Изобретение относится к техническим средствам обучения устному счету в математике.
Назначением таблицы умножения (ТУ) является получение результата умножения по двум сомножителям или результата целочисленного деления по делимому и делителю. В стандартном изображении результаты умножения на однозначные цифры расположены в 9 рядов и 9 столбцов. Использование вращающейся плоскости позволяет показать новые связи и свойства результатов умножения.
Наиболее близким аналогом изобретения является таблица умножения, содержащая поворотную и неподвижную плоскость с изображениями цифр и с прорезями в неподвижной плоскости, через которые видны цифры на подвижной плоскости, показывающие результат действия.
Недостатком известного устройства является размещение исходных данных и результата действия на разных сторонах вращающейся плоскости, что делает невозможным одновременное наглядное сопоставление цифр исходных данных с результатами или указание закономерностей для цифр десятков и единиц результатов умножения/деления.
Техническим результатом изобретения является явное указание зависимостей и симметрий в связях исходных данных с результатами умножения/деления, сокращение объема количества цифр вращающейся таблицы умножения/деления за счет их многократного использования при умножении на разные сомножители, геометрическая интерпретация умножения, в которой места исходных сомножителей определяют места нахождения результата действия. Вращающаяся ТУ по сравнению с обычной ТУ существенно уменьшает объем запоминаемой и обрабатываемой информации при устном счете и сводит проблему определения единиц результата умножения к простому повороту таблицы единиц T или удвоенной таблицы D=2xT, содержащей четные числа. В устройстве вращающейся таблицы умножения результаты становятся более компактными, наглядными, простыми в изучении и использовании.
Указанный технический результат достигается за счет использования специальных свойств чисел при умножении. По сравнению с известной таблицей умножения/деления целых чисел, содержащей поворотную и неподвижную плоскость с изображениями цифр и с прорезями в неподвижной плоскости, через которые видны цифры на подвижной плоскости, показывающие результат действия, согласно изобретению, на одной стороне поворотной плоскости изображена квадратная матрица размера (wxw), где w=3(mod10) или w=7(mod10), с расположенной в ней последовательностью цифр, являющихся единицами или десятками и единицами результатов умножения/деления на нечетные цифры 1, 3, 7, 9, при этом повороты на 90o плоскости с матрицей единиц T результатов умножения на 1 обеспечивают совпадение T после ее поворота с матрицами единиц результатов умножения на 3, 7, 9.
На другой стороне поворотной плоскости или на другой поворотной плоскости изображена матрица с последовательностью четных цифр, являющихся единицами или десятками и единицами результатов умножения/деления на четные цифры 2, 4, 6, 8, при этом повороты на 90o плоскости с матрицей единиц D результатов умножения на 2 обеспечивают совпадение D после ее поворота с матрицами единиц результатов умножения на 4, 6, 8.
Результат умножения получается путем простого поворота вращающейся плоскости так, чтобы первый сомножитель оказался в левом верхнем углу, и чтения результата в ячейке на месте второго сомножителя.
Изобретение поясняется следующими фигурами.
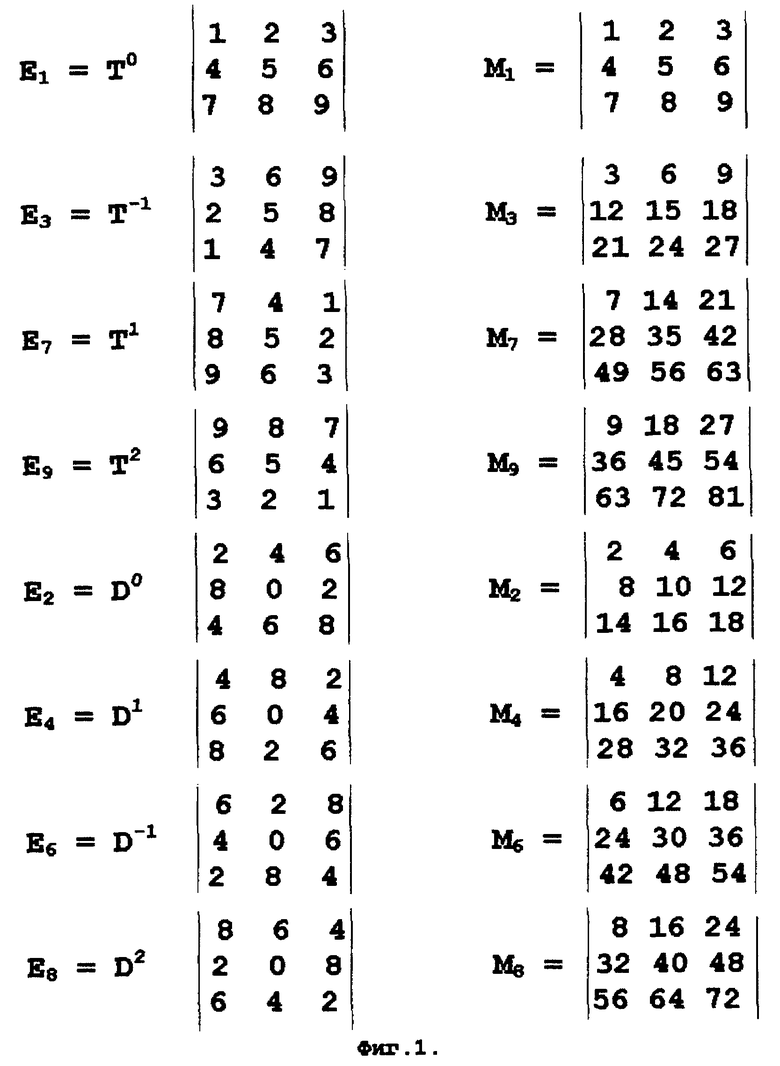
На фиг. 1 изображены матрицы единиц Eh и исходные таблицы умножения Mh для вращающейся таблицы умножения размера (3х3). Выделены матрицы единиц и показаны повороты матрицы единиц результатов умножения.
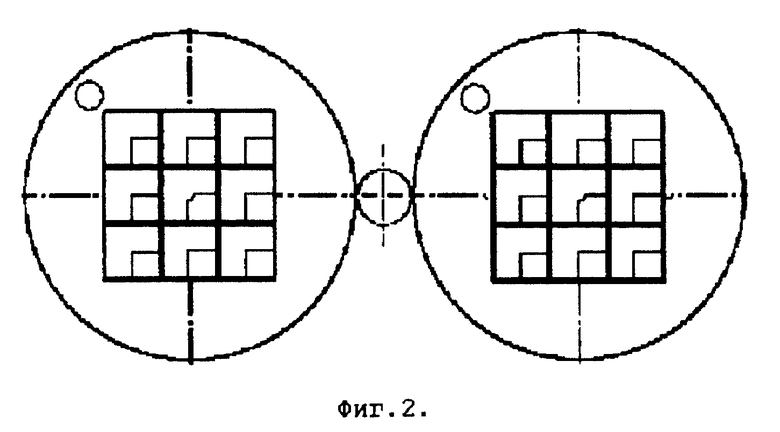
На фиг. 2 изображен шаблон для вращающейся таблицы умножения (вариант 2). Два вращающихся круга с таблицами десятков и единиц соединены шестеренчатой передачей для синхронного вращения в одну сторону. Показаны способ соединения вращающихся кругов с помощью дополнительной шестерни и места для прорезей в неподвижных плоскостях.
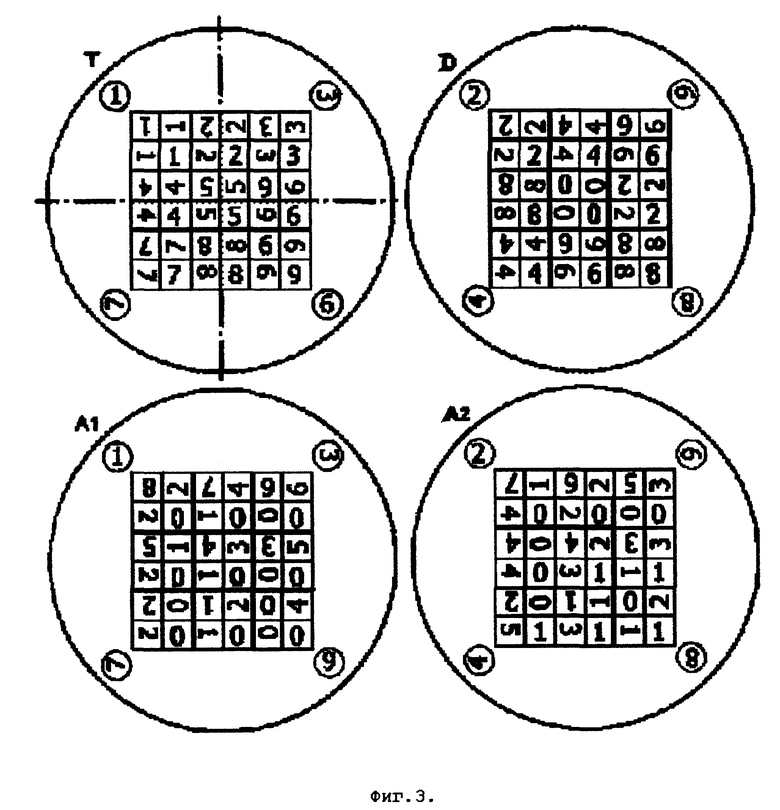
На фиг. 3 дан вид таблиц, изображенных на подвижных кругах (вариант 2) с возможностью чтения на дополнительном левом круге явной записи десятков результата, а на основном правом круге - единиц результата. Показаны четыре таблицы, расположенные по две на каждой стороне устройства, A1 и T - для одной стороны, A2 и D - для оборотной стороны.
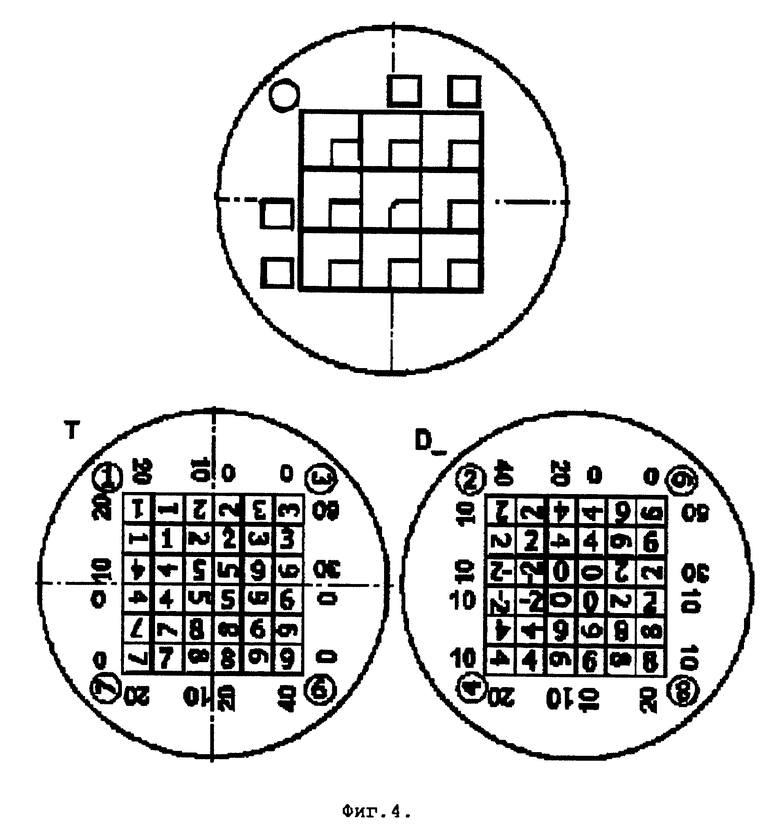
На фиг. 4 показана вращающаяся таблица умножения (вариант 3) с возможностью определения десятков результата методом устного счета. Шаблон для прорезей в неподвижных плоскостях показывает с одной стороны подвижной плоскости цифры T-табло и вспомогательные цифры для устного подсчета десятков при умножении на нечетные сомножители. С другой стороны подвижной плоскости имеются цифры D_-табло и вспомогательные цифры для устного подсчета десятков результата умножения на четные сомножители.
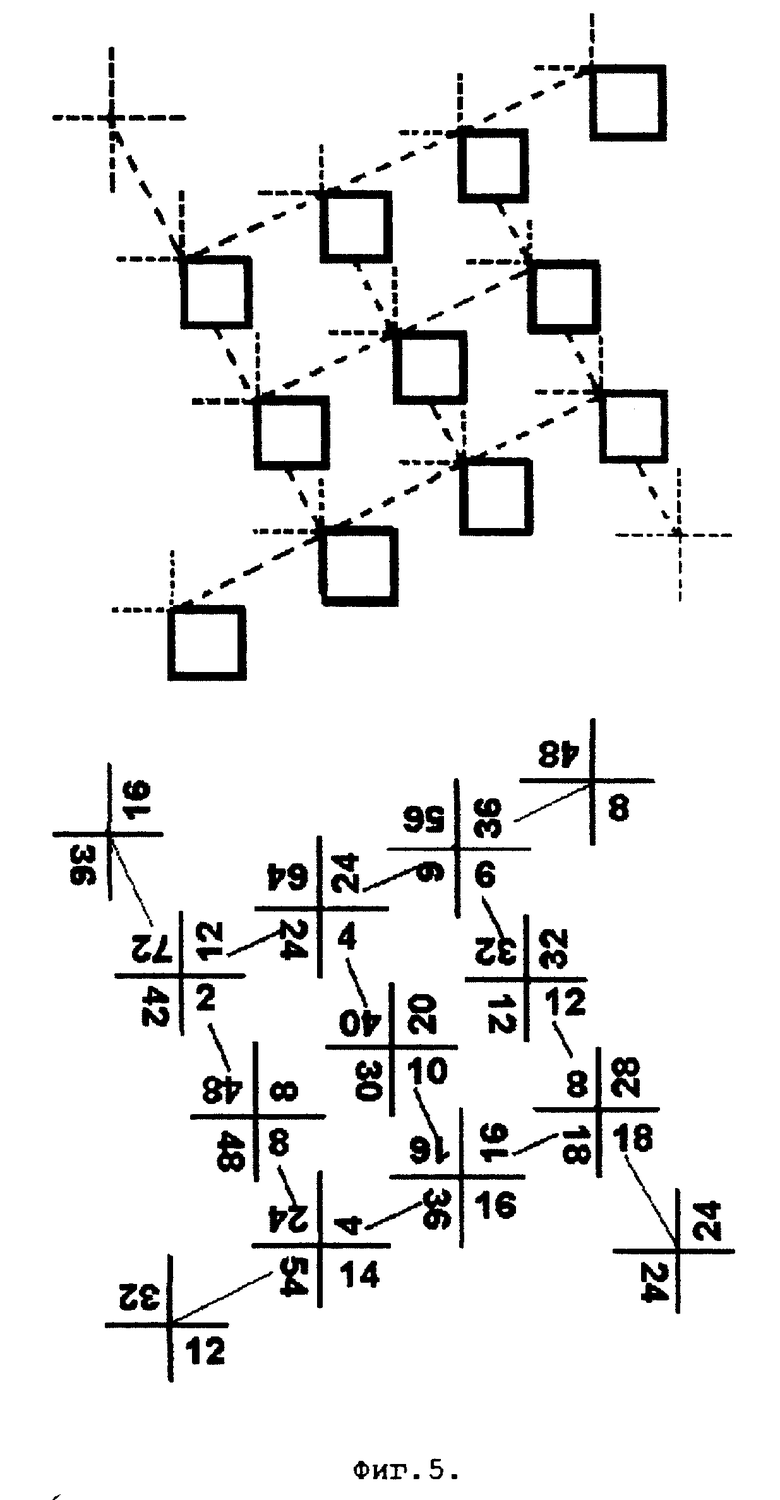
На фиг. 5 приведен вид четной стороны вращающихся таблиц умножения (вариант 4) под углом к горизонтали, при котором сомножители, отличающиеся на 5, находятся на одной вертикали.
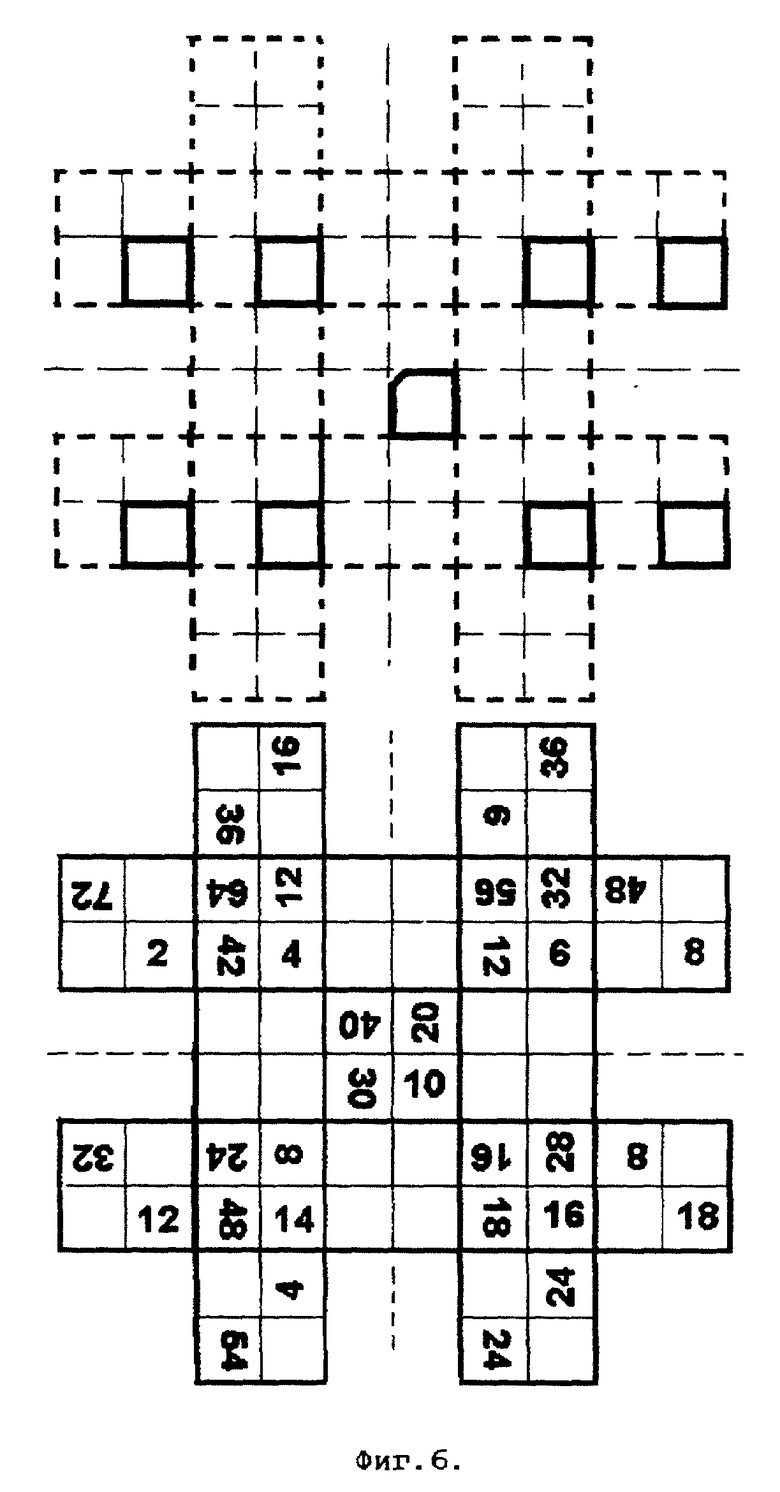
На фиг. 6 изображен вид четной стороны вращающейся таблицы умножения (вариант 5) вместе с шаблоном, имеющим прорези, ячейки которых расположены в горизонтальных рядах в матрице размером (3х5).
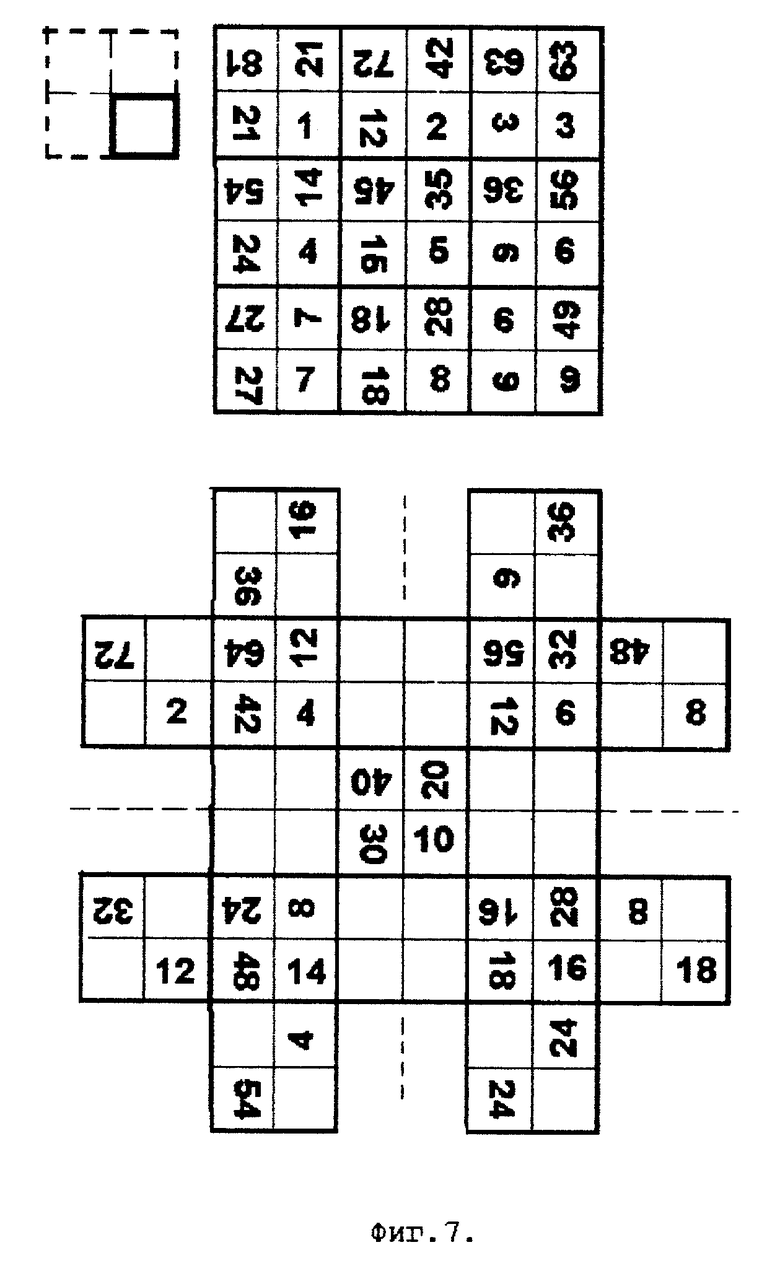
На фиг. 7 показаны две стороны вращающейся таблицы умножения (вариант 5), в котором таблица для нечетной стороны имеет размер (3x3), а для четной стороны результаты таблицы умножения записаны в симметрично заполненные ячейки матрицы размера (3x5).
Вращающаяся таблица умножения/деления (ВТУ) в основном варианте реализации имеет две параллельные расположенные рядом неподвижные плоскости и вращающийся круг между ними. На плоскостях нарисованы квадратные матрицы размера (wxw) с ячейками и общей осью вращения, перпендикулярной плоскостям и проходящей через центры таблиц разных плоскостей. В прорезях внешних неподвижных плоскостей можно увидеть изображенные на подвижном круге ячейки и цифры в ячейках. С одной стороны поворотной плоскости находится табло для умножения на нечетные цифры, а с другой стороны - на четные цифры. Таблицы на поворотной плоскости позволяют получить результат умножения способом простого поворота круга относительно неподвижных плоскостей вокруг оси, проходящей через центры таблиц.
Вращающаяся таблица умножения/деления размером (wxw), где W=3+10•k или W=7+10•k (k=0, 1, 2, 3,...) использует специальные свойства чисел при умножении и закономерности в числах единиц и десятков результатов. Умножение однозначных чисел обеспечивается таблицей размера 3x3.
Имеется два главных случая умножения однозначных чисел axb, когда первый сомножитель - нечетное число а=1, 3, 7, 9, и когда первый сомножитель - четное число а=2, 4, 6, 8, а также исключение а=5. Поскольку умножение коммутативно a•b= b•a, то, например, единственным случаем, не охватываемым в ВТУ размера 3, является пара сомножителей 5•5.
ВТУ размера 3x3 позволяет получить результат умножения a•b для однозначных чисел от 1 до 9, таблица размера 7x7 дает умножение однозначных чисел а на b=1, 2, ..., 49, для 13 - получаем 13•13=169 и т.д.
Обозначения. Будем рассматривать квадратные матрицы размера (wxw) с целочисленными элементами. Матрицы обозначаются прописными буквами T, E,...
Обозначим T-табло  где (i, j=1, 2, 3, ..., w), матрицу элементов bi,j, в которой bi,j являются последовательными натуральными числами, записанными по строкам
где (i, j=1, 2, 3, ..., w), матрицу элементов bi,j, в которой bi,j являются последовательными натуральными числами, записанными по строкам
bi,j= (w•(i-1)+j) (mod 10),
т.е. с отброшенными числами десятков. Число
S = w•(i-1)+j
назовем номером элемента bi,j.
Для размеров таблицы w=3 описанное T-табло представляет собой обычную панель цифрового телефона с цифрами от 1 до 9, расположенными в три ряда.
Пусть h - натуральное число h=1, 2, ..., 9. Обозначим матрицы единиц Eh при умножении на сомножитель h
На месте s в матрице находится результат умножения h•s, но в матрице Eh используются только единицы этого результата.
Повороты квадратной матрицы в положительном направлении (по часовой стрелке) вокруг центра на 90o имеют четыре положения, которые обозначаются верхним индексом г=0, 1, 2, 3. Повороты Tr выглядят так: T0 - нет поворота, T1 - поворот на 90o, T2 - поворот на 180o, T3 - поворот на 270o по часовой стрелке. Для индекса поворота г<0 поворот осуществляется против часовой стрелки T-1=T3.
Обозначим D= E2 - матрицу единиц умножения на 2. Четыре положения при повороте D в положительном направлении обозначаются: D0=D - нет поворота, D1, D2, D3=D-1.
Совпадение матриц единиц Eh результатов умножения при поворотах. Для матриц размера (3x3) изображения таблиц единиц Eh приведены на фиг.1 вместе с матрицами
Mh = h•E1,
которые являются полными таблицами умножения, содержащими десятки и единицы результатов умножения.
Единицы результата умножения на нечетный первый сомножитель, не равный 5, задаются поворотами матрицы T
E1=T0, E3=T-1, E7=T1, E9=T2.
Единицы результата умножения на четный первый сомножитель задаются поворотами матрицы D
E2=D0, E4=D1, E6=D-1, E8=D2.
Матрица E5 при поворотах не меняется.
Для матриц размером (wxw), где w>3, указанные свойства совпадения единиц результатов умножения при поворотах матрицы Т выполняются только для размеров квадратных матриц w=3 (mod10) или w=7 (mod10).
Применение матриц T и D для умножения и деления.
Назовем главным поворотом нечетного числа x=1, 3, 7, 9 в матрице T такой поворот, при котором число x оказывается в левом верхнем углу. Аналогично главным поворотом четного числа x=2, 4, 6, 8 в матрице D является такой поворот, при котором число x оказывается в левом верхнем углу.
Для того, чтобы с помощью ВТУ получить единицы результата умножения чисел x и y, причем x не равно 5, необходимо определить четность числа x:
- для нечетных x взять матрицу T, для четных x матрицу D - это одна из сторон вращающейся плоскости;
- сделать поворот плоскости с матрицей, содержащей число x, так, чтобы число x оказалось в левом верхнем углу.
Тогда в таблице рядом с номерами ячеек y, читаемых на неподвижном табло, на повернутом табло окажутся цифры единиц результата умножения x•y.
После определения единиц результата умножения необходимо найти число десятков результата. Варианты определения числа десятков зависят от способа реализации ВТУ:
- либо используется явная запись десятков в виде отсылочной справки,
- либо к устройству добавляется приспособление для показа явной записи результата десятков,
- либо применяется алгоритм определения значения десятков с помощью простого устного счета, использующего вспомогательные данные, геометрические свойства и параметры самой таблицы (строка, столбец, нахождение в выделенной области и др.).
Для деления можно выполнить те же действия по повороту делителя вращающейся матрицы в левый верхний угол и по известному результату, находящемуся в таблице, определить частное как номер ячейки.
Частное при делении по делимому и делителю можно получить, используя только единицы матриц Т и D. Для наиболее важного случая ТУ однозначных чисел (w= 3) для нечетного делителя (матрица T) результат деления однозначный, для четного делителя (матрица D) - один из двух ответов: меньше 5 или больше 5.
Раскрашивание. Поскольку ВТУ содержит две практически одинаковые матрицы T - одну на подвижной плоскости, другую на неподвижной, то эти матрицы необходимо различать. Удобным способом является раскрашивание цифр матриц в различные цвета (условно) красные цифры - на неподвижном T-табло, синие - на подвижном Т и D табло. Для облегчения применения методов устных вычислений возможно раскрашивание плоскости ячеек с выделением специальными цветами части ячеек матриц (границы, центр, повторяющиеся цифры D-табло и др.).
Сопоставление ячеек. Квадраты на разных плоскостях должны сопоставляться друг с другом, обеспечивая смысловое единство, т.е. устанавливать явные взаимосвязи между ячейками для одновременного восприятия их содержимого путем наложения, либо совпадения части площадей квадратов, либо размещения рядом или другим понятным из контекста способом, в том числе с помощью знаковой имитации поворота в виде стрелок, пиктограмм или текста.
Поскольку при повороте вокруг оси твердой плоскости относительно другой неподвижной плоскости все знаки на подвижной плоскости поворачиваются, то необходимо каким-либо способом обеспечить удобное чтение цифры в ячейке, т. е. сохранить возможность нормального восприятия содержимого этих ячеек. Если в поворачиваемом на 90o квадрате для показа использовать только четверть, например правый нижний угол, тогда в каждом из четырех положений поворота в выделенном углу можно записать правильно развернутую сверху вниз цифру, что обеспечит безошибочное естественное чтение (6 и 9 похожи при перевороте). Следует оговорить, что подобное формальное увеличение количества строк и столбцов, в указанном случае в два раза, не является содержательно значимым увеличением размеров таблицы. Подобное повторение цифр в разных видах поворота в ячейке или формальное введение новых строк и столбцов, не участвующих в получении единиц результата умножения, следует считать состоянием, не увеличивающим количества строк и столбцов таблицы умножения.
Первый вариант вращающейся таблицы умножения размера (w•w).
Устройство содержит два круга, поворачивающихся в вертикальной плоскости на двух разных горизонтальных осях, проходящих через центры таблиц. Площади кругов не должны загораживать друг друга.
На круге 1 нарисована матрица, содержащая (wxw) ячеек, где расположены цифры T-табло. На круге 2 нарисована подобная первой матрица, где расположены цифры D-табло. В центрах ячеек матриц имеются скрепленные с кругами как единое целое короткие оси, на которых висят жетончики с цифрами матриц T и D, похожими на гардеробные - с круглым отверстием в верхней части для надевания на ось.
При повороте круга 1 или 2 вокруг оси на 90o жетончики с цифрами матриц T или D под действием силы тяжести поворачиваются вокруг оси подвески, сохраняя естественное для чтения вертикальное расположение.
В результате поворота кругов с таблицами T и D в ячейках получаются изображенные на жетончиках цифры единиц результата умножения, где первый сомножитель - это число, находящееся в левом верхнем углу, второй сомножитель - номер ячейки, считаемой слева направо и сверху вниз. Десятки результата умножения в этом варианте реализации не показаны.
Второй вариант вращающейся таблицы умножения размера (wxw). Устройство содержит две неподвижные плоскости, закрывающие с обеих сторон два равных круга, поворачивающихся на двух разных параллельных осях. Круги являются шестеренками с зубцами на окружности. Между большими кругами имеется еще одна синхронизирующая шестерня, обеспечивающая одновременный поворот больших кругов в одну сторону (фиг. 2).
На неподвижной плоскости нарисованы две матрицы (wxw) так, что оси вращения проходят через центры кругов, на подвижных кругах также нарисованы матрицы (wxw), оси вращения которых проходят через центры кругов. Подвижные матрицы равны по размеру неподвижным матрицам. В неподвижной плоскости сделаны прорези в правой нижней четверти ячейки, через которые видны цифры на внутренних вращающихся кругах.
На левом подвижном кругу изображена матрица A1 с цифрами десятков, на правом кругу матрица T с цифрами единиц результата умножения на нечетные цифры у= 1, 3, 7, 9, а именно - числа, находящегося в левом верхнем углу таблицы T на сомножитель, равный номеру ячейки в матрице T (фиг. 3).
Умножение заключается в повороте нужного угла матрицы с числом y в главное положение. Тогда в прорезях левого круга видны цифры десятков, справа - цифры единиц результата умножения.
Умножение на четные цифры y=2, 4, 6, 8 производится на оборотной стороне устройства, повторяющего лицевую сторону по форме, с тем отличием, что вместо матриц A1 и T - на левом кругу находится A2, а на правом кругу - матрица D (фиг.3).
Третий вариант вращающейся таблицы умножения размера (3x3). Устройство содержит две неподвижные плоскости, закрывающие с обеих сторон круг, поворачивающийся на оси, перпендикулярной к плоскости.
На неподвижной плоскости нарисована матрица T с (3x3) ячейками и осью в центре круга с цифрами, раскрашенными в (условно) красным цвет. На подвижном круге находится матрица T с (3x3) ячейками с осью в центре круга с (условно) синими цифрами. В неподвижной плоскости сделаны прорези в правой нижней четверти ячейки, через которые видны цифры на внутреннем вращающемся круге.
Сбоку в каждом ряду, кроме первого, сделаны прорези для вспомогательного числа vi, используемого для устных вычислений десятков. Сверху над всеми столбцами, кроме первого, сделаны прорези для вспомогательного числа hj, используемого как второй параметр для устных вычислений десятков (фиг. 4).
Умножение заключается в повороте нужного угла матрицы в главное положение.
Пусть происходит умножение на нечетное y=1, 3, 7, 9, тогда для поворота выбирается матрица T. Выполняется поворот y в главное положение для T на подвижном кругу. В прорезях появляются цифры единиц результата умножения (фиг. 4).
С помощью устного счета число десятков определяется по следующему правилу: в строке i и столбце j число десятков
di,j = vi + hj,
где числа vi и hj равны следующим: v1=0; h1=0;
для умножения на 1 v2=0; v3=0; h2=0; h3=0;
для умножения на 3 v2=1; v3=2; h2=0; h3=0;
для умножения на 7 v2=2; v3=4; h2=1; h3=2;
для умножения на 9 v2=3; v3=6; h2=1; h3=2.
Пусть происходит умножение на y=2, 4, 6, 8, тогда для поворота выбирается матрица D_ . Эта матрица отличается от D отрицательным числом -2 во 2 строке и 1 столбце. Отметим, что -2=8 (mod10). Выполняется поворот числа у в главное положение для D_. В прорезях видны цифры единиц результата умножения (фиг.4).
С помощью устного счета число десятков определяется как и выше. Числа vi и hj равны следующим: v1=0; h1=0;
для умножения на 2 v2=1; v3=1; h2=0; h3=0;
для умножения на 4 v2=1; v3=2; h2=1; h3=1;
для умножения на 6 v2=2; v3=4; h2=1; h3=1;
для умножения на 8 v2=3; v3=5; h2=1; h3=2.
В том месте, где стоит -2, нужно выполнить вычитание: 10•di,j-2.
Таким образом, однозначно определяется результат умножения: число десятков и число единиц.
Четвертый вариант вращающейся таблицы умножения.
Для изучения таблицы умножения на четные цифры 2, 4, 6, 8 удобно представить ВТУ в таком виде, в котором результаты умножения на сомножители, отличающиеся на 5, находятся один под другим по вертикали: 1 и 6, 2 и 7, 3 и 8, 4 и 9. Достигается указанный эффект наклоном основной матрицы размера (3x3) под углом к горизонтали и введением двух дублирующих ячеек - в конце верхней строки и в начале нижней строки (фиг. 5). В правой верхней ячейке будет находиться результат умножения на 4, а в левой нижней ячейке - на 6, причем правая верхняя ячейка будет находиться над ячейкой 9, а левая нижняя ячейка окажется под ячейкой с номером 1.
Основным достоинством данного варианта является сопоставление единиц результатов умножения на сомножители, отличающиеся на 5. Непосредственно видно совпадение единиц результатов умножения для этих пар.
В данном варианте реализации поворотный круг ВТУ с четными цифрами должен быть закрыт с лицевой стороны неподвижным шаблоном с прорезями (фиг. 5), показывающим четыре ячейки в верхнем ряду и четыре ячейки в нижнем ряду, наклоненные к горизонтали для того, чтобы пары сомножителей, отличающихся на 5, находились бы друг под другом по вертикали. Одна прорезь шаблона остается в центре и показывает результат умножения на 5. Целесообразно оставить прорези для ячеек в среднем ряду с номерами 4 и 6, чтобы не нарушалось восприятие поворота подвижного квадрата единиц таблиц умножения как единого целого.
Пятый вариант вращающейся таблицы умножения. Этот вариант похож на четвертый вариант таблиц умножения с четными цифрами, но располагает ячейки шаблонов не под углом, а параллельно горизонтали. Матрица расположения четных цифр имеет здесь 3 строки и 5 столбцов. Средняя ячейка в верхней и нижней строке, находящаяся над и под ячейкой 5, не заполняется. Такой вид более привычен для таблиц, однако теряется зрительная информация о повороте подвижного круга единиц умножения на числа 2, 4, 6, 8 как единого целого. Наглядной остается связь при поворотах на 180o пар таблиц 2 и 8, и 4 и 6.
В данном варианте поворотный круг ВТУ для стороны, показывающей умножение на четный первый сомножитель, должен быть закрыт с лицевой стороны неподвижным шаблоном с прорезями (фиг. 6), показывающим четыре ячейки в верхнем ряду и четыре ячейки в нижнем ряду, и одну для умножения на 5 в центре.
На фиг.7 показаны две стороны ВТУ для варианта 5, в котором таблица для нечетной стороны имеет размер (3х3), а для четной стороны результаты таблицы умножения записаны в симметрично заполненные ячейки матрицы размера (3x5). В ячейках показаны не только единицы, но и десятки результата умножения.
Устройство предназначено для обучения в математике устному счету и позволяет явно указать зависимости и симметрии в связях исходных данных с результатами. Получение единиц результата умножения/деления с помощью вращающейся таблицы умножения (ВТУ) сводится к простому повороту диска. ВТУ состоит из двух неподвижно расположенных плоскостей и поворотного круга между. Поворотные таблицы размера (w•w) видны через прорези в неподвижных плоскостях. Для умножения/деления однозначных чисел w=3. С одной стороны ВТУ заполнены единицами или десятками и единицами результатов умножения на нечетные цифры 1,3,7,9, а с другой стороны плоскости - на четные цифры. Матрицы единиц результатов в ТУ для первого сомножителя х обозначим Еx, Т=Е1, D=Е2 и Тk, Dk повороты на 90o. Тогда Е1=Тo, Е3=Т-1, Е7=Т1, Е9=Т2, Е2=Do, Е4=D1, Е6=D-1, Е8= D2. Пара 5•5=25 - исключение. Для w=3 Т - табло состоит из 3 рядов и 3 столбцов с цифрами 1,2,... 9. Определение единиц результата умножения выполняется поворотом матрицы Т - для нечетных х, или матрицы D - для четных х так, чтобы первый сомножитель оказался в левом верхнем углу. Есть конструктивные варианты ВТУ с подсказкой десятков результата умножения. 1 з.п. ф-лы, 7 ил.
| Новый вариант белка семейства транспортера цианата и способ получения L-триптофана с его применением | 2021 |
|
RU2797499C1 |
| Приспособление к счетам для умножения и деления | 1948 |
|
SU80266A1 |
| DE 3338646 A1, 02.05.85. | |||
Авторы
Даты
1999-10-10—Публикация
1999-02-09—Подача