Изобретение относится к области вычислительной техники и может быть использовано для устного и письменного перемножения много разрядных десятичных чисел, а также для умножения на ЭВМ позиционных чисел с большой разрядностью (40000…50000 цифр).
Известен способ перекрестного умножения двузначных чисел, при котором вычисляют промежуточный результат - произведение старших разрядов, умноженное на 100, далее «крест на крест» перемножают старший разряд одного множителя на младший разряд второго множителя и на оборот, затем результаты перекрестного умножения суммируют и умножают на 10, полученную сумму прибавляют к промежуточному результату. Для получения произведения двузначных чисел к текущему промежуточному результату добавляют произведение младших разрядов [1].
Недостатком известного способа являются его ограниченные функциональные (вычислительные) возможности перемножать только двузначные десятичные числа.
Наиболее близким к заявляемому известным техническим решением является способ умножения чисел, примером технической реализации которого является ассоциативный умножитель чисел [2]. Известный способ характеризуется тем, что запоминают n и m разрядные сомножители, упорядочивают диагональные срезы запомненных разрядов сомножителей путем суммирования в каждой диагонали частных сумм элементов моментом времени, при котором двоичного кода «1» и «0» с выходов регистров памяти соответствующих n и m разрядных сомножителей с одновременным выявлением признака нечетности числа единиц, переносят единицы по признаку положения границы между нулями и единицами в упорядоченном диагональном срезе в каждый последующий такт работы генератора синхроимпульсов, число тактов работы которого определяется моментом времени, при котором отсутствуют единицы среди символов переноса, формируют произведение сомножителей в момент последнего такта отсутствия единиц среди символов переносов. За счет одновременной обработки всех разрядов двух сомножителей двоичного кода сокращается время их перемножения.
Недостаток прототипа состоит в том, что перемножение сомножителей происходит в двоичном коде и при условии обязательного равенства числа разрядов сомножителей (n=m). При этом, если число разрядов сомножителей измеряется десятками тысяч, то перемножение сомножителей в двоичном коде требует больших затрат времени и сложной технической реализации, так как количество разрядов двоичного кода определяется по формуле 2К, где К - число перемножаемых величин в десятичном коде (исчислении).
Целью изобретения является повышение оперативности вычисления произведения сомножителей десятичных чисел разной длины и с большой (десятки тысяч) разрядностью путем исключения большого объема промежуточных вычислительных операций, а также другой целью изобретения является обеспечение условий для возможного устного и письменного умножения десятичных чисел за счет упрощения алгоритма их умножения.
Сущность изобретения заключается в том, что, кроме известных и общих операций по запоминанию n и m разрядных сомножителей и упорядочивания диагональных срезов, предлагается новая совокупность операций, которая характеризуется тем, что составляют прямоугольную матрицу размером n×m ячеек, в каждой из которых запоминают как однозначные, так и двузначные поразрядные произведения сомножителей n и m, упорядочивают диагональные срезы n×m ячеек прямоугольной матрицы путем их последовательного диагонального иерархического обхода, начиная с верхней левой ячейки, которая является верхним уровнем иерархического построения ячеек, и, заканчивая нижней правой ячейкой прямоугольной матрицы, которая является нижним уровнем иерархического построения ячеек, суммируют на каждом уровне иерархии как однозначные, так и двузначные десятичные символы чисел ранее запомненных поразрядных произведений, сдвигают поразрядно вверх все старшие разряды просуммированных символов десятичных чисел на число иерархических уровней, равное порядковому номеру сдвигаемого разряда просуммированных символов десятичных чисел, суммируют на каждом уровне сдвинутого иерархического построения десятичные числа, формируют результат произведения сомножителей n и m поразрядно, начиная с нижнего уровня сдвинутого иерархического построения в качестве младшего разряда произведения, путем последовательного считывания одноразрядных чисел и с одновременным переносом вверх на один уровень сдвинутой иерархии всех старших разрядов десятичных чисел для их последующего суммирования с десятичными числами на вышестоящем уровне сдвинутой иерархии.
Новизна изобретения состоит в том, что составляют прямоугольную матрицу размером n×m ячеек, в каждой из которых запоминают как однозначные, так и двузначные поразрядные произведения сомножителей n и m, упорядочивают диагональные срезы n×m ячеек прямоугольной матрицы путем их последовательного диагонального иерархического обхода, начиная с верхней левой ячейки, которая является верхним уровнем иерархического построения ячеек, и, заканчивая нижней правой ячейкой прямоугольной матрицы, которая является нижним уровнем иерархического построения ячеек, суммируют на каждом уровне иерархии как однозначные, так и двузначные десятичные символы чисел ранее запомненных поразрядных произведений, сдвигают поразрядно вверх все старшие разряды просуммированных символов десятичных чисел на число иерархических уровней, равное порядковому номеру сдвигаемого разряда просуммированных символов десятичных чисел, суммируют на каждом уровне сдвинутого иерархического построения десятичные числа, формируют результат произведения сомножителей n и m поразрядно, начиная с нижнего уровня сдвинутого иерархического построения в качестве младшего разряда произведения, путем последовательного считывания одноразрядных чисел и с одновременным переносом вверх на один уровень сдвинутой иерархии всех старших разрядов десятичных чисел для их последующего суммирования с десятичными числами на вышестоящем уровне сдвинутой иерархии, что обеспечивает повышение оперативности вычисления произведения сомножителей десятичных чисел разной длины за счет упрощения порядка вычислений.
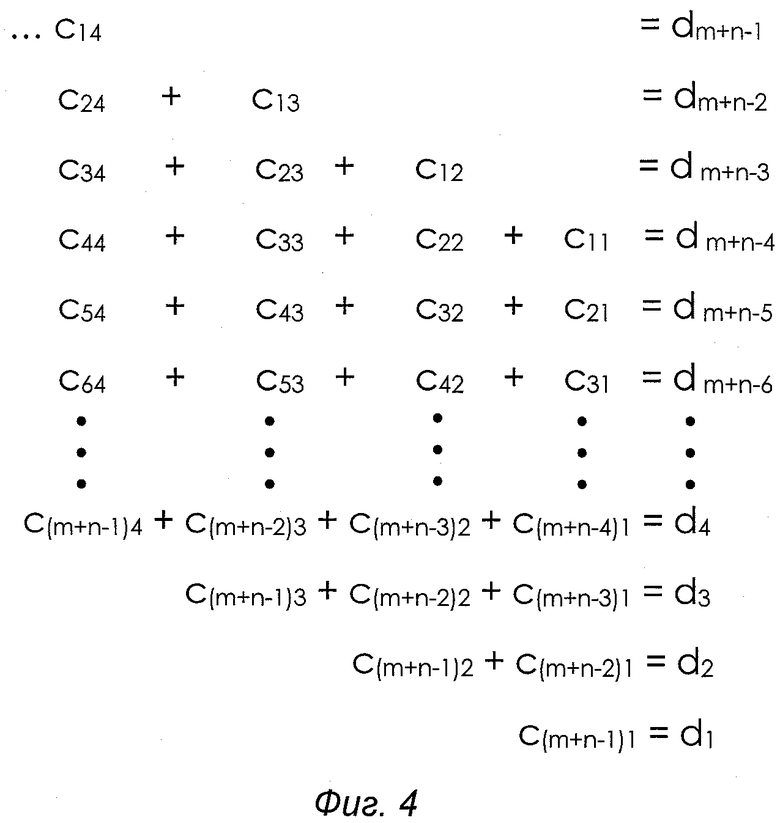
На прилагаемых чертежах показано: фиг.1 - прямоугольная матрица размером n×m ячеек, в каждой из которых хранятся символы как однозначных, так и двузначных десятичных чисел соответствующих поразрядных произведений сомножителей m и n, фиг.2 - упорядоченное иерархическое построение диагональных срезов прямоугольной матрицы поразрядных произведений сомножителей m и n, в котором верхний уровень иерархии равен левому верхнему элементу a11 прямоугольной матрицы поразрядных произведений сомножителей m и n, а нижний уровень иерархии равен правому нижнему элементу amn прямоугольной матрицы поразрядных произведений сомножителей m и n, а также суммы поразрядных произведений сомножителей m и n на каждом уровне иерархического построения; Фиг.3 - поразрядная запись сумм поразрядных произведений сомножителей m и n на каждом уровне иерархического построения; фиг.4 - поразрядные суммы десятичных чисел, сдвинутых по отношению к соседним младшим разрядам вверх по иерархии на число уровней, равных порядковому номеру старших разрядов; фиг.5 - запись для считывания результата произведения сомножителей m и n; фиг.6 - числовой пример перемножения десятичных чисел; фиг.7 - функциональная схема примера технической реализации заявляемого способа перемножения десятичных чисел m и n, где обозначено: 1 и 2 - блоки (регистры) перемножаемых сомножителей m и n десятичных чисел; 3 - блок поразрядного перемножения сомножителей m и n десятичных чисел; 4 - прямоугольная матрица размером m×n ячеек, в каждой из которых хранятся символы как однозначных, так и двузначных десятичных чисел соответствующих поразрядным произведениям сомножителей m и n; 5 - блок упорядоченного иерархического построения диагональных срезов прямоугольной матрицы поразрядных произведений сомножителей m и n с суммированием на каждом, кроме верхнего и нижнего, уровне иерархического построения десятичных чисел; 6 - блок поразрядно сдвинутого иерархического построения диагональных срезов; 7 - блок суммирования десятичных чисел диагональных срезов на каждом уровне сдвинутого иерархического построения dJ, где J=1, 2, …, m+n-1; 8 - генератор (датчик) поразрядных сдвигов вверх по иерархии, начиная с нулевого сдвига для младшего (единичного) разряда и завершая К сдвигами для старших разрядов десятичных чисел; 9 - блок считывания результата перемножения сомножителей m и n десятичных чисел; 10 - блок управления работой матрицы 4; 11 - линия задержки на время выполнения операций сложения десятичных чисел в блоке 5.
Предлагаемый способ умножения десятичных чисел реализуется следующим образом.
Сомножители m и n десятичных чисел, например 861 и 489, из соответствующих регистров 1 и 2 поступают через блок 3 поразрядного перемножения на входы 4.1, 4.2, …, 4. m×n запоминающих ячеек прямоугольной матрицы 4 размером 3×3 (фиг.6) или m×n (фиг.1 и 7), что реализует операцию построения (составления) прямоугольной матрицы размером m×n ячеек с запомненными поразрядными произведениями сомножителей, которые могут быть только одно или двухразрядными. При появлении управляющего сигнала на выходе блока управления 10 в прямоугольной матрице 4 происходит обход ее ячеек по диагоналям, начиная с левой верхней a11, и, заканчивая правой нижней amn ячейкой. Результат этого обхода ячеек фиксируется через входы 5.1, 5.2, …, 5.m+n-1 в ячейках памяти блока 5 упорядоченного иерархического построения диагональных срезов с одновременным суммированием десятичных чисел на каждом уровне иерархии, кроме верхнего и нижнего уровней, в виде символов bi, где i=1, 2, …, m+n-1 (фиг.2 или фиг.7). Выходные символы десятичных чисел блока 5 в виде электрических импульсов поступают на входы 6.1, 6.2, …, 6. m+n-1 блока 6 для поразрядного сдвига иерархического построения.
По истечении времени небольшой задержки, необходимой для суммирования десятичных чисел на каждом уровне иерархического построения символов десятичных чисел в блоке 5, выходной сигнал блока 11 включает в работу генератор 8 поразрядного сдвига вверх по иерархии, начиная с нулевого сдвига «0» для младшего (единичного) разряда и завершая 1, 2, …, К сдвигами для старших разрядов десятичных чисел. В ячейках блока 6 происходит сдвиг старших разрядов на один уровень вверх по отношению к соседним младшим разрядам десятичных чисел. По завершению сдвигов символы сдвинутой иерархии десятичных чисел через входы 7.1, 7.2, …, 7.m+n-1 поступают в соответствующие ячейки блока 7.
Далее в сдвинутом иерархическом построении суммируют с помощью блока 7 (фиг.7) десятичные числа на каждом уровне сдвинутой иерархии (фиг.4). После суммирования десятичных чисел на каждом уровне сдвинутого иерархического построения чисел становится возможной реализация операции формирования результата произведения сомножителей m×n. Для этого последовательно, начиная с нижнего уровня сдвинутой иерархии dm+n-1, считывают с помощью блока 9 только одноразрядные числа среди сдвинутых и просуммированных на каждом уровне сдвинутой иерархии чисел dJ, где J=1, 2, …, m+n-1 (фиг.5 и 7). Если в процессе последовательного считывания одноразрядных чисел окажутся многоразрядные числа dJ, то одновременно со считыванием единичного (младшего) разряда переносится вверх на один уровень сдвинутой иерархии все старшие разряды считываемых десятичных чисел для их последующего суммирования с десятичными числами на вышестоящем уровне сдвинутой иерархии. Для перемножения других сомножителей необходимо привести в исходное положение блоки 1…10, например, путем кратковременного отключения их электрического питания.
Продолжительность вычисления произведения сомножителей m и n десятичных чисел согласно предлагаемому способу складывается из: времени заполнения прямоугольной матрицы m×n результатами поразрядного перемножения каждого одноразрядного числа одного сомножителя на каждое одноразрядное число другого сомножителя (T1); времени упорядочения диагональных срезов прямоугольной матрицы m×n с одновременным суммированием чисел на каждом уровне упорядоченной иерархии десятичных чисел (T2); времени поразрядного сдвига упорядоченной иерархии десятичных чисел (T3); времени сложения десятичных чисел на каждом уровне сдвинутого иерархического построения (T4); времени последовательного считывания результата произведения сомножителей m и n десятичных чисел (T5).
Время поразрядного сдвига T3 и последовательного считывания результата перемножения сомножителей T5 незначительно отличается от времени, расходуемого на выполнение известных аналогичных операций при умножении десятичных чисел [3]. Время T1 заполнения ячеек прямоугольной матрицы m×n пренебрежимо мало по сравнению со временем перемножения сомножителей m и n, так как в ячейках запоминаются только короткие числа (одно или двузначные) и эта операция единственная и не повторяющаяся.
Отметим, что известный порядок перемножения десятичных чисел [3] требует обязательного поразрядного перемножения сомножителей, которое повторяется по числу разрядов сомножителей, и при этом поразрядном перемножении текущие старшие разряды поразрядных произведений вначале оперативно запоминаются, а потом суммируются с результатом последующего поразрядного перемножения, на что расходуется m·(T1+T0) машинного времени, где T0 - время оперативного управления ячейками памяти. Другая операция известного порядка [3] вычисления произведения сомножителей десятичных чисел заключается в поразрядном суммировании сдвинутых на один разряд произведений десятичных чисел при этом старшие разряды суммы вначале оперативно запоминаются, а потом суммируются с результатом последующего поразрядного суммирования, на что расходуется n·(T4+T0) машинного времени.
Относительный выигрыш во времени предлагаемого перемножения десятичных чисел можно оценить с помощью выражения
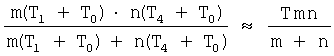 ,
,
где T≈T1≈T4; T0≈0.
Промышленная осуществимость предлагаемого способа перемножения десятичных чисел обосновывается тем, что в примере его технической реализации используются известные в аналоге [1] и прототипе [2] узлы и блоки по своему прямому функциональному назначению.
Положительный эффект от использования изобретения состоит в том, что сокращается не менее чем на 40…60% время перемножения десятичных чисел за счет уменьшения числа вычислительных операций, связанных с оперативным запоминаем результатов промежуточных перемножений.
Источники информации:
1. Считайте в уме как компьютер / Б. Хендли; пер. С англ. Е.А. Самсонов. - Мн.: "Попури", 2006, с.257-261, (аналог).
2. Заявка на изобретение 95104047 RU, Ассоциативный умножитель чисел, МПК G06F 7/52, приоритет: 20.01.1997, заявитель: Серпуховское ВВКИУРВ им. Ленинского комсомола, авторы: Васильев Г.И., Самуилов М.В., (прототип).
3. ru.wikipedia.org/wiki (математика), 2010 г.
| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для умножения двоичных чисел | 1980 |
|
SU938282A1 |
| СПОСОБ ОБРАБОТКИ ИНФОРМАЦИИ И ВЫЧИСЛЕНИЯ КУВЫРКОВА (ВАРИАНТЫ) И УСТРОЙСТВО "ГЕНЕРАЛИЗАТОР" ДЛЯ ОСУЩЕСТВЛЕНИЯ СПОСОБА | 2012 |
|
RU2494445C1 |
| Устройство для умножения | 1989 |
|
SU1668979A1 |
| СПОСОБ ОРГАНИЗАЦИИ УМНОЖЕНИЯ ЧИСЕЛ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2012 |
|
RU2500018C1 |
| УСТРОЙСТВО ДЛЯ УМНОЖЕНИЯ ЧИСЕЛ В КОДЕ "1 ИЗ 4" | 2003 |
|
RU2251144C1 |
| Вычислительное устройство | 1988 |
|
SU1647553A1 |
| Устройство для умножения чисел | 1985 |
|
SU1259254A1 |
| ЯЧЕЙКА ОДНОРОДНОЙ ВЫЧИСЛИТЕЛЬНОЙ СРЕДЫ, ОДНОРОДНАЯ ВЫЧИСЛИТЕЛЬНАЯ СРЕДА И УСТРОЙСТВО ДЛЯ КОНВЕЙЕРНЫХ ВЫЧИСЛЕНИЙ СУММЫ м n-РАЗРЯДНЫХ ЧИСЕЛ | 2011 |
|
RU2475815C1 |
| Последовательное множительное устройство | 1985 |
|
SU1307455A1 |
| Устройство для умножения | 1983 |
|
SU1180881A1 |

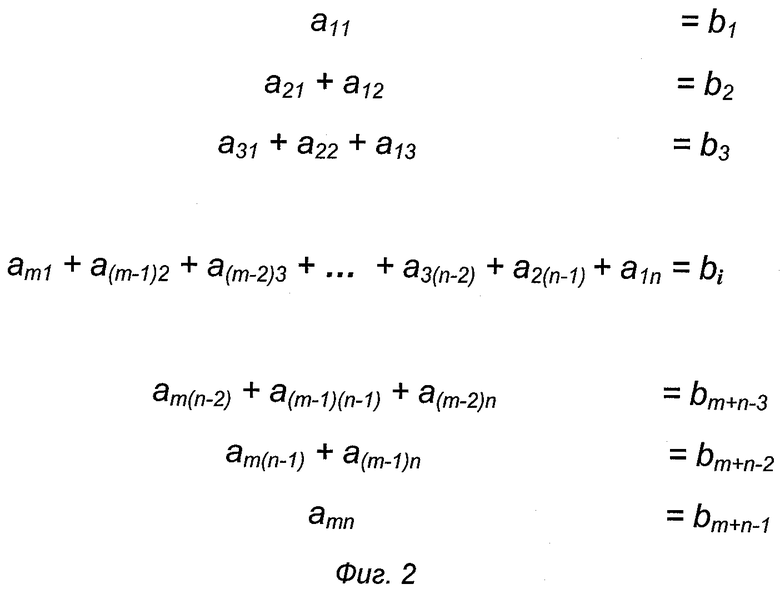

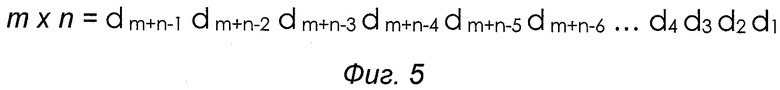

Изобретение относится к области вычислительной техники и может быть использовано для перемножения многоразрядных десятичных чисел. Техническим результатом является повышение быстродействия. Способ заключается в следующем: составляют прямоугольную матрицу размером n×m ячеек, в каждой из которых запоминают поразрядные произведения сомножителей n и m, упорядочивают диагональные срезы ячеек прямоугольной матрицы, суммируют на каждом уровне иерархии ранее запомненные произведения, сдвигают поразрядно вверх все старшие разряды просуммированных десятичных чисел на число иерархических уровней, равное порядковому номеру сдвигаемого разряда, суммируют на каждом уровне сдвинутого иерархического построения десятичные числа и формируют результат произведения начиная с младшего разряда путем последовательного считывания одноразрядных чисел. 7 ил.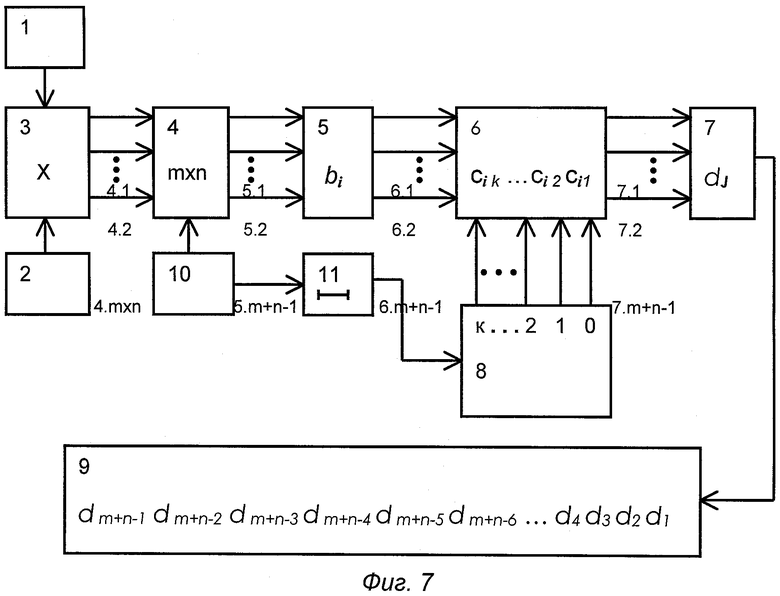
Способ умножения десятичных чисел, характеризующийся тем, что запоминают n и m разрядные сомножители и упорядочивают диагональные срезы, отличающийся тем, что составляют прямоугольную матрицу размером n×m ячеек, в каждой из которых запоминают как однозначные, так и двузначные поразрядные произведения сомножителей n и m, упорядочивают диагональные срезы n×m ячеек прямоугольной матрицы путем их последовательного диагонального иерархического обхода, начиная с верхней левой ячейки, которая является верхним уровнем иерархического построения ячеек, и заканчивая нижней правой ячейкой прямоугольной матрицы, которая является нижним уровнем иерархического построения ячеек, суммируют на каждом уровне иерархии как однозначные, так и двузначные десятичные символы чисел ранее запомненных поразрядных произведений, сдвигают поразрядно вверх все старшие разряды просуммированных символов десятичных чисел на число иерархических уровней, равное порядковому номеру сдвигаемого разряда просуммированных символов десятичных чисел, суммируют на каждом уровне сдвинутого иерархического построения десятичные числа, формируют результат произведения сомножителей n и m поразрядно, начиная с нижнего уровня сдвинутого иерархического построения в качестве младшего разряда произведения, путем последовательного считывания одноразрядных чисел и с одновременным переносом вверх на один уровень сдвинутой иерархии всех старших разрядов десятичных чисел для их последующего суммирования с десятичными числами на вышестоящем уровне сдвинутой иерархии.
| US 6633896 B1, 14.10.2003 | |||
| JP 7160477 A, 23.06.1995 | |||
| US 2007266072 A1, 15.11.2007 | |||
| RU 95104047 A1, 20.01.1997 | |||
| Устройство для умножения десятичных чисел | 1984 |
|
SU1236462A1 |
| Устройство для умножения чисел | 1989 |
|
SU1817091A1 |
Авторы
Даты
2014-08-20—Публикация
2010-12-09—Подача