Изобретение относится к техническим средствам обучения устному счету в математике. Назначением таблицы умножения (ТУ) является получение результата умножения по двум сомножителям или результата целочисленного деления по делимому и делителю.
Наиболее близким аналогом изобретения является вращающаяся таблица умножения, содержащая поворотную и неподвижную плоскость с изображениями цифр от 1 до 9, расположенными в виде матрицы единиц в три ряда и три столбца, и с прорезями в неподвижной плоскости, через которые видны цифры на подвижной плоскости, показывающие результат действия, причем единицы результата умножения возникают, как повороты матрицы единиц, размещенной на подвижной плоскости (см. патент RU N 2139574, МПК 6 G 09 B 19/02, 1999).
Недостаток известного устройства заключается в том, что для получения результата умножения двух чисел приходится использовать не только два заданных числа, но и всю поворотную матрицу из девяти результатов умножения.
Техническим результатом изобретения в динамической модели умножения является существенное уменьшение объема запоминаемой и обрабатываемой информации при устном счете, что увеличивает скорость вычислений в уме и сводит задачу определения единиц результата умножения к простому повороту геометрических фигур, соответствующих цифрам A и B. Устройство динамической ТУ с перемещаемыми фигурами цифр делает получение результатов умножения и деления более наглядным, простым в изучении и использовании. Результат достигается за счет использования специальных свойств чисел при умножении, которые выражают угловые меры цифр, записанных в матрице телефонного табло размера 3х3. Фигуры для цифр, выражающие угловые меры, могут использоваться в процессе коммуникации при визуальной передаче цифровой информации.
Указанный технический результат достигается тем, что в известной динамической модели, предназначенной для получения результата умножения A•B однозначных чисел, содержащей перемещаемые и поворачиваемые фигуры, соответствующие цифрам квадратного телефонного табло размером 3х3, согласно изобретению фигуры представляют собой части телефонного табло, приписывающие каждой цифре одно из восьми направлений из центра табло, которые отсчитывают углы α (A) для каждой цифры A, при этом для нечетных цифр A = 1, 3, 7, 9 угол α (A) отсчитывается от направления, указывающего цифру 1, для четных цифр A = 2, 4, 6, 8 - от направления на цифру 6, цифрам 5 и 0 не приписывается конечного значения угла, причем единицы результата умножения A•B определяются величиной угла α (A•B), равной сумме углов α (A) и α (B), α (A•B) = α (A) + α (B).
В варианте модели, показывающей величину десятков D результатов умножения, на фигурах для цифр имеются по меньшей мере две ячейки, которым соответствуют различные пары сомножителей, между ячейками указаны линии границ, разделяющие ячейки с различными величинами десятков, при этом граница между соседними ячейками, содержащими значения результатов умножения A•B = 10•D0 + E0 и A•(B+1) = 10•D1+E1, где D - десятки, E - единицы, определяется в результате сравнения значений единиц E0, E1 и границы десятков возникают при инверсии порядка единиц E0 > E1.
Имеется вариант модели, в которой границы десятков, разделяющие ячейки, отвечающие результатам умножения A•1, A•2, ..., A•9 с одинаковыми значениями сомножителя A, указываются с помощью прямолинейных параллельных отрезков, которые шарнирами прикреплены к сторонам параллелограмма, при этом параллелограмм одним основанием закреплен на плоскости, а его стороны поворачиваются на фиксированные углы, соответствующие сомножителю A = 1, 2, ..., 9, причем в фиксированных положениях отрезки указывают границы десятков между ячейками.
Изобретение поясняется следующими фигурами.
На фиг. 1 показано расположение цифр в ячейках T-табло и выделенные направления, приписанные цифрам, а также косой нечетный крест ячеек и прямой четный крест ячеек на T-табло.
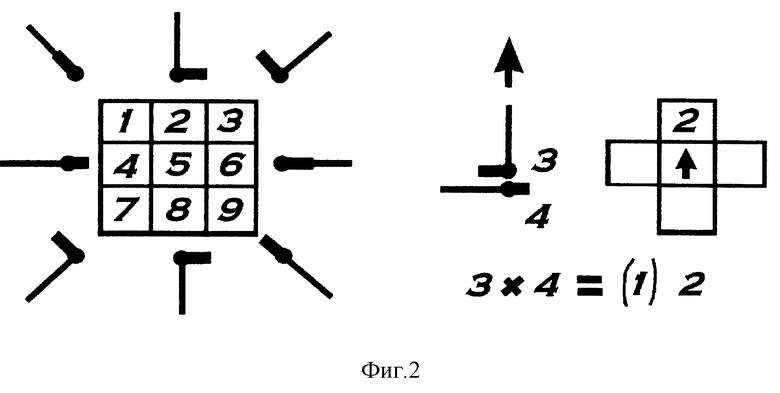
Фиг. 2 изображает фигуры, использующие для обозначения цифр указатели углов между вспомогательным направлением и выделенным направлением цифры. На примере показан способ определения единиц произведения 3х4 путем совмещения знаков 3 и 4.
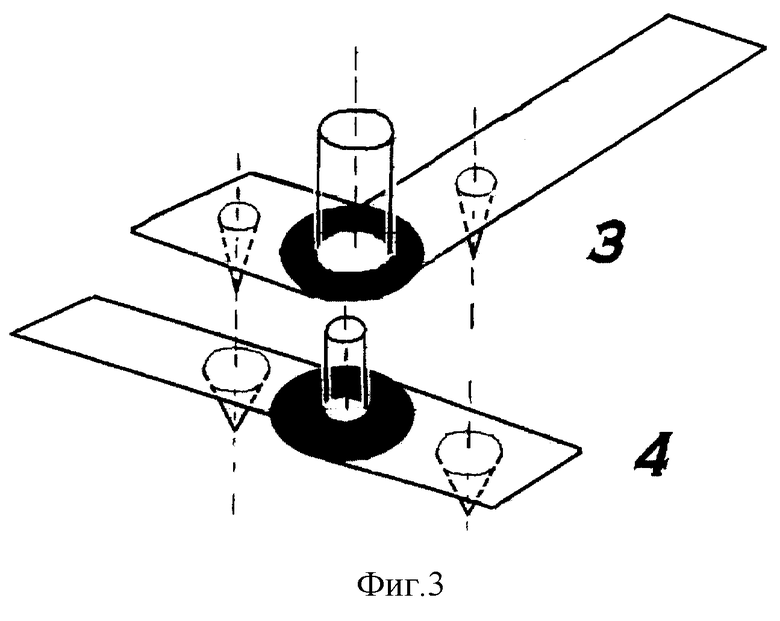
Фиг. 3 предлагает способ соединения фигур, соответствующих цифрам, с помощью шипов, допускающий соединения чисел нечет-нечет, нечет (сверху) - чет (снизу), чет-чет и запрещающий наложение фигур для четных цифр на фигуры нечетных цифр.
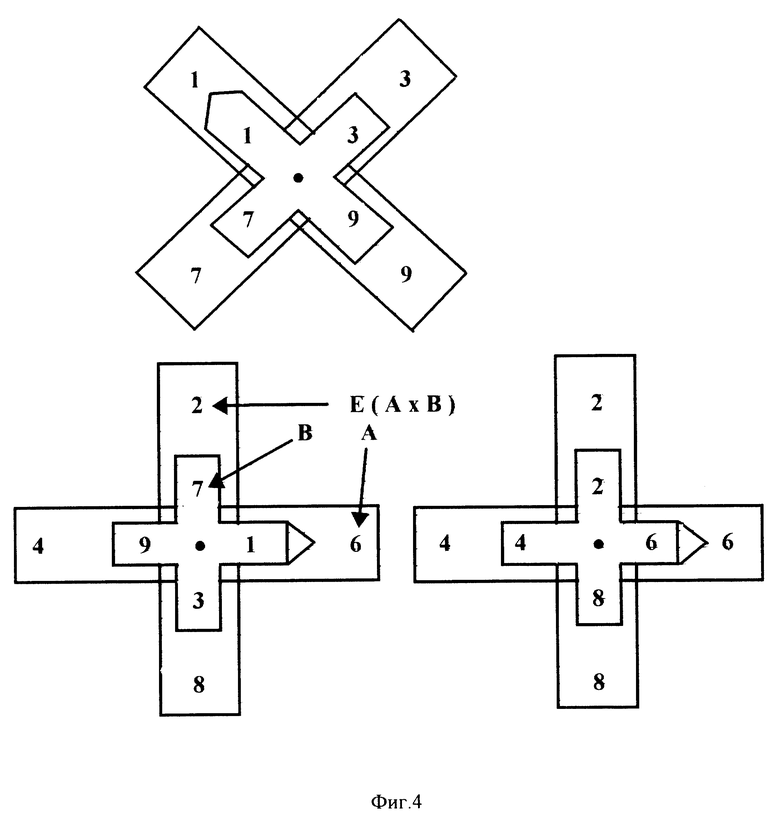
Фиг. 4 показывает конструкции "вертушек умножения" для различных сочетаний четности сомножителей A и B. Указатель подвижной вертушки показывает сомножитель A на большой неподвижной вертушке. Сомножитель B расположен на подвижной вертушке, единицы E результата умножения A•B находятся на неподвижной вертушке напротив цифры B.
Фиг. 5 демонстрирует модель "часов умножения". Угол первого сомножителя показан на первом циферблате "часов". Угол второго сомножителя B отсчитывается от направления A. Единицы E результата умножения A•B читаются на втором циферблате "часов умножения".
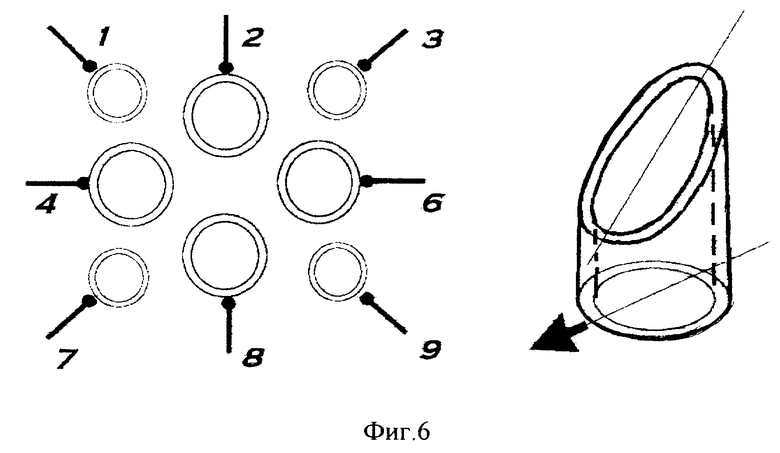
Фиг. 6 показывает расположение корзин модели "баскетбол умножения". Корзины, имеющие направляющую канву, пронумерованы номером второго сомножителя B.
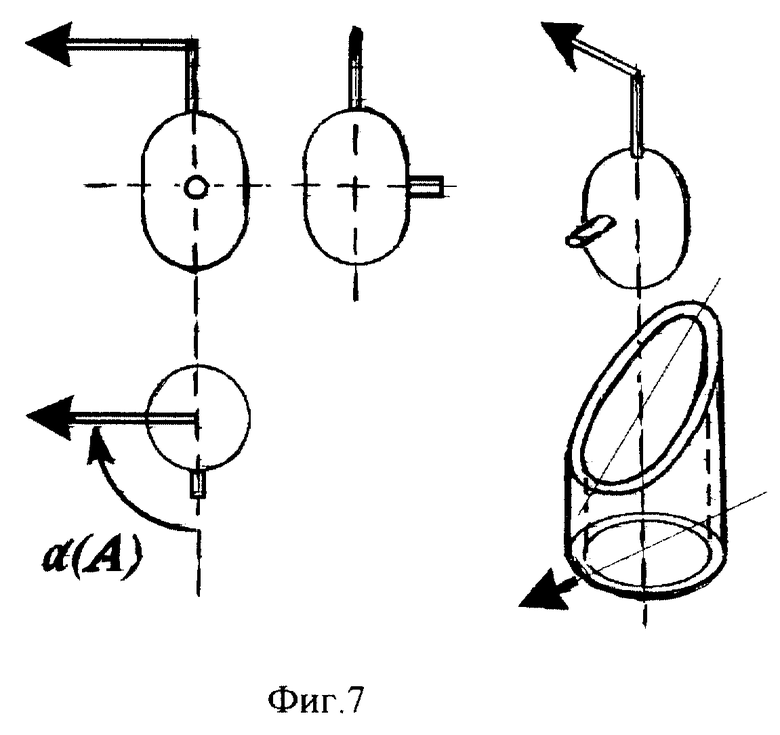
Фиг. 7 изображает конструкцию объемной фигуры модели "баскетбол умножения", соответствующей сомножителю A, позволяющей ей поворачиваться на заданный угол при опускании в корзину B. На чертеже угол α (A) зависит от цифры A.
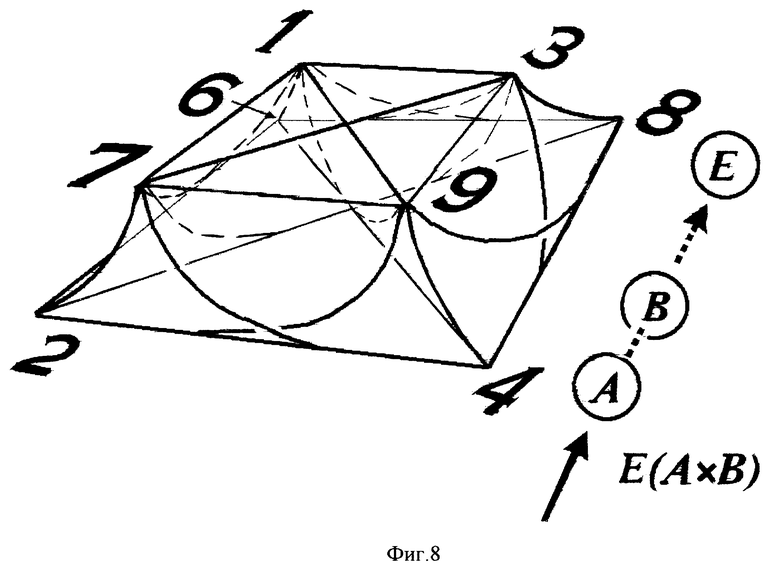
Фиг. 8 дает объемное изображение модели "биллиарда умножения" на двух горизонтальных плоскостях. Рядом с лузой B располагается шар, имеющий такой же номер B. Шар A выполняет удар по шару B в заданном направлении. Шар B перекатывается по направляющим дорожкам и попадает в лузу с номером E(A•B), равным единицам результата умножения A•B.
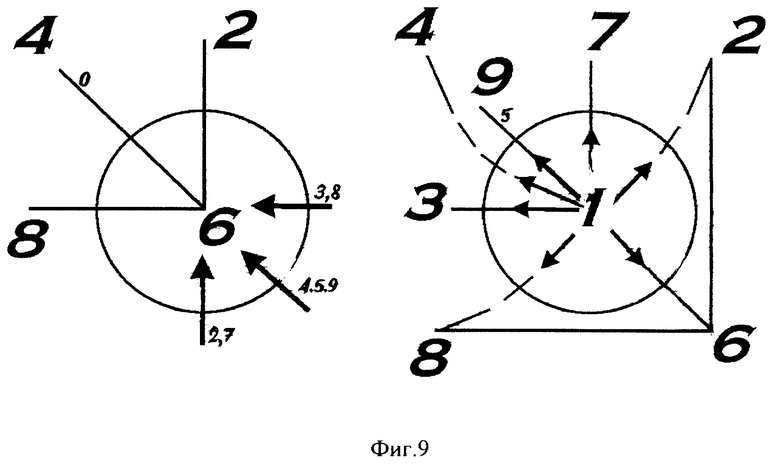
Фиг. 9 для модели "биллиарда умножения" отмечает направления удара шаром с номером A, выстреливаемого разгонным устройством, по шару с номером B, для получения единиц E произведения A•B.
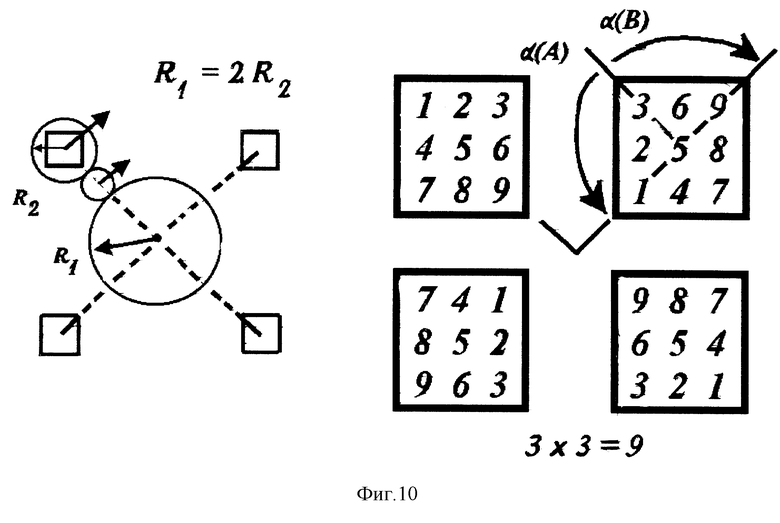
На фиг. 10 показана модель "планетарного вращения единиц", соответствующая нечетному первому сомножителю A = 1, 3, 7, 9. Поворот штанги с T-табло вокруг неподвижного центра на угол α (A) приводит к одновременному вращению T-табло вокруг своего центра на угол -α (A), отсчитываемый в противоположном направлении. Показан пример 3•3 = 9.
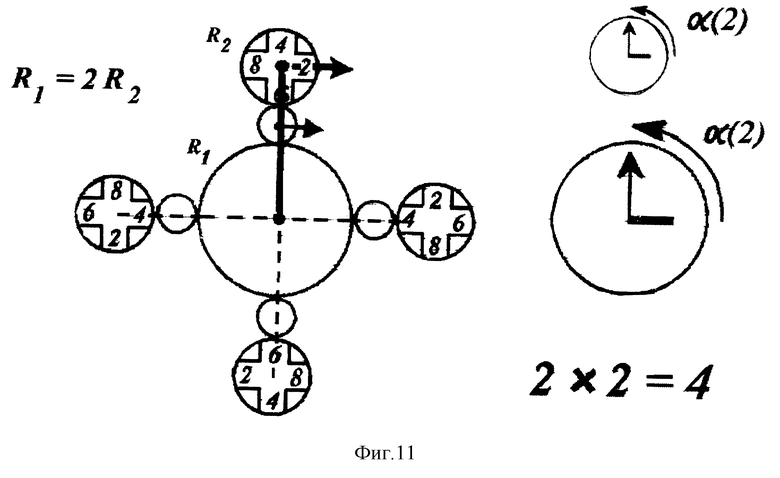
На фиг. 11 приведен вариант модели "планетарного вращения единиц", соответствующей поворотам четной вертушки умножения для значения A = 2, 4, 6, 8. Поворот штанги с вертушкой вокруг неподвижного центра на угол α (A) приводит к одновременному вращению вертушки вокруг своего центра на угол -α (A), отсчитываемый в противоположном направлении. Демонстрируется пример геометрического умножения 2•2 = 4.
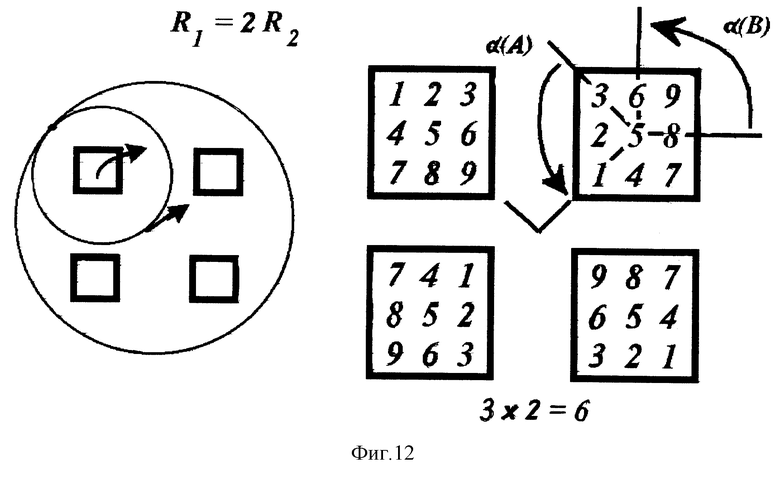
Фиг. 12 дает вариант модели "планетарного вращения внутри окружности". Показано вращение круга с T-табло по внутренней части неподвижной окружности двойного радиуса. Отсчет угла четного сомножителя B начинается от вспомогательного направления для четных цифр.
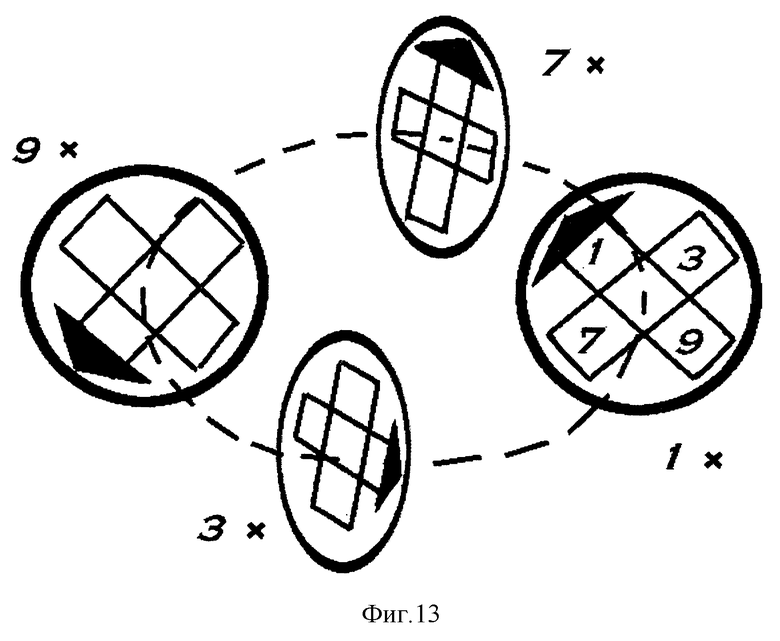
Фиг. 13 показывает объемный вариант модели "бублик умножения". Вертушки умножения располагаются на поперечных срезах тора. Вертушки перемещаются по ободу тора, совершая винтовое вращение. Схема показывает вращение вертушки нечетного креста.
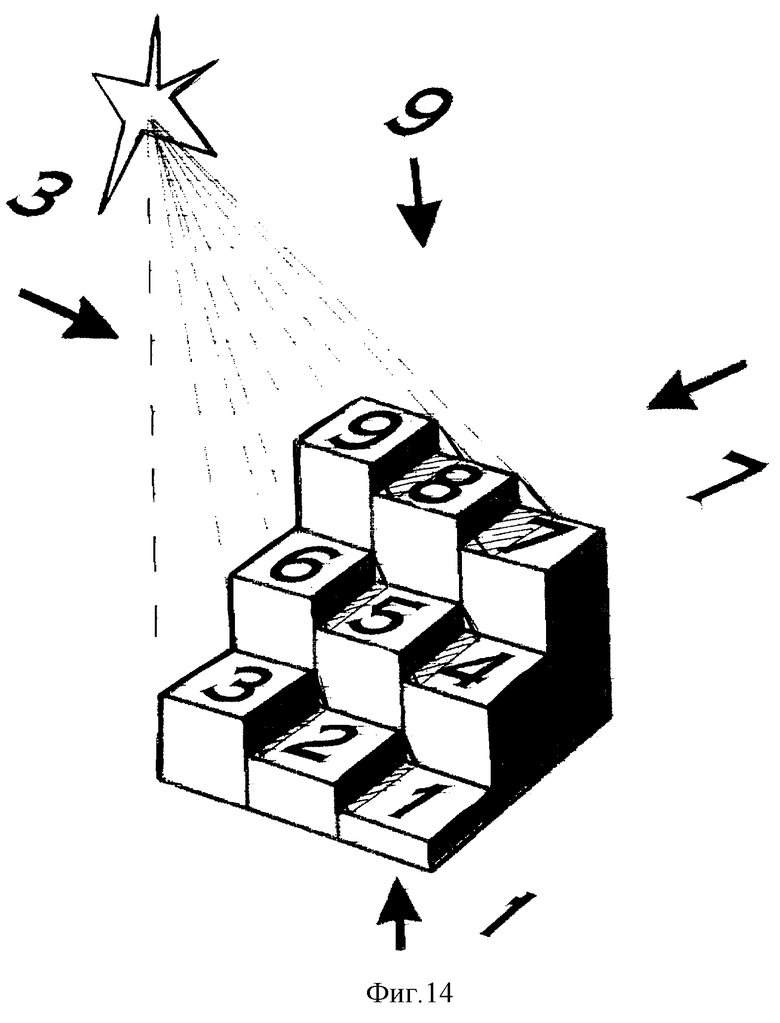
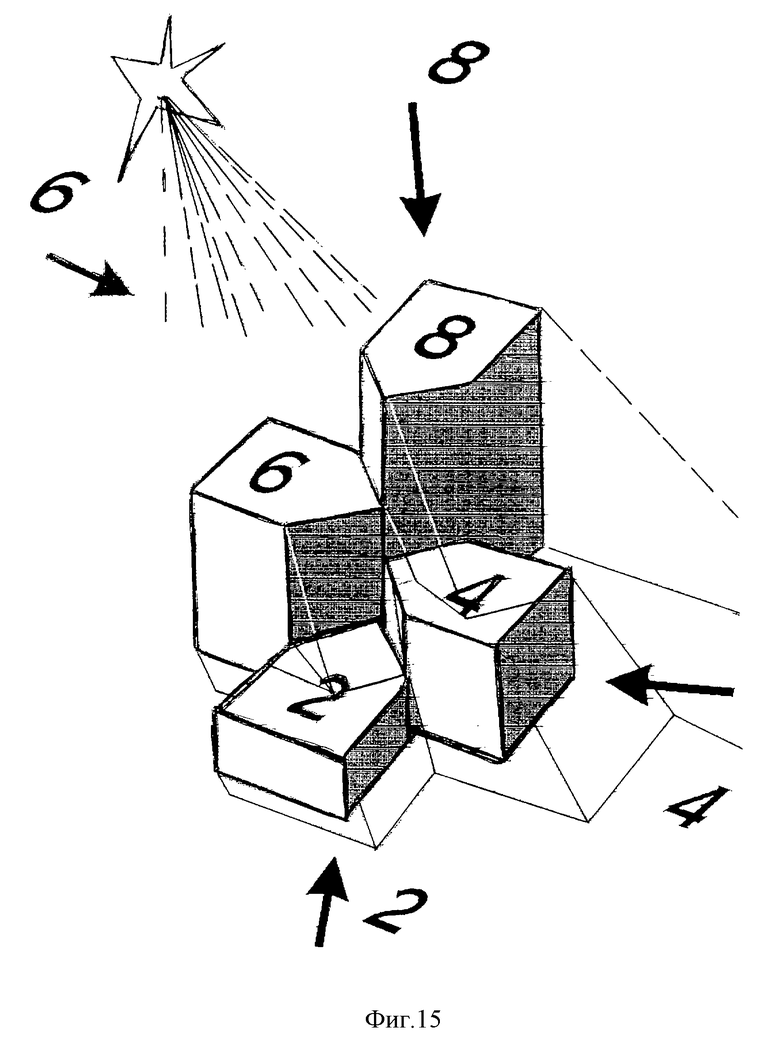
На фиг. 14 изображен вариант модели "город, освещенный солнцем" для нечетного сомножителя A и на фиг. 15 - для четного числа A. Десятки возрастают там, где между последовательными результатами A•B и A•(B+1) имеется тень.
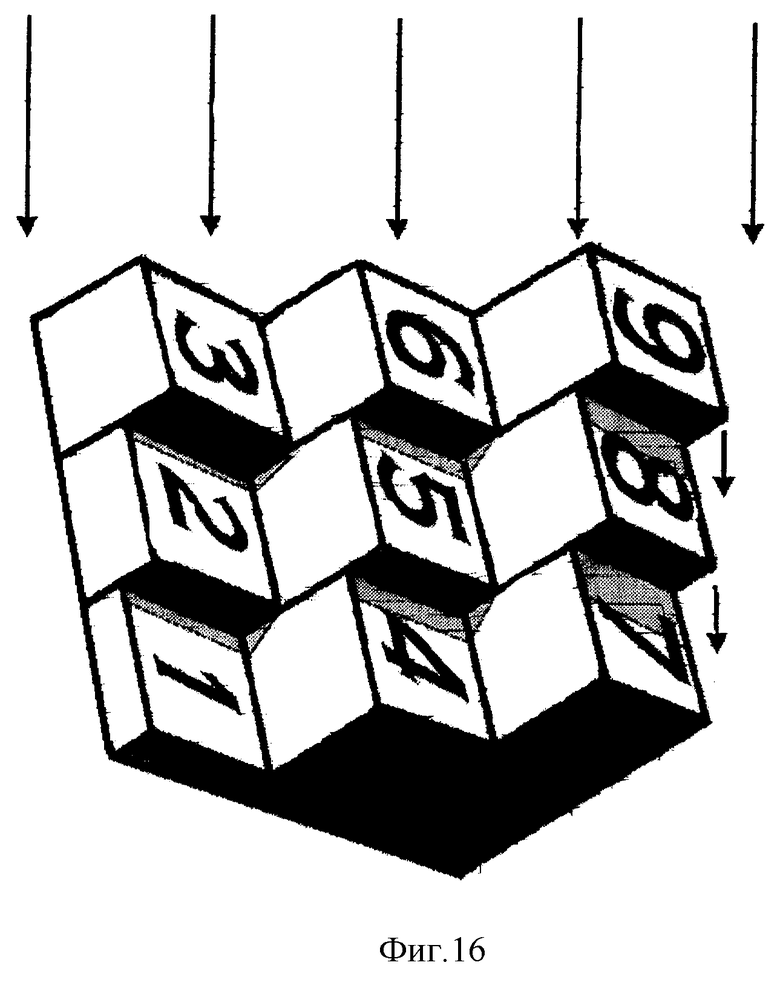
Фиг. 16 показывает модификацию предыдущего варианта "город под дождем" в положении, демонстрирующем границы десятков умножения на A = 3 в виде стенок, защищенных навесом от падающей сверху воды.
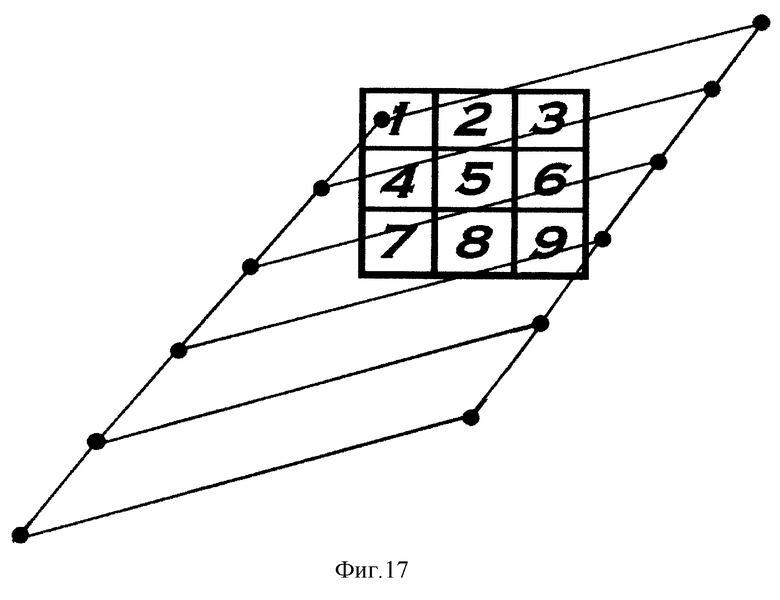
Фиг. 17 объясняет конструкцию модели "параллелограмм границ" в случае умножения на A = 3.
Для точного описания свойств чисел, используемых в изобретении, введем следующую терминологию. Назовем квадратную матрицу размера (3•3) с последовательно заполненными в ней цифрами от 1 до 9 матрицей T-табло (фиг. 1), она является основой цифрового телефонного табло. Выделим из матрицы T-табло четные ячейки 2, 4, 6, 8, которые образуют прямой четный крест H, и угловые нечетные ячейки 1, 3, 7, 9, образующие косой нечетный крест X. На T-табло каждой цифре A однозначно приписывается одно из восьми направлений из центра, расположенного в ячейке с номером 5. Цифре 1 соответствует вектор-направление налево вверх, цифре 2 - вектор-направление вверх и. т.д. (фиг. 1). Эти направления, указывающие цифры, совпадают с одним из направлений осей симметрии квадратной матрицы телефонного табло размера 3х3.
Зададим для чисел A = 0, 1, 2, ..., 9 функцию угол числа A, обозначаемую α (A). Для нечетных цифр A = 1, 3, 7, 9 (фиг. 2) угол α (A) отсчитывается по часовой стрелке от направления, указывающего цифру 1, для четных цифр A = 2, 4, 6, 8 (фиг. 2) - от направления на цифру 6, цифрам 5 и 0 не приписывается конечного значения угла. Таким образом, угол числа для значений A = 1, 3, 7, 9 на косом кресте X равен
α(1)=0, α(3)=1, α(9)=2, α(7)=3.
Угол числа для значений A = 2, 4, 6, 8 на прямом кресте H равен
α(6)=0, α(8)=1, α(4)=2, α(2)=3.
Направление, приписанное самой цифре A, называется основным направлением для цифры A. Направление, от которого начинается отсчет угла для цифры A, называется вспомогательным.
Угол измеряется целым числом, кратным прямому углу 90o, причем прямому углу приписывается угловая мера, равная 1. После полного оборота на 360o отсчет угловой меры начинается опять с нуля, что записывается равенством для углов по модулю 4
4 = 0(mod 4).
Числам 5 и 0 не приписывается конечных значений угла α (5) и α (0) или условно приписывается бесконечное значение ∞.
Отметим, что угловая мера чисел может быть получена из степеней числа 3 для цифр нечетного косого креста X
31 = 3, 32 = 9, 33 = 27 = 7(mod 10), 34 = 81 = 1(mod 10),
и из степеней числа 8 для цифр прямого четного креста H
81 = 8, 82 = 64 = 4(mod 10), 83 = 512 = 2(mod 10), 84 = 4096 = 6(mod 10).
Единицы результата умножения A•B определяются по углу α (A•B), равному сумме углов α (A) и α (B),
α(A×B) = α(A) + α(B).
Это равенство называется формулой углов.
Исключения в формуле углов для однозначных чисел имеются только в случае равенства одного из сомножителей A или B числам 5 или 0. Однако, если считать, что значения угла α для чисел 5 и 0 равны бесконечности
α(5)=∞, α(0)=∞,
и сложение конечного числа α (A) с бесконечностью равно бесконечности
α(A) + α(5) = α(A) + ∞ = ∞,
тогда линейная формула углов для произведения A•B верна во всех случаях.
Единицы E результата умножения A•B однозначно определяются двумя правилами
(E1) формулой углов
α(A×B) = α(A) + α(B);
(E2) согласованием четностей, а именно единицы E произведения чисел A•B являются четным числом, тогда и только тогда, когда одно из чисел A или B четно.
В изобретении оба приведенных выше свойства (E1), (E2) реализованы в конструктивных особенностях фигур динамической модели ТУ.
Вариант 1 динамической модели ТУ использует перемещаемые и поворачиваемые фигуры с двумя планками, изображающие цифры A = 1, 2, 3, 4, 6, 7, 8, 9, представляющие собой жесткие соединения двух прямых планок, угол между которыми определяется угловой мерой α (A) (фиг. 2). Точка соединения планок называется центром фигуры, изображающей цифру. Поскольку угол имеет направление измерения, то планки должны различаться по виду для наглядного различия начального и конечного луча изображаемого угла. Предлагается в данном варианте модели ТУ укоротить планку, указывающую вспомогательное направление, по сравнению с планкой основного направления.
Для фигур, отвечающих цифрам 5 и 0, не выделяется направлений, они представлены фигурами вращения. Например, цифре 5 можно сопоставить закрашенный круг • , а цифра 0 остается окружностью ○ .
Фигуры, соответствующие цифрам, могут перемещаться и поворачиваться, при этом допускается совмещение короткой планки одной цифры с длинной планкой другой цифры. Фигуры представляют собой части плоского телефонного табло, жестко фиксируют относительное расположение осей симметрий квадратного табло и показывают углы α (A) для каждой цифры A,
Процедура определения единиц результата умножения A•B выглядит как простое прикладывание фигуры, соответствующей одной цифре A к фигуре другой цифры B с соблюдением двух условий:
(M1) центры совмещаемых фигур накладываются друг на друга, короткая планка цифры B совмещается с длинной планкой цифры A,
(M2) допускается наложение фигуры нечетной цифры на нечетную или на четную, но не допускается наложение фигуры четной цифры на нечетную цифру.
Первое условие (M1) показывает, что углы, приписанные фигурам, складываются по формуле углов. Второе условие (M2) гарантирует, что произведение четных чисел будет указывать четную цифру единиц E результата A•B, если один из сомножителей является четным числом.
Ответ читается как указание длинной планкой фигуры B на направление, соответствующее единицам E произведения A•B.
При умножении 5 или 0 на число B направления планок в фигурах несущественны, можно считать, что, например, фигура цифры 5 при наложении ее на другую фигуру закрывает сверху все направления, то есть указывает на отсутствие выделенных направлений у результата A•B, что реализуется только для ответа E = 5 или E = 0.
Конструктивно условие соединения фигур для нечетных чисел с любыми фигурами и запрещение накладывать фигуру четной цифры на фигуру для нечетной цифры предлагается реализовать как шип на короткой планке в виде конуса с тонкой стенкой. Если конус шипа для фигуры нечетной цифры имеет узкое основание, а шип для фигуры четной цифры имеет широкое основание, тогда допускаются соединения типа нечет-нечет, нечет (сверху) - чет (снизу), чет-чет, но нельзя плотно наложить фигуру для четной цифры с широким шипом на фигуру для нечетной цифры с узким отверстием ответной части шипа (фиг. 3). Тот же эффект достигается, если центр фигуры, соответствующей числу A, имеет отверстие, позволяющее надевать фигуры на центровочные штыри, причем центровочное отверстие для фигуры нечетной цифры - широкое, а для фигуры четной цифры - узкое. Тогда фигуру четной цифры с узким отверстием нельзя надеть сверху на широкий центровочный стержень нечетной цифры.
Вариант 2 модель "вертушек умножения". В данном варианте динамическая модель ТУ состоит из поворачивающегося косого нечетного креста или прямого четного креста и неподвижной плоскости с цифрами в ячейках, которые находятся на параллельных близко расположенных плоскостях (фиг. 4). У косого креста отмечается выделенное направление на цифру 1, у прямого креста выделенный вектор-направление указывает на цифру 6. Указатели углов U1 и U2 для сомножителей A и B могут быть реализованы как дополнительные приспособления в виде стрелок, отсчитывающие угол от выделенного направления.
Для получения результата умножения нужно выбрать комбинацию вертушек той четности, которые совпадают с четностью сомножителей A и B: нечет-нечет, нечет-чет или чет-чет. Вектор-направление цифры A (стрелка U1, отсчитывающая угол α (A)) на первой вертушке, должен совпадать с вспомогательным вектором сомножителя B второй вертушки, от которого стрелкой Uz отсчитывается угол α (B). Тогда единицы ответа A•B указываются вектором цифры B, читаемым на первой вертушке (фиг. 4). Условие (M2) согласования четности результатов умножения требует, чтобы в случае наличия четного сомножителя A или B, ответ читался бы на четной вертушке.
Вариант 3 "часы умножения". Эта конструкция динамической модели ТУ незначительно отличается от варианта 2 "вертушек умножения" видом плоскостей с цифрами (фиг. 5), напоминающим часы с двумя стрелками. Углы между малой и большой стрелками на циферблатах "часов" равны углам, приписанным сомножителям α (A) и α (B). Угол α (A) указывается на первом циферблате, а угол α (B) - на втором циферблате "часов". Сложение углов α(A) + α(B) дает возможность определить единицы произведения A•B по формуле углов. Например, единицы умножения A•B для A = 3 получаются простым правилом "плюс четверть часа к углу для числа B".
Вариант 4 "баскетбол умножения". В данном варианте модели ТУ проводится аналогия с игрой в баскетбол. Поле содержит девять корзин для мячей, пронумерованных вторым сомножителем B, расположенных в три ряда и три столбца в центрах ячеек T-табло (фиг. 6). Фигура, представляющая первый сомножитель A, выглядит как продолговатый цилиндр с двумя штырями (фиг. 7). Первый штырь является коротким и направлен перпендикулярно вертикальной оси фигуры. Второй штырь - длинный, он прикреплен к фигуре сверху и направлен перпендикулярно вертикальной оси фигуры. Угол между штырями в проекции сверху равен углу α (A), приписанному числу A.
Конструкция корзины с номером B, в которую попадает фигура A, обеспечивает вертикальную ориентацию фигуры A и поворот ее короткого штыря в направлении основного вектора цифры B в интервал времени, пока фигура под действием силы тяжести проходит путь до низа корзины. Такой поворот вокруг вертикальной оси обеспечивается наклонной канвой на стенках корзины B, поворачивающей опускающуюся фигуру A за короткий стержень (фиг. 6).
Процесс определения единиц E результата умножения A•B представляется как баскетбольное забрасывание фигуры для цифры A в корзину с номером B. Фигура, соответствующая цифре A, в процессе продвижения вниз по каналу корзины ориентируется так, что короткий штырь цифры A оказывается направленным по вектору-направлению цифры B. Результат E однозначно определяется как вектор-направление длинного штыря фигуры для цифры A (фиг. 7).
Для того, чтобы соблюдать условие четности (M2), сформулированное выше, вводится ограничение, запрещающее бросать фигуру для четной цифры в корзину, имеющую нечетный номер. Технически этого можно достичь, уменьшая диаметр нечетных корзин и, соответственно, диаметр нечетных фигур, тогда более широкие фигуры для четных цифр не смогут провалиться в корзины с нечетными номерами.
Вариант 5 "биллиард умножения". Этот вариант модели ТУ имеет аналогию с игрой в билллиард. Первый сомножитель A является шаром с нарисованной на его поверхности цифрой A, который бьет по второму шару с изображенной на нем цифрой B, причем направление удара отсчитывается от направления на центр всей конструкции и не зависит от номера шара B. Шар B под действием удара перекатывается по биллиардному полю и попадает в лузу, номер которой равен E, единицам произведения A•B.
Поскольку умножение четного числа A или B на любое другое число всегда даст в ответе четные единицы (см. условие (M2)), то "биллиард умножения" удобно реализовывать как конструкцию на двух ярусах. Верхняя плоскость содержит лузы, пронумерованные нечетными цифрами, нижняя плоскость имеет лузы, пронумерованные четными цифрами (фиг. 8).
Система дорожек между лузами реализуется в виде двух квадратов, каждая сторона и диагональ которых позволяет шарам катиться вдоль них как по направляющим. Между верхним и нижним ярусами имеются переходные дорожки, которые позволяют шару перекатиться с верхнего яруса на нижний и попасть в нужную лузу.
В начальном положении шар B располагается возле лузы с номером B. Шар A помещается в разгонное устройство на позицию, соответствующую номеру A.
Разгонное устройство выстреливает шар A в заданном направлении, который ударяет по шару B и тот катится по направляющим дорожкам до лузы E, равной единицам произведения A•B. Разгонное устройство закрепляется на вертикальной поворотной оси, проходящей через центр всей конструкции. Разгонное устройство предлагается реализовать в виде полусферы с пронумерованными дорожками, которые ведут шар A по поверхности полусферы вниз и шар A приобретает скорость под действием силы тяжести. Разгонное устройство поворачивается так, чтобы шар A ударил по шару B в нужном направлении (фиг. 9). В предлагаемом варианте модели "биллиарда умножения" имеется два разгонных устройства для верхнего яруса с нечетными лузами B и нижнего яруса с четными лузами B. Их различие состоит в том, что разгонное устройство нижнего яруса для четных цифр можно реализовать с меньшим количеством выделенных направлений для выстреливания шара A.
Умножение на число 5 имеет особенность, заключающуюся в том, что шар A должен останавливаться в центре конструкции на верхнем ярусе для нечетного B, где находится луза с числом 5, или в центре нижнего яруса для четного B, там находится луза с числом "нуль". Остановку шара в центре можно реализовать с помощью выдвигаемой дополнительной ограничительной стенки (на схеме не показана).
Вариант 6 "планетарное вращение единиц умножения". В данном варианте динамической модели умножения имеется подвижный круг радиуса R, неподвижный круг радиуса 2R и передаточная шестерня. На подвижном круге могут находиться матрицы T-табло (фиг. 10), которые удобны для получения ответа, если сомножитель A - нечетное число, или вертушки умножения (фиг. 11), здесь показан случай умножения четных чисел A•B. Круги с ячейками для цифр снабжены указателями углов, соответствующих углу первого сомножителя α (A) и углу второго сомножителя α (B). Углы отсчитываются для нечетных чисел от вектора-направления цифры 1, а для четных чисел - от вектора направления цифры 6.
Эффект планетарного вращения единиц умножения заключается в том, что поворот штанги вокруг неподвижного центра O на угол α приводит к перемещению центра T-табло или вертушки, находящихся на конце штанги, и одновременно вызывает их вращение вокруг своего центра на угол -α, то есть на угол α, отсчитываемый в противоположном направлении.
Результат - единицы E произведения A•B получаются в модели "планетарного вращения единиц" в два действия. Из начального положения указатель угла для сомножителя A поворачивается на угол α (A). Затем указатель угла для числа B поворачивается на угол α (B), указывая единицы E произведения A•B.
Вариант 7 "планетарное вращение внутри окружности". Данный вариант отличается от предыдущего тем, что круг радиуса R, несущий T-табло катится по внутренней части неподвижной окружности радиуса 2R без промежуточной шестерни (фиг. 12).
Вариант 8 "бублик умножения". Этот вариант динамической модели умножения является модификацией варианта 2 конструкции, названной "вертушками умножения". Кресты с цифрами вертушек располагаются своими центрами на ободе тора, причем их плоскости являются поперечными срезами тора и центр тора находится в плоскости каждой вертушки. Вертушки могут перемещаться по ободу тора, совершая при поступательном движении винтовое вращение - один оборот вокруг своей оси за каждый оборот по ободу тора (фиг. 13). Определение результата происходит так же, как и в варианте 2.
Вариант 9 динамической модели "город, освещенный солнцем", предназначен для явного задания границ десятков между ячейками с последовательными результатами A•B и A•(B+1). В этом варианте на фигурах для цифр имеются по меньшей мере две ячейки, которым соответствуют различные пары сомножителей, между ячейками указаны линии границ, разделяющие ячейки с различными величинами десятков, при этом граница между соседними ячейками, содержащими значения результатов умножения A•B = 10•D0 + E0 и A•(B+1) = 10•D1 + E1, где D - десятки, E - единицы, существует там, где имеется инверсия порядка единиц E0 > E1.
Значения единиц E могут быть показаны, как число этажей многоэтажных "домов" из кубиков, надстроенных над ячейкой с результатом A•B = 10•D + E.
Расположим в формате T-табло ячейки, пронумерованные индексом B. Над каждой ячейкой надстроим "дома", содержащие B этажей-кубиков (фиг. 14). Четыре поворота данной объемной модели на 90o вокруг вертикальной оси можно рассматривать как единицы умножения A = 1, 3, 9, 7 на B (см., например, вариант 2).
Сравнение значений E0 и E1 выполняется с помощью лучей лампочки освещения, расположенной за сторонами T-табло в направлении вектора, указанного цифрой A (фиг. 14) и создающей тени от более высоких объектов. При достаточно высоком расположении лампочки тени от более высоких столбцов-домов падают на крыши соседних столбцов-домов, именно в этих местах и находятся границы десятков между соседними результатами A•B и A•(B+1).
Для указания границ десятков в случае первого сомножителя A = 2, 4, 6, 8 берется за основу "город" из "домов", построенных на ячейках прямого четного креста (фиг. 15).
Вариант 10 "город под дождем" динамической модели ТУ указывает десятки на объемных фигурах, названных в варианте 9 "городом", с той разницей, что для сравнения величин единиц используется не свет, а поток падающей вниз (или текущей по поверхности) воды. Модель города располагается под углом к вертикальному потоку воды. Если капли потока, падая вертикально, не затекают на навесные стены, что можно достичь с помощью карнизов, то стены более высоких нависающих "домов" останутся сухими, показывая наличие здесь границы десятков между ячейками (фиг. 16).
Вариант 11 "параллелограмм границ" использует прямолинейные отрезки границ, разделяющих ячейки с результатами A•B, имеющими различное число десятков. Отрезки закреплены на сторонах параллелограмма, который одним основанием закреплен на плоскости, а боковые стороны параллелограмма поворачиваются на шарнирах на фиксированные углы, соответствующие сомножителю A = 1, 2,...,9, причем в фиксированных положениях отрезки указывают границы десятков между ячейками. На фиг. 17 показаны границы десятков при умножении на число A = 3.
Модель указывает десятки D результатов умножения A•B = 10•D + E для фиксированных значений A и девяти ячеек, пронумерованных индексом B, с помощью прямолинейных параллельных отрезков, закрепленных на параллелограмме, которые изображают линии границ десятков.
Приведенные выше варианты конструкции динамической модели умножения могут использоваться для демонстрации геометрических действий при получении ответа произведения сомножителей A•B с фигурами только для двух конкретных цифр A и B без использования знаков остальных цифр.
Основное назначение указателей цифр, выполненных в динамической модели ТУ в виде материальных фигур специальной формы, заключается в возможности обучения детей основам арифметики с помощью игровых методик. Повороты, перемещения или непосредственное прикладывание одного знака, соответствующего цифре A, к другому знаку для цифры B указывает правильные цифры единиц E произведения A•B. Принципиально важно, что результат умножения возникает здесь даже без произнесения аудио-моторных словесных формул типа "четырежды три равно двенадцать" только на основе зрительного восприятия сложенных вместе знаков двух сомножителей (например, фиг. 2), позволяя использовать исключительно зрительную память при устном счете, многократно ускоряя скорость устных вычислений.
Соответствие универсальных фигур, состоящих из двух направлений, конкретным цифрам расшифровывается вполне определенно. Изображения цифр (фиг. 2) однозначно указывают, что они записаны в десятичной системе счисления. По угловым мерам, отраженным в фигурах для цифр, можно расшифровать и отождествить соответствие фигур знаков и цифр 1, 2, ..., 9.
Выделение для обозначений цифр восьми фиксированных направлений на плоскости непосредственно следует из симметрий плоских фигур. Таким образом, фигуры для цифр в виде уголков (фиг. 2) создают знаковую цифровую систему, пригодную для визуальной коммуникации или для письменных сообщений. Высокоразвитое разумное существо, например инопланетянин, который знает о математических свойствах угловых мер чисел, может непосредственно понимать производимые человеком числовые действия, наблюдая манипуляции с универсальными указателями цифр. Именно в этом смысле указатели цифр, использующие угловые меры, основанные на универсальных симметриях плоскости, понятны инопланетянам, поскольку не требуют устной речи для их названий в процессе общения или в письменных сообщениях.
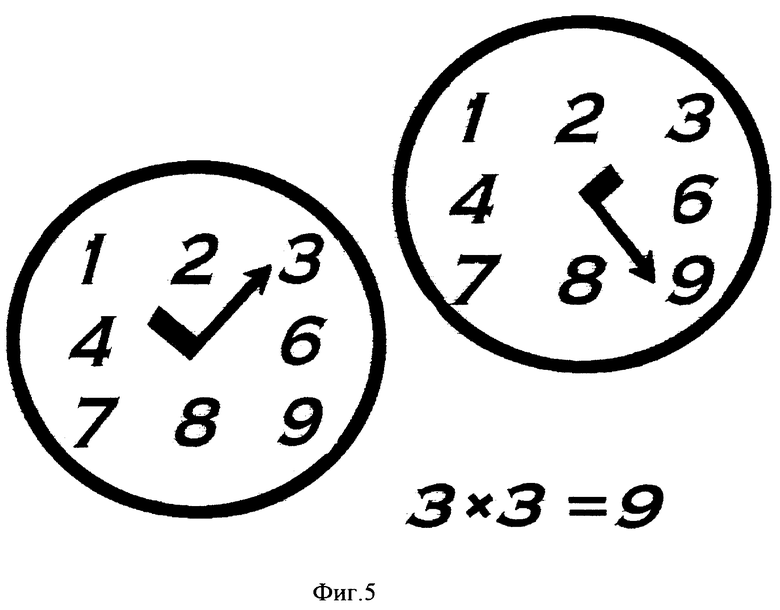
Динамическая модель предназначена для обучения устному счету и позволяет повысить эффективность обучения. Перемещаемые фигуры сопоставляют каждой цифре одно из направлений осей симметрии квадратного табло размером 3 х 3. Фигуры представляют собой части телефонного табло. Фигуры жестко фиксируют относительное расположение осей симметрии табло и показывают углы α (А) для каждой цифры А. Для нечетных цифр А = 1, 3, 7, 9 угол α (А) отсчитывается от направления, указывающего цифру 1. Для четных цифр А = 2, 4, 6, 8 - от направления на цифру 6. Цифрам 5 и 0 не приписывается конечного значения угла. Единицы результата умножения А х В определяются величиной угла α (А х В), равной сумме углов α (А) и α (В), α(A×B) = α(A) + α(B). На фигурах для цифр могут быть, по меньшей мере, две ячейки, которым соответствуют различные пары сомножителей. Между ячейками указаны линии границ, разделяющие ячейки с различными величинами десятков. Граница между соседними ячейками, содержащими значения результатов умножения А х В = 10 х D0 + Е0 и А х (В + 1) = 10 х D1 + Е1, где D - десятки, Е - единицы, существует там, где имеется инверсия порядка единиц Е0 > Е1. Границы десятков, разделяющих ячейки, соответствующие результатам умножения А х 1, А х 2, ..., А х 9 с одинаковыми значениями сомножителя А, указываются с помощью прямолинейных параллельных отрезков. Отрезки шарнирами прикреплены к сторонам параллелограмма. Параллелограмм одним основанием закреплен на полости. Стороны параллелограмма поворачиваются на фиксированные углы, соответствующие сомножителю А = 1, 2, .. . , 9. В фиксированных положениях отрезки указывают границы десятков между ячейками. 2 з.п.ф-лы, 17 ил.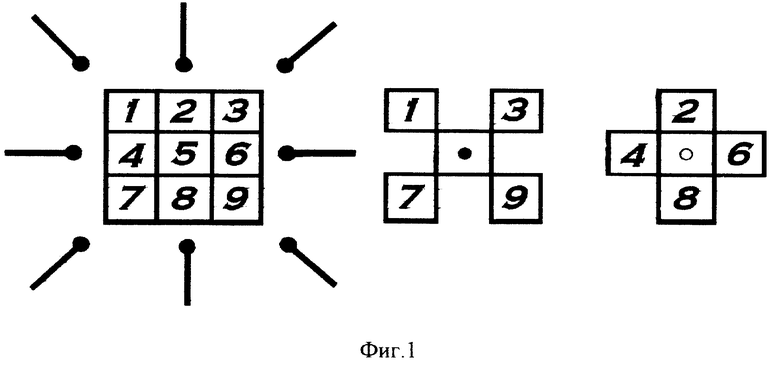
α(A×B) = α(A) + α(B).
2. Модель по п.1, отличающаяся тем, что на фигурах для цифр имеются по меньшей мере две ячейки, которым соответствуют различные пары сомножителей, между ячейками указаны линии границ, разделяющие ячейки с различными величинами десятков, при этом граница между соседними ячейками, содержащими значения результатов умножения AхB=10хD0 + E0 и Aх(B+ 1) = 10хD1+E1, где D - десятки, E - единицы, определяются в результате сравнения значений единиц E0, E1 и границы десятков возникают при инверсии порядка единиц E0>E1.
| ВРАЩАЮЩАЯСЯ ТАБЛИЦА УМНОЖЕНИЯ/ДЕЛЕНИЯ РАЗМЕРОМ (W • W), ГДЕ W = 3(MOD 10) ИЛИ W = 7(MOD 10) | 1999 |
|
RU2139574C1 |
| СПОСОБ ОБУЧЕНИЯ И МОДЕЛЬ ТАБЛИЦЫ УМНОЖЕНИЯ/ДЕЛЕНИЯ НА ОСНОВЕ ДЕВЯТИ МАТРИЦ - ДЕВЯТИЛИСТНИКА, ОБЛАДАЮЩЕГО ДВУХУРОВНЕВЫМИ ЛОКАЛЬНЫМИ И ГЛОБАЛЬНЫМИ СИММЕТРИЯМИ | 1999 |
|
RU2139575C1 |
| ПЕРЕНОСНОЕ СКОЛЬЗЯЩЕЕ ПЕРЕМЕЩАЮЩЕЕ УСТРОЙСТВО | 1991 |
|
RU2066547C1 |
| ПЛАНЕТАРНЫЙ СМЕСИТЕЛЬ ВЯЗКИХ МАТЕРИАЛОВ | 2004 |
|
RU2253507C1 |
| US 3766667 A, 23.10.1973 | |||
| US 3787988 A, 29.01.1974 | |||
| СПОСОБ ПОДГОТОВКИ К ХРАНЕНИЮ ТОМАТОВ СВЕЖИХ СПЕЦИАЛЬНОГО НАЗНАЧЕНИЯ | 2006 |
|
RU2322005C1 |
Авторы
Даты
2001-10-10—Публикация
2000-04-24—Подача