Изобретение относится к техническим средствам обучения устному счету в математике.
Назначением таблиц умножения (ТУ) является получение результата умножения по двум сомножителям. Использование симметрий вращения и симметрий дополнения для единиц или десятков результатов умножения на различные сомножители показывает новые связи и свойства.
Наиболее близким аналогом изобретения является таблица умножения на однозначные числа от 1 до 9, содержащая плоскости с матрицами, состоящими из ячеек, в которых изображены цифры, показывающие результаты действий.
Недостатком известного устройства является размещение исходных данных и результата действия на разных сторонах плоскости и одновременный показ только некоторых результатов, что делает невозможным одновременное наглядное сопоставление цифр исходных данных с результатами для всей таблицы умножения/деления.
Техническим результатом изобретения является явное указание зависимостей и симметрий в связях для всех исходных данных и результатов умножения/деления одновременно, геометрическая интерпретация умножения, в которой места исходных сомножителей определяют места нахождения результата действия. По сравнению с обычной таблицей умножения, не использующей симметричных взаимосвязей, новое расположение в форме девятилистника, существенно уменьшает объем запоминаемой и обрабатываемой информации при устном счете. В модели таблицы умножения, содержащей поворотные плоскости, связь исходных данных и результатов становятся более наглядной, простой в изучении.
Использование симметричного вида таблицы умножения позволяет получать по определенным алгоритмам число десятков результата умножения и число единиц результата умножения как значения, определяемые местом сомножителей в таблицах умножения в форме девятилистника, фактически, независимо друг от друга. В этом смысле новая структура умножения является не улучшением "старой" структуры, а независимым обоснованием для аксиоматического введения результата умножения, которое не требует анализа содержания самого умножения (axb) как сложения а раз числа b.
Указанный технический результат достигается за счет использования специальных свойств чисел при умножении. В отличие от известной таблицы умножения на однозначные числа от 1 до 9, содержащей плоскости с матрицами, состоящими из ячеек, в которых изображены цифры, показывающие результаты действий, согласно изобретению, ячейки с результатами действий составляют девять таблиц умножения, записанных в виде матриц Мh, где h - первый сомножитель, при этом ячейки каждой матрицы Мh расположены симметрично относительно центра матрицы (hx5), ячейки каждой пары матриц Мh и M10-h расположены симметрично относительно общего центра (5х5) таблицы М5, что определяет совпадение единиц результатов умножения на 3 с поворотом против часовой стрелки на 90o матрицы Т, где Т - матрица единиц для M1, единиц умножения на 7 с поворотом по часовой стрелки на 90o матрицы Т, единиц умножения на 9 с поворотом на 180o матрицы Т, единиц умножения на 4 с поворотом по часовой стрелки на 90o матрицы единиц D для матрицы М2 результатов умножения на 2, единиц умножения на 6 с поворотом против часовой стрелки на 90o матрицы D, единиц умножения на 8 с поворотом на 180o матрицы D.
В варианте реализации модели таблицы умножения на четные цифры на плоскостях имеются симметричные матрицы размера 3х5, где ячейка 4 расположена в конце верхнего ряда, а ячейка 6 в начале нижнего ряда.
Дан статический вариант модели результатов умножения в виде графовой структуры, в вершинах которой размещены результаты умножения двух сомножителей, при этом вершины образуют симметричную относительно центра (5х5) фигуру для всех результатов, кроме четырех пар сомножителей (1х9), (2х8), (3х7), (4х6), которые расположены вблизи центра симметрии (5х5) и образуют отклонение от симметрии.
Предложен способ обучения умножению целых чисел, при котором используют симметричное расположение на плоскостях ячеек с результатами умножения, отличающийся тем, что используют повороты плоскостей с ячейками для указания связи пары ячеек, для которых единицы ehxb и ehx(10-b) результатов умножения чисел h, b и (10-b) удовлетворяют формуле
ehxb + ehx(10-b) = 0 (mod10), (5)
и десятки результатов умножения ahxb и ahx(10-b) результатов умножения удовлетворяют формуле дополнения десятков
ahxb + ahx(10-b) = h-1+V(h,b), (6)
где "функция десятки" V(h,b) зависит от чисел h и b и равна 1, если hxb = 0 (mod10), и V(h,b) равна 0 в остальных случаях.
Вариант способа обучения отличается тем, что используют повороты плоскостей с ячейками для указания связи пары ячеек, для которых единицы ehxb и e(10-h) x(10-b) результатов умножения чисел h, b, (10-h) и (10-b) удовлетворяют формуле
ehxb = e(10-h) x(10-b)
Предлагается способ обучения, использующий связь десятков результатов умножения ahxb и ahxc в ячейках (hxb) (hxc) в соответствии с формулой
ahxb = ahxc + ind (hxc, hxb),
где индекс пути ind равен числу пересечений границ десятков в матрицах Мh.
Изобретение поясняется следующими чертежами.
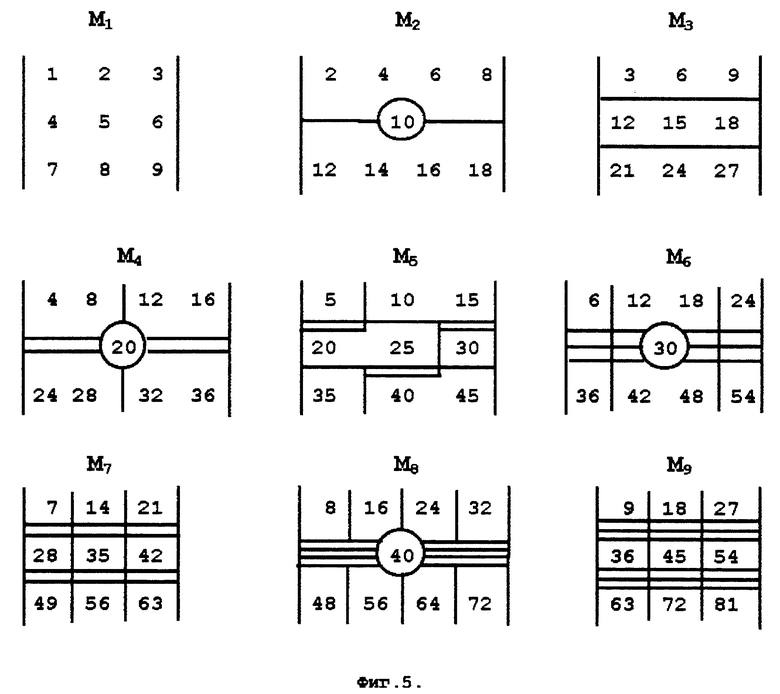
На фиг. 1 изображены матрицы таблиц умножения Мh, матрицы десятков Аh и матрицы единиц Eh, где h=1,2,...9. Показан поворот матриц единиц для разных таблиц.
Фиг. 2 дает представление таблицы умножения в форме девятилистника. Использование данного представления показывает локальные и глобальные симметрии и дополнения результатов умножения.
Фиг. 3 отмечает регулярные и нерегулярные границы десятков на девятилистнике таблицы умножения. Области нерегулярности в четных таблицах умножения образуются как взаимные повороты.
Фиг. 4. приведены пиктограммы способа подсчета числа десятков результата умножения как индекса пересечения границ. Десятки результата умножения равны числу пересекаемых границ с учетом кратности, задаваемой количеством стрелок в данном направлении. В таблицах умножения на 4 и на 8 граница нерегулярности берется с минусом.
Фиг. 5 показывает вариант симметричного представления таблицы умножения на четные цифры в виде матрицы размером (5х3). Данный вид упрощает изучение свойств умножения на четные цифры.
Фиг. 6 изображает девятилистник таблицы умножения в форме восьмиугольника. Представление таблицы умножения в форме восьмиугольника показывает равноправие между "углами" и "сторонами" таблиц.
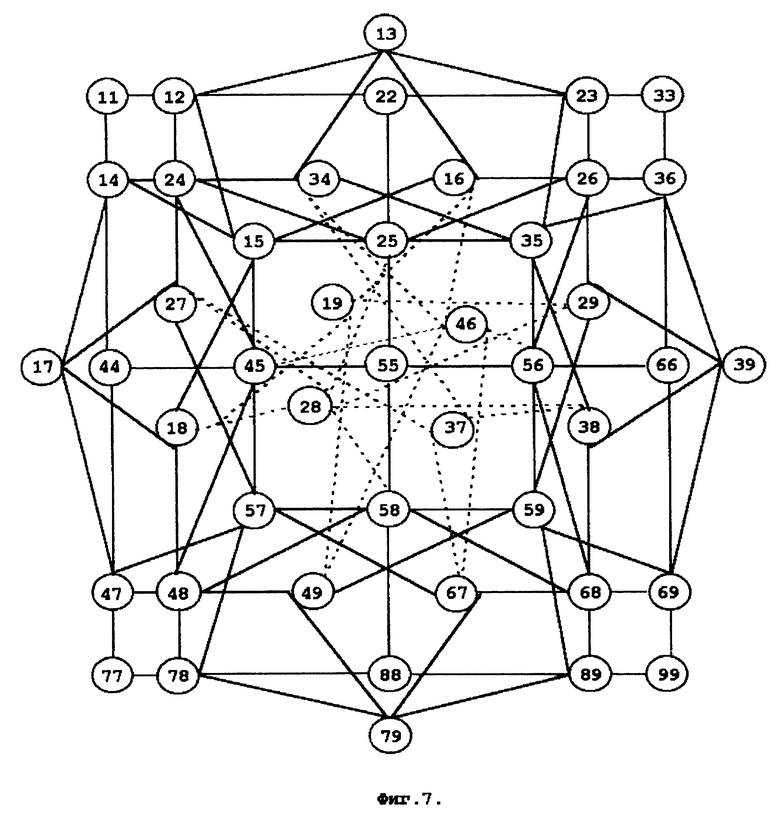
Фиг. 7 изображает симметричную топологическая модель девятилистника таблицы умножения в виде графа результатов умножения. Показаны симметрии статической модели таблицы умножения относительно центра.
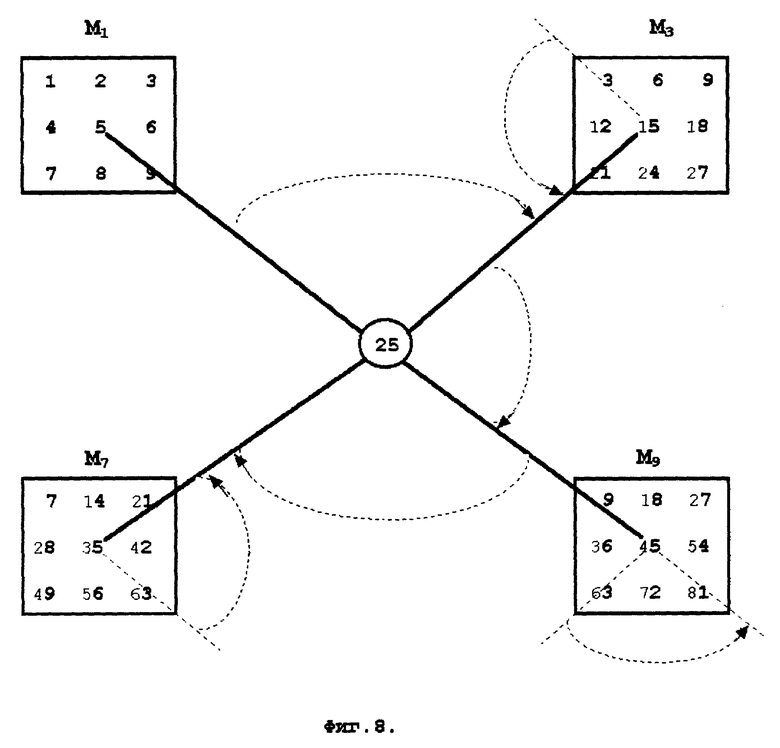
На фиг. 8 показана модель вращения матрицы единиц результатов умножения для различных сомножителей. Поворот матриц единиц выполняется вокруг центра симметрии девятилистника (5х5) и одновременно на такой же угол в противоположном направлении вокруг своего центра.
Модель таблицы умножения на однозначные числа от 1 до 9 содержит плоскости с ячейками, в которых изображены цифры, показывающие результаты действий. Плоскости содержат одну или несколько ячеек, сгруппированных в таблицы умножения на разные сомножители. Плоскости могут поворачиваться, что позволяет сопоставлять совмещаемые при повороте пары ячеек.
Модель таблицы умножения, расположенная в форме девяти таблиц Тa, использует специальные свойства чисел при умножении. Умножение однозначных чисел обеспечивается таблицами Тa размера 3х3. Везде далее предполагается, что таблицы умножения Тa могут иметь размер (wxw), где w==3 (mod10) или w=7 (mod10), однако изложение примеров будет демонстрироваться для основного варианта w= 3. При увеличении размера w до 7 таблица умножения показывает произведение однозначного сомножителя на число от 1 до 49, при w=13 - на число от 1 до 13х13=169 и т.д.
Введем обозначения и построим математическую структуру, которую будем называть девятилистником, описывающую симметрии таблицы умножения и реализующую правила получения результатов умножения.
Обозначения. Будем рассматривать квадратные матрицы размера (wxw) с целочисленными элементами. Матрицы обозначаются прописными буквами Т, Е,.... Обозначим Т-табло T= (bi,j), где (i, j =1, 2, 3,..., w), матрицу элементов bi,j, в которой bi,j являются последовательными натуральными числами, записанными по строкам bi,j = (x x(i-1)+j) (mod 10), т.е. с отброшенными числами десятков. Число S= w x (i-1)-+j назовем номером элемента bi,j.
Для размеров таблицы w=3 описанное Т-табло представляет собой обычную панель цифрового телефона с цифрами от 1 до 9, расположенными в три ряда.
Пусть h - натуральное число h=1,2,...,9. Обозначим таблицы умножения на сомножитель h матрицами
Mh=hxE1.
В ячейках матрицы Мh находятся результаты умножения числа h на номер места в таблице умножения (фиг.1). Обозначим матрицы единиц при умножении на сомножитель h
Eh = h x Т - (h x bi,j (mod 10)) = (h x s (mod 10)).
На месте s в матрице находится результат умножения hxs, но в матрице Eh используются только единицы этого результата (фиг.1). Ячейку с результатом умножения (hxs) можно обозначить (h,s).
Обозначим через Ah матрицу десятков таблицы умножения Mh. Тогда в матричном виде можно записать, что
Mh = 10 x Ah + Eh.
Из обозначений следует, что T=E1 где E1 матрица единиц умножения на 1.
Повороти плоскостей квадратной матрицы в положительном направлении (по часовой стрелке) вокруг центра на 90 имеют четыре положения, которые обозначаются верхним индексом r= 0,1,2,3. Повороты Тr выглядят так: Т0 - нет поворота, Т1 - поворот на 90o, Т2 - поворот на 180o, Т3 - поворот на 270o по часовой стрелке. Для индекса числа поворотов r<0 поворот осуществляется против часовой стрелки; Т-1=Т3.
Обозначим D=E2 матрицу единиц умножения на 2. Четыре положения при повороте D в положительном направлении обозначаются: D0 = D, D1, D2, D3 = D-1.
Построение девятилистника. Симметричное расположение относительно центра матрицы (hx5) сомножителей (hxb) и (hx(10-b)) для b не равного 5 в таблице Мh
будем называть локальной симметричной парой.
Расположим таблицы умножения Мh, где h от 1 до 9, в три ряда по три матрицы в каждом ряду:
Назовем девятилистником (фиг.2) взаимное расположение на плоскостях девяти матриц Мh составленных из ячеек, где h - первый сомножитель, при котором ячейки каждой матрицы Мh расположены симметрично относительно центра матрицы (hx5), а ячейки каждой пары матриц Мh и M10-h расположены симметрично относительно общего центра (5х5) матрицы M5.
В том же формате можно составить девятилистник десятков результатов умножения и девятилистник единиц результатов умножения:
Пару сомножителей (axb) в таблице Мa и (10-а)x(10-b) в таблице М10-a будем называть глобально симметричной парой в девятилистнике (2), эти пары являются центрально-симметричными парами относительно общего центра девятилистника (5х5) таблицы М5.
Совпадение матриц единиц Eh результатов умножения при поворотах. Для матриц размера (3х3) изображения таблиц единиц Eh приведены на фиг. 1 вместе с матрицами Мh =- hxE1, которые являются полными таблицами умножения.
Непосредственно проверяется, что Eh действительно являются единицами для таблиц умножения Мh. Единицы результата умножения на нечетный первый сомножитель, не равный 5, являются поворотами плоскостей с находящимися на них матрицами единиц Т: E1-T0, E3=Т-1, E7=Т1, E9 = Т2 (фиг.8).
Единицы результата умножения на четный первый сомножитель являются поворотами плоскостей с находящимися на них матрицами единиц D: E2=D0, E4=D1, E6=D-1, E8=D2.
Таким образом, из свойств матриц Eh следует, что единицы результатов таблиц умножения девятилистника определяются поворотами плоскостей с матрицами единиц Т и D на углы 0o, 90o, 180o или 270o, задаваемые формулами
Следовательно, повороты определяют совпадение единиц результатов умножения на 3 с поворотом против часовой стрелки на 90o матрицы Т, единиц результатов умножения на 7 с поворотом по часовой стрелки на 90o матрицы Т, единиц результатов умножения на 9 с поворотом на 180o матрицы Т,
единиц результатов умножения на 4 с поворотом по часовой стрелки на 90o матрицы D, единиц результатов умножения на 6 с поворотом против часовой стрелки на 90o матрицы D, единиц результатов умножения на 8 с поворотом на 180o матрицы D.
В способе обучения умножению целых чисел используют симметричное расположение на плоскостях ячеек с результатами умножения, чтобы посредством поворотов плоскостей с ячейками указать локально-симметричные или глобально симметричные пары ячеек, цифры десятков и единиц которых связаны формулами.
Локальная симметрия результатов. Повороты плоскостей с ячейками для указания связи пар локально-симметричных ячеек, содержащих числа (hxb) и (hx(10-b)) в матрице Мh показывают, что единицы ehxb и ehx(10-b) результатов умножения чисел h, b и (10-b) удовлетворяют формуле
ehxb + ehx(10-b) = 0 (mod10), (5)
и десятки результатов умножения ahxb и ahx(10-b) результатов умножения удовлетворяют формуле дополнения десятков
ahxb + ahx(10-b) = h-l+V(h,b),
где "функция десятки" V(h,b) зависит от чисел h и b и
V(h,b) равна 1, если hxb = 0(mod10) и
V(h,b) равна 0, в остальных случаях.
Таким образом, локально-симметричные пары единиц в каждой матрице Мh в сумме дают 10 или 0, а локально-симметричные пары десятков, если единицы результата не равны 0, в сумме дают константу (h-1).
Глобальная симметрия результатов. Повороты плоскостей с ячейками позволяют указать связи глобально-симметричных пар ячеек (hxb) и (10-h)x(10-b), для которых единицы ehxb и e(10-h) x(10-b) результатов умножения чисел h, b, (10-h) и (10-b) удовлетворяют равенству
ehxb и e(10-h) x(10-b)
Сумму десятков глобально-симметричных пар результатов умножения можно получить с помощью двойного применения формулы (6).
Границы в матрице десятков Аh и индекс пути как число пересечения границ. Границы ячеек в матрице Ah дают важную информацию о значении десятков результата умножения. Граница области проходит по сторонам квадрата, ограничивающего ячейку с результатом умножения hxb. Выделим два типа границ.
Регулярные границы определяются только сомножителем h и представляют собой горизонтальные и вертикальные линии в матрице Аh, проходящие между строками и столбцами матрицы. Регулярные границы могут иметь кратность 1, 2 или 3. Например, при кратности равной 2, пересечение границы должно считаться дважды. Если граница пересекается сверху вниз или слева направо (положительное направление), то подсчет пересечений выполняется с плюсом, если в обратном направлении, то с минусом.
Нерегулярные границы возникают при умножении на четные цифры 2, 4, 6, 8. При умножении на нечетные цифры областей нерегулярности не возникает.
Определим области нерегулярности в таблице десятков А2 для матриц размером 3х3. Областью "чудес" U2 назовем ячейки в таблице A2 (или M2, или E2), десятки в которых равны 1 (фиг. 3).
Граница области "чудес" U2 в матрице А2 проходит на стыке следующих пар ячеек: (4,7), (4,5), (2,5), (3,6). Если использовать номера ячеек, то области "чудес" в матрицах умножения на четные цифры определяются следующими наборами ячеек
U2={5, 6, 7, 8, 9};
U4={1, 4, 5, 7, 8};
U6={2, 3, 5, 6, 9};
U8={1, 2, 3, 4, 5}.
На фиг. 3 показано, что области "чудес" в матрицах А4, А6, A8 являются поворотами нерегулярной области U2 из матрицы А2.
Путь в матрице десятков. Путь в матрице Аh определяется как переход из ячейки в ячейку в направлении горизонтали или вертикали. Для номеров i, j, равных 1, 2, 3, и шагов, не выводящих за границы матрицы, получаем:
(i, j) ---> (i+1,j), (i,j) ---> (i,j+1),
(i, j) ---> (i-1,j), (i,j) ---> (i,j-1).
Индекс пути. Индекс пути равен алгебраической сумме числа пересечений границы с учетом кратности границы, считаемой в положительном направлении с плюсом, в противоположном направлении с минусом.
Обозначается индекс пути, проходящий в матрице Аh из ячейки (h,a) в (h, b) с помощью выражения
ind ((h,a), (h,b)).
Формула десятков в матрице Аh. Введение областей, границ и индекса пути оправдывается следующей формулой. Для любой матрицы Аh число десятков ahxc и ahxb в ячейках (hxb) и (hxc) связаны формулой
ahxc = ahxb + ind ((hxb), (hxc)),
причем значение индекса не зависит от вида пути, соединяющего (hxb) и (hxc).
Поскольку для всех однозначных чисел h результат умножения hx1 имеет число десятков равное нулю, то в левом верхнем углу любой матрицы Аh находится
ahx1 = 0.
Поэтому формула десятков (7) для пути, начинающегося в левом верхнем углу матрицы Аh имеет вид
ahxb = ind((hx1), (hxb)).
Таким образом, для определения числа десятков результата умножения (hxb) достаточно пройти в матрице Аh по пути из левого верхнего угла в ячейку (hxb) и подсчитать число пересечений границ.
Границы десятков при умножении на нечетные числа 1, 3, 7, 9. Матрица умножения на 1 границ не имеет. Границы матрицы умножения на 3 состоят только из регулярных горизонтальных линий (фиг.3). Границы матрицы умножения на 7 имеют двойные регулярные горизонтальные линии и одиночные вертикальные линии (фиг. 3). Границы матрицы умножения на 9 состоят из тройных регулярных горизонтальных линий и одиночных вертикальных линий (фиг. 3).
Границы десятков при умножении на четные числа 2, 4, 6, 8. Матрица умножения на 2 регулярных границ не имеет, нерегулярная граница определяются областью "чудес" U2 (фиг.3). Матрица умножения на 4 имеет однократные горизонтальные регулярные границы и однократные вертикальные регулярные границы. Нерегулярная граница области "чудес" определяется поворотом U2 по часовой стрелке на 90o (фиг.3), что можно записать в виде
U4=T1(U2).
Поскольку левый верхний угол матрицы умножения на 4 лежит в области "чудес" то нерегулярная граница при ее пересечении в положительном направлении сверху вниз или слева направо дает минус 1 в формуле десятков умножения на 4.
Матрица умножения на 6 имеет двукратные горизонтальные регулярные границы, нерегулярная границы области "чудес" определяется поворотом U2 против часовой стрелки на 90o (фиг. 3), что можно записать в виде
U6=Т-1(U2).
Матрица умножения на 8 имеет трехкратные горизонтальные регулярные границы и однократные вертикальные регулярные границы, нерегулярная границы области "чудес" определяется поворотом U2 на 180o (фиг. 3), что можно записать в виде
U8=Т2(U2).
Как и в случае 4, поскольку левый верхний угол матрицы умножения на 8 лежит в области "чудес", то нерегулярная граница при ее пересечении в положительном направлении сверху вниз или слева направо дает минус 1 в формуле десятков умножения на 8.
Границы десятков при умножении на 5. Граница перехода десятков в матрице умножения на 5 отличается по виду от других таблиц. Кратность границ в матрице умножения на 5 следует определить как прирост числа десятков при переходе в соседнюю ячейку (фиг.3).
Пиктограммы для подсчета числа десятков результата умножения как индекса пересечения границ. Заданные на матрице десятков Аh границы позволяют кратко в графическом виде обозначить правила получения числа десятков для каждой таблицы умножения в виде специальных пиктограмм.
Пиктограммы состоят из конечного набора повторяющихся элементов:
для правила определения десятков, связанного с подсчетом топологической характеристики количества пересечений путей с границами, используются изображения эквивалентные следующим: "стрелка вниз", "стрелка направо", "граница с плюсом", "граница с минусом" и "кратная граница";
для правила определения единиц, связанного с поворотами матрицы единиц на 90o, используются изображения эквивалентные следующим: "вращение направо", "вращение налево" (фиг. 4).
Частный случай представления таблицы умножения на четные цифры в виде матрицы размера (5х3).
Для облегчения запоминания правил десятков при обучении умножению на четные цифры можно предложить вариант расположения таблиц умножения в симметричном виде в матрице размера (5х3) (фиг.5).
В данном представлении ячейка 4 перенесена в конец верхнего ряда, а ячейка 6 - в начало нижнего ряда. В этом варианте затруднительно проследить вид области "чудес" в том виде, как в таблицах размещения (3х3). Здесь имеется повторяемость единиц в верхнем и нижнем ряду.
Представление таблиц умножения в форме восьмиугольника. Еще одним из способов симметричного представления результатов таблицы умножения является расположение ячеек в каждой таблице Мh (1) и/или всего девятилистника (2) в форме восьмиугольника (фиг.6). Подобный восьмиугольный цветок полностью стирает различие между углом и стороной "квадрата" девятилистника (2), делая их равноправными.
Топологическая модель девятилистника. Формула десятков, приведенная в (7), не позволяет перейти от таблицы умножения на h в таблицу умножения на другое число g. Эту проблему решает построение единой топологической модели таблицы умножения для всего девятилистника, которая может быть построена в форме графа, содержащего вершины и ребра.
Топологическая модель-изображение для таблицы умножения в форме девятилистника состоит из ячеек таблиц с результатами. В каждой вершине графа находится только один результат умножения двух сомножителей (axb)=(bxa). Таким образом, ячейка (axb), которая находится в таблице умножения Та на сомножитель а, отождествляется с ячейкой (bxa), которая находится в таблице умножения Тb на сомножитель b.
Ближайшие друг к другу "точки" в топологический модели девятилистника определяются выбранными критериями близости ячеек в локальных топологиях каждой из таблиц Тa и Тb. На плоскости симметричное расположение результатов умножения в графовой структуре может иметь вид, представленный на фиг 7. Отклонение от симметрии имеется только для четырех результатов (1х9), (3х7), (2х8), (4х6), которые должны находиться вне основной плоскости модели рядом с вершиной (5,5).
В построенной модели между любыми парами результатов умножения можно найти соединяющий их путь по ребрам топологического девятилистника. Поскольку каждая точка имеет несколько соседей, путей между двумя фиксированными точками несколько, однако, результат не зависит от вида пути.
Формула десятков на девятилистнике может быть выражена в более общем виде, чем формула (7) для одной таблицы умножения:
agxb = ahxc + ind((hxc), (gxb)
Системообразующие принципы симметрии и дополнения.
Результат, объединяющий в единую систему построенную выше модель девятилистника для таблицы умножения, принципы дополнения и симметрии, заключается в следующей теореме, которая может быть доказана строго математически:
В модели девятилистника принцип симметрии поворотов единиц результатов умножения и принцип дополнения десятков результатов умножения однозначно определяют всю таблицу умножения.





Способ обучения и модель таблицы умножения предназначены для обучения устному счету при умножении на однозначные цифры А от 1 до 9 и позволяют явно указать зависимости и симметрии для всех исходных данных и результатов. Девять таблиц умножения Тa расположены на плоскостях в форме девятилистника - ячейки каждой из таблиц Тa центрально-симметричны относительно центра (Ах5) и все ячейки таблиц Тa и Т10-a центрально-симметричны относительно общего центра (5х5) в центральной таблице Т5 Единицы результатов умножения на 1,3,7,9 являются поворотами на 90o единиц результатов умножения на 1. Единицы результатов умножения на 2,4,6,8 могут являться поворотами на 90o или на 180o единиц результатов умножения на 2. Модель таблицы умножения допускает представление в виде симметричной графовой конструкции, содержащей вершины и ребра. Способ обучения умножению заключается в использовании поворотов плоскостей для указания симметрично расположенных совмещаемых пар ячеек, у которых сумма единиц как и сумма десятков результатов умножения образуют функциональные зависимости. Число десятков результатов умножения может определяться способом пошагового подсчета пересекаемых границ десятков на девятилистнике. 2 с. и 4 з.п.ф-лы, 8 ил.
ehxb + ehx(10-b) = 0(mod10),
и десятки результатов умножения ahxb и ahx(10-b) удовлетворяют формуле
ahxb+ ahx(10-b) = h-1 + V(h,b),
где функция V(h,b) зависит от чисел h и b и равна 1, если hxb = 0(mod10) и V(h,b) равна 0 в остальных случаях.
ehxb = e(10-h) x(10-b).
ahxb = ahxc + ind [(hxb), (hxc)],
где индекс пути ind равен числу пересечений границ десятков в матрицах Mh.
| DE 3338646 A1, 02.05.85 | |||
| Приспособление к счетам для умножения и деления | 1948 |
|
SU80266A1 |
| Новый вариант белка семейства транспортера цианата и способ получения L-триптофана с его применением | 2021 |
|
RU2797499C1 |
| СПОСОБ ПОДГОТОВКИ К ХРАНЕНИЮ ТОМАТОВ СВЕЖИХ СПЕЦИАЛЬНОГО НАЗНАЧЕНИЯ | 2006 |
|
RU2322005C1 |
Авторы
Даты
1999-10-10—Публикация
1999-02-26—Подача