Область техники, к которой относится изобретение
Изобретение относится к медицине, а именно к кардиологии, сердечно-сосудистой хирургии и функциональной диагностике (клинической физиологии), и предназначено для проведения диагностической процедуры - неинвазивного электрофизиологического исследования сердца. Более точно, изобретение предназначено для реконструкции динамики электрического поля сердца во внутренних точках грудной клетки, в частности, для получения внутрипищеводных и эпикардиальных электрограмм, а также для осуществления активационного эпикардиального картирования - получения эпикардиальных изопотенциальных и изохронных карт (паттернов активации миокарда) неинвазивным путем, т.е. без введения регистрирующих устройств в камеры сердца, полость перикарда, полость пищевода и т.п.
Уровень техники
Основным методом диагностики электрофизиологических процессов сердца, рутинно использующимся в клинической практике, является электрокардиография (ЭКГ) в 12 стандартных отведениях. Простота и низкая себестоимость в сочетании с относительно высокой информативностью стандартного электрокардиографического исследования привела к чрезвычайно широкому его использованию в повседневной практике.
Однако электрокардиографический метод имеет принципиальные ограничения. Активность определенных отделов миокарда незначительно отражается в электрокардиографических сигналах, зарегистрированных в стандартных отведениях. Примером является трудность ЭКГ-диагностики инфаркта миокарда заднебазальных отделов левого желудочка. Кроме того, согласно принципу суперпозиции в электродинамике, электрокардиограмма является суммой электрических потенциалов, возникающих от источников во множестве точек миокарда. Так как электрофизиологические процессы в различных участках сердечной мышцы протекают одновременно, по стандартным ЭКГ-отведениям весьма сложно определить локальную электрическую активность миокарда. Например, волна реполяризации предсердий у человека в условиях нормального ритма не выявляется на ЭКГ, так как она "скрыта" высокоамплитудным комплексом QRS, отражающим деполяризацию желудочков. Аналогичными ограничениями характеризуется и метод векторэлектрокардиографии.
Более широкими возможностями обладает метод поверхностного электрокардиографического картирования грудной клетки. Метод заключается в синхронной регистрации множества (от 40 до 250 и более) однополюсных ЭКГ-отведений с поверхности грудной клетки и построении путем интерполяции для каждого момента времени кардиоцикла карт распределения электрического потенциала на поверхности грудной клетки.
Однако указанный метод не позволяет точно определять локальную электрическую активность миокарда. Если электрод расположен на поверхности грудной клетки, вклады в ЭКГ-сигнал от ближайшего и наиболее удаленного по отношению к регистрирующему электроду сегмента миокарда отличаются примерно на один порядок. Для электрода, помещенного на поверхность сердца, это различие составляет три порядка. В связи с этим для выявления локальной электрической активности сердца используют методы инвазивной регистрации ЭКГ, стремясь максимально приблизить электроды к поверхности сердца.
Чреспищеводное электрофизиологическое исследование сердца основано на введении зонда с регистрирующими электродами в полость пищевода. Пищевод на определенном участке достаточно плотно прилежит к задней стенке левого предсердия и задней стенке левого желудочка, поэтому внутрипищеводные ЭКГ-сигналы избирательно регистрируют активность этих отделов сердца. Внутрипищеводная электрокардиография применяется, в частности, для дифференциальной диагностики наджелудочковых и желудочковых аритмий (Чреспищеводная электрическая стимуляция сердца /Под ред. В.А.Сулимова, В.И.Маколкина. - М.: Медицина, 2001. - 208 с.).
Однако указанный метод позволяет выявить локальную электрическую активность лишь отдельных сердечных структур.
Для комплексной оценки электрофизиологических процессов сердца и топической диагностики нарушений сердечного ритма используется инвазивное электрофизиологическое исследование сердца, основанное на прямой регистрации комплекса электрограмм с эпикардиальной или эндокардиальной поверхности сердца. Указанные методы могут применяться на «открытом сердце» в условиях торакотомии, а также на основе интервенционных технологий введения регистрирующих устройств (катетеров) в полости сердца чрессосудистым доступом или в полость перикарда путем его чрескожной пункции под флюороскопическим контролем.
Современные реализации указанных методов предусматривают точное определение трехмерных координат регистрирующих электродов нефлюороскопическими методами и визуализацию результатов в виде изопотенциальных и изохронных карт на моделях отделов сердца средствами компьютерной графики. Компьютерные модели отделов сердца строятся по множеству точек регистрации электрограмм с известными координатами, а также на основе данных компьютерной (КТ) или магнитно-резонансной (МРТ) томографии сердца (Ревишвили А.Ш., Рзаев Ф.Г., Джетыбаева С.К. Электрофизиологическая диагностика и интервенционное лечение сложных форм нарушения ритма сердца с использованием системы трехмерного электроанатомического картирования. - Вестник аритмологии 2004; 34:32-37; Покушалов Е.А., Туров А.Н., Шугаев П.Л., Артеменко С.Л. Радиочастотная аблация желудочковой тахикардии трансперикардиальным доступом. - Вестник аритмологии. 2006; 44: 58-62).
К этой же группе относятся способы бесконтактного эндокардиального картирования, основанные на введении в полости сердца «плавающего» баллонного катетера, регистрации комплекса электрограмм на его поверхности и реконструкции вычислительным путем по полученным данным эндокардиальных электрограмм (Schilling R.J., Kadish А.Н., Peters N.S. et al. Endocardial mapping of atrial fibrillation in the human right atrium using a non-contact catheter. - European Heart Journal. 2000; 21: 550-564).
Недостатком указанных способов, преодолеваемым в настоящем изобретении, является их инвазивный характер.
Аналогами изобретения являются способы реконструкции электрограмм во внутренних точках грудной клетки вычислительным путем по данным синхронной регистрации комплекса ЭКГ на поверхности грудной клетки.
Указанные способы основаны на решении обратной задачи электрокардиографии. Постановка обратной задачи электрокардиографии (ОЗ ЭКГ) сформулирована в работах (Барр Д., Спек М. Решения обратной задачи, выраженные непосредственно в форме потенциала //Теоретические основы электрокардиологии: Пер. с англ. /Под ред. К.В.Нельсона и Д.В.Гезеловица. - М.: Медицина, 1979. - С.341-352; MacLeod R.S., Brooks D.H. Recent progress in inverse problem in electrocardiology// IEEE Eng. in Med. Bio. Mag. 17:1, pp.78-83, Jan. 1998; Rudy Y., Messinger-Rapport B.J. The inverse problem in electrocardiography: Solutions in terms of epicardial potentials. CRC Crit. Rev. Biomed. Eng. 1988; 16: 216-268).
ОЗ ЭКГ с математической точки зрения является задачей гармонического продолжения потенциала в сторону источников, т.е. задачей Коши для уравнения Лапласа. Расчетной областью, в которой задается уравнение Лапласа, является часть грудной клетки, ограниченная внешней поверхностью сердца, поверхностью грудной клетки, на которой доступна регистрация ЭКГ и воображаемыми поперечными сечениями грудной клетки на уровне диафрагмы и ключиц.
На части поверхности грудной клетки, где доступна регистрация ЭКГ, задаются полученные в результате ЭКГ-картирования значения электрического потенциала, а также условие равенства нулю нормальной производной потенциала. Эти данные составляют условия Коши.
Задача Коши заключается в нахождении потенциала электрического поля в указанной области и его следа на поверхности сердца и поперечных сечениях грудной клетки таким образом, чтобы потенциал в расчетной области удовлетворял уравнению Лапласа, а на поверхности торса, где доступна регистрация ЭКГ - условиям Коши.
Задача Коши для уравнения Лапласа является некорректно поставленной по Адамару: сколь угодно малые погрешности условия могут привести к произвольно большим погрешностям решения. При решении задачи Коши для уравнения Лапласа необходимо применять специальные, т.н. регуляризирующие алгоритмы (Денисов A.M. Введение в теорию обратных задач. - М.: Изд-во Моск. ун-та, 1994; Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. - М.: Наука, 1986. - 312 с.).
Решить задачу Коши для уравнения Лапласа в указанной постановке (обратную задачу электрокардиографии) аналитическим способом не представляется возможным. Поэтому обратная задача электрокардиографии решается численно средствами вычислительной математики с использованием компьютерной техники.
Один из способов решения обратной задачи электрокардиографии - метод реконструкции электрического поля на «квазиэпикарде» - условной сферической поверхности, окружающей сердце. С математической точки зрения метод основан на представлении потенциала электрического поля сердца в виде гармонического полинома (шаровой функции), коэффициенты которого находятся из условия равенства (или минимума среднеквадратичного отклонения) значений полинома и значений ЭКГ-сигнала в точках его регистрации с учетом равенства нулю нормальной производной потенциала на поверхности грудной клетки. Для обеспечения устойчивости решения используется полином не выше 4 степени. Способ обладает существенным недостатком: при уменьшении радиуса сферы, т.е. по мере приближения поверхности «квазиэпикарда» к реальной поверхности сердца точность реконструкции потенциала резко падает. При приближении поверхности квазиэпикарда к поверхности грудной клетки снижается разрешающая способность метода в плане выявления локальной электрической активности миокарда (Титомир Л.И., Кнеппо П. Математическое моделирование биоэлектрического генератора сердца. - М.: Наука. Физматлит, 1999. - 448 с.; Титомир Л.И., Трунов В.Г., Айду Э.А.И. Неинвазивная электрокардиотопография. - М.: Наука, 2003. - 198 с.).
Для решения граничных задач для уравнения Лапласа широко используются методы интегральных уравнений теории потенциала, в англоязычной литературе более известные как методы граничных элементов (Бреббия К., Теллес Ж., Вроубел Л. Методы граничных элементов. - Пер. с англ. М.: Мир, 1987). Данный подход для решения ОЗ ЭКГ предложен в работах Е.Таккарди, Р.Плонзи, Р.Барра (Барр Д., Спек М. Решения обратной задачи, выраженные непосредственно в форме потенциала // Теоретические основы электрокардиологии: Пер. с англ. / Под ред. К.В.Нельсона и Д.В.Гезеловица. - М.: Медицина, 1979.- С.341-352). Указанные методы, в частности, предполагают представление поверхностей сердца и торса в виде полигональных поверхностей, т.е. разбиение граничных поверхностей на множество треугольных элементов. Согласно методу граничных элементов ОЗ ЭКГ для однородной модели грудной клетки сводится к решению системы двух интегральных уравнений Фредгольма I и II рода, которая приближенно заменяется системой матрично-векторных уравнений

где Ai,j - известные матрицы, х1, х2 - неизвестные векторы, имеющие смысл искомых значений потенциала и его нормальных производных в узлах триангуляционных сеток, аппроксимирующих поверхности сердца и поперечных сечений торса, с1, с2 - известные векторы, рассчитываемые по известным данным задачи.
В способе неинвазивного эпикардиального картирования, предложенном В.В. Шакиным и соавт., использовался следующий алгоритм решения ОЗ ЭКГ.
Система матрично-векторных уравнений (1) путем тождественных преобразований сводилась к системе линейных алгебраических уравнений, которая разрешалась в явном виде

где ФН - неизвестный вектор, имеющий смысл искомых значений потенциала в узлах триангуляционных сеток, аппроксимирующих поверхности сердца и поперечных сечений торса, ZHB - известная матрица, ФB - известный вектор. Для вычисления матрицы ZHB необходимо использовать процедуру обращения матриц, входящих в систему (1), причем одна из обращаемых матриц является неквадратной и плохо обусловленной. Для выполнения указанной процедуры использовалось построение псевдообратной матрицы Мура-Пенроуза на основе SVD-разложения исходной матрицы и замена нулями малых сингулярных чисел.
Поверхности сердца торса представлялись упрощенными моделями в виде цилиндрической и эллипсоидальной поверхностей, строившихся на основе рентгенографии грудной клетки в двух проекциях. Результаты картирования в виде изопотенциальных и изохронных карт накладывались на модельные схемы-развертки отделов сердца. Методика применялась для выявления локализации ДПП при манифестирующем синдроме WPW и эктопических источников при желудочковой экстрасистолии (Щакин В.В. Вычислительная электрокардиография. - М.: Наука, 1980).
В работах В.В.Шакина указывалось на перспективность применения компьютерно-томографических методик для точного построения поверхностей торса и сердца, однако из-за недостаточного развития методов компьютерной томографии сердца этот подход не применялся.
Наиболее близким к заявляемому способу (прототип) является методика неинвазивного электрокардиографического картирования (Noninvasive Electrocardiographic Imaging, ECGI).
В указанном способе поверхностное картирование осуществляется с использованием 224 однополярных электродов, размещенных на специальном жилете, который надевается на пациента во время исследования. Поверхности торса и сердца определяются на основе компьютерной или МРТ-томографии грудной клетки. Алгоритм реконструкции основан на решении обратной задачи электрокардиографии методом граничных элементов.
Поверхности сердца и торса в приближенно представляются в виде полигональных поверхностей. Для решения ОЗ ЭКГ также используется система матрично-векторных уравнений (1), которая путем элементарных преобразований сводится к системе линейных алгебраических уравнений

где х - неизвестный вектор, имеющий смысл искомых значений потенциала в узлах триангуляционных сеток, аппроксимирующих поверхности сердца и поперечных сечений торса, А - известная матрица, с - известный вектор.
Система линейных алгебраических уравнений (3) является плохообусловленной. Для ее решения используется метод регуляризации А.Н.Тихонова и метод итерационной регуляризации на основе GMRes-алгоритма. Метод Тихонова основан на решении вместо системы (3) системы

где AT- матрица, транспонированная по отношению к матрице А, Е - единичная матрица, α - параметр регуляризации (малое положительное действительное число).
Метод итерационной регуляризации основан на решении системы (3) методом последовательных приближений с ограничением числа итераций на основе GMRes-алгоритма, относящегося к группе методов подпространств Крылова (Ramanathan С., Ghanem, R.N., Jia P., Ryu К., Rudy Y. Electrocardiographic Imaging (ECGI): A Noninvasive Imaging Modality for Cardiac Electrophysiology and Arrhythmia// Nature Medicine, 2004; 10:422-428; Rudy Y, Ramanathan C., Ghanem R.N., Jia P. System and method for noninvasive electrocardiographic imaging (ECGI) using generalized minimum residual (GMRES) //United states patent №7016719 B2, 2006).
Аналогичный способ использовался в работе (Berger Т., Fisher G., Pfeifer В. et all. Single-Beat Noninvasive Imaging of Cardiac Electrophysiology of Ventricular Pre-Exitation/J.Am.Coll.Cardiol, 2006; 48: 2045-2052).
Способ применялся для выявления локализации Дополнительных проводящих путей (ДПП) при манифестирующем синдроме WPW, эктопических источников при желудочковой экстрасистолии и тахикардии, реконструкции динамики активации миокарда при трепетании предсердий.
Существенным недостатком рассмотренного способа является использование модели грудной клетки с постоянным коэффициентом удельной электропроводности. Удельная электропроводность различных органов и тканей грудной клетки существенно различается. Переменный коэффициент электропроводности биологических тканей оказывает достаточно большое влияние на электрическое поле сердца в грудной клетке, что подтверждается данными экспериментальных исследований (Rudy Y., Wood R., Plonsey R., Liebman J. The effect of high lung conductivity on electrocardiographic potentials. Results from human subjects undergoing bronchopulmonary lavage // Circulation 1982; 65: 440-445). Наибольшую роль играет различие электропроводности легких и окружающих мягких тканей (в 4-5 раз). Потенциалы электрического поля сердца модельных источников, рассчитанные для однородной и неоднородной моделей грудной клетки, различаются на 15%-20% (Титомир Л.И., Кнеппо П. Математическое моделирование биоэлектрического генератора сердца. - М.: Наука. Физматлит, 1999. - 448 с.). Таким образом, пренебрежение электрической неоднородностью тканей грудной клетки приводит к большим погрешностям реконструкции электрического поля сердца.
Целью настоящего изобретения является повышение точности неинвазивного электрофизиологического исследования сердца за счет учета различного коэффициента электропроводности тканей грудной клетки.
Сущность изобретения
Для проведения электрофизиологического исследования сердца необходима регистрация комплекса электрограмм с поверхности сердца, на основе которых строятся изопотенциальные, изохронные карты и осуществляется диагностика электрофизиологических процессов в сердечной мышце. Для получения электрограмм используется инвазивный путь - введение специальных регистрирующих устройств в камеры сердца или полость перикарда.
Сущность настоящего изобретения состоит в том, что электрограммы, экспериментальная регистрации которых требует инвазивного доступа, реконструируются вычислительным путем по однополюсным ЭКГ, записанным в 80 и более точках поверхности грудной клетки. По набору поверхностных электрокардиограмм для каждого дискретного момента времени кардиоцикла определяются значения потенциала электрического поля сердца в точках записи ЭКГ и путем интерполяции рассчитывается значение потенциала электрического поля в каждой точке поверхности грудной клетки. По данным какой-либо визуализационной методики (компьютерная томография (КТ), магнитно-резонансная томография (МРТ)) определяются границы поверхностей грудной клетки, эпикардиальной поверхности сердца и крупных анатомических структур грудной клетки, а также средние значения удельной электропроводности ткани органов грудной клетки.
Далее вычислительным путем на основе решения задачи Коши для уравнения Лапласа в неоднородной среде осуществляется продолжение потенциала электрического поля на всю область грудной клетки вплоть до эпикардиальной поверхности сердца. Для решения задачи Коши для уравнения Лапласа используется модель грудной клетки, ткани которой в пределах крупных анатомических структур (легкие, средостение, позвоночник) имеют усредненный постоянный коэффициент удельной электропроводности. При этом потенциал электрического поля сердца в каждой из областей с постоянным коэффициентом электропроводности является гармонической функцией, а на границе областей удовлетворяет условиям сопряжения (непрерывности потенциала и тока).
Для решения задачи Коши для уравнения Лапласа используется метод граничных элементов, на основе которого исходная задача сводится к задаче решения системы матрично-векторных уравнений. Для повышения точности способа применяется итерационный алгоритм решения системы матрично-векторных уравнений. На каждом шаге итерационной процедуры решается система линейных алгебраических уравнений (СЛАУ) на основе регуляризирующих алгоритмов. Для выполнения операции матрично-векторного умножения применяется «быстрый мультипольный метод», позволяющий существенно увеличить скорость вычислений для матриц большой размерности.
Описанную выше последовательность процедур повторяют для каждого момента времени кардиоцикла. По полученным значениям потенциала в заданных внутренних точках грудной клетки путем интерполяции реконструируют требуемые электрограммы. На основе реконструированных электрограмм строятся изопотенциальные, изохронные карты на реалистичных моделях сердца, реконструируется динамика возбуждения миокарда и осуществляется диагностика электрофизиологических процессов в сердечной мышце.
Краткое описание иллюстраций
Фиг.1 иллюстрирует общую схему способа.
На фиг.2 представлена схема методики поверхностного картирования ЭКГ.
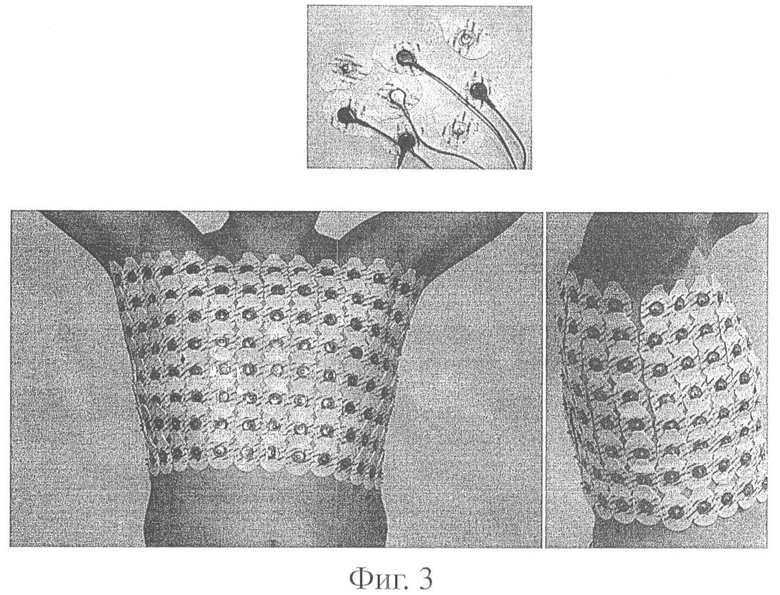
Фиг.3 иллюстрирует схему наложения электродов на поверхность грудной клетки.
На фиг.4 представлены основные этапы компьютерной обработки информации.
Фиг.5 иллюстрирует обработку ЭКГ-сигналов в процессе ЭКГ картирования в режиме реального времени. На верхнем рисунке показаны сетевые наводки, на нижнем рисунке - мышечные наводки. Фиг 5. (продолжение). На верхнем рисунке показан дрейф изолинии, на нижнем рисунке - результирующий отфильтрованный сигнал.
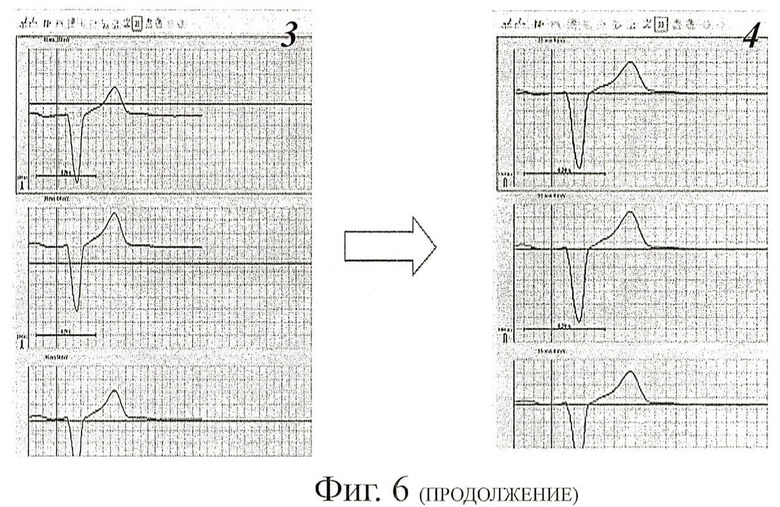
Фиг.6 иллюстрирует ретроспективную обработку ЭКГ-сигналов.
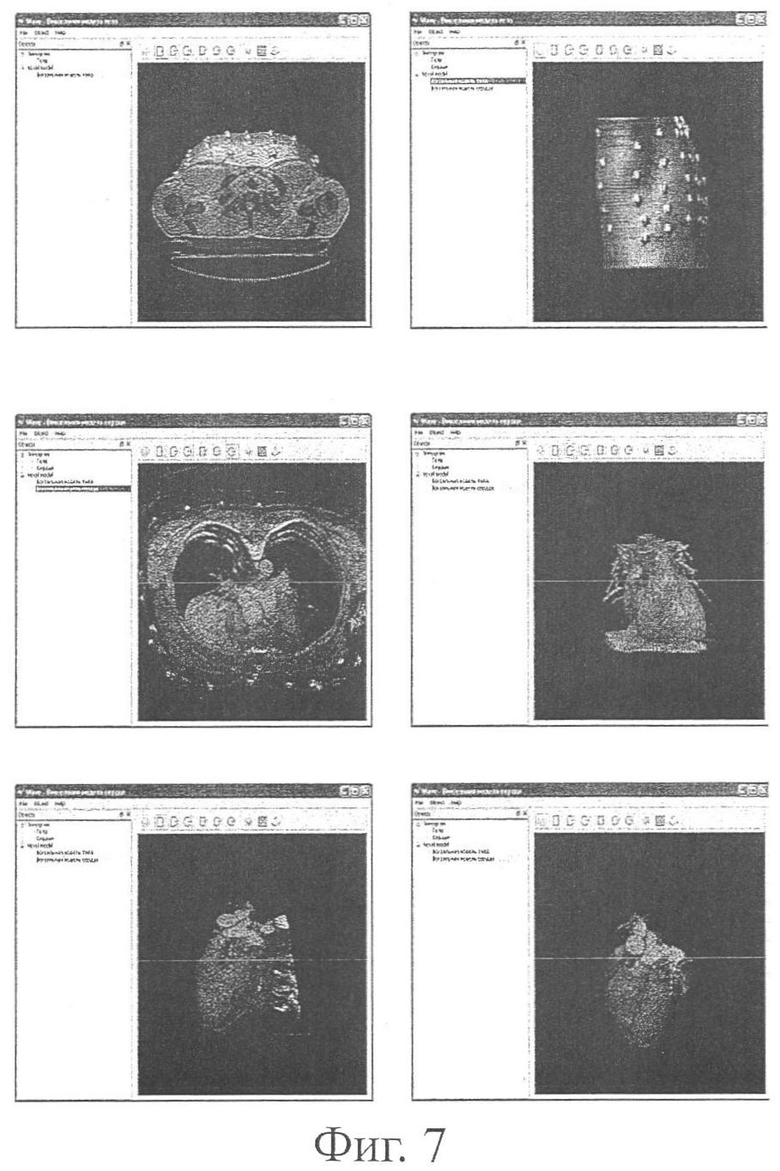
На фиг.7 показано построение вексельной модели торса, сердца и легких в редакторе вексельной графики.
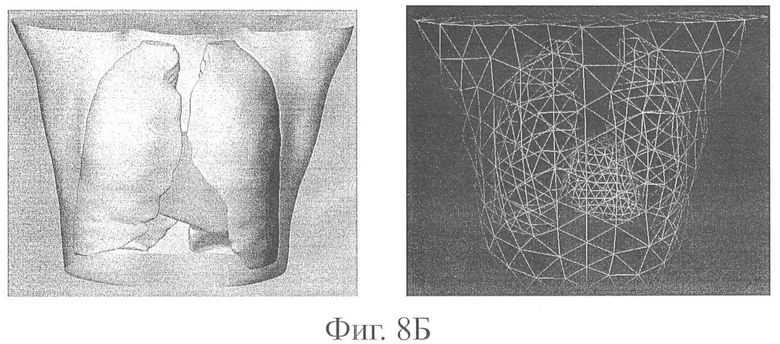
Фиг.8 иллюстрирует построение полигональных поверхностей (триангуляционных сеток) торса, сердца (8а) и легких (8б) на основе вексельных моделей. Фиг 8А. В левом столбце показаны этапы построения полигональной сетки сердца: исходная сетка (350 тыс.элементов), реконструированная сетка (20 тыс.элементов), разреженная сетка (3 тыс.элементов). В правом столбце показаны этапы построения полигональной сетки торса: исходная сетка (900 тыс.элементов), реконструированная сетка (20 тыс.элементов) и разреженная сетка (3 тыс.элементов).
На фиг.9 показано автоматическое определение координат электродов по данным КТ или МРТ грудной клетки.
На фиг.10 представлены изопотенциальные карты на поверхности торса.
Фиг.11 иллюстрирует геометрические соотношения грудной клетки, использующиеся в методе граничных элементов.
На фиг.12 приведена блок-схема вычислительного алгоритма решения обратной задачи электрокардиографии на основе итерационного алгоритма.
На фиг.13 приведены графики сходимости итерационного алгоритма с использованием регуляризации Тихонова. На верхнем рисунке показана сходимость алгоритма без уточнения параметра регуляризации α на каждом шаге итерационной процедуры. На нижнем рисунке показана сходимость алгоритма с уточнением параметра регуляризации α на каждом шаге итерационной процедуры.
На фиг.14 приведены графики погрешностей реконструкции электрического поля для однородной и кусочно-однородной моделей грудной клетки в сравнении с точными данными.
На фиг.15 представлены изопотенциальные карты реконструированного электрического поля сердца для кусочно-однородной модели грудной клетки на поперечных и фронтальных сечениях торса.
На фиг.16 приведены результаты реконструкции электрического поля на поверхности сердца для однородной и неоднородной моделей грудной клетки в сравнении с точными данными.
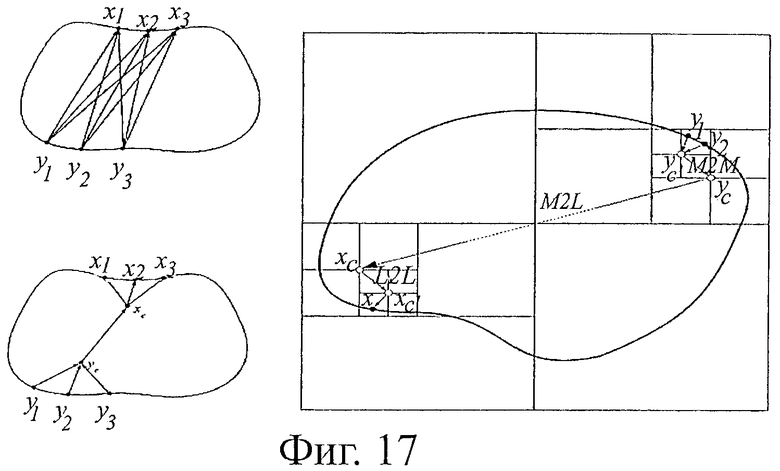
Фиг.17 иллюстрирует основные принципы «быстрого мультипольного метода». В левом столбце сверху показана схема операций при реализации классического ВЕМ, снизу - схема операций при реализации FMM ВЕМ. В правом столбце изображена схема иерархического разбиения пространства и детали реализации метода FMM ВЕМ. Фиг.17 (продолжение). На рисунке приводится сравнение времени выполнения классического алгоритма ВЕМ и FMM ВЕМ.
На фиг.18 представлены примеры визуализации результатов неинвазивного электрофизиологического исследования сердца.
На фиг.19 представлен пример топической диагностики аритмогенного источника.
Подробное описание
Чтобы обеспечить полное понимание изобретения, далее будут описаны конкретные иллюстративные его воплощения, однако специалисту в данной области должно быть ясно, что системы и методы могут быть модифицированы в пределах, не выходящих за рамки описанных в формуле изобретения.
Раскрытые методы и системы используют устройство поверхностного картирования ЭКГ, визуализационную технику компьютерной (КТ) или магнитно-резонансной (МРТ) томографии, вычислительную технику, а также математические алгоритмы решения обратной задачи электрокардиографии для неинвазивной реконструкции электрограмм во внутренних точках грудной клетки и на эпикардиальной поверхности сердца и для построения изопотенциальных и изохронных эпикардиальных карт на реалистичной трехмерной компьютерной модели сердца.
Фиг.1 иллюстрирует общую схему способа. Способ включает регистрацию от 80 до 240 однополюсных ЭКГ на поверхности грудной клетки (1), проведение КТ или МРТ грудной клетки (2), обработку данных поверхностного картирования ЭКГ и КТ (МРТ) средствами вычислительной техники (3) и представление полученной электрофизиологической информации методами компьютерной графики (4).
Фиг.2 иллюстрирует схему методики поверхностного картирования ЭКГ. Устройство картирования включает цифровой многоканальный электрокардиограф (1), соединенный с персональным компьютером (2). Цифровой многоканальный электрокардиограф позволяет регистрировать ЭКГ-сигналы в 12 стандартных отведениях и до 240 однополюсных отведениях с поверхности грудной клетки.
Фиг.3 иллюстрирует схему наложения электродов. Для поверхностного картирования ЭКГ используются одноразовые металлические хлор-серебряные электроды (1) (при компьютерной томографии) или одноразовые графитовые электроды (при магнитно-резонансной томографии). Электроды накладываются в виде 5-8 горизонтальных поясов, расположенных на одинаковых расстояниях по вертикали. Верхний пояс располагается на уровне грудинно-ключичного сочленения, нижний пояс - на уровне нижнего края реберной дуги. Каждый пояс включает от 16 до 30 электродов, расположенных на одинаковых расстояниях по окружности грудной клетки (2).
Фиг.4 иллюстрирует основные этапы компьютерной обработки информации. Первый этап (1) - обработка ЭКГ-сигналов в режиме реального времени в процессе многоканальной регистрации ЭКГ с поверхности грудной клетки. Второй этап (2) - ретроспективная обработка ЭКГ-сигналов. Третий этап (3) - построение вексельных моделей грудной клетки, сердца и его отделов по данным КТ или МРТ. Четвертый этап (4) - построение полигональных поверхностей грудной клетки, сердца и его отделов. Пятый этап (5) - автоматическое определение координат регистрирующих электродов на поверхности грудной клетки по данным КТ или МРТ. На шестом этапе (6) осуществляется поверхностная интерполяция значений ЭКГ-сигналов поверхностного картирования в каждый момент времени и построение изопотенциальных карт на поверхности грудной клетки. Седьмой этап (7) включает вычислительную реконструкцию потенциала электрического поля сердца во внутренних точках грудной клетки и на эпикардиальной поверхности сердца. На последнем этапе осуществляется реконструкция эпикардиальных электрограмм (8) и построение средствами компьютерной графики эпикардиальных изопотенциальных, изохронных карт (9) на реалистичной компьютерной модели сердца и визуализация динамики электрофизиологических процессов миокарда в анимационном режиме (propagation mapping) (10).
Фиг.5 иллюстрирует обработку ЭКГ-сигналов в процессе ЭКГ картирования в режиме реального времени. Регистрируемые ЭКГ-сигналы отображаются на дисплее компьютера. Оператор контролирует качество ЭКГ-сигнала в каждом из отведений, при необходимости используется программное подавление сетевых (1) и мышечных (2) наводок и дрейфа изолинии (3). Также осуществляется автоматический контроль контакта электрода с кожей и правильности наложения электродов на основе спектрального и взаимно-корреляционного анализа сигналов ЭКГ. Результатом первого этапа являются оцифрованные и отфильтрованные значения ЭКГ-сигналов в 80-240 однополюсных отведений с поверхности грудной клетки и в 12 стандартных отведениях длительностью до 30 минут.
Фиг.6 иллюстрирует ретроспективную обработку ЭКГ-сигналов.
Оператор просматривает зарегистрированные ЭКГ-сигналы и выбирает для дальнейшей обработки один или несколько кардиоциклов (1, 2). Далее осуществляется приведение ЭКГ к единой изолинии (3, 4): оператор на одной из ЭКГ выбирает интервал времени τ, в пределах которого ЭКГ-сигнал совпадает с изолинией (как правило, этот интервал принадлежит сегменту PQ). Коррекция ЭКГ-сигналов осуществляется по формуле

где U0(t) - корригированный ЭКГ-сигнал, U(t)-исходный ЭКГ-сигнал, u0 - среднее значение исходного ЭКГ-сигнала на интервале времени τ.
После чего оператор выбирает интересующий фрагмент кардиоцикла для дальнейших расчетов.
Фиг.7 иллюстрирует построение вексельной модели торса и сердца в редакторе вексельной графики.
По данным КТ или МРТ грудной клетки и сердца осуществляется вексельный рендеринг анатомических структур грудной клетки. Для этой цели используется алгоритм факторизации «сдвиг-деформация» для преобразования просмотра (Shear-Warp Factorization of the Viewing Transformation), относящийся к группе методов преобразования растровой строки (a scanline-order volume rendering algorithm).
Концепция используемого метода вексельного рендеринга заключается в трех основных шагах (Philippe Lacroute Fast Volume Rendering Using a Shear-Warp Factorization of the Viewing Transformation. - Ph.D. dissertation. Technical Report CSL-TR-95-678, Stanford University, 1995).
На первом шаге объемные данные преобразуются сдвиговой матрицей в соответствующее объектное пространство. При этом каждый параллельный срез объемных данных после преобразования проходит через специальный фильтр для снижения искажений.
На втором шаге из набора отфильтрованных и сдвинутых срезов совместно путем их наложения в прямом порядке формируется промежуточное 2D изображение в том же сдвиговом пространстве.
На третьем шаге полученное промежуточное 2D изображение переводится в нормальное пространство изображения с использованием матрицы деформации и далее проходит опять через фильтр для формирования финального изображения.
Оператор, пользуясь инструментами вексельного редактирования, подготавливает вексельную модель торса, сердца или одной из его структур.
Фиг.8 иллюстрирует построение полигональных поверхностей (триангуляционных сеток) торса, сердца и легких на основе вексельных моделей.
На основе полученных вексельных моделей автоматически строятся полигональные поверхности, состоящие из объединения плоских треугольников. Исходные данные представляют собой трехмерное скалярное поле плотностей в вексельном представлении, т.е. трехмерную прямоугольную сетку, в узлах которой заданы значения условных плотностей тканей грудной клетки. Построение триангуляционных сеток торса и органов грудной клетки представляет собой построение полигональных поверхностей, которые наиболее близким образом повторяют поверхности указанных структур, заданных определенным уровнем плотности.
Процедура построения полигональных поверхностей включает следующие этапы:
- фильтрация исходных вексельных моделей для уменьшения уровня случайного шума;
- построение триангуляционной поверхности на основе алгоритма «марширующих кубов» и «метода исчерпывания», в англоязычной литературе более известного как алгоритм «распространяющегося фронта» («advancing front method») (1);
- сглаживание сетки, т.е. построение полигональной поверхности, близкой к исходной, но отличающейся более низкими величинами углов между нормальными векторами соседних треугольников (2);
- разреживание и улучшения качества сетки, т.е. построение полигональной поверхности с меньшим числом более крупных треугольников, которые, в свою очередь, наиболее близки к равносторонним (3).
Алгоритм «марширующих кубов» позволяет строить полигональное представление изоповерхностей, заданных трехмерным скалярным полем плотностей (W.Lorensen, H.Cline Marching Cubes: A High Resolution 3D Surface Construction Algorithm Computer Graphics, 21 (4): 163-169, July, 1987).
Пространство исследуется перемещением кубика построения. На каждом шаге в вершинах этого кубика определяются значения плотности. Если значение плотности в одной из вершин ребра куба меньше, а в другой больше изоуровня, то делается вывод о том, что поверхность пересекает это ребро. После сравнения значений плотности для всех вершин кубика построения определяется, какие ребра пересечены изоповерхностью. Каждый вариант пересечения кубика построения и изоповерхности задает известный набор треугольников, которые добавляются в результирующую сетку.
Для улучшения качества триангуляционной сетки используется алгоритм «распространяющегося фронта» («advancing front method»), при помощи которого на основе сетки, полученной методом «марширующих кубов» осуществляется построение новой сетки с управляемыми параметрами. Подробное описание алгоритма «распространяющегося фронта» (см.: S.H.Lo.Volume Discretization into Tetrahedra - II. 3D Triangulation by Advancing Front Approach //Computers and Structures, Pergamon, Vol.39, №5, p.p.501-511, 1991. A.Rassineux Generation and Optimization of Tetrahedral Meshes by Advancing Front Technique //International Journal for Numerical Methods in Engineering, Wiley, Vol.41, p.p.651-674, 1998. Гольник Э.Р., Вдовиченко А.А., Успехов А.А. Построение и применение препроцессора генерации, управления качеством и оптимизации сеток триангуляции контактных систем //Информационные технологии. - 2004. - №4. - С.2-10).
Алгоритм сглаживания триангуляционной сетки состоит в следующем. Для каждого узла сетки с координатами Р0=(х0,y0,z0) определяются N ближайших узлов Pj=(xi,yj,zj), j=1, 2,…, N. Вычисляется точка Q=(х, у, z), являющаяся усредненным положением этого узла Р0 и его соседей

Далее для узла Р0 вычисляется вектор r, направленный из узла в точку Q. На каждом i-м шаге итерационного процесса P0 перемещается по направлению вектора r
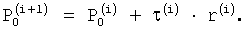
Параметр τ выбирается таким образом, чтобы новый узел 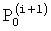 был максимально близок к точке Q(i) с учетом ограничения: вектор перемещения τ(i)·r(i) не должен выходить за пределы кубика построения, используемого в алгоритме марширующих кубов:
был максимально близок к точке Q(i) с учетом ограничения: вектор перемещения τ(i)·r(i) не должен выходить за пределы кубика построения, используемого в алгоритме марширующих кубов:  , где
, где  - евклидова норма вектора, λ - длина ребра кубика построения.
- евклидова норма вектора, λ - длина ребра кубика построения.
Операция повторяется до тех пор, пока перемещение узла на i-й итерации не станет меньшим, чем заданное значение остановки ε

Также используется алгоритм построения сглаженной изоповерхности, основанный на решении уравнения Пуассона (М. Kazhdan, M.Bolitho and Н.Норре Poisson Surface Reconstruction. - Eurographics Symposium on Geometry Processing, 2006). Алгоритм может применяться как к исходному вексельному полю, так и к триангуляционной поверхности с низким качеством.
Проводится иерархическое разбиение пространства на кубические области - построение октарного дерева (oct-tree), так, что в каждой терминальной ветви дерева содержится не больше N элементов. От числа N зависит выраженность сглаживающего эффекта. Узлы сетки рассматриваются как ориентированные точки (вектора) Vi, равные единичным нормальным векторам к аппроксимируемой поверхности. В центре каждого j-го кубического элемента задается т.н. трехмерная радиальная базисная функция (РБФ). В качестве РБФ возможно использование функции Коши

где 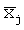 - центр кубического элемента, х - произвольная точка пространства,
- центр кубического элемента, х - произвольная точка пространства,  - евклидово расстояние между точками, а также иных видов трехмерных РБФ на основе кривой Гаусса и др.
- евклидово расстояние между точками, а также иных видов трехмерных РБФ на основе кривой Гаусса и др.
В расчетной Ω области вводится векторное поле U(x)=(Ux(x), Uy(x), Uz(х))T. Векторное поле представляется в виде разложения по системе РБФ функций
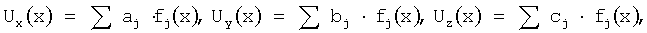
где aj, bj, cj - неопределенные коэффициенты, которые находятся из условия минимума среднеквадратичного отклонения вектор-функции U(x) от векторов Vi.
На основе полученной вектор-функции U(x) находится скалярная функция φ(х), удовлетворяющая условию  . Функция φ(х) находится как решения уравнения Пуассона
. Функция φ(х) находится как решения уравнения Пуассона

в расчетной области Ω с естественными граничными условиями, где q(x)=diνU(x).
Для решения уравнения Пуассона используется проекционный метод Галеркина, использующий в качестве весовых функций введенную выше систему РБФ. Далее к полученной функции φ(х) применяется алгоритм марширующих кубов, строящий новую полигональную аппроксимацию изоповерхности.
Разреживание полигональных сеток производится по следующему алгоритму.
Для каждого треугольника сетки вычисляется параметр χ, характеризующий качество треугольника, по одной из следующих формул:
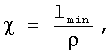
где lmin - минимальная сторона треугольника, ρ - радиус вписанной в треугольник окружности;

где ρ1 - радиус описанной окружности, ρ2 - радиус вписанной окружности;

где lmin - длина наименьшей стороны треугольника, lmax - длина наибольшей стороны треугольника.
Далее для каждого треугольника вычисляется параметр  по формуле
по формуле

где SΔ - площадь треугольника, а1, а2 - числовые коэффициенты, выбираемые в зависимости используемой формулы для вычисления χ и от требуемого качества сетки.
Далее для каждого узла сетки рассчитывается вес ω как среднее арифметическое значений параметров 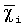 N треугольников, для которых данный узел сетки является вершиной
N треугольников, для которых данный узел сетки является вершиной

Затем удаляется узел сетки с наименьшим весом ω, получившееся отверстие триангулируется, и пересчитываются изменившиеся веса узлов сетки. Процедура повторяется до тех пор, пока количество треугольников в сетке не удовлетворит заданному.
На следующем этапе для каждой анатомической структуры грудной клетки определялся коэффициент удельной электропроводности биологической ткани.
Приведем значения удельной электропроводности для основных типов тканей грудной клетки (М.Хофер. Компьютерная томография. Базовое руководство./Пер с англ. М.: Медицинская литература, 2006. Э.Г.Мартиросов, Д.В.Николаев, С.Г.Руднев. Технологии и методы определения состава тела человека. - М.: Наука, 2006).
Таблица 1
Фиг.10 иллюстрирует построение изопотенциальных карт на поверхности торса.
Построение изопотенциальных карт осуществляется путем поверхностной интерполяции значений ЭКГ-сигналов в каждый момент времени с использованием радиальных базисных функций.
Потенциал электрического поля на поверхности грудной клетки S представляется в виде разложения по системе радиальный базисных функций (РБФ)

где U(х) - потенциал электрического поля, fj(х)- радиальные базисные функции, аj - неопределенные коэффициенты.
В качестве РБФ используются функции следующего вида, заданные в точках регистрации ЭКГ
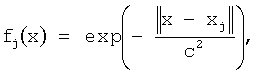
где х - произвольная точка на поверхности тела, хj - точки регистрации ЭКГ, 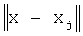 - наименьшая длина линии, принадлежащей поверхности S и соединяющей точки х и хj, с - экспериментально подбираемый коэффициент, определяющий аппроксимационные свойства функции.
- наименьшая длина линии, принадлежащей поверхности S и соединяющей точки х и хj, с - экспериментально подбираемый коэффициент, определяющий аппроксимационные свойства функции.
Коэффициенты аj находятся из условия минимума функционала J

при условии
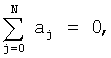
где U(xi)- значения потенциала электрического поля в хi, точках регистрации ЭКГ на поверхности грудной клетки, N - число точек регистрации ЭКГ.
Для нахождения коэффициентов ai решается соответствующая система линейных алгебраических уравнений (СЛАУ) с матрицей размерностью N×N.
Потенциал U(xi) рассчитывается в узлах триангуляционной поверхности торса хi по формуле  .
.
Для расчета потенциала в каждой точке поверхности торса используется билинейная интерполяция по значениям в вершинах треугольника сетки, которому принадлежит точка.
Заявляемый способ включает метод неинвазивной реконструкции потенциала электрического поля сердца во внутренних точках грудной клетки по измеренным значениям потенциала электрического поля на поверхности грудной клетки путем численного решения обратной задачи электрокардиографии для модели грудной клетки с кусочно-постоянным коэффициентом электропроводности методом конечных элементов на основе итерационных алгоритмов.
В качестве примера реализации метода используем модель грудной клетки, в которой учитывается низкая электропроводность легких. Пусть Ω∈R3- часть грудной клетки, ограниченная достаточно гладкой границей ∂Ω, включающей поверхность торса, контактирующую с внешней средой Г0, поперечные сечения грудной клетки на уровне диафрагмы и ключиц ГT1 и ГT2, а также эпикардиальную поверхность сердца ГE. Ведем также поверхность Г3, состоящую из поверхностей ГT1, ГT2 и ГE: Г3=ГT1∪ГT2∪ГE; Обозначим:  .
.
В области Ω выделим две подобласти Ω1и Ω2 c достаточно гладкими границами Г1 и Г2, соответствующие правому и левому легкому. Выделим также подобласть Ω0=Ω/(Ω1∪Ω2), представляющую собой пространство грудной клетки между ее наружной поверхностью и сердцем, не занятое легкими. В каждой из областей Ω0, Ω1, Ω2 биологические ткани имеют удельную электропроводность k0, k1, k2. Коэффициенты k1 и k2 соответствуют электропроводности правого и левого легкого, k1=k2. Коэффициент k0 соответствует усредненному значению электропроводности тканей грудной клетки без легких. Указанные геометрические соотношения приведены на фиг.11.
Допускается, что потенциал электрического поля сердца в каждой из областей Ωi, i=0, 1, 2 удовлетворяет уравнению Лапласа

где x=(x1,x2,x3)T∈Ωi⊂R3 - точка в трехмерном пространстве,
 - оператор Лапласа в R3.
- оператор Лапласа в R3.
На части границы Г0 области Ω считается известным условие Дирихле - потенциал электрического поля (измеренный в результате поверхностного картирования ЭКГ)

Условие Дирихле как результат экспериментальных измерений, содержит шумовую составляющую

где u0(х) - точное значение потенциала на поверхности грудной клетки, ξ(х) -погрешность измерения, для которой известна оценка:  .
.
На этой же части границы известно условие Неймана

где  - производная потенциала u(х) по направлению внешней нормали к поверхности.
- производная потенциала u(х) по направлению внешней нормали к поверхности.
На границах раздела сред с различной электропроводностью Гi, i=1, 2, 3 справедливы условия непрерывности потенциала и электрического тока
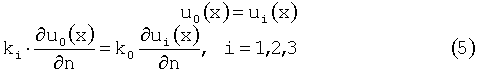
Обратная задача электрокардиографии заключается в следующем: требуется найти функцию u(х), в каждой из областей Ωi, i=0, 1, 2 удовлетворяющую уравнению Лапласа (1), на границе Г0 - граничным условиям (2), (4) и на границах Гi, i=1, 2, 3 - условиям (5).
Поставленная задача известна как задача Коши для уравнения Лапласа в кусочно-однородной среде.
Для решения обратной задачи электрокардиографии используется метод граничных элементов (Бреббия К., Теллес Ж., Вроубел Л. Методы граничных элементов: Пер. с англ. - М.: Мир, 1987).
Внешняя поверхность грудной клетки, сердца и поверхности легких приближенно заменяются гранично-элементной сеткой - полигональной поверхностью, состоящей из 2·103-5·103 плоских треугольников. Каждая из поверхностей Гi разбивается на Ni граничных элементов ωj:  . Потенциал u(s) и нормальная производная потенциала q(s) на поверхностях Гi представляется в виде разложения по системе линейно независимых финитных базисных функций φj(s)
. Потенциал u(s) и нормальная производная потенциала q(s) на поверхностях Гi представляется в виде разложения по системе линейно независимых финитных базисных функций φj(s)

где коэффициенты разложения uj и qj и - суть значения потенциала u(s) и его нормальной производной q(s) в узлах гранично-элементной сетки.
В результате формируются четыре вектора u0, u1, u2, u3 четыре вектора q0, q1, q2, q3, соответствующие значениям потенциала и его нормальной производной на поверхностях Г0, Г1, Г2, Г3. Из них два вектора u0 и q0 известны из граничных условий (2), (4)

Прямой метод граничных элементов непосредственно использует третью (основную) формулу Грина, связывающую значения потенциала и нормальной производной на граничных поверхностях Г и значения потенциала внутри расчетной области Ω в виде интегрального соотношения

где x=(x1,x2,x3)T - фиксированная, y=(y1,y2,y3)T - «скользящая» точки на поверхности Г,
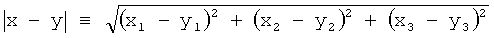 - евклидово расстояние между точками х и у,
- евклидово расстояние между точками х и у,  - нормальная производная потенциала в точке у,
- нормальная производная потенциала в точке у,  - оператор дифференцирования по направлению единичного нормального вектора к поверхности Г в точке у∈Г, ds - дифференциальный элемент поверхности Г.
- оператор дифференцирования по направлению единичного нормального вектора к поверхности Г в точке у∈Г, ds - дифференциальный элемент поверхности Г.
Применяя третью формулу Грина для точек, лежащих на поверхностях Гi, получаем систему интегральных уравнений Фредгольма (I и II родов). После гранично-элементной дискретизации функций u(s) и q(s) согласно формулам (8) и преобразований, учитывающих условия (5) и (7), система интегральных уравнений записывается в виде системы четырех матрично-векторных уравнений с четырьмя неизвестными векторами u1, u2, u3 и q3

Здесь использованы следующие обозначения:
Gi - матрицы, полученные в результате дискретизации интегралов 
Нi - матрицы, полученные в результате дискретизации интегралов вида

Е - единичная матрица,
Rij - матрицы, имеющие структуру: 
где
 ,
,  ,
,
сi - известные векторы вида: 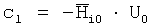 .
.
Для решения системы матрично-векторных уравнений используется следующий итерационный алгоритм, являющийся аналогом метода Зейделя для решения систем линейных алгебраических уравнений:




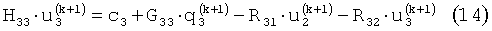
где f1, f2, f3, f4 - произвольно задаваемые векторы начального приближения, k=1, 2,…, n - номера итераций.
Для определения числа итераций используется принцип невязки (принцип Морозова): процедура останавливается на итерации k, начиная с которой норма по первому уравнению невязки не превышает абсолютной погрешности свободного члена:

где δ - абсолютная погрешность определения потенциала электрического поля на поверхности грудной клетки,  - евклидова векторная норма.
- евклидова векторная норма.
Решение матрично-векторных уравнений (12), (13), (14) на каждом шаге итерационной процедуры осуществляется на основе стандартных алгоритмов вычислительной линейной алгебры (LU - разложение, QR - разложение и др.).
Решение матрично-векторного уравнения (11) на каждом шаге итерационной процедуры вычисляется на основе регуляризирующего метода А.Н.Тихонова: регуляризированное решение 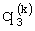 , зависящее от параметра регуляризации α, находится как решение следующего матрично-векторного уравнения:
, зависящее от параметра регуляризации α, находится как решение следующего матрично-векторного уравнения:
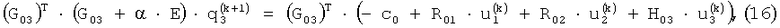
где (G03)T - матрица, транспонированная по отношению к матрице G03, Е - единичная матрица.
Параметр регуляризации α (положительное действительное число) вычисляется по формуле

где α0 - малый действительный параметр, зависящий от погрешности задания граничных условий обратной задачи электрокардиографии, ρ - положительный действительный параметр, зависящий от скорости сходимости итерационной процедуры, β - положительный действительный параметр, зависящий от точности начального приближения в итерационной процедуре, k - номер итерации.
Блок-схема алгоритма приведена на фиг.12.
На фиг.13 приведены графики сходимости итерационной процедуры с постоянным параметром регуляризации α (12а) и с уточнением параметра на каждом шаге итерации α по приведенной выше формуле (фиг.12б). Использовались следующие параметры α0=10-7, β=102, ρ=3.0.
В расчетах использовалась модель торса, сердца и легких реального пациента. Общее число треугольных элементов в сетке для торса, сердца и легких составило 3200. Для моделирования эталонного электрического поля сердца использовался квадрупольный источник, помещенный в геометрический центр сердца. Удельная электропроводности легких принималась равной 0.04300 См/м (легкие на вдохе), усредненная электропроводность тканей грудной клетки без легких - 0.22 См/м.
На фиг.14А приведены графики эталонного потенциала и реконструированного раскрываемым в настоящем патенте алгоритмом для кусочно-однородной модели грудной клетки. На фиг.14Б приведены графики эталонного потенциала и потенциала, реконструированного для модели однородной среды. Использовался тот же алгоритм, но электропроводность легких полагалась равной усредненной электропроводности тканей грудной клетки. По оси абсцисс - порядковый номер узла граничного элемента, по оси ординат - значение потенциала в соответствующем узле. Узлы упорядочены в соответствии с точными значениями потенциала в узле. Красным цветом обозначено точное значение потенциала, а синим - реконструированное значение потенциала.
На фиг.15 приведено распределение изопотенциальных линий на поперечном и фронтальном сечении торса для кусочно-однородной модели грудной клетки. На фиг.16 приведены наложенные на реалистичные модели сердца изопотенциальные карты точного электрического потенциала (16А), рассчитанного раскрываемым в настоящем патенте алгоритмом для кусочно-однородной модели грудной клетки и (16Б), реконструированная этим же алгоритмом для однородной модели грудной клетки (16В). Верхний ряд - вид спереди, нижний ряд - вид сзади.
Способ включает итерационный метод решения системы матрично-векторных уравнений (10-14), в котором на каждом шаге уравнение (11) решается с использованием псевдообращения матрицы на основе SVD-разложения с фильтрацией малых по модулю сингулярных чисел.
Регуляризирующее решение матрично-векторного уравнения (11)  , зависящее от параметра ε, находится по формуле
, зависящее от параметра ε, находится по формуле

где  - регуляризированная псевдообратная матрица, зависящая от параметра ε.
- регуляризированная псевдообратная матрица, зависящая от параметра ε.
Матрица  вычисляется следующим образом. Матрица G03 размерности М×N представляется в виде SVD-разложения: G03=UΣVT, где U - ортогональная матрица размерности М×М, V - ортогональная матрица размерности N×N, Σ - диагональная матрица размерности M×N, на главной диагонали которой расположены в порядке убывания сингулярные числа матрицы G03, остальные элементы равны нулю. Вычисление SVD-разложения матрицы G03 осуществляется одним из стандартных алгоритмов вычислительной линейной алгебры (QL-алгоритм, QR- алгоритм и др.).
вычисляется следующим образом. Матрица G03 размерности М×N представляется в виде SVD-разложения: G03=UΣVT, где U - ортогональная матрица размерности М×М, V - ортогональная матрица размерности N×N, Σ - диагональная матрица размерности M×N, на главной диагонали которой расположены в порядке убывания сингулярные числа матрицы G03, остальные элементы равны нулю. Вычисление SVD-разложения матрицы G03 осуществляется одним из стандартных алгоритмов вычислительной линейной алгебры (QL-алгоритм, QR- алгоритм и др.).
Все ненулевые сингулярные числа σj матрицы Σ, для которых справедливо условие: σj<ε, заменяются нулями. Далее строится регуляризованная псевдообратная матрица Σ+: ненулевым диагональным элементам σj матрицы Σ присваивается значения 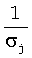 . После чего строится зависящая от параметра ε регуляризованная псевдообратная матрица
. После чего строится зависящая от параметра ε регуляризованная псевдообратная матрица  по формуле
по формуле
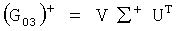 .
.
Параметр ε, играющий роль параметра регуляризации, определяется согласно формуле
ε=ε0+β·ρ-(k), где ε0 - малый действительный параметр, зависящий от погрешности задания граничных условий обратной задачи электрокардиографии, ρ - положительный действительный параметр, зависящий от скорости сходимости итерационной процедуры, β - положительный действительный параметр, зависящий от точности начального приближения в итерационной процедуре, k - номер итерации.
Способ включает итерационный метод решения рассмотренной системы матрично-векторных уравнений (10)-(14), в котором на каждом шаге уравнение (11) решаются итерационным методом на основе алгоритма обобщенных минимальных невязок (Generalized minimal residual (GMRes) method).
Описание используемого в изобретении GMRes - алгоритма - см. (Y.Saad. Iterative Methods for Sparse Linear Systems (2nd ed.), SIAM, Philadelphia, 2003).
При решении уравнения (11) итерации GMRes-алгоритма останавливаются при выполнении условия
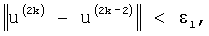
где  - евклидова норма вектора, k - номер итерации, ε1, - малый параметр, зависящий от машинной точности.
- евклидова норма вектора, k - номер итерации, ε1, - малый параметр, зависящий от машинной точности.
При решении СЛАУ (11) число итераций GMRes-алгоритма определяется по формуле

где n - число итераций GMRes -алгоритма, k - номер итерации в процедуре (10)-(14), n0 и λ - положительные целые числа, зависящие от точности начального приближения и скорости сходимости процедуры (11)-(13).
Способ включает итерационный метод решения системы матрично-векторных уравнений (10)-(14) с матрицами большой размерности, в котором на каждом шаге итерационной процедуры уравнения решаются на основе быстрого мультипольного метода (Fast Multipole Method).
Для решения матрично-векторных уравнений (10)-(14) на каждом шаге итерационной процедуры используется итерационный метод, включающий только операции матрично-векторного сложения (вычитания) и умножения, например алгоритм обобщенных минимальных невязок (Generalized minimal residual (GMRes) method).
Для реализации операция умножения матрицы на вектор используется быстрый мультипольный метод (Fast Multipole Method), представленный на фиг.17. Его детальное описание см. (Yoshida К. Applications of fast multipole method to boundary integral equation method. Ph.D.Dissertation, Department of Global Environment Engineering, Kyoto University, 2001). Основная идея метода показа на фиг.17.1.
Реализация быстрого мультипольного метода включает следующие этапы (фиг.17.2):
1. Осуществляется иерархическое разбиение расчетной области Ω на подобласти, т.е. построение октарного дерева (oct-tree).
Ядра интегралов


в результате дискретизации которых формируются матрицы Нij и Gij, разделяются по переменным х и у на основе разложения в ряд по системе сферических функций (мультипольное разложение) относительно заданных узлов xс и yс в подобластях иерархичеcкого разбиения расчетной области;
2. Вычисляются мультипольные моменты в листьях октарного дерева на основе вышеописанного мультипольного разложения;
3. Вычисляются мультипольные моменты для родительских уровней дерева на основе ранее вычисленных мультипольных моментов (М2М);
4. Вычисляются значения функций в удаленных точках на основе ранее вычисленных мультипольных моментов (M2L, L2L).
Сравнительный график временной сложности классического метода граничных элементов и метода быстрого мультипольного разложения приведен на фиг.17.3.
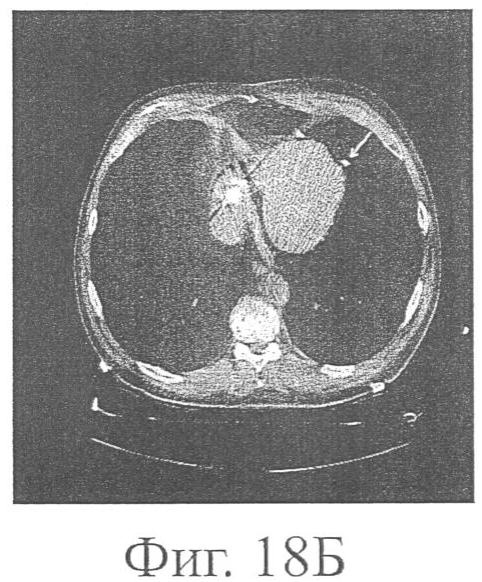
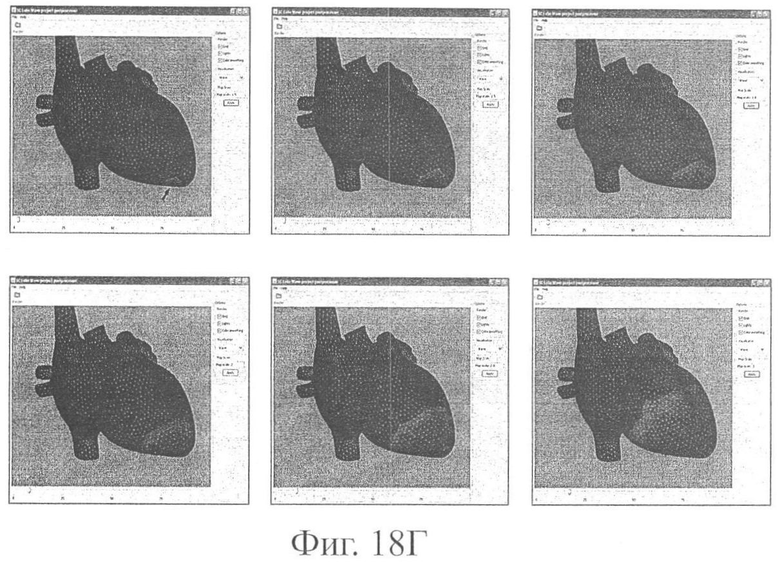
На фиг.18 представлены примеры визуализации результатов неинвазивного электрофизиологического исследования сердца.
Используются следующие типы визуального отображения:
1. Построение электрограмм в интерактивно выбранных точках эпикардиальной поверхности сердца, эндокардиальных поверхностей межжелудочковой и межпредсердной перегородок, а также внутренних точках грудной клетки на поперечных томографических срезах (фиг.18А);
2. Построение изопотенциальных карт на поперечных томографических срезах грудной клетки (фиг.18Б);
3. Построение изопотенциальных и изохронных карт на эпикардиальной поверхности сердца, эндокардиальных поверхностей межжелудочковой и межпредсердной перегородок (фиг.18В);
4. Визуализация динамики возбуждения миокарда на эпикардиальной поверхности сердца, эндокардиальных поверхностях межжелудочковой и межпредсердной перегородок в анимационном режиме (propagation maps) (фиг.18Г).
Монополярные электрограммы строятся путем интерполяции вычисленных значений потенциала электрического поля сердца для всех моментов времени кардиоцикла в заданной точке. Биполярные электрограммы строятся как разность электрограмм в выбранном узле и в точке, находящейся в окрестности узла на расстоянии Δl по направлению I. Параметры Δl и I задаются интерактивно.
Изопотенциальные карты строятся на основе билинейной интерполяции вычисленных значений потенциала электрического поля сердца в узлах сетки в заданный момент времени кардиоцикла методом градиентной закраски или построения изопотенциальных линий.
Для построения изохронных карт предусмотрены два режима: ручной и автоматический. В ручном режиме в интерактивно выбранном узле сетки реконструируются: монополярная электрограмма U(t), биполярная электрограмма Ub=U1(t)-U2(t), а также дифференциальная электрограмма  - график первой производной монополярной электрограммы по времени. Оператор в интерактивном режиме отмечает на указанных графиках момент времени τ, соответствующий началу активации миокарда в данной точке. В автоматическом режиме выбор соответствующей отметки времени τ осуществляется без вмешательства оператора. Момент времени τ определяется как максимум отрицательной дифференциальной монополярной электрограммы
- график первой производной монополярной электрограммы по времени. Оператор в интерактивном режиме отмечает на указанных графиках момент времени τ, соответствующий началу активации миокарда в данной точке. В автоматическом режиме выбор соответствующей отметки времени τ осуществляется без вмешательства оператора. Момент времени τ определяется как максимум отрицательной дифференциальной монополярной электрограммы
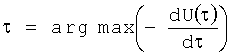 .
.
На основе билинейной интерполяции значений τ в узлах сетки визуализируются изохронные карты путем градиентной закраски или построения изохронных линий. Эти же данные представляются в анимационном режиме в виде т.н. карт распространения возбуждения (propagation maps).
На фиг.19 представлены реконструированные описанным способом эпикардиальные изохронные карты при экстрасистолии, вызванной эктопическим источником в области выводного тракта правого желудочка. Стрелкой указана локализация аблационного электрода, при помощи которого была выполнена успешная радиочастотная аблация эктопического источника.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ НЕИНВАЗИВНОГО ЭЛЕКТРОФИЗИОЛОГИЧЕСКОГО ИССЛЕДОВАНИЯ СЕРДЦА | 2008 |
|
RU2409313C2 |
| СПОСОБ НЕИНВАЗИВНОГО ЭЛЕКТРОФИЗИОЛОГИЧЕСКОГО ИССЛЕДОВАНИЯ СЕРДЦА | 2008 |
|
RU2417051C2 |
| СПОСОБ ДИАГНОСТИКИ И КОНТРОЛЯ ЛЕЧЕНИЯ СЕРДЕЧНЫХ ПАТОЛОГИЙ | 2022 |
|
RU2790406C1 |
| ЭЛЕКТРОКАРДИОГРАФ С ИЗМЕРЕНИЕМ КООРДИНАТ И ПАРАМЕТРОВ ИСТОЧНИКА ЭЛЕКТРИЧЕСКОЙ АКТИВНОСТИ СЕРДЦА | 2010 |
|
RU2448643C2 |
| СПОСОБ ТРЕХМЕРНОГО КАРТИРОВАНИЯ КАМЕР СЕРДЦА С ИСПОЛЬЗОВАНИЕМ НАВИГАЦИОННОЙ СИСТЕМЫ "АСТРОКАРД" ДЛЯ ЛЕЧЕНИЯ ПАЦИЕНТОВ С НАРУШЕНИЕМ РИТМА СЕРДЦА | 2019 |
|
RU2724191C1 |
| СПОСОБ НЕИНВАЗИВНОГО ОПРЕДЕЛЕНИЯ ЭЛЕКТРОФИЗИОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК СЕРДЦА | 2011 |
|
RU2489083C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЭЛЕКТРИЧЕСКОЙ АКТИВНОСТИ СЕРДЦА | 2007 |
|
RU2360597C2 |
| СПОСОБ НЕИНВАЗИВНОГО ОПРЕДЕЛЕНИЯ ЭЛЕКТРОФИЗИОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК СЕРДЦА | 2017 |
|
RU2651068C1 |
| СПОСОБ НЕИНВАЗИВНОЙ АБЛЯЦИИ И ДЕСТРУКЦИИ УЧАСТКОВ ДИЭЛЕКТРИЧЕСКОГО ТЕЛА С ПОТЕРЯМИ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2011 |
|
RU2465860C1 |
| ИТЕРАЦИОННОЕ КОГЕРЕНТНОЕ КАРТИРОВАНИЕ ЭЛЕКТРОФИЗИОЛОГИЧЕСКОЙ АКТИВАЦИИ СЕРДЦА, ВКЛЮЧАЯ ЭФФЕКТЫ РУБЦА | 2019 |
|
RU2772201C2 |
























Изобретение относится к кардиологии, сердечно-сосудистой хирургии, функциональной диагностике и клинической электрофизиологии сердца. Способ неинвазивного электрофизиологического исследования сердца включает следующие стадии: закрепление регистрирующих электродов на поверхности грудной клетки; регистрация ЭКГ; обработка ЭКГ-сигналов в режиме реального времени; ретроспективная обработка полученных ЭКГ; компьютерная или магнитно-резонансная томография грудной клетки; построение и редактирование компьютерных воксельных моделей органов грудной клетки и сердца; построение полигональных моделей торса, сердца, легких и других органов грудной клетки; определение удельной электропроводности для крупных анатомических областей грудной клетки по данным КТ или МРТ на основе известных соответствий между типом биологической ткани и числом Хаунсфилда при КТ или интенсивностью МР-сигнала при МРТ и типом биологической ткани; определение координат регистрирующих электродов на поверхности грудной клетки; интерполяция значений ЭКГ-сигналов в узлы полигональной сетки; реконструкция потенциала электрического поля в заданных точках с использованием условий непрерывности потенциала и электрического тока на границах раздела сред с различной электропроводностью согласно уравнениям

где u0(x) и ui(x) - потенциал электрического поля в анатомических структурах 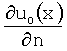 и
и 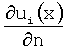 грудной клетки, нормальные производные потенциала электрического поля на границах анатомических структур, k0, ki - значения электропроводности в анатомических структурах; визуализация результатов реконструкции электрического поля сердца; клиническая оценка результатов. Изобретение позволяет повысить точность неинвазивной диагностики нарушений сердечного ритма и других сердечно-сосудистых заболеваний. 12 з.п. ф-лы, 19 ил., 1 табл.
грудной клетки, нормальные производные потенциала электрического поля на границах анатомических структур, k0, ki - значения электропроводности в анатомических структурах; визуализация результатов реконструкции электрического поля сердца; клиническая оценка результатов. Изобретение позволяет повысить точность неинвазивной диагностики нарушений сердечного ритма и других сердечно-сосудистых заболеваний. 12 з.п. ф-лы, 19 ил., 1 табл.
1. Способ неинвазивного электрофизиологического исследования сердца, включающий следующие стадии:
- закрепление одноразовых регистрирующих электродов на поверхности грудной клетки;
- регистрация ЭКГ во множестве однополюсных отведений с поверхности грудной клетки;
- обработка ЭКГ-сигналов в режиме реального времени;
- ретроспективная обработка полученных ЭКГ;
- КТ или МРТ грудной клетки пациента закрепленными электродами;
- построение и редактирование компьютерных вексельных моделей органов грудной клетки и сердца;
- построение при помощи компьютерной программы полигональных моделей торса, сердца, легких и других органов грудной клетки;
- определение удельной электропроводности для крупных анатомических областей грудной клетки по данным КТ или МРТ на основе известных соответствий между типом биологической ткани и числом Хаунсфилда при КТ или интенсивностью MP-сигнала при МРТ и типом биологической ткани;
- определение координат регистрирующих электродов на поверхности грудной клетки;
- интерполяция значений ЭКГ-сигналов в узлы полигональной сетки (получение изопотенциальных карт на полигональной модели торса);
- реконструкция потенциала электрического поля в заданных точках грудной клетки, эпикардиальной поверхности сердца, поверхности межжелудочковой и межпредсердной перегородок с использованием условий непрерывности потенциала и электрического тока на границах раздела сред с различной электропроводностью согласно уравнениям:

где u0(x) и ui(x) - потенциал электрического поля в анатомических структурах грудной клетки,
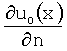 и
и 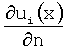 - нормальные производные
- нормальные производные
потенциала электрического поля на границах анатомических структур,
k0,ki- значения электропроводности в анатомических структурах;
- визуализация результатов реконструкции электрического поля сердца в виде эпикардиальных электрограмм, изохронных и изопотенциальных карт, а также динамических карт (propagation maps) на полигональных моделях сердца и его структур;
- клиническая оценка результатов.
2. Способ по п.1, в котором для КТ используют наклеиваемые металлические хлор-серебряные электроды, а для МРТ - наклеиваемые графитовые электроды.
3. Способ по п.1, в котором одноразовые электроды закрепляют в виде горизонтальных пяти - восьми поясов, расположенных на одинаковых расстояниях по вертикали, причем первый пояс располагают на уровне грудинно-ключичного сочленения, а последний пояс - на уровне нижнего края реберной поверхности, и каждый пояс включает от 16 до 30 электродов, расположенных на одинаковых расстояниях по окружности грудной клетки.
4. Способ по п.1, в котором для построения воксельной модели используют алгоритм факторизации «сдвиг-деформация» для преобразования просмотра (Shear-Warp Factorization of the Viewing Transformation).
5. Способ по п.1, в котором стадия построения полигональных моделей включает следующие этапы:
- фильтрация исходных воксельных моделей для уменьшения уровня случайного шума;
- построение триангуляционной поверхности методом «марширующих кубов» или «методом исчерпывания» («advancing front method»);
- разреживание и улучшение качества сетки с использованием метода пуассоновской реконструкции (Poisson Surface Reconstruction).
6. Способ по п.1, в котором определение удельной электропроводности каждой точки грудной клетки определяют на основе известных соответствий между типом биологической ткани и числом Хаунсфилда (при КТ) или интенсивностью MP-сигнала (при МРТ), с одной стороны, и типом биологической ткани и ее удельной электропроводностью, с другой стороны.
7. Способ по п.1, в котором определение координат регистрирующих электродов проводится в автоматическом режиме по данным КТ или МТР грудной клетки.
8. Способ по п.1, в котором интерполяцию значений ЭКГ-сигналов полигональной сетки осуществляют с использованием радиальных базисных функций.
9. Способ по п.1, в котором реконструкцию потенциала электрического поля сердца проводят путем численного решения задачи Коши для уравнения Лапласа методом граничных элементов, при котором при формировании матриц итоговой системы матрично-векторных уравнений используются найденные значения удельной электропроводности крупных анатомических структур грудной клетки, и включающим итерационное решение итоговой системы матрично-векторных уравнений, причем для решения тех уравнений системы, матрицы которых характеризуются большим числом обусловленности, используют регуляризирующие методы и общее число итераций алгоритма определяют по принципу невязки (принцип Морозова).
10. Способ по п.9, в котором для решения тех уравнений из системы матрично-векторных уравнений, матрицы которых характеризуются большим числом обусловленности, используется метод регуляризации Тихонова, причем параметр регуляризации определяют по формуле

где α - параметр регуляризации, α0 - малый действительный параметр, зависящий от погрешности задания граничных условий обратной задачи электрокардиографии, ρ - положительный действительный параметр, зависящий от скорости сходимости итерационной процедуры (10)-(14)




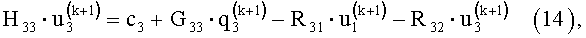
решения итоговой матрично-векторной системы (9)
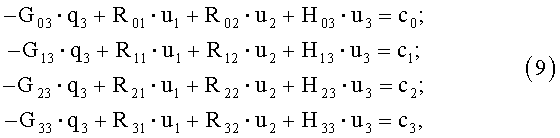
β - положительный действительный параметр, зависящий от точности начального приближения (10)

в итерационной процедуре (10)-(14),
k - номер итерации в итерационной процедуре (10)-(14).
11. Способ по п.9, в котором для решения тех уравнений из системы матрично-векторных уравнений (9), матрицы которых характеризуются большим числом обусловленности, используется регуляризирующий алгоритм на основе SVD-разложения матрицы уравнения с заменой нулями сингулярных чисел, меньших заданного положительного числа ε, причем параметр ε определяют согласно формуле:
ε=ε0+β·ρ-(k/2),
где ε0 - малый действительный параметр, зависящий от погрешности задания граничных условий обратной задачи электрокардиографии,
ρ - положительный действительный параметр, зависящий от скорости сходимости итерационной процедуры (10)-(14) решения итоговой матрично-векторной системы (9), β - положительный действительный параметр, зависящий от точности начального приближения (10) в итерационной процедуре (10)-(14),
k - номер итерации в итерационной процедуре (10)-(14).
12. Способ по п.9, в котором для решения тех уравнений из системы матрично-векторных уравнений, матрицы которых характеризуются большим числом обусловленности, используется регуляризирующий алгоритм на основе итерационного метода обобщенных минимальных невязок (Generalized minimal residual method) с ограничением числа итераций, причем требуемое число итераций определяют по формуле n=n0+λ·k,
где n - число итераций алгоритма обобщенных минимальных невязок, k -номер итерации в общей итерационной процедуре (10)-(14) решения итоговой матрично-векторной системы (9), n0 и λ - положительные целые числа, зависящие от точности начального приближения (10) и скорости сходимости итерационной процедуры (10)-(14) решения итоговой матрично-векторной системы (9).
13. Способ по п.9, в котором уравнения системы матрично-векторных уравнений решаются на основе «быстрого мультипольного метода» (Fast Multipole Method).
| РЕВИШВИЛИ А.Ш | |||
| и др | |||
| Верификация новой методики неинвазивного электрофизиологического исследования сердца, основанной на решении обратной задачи электрокардиографии // Вестник аритмологии | |||
| Станок для изготовления деревянных ниточных катушек из цилиндрических, снабженных осевым отверстием, заготовок | 1923 |
|
SU2008A1 |
| ДЕНИСОВ A.M | |||
| и др | |||
| Применение метода | |||
Авторы
Даты
2011-12-10—Публикация
2008-11-27—Подача