Изобретение относится к способу кодирования сообщения K' данных для передачи от передающей станции к принимающей станции, а также к способу для декодирования, соответствующей передающей станции, соответствующей принимающей станции и соответствующему программному обеспечению.
Создание хороших имеющих малую плотность кодов проверки четности (кодов LDPC) стало в последнее время одной из самых насущных тем исследований в теории кодирования. Несмотря на существенный прогресс в асимптотическом анализе кодов LDPC [1], создание практических кодов короткой и умеренной длины все еще остается открытой проблемой. Главная причина этого состоит в том, что анализ эволюции плотности требует формирования нерегулярных кодов LDPC, в то время как большинство способов проектирования алгебраических кодов, разработанных до сих пор, может сформировать только регулярные конструкции, которым внутренне присущ недостаток в поведении приближения к возможностям. Кроме того, характеристика практической длины кодов LDPC зависит не только от порога асимптотического итерационного декодирования, но также и от кодового минимального расстояния.
Для высокоскоростных кодов минимальное расстояние представляется доминирующим фактором. Это позволяет решать проблему конструирования кодов с использованием традиционных способов теории кодирования, таких как конечные геометрии, разностные наборы и т.д. (см., например, [2, 3, 4]). Но для более низкоскоростных кодов (например, со скоростью 1/2) нужно найти компромисс между минимальным расстоянием и порогом итерационного декодирования. Это типично достигается выполнением некоторого рода обусловленного случайного поиска [5, 6, 7]. Коды, получаемые этими способами, демонстрируют очень хорошие характеристики, но являются очень трудными для реализации из-за отсутствия какой-либо структуры. Один способ решить эту проблему состоит в том, чтобы изменить структурированную регулярную матрицу проверки четности так, чтобы она стала нерегулярной [8, 9]. Однако нет никакого формализованного способа выполнить такую модификацию, и много испытаний необходимо выполнить, прежде чем будет найден хороший код.
Коды LDPC представляют подкласс линейных кодов. Любое кодовое слово c линейного кода удовлетворяет уравнение HcT=0, где H - матрица проверки четности кода. С другой стороны, для заданного сообщения К данных соответствующее кодовое слово может быть получено как с=KG, где G - генераторная матрица кода. Это подразумевает, что матрица Н проверки четности и генераторная матрица G должны удовлетворять уравнению HGT=0. Для заданной матрицы Н проверки четности можно сконструировать много различных генераторных матриц G. Всегда возможно (вероятно, после применения перестановки столбцов к матрице Н проверки) сконструировать генераторную матрицу формы G=[A I], где I - единичная матрица, и A - некоторая другая матрица. В этом случае кодовое слово, соответствующее сообщению К данных, подобно с=KG=[KA K], то есть сообщение К данных появляется как подвектор кодового слова. Это известно как систематическое кодирование. Преимущество систематического кодирования состоит в том, что, как только все ошибки канала удалены из кодового слова, сообщение данных может быть немедленно извлечено из него, без какой-либо постобработки. В некоторых случаях можно сконструировать другие способы для систематического кодирования сообщений данных, более эффективные, чем умножение на генераторную матрицу в систематической форме. Однако способ кодирования не влияет на способность исправления ошибок кода.
Также верно, что если H - матрица проверки четности некоторого линейного кода, то произведение SH также является матрицей проверки четности для того же самого кода, где S - несингулярная матрица. В частности, если S - матрица перестановки, и H - матрица низкой плотности, исполнение алгоритма декодирования LDPC распространения достоверности [10] на матрице SH дало бы те же самые результаты, что и для случая исходной матрицы H. Многие конструкции кода LDPC основаны на расширении матрицы Р шаблона путем подстановки вместо заданных записей pij матриц перестановки p×p, где p - коэффициент расширения. Используя конструкцию согласно фиг. 2-8, могут генерироваться коды с различной длиной, но той же самой скорости, начиная с единственной матрицы шаблона. Более определенно, их матрица проверки четности задана двумя подматрицами, первая Hz является двойной диагональной матрицей, реализующей так называемый зигзагообразный шаблон, и вторая Hi сконструирована на основе расширения матрицы шаблона, то есть путем замены элементов перестановкой и нулевыми матрицами. Путем изменения коэффициента расширения получаются коды различных длин. Очевидно, это требует использования различных матриц перестановок. Несмотря на простоту этой операции, изменение коэффициента расширения требует переадресации краев в графе Таннера соответственно матрице проверки четности. Так как структура графа Таннера реализована для так называемого декодирования "прохождения сообщения" или "распространения достоверности" в приемнике, изменение в его структуре может привести к существенной сложности аппаратных средств при рассмотрении всего семейства кодов.
Возможность получить более длинные коды из более коротких кодов обеспечивается посредством конкатенированного кодирования [3]. Однако это обычно изменяет также кодовую скорость. Кроме того, коды LDPC, как известно, работают не так хорошо, если используются в конкатенированных кодовых конструкциях. Причина состоит в том, что чрезвычайно трудно получить хорошее распределение степени узлов в графе Таннера конкатенированного кода.
Целью настоящего изобретения является создание улучшенного способа для кодирования сообщения данных с использованием кода, длина которого может быть выбрана таким образом, чтобы можно было преодолеть вышеупомянутые недостатки относительно структуры декодера и кодовой скорости. Другой целью изобретения является создание соответствующего способа для декодирования, соответствующей передающей станции и соответствующей принимающей станции, а также соответствующего программного обеспечения.
Цель достигается способом для кодирования, способом для декодирования, передающей станцией, принимающей станцией и программным обеспечением согласно независимым пунктам формулы изобретения.
Предпочтительные варианты осуществления представлены в зависимых пунктах формулы изобретения.
Согласно заявленному способу для кодирования сообщения K' данных для передачи от передающей станции к принимающей станции, кодирование генерирует кодовое слово c' длины n=w·n0, где w и n0 - целые числа, и генерация кодового слова c' реализуется и/или математически записывается как умножение сообщения K' данных на генераторную матрицу G', c'=K'G', тогда как генераторная матрица G' является решением матричного уравнения H'G'T=0, при H'=[Hz' Hi'], где Hz' является матрицей w·m0×w·m0 с двумя смежными диагоналями из 1, имеющей 0 во всех других позициях, и Hi' является матрицей w·m0×w·(n0-m0), и Hi' является матрицей, полученной чередованием строк блочно-диагональной матрицы Hi'(w), имеющей w матриц Hi размера m0×(n0-m0) на диагонали и 0 во всех других позициях, причем Hi дополнительно выбрана таким образом, что H=[Hz Hi] является матрицей проверки четности кода с длиной n0, где Hz является матрицей m0×m0 с двумя смежными диагоналями из 1, имеющей 0 во всех других позициях.
Изобретение обеспечивает возможность создания кодов с w-кратной длиной кода-прототипа с длиной n0, не изменяя соответствующую структуру графа Таннера. Поэтому структура декодера, например, компоненты аппаратных средств, используемые для кода-прототипа длиной n0, могут также использоваться для декодирования кодовых слов, кодированных согласно заявленному способу.
В дополнение к чередованию строк, также возможно чередовать столбцы матрицы H'. Получающийся код эквивалентен и имеет ту же самую характеристику, что и код, генерированный без чередования столбцов.
Предпочтительным образом Hi дополнительно выбирается таким образом, что кодирование сообщения К данных, используя генераторную матрицу G, генерирует кодовое слово c длины n0, с=KG, где генераторная матрица G является решением матричного уравнения HGT=0, при H=[Hz Hi], где Hz является матрицей m0 x m0 с двумя смежными диагоналями из 1, имеющей 0 во всех других позициях.
Предпочтительным образом Hi получается чередованием строк первой матрицы Hu, которая является блочной матрицей, состоящей из матриц перестановки и нулевых матриц.
Это означает, что матрица H проверки четности соответствующего кода определяется как H=[Hz SHu]=S[S-1Hz Hu], где S - матрица перестановки, используемая для чередования строк первой матрицы Hu. Поскольку перестановка строк матрицы проверки четности не изменяет код, можно использовать также матрицу проверки четности в форме [S-1Hz Hu].
Предпочтительным образом используется генераторная матрица G', которая удовлетворяет условию G'=[((Hz')-1 Hi')T I].
Поэтому, если кодовое слово c' математически записано как c'=[cz' ci'], то умножение сообщения K' данных и этой генераторной матрицы G' приводит к ci', являющемуся сообщением K' данных, в то время как cz' задается как cz'T=(Hz')-1Hi'K'T. Умножение на подматрицу (Hz')-1Hi' может быть реализовано или прямо, или как последовательность следующих преобразований. Поскольку Hi'=S'Hi'(w), где S' - матрица перестановки, используемая для чередования строк блочно-диагональной матрицы Hi'(w), можно или умножить вектор K'T (сообщение данных) непосредственно на Hi' или умножить его сначала на Hi'(w) и затем чередовать элементы полученного вектора. Умножение вектора на матрицу Hz'-1 может быть осуществлено посредством фильтра с передаточной функцией 1/(1+D').
Предпочтительным образом прямоугольный перемежитель используется для перемежения (чередования) строк блочно-диагональной матрицы Hi'(w), то есть с использованием перестановки

Предпочтительным образом первая матрица Hu сгенерирована расширением матрицы Р шаблона размером s×t, причем расширение выполняется заменой всех элементов pij матрицы Р шаблона, которые удовлетворяют условию 0≤pij<∞, матрицами циклических перестановок размера p x p, имеющими значение 1 в позициях (r, (pij+r) mod p), при r=0.. p-l, i=0.. s-l и j=0.. t-1, и заменой всех других элементов P, которые удовлетворяют условию pij=∞ или pij<0, нулевыми матрицами размера p x p.
Изменяя коэффициент расширения p, различные значения для n0 могут быть выбраны, потому что изменение p изменяет размер Hi и Hz, то есть n0 и m0.
Предпочтительным образом прямоугольный перемежитель используется для перемежения (чередования) строк блочно-диагональной матрицы Hu, то есть с использованием перестановки
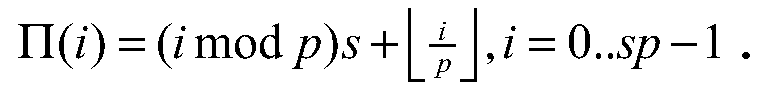
Заявленный способ для декодирования сообщения K' данных из кодового слова c', принятого от передающей станции, показывает все необходимые этапы для декодирования кодового слова c' и использует матрицу Н' проверки четности, которая построена согласно заявленному способу для кодирования. Согласно заявленному способу для кодирования, матрица H' проверки четности используется в уравнении H'G'T =0, которому должна удовлетворять генераторная матрица G', которая используется для того, чтобы математически выразить кодирование сообщения K' данных.
Соответствующая изобретению передающая станция содержит блок кодирования, чтобы кодировать сообщение K' данных в кодовое слово c' длины n=w·n0, где w и n0 - целые числа, и генерация кодового слова c' реализуется и/или математически записывается как умножение сообщения K' данных на генераторную матрицу G', c'=K'G', тогда как генераторная матрица G' является решением матричного уравнения H'G'T=0, при H'=[Hz' Hi'], где Hz' является матрицей w·m0×w·m0 с двумя смежными диагоналями из 1, имеющей 0 во всех других позициях, и Hi' является матрицей w·m0×w·(n0-m0), и Hi' является матрицей, полученной чередованием строк блочно-диагональной матрицы Hi'(w), имеющей w матриц Hi размера m0 x (n0-m0) на диагонали и 0 во всех других позициях, причем Hi дополнительно выбрана таким образом, что H=[Hz Hi] является матрицей проверки четности кода с длиной n0, где Hz является матрицей m0×m0 с двумя смежными диагоналями из 1, имеющей 0 во всех других позициях.
Заявленная принимающая станция содержит средство декодирования для декодирования кодового слова c', принятого от передающей станции, используя матрицу H' проверки четности, построенную согласно заявленному способу для кодирования, для проверки четности кодового слова c'.
Соответствующее изобретению программное обеспечение для кодирования сообщения K' данных содержит код программы, который выводит кодовое слово c' из входного сообщения K' данных, если программное обеспечение исполняется на компьютере, с использованием заявленного способа для кодирования. Далее, соответствующее изобретению программное обеспечение декодирования кодового слова c' содержит код программы, который выводит сообщение K' данных из входного кодового слова c' и использует матрицу H' проверки четности, построенную согласно заявленному способу для кодирования, если программное обеспечение исполняется на компьютере.
Далее изобретение описано согласно вариантам осуществления, показанным на чертежах:
Фиг. 1 - граф Таннера приведенного для примера кода (уровень техники),
Фиг. 2 - матрица проверки четности и граф Таннера с зигзагообразным шаблоном,
Фиг. 3 - первый вариант осуществления кодера,
Фиг. 4 - второй вариант осуществления кодера,
Фиг. 5 - матрица Р шаблона для кодов 1/2 скорости,
Фиг. 6 - характеристика кодов 1/2 скорости,
Фиг. 7 - характеристика кодов 2/3 скорости,
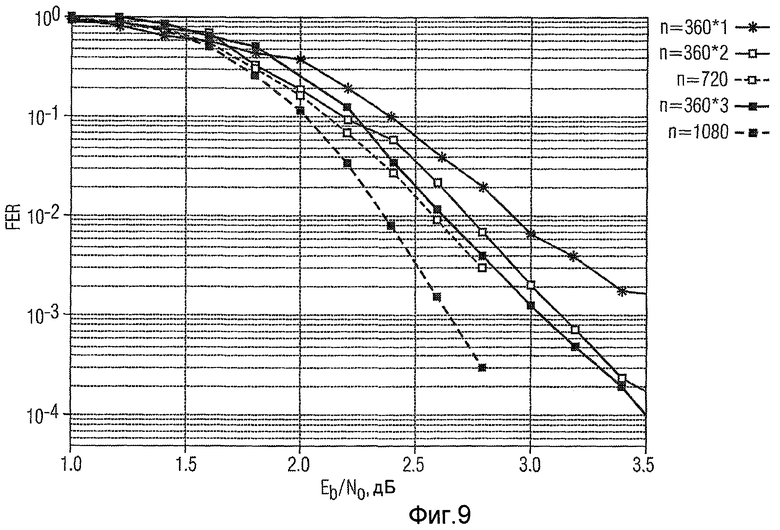
Фиг. 9 - характеристика кодов 2/3 скорости с длинами w·360, w=1, 2, 3, построенных согласно заявленному способу кодирования, и кодов 2/3 скорости с длинами 720 и 1080, построенных с использованием различных коэффициентов р расширения.
Передающая станция является, например, терминалом или базовой станцией системы радиосвязи.
Принимающая станция является, например, терминалом или базовой станцией системы радиосвязи.
Терминал является, например, мобильным радиотерминалом, в частности, мобильным телефоном или адаптером стационарного устройства, для передачи данных изображений и/или звуковых данных, для факсимильной передачи, сообщений службы коротких сообщений (SMS) и/или сообщений электронной почты, и/или для доступа в Интернет.
Изобретение может предпочтительным образом использоваться в коммуникационной системе любого типа. Коммуникационная система является, например, компьютерной сетью или системой радиосвязи.
Системы радиосвязи представляют собой системы, в которых передача данных между терминалами выполняется по воздушному интерфейсу. Передача данных может быть двунаправленной и однонаправленной. Системы радиосвязи являются, в частности, системами сотовой радиосвязи, например, согласно стандарту GSM (Глобальная Система для Мобильных Коммуникаций) или стандарту UMTS (Универсальная Мобильная Телекоммуникационная Система).
Также будущие мобильные системы радиосвязи, например, согласно четвертому поколению, а также самоорганизующиеся (ad hoc) сети должны пониматься как системы радиосвязи. Системами радиосвязи также являются беспроводные локальные сети (WLAN) согласно стандартам Института инженеров по электротехнике и радиоэлектронике (IEEE), таким как 802.11a-i, Hiper-LANl и HiperLAN2 (Локальная радио сеть высокой эффективности), а также сети Bluetooth.
Краткий обзор кодов LDPC
Коды LDPC определены как класс линейных двоичных кодов, имеющих разреженную m 0 ×n 0 матрицу Н проверки четности. Размер кода задается выражением k≥n 0 -m 0. Альтернативно, код LDPC может быть охарактеризован двудольным графом (графом Таннера) с n0 узлами переменных и m0 узлами проверки [10]. Ребро соединяет узел j переменной с узлом i проверки, если и только если H ij =1 . Например, рассмотрим следующую матрицу проверки четности:

Фиг. 1 представляет ассоциированный граф Таннера.
Степень узла в графе - это число ребер, связанных с этим узлом. Если различные узлы в графе Таннера имеют различную степень, то код называют нерегулярным. В противном случае код является регулярным. Граф Таннера характеризуется своими распределениями степени узлов переменной и проверки  и
и  , где
, где  и
и 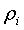 - доли ребер, соединенных с узлами переменной и проверки степени i, соответственно. Эти перспективные распределения ребер могут быть преобразованы в перспективные распределения узлов
- доли ребер, соединенных с узлами переменной и проверки степени i, соответственно. Эти перспективные распределения ребер могут быть преобразованы в перспективные распределения узлов  и
и  , где
, где  и
и  - доли узлов переменной и проверки степени i. Основанное на графе описание кода LDPC позволяет проектировать алгоритм декодирования с итеративным прохождением сообщения [10]. Этот алгоритм был проанализирован в [11] для случая бесконечно длинных кодов и двоичных по входу, без запоминания и симметричных по выходу каналов. Было показано, что для данного ансамбля кодов LDPC существует значение параметра канала (например, отношение сигнала к шуму) такое, что итеративное декодирование успешно для всех значений параметра, превышающих этот порог. Возможно проектировать численный алгоритм для вычисления порога для заданных распределений степени узлов и даже выполнить их оптимизацию, чтобы минимизировать его [11].
- доли узлов переменной и проверки степени i. Основанное на графе описание кода LDPC позволяет проектировать алгоритм декодирования с итеративным прохождением сообщения [10]. Этот алгоритм был проанализирован в [11] для случая бесконечно длинных кодов и двоичных по входу, без запоминания и симметричных по выходу каналов. Было показано, что для данного ансамбля кодов LDPC существует значение параметра канала (например, отношение сигнала к шуму) такое, что итеративное декодирование успешно для всех значений параметра, превышающих этот порог. Возможно проектировать численный алгоритм для вычисления порога для заданных распределений степени узлов и даже выполнить их оптимизацию, чтобы минимизировать его [11].
Для кодов LDPC конечной длины эффективность зависит не только от асимптотического порога итеративного декодирования, но также и от структуры цикла кода. Обхват графа Таннера представляет собой минимальную длину цикла графа. Обхват графа на фиг. 1 равен 6, так как имеется цикл длиной 6 v1-c1-v2-c3-v5-c2-v1, соединяющий его вершины. Короткие (в частности, длины 4) циклы, как известно, оказывают негативное воздействие на эффективность алгоритма декодирования прохождения сообщения, так что таких графов Таннера нужно, в принципе, избегать. Однако в [6] было показано, что не все короткие циклы одинаково вредны. Если узлы в цикле связаны с узлами, не участвующими в этом цикле, то внешняя информация может все еще проходить по графу Таннера, и декодирование может продолжиться. Возможно ввести приближенную степень внешних для цикла сообщений (АСЕ) контура, как [6]

где суммирование выполнено по всем переменным узлам в контуре, и d i - степень i-го переменного узла. Можно наложить ограничение ACE min >η на минимальное значение АСЕ по всем циклам длины l≤2l ACE в построенном графе Таннера. В [12] было показано, что в этом случае число наборов остановки (то есть конфигурации стирания, невосстанавливаемые алгоритмом прохождения сообщения) размером ≤l ACE уменьшается по экспоненте с уменьшением η . Так как позиции ненулевых символов любого кодового слова также составляют набор остановки, кондиционирование АСЕ также улучшает кодовое минимальное расстояние (и, вообще, спектр весов).
Уравнение (1) подразумевает, что АСЕ цикла, использующего только узлы степени 2, равна нулю. Кроме того, известно, что любой цикл длиной 2l степени в части степени 2 графа Таннера соответствует кодовому слову веса l . Так как оптимизированные распределения степеней узлов обычно имеют 1>Λ 2 >>0 (то есть должно быть существенное количество узлов степени 2), особенно важно максимизировать длину циклов, проходящих через часть степени 2 графа Таннера. Это может быть достигнуто путем упорядочения по возможности большего количества узлов степени 2 узла в зигзагообразный шаблон, показанный на фиг. 2. Если необходимо, остальные узлы степени 2 могут быть упакованы в часть H i. Зигзагообразный шаблон также не требует использования всех узлов проверки. Это подразумевает, что зигзагообразный шаблон является очень хорошей отправной точкой в проектировании кода LDPC.
Следует отметить, что систематическое кодирование сообщения К данных с таким кодом может быть выполнено путем умножения K на генераторную матрицу G = [(Hz -1 Hi)TI].
Описание вариантов осуществления, показывающих возможную конструкцию кодов LDPC
Матрица H i должна быть построена при следующих ограничениях:
1) граф Таннера полученной матрицы Н=[H z H i ] должен иметь распределение степеней узлов, приблизительно равное целевому распределению;
2) следует избегать кодовых слов низкого веса;
3) в более широком смысле, следует избегать малых наборов остановки в H , то есть ограничение ACE≥η для некоторых η должно быть удовлетворено;
4) следует избегать циклов длиной 4;
5) H i должно быть структурировано.
Эти руководящие принципы осуществлены в алгоритме для построения H i.
Предлагается построить H i двумя этапами. Во-первых, расширим s x t матрицу шаблона P , то есть заменим ее элементы pij, которые удовлетворяют условию 0≤pij<∞, матрицами циклических перестановок размера p×p, имеющими значение 1 в позициях (r,(p ij +r)mod p), r=0.. p-l, i=0.. s-l и j=0.. t-1. Заменим все другие элементы P нулевыми матрицами размера p×p . Первая матрица H u получена расширением матрицы Р шаблона. Во-вторых, выполним перестановку (чередование) строк первой матрицы H u. Это приводит к sp×tp матрице H i. Одна возможная перестановка строк задана прямоугольным перемежителем:

Здесь s, p и t являются параметрами построения. Применяя m 0 столбцов зигзага к H i, получаем m 0 ×n 0 матрицу Н проверки четности с m 0 =sp, n 0 =tp+m 0. Матрица Р шаблона является результатом процесса оптимизации, описанного ниже, с использованием матрицы-прототипа М, имеющей 1 в позициях (i, j): 0≤pij<∞ и 0 в других позициях.
Отметим, что
H
i может быть определена с максимум  целых чисел
p
ij, где
целых чисел
p
ij, где  является числом «1» в матрице-прототипе
М
.
является числом «1» в матрице-прототипе
М
.
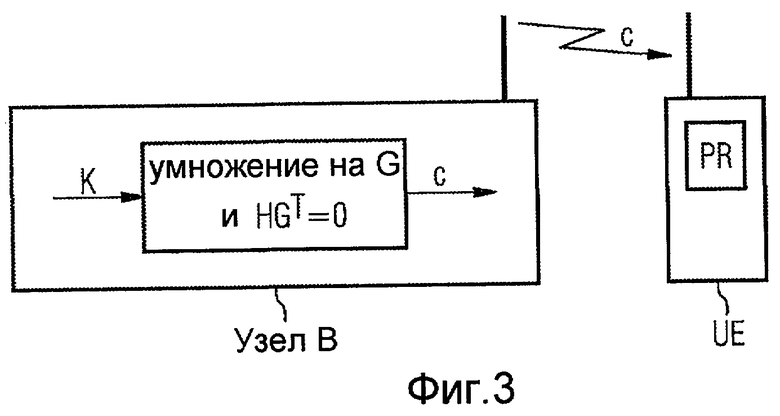
Фиг. 3 и фиг. 4 иллюстрируют варианты осуществления кодера для описанного кода, используемого для кодирования сообщения К данных в кодовое слово c. Сообщение К данных является, например, вектором k битов, который должен быть передан от передающей станции Узел B к принимающей станции UE. Принимающая станция UE содержит процессор PR для декодирования кодового слова c, в то время как декодирование включает использование матрицы Н проверки четности для выполнения алгоритма декодирования распространения достоверности и проверки четности кодового слова c.
На фиг. 3 кодовое слово c, которое может быть математически записано как c=[cz ci], генерируется умножением сообщения К данных на генераторную матрицу HGT=0. Матрица H=[H z H i ] проверки четности строится, как описано в самом последнем разделе.
На фиг. 4 еще более эффективный подход представлен при использовании генераторной матрицы G=[(Hz -1 Hi)TI]. Поэтому, если кодовое слово c математически записано как c=[cz ci], то умножение сообщения К данных и этой генераторной матрицы G дает в результате первый компонент ci, являющийся сообщением К данных, в то время как второй компонент cz задается как cz T = Hz -1HiKT. То есть второй компонент cz кодового слова c вычисляется с использованием перестановки строк путем умножения сообщения К данных на первую матрицу Hu и перестановки строк результата этого умножения и фильтрации результата. Альтернативно, перестановка строк может применяться к первой матрице Hu перед умножением на сообщение К данных. Матрица Н проверки четности, то есть матрицы Hi и Hz строятся таким же образом, как описано для фиг. 3.
Матрица-прототип М может быть построена различными способами, например вручную или с использованием алгоритма PEG [5], так чтобы она удовлетворяла приблизительно данную пару распределений степени узлов (Λ(x),R(x)) . Конкретные значения p ij целых чисел в матрице Р шаблона должны быть выбраны так, чтобы полученная матрица Н проверки четности удовлетворяла требованиям 1-5, представленным выше. Следующий раздел представляет рандомизированный алгоритм для их вычисления.
Алгоритм оптимизации
Идея алгоритма оптимизации, представленного ниже, заключается в том, что входные слова низкого веса после умножения на первую матрицу H u, перемежитель и 1/(1+D) фильтр, как показано на фиг. 4, не должны преобразовываться в векторы (cz,ci) низкого веса. Это весьма сходно с задачей конструирования перемежителей для турбо кодов.
Структура зигзагообразного шаблона образца позволяет вычислять вес вектора y = H z -1 x как
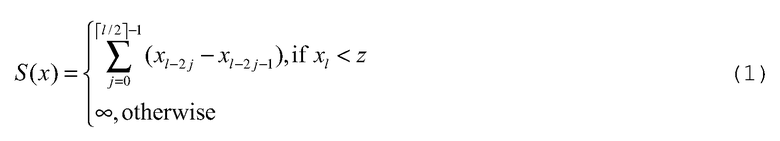
где z - число переменных узлов в зигзагообразном шаблоне, x j : 1≤x j <x j+1 <…≤ m, j = 1…l позиции ненулевых битов в векторе x на входе зигзагообразного кодера, и х 0 =0 . Это выражение принимает во внимание случай зигзагообразного шаблона, не покрывающего все узлы проверки в графе, и случай линейно зависимых столбцов в H i.
В принципе, это позволяет учитывать все возможные входные шаблоны, вычислять для данного набора p ij входной вектор x=H i c i T для 1/(1+D) фильтра, находить вес выхода фильтра и выводить минимальное расстояние d min полученного кода. Тогда можно выполнить максимизацию d min по всем возможным значениям p ij. Однако этот подход весьма непрактичен из-за экспоненциального числа входных шаблонов и огромного размера пространства поиска. Поэтому нужно ограничить область поиска сообщениями К данных из k битов, имеющими достаточно малый вес wt(K)≤α . Кроме того, оптимизация значений p ij может быть выполнена на основе столбец за столбцом, используя изменение генетического алгоритма:
1. Построить матрицу-прототип М с необходимым распределением степеней столбцов и строк.
2. Принять j: = 0 .
3. Генерировать p ij случайным образом для всех i s.t. M ij =1.
4. Удостовериться, что матрица  , полученная расширением первых j+1 столбцов матрицы Р шаблона и перестановкой строк расширенной матрицы соответствующим образом, не имеет циклов длины 4, и ее минимальная АСЕ не меньше, чем данный порог
η
. Это может быть осуществлено, эффективно используя алгоритмы, представленные в [13, 6]. При неудаче перейти к этапу 3.
, полученная расширением первых j+1 столбцов матрицы Р шаблона и перестановкой строк расширенной матрицы соответствующим образом, не имеет циклов длины 4, и ее минимальная АСЕ не меньше, чем данный порог
η
. Это может быть осуществлено, эффективно используя алгоритмы, представленные в [13, 6]. При неудаче перейти к этапу 3.
5. Учесть все возможные входные шаблоны.

Определить вес ассоциированных выходных векторов зигзагообразного кодера, используя (1), и найти минимальный вес кодового слова, который обозначен здесь S min.
6. Повторить этапы 3-5 данное количество раз и выбрать значения
p
ij, максимизирующие
S
min. Пусть  будет максимальным значением
S
min
.
будет максимальным значением
S
min
.
7. Пусть j:=j+1 .
8. Если j <t , перейти к этапу 1.
Отметим, что  задает верхнюю границу для минимального расстояния полученного кода. Ясно, что увеличение α, веса анализируемых входных векторов, улучшает точность этой оценки. На практике, для хорошо выбранных матриц-прототипов M, достаточно установить α≈5, чтобы получить
задает верхнюю границу для минимального расстояния полученного кода. Ясно, что увеличение α, веса анализируемых входных векторов, улучшает точность этой оценки. На практике, для хорошо выбранных матриц-прототипов M, достаточно установить α≈5, чтобы получить  , очень близкое к истинному минимальному расстоянию кода.
, очень близкое к истинному минимальному расстоянию кода.
Алгоритм, представленный выше, оптимизирует матрицу Р шаблона для фиксированного значения коэффициента р расширения. Однако возможно учесть одновременно несколько различных коэффициентов расширения, максимизирующих на этапе 6 взвешенную сумму оцененных минимальных расстояний кодов, полученных для той же самой матрицы Р шаблона, но различных коэффициентов р расширения. Как следствие, получается уникальная матрица Р шаблона для матриц проверки четности для ряда различных длин кода, но той же скорости.
Предложенный алгоритм обобщает методы, представленные в [8, 9, 14] несколькими путями. Во-первых, чередование строк первой матрицы H u можно рассматривать как дополнительную степень свободы в оптимизации кода LDPC. Алгоритм оптимизации, представленный выше, не зависит от этого явно. Во-вторых, нет никаких искусственных ограничений для значений p ij, получаемых из исходных алгебраических конструкций LDPC (сравни [8, 15]). Ценой этого является отсутствие выраженного в явной форме алгоритма для вычисления p ij. Но так как число этих значений является весьма малым по сравнению с размером матрицы Р шаблона (см. фиг. 5 и 8), это не представляет серьезного недостатка. В-третьих, процесс отыскания хороших кодов формализован, и количество попыток методом проб и ошибок сокращается. При условии, что доступна достаточная вычислительная мощность, предложенный алгоритм может сформировать надежные оценки минимального расстояния полученного кода, предоставляя таким образом ценную обратную связь разработчику кодов.
Численные результаты
Матрица Р шаблона на фиг. 5 может использоваться для конструирования кодов скорости 1/2, которые будут использоваться, например, в вариантах осуществления согласно фиг. 3 или 4. Каждый целочисленный элемент записи p ij должен быть заменен p×p циклической матрицей перестановки, заданной посредством p ij, в то время как элементы записи ∞ должны быть заменены p×p нулевыми матрицами. m0=s·p столбцов зигзага должны быть добавлены к ней после ее расширения и перестановки строк.
Используемая перестановка строк (прямоугольный перемежитель) представляет собой

Фиг. 6 представляет результаты моделирования, иллюстрирующие характеристики полученных кодов в канале AWGN, а также характеристики кодов PEG и IEEE 802.16 [16] с подобными параметрами.
Можно заметить, что предложенный код превосходит коды IEEE, и в некоторых случаях даже полностью случайные коды PEG, которые в настоящее время считаются лучшими с точки зрения характеристик.
Фиг. 7 иллюстрирует характеристики кода скорости 2/3, и фиг. 8 представляет компактное представление соответствующей матрицы Р шаблона. Используемая перестановка строк (прямоугольный перемежитель) имеет вид:

Можно видеть, что предложенный код значительно превосходит код IEEE.
Был представлен способ формирования структурированных нерегулярных кодов LDPC. Формирование кода основано на матрице блочной перестановки с дополнительной перестановкой строк. Параметры матрицы перестановки заполняются посредством алгоритма оптимизации, который пытается максимизировать кодовое минимальное расстояние. Числовые результаты указывают, что коды, полученные этим способом, имеют превосходное минимальное расстояние и никакого видимого минимального уровня ошибок.
Предложенный метод формирования допускает множество обобщений и усовершенствований. Например, возможно заменить матрицы циклических перестановок некоторыми другими параметрическими перестановками, например, основанными на полиномах перестановки. Во-вторых, дополнительные критерии эффективности LDPC могут быть объединены в алгоритм оптимизации.
Соответствующее изобретению формирование кодов с различными длинами
Изобретателями установлено, что, начиная с матрицы H=[Hz Hi] проверки четности кода с длиной n0, где Hz представляет собой матрицу m0×m0 с двумя смежными диагоналями из l, имеющую во всех других позициях 0, и Hi представляет собой матрицу m0×(n0×m0), коды с длиной w·m0 могут быть сконструированы с использованием матрицы проверки четности H'=[Hz' Hi'], если Hz' выбрана как матрица w·m0×w·m0 с двумя смежными диагоналями из 1, имеющая 0 во всех других позициях, и Hi' является матрицей w·m0×w·(n0-m0), полученной чередованием строк блочно-диагональной матрицы Hi'(w), имеющей w матриц Hi размера m0×(n0-m0) на диагонали и 0 во всех других позициях.
Матрица Н, в частности Hi, может быть сконструирована, как описано выше со ссылками на фиг. 2-8. Разумеется, также другие конструкции Н могут быть использованы для изобретения.
Если, например, w=2, Hi '(2) задается следующим образом:
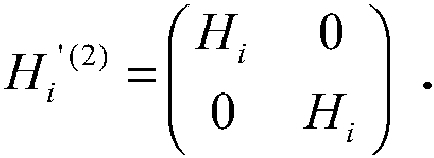
И H' в этом случае задается соотношением H'=[Hz' Π Hi'(2)], например, с перестановкой

Кодовое слово c', которое может математически быть записано как c'=[cz' ci'], генерируется умножением сообщения K' данных на генераторную матрицу G', которая должна удовлетворять уравнению H'G'T=0.
Заметим, что систематическое кодирование сообщения K' данных может быть выполнено умножением K' на генераторную матрицу G', согласно уравнению G'=[((Hz')-1 Hi')T I].
Кодирование и декодирование для генерации кодового слова c' с длиной w·n0 эквивалентно выполняются, как описано в связи с фиг. 3 и 4, используя H' и G' вместо H и G.
Для примера, характеристика FER (частота ошибок кадров как функция отношения сигнала к шуму Eb/N0) кодов скорости 2/3, построенных согласно изобретению и имеющих длины w·360, w=l, 2, 3, и характеристика кодов тех же самых длин, построенных с использованием различных коэффициентов р расширения, показаны на фиг. 9. Характеристика соответствующих изобретению кодов лишь незначительно хуже, чем характеристика кодов, использующих соответствующие коэффициенты р расширения. Но преимущество состоит в том, что структура декодера, которая может использоваться для кода с длиной 360 и которая обычно реализуется соответствующими компонентами аппаратных средств, может поддерживаться для кодов с длиной w·360, тогда как структура декодера изменяется для кодов той же самой длины, построенных путем выбора соответствующего коэффициента р расширения.
Заявленный способ для получения более длинных кодов LDPC может быть основан на других основанных на зигзаге конструкциях, как, например, в [14].
Список литературы








Изобретение относится к способам кодирования и декодирования сообщения К' данных для передачи от передающей станции к принимающей станции. Представлена новая конструкция нерегулярных кодов LDPC, которая позволяет получать ряд кодов с различной длиной из единственного кода-прототипа с матрицей проверки четности, заданной как H=[Hz Hi], где Hz определяет хорошо известный шаблон соответствующего графа Таннера. Матрицы проверки четности для более длинных кодов получаются как [Hz' П diag(Hi,…,Hi), где Hz' определяет более длинный зигзагообразный шаблон в зависимости от числа использованных матриц Нi, и П представляет некоторую перестановку. Технический результат - создание улучшенного способа для кодирования и декодирования сообщения данных для более длинного кода путем повторного использования компонентов аппаратных средств, разработанных для декодирования кода-прототипа. 4 н. и 8 з.п. ф-лы, 9 ил.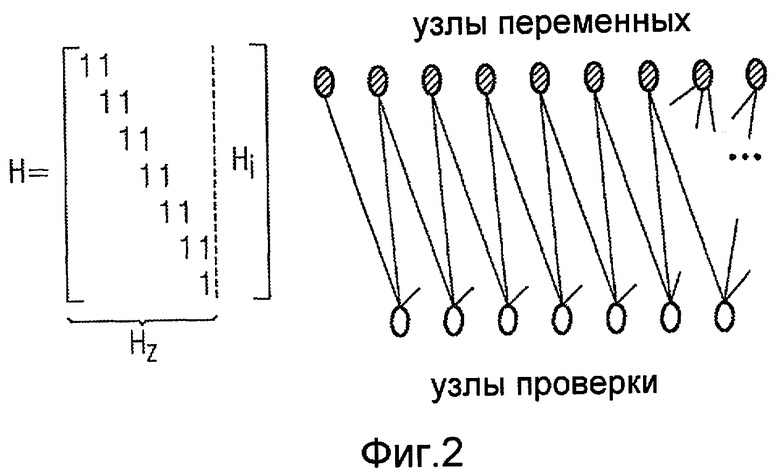
1. Способ кодирования сообщения К' данных в передающей станции, для передачи от принимающей станции к принимающей станции, в котором в передающей станции генерируют кодовое слово с' длины n=w·n0, где w и n0 - целые числа, причем генерация кодового слова с' реализуется посредством умножения, выполняемого блоком кодирования передающей станции, сообщения К' данных на генераторную матрицу G', c'=K'G', причем генераторная матрица G является решением матричного уравнения H'G'T=0, при H'=[Hz' Hi'], где Hz' является матрицей w·m0×w·m0 с двумя смежными диагоналями из 1, имеющей 0 во всех других позициях, и Hi' является матрицей w·m0×w·(n0-m0),
отличающийся тем, что
Нi' является матрицей, полученной чередованием строк блочно-диагональной матрицы Нi'(w), имеющей w матриц Нi размера m0×(n0-m0) на диагонали и 0 во всех других позициях, причем Нi дополнительно выбрана таким образом, что H=[Hz Нi] является матрицей проверки четности кода с длиной n0, где Hz является матрицей m0×m0 с двумя смежными диагоналями из 1, имеющей 0 во всех других позициях.
2. Способ по п.1, в котором Нi дополнительно выбирается таким образом, что при кодировании сообщения К данных, используя генераторную матрицу G, передающая станция генерирует кодовое слово с длины n0, c=KG, где генераторная матрица G является решением матричного уравнения HGT=0, при H=[Hz Hi], где Hz является матрицей m0×m0 с двумя смежными диагоналями из 1, имеющей 0 во всех других позициях.
3. Способ по п.1, в котором Hi получается чередованием строк первой матрицы Нu, которая является блочной матрицей, состоящей из матриц перестановки и нулевых матриц.
4. Способ по любому из пп.1-3, в котором передающая станция использует генераторную матрицу G', которая удовлетворяет условию G'=[((Hz')-1Hi')TI].
5. Способ по любому из пп.1-3, в котором передающая станция использует прямоугольный перемежитель для перемежения строк блочно-диагональной матрицы Нi'(w), то есть использует перестановку
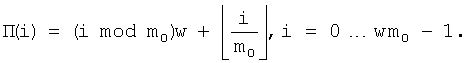
6. Способ по п.4, в котором первая матрица Нu генерируется передающей станцией посредством расширения матрицы Р шаблона размера s×t, причем расширение выполняется заменой всех элементов рij матрицы Р шаблона, которые удовлетворяют условию 0≤рij<∞, матрицами циклических перестановок размера р×р, имеющими значение 1 в позициях (r,(рij+r) mod р), при r=0… p-1, i=0… s-1 и j=0… t-1, и заменой всех других элементов рij, которые удовлетворяют условию рij=∞, или рij<0, нулевыми матрицами размера р×р, где рij - некоторые целые числа.
7. Способ по п.5, в котором первая матрица Нu генерируется передающей станцией посредством расширения матрицы Р шаблона размера s×t, причем расширение выполняется заменой всех элементов рij матрицы Р шаблона, которые удовлетворяют условию 0≤рij<∞, матрицами циклических перестановок размера р × р, имеющими значение 1 в позициях (r,(рij+r) mod р), при r=0…p-1, i=0…s-1 и j=0…t-1, и заменой всех других элементов рij, которые удовлетворяют условию рij=∞, или рij<0, нулевыми матрицами размера р×р, где рij - некоторые целые числа.
8. Способ по п.6, в котором передающая станция использует прямоугольный перемежитель для перемежения строк первой матрицы Нu, то есть использует перестановку

9. Способ по п.7, в котором передающая станция использует прямоугольный перемежитель для перемежения строк первой матрицы Нu, то есть использует перестановку
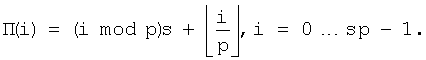
10. Передающая станция, содержащая:
блок кодирования, чтобы кодировать сообщение К' данных в кодовое слово с' длины n=w·n0, где w и n0 - целые числа, причем блок кодирования генерирует кодовое слово с' посредством умножения сообщения К' данных на генераторную матрицу G', c'=K'G', при этом генераторная матрица G' является решением матричного уравнения H'G'T=0, при H'=[Hz' Hi'], где Hz' является матрицей w·m0×w·m0 с двумя смежными диагоналями из 1, имеющей 0 во всех других позициях, и Нi' является матрицей w·m0×w·(n0-m0),
отличающаяся тем, что
Hi' является матрицей, полученной чередованием строк блочно-диагональной матрицы Нi'(w), имеющей w матриц Нi размера m0×(n0-m0) на диагонали и 0 во всех других позициях, причем Нi дополнительно выбрана таким образом, что H=[Hz Hi] является матрицей проверки четности кода с длиной n0, где Hz является матрицей m0×m0 с двумя смежными диагоналями из 1, имеющей 0 во всех других позициях.
11. Способ для декодирования сообщения К' данных из кодового слова с', принятого от передающей станции, в которой принимающая станция использует матрицы Н' проверки четности, сформированную согласно одному из пп.1-3.
12. Принимающая станция, содержащая средство для декодирования кодового слова с', принятого от передающей станции, причем средство для декодирования осуществляет декодирование с использованием матрицы Н' проверки четности, сформированной согласно одному из пп.1-3, для проверки четности кодового слова с'.
| Пломбировальные щипцы | 1923 |
|
SU2006A1 |
| СИСТЕМА ДЛЯ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ С ИСПРАВЛЕНИЕМ ОШИБОК | 1991 |
|
RU2007042C1 |
| Способ обработки целлюлозных материалов, с целью тонкого измельчения или переведения в коллоидальный раствор | 1923 |
|
SU2005A1 |
| US 2002042899 A1, 2002.04.11 | |||
| Подмости | 1979 |
|
SU806839A1 |
| СПОСОБ СЖАТИЯ И ВОССТАНОВЛЕНИЯ СООБЩЕНИЙ | 2003 |
|
RU2246798C1 |
Авторы
Даты
2011-12-27—Публикация
2007-04-26—Подача