Область техники, к которой относится изобретение
Настоящее изобретение относится к системам записи информации для записи информации большого объема, когда используются наборы из нескольких запоминающих устройств, чаще всего дисковых. В частности, данное изобретение к способу и системе восстановления записей в запоминающем устройстве и к машиночитаемому носителю с соответствующей программой.
Уровень техники
Для запоминания больших объемов информации используются запоминающие устройства, составленные из дисковых массивов. Эти массивы из нескольких дисков обычно построены по технологии RAID (Redundant Array of Inexpensive Disks, массив резервных недорогих дисков; иногда это сокращение раскрывают как Redundant Array of Independent Disks, массив резервных независимых дисков). Такие массивы состоят из нескольких дисков, управляемых контроллером и взаимосвязанных скоростными каналами передачи данных. Внешняя система «воспринимает» такой массив как единое целое. В настоящее время применяется технология RAID-6, согласно которой в набор дисков добавляют два дополнительных диска, хранящих постоянно обновляемые контрольные суммы. Благодаря этому обеспечивается возможность восстановления информации в случае выхода из строя одного или двух дисков в массиве (См., например, Anvin, H.P. (21 May 2009 г.). The mathematics of RAID-6. Получено 18 ноября 2009 года по адресу http://ftp.kernel.org/pub/linux/kernel/people/hpa/raid6.pdf).
Способы и системы восстановления записей в массивах RAID-6 описаны в таких патентных документах: патенты США №№5499253 (опубл. 12.03.1996), 5948110 (опубл. 07.09.1999), 6148430 (опубл. 14.11.2000), 6823425 (опубл. 23.11.2004), 6891690 (опубл. 10.05.2005), 6959413 (опубл. 25.10.2005), 7076606 (опубл. 11.07.2006), 7343546 (опубл. 11.03.2008), 7360143 (опубл. 15.04.2008), 7392458 (опубл. 24.06.2008), 7437658 (опубл. 14.10.2008), 7600176 (опубл. 06.10.2009); в заявках на патент США №№2008/0177815 (опубл. 28.07.2008), 2009/0024879 (опубл. 22.01.2009), 2009/0132851 (опубл. 21.05.2009); в заявке Великобритании №2429809 (опубл. 07.03.2007); в выложенных заявках Японии №№08-171463 (опубл. 02.07.1996) и 2000-259359 (опубл. 22.09.2000).
Однако все эти технические решения весьма сложны вследствие того, что вычисления в них выполняются с использованием арифметики конечных полей или полей Галуа, и все ухищрения в этих и некоторых иных патентных документах направлены на некоторые упрощения при таких вычислениях. Поясним это утверждение следующим образом.
Как показано на чертеже, дисковый массив состоит из N дисков данных, обозначенных D1, D2, …, DN, и два контрольных диска, обозначенных Р и Q. Каждый диск в наборе рассматривается как набор из S байтов, причем все диски имеют одинаковый размер, т.е. содержат одинаковое количество байтов S. Байт с номером j на i-м диске Di данных обозначен как dij. Для байтов с одинаковыми номерами i с каждого диска Di рассчитываются две контрольные суммы по специальному алгоритму. Каждая сумма тоже имеет размер один байт. Эти два байта (на фиг.1 они обозначены как р и q) записываются на контрольные диски Р и Q под тем же номером j.
Вычисления контрольных сумм производится по нижеследующим формулам (1'), (2'):
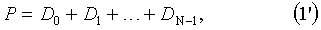
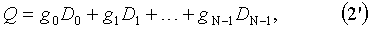
где gi есть некоторые коэффициенты.
Тогда в случае отказа двух дисков данных с номерами х и y для восстановления утраченной информации необходимо решить данную систему уравнений относительно DX и DY.
Технически это выглядит таким образом, что при попытке чтения информации с отказавших дисков данных производится решение системы уравнений (1') и (2') относительно DX и DY и полученный результат возвращается в качестве результата операции чтения.
Однако сложность указанных вычислений существенно возрастает с размером слова. Поэтому используются слова размером всего в один байт. Причина роста сложности состоит в необходимости применять арифметику конечных полей (полей Галуа), а в наборе команд современных компьютеров нет соответствующих команд. Поля Галуа «большого размера» очень сложно построить, но еще сложнее производить в них вычисления.
В данном контексте сложность следует понимать как необходимость большого количества вычислений, которые требуют временных затрат и, соответственно, снижают производительность дисковых массивов.
В действительности вычисления в полях Галуа организуются как вычисления с многочленами по модулю некоторого неприводимого многочлена. Т.е. каждый байт рассматривается как набор коэффициентов многочлена. Например, байт 10011011, у которого разряды соответствуют степеням двойки, начиная с 0 (справа) и кончая 7 (слева), можно рассматривать как следующий многочлен: х7+х4+х3+х1+1. Соответственно, коэффициенты могут быть равны только нулю и единице, а для операций сложения, умножения и деления необходимо создавать специальные подпрограммы. Эти подпрограммы должны осуществлять обычные арифметические операции с многочленами (сложение, умножение), после чего находить остаток от деления результата на некоторый специальный многочлен, именуемый «порождающим». Этот многочлен должен обладать важным свойством: он должен быть неразложим на множители.
Существенно, что при вычислениях по наиболее трудоемким формулам (2') и (3') основными операциями являются операция умножения на многочлен х и нахождение остатка от деления на «порождающий» многочлен.
Для ускорения вычислений могут использоваться заранее подготовленные таблицы умножения. Таблицы помогают ускорить вычисления, но их размер слишком быстро возрастает с размером поля, и поэтому практически они могут быть использованы только с полями, элементы которых имеют размер в один байт. В существующих реализациях диски данных разбиваются на байты, и вычисления повторяются столько раз, сколько имеется байтов на диске данных.
Раскрытие изобретения
Таким образом, имеется необходимость в разработке такого технического решения, которое обеспечивало бы существенное увеличение скорости расчетов при восстановлении дисков. Следует отметить, что диски в принципе являются лишь одним из наиболее распространенных вариантов объемной памяти, так что предлагаемое изобретение направлено в общем случае на любое запоминающее устройство.
Для решения поставленной задачи и достижения вышеуказанного технического результата в первом объекте по настоящему изобретению предложен способ восстановления записей в запоминающем устройстве, заключающийся в том, что: разделяют область памяти запоминающего устройства на информационные зоны и контрольные зоны; записывают каждую группу подлежащих запоминанию данных в виде набора кодовых слов в соответствующую информационную зону; находят при каждой записи подлежащих запоминанию данных в запоминающее устройство с помощью соответствующего вычислительного блока по меньшей мере две эталонных контрольных суммы, каждую по соответствующей заранее установленной формуле, для каждого набора кодовых слов с одинаковыми номерами во всех информационных зонах; записывают каждую из найденных контрольных сумм в виде кодового слова с тем же номером в соответствующую контрольную зону; в процессе использования запоминающего устройства неоднократно вычисляют с помощью вычислительного блока текущие контрольные суммы по заранее установленным формулам для каждого набора кодовых слов с одинаковыми номерами во всех информационных зонах; сравнивают с помощью вычислительного блока каждую из вычисленных текущих контрольных сумм с соответствующей эталонной контрольной суммой для набора кодовых слов с теми же номерами, записанной в соответствующую контрольную зону, для определения синдрома ошибок; при определении синдрома ошибок заменяют выявленные ошибки записи правильными значениями; при этом выявление ошибок записи производят путем соответствующих вычислений с помощью вычислительного блока над многочленами, в которых в качестве коэффициентов используют кодовые слова с одинаковыми номерами во всех информационных зонах, а в качестве порождающего многочлена, по модулю которого производят соответствующие вычисления над многочленами, используют такой многочлен, который не обладает свойством неразложимости на множители и порождает конечное кольцо.
Для решения той же задачи и достижения того же технического результата во втором объекте по настоящему изобретению предложена система для восстановления записей в запоминающем устройстве, содержащая запоминающее устройство, включающее в себя N информационных зон и по меньшей мере две контрольные зоны, и вычислительный блок, при этом каждая из N информационных зон запоминающего устройства выполнена с возможностью записи в нее группы подлежащих запоминанию данных в виде набора кодовых слов; каждая из по меньшей мере двух контрольных зон запоминающего устройства выполнена с возможностью записи в нее соответствующей контрольной суммы; вычислительный блок выполнен с возможностью нахождения по меньшей мере двух эталонных контрольных сумм, каждую по соответствующей заранее установленной формуле, для каждого i-го набора кодовых слов, где i=0, …, N-1, во всех N информационных зонах при каждой записи подлежащих запоминанию данных в запоминающее устройство; неоднократного вычисления, в процессе использования запоминающего устройства, текущих контрольных сумм по заранее установленным формулам для каждого i-го набора кодовых слов во всех N информационных зонах; сравнения каждой из вычисленных текущих контрольных сумм с соответствующей эталонной контрольной суммой, записанной в соответствующую из контрольных зон, для определения синдрома ошибок; выявления ошибок записи путем соответствующих вычислений над многочленами, при которых в качестве коэффициентов используют кодовые слова с одинаковыми номерами во всех N информационных зонах, а в качестве порождающего многочлена, по модулю которого производят соответствующие вычисления над многочленами, используют такой многочлен, который не обладает свойством неразложимости на множители и порождает конечное кольцо.
Особенность как способа, так и системы по настоящему изобретению состоит в том, что количество вычисляемых контрольных сумм может быть равно двум, в качестве заранее установленных формул для вычисления контрольных сумм можно использовать формулы
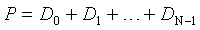 и
и
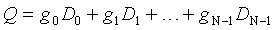 ,
,
где Di - i-ая информационная зона, в которую записаны кодовые слова di1, di2, …, diS; i=0, …, N-1; gi - коэффициент, S - количество кодовых слов, которое можно записать в i-ую информационную зону, а ошибки записи выявляют путем решения получающейся из этих формул системы уравнений. При этом в качестве порождающего многочлена можно использовать многочлен вида х128+х7+х2+х+1.
Еще одна особенность как способа, так и системы по настоящему изобретению состоит в том, что вычислительный блок может как входить в состав запоминающего устройства, так и быть внешним блоком по отношению к запоминающему устройству.
Наконец, для решения той же задачи и достижения того же технического результата в третьем объекте по настоящему изобретению предложен машиночитаемый носитель, предназначенный для непосредственного участия в работе компьютера и содержащий компьютерную программу, при исполнении которой в компьютере выполняются действия вышеупомянутого способа.
Краткое описание чертежей
Настоящее изобретение иллюстрируется чертежом, который условно показывает известный в уровне техники дисковый массив в качестве запоминающего устройства.
Подробное описание варианта осуществления изобретения
Нижеследующее подробное описание сделано на основе иллюстративного примера, в котором запоминающее устройство представляет собой дисковый массив, построенный по технологии RAID-6. He надо, однако, думать, что настоящее изобретение ограничивается только такими запоминающими устройствами. Разумеется, настоящее изобретение может быть не менее эффективно применено и к запоминающим устройствам иного типа, например к запоминающим устройствам, построенным на основе флэш-памяти.
Суть настоящего изобретения заключается в предложении использовать не поля Галуа, а конечные кольца, в которых имеется достаточное количество обратимых элементов, чтобы было возможно решить уравнения (1') и (2'), а также использовать многочлен, не обладающий свойством неразложимости на множители, в качестве порождающего многочлена.
Рассмотрим вначале подробнее те преобразования, которые осуществляются при вычислениях в полях Галуа для дискового массива.
Каждый диск массива будем рассматривать как множество слов и будем рассматривать вычисления внутри одного слова, подразумевая, что одинаковые вычисления производятся над всеми словами.
Пусть имеется N дисков данных D0, D1, D2, …, DN-1.
Вычислим значение величины Р, именуемой синдромом
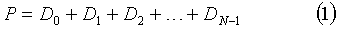
Тогда в случае утраты одного диска Dx данных для его восстановления достаточно будет решить уравнение (1) относительно этого диска. Если в качестве операции сложения использовать операцию побитового сложения по модулю два, то можно записать
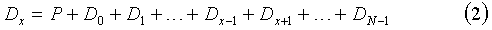
Для защиты от утраты двух или более дисков необходимо составить систему из линейно независимых уравнений, решение которых позволит восстановить утраченные диски в количестве, равном количеству уравнений в системе. Для нас практический интерес представляет система из двух уравнений, позволяющая восстанавливать данные в случае потери двух дисков
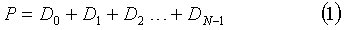
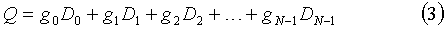
Если обозначить потерянные диски Dx и Dy, то для восстановления Dy имеем
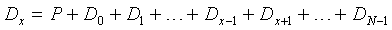
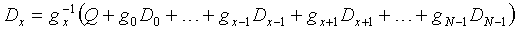
Объединив эти два уравнения и учитывая, что в качестве операции сложения используем побитовое сложение по модулю два, имеем
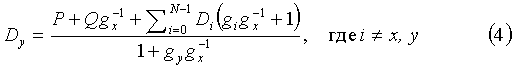
Имея значение Dy и используя (2), можно восстановить и значение Dx. Но для того, чтобы вычисления по формуле (3) состоялись, кроме операции сложения нам необходимо иметь в своем распоряжении операцию умножения, а для вычислений по формуле (4) еще и операцию нахождения обратного элемента (деление). Поэтому для построения массивов RAID-6 обычно используется арифметика конечных полей (полей Галуа), т.к. именно поля представляют собой алгебраические структуры, которые имеют операции умножения, сложения и деления на ненулевой элемент и замкнуты относительно этих операций.
Здесь важен тот факт, что требование обратимости всех ненулевых элементов для вычислений по формуле (4) является избыточным. Достаточно того, чтобы обратимыми были выражения gx и 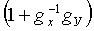 для х≠y, 0<х, y<N. Иными словами, нет необходимости строить поле Галуа, достаточно найти подходящее кольцо.
для х≠y, 0<х, y<N. Иными словами, нет необходимости строить поле Галуа, достаточно найти подходящее кольцо.
Обратимся теперь к общей структуре и расширениям полей Галуа.
Пусть имеется простое поле GF(p). Его расширение до поля CF(ps) может осуществляться путем присоединения корней многочлена xq-1-1, где q=ps. При этом мультипликативная группа поля состоит из корней из единицы в степени s. Рассмотрим случай, когда s разлагается на множители s=nk. Все корни из единицы степени n являются и корнями степени s=nk. Это означает, что поле GF(pn) лежит в поле GF(pnk). Говоря иными словами, поле GF(pnk) является расширением поля GF(pn) степени k. Соответственно, оно может быть получено построением кольца многочленов GF(pn)[x] и дальнейшей факторизацией по модулю некоторого многочлена φ(х) степени k, неприводимого над GF(pn).
Прикладное значение этого факта состоит в том, что, имея реализацию вычислений в поле GF(pn) можно свести вычисления в большем поле GF(pnk) к полиномиальной арифметике по модулю φ(х).
Сейчас важно обратить внимание на факт замкнутости поля относительно операций сложения, умножения и деления. Поскольку операции с многочленами сводятся к последовательности операций с их коэффициентами, кольцо многочленов над GF(pn) лежит внутри кольца многочленов над GF(pnk). Это же наблюдение в полной мере относится и к конечным кольцам многочленов, полученных путем факторизации по модулю многочлена над GF(pn). А отсюда немедленно следует важное прикладное утверждение:
Лемма 1. Пусть ℜ[х]/φ(х) - конечное кольцо многочленов над GF(pn) по модулю некоторого многочлена φ(х), а ℜ'[х]/φ(х) - конечное кольцо многочленов над GF(pnk) по модулю того же многочлена. Тогда, если элемент ν∈ℜ[x]/φ(х) обратим в ℜ[х]/φ(х), то он обратим и в ℜ[х]/φ(х).
У этой леммы есть два интересных в прикладном смысле частных случая.
Во-первых, если φ(х) неприводим над ℜ[х], то ℜ[х]/φ(х) является полем, а значит в нем обратимы все ненулевые элементы. В соответствии с вышеприведенной леммой они же будут обратимы и в расширении ℜ'[x]/φ(x). Это означает, что если для вычисления синдрома (3) выбраны gi из некоторого поля, то можно использовать их и для вычислений в расширении этого поля.
Во-вторых, при р=2 и n=1 все элементы ℜ[х]/φ(х) являются многочленами с коэффициентами из GF(2), т.е равны 0 или 1. Это означает, что и в расширении ℜ'[x]/φ(x) при вычислении по уравнениям (3) и (4) все операции умножения сводятся к умножению на 0 и 1, которое можно считать умножением только в фундаментальном смысле. Опираясь на данный факт, при построении дисковых массивов RAID-6 можно вообще исключить трудоемкую операцию умножения в полях Галуа.
В дальнейшем нас будут интересовать только различные расширения поля GF(2). Элементы этого поля будем обозначать 0 и 1, и в качестве операций поля будем использовать сложение по модулю два и логическое умножение (конъюнкцию).
Многочлены с коэффициентами GF(2) будем записывать в виде последовательности нулей и единиц, начиная со старшего коэффициента, и для краткости записи естественным образом преобразовывать их в шестнадцатиричное число. Например
x5+x2+1→100101→25
х4+х+1→10011→13.
Поскольку элементы поля GF(2n) и вообще произвольного конечного кольца GF(2)[x]/φ(x) можно представить в виде многочленов, естественным образом распространим на них эту форму записи.
В дальнейшем записанное таким образом поле (или кольцо) будем называть базовым.
Продолжим расширение базового поля до кольца многочленов GF(2n)[y]. Будем записывать элементы этого кольца в виде набора коэффициентов из базового поля, начиная с младшего. Например
7y2+y+12→(12, 1, 7)
25y4+13y2+1→(1, 0, 13, 25)
Так как элементы произвольного конечного кольца GF(2n)[y]/ψ(y) (в том числе и элементы поля GF(2nk)) можно, в свою очередь, представить как многочлены над GF(2n), распространим на них эту же форму записи.
Операции умножения и сложения в кольцах многочленов сводятся к операциям сложения и умножения их коэффициентов в базовом поле. При вычислениях в конечных кольцах возникает необходимость использовать и операцию нахождения остатка от деления на многочлен, по модулю которого построено кольцо. Это, в свою очередь, влечет за собой необходимость использования операции деления на старший коэффициент ψ(х). В дальнейшем при построении конечного кольца всегда будем использовать многочлен со старшим коэффициентом, равным единице (Это, кстати, позволяет аналогичным образом строить расширения не только полей Галуа, но и любых конечных коммутативных колец с единицей).
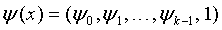
Для вычислений синдрома Q по формуле (3) удобно выбрать некий элемент g и построить все необходимые элементы gi по формуле
gi=gi+1, где i=0, …, n-1.
Тогда вычисления синдрома Q можно будет проводить по схеме Горнера
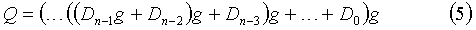
Формула (4) для вычисления потерянного диска при этом может быть записана следующим образом
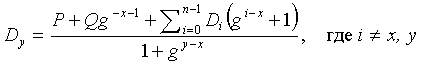
Или
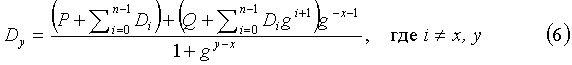
Запись в виде (6) позволяет также использовать схему Горнера при вычислении наиболее трудоемкой части, а именно второй суммы в числителе.
Нужно только быть уверенным в том, что все gi - разные. С алгебраической точки зрения это означает, что порядок выбранного элемента g в кольце должен быть меньше количества защищаемых дисков. Т.е.
gi≠g, где ∀i: 0<i<N.
В качестве элемента g удобно выбрать многочлен (0, 1). Тогда умножение произвольного многочлена на этот многочлен в нашей форме записи сводится к сдвигу на один разряд вправо и сложению
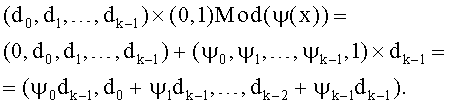
Для выполнения этой операции в общем случае требуется k операций умножения и k-1 операций сложения. Но есть шанс найти такой полином ψ(х), коэффициенты которого равны только 0 и 1, причем количество нулей достаточно велико. Действительно, в соответствии с леммой 1 достаточно найти ψ(x) с коэффициентами из GF(2) и затем использовать его в расширении GF(2n), причем n может быть сколь угодно большим. При этом не нужно даже проверять неприводимость полинома, достаточно проверить, что элемент g=(0, 1) обратим, а также обратимы все (1+gy-x) для х≠y, 0<x, y<N.
Таким свойством при N=100 обладает, например, полином
x128+x7+x2+x+1.
Для выполнения операции умножения на элемент (0,1) по модулю этого многочлена необходимо осуществить четыре операции сложения в базовом поле. На самом деле, поскольку в базовом поле умножения не осуществляется, задачи построения поля вообще не существует. В качестве элементов этого базового поля можно использовать сколь угодно большую последовательность битов с операцией сложения по модулю два.
Для сравнения выберем элемент g из базового поля g=(g0). Тогда операция умножения сведется к умножению всех коэффициентов на g0 в базовом поле
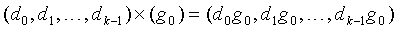 .
.
Именно таким образом производятся вычисления в классическом варианте. Каждый диск разбивается на байты, вычисления в которых производятся независимо друг от друга. Здесь же это частный случай. Для осуществления одной операции умножения на g он требует k операций умножения в базовом поле. Для сравнения, в предыдущем примере, который требовал только четырех операций сложения, k=128. При этом в отличие от предыдущего варианта g0 не может быть равным единице и, соответственно, операции умножения нетривиальны.
Итак, суть предложенного метода вычислений состоит в том, что вычисления будут осуществляться с многочленами, но в качестве коэффициентов этих многочленов будем брать не отдельные биты, а элементы «небольших полей» целиком, то есть, например, байты. Для следующих четырех байтов 10011011, 11011001, 00010011, 10100111 (половинки которых можно обозначить шестнадцатеричными цифрами: 9В, D9, 13, А7) получим при этом следующий полином: 9Вх3+D9x2+13х1+А7.
Набор байтов, таким образом, рассматривается как набор коэффициентов многочлена. В существующем решении вычисления в каждом байте производятся независимо, тогда как в нашем случае набор отдельных байтов объединяется в многочлен и вычисления по формулам (1)-(4) теперь производятся не с каждым байтом по отдельности, а целиком со всем набором. При этом, как и в существующем решении, самыми часто употребимыми операциями являются умножение на многочлен х и деление на «порождающий» многочлен. В случае, если порождающий многочлен является разреженным (то есть имеющим большое количество нулевых коэффициентов) количество необходимых вычислений с коэффициентами оказывается намного меньшим, чем в существующем решении.
В качестве «порождающего» многочлена используется многочлен, не обладающий свойством неразложимости. При этом данный многочлен порождает не поле, а другую структуру, именуемую кольцом. Существенное отличие кольца от поля состоит в том, что в кольце не на все элементы можно делить. Но требование делимости на все элементы является избыточным. В соответствии с формулой (3) достаточно иметь возможность осуществлять деление только на некоторые элементы. Например, уже упоминавшийся многочлен
x128+x7+x2+х+1
имеет 124 нулевых коэффициента, 5 единичных и больше никаких. Нахождение остатка от деления на этот многочлен сводится к выполнению всего четырех операций сложения и позволяет «обработать» этими четырьмя сложениями 128 байт.
Итак, способ восстановления записей в запоминающем устройстве согласно настоящему изобретению осуществляется следующим образом.
В запоминающем устройстве область памяти разделяют на информационные зоны и контрольные зоны. Запоминающее устройство может быть, например, дисковым массивом, построенным по технологии RAID-6, тогда каждая из информационных и контрольных зон представляет собой отдельный диск. В случае, когда запоминающее устройство выполнено по-другому - например, по технологии флэш-памяти, - информационные и контрольные зоны могут быть выделены в общем объеме этой памяти. Важно лишь, чтобы информационные и контрольные зоны имели каждая одинаковый объем памяти и несовпадающие адреса в каждой из этих зон для соответствующих ячеек.
Разумеется, все информационные и контрольные зоны соединены между собой и работают под управлением одного и того же контроллера (или иного управляющего средства), который как раз и обеспечивает все последующие операции данного способа. Этот контроллер именуется далее (в том числе и в формуле изобретения) вычислительным блоком.
В соответствующую информационную зону записывают каждую группу подлежащих запоминанию данных в виде набора кодовых слов. Такие записи производят по мере поступления новых данных, как путем добавления записей в свободное место уже записанной информационной зоны, так и путем перезаписи всех данных, записанных в эту информационную зону. Эти записи могут осуществляться как автоматически (например, с заданным временным периодом), так и принудительно оператором.
При каждой очередной записи подлежащих запоминанию данных в упомянутое запоминающее устройство находят с помощью соответствующего вычислительного блока по меньшей мере две эталонных контрольных суммы. Каждая из этих эталонных контрольных сумм вычисляется по соответствующей заранее установленной формуле (например, по вышеуказанным формулам (1) и (2)) для каждого набора кодовых слов с одинаковыми номерами во всех информационных зонах. К примеру, две эталонные контрольные суммы вычисляются для всех первых ячеек во всех информационных зонах, еще две эталонные контрольные суммы вычисляются для всех вторых ячеек во всех информационных зонах (по тем же формулам, что и для первых ячеек) и так далее.
Каждую из найденных таким образом эталонных контрольных сумм записывают в виде кодового слова с тем же номером в соответствующую контрольную зону. В приведенном выше примере первую эталонную контрольную сумму (вычисленную, к примеру, по формуле (1)) для всех первых ячеек записывают в первую ячейку первой контрольной зоны, первую эталонную контрольную сумму для всех вторых ячеек записывают во вторую ячейку этой же первой контрольной зоны и т.д. А вот вторые эталонные контрольные суммы (вычисленные, в данном случае, по формуле (2)) для тех же ячеек записывают в ячейки с теми же номерами, но уже во вторую контрольную зону. Эти вычисления эталонных контрольных сумм производятся автоматически при каждой очередной записи в любую информационную зону.
В процессе использования запоминающего устройства неоднократно с помощью вычислительного блока вычисляют текущие контрольные суммы по заранее установленным формулам для каждого набора кодовых слов с одинаковыми номерами во всех информационных зонах. Т.е. при работе запоминающего устройства между очередными записями данных вычисляют - либо периодически, либо принудительно - текущие контрольные суммы. Для этого используют те же самые заранее установленные формулы (например, формулы (1) и (2)).
Далее каждую из вычисленных текущих контрольных сумм сравнивают с помощью того же вычислительного блока с соответствующей эталонной контрольной суммой для набора кодовых слов с теми же номерами, записанной в соответствующую контрольную зону, для определения синдрома ошибок.
Если синдром оказывается нулевым, что свидетельствует об отсутствии ошибок или сбоев, работу запоминающего устройства продолжают по-прежнему.
Если же при таком сравнении определено, что синдром ошибок имеет ненулевое значение, найденные по этому синдрому ошибки заменяют записи правильными значениями. Такое исправление ошибок является общеизвестным для специалистов в области кодирования с исправлением ошибок.
Отличие данного способа от известных состоит в том, что выявление ошибок записи с использованием ненулевого синдрома производят с помощью вычислительного блока путем соответствующих вычислений над многочленами, в которых в качестве коэффициентов используют кодовые слова с одинаковыми номерами во всех информационных зонах, а в качестве порождающего многочлена, по модулю которого производят соответствующие вычисления над этими многочленами, используют такой многочлен, который не обладает свойством неразложимости на множители и порождает конечное кольцо. Конкретные пояснения последнего действия приведены ранее.
Можно отметить, что вычислительный блок может входить в состав запоминающего устройства, т.е. быть его составной частью, но может быть и внешним средством по отношению к этому запоминающему устройству, например, в случаях, когда запоминающее устройство организовано в процессе работы из нескольких самостоятельных устройств. Так, внешнее средство в данном случае может быть сетевым сервером, управляющим работой нескольких баз данных, соединенных обслуживаемой им сетью.
Следует в заключение отметить, что по приведенному здесь описанию специалист может составить соответствующую программу, при исполнении которой в компьютере будут осуществляться действия способа по настоящему изобретению. Поэтому машиночитаемый носитель с такой программой, предназначенный для непосредственного участия в работе компьютера, является одним из объектов настоящего изобретения.
Еще одним объектом настоящего изобретения является система, содержащая вышеописанное запоминающее устройство и вычислительный блок, обеспечивающий описанное выше функционирование.
Можно добавить, что для ускорения вычислений по формуле (6) полезно заранее подготовить набор величин для gx-1 и (1+gy-x), где х, y=0, …, n-1, х≠y. Основных результатов можно достичь при организации параллельных вычислений, поскольку предложенный способ подразумевает большое количество сложений независимых данных любого размера.
| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для вычисления синдромов кода Рида-Соломона | 1990 |
|
SU1751860A1 |
| СПОСОБ И ДЕКОДИРУЮЩЕЕ УСТРОЙСТВО ИСПРАВЛЕНИЯ ДВУХ ОШИБОК В ПРИНИМАЕМОМ КОДЕ | 2006 |
|
RU2336559C2 |
| УСТРОЙСТВО ДЕКОДИРОВАНИЯ КОДОВ РИДА-СОЛОМОНА | 2006 |
|
RU2314639C1 |
| УСТРОЙСТВО КОДИРОВАНИЯ-ДЕКОДИРОВАНИЯ ИНФОРМАЦИИ | 1994 |
|
RU2115231C1 |
| Устройство для декодирования кодов Рида-Соломона | 1985 |
|
SU1309317A1 |
| Устройство кодирования и вычисления синдромов помехоустойчивых кодов для коррекции ошибок во внешней памяти ЭВМ | 1989 |
|
SU1656689A1 |
| Устройство мажоритарного декодирования кода Рида-Соломона по k-элементным участкам кодовой комбинации | 2015 |
|
RU2613760C2 |
| СПОСОБ ВОССТАНОВЛЕНИЯ ЗАПИСЕЙ В ЗАПОМИНАЮЩЕМ УСТРОЙСТВЕ И СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2012 |
|
RU2502124C1 |
| СПОСОБ КОНТРОЛЯ ЦЕЛОСТНОСТИ ДАННЫХ НА ОСНОВЕ НЕРАВНОМЕРНОГО КОДИРОВАНИЯ | 2023 |
|
RU2808759C1 |
| Устройство для кодирования циклических кодов | 1988 |
|
SU1569997A1 |
Изобретение относится к вычислительной технике. Технический результат заключается в увеличении скорости расчетов при восстановлении дисков. Способ восстановления записей в запоминающем устройстве, в котором при записи данных в информационные зоны запоминающего устройства в его соответствующие контрольные зоны заносят по меньшей мере две эталонных контрольных суммы, вычисленные по заранее установленным формулам, а в процессе использования запоминающего устройства неоднократно вычисляют с помощью вычислительного блока текущие контрольные суммы по тем же формулам для каждого набора кодовых слов с одинаковыми номерами во всех информационных зонах и сравнивают каждую из вычисленных текущих контрольных сумм с соответствующей эталонной контрольной суммой для нахождения синдрома ошибок и замены выявленных ошибок записи правильными значениями. 3 н. и 8 з.п. ф-лы, 1 ил.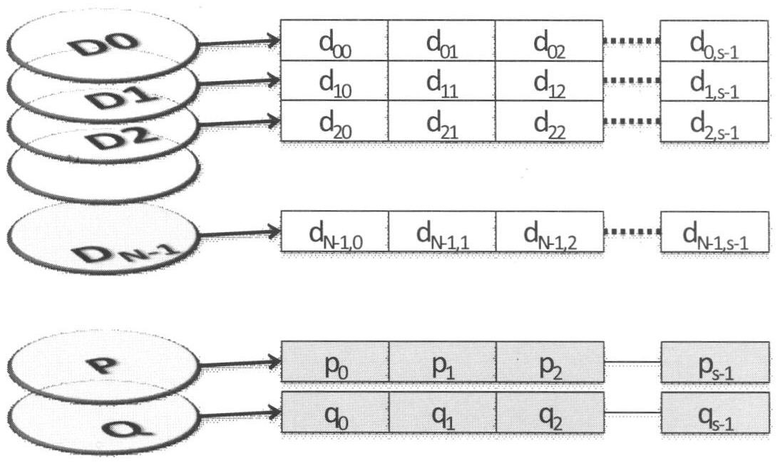
1. Способ восстановления записей в запоминающем устройстве, заключающийся в том, что:
разделяют область памяти упомянутого запоминающего устройства на информационные зоны и контрольные зоны;
записывают каждую группу подлежащих запоминанию данных в виде набора кодовых слов в соответствующую информационную зону;
находят при каждой записи подлежащих запоминанию данных в упомянутое запоминающее устройство с помощью соответствующего вычислительного блока по меньшей мере две эталонных контрольных суммы, каждую по соответствующей заранее установленной формуле, для каждого набора кодовых слов с одинаковыми номерами во всех упомянутых информационных зонах;
записывают каждую из найденных контрольных сумм в виде кодового слова с тем же номером в соответствующую контрольную зону;
в процессе использования упомянутого запоминающего устройства неоднократно вычисляют с помощью упомянутого вычислительного блока текущие контрольные суммы по упомянутым заранее установленным формулам для каждого набора кодовых слов с одинаковыми номерами во всех информационных зонах;
сравнивают с помощью упомянутого вычислительного блока каждую из вычисленных текущих контрольных сумм с соответствующей эталонной контрольной суммой для набора кодовых слов с теми же номерами, записанной в соответствующую контрольную зону, для нахождения синдрома ошибок;
при нахождении упомянутого синдрома ошибок заменяют выявленные ошибки записи правильными значениями;
при этом упомянутое выявление ошибок записи производят путем соответствующих вычислений с помощью упомянутого вычислительного блока над многочленами, в которых в качестве коэффициентов используют упомянутые кодовые слова с одинаковыми номерами во всех информационных зонах, а в качестве порождающего многочлена, по модулю которого производят соответствующие вычисления над упомянутыми многочленами, используют такой многочлен, который не обладает свойством неразложимости на множители и порождает конечное кольцо.
2. Способ по п.1, в котором количество вычисляемых контрольных сумм равно двум, в качестве упомянутых заранее установленных формул для вычисления контрольных сумм используют формулы:
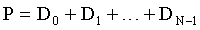 и
и
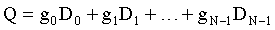 ,
,
где Di - i-я информационная зона, в которую записаны кодовые слова di1, di2, …, diS; i=0, …, N-1; gi - коэффициент, S - количество кодовых слов, которое можно записать в i-ю информационную зону,
а ошибки записи выявляют путем решения получающейся из этих формул системы уравнений.
3. Способ по п.2, в котором в качестве упомянутого порождающего многочлена используют многочлен:
x128+x7+x2+x+1.
4. Способ по любому из пп.1-3, в котором упомянутый вычислительный блок входит в состав упомянутого запоминающего устройства.
5. Способ по любому из пп.1-3, в котором упомянутый вычислительный блок является внешним по отношению к упомянутому запоминающему устройству.
6. Система для восстановления записей в запоминающем устройстве, содержащая упомянутое запоминающее устройство, включающее в себя N информационных зон и по меньшей мере две контрольные зоны, и вычислительный блок, при этом:
каждая из упомянутых N информационных зон запоминающего устройства выполнена с возможностью записи в нее группы подлежащих запоминанию данных в виде набора кодовых слов;
каждая из упомянутых по меньшей мере двух контрольных зон запоминающего устройства выполнена с возможностью записи в нее соответствующей контрольной суммы;
упомянутый вычислительный блок выполнен с возможностью:
нахождения по меньшей мере двух эталонных контрольных сумм, каждую по соответствующей заранее установленной формуле, для каждого i-го набора кодовых слов, где i=0, …, N-1, во всех упомянутых N информационных зонах при каждой записи подлежащих запоминанию данных в упомянутое запоминающее устройство;
неоднократного вычисления в процессе использования упомянутого запоминающего устройства текущих контрольных сумм по упомянутым заранее установленным формулам для каждого i-го набора кодовых слов во всех упомянутых N информационных зонах;
сравнения каждой из вычисленных текущих контрольных сумм с соответствующей эталонной контрольной суммой, записанной в соответствующую из упомянутых контрольных зон, для нахождения синдрома ошибок;
выявления ошибок записи по найденному синдрому ошибок и замены выявленных ошибок записи правильными значениями путем соответствующих вычислений над многочленами, при которых в качестве коэффициентов используют упомянутые кодовые слова с одинаковыми номерами во всех N информационных зонах, а в качестве порождающего многочлена, по модулю которого производят соответствующие вычисления над упомянутыми многочленами, используют такой многочлен, который не обладает свойством неразложимости на множители и порождает конечное кольцо.
7. Система по п.6, в которой количество вычисляемых контрольных сумм равно двум, в качестве упомянутых заранее установленных формул для вычисления контрольных сумм используют формулы:
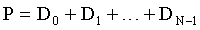 и
и
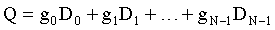 ,
,
где Di - i-я информационная зона, в которую записаны кодовые слова di1, di2, …, diS; i=0, …, N-1; gi - коэффициент, S - количество кодовых слов, которое можно записать в i-ю информационную зону,
а ошибки записи выявляют путем решения получающейся из этих формул системы уравнений.
8. Система по п.7, в которой в качестве упомянутого порождающего многочлена используют многочлен:
x128+x7+x2+x+1.
9. Система по любому из пп.6-8, в которой упомянутый вычислительный блок входит в состав упомянутого запоминающего устройства.
10. Система по любому из пп.6-8, в которой упомянутый вычислительный блок является внешним по отношению к упомянутому запоминающему устройству.
11. Машиночитаемый носитель, предназначенный для непосредственного участия в работе компьютера и содержащий компьютерную программу, при исполнении которой в компьютере выполняются действия способа по любому из пп.1-3.
| Гидравлический пресс | 1980 |
|
SU1232499A2 |
| ЕР 1976180 А2, 01.10.2008 | |||
| US 7343546 В2, 11.03.2008 | |||
| US 7096389 B2, 22.08.2006 | |||
| RU 2007149316 A, 20.07.2009 | |||
| RU 2005134020 A, 10.09.2006. | |||
Авторы
Даты
2012-04-20—Публикация
2010-07-01—Подача