Настоящая заявка притязает на приоритет Предварительной заявки (США) серийный номер 60/787562, озаглавленной "CONVERGENCE OF SCALED AND NON-SCALED IDCT ARCHITECTURES", зарегистрированной 29 марта 2006 года, назначенной правопреемнику этой заявки и содержащейся в данном документе по ссылке.
Уровень техники
Область техники, к которой относится изобретение
Настоящее изобретение, в общем, относится к обработке, а более конкретно, к методикам выполнения преобразования данных.
Уровень техники
Преобразования, в общем, используются для того, чтобы преобразовывать данные из одной области в другую область. Например, дискретное косинусное преобразование (DCT), в общем, используется для того, чтобы преобразовывать данные из пространственной области в частотную область, а обратное дискретное косинусное преобразование (IDCT), в общем, используется для того, чтобы преобразовывать данные из частотной области в пространственную область. DCT широко используется для сжатия изображений/видео, чтобы пространственно декоррелировать блоки элементов изображений (пикселов) в изображениях или видеокадрах. Результирующие коэффициенты преобразования в типичном варианте гораздо меньше зависят друг от друга, что делает эти коэффициенты более подходящими для квантования и кодирования. DCT также использует свойство энергетического сжатия, которое является способностью сопоставлять большую часть энергии блока пикселов только с несколькими (в типичном варианте младшего порядка) коэффициентами преобразования. Это свойство энергетического сжатия позволяет упростить проектирование алгоритмов кодирования.
Преобразования, такие как DCT и IDCT, могут быть использованы для различных вариантов применения, которые могут поддерживать различные стандарты кодирования изображений и видео. Следовательно, желательно предоставить интерфейсы, которые могут принимать и предоставлять данные в форматах, подходящих для этих вариантов применения. Более того, поскольку преобразования могут выполняться с большим объемом данных, желательно выполнять преобразования максимально эффективно.
Сущность изобретения
Методики эффективного выполнения полных и масштабированных преобразований с данными, принимаемыми посредством полных и масштабированных интерфейсов, соответственно, описываются в данном документе. Полное преобразование - это преобразование, которое реализует полное математическое описание преобразования. Полное преобразование оперирует с или предоставляет коэффициенты полного преобразования (или просто коэффициенты преобразования). Полное преобразование также может упоминаться как немасштабированное преобразование, законченное преобразование и т.д. Масштабированное преобразование - это преобразование, которое оперирует с или предоставляет коэффициенты масштабированного преобразования, которые являются масштабированными версиями коэффициентов полного преобразования. Масштабированное преобразование может иметь меньшую вычислительную сложность и может быть использовано вариантами применения, которые могут принимать коэффициенты масштабированного преобразования. Полное преобразование может быть использовано вариантами применения, которые хотят обмениваться полными коэффициентами преобразования. Полные и масштабированные преобразования могут быть для двумерного (2D) IDCT, которое может быть реализовано разделимым способом с одномерными (1D) IDCT. Полные и масштабированные преобразования могут также быть для 2D DCT, которое может быть реализовано разделимым способом с преобразованиями 1D DCT. Преобразования 1D IDCT и преобразования 1D DCT могут быть реализованы вычислительно эффективным способом, как описано ниже.
Далее более подробно описаны различные аспекты и признаки изобретения.
Краткое описание чертежей
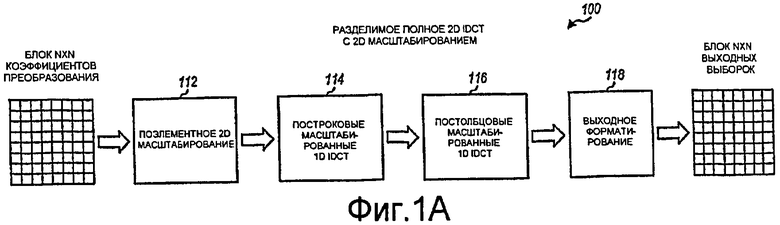
Фиг.1A иллюстрирует разделимое полное 2D IDCT с 2D масштабированием.
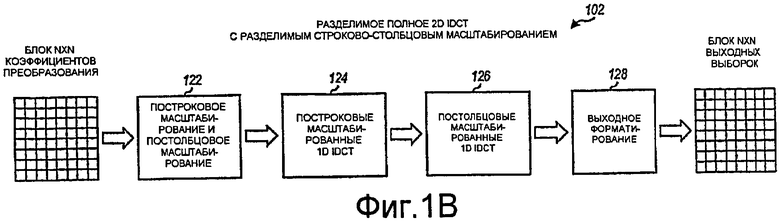
Фиг.1B иллюстрирует разделимое полное 2D IDCT со строково-столбцовым масштабированием.
Фиг.1B иллюстрирует разделимое полное 2D IDCT с 1D масштабированием.
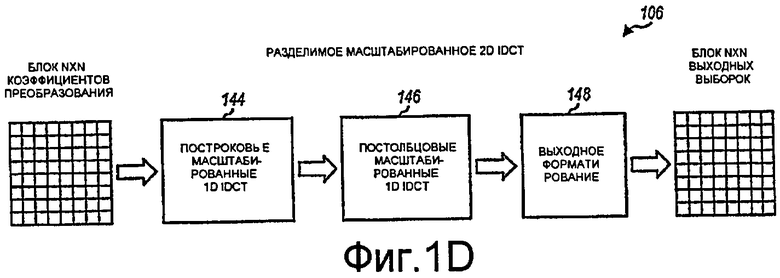
Фиг.1D иллюстрирует разделимое масштабированное 2D IDCT.
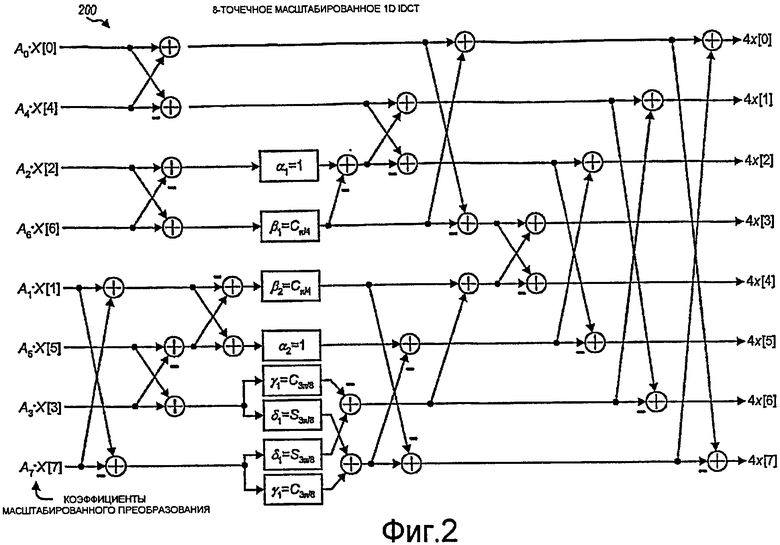
Фиг.2 иллюстрирует блок-схему факторизации 8-точечного 1D IDCT.
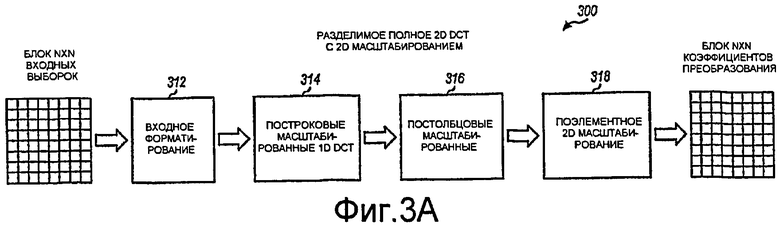
Фиг.3A иллюстрирует разделимое полное 2D DCT с 2D масштабированием.
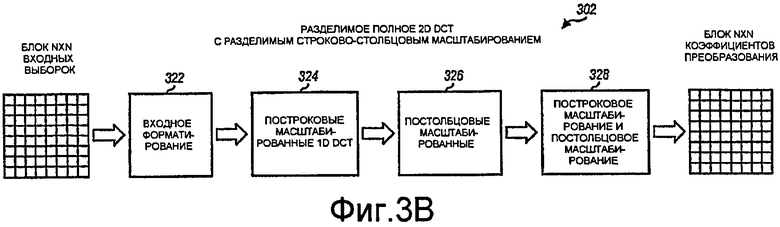
Фиг.3B иллюстрирует разделимое полное 2D DCT со строково-столбцовым масштабированием.
Фиг.3B иллюстрирует разделимое полное 2D DCT с 1D масштабированием.
Фиг.3D иллюстрирует разделимое масштабированное 2D DCT.
Фиг.4 иллюстрирует блок-схему факторизации 8-точечного 1D DCT.
Фиг.5 иллюстрирует IDCT-процессор, поддерживающий полный и масштабированный интерфейсы.
Фиг.6 иллюстрирует DCT-процессор, поддерживающий полный и масштабированный интерфейсы.
Фиг.7 иллюстрирует процесс выполнения преобразования.
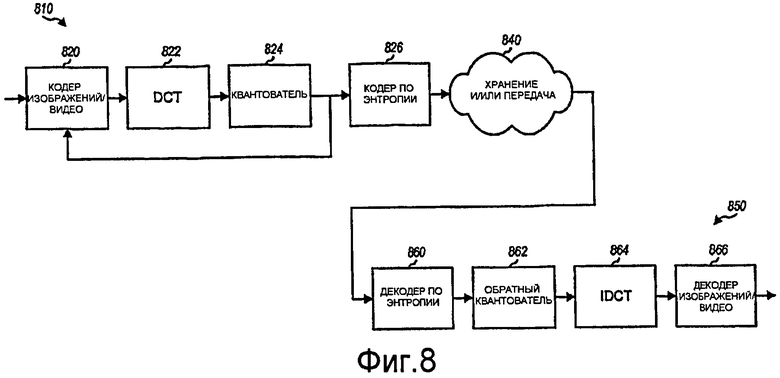
Фиг.8 иллюстрирует систему кодирования и систему декодирования.
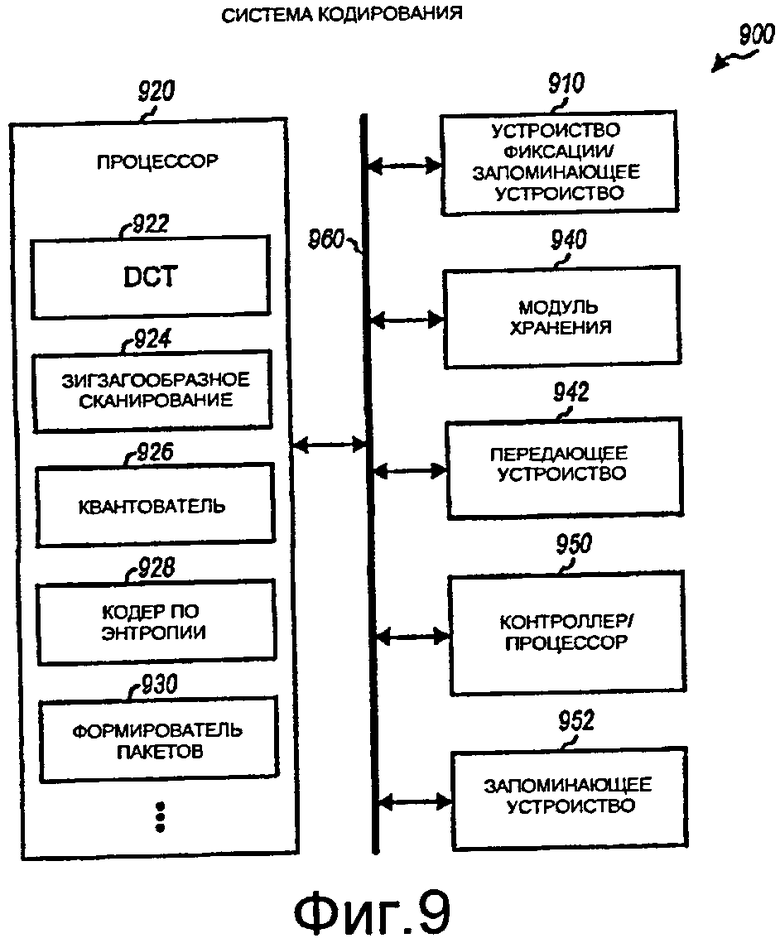
Фиг.9 иллюстрирует блок-схему системы кодирования.
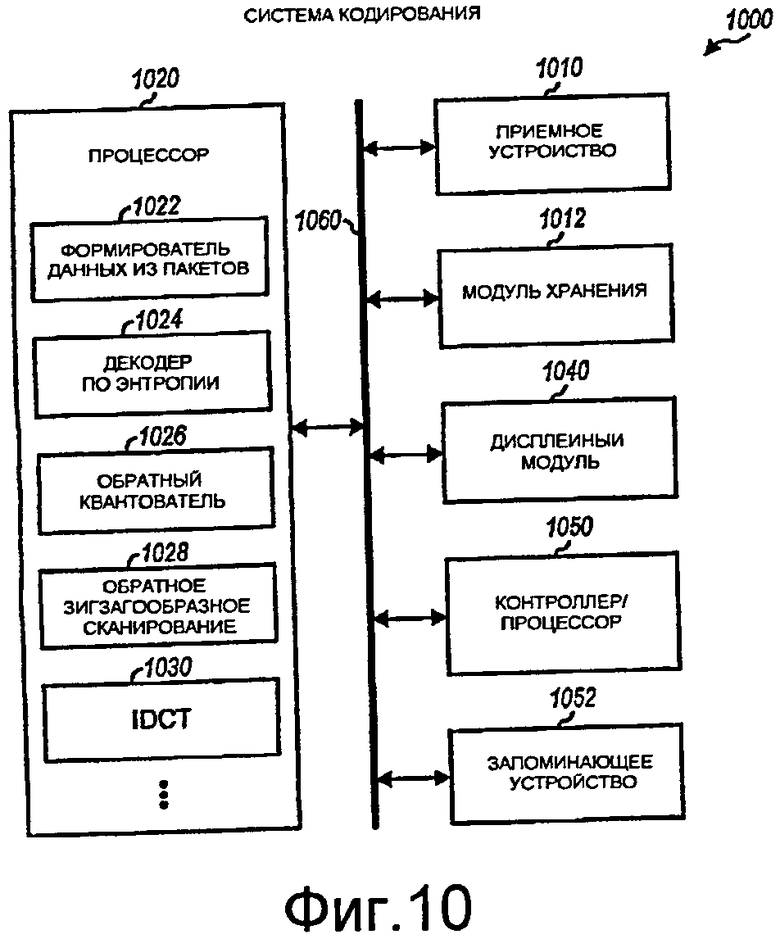
Фиг.10 иллюстрирует блок-схему системы декодирования.
Подробное описание изобретения
Методики, описанные в данном документе, могут быть использованы для различных типов преобразования, таких как DCT, IDCT, дискретное преобразование Фурье (DFT), обратное DFT (IDFT), модулированное перекрывающееся преобразование (MLT), обратное MLT, модулированное комплексное перекрывающееся преобразование (MCLT), обратное MCLT и т.д. Методики также могут быть использованы для различных вариантов применения, таких как обработка изображений, видео и аудио, связь, сети данных, хранение данных, графики и т.д. В общем, методики могут быть использованы для любого варианта применения, который использует преобразование. Для понятности, методики описаны ниже для DCT и IDCT, которые, как правило, используются в обработке изображений и видео.
N-точечное 1D DCT и N-точечное 1D IDCT типа II может быть задано следующим образом:
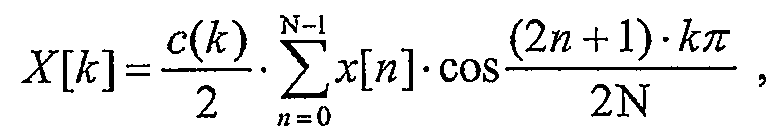 уравнение (1)
уравнение (1)
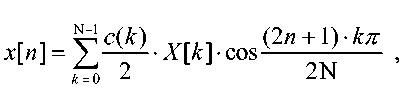 уравнение (2)
уравнение (2)
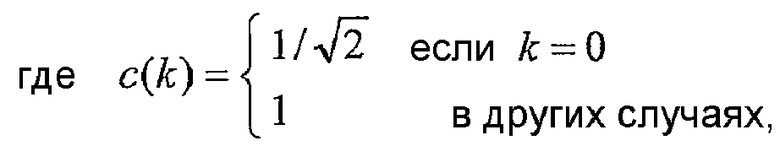
x[n] - это функция 1D пространственной области, а X[k] - это функция 1D частотной области.
1D DCT в уравнении (1) оперирует с N входными выборками или значениями пространственной области от x[0] до x[N-1] и формирует N коэффициентов преобразования от X[0] до X[N-1]. 1D IDCT в уравнении (2) оперирует с N коэффициентами преобразования и формирует N выходных выборок. DCT типа II - это один тип преобразования, и он, в общем, считается одним из наиболее эффективных преобразований из различных преобразований с энергетическим сжатием, часто предлагаемых для сжатия изображений/видео.
1D DCT и 1D IDCT могут быть реализованы в своих исходных формах, показанных в уравнениях (1) и (2), соответственно. Тем не менее, существенное снижение вычислительной сложности может быть реализовано посредством нахождения факторизаций, которые приводят к наименьшему возможному числу умножений и сложений, как описано ниже.
1D DCT в уравнении (1) может быть выражено в матричной форме следующим образом:
x = T y , уравнение (3)
где y - это вектор Nx1 входных выборок,
T - это матрица NxN полного 1D DCT, и
x - это вектор Nx1 коэффициентов преобразования.
y содержит входные выборки от x[0] до x[N-1], а x содержит коэффициенты преобразования от X[0] до X[N-1]. Элементы T могут быть получены на основе уравнения (1).
1D DCT может быть факторизовано в произведение матриц следующим образом:
T = S T S, уравнение (4)
где S = diag (A 0 ,..., A N-1 ) - это диагональная матрица множителей масштабирования, а T S - это матрица NxN масштабированного 1D DCT.
Уравнения (3) и (4) указывают то, что полное 1D DCT может выполняться для y посредством выполнения сначала масштабированного 1D DCT для y и последующего масштабирования результатов с помощью S .
Преимущество декомпозиции полного преобразования в масштабированное преобразование и операцию масштабирования, к примеру, как показано в уравнении (4), заключается в том, что посредством надлежащего выбора множителей масштабирования мультипликативная сложность масштабированного преобразования может быть уменьшена. Например, хорошо известное разложение Arai, Agui и Nakajima (AAN) в "A Fast DCT-SQ Scheme for Images", Transactions of the IEICE, November 1988, формирует масштабированное 8-точечное DCT, которое может быть реализовано только с помощью пяти умножений на иррациональные множители. В отличие от этого, наилучшее известное полное 8-точечное DCT требует 11 таких умножений.
NxN 2D DCT может быть задано следующим образом:
T
 T
= (
S
T
S)
T
= (
S
T
S) 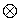 (
S
T
S) = (
S
(
S
T
S) = (
S
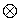 S
)(
T
S
S
)(
T
S
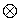 T
S), уравнение (5)
T
S), уравнение (5)
где
T
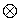 T
- это кронекеровское произведение
T
с собой и является матрицей полного 2D DCT,
T
- это кронекеровское произведение
T
с собой и является матрицей полного 2D DCT, 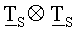 - это матрица масштабированного 2D DCT, а
- это матрица масштабированного 2D DCT, а 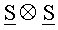 - это матрица множителей масштабирования для масштабированного 2D DCT.
- это матрица множителей масштабирования для масштабированного 2D DCT.
Результат операции в уравнении (5) - это матрица NxN 2D DCT.
2D DCT может выполняться для матрицы N×N входных выборок Y разделимым способом, для одной размерности за раз. Например, 1D DCT может выполняться для каждой строки Y , чтобы получить промежуточную матрицу, и 1D DCT затем может быть выполнено для каждого столбца промежуточной матрицы. Альтернативно, 1D DCT может выполняться для каждого столбца Y , после чего выполняется 1D DCT для каждой строки промежуточной матрицы.
Уравнение (5) указывает то, что 2D DCT может выполняться для
Y
посредством выполнения сначала 2D DCT для
Y
, а затем масштабирования результатов. Уравнение (5) также указывает то, что масштабирование для строковых и столбцовых 1D DCT может объединяться в один этап (который является матричным произведением
S
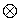 S
), применяемым к результатам масштабированного 2D DCT.
S
), применяемым к результатам масштабированного 2D DCT.
1D IDCT в уравнении (2) может быть выражено в матричной форме следующим образом:
T -1 = T t = T t S S , уравнение (6)
где T t - это матрица N×N полного 1D IDCT, и "t" означает транспонирование.
2D IDCT может выражаться следующим образом:
(
T
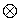 T
)-1 =
T
-1
T
)-1 =
T
-1
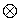 T
-1 = (
T
t S
S
)
T
-1 = (
T
t S
S
)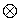 (
T
t S
S
) = (
T
t S
(
T
t S
S
) = (
T
t S
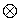 T
t S)(
S
T
t S)(
S
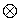 S
) уравнение (7)
S
) уравнение (7)
Уравнение (7) указывает то, что 2D IDCT может выполняться для матрицы N×N коэффициентов преобразования X посредством масштабирования сначала коэффициентов преобразования и последующего выполнения масштабированного 2D IDCT по масштабированным коэффициентам преобразования. Уравнение (7) также указывает то, что масштабирование для строковых и столбцовых 1D IDCT может объединяться в один этап, предшествующий масштабированному 2D IDCT.
Масштабированная архитектура - это структура, которая использует масштабированное преобразование, а полная архитектура - это структура, которая использует полное преобразование. Масштабированная архитектура может иметь меньшую мультипликативную сложность, чем полная архитектура. Например, масштабированная архитектура может выполнять масштабированное 2D IDCT (
T
t S
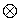 T
t S) разделимым строково-столбцовым способом и может использовать 8-точечное масштабированное ID IDCT
T
S из разложения AAN для каждой строки и каждого столбца. Мультипликативная сложность этой масштабированной архитектуры может быть 8·8+16·5=64+80=144, или 64 умножения для масштабирования и 5 умножений для каждой из 8 строк и 8 столбцов. В определенных ситуациях масштабирование может быть комбинировано с квантованием, и при этом мультипликативная сложность масштабированной архитектуры может быть уменьшена до примерно 80 умножений. Полная архитектура может выполнять 2D IDCT (
T
T
t S) разделимым строково-столбцовым способом и может использовать 8-точечное масштабированное ID IDCT
T
S из разложения AAN для каждой строки и каждого столбца. Мультипликативная сложность этой масштабированной архитектуры может быть 8·8+16·5=64+80=144, или 64 умножения для масштабирования и 5 умножений для каждой из 8 строк и 8 столбцов. В определенных ситуациях масштабирование может быть комбинировано с квантованием, и при этом мультипликативная сложность масштабированной архитектуры может быть уменьшена до примерно 80 умножений. Полная архитектура может выполнять 2D IDCT (
T
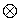 T
) строково-столбцовым способом и может использовать наилучшее известное полное 8-точечное ID IDCT
T для каждой строки и каждого столбца. Мультипликативная сложность этой полной архитектуры может составлять 16·11=176, или 11 для каждой из 8 строк и 8 столбцов. Для разделимой реализации масштабированная архитектура может иметь меньшую мультипликативную сложность, чем полная архитектура.
T
) строково-столбцовым способом и может использовать наилучшее известное полное 8-точечное ID IDCT
T для каждой строки и каждого столбца. Мультипликативная сложность этой полной архитектуры может составлять 16·11=176, или 11 для каждой из 8 строк и 8 столбцов. Для разделимой реализации масштабированная архитектура может иметь меньшую мультипликативную сложность, чем полная архитектура.
Масштабированная архитектура может использоваться в структурах, которые предпочитают низкую сложность. Масштабированная архитектура может быть преимущественной, когда имеется только несколько коэффициентов преобразования, чтобы масштабировать, что часто может иметь место для 2D IDCT в декодере изображений/видео. Масштабированная архитектура также может быть преимущественной в структурах, которые предоставляют возможность масштабирования коэффициентов преобразования, которые должны быть комбинированы с квантованием и/или обратным квантованием в кодере/декодере (кодеке) изображений/видео, к примеру, как показано на фиг.8.
Полная архитектура может быть желательной в структурах, которые предпочитают простоту использования. Например, многие вычислительные окружения и приложения могут поддерживать несколько стандартов кодирования изображений и видео. В этих случаях может быть более удобным иметь механизм преобразования, который реализует полное преобразование, и предоставлять гибкий интерфейс ввода/вывода, чтобы дать возможность использования механизма преобразования с различными квантователями и кодеками. Полная архитектура может предоставлять простой интерфейс и может быть более подходящей в таких окружениях.
Структура преобразования, которая может гибко поддерживать различные варианты применения посредством масштабированного и полного интерфейса, описана в данном документе. Структура преобразования может принимать полные входные значения посредством полного интерфейса, выполнять полное преобразование для этих входных значений и предоставлять полные выходные значения, аналогично полной архитектуре. Структура преобразования также может принимать масштабированные входные значения через масштабированный интерфейс, выполнять масштабированное преобразование для этих входных значений и предоставлять масштабированные выходные значения, аналогично масштабированной архитектуре. Структура преобразования внутренне может реализовывать разделимое масштабированное преобразование, чтобы потенциально достигать меньшей сложности и/или повышенной точности. Структура преобразования тем самым может достигать меньшей сложности для определенных вариантов применения, предоставлять простоту применения для других вариантов применения или предоставлять и меньшую сложность, и простоту применения в определенных случаях. Структура преобразования может быть использована как для прямых преобразований (к примеру, DCT), так и для обратных преобразований (к примеру, IDCT). Для простоты структура преобразования конкретно описана ниже для IDCT.
Архитектуры масштабированного и немасштабированного/полного 2D IDCT могут быть выражены следующим образом:
масштабированное 2D IDCT:
T
-1
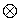 T
-1 = (
T
t S
T
-1 = (
T
t S
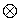 T
t S)(
S
T
t S)(
S
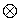 S
), уравнение (8)
S
), уравнение (8)
немасштабированное 2D IDCT:
T
-1
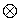 T
-1 = (
T
t S
S
)
T
-1 = (
T
t S
S
)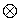 (
T
t S
S
) уравнение (9)
(
T
t S
S
) уравнение (9)
Полный/немасштабированный интерфейс может принимать коэффициенты преобразования. Полное 2D IDCT может выполняться для этих коэффициентов преобразования следующим образом:
Y = Θ( X )≈ T t X T , уравнение (10)
где X - это матрица коэффициентов преобразования,
Θ (.) - это аппроксимация полного 2D IDCT, а
Y - это матрица выходных выборок.
Операторная запись (.) в уравнении (10) используется для того, чтобы указывать то, что аппроксимации с фиксированной запятой могут не основываться исключительно на линейных операциях.
Полное 2D IDCT может осуществляться посредством выполнения полного 1D IDCT для каждой строки и каждого столбца X следующим образом:
θ( x i) ≈ T t x i, уравнение (11)
где x i - это i-я строка или столбец X , и
θ (.) - это аппроксимация полного 1D IDCT.
θ (.) может быть использована для строково-столбцовой реализации 2D оператора Θ(.).
Масштабированный интерфейс может принимать коэффициенты масштабированного преобразования, которые могут получаться следующим образом:
X S = Σ ( X ) ≈ S t X S , уравнение (12)
где Σ(.) - это аппроксимация операции 2D масштабирования, а X S - это матрица коэффициентов масштабированного преобразования.
Масштабированное 2D IDCT может выполняться для коэффициентов масштабированного преобразования следующим образом:
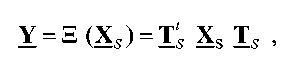 уравнение (13)
уравнение (13)
где Ξ(.) - это аппроксимация масштабированного 2D IDCT.
Масштабированное 2D IDCT может осуществляться посредством выполнения масштабированного 1D IDCT для каждой строки и каждого столбца X s следующим образом:
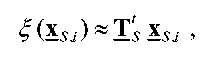 уравнение (14)
уравнение (14)
где x S,i - это i-я строка или столбец X s, и
ξ (.) - это аппроксимация масштабированного 1D IDCT.
ξ(.) может быть использована для строково-столбцовой реализации 2D оператора Ξ(.).
Как показано в уравнении (13), масштабированный интерфейс может быть реализован посредством реализации 2D оператора Ξ(.). Как показано в уравнениях (12) и (13), полный интерфейс может быть реализован посредством реализации оператора 2D масштабирования Σ(.) помимо 2D оператора Ξ(.). Полное 2D IDCT затем может выполняться следующим образом:
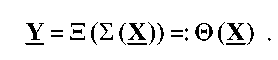 уравнение (15)
уравнение (15)
Уравнение (15) указывает то, что полное 2D IDCT может выполняться для коэффициентов полного преобразования X посредством сначала масштабирования этих коэффициентов преобразования с помощью оператора 2D масштабирования Σ(.) и последующего выполнения 2D IDCT для масштабированных преобразованных коэффициентов с помощью 2D оператора Ξ(.). 2D оператор Ξ(.), в свою очередь, может быть реализован посредством строково-столбцового каскада 1D операторов ξ(.).
2D оператор Θ(.) для разделимого полного 2D IDCT тем самым может быть реализован с помощью 2D оператора Ξ(.) для разделимого масштабированного 2D IDCT и оператора 2D масштабирования Σ(.). 2D масштабирование может быть реализовано различными способами, как описано ниже. Результирующая сложность и производительность разделимого полного 2D IDCT, реализованного с помощью разделимого масштабированного 2D IDCT и 2D масштабирования может быть сравнима с собственным реализованным 2D IDCT.
Фиг.1A иллюстрирует структуру разделимого полного 2D IDCT 100 с 2D масштабированием. 2D IDCT 100 содержит стадию 112 2D масштабирования, за которой следует стадия 114 1D IDCT для строк (или столбцов), за которой дополнительно следует стадия 116 масштабированного 1D IDCT для столбцов (или строк), и завершается стадией 118 выходного форматирования. Стадия 112 2D масштабирования принимает блок NxN коэффициентов преобразования X и может умножать каждый коэффициент преобразования X ij на множитель масштабирования A ij и дополнительно сдвигать каждый коэффициент масштабированного преобразования на P битов влево, где P обозначает число зарезервированных битов "мантиссы". После масштабирования величина C=2 P-1 может быть добавлена в коэффициент DC-преобразования, чтобы добиться надлежащего округления выходных выборок. Чтобы повысить точность масштабирования, S=P+R битов могут быть использованы при преобразовании множителей масштабирования в целые числа, и надлежащие сдвиги на R битов могут быть выполнены после умножения. S может быть любым надлежащим значением, которое может упрощать реализации на аппаратных платформах, к примеру, S может быть равно 15 или 16 для платформ с 16-битовых множителей без знака.
Стадия 114 IDCT выполняет N-точечное масштабированное 1D IDCT для каждой строки блока коэффициентов масштабированного преобразования из стадии 112 2D масштабирования. Стадия 112 IDCT выполняет N-точечное масштабированное 1D IDCT для каждого столбца промежуточного блока, сформированного посредством стадии 114 IDCT. Масштабированные 1D IDCT для стадий 114 и 116 могут оперировать непосредственно со своими входными данными без выполнения какого-либо внутреннего пре- или пост-масштабирования. После того как все строки и столбцы масштабированы, стадия 118 выходного форматирования может сдвигать результирующие величины из стадии 116 IDCT на P битов вправо, чтобы сформировать блок NxN выходных выборок Y для полного 2D IDCT. Множители масштабирования и константа точности P могут выбираться таким образом, что полное 2D IDCT может быть реализовано с помощью регистров требуемой ширины.
2D масштабирование на стадии 112 может быть выражено следующим образом:
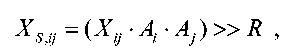 уравнение (16)
уравнение (16)
где X ij - это коэффициент преобразования в i-й строке и j-том столбце X , A i и A j - это i-й и j-й диагональные элементы, соответственно, S , X S,ij - это коэффициент масштабированного преобразования в i-й строке и j-м столбце X s, а ">>R" обозначает операцию сдвига вправо со знаком на R битов. R - это константа, обеспечивающая P битов добавленной точности с фиксированной запятой в коэффициентах масштабированного преобразования X S,ij.
Таблица может сохранять множители масштабирования A ij =A i A j , для i = 0,..., N-1 и j = 0,..., N-1. Каждый элемент X может быть умножен на соответствующий множитель масштабирования в таблице. До N·N умножений может быть выполнено для N·N элементов X .
Фиг.1B иллюстрирует структуру разделимого полного 2D IDCT 102 с разделимым строково-столбцовым масштабированием. 2D IDCT 102 содержит стадию 122 разделимого строкового-столбцового масштабирования, за которой следует стадия 124 масштабированного 1D IDCT для строк (или столбцов), за которой дополнительно следует стадия 126 масштабированного 1D IDCT для столбцов (или строк), и завершается стадией 128 выходного форматирования. Стадия 122 принимает блок NxN коэффициентов преобразования X и может умножать каждый коэффициент преобразования Xij в каждой строке i на множитель масштабирования Ai, и затем умножать каждый результирующий коэффициент в каждом столбце j на множитель масштабирования Aj, чтобы получить коэффициенты масштабированного преобразования, следующим образом:
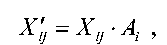 уравнение (17)
уравнение (17)
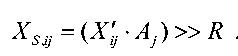
Стадия 122 масштабирования тем самым может выполнять 2D масштабирование разделимым способом для строк, за которыми следуют столбцы (или столбцов, за которыми следуют строки). Разделимое строково-столбцовое масштабирование может давать возможность одному и тому же оборудованию быть использованным для масштабирования строк и масштабирования столбцов, что позволяет уменьшать сложность реализации. До 2-N-N умножений может быть выполнено для N·N элементов X . Тем не менее, фактическое число умножений может быть гораздо меньше 2-N-N, поскольку некоторые из множителей масштабирования от A 0 до A N-1 могут иметь тривиальные значения (к примеру, 256), и умножение на эти тривиальные множители масштабирования может быть реализовано с помощью простых операций сдвига. Стадии 124, 126 и 128 могут работать таким же образом, что и стадии 114, 116 и 118, соответственно, на фиг.1A.
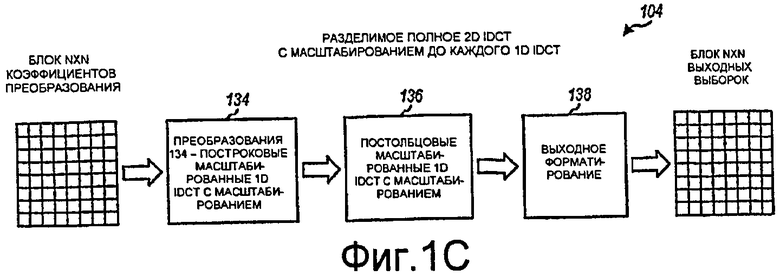
Фиг.1C иллюстрирует структуру разделимого полного 2D IDCT 104 с масштабированием перед каждым масштабированным 1D IDCT. 2D IDCT 104 содержит масштабированное 1D IDCT со стадией 134 масштабирования для строк (или столбцов), за которой следует масштабированное 1D IDCT со стадией 136 масштабирования для столбцов (или строк), и завершается стадией 138. Стадия 134 IDCT выполняет масштабирование до N-точечного масштабированного 1D IDCT для каждой строки блока коэффициентов преобразования. Стадия 136 IDCT выполняет масштабирование до N-точечного масштабированного 1D IDCT для каждого столбца промежуточного блока, сформированного посредством стадии 134 DCT. Стадии 134 и 136, по сути, выполняют полные 1D IDCT с помощью масштабированных 1D IDCT. Множители масштабирования от A 0 до A N-1 и постоянные множители в масштабированном 1D IDCT могут выбираться так, чтобы снижать сложность и/или повышать точность полного 1D IDCT, как описано ниже. Стадия 138 может работать таким же образом, что и стадия 118 на фиг.1A.
Фиг.1D иллюстрирует структуру разделимого масштабированного 2D IDCT 106. 2D IDCT 106 содержит стадию 144 масштабированного 1D IDCT для строк (или столбцов), за которой следует стадия 146 масштабированного 1D IDCT для столбцов (или строк), и завершается стадией 148 выходного масштабирования. Стадия 144 IDCT выполняет N-точечное масштабированное 1D IDCT для каждой строки блока NxN коэффициентов масштабированного преобразования X s. Стадия 146 IDCT выполняет N-точечное масштабированное 1D IDCT для каждого столбца промежуточного блока, сформированного посредством стадии 144 IDCT. Стадия 148 может работать таким же образом, что и стадия 118 на фиг.1A.
Как проиллюстрировано на фиг.1A-1C, масштабирование для полного 2D IDCT может осуществляться различными способами, например, с помощью 2D масштабирования перед строково-столбцовыми 1D IDCT на фиг. 1A, с помощью строкового-столбцового масштабирования перед строково-столбцовыми 1D IDCT на фиг.1B или с помощью масштабирования перед каждым 1D IDCT на фиг.1C. Масштабирование также может осуществляться другими способами. Как показано на фиг.1D, масштабированное 2D IDCT может выполняться посредством простого пропуска масштабирования и выполнения преобразований 1D IDCT для строк и столбцов.
Различные типы масштабированного 1D IDCT могут быть использованы для строково-столбцовых 1D IDCT на фиг.1A-1D. Например, масштабированное 1D IDCT на основе разложения AAN может быть использовано. Другое масштабированное IDCT с возможно меньшей сложностью описано ниже.
Фиг.2 иллюстрирует блок-схему 200 примерной факторизации 8-точечного 1D IDCT. На блок-схеме 200 каждое сложение представляется символом "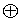 ", а каждое умножение представляется прямоугольником. Каждое сложение суммирует или вычитает два входных значения и предоставляет выходное значение. Каждое умножение умножает входное значение на постоянный множитель в прямоугольнике и предоставляет выходное значение. Факторизация на фиг.2 имеет умножения на следующие постоянные множители:
", а каждое умножение представляется прямоугольником. Каждое сложение суммирует или вычитает два входных значения и предоставляет выходное значение. Каждое умножение умножает входное значение на постоянный множитель в прямоугольнике и предоставляет выходное значение. Факторизация на фиг.2 имеет умножения на следующие постоянные множители:
α 1 = α 2 = 1,Уравнение (18)
β 1 = β 2 = C π/4 = cos(π/4) ≈ 0,707106781,
γ 1 = C 3π/8 = cos(3π/8) ≈ 0,382683432 и
δ 1 = S 3π/8 = sin(3π/8) ≈ 0,923879533.
Блок-схема 200 может принимать восемь коэффициентов преобразования от X[0] до X[7] и масштабировать эти коэффициенты преобразования с помощью множителей масштабирования от A 0 до A 7, чтобы получить восемь масштабированных коэффициентов преобразования от A 0 X[0] до A 7 X[7]. Альтернативно, блок-схема 200 может напрямую принимать восемь коэффициентов масштабированного преобразования. В любом случае, блок-схема 200 выполняет 8-точечное 1D IDCT для восьми коэффициентов масштабированного преобразования и формирует восемь выходных выборок от x[0] до x[7]. Множители масштабирования от A 0 до A 7 следующие:

Блок-схема 200 включает в себя ряд операций бабочки. Операция бабочки принимает два входных значения и формирует два выходных значения, где одно выходное значение - это сумма двух входных значений, а другое выходное значение - это разность двух входных значений. Например, операция бабочки для входных значений A 0 X[0] и A 4 X[4] формирует выходное значение A 0 X[0] + A 4 X[4] для верхней ветви и выходное значение A 0 X[0] - A 4 X[4] для нижней ветви.
Факторизация, показанная на фиг.2, приводит всего к 6 умножениям и 28 сложениям, что значительно меньше числа умножений и сложений, требуемых для прямых расчетов по уравнению (2). Умножения выполняются с иррациональными константами, представляющими синус и косинус различных углов, которые являются кратными π/8 для 8-точечного ID IDCT. Иррациональная константа - это константа, которая не является соотношением двух целых чисел. Умножения на иррациональные константы могут эффективно выполняться в целочисленной арифметике с фиксированной запятой, когда иррациональная константа аппроксимируется посредством двоично-рациональной константы. Двоично-рациональная константа - это константа с двоичным знаменателем, и она имеет форму c/2 b, где b и c - это целые числа, и b>0.
Умножение целочисленной переменной x на иррациональную константу μ в целочисленной арифметике с фиксированной запятой может выполняться посредством аппроксимации иррациональной константы с помощью двоично-рациональной константы следующим образом:
μ ≈ c / 2b , уравнение (19)
где μ - это иррациональная константа, которая должна быть аппроксимирована, а c/2 b - это двоично-рациональная константа.
При условии целочисленной переменной x и двоично-рациональной константы u = c/2 b целочисленное произведение
y = (x · c) / 2b , уравнение (20)
может быть аппроксимировано с помощью последовательности промежуточных значений
x 0, x 1, x 2, …, x t, уравнение (21)
где x0=0, x 1 =x, и для всех 2 ≤ i ≤ t значений x i получается следующим образом:
x i = ±x j ± x k · 2Si, с j, k<i, уравнение (22)
где x k 2 Si подразумевает сдвиг влево или вправо (в зависимости от знака константы s i ) промежуточного значения x k на |s i| битов.
В уравнении (22) x i может быть равно x j + x k · 2 Si, x j - x k · 2 Si или - x j + x k · 2 Si. Каждое промежуточное значение x i в последовательности может быть извлечено на основе двух предыдущих промежуточных значений x j и x k в последовательности, где x j или x k может быть равно нулю. Каждое промежуточное значение x i может быть получено с одним сдвигом и/или одним сложением. Сдвиг не требуется, если s i равно нулю. Сложение не требуется, если x j=x 0 =0.
Общее число сложений и сдвигов для умножения определяется посредством числа промежуточных значений в последовательности, которое равно t, а также выражения, используемого для каждого промежуточного значения. Умножение на двоично-рациональную константу u, по сути, разворачивается в последовательность операций сдвига и сложения. Последовательности задаются таким образом, что конечное значение в последовательности становится требуемым целочисленным произведением, или:
x t ≈ y, уравнение (23)
Умножение целочисленной переменной x на две иррациональные константы μ и η в целочисленной арифметике с фиксированной запятой может выполняться посредством аппроксимации иррациональных констант с помощью двоично-рациональной константы следующим образом:
μ ≈ c / 2b и η ≈ e / 2d , уравнение (24)
где c/2 b и e/2 d - это две двоично-рациональные константы, а b, c, d и e - это целые числа, при b>0 и d>0.
При условии целочисленной переменной x и двоично-рациональных констант u = c/2 b и v = e/2 d целочисленные произведения
y = (x · c) / 2b и z = (x · e) / 2d, уравнение (25)
могут быть аппроксимированы с помощью последовательности промежуточных значений
x 0, x 1, x 2, …, x t, уравнение (26)
где x0=0, x 1 =x, и для всех 2 ≤ i ≤ t значений x i получается следующим образом:
x i = ±x j ± x k · 2Si, с j, k<i, уравнение (27)
Последовательность задается таким образом, чтобы требуемые целочисленные произведения получались на этапах m и n следующим образом:
x m ≈ y и x n ≈ z, уравнение (28)
где m, n≤ t и либо m, либо n не равно t.
Как показано в уравнениях (24)-(28), умножение целочисленной переменной на x на иррациональные константы μ и η может быть аппроксимировано с помощью общей последовательности промежуточных значений, сформированных посредством операций сдвига и сложения и с помощью промежуточных результатов, чтобы уменьшить общее число операций.
В описанных выше вычислениях тривиальные операции, такие как сложения и вычитания нулей и сдвиги на нуль битов, могут быть опущены. Могут быть сделаны следующие упрощения:
x i = ±x 0 ± x k · 2Si => x i = ± x k · 2Si, уравнение (29)
x i = ±x i ± x k · 20 => x i = ±x i ± x k. уравнение (30)
В уравнении (29) выражение слева от "=>" влечет за собой сложение или вычитание нуля (обозначенного как x0) и может выполняться с помощью одного сдвига, как показано посредством выражения справа от "=>". В уравнении (30) выражение слева от "=>" влечет за собой сдвиг на нуль битов (обозначенный как 20) и может выполняться с помощью одного сложения, как показано посредством выражения справа от "=>". Уравнения (29) и (30) могут быть применены к уравнениям (22) и (27) при вычислении x i.
Чтобы уменьшить вычисления, первый общий множитель F1 может быть применен к постоянным множителям α1 и β1 на блок-схеме 200, а второй общий множитель F2 может быть применен к постоянным множителям α2, β2, β1 и γ1 следующим образом:
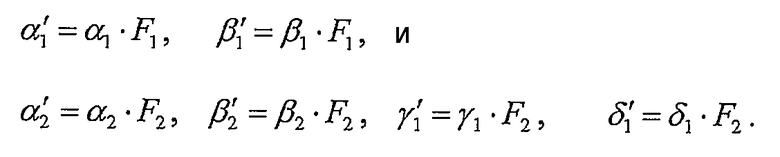 уравнение (31)
уравнение (31)
Множители масштабирования A 0 и A 7 также могут быть масштабированы так, чтобы учитывать общие множители F 1 и F 2 следующим образом:
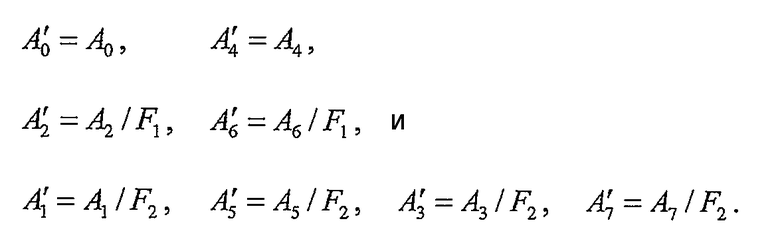 уравнение (32)
уравнение (32)
Различные комбинации значений для общих множителей F 1 и F 2 могут быть оценены. Для каждой комбинации значений F 1 и F 2 общее число логических и арифметических операций для 1D IDCT и точность выходных выборок может быть оценена.
Таблица 1 показывает примерную аппроксимацию с фиксированной запятой для 1D IDCT на фиг.2 при F 1 =2523/2048 и F 2 =2607/2048. В таблице 1 множители масштабирования от A' 0 до A' 7 и масштабированные общие множители приведены в первом столбце. Каждый множитель может быть аппроксимирован с помощью двоично-рациональной константы, приведенной во втором столбце. Последовательность промежуточных значений для умножения переменой x на одну или две двоично-рациональные константы приведена в третьем столбце. Число операций сложения и сдвига для каждого умножения приведено в четвертом и пятом столбцах, соответственно. Число раз, когда каждое умножение используется для 1D IDCT, приведено в шестом столбце. Общее число операций сложения для 1D IDCT равно сумме числа операций сложения в четвертом столбце, умноженной на число, приведенное в шестом столбце. Общее число операций сдвига для 1D IDCT равно сумме числа операций сдвига в пятом столбце, умноженной на число, приведенное в шестом столбце.
В таблице 1 сдвиг вправо на 8 компенсирует умножение на множитель 256 в множителях масштабирования A' 0 , A' 1 , A' 2 и A' 4, что предоставляет дополнительное уменьшение сложности.
В структуре, показанной в таблице 1, 8-точечное масштабированное 1D IDCT может быть выполнено с помощью 50 операций сложения и 24 операций сдвига. 8-точечное полное 1D IDCT может быть выполнено с помощью 61 операции сложения и 39 операций сдвига. Масштабирование с помощью множителей масштабирования от A' 0 до A' 7 может выполняться до масштабированного 1D IDCT (как показано на фиг.1C) или может выполняться до строково-столбцовых 1D IDCT (как показано на фиг.1A и 1B). 8x8 полное 2D IDCT может быть выполнено с помощью 977 операций сложения и 688 операций сдвига. 977 операций сложения включают в себя 61 сложение для каждого из 16 1D IDCT для 8 строк и 8 столбцов плюс 1 сложение для того, чтобы суммировать 2P-1 с коэффициентом DC-преобразования после масштабирования. 688 операций сдвига включают в себя 39 сдвигов для каждого из 16 IDCT для 8 строк и 8 столбцов плюс 64 сдвига для того, чтобы сдвигать 64 значения из второй стадии IDCT на P битов. Структура, показанная на фиг.1, удовлетворяет или превышает показатели точности, заданные в стандарте IEEE 1180-1190 и его ожидающей рассмотрение замене.
Таблица 1 показывает примерную аппроксимацию с фиксированной запятой для 1D IDCT на фиг.2. Множители масштабирования от A 0 и A 7 и постоянные множители α 1 , β 1 , α 2 , β 2 , β 1 и γ 1 также могут быть аппроксимированы с помощью других двоично-рациональных констант, которые могут иметь другую сложность и/или точность. Другие типы масштабированного IDCT также могут быть использованы для того, чтобы реализовать разделимые масштабированные и полные 2D IDCT.
Фиг.3A иллюстрирует структуру разделимого полного 2D DCT 300 с 2D масштабированием. 2D DCT 300 содержит стадию 312 входного форматирования, за которой следует стадия 314 масштабированного 1D DCT для строк (или столбцов), за которой дополнительно следует стадия 316 масштабированного 1D DCT для столбцов (или строк), и завершается стадией 318 2D масштабирования. Стадия 312 входного форматирования может умножить в обратном порядке блок NxN входных выборок. Стадия 314 DCT выполняет N-точечное масштабированное 1D DCT для каждой строки блока умноженных в обратном порядке выборок из стадии 312 и формирует первый промежуточный блок. Стадия 316 DCT выполняет N-точечное масштабированное 1D DCT для каждого столбца первого промежуточного блока и формирует второй промежуточный блок. Стадия 318 масштабирования масштабирует каждый элемент второй промежуточной матрицы и предоставляет блок преобразованных коэффициентов для полного 2D DCT.
Фиг.3B иллюстрирует структуру разделимого полного 2D DCT 302 с разделимым строково-столбцовым масштабированием. 2D DCT 302 содержит стадию 322 входного форматирования, за которой следует стадия 324 масштабированного 1D DCT для строк (или столбцов), за которой дополнительно следует стадия 326 масштабированного 1D DCT для столбцов (или строк), и завершается стадией 328 разделимого строкового-столбцового масштабирования. Стадии 322, 324 и 326 могут работать таким же образом, что и стадии 312, 314 и 316, соответственно, на фиг.3A. Стадия 328 масштабирования может масштабировать второй промежуточный блок из стадии 326 DCT построково, а затем постолбцово, чтобы сформировать блок преобразованных коэффициентов для полного 2D DCT.
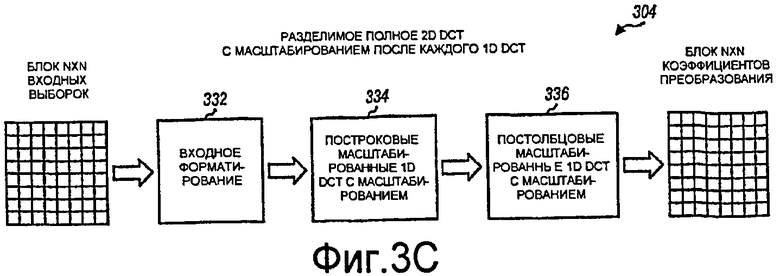
Фиг.3C иллюстрирует структуру разделимого полного 2D DCT 304 с масштабированием после каждого масштабированного 1D DCT. 2D DCT 304 содержит стадию 332 входного форматирования, за которой следует масштабированное 1D DCT с помощью стадии 334 масштабирования для строк (или столбцов), за которой дополнительно следует масштабированное 1D DCT с помощью стадии 336 масштабирования для столбцов (или строк). Стадия 332 может работать таким же образом, что и стадия 312 на фиг.3A. Стадия 334 DCT выполняет N-точечное масштабированное 1D DCT, за которым следует масштабирование, для каждой строки блока умноженных в обратном порядке выборок из стадии 332. Стадия 336 DCT выполняет N-точечное масштабированное 1D DCT, за которым следует масштабирование, для каждого столбца промежуточного блока, сформированного посредством стадии 334 DCT.
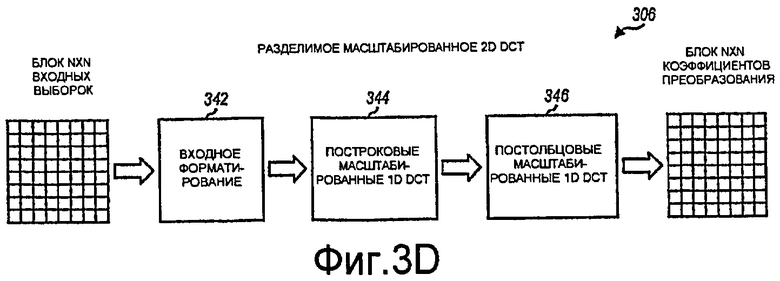
Фиг.3D иллюстрирует структуру разделимого масштабированного 2D DCT 306. 2D DCT 306 содержит стадию 342 входного форматирования, за которой следует стадия 344 масштабированного 1D DCT для строк (или столбцов), за которой дополнительно следует стадия 346 масштабированного 1D DCT для столбцов (или строк). Стадия 342 может работать таким же образом, что и стадия 312 на фиг.3A. Стадия 344 DCT выполняет N-точечное масштабированное 1D DCT для каждой строки блока умноженных в обратном порядке выборок из стадии 342. Стадия 346 DCT выполняет N-точечное масштабированное 1D DCT для каждого столбца промежуточного блока, сформированного посредством стадии 344 DCT.
Как проиллюстрировано на фиг.3A-3C, масштабирование для полного 2D DCT может осуществляться различными способами, например, с помощью 2D масштабирования после строково-столбцовых 1D DCT на фиг.3A, с помощью разделимого строкового-столбцового масштабирования после строково-столбцовых 1D IDCT на фиг.3B или с помощью масштабирования после каждого 1D DCT на фиг.3C. Масштабирование также может осуществляться другими способами. Как показано на фиг.3D, масштабированное 2D DCT может выполняться посредством простого пропуска масштабирования и выполнения преобразований 1D DCT для строк и столбцов.
Различные типы масштабированного 1D DCT могут быть использованы для масштабированных 1D DCT на фиг.3A-3D. Примерное масштабированное DCT с низкой сложностью описано ниже.
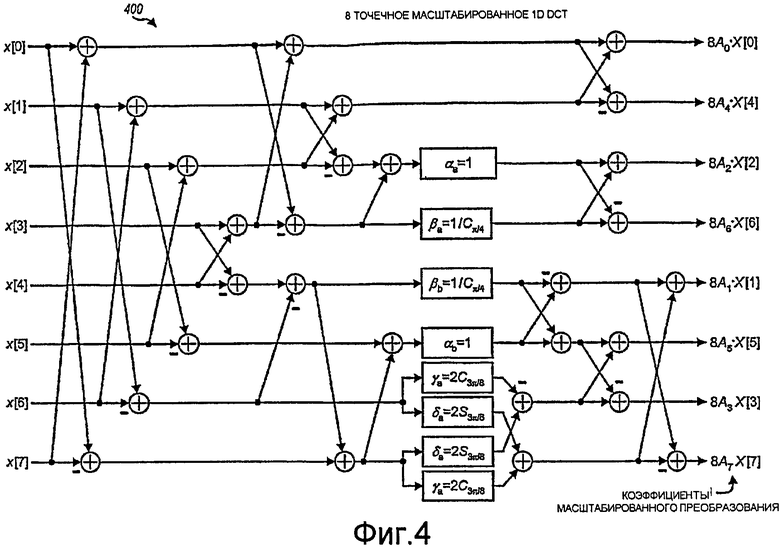
Фиг.4 иллюстрирует блок-схему 400 примерной факторизации 8-точечного 1D DCT. Блок-схема 400 принимает восемь входных выборок от x[0] до x[7], выполняет 8-точечное масштабированное 1D DCT для этих входных выборок и формирует восемь коэффициентов масштабированного преобразования от 8A 0 X[0] до 8A 7 X[7]. Множители масштабирования от A 0 до A 7 приведены выше. Факторизация на фиг. 4 имеет умножения на следующие постоянные множители:
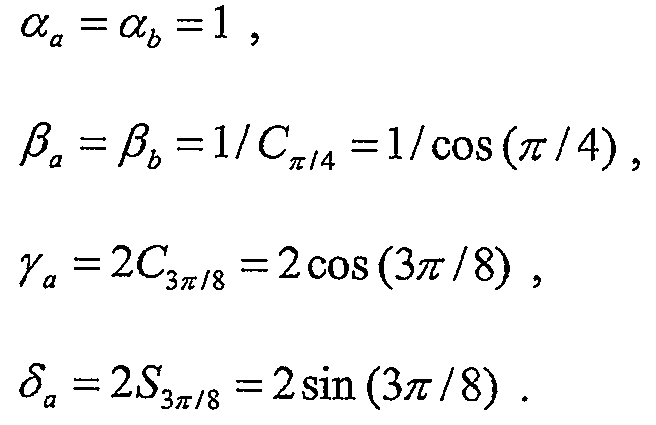 уравнение (33)
уравнение (33)
Блок-схемы для IDCT и DCT на фиг.2 и 4 являются аналогичными и влекут за собой умножения на, по существу, одинаковые постоянные множители (с разницей в 1/2). Эта аналогичность может быть преимущественной для реализации DCT и IDCT в интегральной микросхеме. В частности, аналогичность может предоставлять экономию площади кремния или кристалла, чтобы реализовать бабочки и умножения на постоянные преобразования, которые используются в прямом и обратном преобразовании.
Фиг.5 иллюстрирует блок-схему структуры IDCT-процессора 500, который поддерживает полные и масштабированные интерфейсы. В IDCT-процессоре 500 модуль 510 масштабирования принимает блок коэффициентов преобразования через полный интерфейс, выполняет масштабирование (к примеру, поэлементное 2D масштабирование или разделимое строково-столбцовое масштабирование) для блока коэффициентов преобразования и предоставляет блок масштабированных коэффициентов преобразования. Мультиплексор (Mux) 512 принимает и предоставляет коэффициенты масштабированного преобразования из модуля 510 масштабирования, когда полный интерфейс выбран. Мультиплексор 512 также принимает коэффициенты масштабированного преобразования через масштабированный интерфейс и предоставляет эти коэффициенты масштабированного преобразования, когда масштабированный интерфейс выбран. Мультиплексор 514 предоставляет вывод мультиплексора 512 или вывод буфера 518 в механизм 516 IDCT.
Механизм 516 IDCT может выполнять масштабированные 1D IDCT для строк блока коэффициентов масштабированного преобразования из мультиплексора 512 и предоставлять строки блока промежуточных результатов в буфер 518. Механизм 516 IDCT затем может выполнять масштабированные 1D IDCT для столбцов блока промежуточных результатов и буфера 518 и предоставлять блок конечных результатов в буфер 518. Модуль 520 выполняет выходное форматирование конечных результатов в буфере 518 и предоставляет выходные выборки.
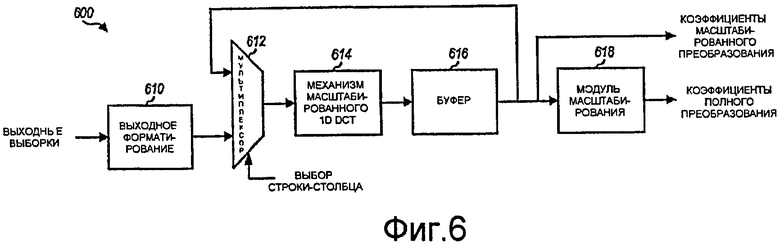
Фиг.6 иллюстрирует блок-схему структуры DCT-процессора 600, который поддерживает полные и масштабированные интерфейсы. В DCT-процессоре 600 модуль 610 выполняет входное форматирование блока входных выборок. Механизм 614 DCT принимает блок входных значений из модуля 610 через мультиплексор 612, выполняет масштабированные 1D DCT для строк блока входных значений и предоставляет блок промежуточных результатов в буфер 616. Механизм 614 DCT затем может выполнять масштабированные 1D DCT для столбцов блока промежуточных результатов из буфера 616 и предоставлять блок коэффициентов масштабированного преобразования в буфер 616. Буфер 616 предоставляет блок коэффициентов масштабированного преобразования для масштабированного интерфейса. Модуль 618 масштабирования принимает и масштабирует блок коэффициентов масштабированного преобразования и предоставляет коэффициенты полного преобразования для полного интерфейса.
Для простоты большая часть описания выше служит для DCT и IDCT. В общем, методики, описанные в данном документе, могут быть использованы для любого типа преобразования, например, DCT, IDCT, DFT, IDFT, MLT, обратное MLT, MCLT, обратное MCLT и т.д. Методики также могут быть использованы для любой факторизации преобразования, при этом несколько примерных факторизаций приведено на фиг.2 и 4. Методики также могут быть использованы для преобразований любого размера, при этом 8-точечные преобразования приведены на фиг.2 и 4. 8x8 DCT и 8x8 IDCT, как правило, используются для обработки изображений и видео. Методики также могут быть использованы для различных стандартов кодирования изображений и видео, таких как JPEG, MPEG-1, MPEG-2, MPEG-4 (P.2), H.261, H.263 и т.д.
Фиг.7 иллюстрирует структуру процесса 700 выполнения преобразования. Первые входные значения принимаются через первый интерфейс (полный или немасштабированный интерфейс) (этап 712). Полное преобразование может быть выполнено для первых входных значений, чтобы получить первые выходные значения (этап 714). Вторые входные значения принимаются через второй интерфейс (масштабированный интерфейс) (этап 716). Масштабированное преобразование может быть выполнено для вторых входных значений, чтобы получить вторые выходные значения (этап 718).
Полным преобразованием может быть полное 2D обратное преобразование. В этом случае блок первых входных значений может быть принят через первый интерфейс и масштабирован так, чтобы получить блок масштабированных входных значений. Масштабированное 1D преобразование может быть выполнено для каждой строки блока масштабированных входных значений, чтобы получить промежуточный блок. Масштабированное 1D преобразование может быть выполнено для каждого столбца промежуточного блока, чтобы получить блок первых выходных значений. Масштабированные 1D преобразования также могут быть выполнены для столбцов, за которыми следуют строки.
Полным преобразованием также может быть полное 2D прямое преобразование. В этом случае блок первых входных значений может быть принят через первый интерфейс. Масштабированное 1D преобразование может быть выполнено для каждой строки блока входных значений, чтобы получить первый промежуточный блок. Масштабированное 1D преобразование может быть выполнено для каждого столбца первого промежуточного блока, чтобы получить второй промежуточный блок. Второй промежуточный блок может быть масштабирован, чтобы получить блок первых выходных значений.
Полным преобразованием может быть полное 2D IDCT. В этом случае блок коэффициентов преобразования может быть принят через первый интерфейс и масштабирован так, чтобы получить блок коэффициентов масштабированного преобразования. Каждый коэффициент преобразования может быть масштабирован с помощью соответствующего множителя масштабирования, чтобы получить соответствующий коэффициент масштабированного преобразования, к примеру, как показано на фиг.1A. Альтернативно, блок коэффициентов преобразования может быть масштабирован построково или постолбцово, чтобы получить блок коэффициентов масштабированного преобразования, к примеру, как показано на фиг. 1B. Масштабированное 1D IDCT может быть выполнено для каждой строки блока коэффициентов масштабированного преобразования, чтобы получить промежуточный блок. Масштабированное 1D IDCT может быть выполнено для каждого столбца промежуточного блока, чтобы получить блок выходных выборок. Альтернативно, масштабирование и масштабированное одно 1D IDCT может быть выполнено для каждой строки коэффициентов преобразования, чтобы получить промежуточный блок, а масштабирование и промежуточное 1D IDCT может быть выполнено для каждого столбца промежуточного блока, к примеру, как показано на фиг.1C.
Масштабированным преобразованием может быть масштабированное 2D IDCT. В этом случае блок коэффициентов масштабированного преобразования может быть принят через второй интерфейс. Масштабированное 1D IDCT может быть выполнено для каждой строки блока коэффициентов масштабированного преобразования, чтобы получить промежуточный блок. Масштабированное 1D IDCT может быть выполнено для каждого столбца промежуточного блока, чтобы получить блок выходных выборок.
Полным преобразованием может быть полное 2D DCT, а масштабированным преобразованием может быть масштабированное 2D DCT. Полное 2D DCT может быть выполнено для блока входных выборок, как описано выше, чтобы получить блок коэффициентов полного преобразования для первого интерфейса. Масштабированное 2D DCT также может быть выполнено для блока входных выборок, чтобы получить блок коэффициентов масштабированного преобразования для второго интерфейса.
Фиг.8 иллюстрирует блок-схему структуры системы 810 кодирования и системы 850 декодирования. В системе 810 кодирования кодер 820 изображений/видео может принимать блоки пикселов и выполнять сжатие каждого блока пикселов в соответствии с конкретным алгоритмом сжатия изображений или видео. Кодер 820 может предоставлять блоки разностных значений пикселов (или остатков) и блоки пикселов. Модуль 822 может принимать остаточные блоки и блоки пикселов в качестве блоков входных выборок, выполнять 2D DCT для каждого блока входных выборок и предоставлять блоки коэффициентов полного или масштабированного преобразования. Модуль 822 может поддерживать полные и масштабированные интерфейсы. Квантователь 824 может квантовать коэффициенты полного или масштабированного преобразования и предоставлять квантованные коэффициенты. Кодер 826 по энтропии может выполнять кодирование по энтропии квантованных коэффициентов и предоставлять сжатые данные в пакетах или потоке битов для передачи посредством канала 840 связи и/или хранения.
В системе 850 декодирования, декодер 860 по энтропии может выполнять декодирование по энтропии сжатых данных способом, комплементарным кодированию по энтропии посредством кодера 826, и предоставлять квантованные коэффициенты. Обратный квантователь 862 может преобразовывать квантованные коэффициенты в коэффициенты полного или масштабированного преобразования. Модуль 862 может выполнять полное 2D IDCT для коэффициентов полного преобразования или масштабированное 2D IDCT для коэффициентов масштабированного преобразования и предоставлять блоки выходных выборок. Модуль 862 может поддерживать полные и масштабированные интерфейсы. Декодер 866 изображений/видео может выполнять распаковку для блоков выходных выборок и предоставлять блоки пикселов.
В системе 810 кодирования, модуль 822 может выполнять масштабированное 2D DCT и предоставлять коэффициенты масштабированного преобразования. Квантователь 824 может выполнять масштабирование (к примеру, стадия 318 на фиг. 3A или стадия 328 на фиг.3B), а также квантование коэффициентов масштабированного преобразования. В системе 850 декодирования, модуль 862 может выполнять обратное квантование, а также масштабирование (к примеру, стадия 112 на фиг.1A или стадия 122 на фиг.1B) для коэффициентов преобразования. Затем модуль 864 может выполнять масштабированное 2D IDCT для коэффициентов масштабированного преобразования из модуля 862.
Фиг.9 иллюстрирует блок-схему системы 900 кодирования, которая может быть использована для системы 810 кодирования по фиг.8. Устройство фиксации/запоминающее устройство 910 может принимать входной сигнал, выполнять преобразование в цифровой формат и предоставлять входные/необработанные данные. Устройством 910 фиксации может быть видеокамера, устройство ввода аналоговых данных или некоторое другое устройство. Процессор 920 обрабатывает необработанные данные и формирует сжатые данные. В процессоре 920 необработанные данные могут быть преобразованы посредством модуля 922 DCT, отсканированы посредством модуля 924 зигзагообразного сканирования, квантованы посредством квантователя 926, кодированы посредством кодера 928 по энтропии и пакетированы посредством формирователя 930 пакетов. Модуль 922 DCT может выполнять преобразования 2D DCT для необработанных данных в соответствии с методиками, описанными в данном документе, и поддерживает полные и масштабированные интерфейсы. Каждый из модулей 922-930 может быть реализован в аппаратных средствах, микропрограммном обеспечении и/или программном обеспечении. Например, модуль 922 DCT может быть реализован с помощью специализированных основных средств, набора команд для арифметического логического устройства (ALU) и т.д.
Модуль 940 хранения может сохранять сжатые данные из процессора 920. Передающее устройство 942 может передавать сжатые данные. Контроллер/процессор 950 управляет работой различных модулей в системе 900 кодирования. Запоминающее устройство 952 сохраняет данные и программные коды для системы 900 кодирования. Одна или более шин 960 соединяет различные модули в системе 900 кодирования.
Фиг.10 иллюстрирует блок-схему системы 1000 декодирования, которая может быть использована для системы 850 декодирования по фиг.8. Приемное устройство 1010 может принимать сжатые данные из системы хранения, и модуль 1012 хранения может сохранять принятые сжатые данные. Процессор 1020 обрабатывает сжатые данные и формирует выходные данные. В процессоре 1020, сжатые данные могут быть депакетированы посредством формирователя 1022 данных из пакетов, декодированы посредством декодера 1024 по энтропии, обратно квантованы посредством обратного квантователя 1026, размещены в надлежащем порядке посредством модуля 1028 обратного зигзагообразного сканирования и преобразованы посредством IDCT-модуля 1030. IDCT-модуль 1030 может выполнять преобразования 2D IDCT для коэффициентов полного или масштабированного преобразования в соответствии с методиками, описанными в данном документе, и может поддерживать полные и масштабированные интерфейсы. Каждый из модулей 1022-1030 может быть реализован в аппаратных средствах, микропрограммном обеспечении и/или программном обеспечении. Например, модуль 1030 IDCT может быть реализован с помощью специализированных основных средств, набора команд для ALU и т.д.
Дисплейный модуль 1040 отображает восстановленные изображения и видео из процессора 1020. Контроллер/процессор 1050 управляет работой различных модулей в системе 1000 декодирования. Запоминающее устройство 1052 сохраняет данные и программные коды для системы 1000 декодирования. Одна или более шин 1060 соединяет различные модули в системе 1000 декодирования.
Процессоры 920 и 1020 могут быть реализованы с помощью одной или нескольких специализированных интегральных схем (ASIC), процессоров цифровых сигналов (DSP) и/или какого-либо другого типа процессоров. Альтернативно, процессоры 920 и 1020 могут быть заменены на одно или более оперативных запоминающих устройств (RAM), постоянных запоминающих устройств (ROM), электрически программируемых ROM (EPROM), электрически стираемых программируемых ROM (EEPROM), магнитных дисков, оптических дисков и/или других типов энергозависимых и энергонезависимых запоминающих устройств, известных в данной области техники.
Методики, описанные в данном документе, могут быть реализованы в различных типах устройств. Например, методики могут быть реализованы в различных типах процессоров, различных типах интегральных микросхем, различных типах электронных устройств, различных типах электронных схем и т.д.
Специалисты в данной области техники должны понимать, что информация и сигналы могут быть представлены с помощью любой из множества различных технологий и методик. Например, данные, инструкции, команды, информация, сигналы, биты, символы и элементарные сигналы, которые могут приводиться в качестве примера по всему описанию выше, могут быть представлены напряжениями, токами, электромагнитными волнами, магнитными полями или частицами, оптическими полями или частицами либо любой их комбинацией.
Специалисты в данной области техники дополнительно должны принимать во внимание, что различные иллюстративные логические блоки, модули, схемы и этапы алгоритма, описанные в связи с изобретением, могут быть реализованы как электронные аппаратные средства, вычислительное программное обеспечение либо их комбинации. Чтобы понятно проиллюстрировать эту взаимозаменяемость аппаратных средств и программного обеспечения, различные иллюстративные компоненты, блоки, модули, схемы и этапы описаны выше, в общем, на основе их функциональности. Реализована эта функциональность в качестве аппаратных средств или программного обеспечения, зависит от конкретного варианта применения и структурных ограничений, накладываемых на систему в целом. Высококвалифицированные специалисты могут реализовать описанную функциональность различными способами для каждого конкретного варианта применения, но такие решения по реализации не должны быть интерпретированы как являющиеся отступлением от области применения настоящего изобретения.
Различные иллюстративные логические блоки, модули и схемы, описанные в связи с изобретением, могут быть реализованы или выполнены с помощью процессора общего назначения, DSP, ASIC, программируемой пользователем матричной БИС (FPGA) или другого программируемого логического устройства, дискретного логического элемента или транзисторной логики, дискретных компонентов аппаратных средств или любой их комбинации, предназначенной для того, чтобы выполнять описанные в данном документе функции. Процессором общего назначения может быть микропроцессор, но в альтернативном варианте, процессором может быть любой традиционный процессор, контроллер, микроконтроллер или конечный автомат. Процессор также может быть реализован как комбинация вычислительных устройств, к примеру, комбинация DSP и микропроцессора, множество микропроцессоров, один или более микропроцессоров вместе с ядром DSP либо любая другая подобная конфигурация.
Этапы способа или алгоритма, описанные в связи с изобретением, могут быть реализованы непосредственно в аппаратных средствах, в программном модуле, приводимом в исполнение посредством процессора, либо в комбинации вышеозначенного. Программный модуль может размещаться в памяти RAM, флэш-памяти, памяти ROM, памяти EPROM, памяти EEPROM, регистрах, на жестком диске, сменном диске, CD-ROM или любой другой форме носителя хранения, известной в данной области техники. Типичный носитель хранения соединяется с процессором, причем процессор может считывать информацию и записывать информацию на носитель хранения. В альтернативном варианте носитель хранения может быть встроен в процессор. Процессор и носитель хранения данных могут постоянно размещаться в ASIC. ASIC может постоянно размещаться в пользовательском терминале. В альтернативном варианте процессор и носитель хранения данных могут постоянно размещаться как дискретные компоненты в пользовательском терминале.
Предшествующее описание изобретения предоставлено для того, чтобы дать возможность любому специалисту в данной области техники создавать или использовать настоящее изобретение. Различные модификации в изобретении могут быть очевидными для специалистов в данной области техники, а описанные в данном документе общие принципы могут быть применены к другим структурам без отступления от духа и области применения изобретения. Таким образом, настоящее изобретение не предназначено, чтобы быть ограниченным показанными в данном документе примерами, а должно удовлетворять самой широкой области применения, согласованной с принципами и новыми признаками, раскрытыми в данном документе.

Изобретение относится к средствам и методам выполнения преобразования данных. Технический результат - уменьшение сложности реализации оборудования для кодирования. Описываются методики эффективного выполнения полных и масштабированных преобразований с данными, принимаемыми через полные и масштабированные интерфейсы, соответственно. Полное преобразование - это преобразование, которое реализует полное математическое описание преобразования. Полное преобразование оперирует с или предоставляет коэффициенты полного преобразования. Масштабированное преобразование - это преобразование, которое оперирует с или предоставляет коэффициенты масштабированного преобразования, которые являются масштабированными версиями коэффициентов полного преобразования. Масштабированное преобразование может иметь меньшую вычислительную сложность, тогда как полное преобразование можно проще использовать посредством вариантов применения. Полные и масштабированные преобразования могут быть для 2D IDСТ, которое может быть реализовано разделимым способом с преобразованиями 1D IDСТ. Полные и масштабированные преобразования могут также быть для 2D DCT, которое может быть реализовано разделимым способом с преобразованиями 1D DCT. Преобразования 1D IDСТ и преобразования 1D DCT могут быть реализованы вычислительно эффективным способом. 4 н. и 22 з.п. ф-лы, 16 ил., 1 табл.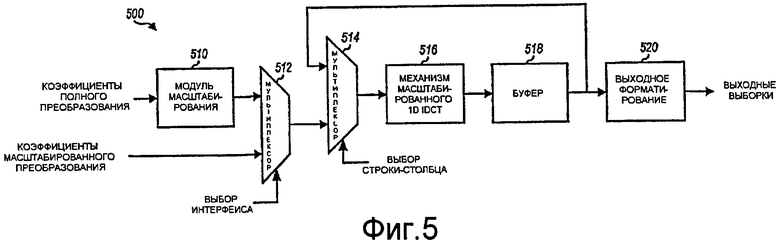
1. Устройство выполнения преобразования данных, содержащее:
- процессор, выполненный с возможностью принимать первые входные значения от кодера через первый интерфейс, выполнять полное двумерное (2D) преобразование первых входных значений, чтобы получить первые выходные значения, используя механизм одномерного (1D) преобразования процессора, принимать вторые входные значения из кодера, отличные от первых входных значений, через второй интерфейс, и выполнять масштабированное преобразование вторых входных значений, чтобы получить вторые выходные значения, используя механизм одномерного (1D) преобразования процессора, причем полное преобразование обеспечивает полное математическое описание преобразования, и причем масштабируемое преобразование выдает значения преобразования, каждый из которых умножен на один из множества различных постоянных множителей, и
- запоминающее устройство, соединенное с процессором для приема и сохранения данных от процессора.
2. Устройство по п.1, в котором процессор выполнен с возможностью принимать блок первых входных значений через первый интерфейс, масштабировать блок первых входных значений, чтобы получить блок масштабированных входных значений, выполнять масштабированное одномерное (1D) преобразование для каждой строки блока масштабированных входных значений, чтобы получить промежуточный блок, используя механизм одномерного (1D) преобразования, и выполнять масштабированное 1D преобразование для каждого столбца промежуточного блока, чтобы получить блок первых выходных значений, используя механизм одномерного (1D) преобразования.
3. Устройство по п.1, в котором процессор выполнен с возможностью принимать блок первых входных значений через первый интерфейс, выполнять масштабированное одномерное (1D) преобразование для каждой строки блока входных значений, чтобы получить первый промежуточный блок, используя механизм одномерного (1D) преобразования, выполнять масштабированное 1D преобразование для каждого столбца первого промежуточного блока, чтобы получить второй промежуточный блок, используя механизм одномерного (1D) преобразования, и масштабировать второй промежуточный блок, чтобы получить блок первых выходных значений.
4. Устройство по п.1, в котором полное преобразование - это полное обратное дискретное косинусное преобразование (IDСТ), а масштабированное преобразование - это масштабированное IDСТ.
5. Устройство по п.1, в котором полное преобразование - это полное двумерное (2D) обратное дискретное косинусное преобразование (IDСТ), а масштабированное преобразование - это масштабированное 2D IDСТ.
6. Устройство по п.5, в котором процессор выполнен с возможностью принимать первый блок коэффициентов преобразования в качестве первых входных значений через первый интерфейс, масштабировать первый блок коэффициентов преобразования, чтобы получить второй блок масштабированных коэффициентов преобразования, выполнять масштабированное одномерное (1D) IDСТ для каждой строки второго блока, чтобы получить промежуточный блок, используя механизм одномерного (1D) преобразования и выполнять масштабированное 1D IDСТ для каждого столбца промежуточного блока, используя механизм одномерного (1D) преобразования.
7. Устройство по п.6, в котором процессор выполнен с возможностью масштабировать каждый коэффициент преобразования в первом блоке с помощью соответствующего множителя масштабирования, чтобы получить соответствующий коэффициент масштабированного преобразования во втором блоке.
8. Устройство по п.6, в котором процессор выполнен с возможностью масштабировать первый блок коэффициентов преобразования построково и постолбцово, чтобы получить второй блок коэффициентов масштабированного преобразования.
9. Устройство по п.5, в котором процессор выполнен с возможностью принимать блок коэффициентов преобразования в качестве первых входных значений через первый интерфейс, выполнять масштабирование и масштабированное одномерное (1D) IDСТ для каждой строки блока коэффициентов преобразования, чтобы получить промежуточный блок, используя механизм одномерного (1D) преобразования и выполнять масштабирование и масштабированное 1D IDСТ для каждого столбца промежуточного блока, используя механизм одномерного (1D) преобразования.
10. Устройство по п.5, в котором процессор выполнен с возможностью принимать блок коэффициентов масштабированного преобразования в качестве вторых входных значений через второй интерфейс, выполнять масштабированное одномерное (1D) IDСТ для каждой строки блока коэффициентов масштабированного преобразования, чтобы получить промежуточный блок, используя механизм одномерного (1D) преобразования и выполнять масштабированное 1D IDСТ для каждого столбца промежуточного блока, используя механизм одномерного (1D) преобразования.
11. Устройство по п.1, в котором полное преобразование - это полное дискретное косинусное преобразование (DCT), а масштабированное преобразование - это масштабированное DCT.
12. Устройство по п.1, в котором полное преобразование - это полное двумерное (2D) дискретное косинусное преобразование (DCT), а масштабированное преобразование - это масштабированное 2D DCT.
13. Устройство по п.12, в котором процессор выполнен с возможностью принимать блок входных выборок в качестве первых входных значений через первый интерфейс, выполнять масштабированное одномерное (1D) IDCT для каждой строки блока входных выборок, чтобы получить первый промежуточный блок, используя механизм одномерного (1D) преобразования, выполнять масштабированное 1D DCT для каждого столбца первого промежуточного блока, чтобы получить второй промежуточный блок, масштабировать второй промежуточный блок, используя механизм одномерного (1D) преобразования, чтобы получить блок коэффициентов преобразования, и предоставлять блок коэффициентов преобразования в качестве первых выходных значений через первый интерфейс.
14. Устройство по п.13, в котором процессор выполнен с возможностью масштабировать каждый элемент во втором промежуточном блоке с помощью соответствующего множителя масштабирования, чтобы получить соответствующий коэффициент преобразования в блоке коэффициентов преобразования.
15. Устройство по п.13, в котором процессор выполнен с возможностью масштабировать второй промежуточный блок построково и постолбцово, чтобы получить блок коэффициентов преобразования.
16. Устройство по п.12, в котором процессор выполнен с возможностью принимать блок входных выборок в качестве первых входных значений через первый интерфейс, выполнять масштабированное одномерное (1D) IDCT и масштабирование для каждой строки блока входных выборок, чтобы получить промежуточный блок, используя механизм одномерного (1D) преобразования, выполнять масштабированное 1D DCT и масштабирование для каждого столбца промежуточного блока, используя механизм одномерного (1D) преобразования, чтобы получить блок коэффициентов преобразования, и предоставлять блок коэффициентов преобразования в качестве первых выходных значений через первый интерфейс.
17. Устройство по п.12, в котором процессор выполнен с возможностью принимать блок входных выборок в качестве вторых входных значений через второй интерфейс, выполнять масштабированное одномерное (1D) IDСТ для каждой строки блока входных выборок, чтобы получить промежуточный блок, используя механизм одномерного (1D) преобразования, выполнять масштабированное 1D DCT для каждого столбца промежуточного блока, чтобы получить блок коэффициентов масштабированного преобразования, используя механизм одномерного (1D) преобразования, и предоставлять блок коэффициентов масштабированного преобразования в качестве вторых выходных значений через второй интерфейс.
18. Способ выполнения преобразования данных, содержащий этапы, на которых:
- принимают с помощью процессора первые входные значения через первый интерфейс из кодера;
- выполняют полное двумерное (2D) преобразование первых входных значений, чтобы получить первые выходные значения, посредством механизма одномерного (1D) преобразования процессора;
- принимают с помощью процессора вторые входные значения, отличные от первых входных значений, через второй интерфейс из кодера; и
- выполняют масштабированное преобразование вторых входных значений, чтобы получить вторые выходные значения, посредством механизма одномерного (1D) преобразования процессора, причем полное преобразование обеспечивает полное математическое описание преобразования, и причем масштабируемое преобразование выдает значения преобразования, каждый из которых умножен на один из множества различных постоянных множителей.
19. Способ по п.18, в котором выполнение полного преобразования для первых входных значений содержит этапы, на которых:
- масштабируют блок первых входных значений, чтобы получить блок масштабированных входных значений,
- выполняют масштабированное одномерное (1D) преобразование для каждой строки блока масштабированных входных значений, чтобы получить промежуточный блок, и
- выполняют масштабированное 1D преобразование для каждого столбца промежуточного блока, чтобы получить блок первых выходных значений.
20. Способ по п.18, в котором выполнение полного преобразования для первых входных значений содержит этапы, на которых:
- выполняют масштабированное одномерное (1D) преобразование для каждой строки блока входных значений, чтобы получить первый промежуточный блок,
- выполняют масштабированное 1D преобразование для каждого столбца первого промежуточного блока, чтобы получить второй промежуточный блок, и
- масштабируют второй промежуточный блок, чтобы получить блок первых выходных значений.
21. Способ по п.18, в котором полное преобразование - это полное двумерное (2D) обратное дискретное косинусное преобразование (IDCT), в котором прием первых входных значений через первый интерфейс содержит этап, на котором принимают первый блок коэффициентов преобразования в качестве первых входных значений через первый интерфейс, и в котором выполнение полного преобразования для первых входных значений содержит этапы, на которых:
- масштабируют первый блок коэффициентов преобразования, чтобы получить второй блок масштабированных коэффициентов преобразования,
- выполняют масштабированное одномерное (1D) IDСТ для каждой строки второго блока, чтобы получить промежуточный блок, и
- выполняют масштабированное 1D IDСТ для каждого столбца промежуточного блока.
22. Способ по п.18, в котором полное преобразование - это полное двумерное (2D) дискретное косинусное преобразование (DCT), в котором прием первых входных значений через первый интерфейс содержит этап, на котором принимают блок входных выборок в качестве первых входных значений через первый интерфейс, и в котором выполнение полного преобразования для первых входных значений содержит этапы, на которых:
- выполняют масштабированное одномерное (1D) преобразование для каждой строки блока входных выборок, чтобы получить первый промежуточный блок,
- выполняют масштабированное 1D преобразование для каждого столбца первого промежуточного блока, чтобы получить второй промежуточный блок,
- масштабируют второй промежуточный блок, чтобы получить блок коэффициентов преобразования, и
- предоставляют блок коэффициентов преобразования в качестве первых выходных значений через первый интерфейс.
23. Устройство для выполнения преобразования данных, содержащее:
- средство приема первых входных значений через первый интерфейс от кодера;
- средство приема вторых входных значений, отличных от первых входных значений, через второй интерфейс из кодера; и
- средство выполнения полного двумерного (2D) преобразования первых входных значений, чтобы получить первые выходные значения, и для выполнения масштабированного преобразования вторых входных значений, чтобы получить вторые выходные значения, причем полное преобразование обеспечивает полное математическое описание преобразования, и причем масштабируемое преобразование выдает значения преобразования, каждый из которых умножен на один из множества различных постоянных множителей, и при этом дополнительно средство для выполнения полного двумерного (2D) преобразования и масштабированного одномерного (1D) преобразования представляет собой механизм одномерного (1D) преобразования.
24. Устройство по п.23, в котором средство выполнения полного 2D преобразования и масштабированного преобразования содержит:
- средство масштабирования блока первых входных значений, чтобы получить блок масштабированных входных значений,
- средство выполнения масштабированного одномерного (1D) преобразования для каждой строки блока масштабированных входных значений, чтобы получить промежуточный блок, и
- средство выполнения масштабированного 1D преобразования для каждого столбца промежуточного блока, чтобы получить блок первых выходных значений.
25. Устройство по п.23, в котором средство выполнения полного 2D преобразования и масштабируемого преобразования содержит:
- средство выполнения масштабированного одномерного (1D) преобразования для каждой строки блока входных значений, чтобы получить первый промежуточный блок,
- средство выполнения масштабированного 1D преобразования для каждого столбца первого промежуточного блока, чтобы получить второй промежуточный блок, и
- средство масштабирования второго промежуточного блока, чтобы получить блок первых выходных значений.
26. Процессорно-читаемый носитель для сохранения команд, исполняемых процессором для выполнения преобразования данных, причем процессор выполнен с возможностью:
- принимать первые входные значения через первый интерфейс из кодера;
- выполнять полное двумерное (2D) преобразование первых входных значений, используя механизм одномерного (1D) преобразования процессора, чтобы получить первые выходные значения;
- принимать вторые входные значения, отличные от первых входных значений, через второй интерфейс от кодера; и
- выполнять масштабированное преобразование вторых входных значений, используя механизм одномерного (1D) преобразования, чтобы получить вторые выходные значения, причем полное преобразование обеспечивает полное математическое описание преобразования, и причем масштабируемое преобразование выдает значения преобразования, каждый из которых умножен на один из множества различных постоянных множителей.
| Способ приготовления мыла | 1923 |
|
SU2004A1 |
| ДРЕНАЖ ДЛЯ ХИРУРГИЧЕСКОГО ЛЕЧЕНИЯ ГЛАУКОМЫ | 2005 |
|
RU2304946C2 |
| Перекатываемый затвор для водоемов | 1922 |
|
SU2001A1 |
| RU 2002115290, 20.04.2004 | |||
| RU 2003114715 А, 20.11.2004 | |||
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
Авторы
Даты
2012-08-27—Публикация
2007-03-29—Подача