Область техники
Настоящее изобретение касается области кодирования и декодирования данных, в частности способа и устройства декодирования кода порождающей матрицы с низкой плотностью.
Уровень техники
Цель кодирования канала заключается в обеспечении надежной передаче информации, сложность осуществления схемы кодирования канала главным образом сосредоточена в стороне декодирования, в обычном случае декодер является основной частей схемы кодирования канала. Декодер может быть выполнен аппаратным обеспечением, т.е. применять логический блок аппаратного обеспечения для создания декодера; также может быть выполнен программным обеспечением, т.е. применять процессор общего назначения (CPU), с помощью программы осуществляется декодер; а также может применять способ сочетания программного обеспечения и аппаратного обеспечения для осуществления декодера.
LDGC (Low Density Generator Matrix Codes, код порождающей матрицы с низкой плотностью) в широком смысле понимается так: порождающая матрица является кодом первого класса редкой двоичной матрицы (т.е. матричными элементами являются 0 или 1), включая структурированный код LDGC, код Raptor (раптор) и другие неструктурированные коды LDGC.
LDGC предназначен для упреждающей коррекции ошибок (FEC) стирающего канала. В процессе передачи данных, в случае если обнаружение ошибок проверки в пакете данных, принимаемых приемным терминалом, то сегмент данных с ошибками отбрасывается, т.е. проводится стирание. Код LDGC может эффективно предотвращать потерю данных.
При этом LDGC является одним линейным блочным кодом, все элементы в порождающей матрице (матрице кодирования) происходят из бинарного поля (поле GF(2)), т.е. элементы порождающей матрицы только состоят из 0 и 1; а также ненулевые элементы обычно являются редкими, т.е. в матрице количество «1» только занимает малый процент от количества общих элементов матрицы; кроме того, LDGC еще является одним системным кодом, т.е. первые К биты кодовых слов, образованные с помощью кодирования К битов информации с применением порождающей матрицы LDGC, равны с данными битами информации. Операция, касающаяся процесса кодирования и декодирования LDGC, является операцией на поле GF(2).
Порождающая матрица структурированного LDGC еще обладает другими характеристиками, может получаться из очень малой основной матрицы с помощью расширенной коррекции; в частности, квадратичная матрица, соответствующая первым L строкам, обычно является одной верхней треугольной матрицей или нижней треугольной матрицей. А порождающие матрицы LDGC без структурированных характеристик у кодов Raptor и т.д. являются случайными бинарными матрицами. В дальнейшем Gldgc используется для единого обозначения порождающей матрицы LDGC, при необходимости отдельного обозначения, Gstruct используется для обозначения транспонирования порождающей матрицы структурированного LDGC, Grandom используется для обозначения транспонирования порождающей матрицы LDGC без структурированных характеристик (можно сокращенно называть как порождающая матрица неструктурированного LDGC), в частности, Grandom включает порождающую матрицу кода Raptor.
В дальнейшем описании всякие «векторы» или «матрицы» с нижним индексом в виде t обозначают транспонирование бывших «векторов» или «матриц», вектор или матрица и их транспонирование являются совершенно одинаковыми по содержанию, иногда они могут выражать одинаковый предмет. Например, определение Gldgct является транспонированием Gldgc, It является транспонированием I, Rt является транспонированием R, поскольку I и R являются вектором строк, где It и Rt являются вектором столбцов; в дальнейшем Gstruct, Grandom используются для отдельного обозначения своих транспонированных порождающих матриц Gldgct.
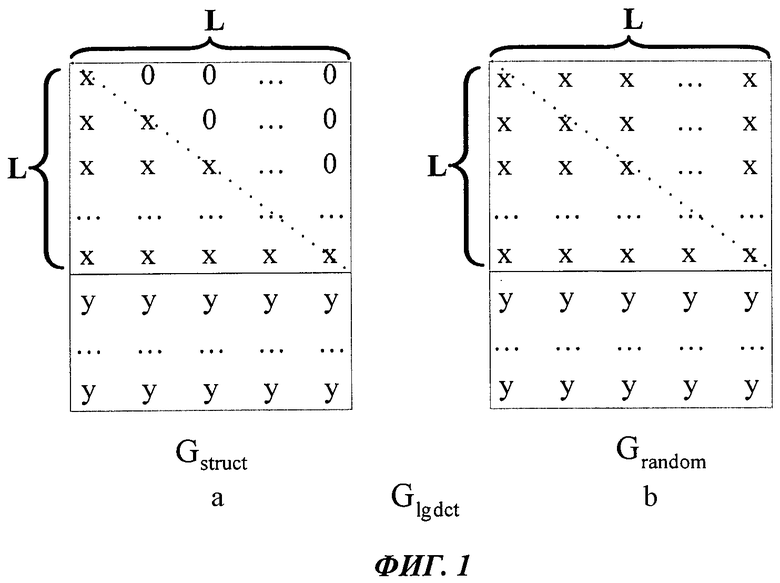
Фиг.1 является схемой транспонированной порождающей матрицы LDGC Gldgct. Как показано на фиг.1а, в структурированной порождающей матрице LDGC Gstruct квадратичная матрица, соответствующая первым L строкам, обычно является одной верхней треугольной матрицей или нижней треугольной матрицей. Как показано на фиг.1b, квадратичная матрица кода Raptor, соответствующая первым L строкам, является случайной матрицей без характеристик верхней треугольной матрицы или нижней треугольной матрицы. В т.ч. в схеме х, у может составлять 0.
Кодирование LDGC получается таким образом, сначала определяется промежуточная переменная с помощью относительного отношения между битами информации (данными, подлежащими передаче) и промежуточной переменной в системном коде, затем промежуточная переменная умножается на порождающую матрицу и получается кодированное кодовое слово. В частности, процесс кодирования заключается в том, что сначала исходная информационная последовательность m битов K заполнена известными битами в количестве d=L-K, после этого получается последовательность s битов L, затем в соответствии с отношением системы уравнений: I×Gldgc(0:L-1,0:L-1)=s, после решения системы уравнений получается последовательность промежуточной переменной битов L, затем промежуточная переменная умножается на порождающую матрицу, т.е. I×Gldgc(0:L-1,0:N+d-1) и получается последовательность 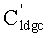 кодовых слов битов N+d (включая заполненные биты в количестве d), для заполненных битов в количестве d
кодовых слов битов N+d (включая заполненные биты в количестве d), для заполненных битов в количестве d 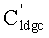 передача не требуется, поэтому в самом деле последовательность Gldgc кодовых слов битов N передается после того, как Gldgc проходит через канал (стирание является возможным), последовательность кодовых слов, принимаемая приемным терминалом, является R. В т.ч. s является вектором 1×L; I является вектором 1×L; R является вектором 1×N, ее транспонирование Rt является вектором N×1; Gldgc(0:L-1,0:L-1) является квадратичной матрицей L×L, в обычной случае, данная квадратичная матрица является одной верхней треугольной матрицей или нижней треугольной матрицей, Gldgc(0:L-1,0:N+d-1) является матрицей L×(N+d). Подробный процесс кодирования приведен в патенте «способ и устройство кодирования и декодирования кода порождающей матрицы с низкой плотностью».
передача не требуется, поэтому в самом деле последовательность Gldgc кодовых слов битов N передается после того, как Gldgc проходит через канал (стирание является возможным), последовательность кодовых слов, принимаемая приемным терминалом, является R. В т.ч. s является вектором 1×L; I является вектором 1×L; R является вектором 1×N, ее транспонирование Rt является вектором N×1; Gldgc(0:L-1,0:L-1) является квадратичной матрицей L×L, в обычной случае, данная квадратичная матрица является одной верхней треугольной матрицей или нижней треугольной матрицей, Gldgc(0:L-1,0:N+d-1) является матрицей L×(N+d). Подробный процесс кодирования приведен в патенте «способ и устройство кодирования и декодирования кода порождающей матрицы с низкой плотностью».
Фиг.2 является технологической схемой способа декодирования кода порождающей матрицы с низкой плотностью. Как показано на фиг.2, процесс декодирования включает в себя следующие шаги:
201: на соответственном месте принятой последовательности кодовых слов Rt заполняется последовательность известных битов длительностью d=L-K, например: 1, 1, …, 1., при этом вычеркиваются символы кодовых слов, стертые каналом и получается Re,
где K является длительностью битов исходной информации, L является длительностью кодирования заполненных битов исходной информации;
202: в соответствии с состоянием стирания принятой последовательности кодовых слов Rt проводится обработка стирания (вычеркивания) над Gldgct и получается порождающая матрица стирания Ge.
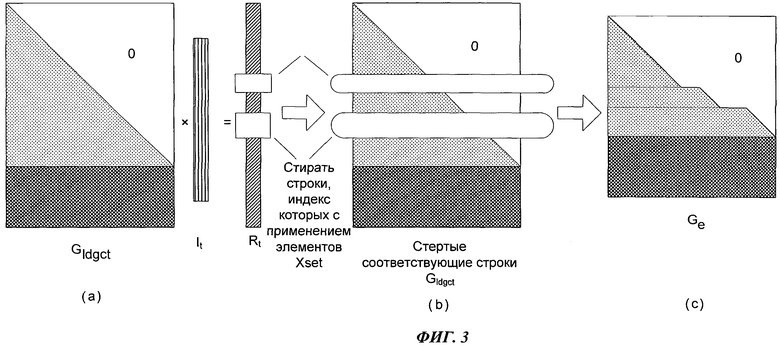
Фиг.3 является схемой проведения обработки стирания порождающей матрицы в соответствии с состоянием стирания принятой последовательности кодовых слов Rt. Как показано на фиг.3, после обработки стирания первые L строки порождающей матрицы Ge больше не являются нижней треугольной матрицей.
Допустим, что символы в количестве XT, заполненные последовательностью известных битов в формуляре R=(r0, r1,…… rN+d-1)T:{ri, rj,…, rp…rx}, стираются каналом, где символы в количестве XL в первых L символах {ri, rj,…, rp} стираются каналом, то Xset={i, j,…, р,…, х}; XsetL={i, j,… p}. Соответственно, стирать {i-ю, j-ю, …, р-ю, …, х-ю} строку в Gldgct, то получается Ge, при этом из-за того что некоторые строки стерты, то матрица над Ge не является строгой диагонализацией, как показано на фиг.3 (с),
203: в соответствии с отношением системы уравнений Ge×It=Re решается система уравнений и определяется промежуточная переменная It;
204: в соответствии с отношением системы уравнений Gldgct(0:L-1,0:L-1)×It=st определяется st, а также, если из st вычеркивать вышеуказанные заполненные известные биты в количестве d, получается исходная информационная последовательность m битов K и декодирование LDGC выполняется.
В вышеуказанном процессе декодирования самым ключевым шагом является определение промежуточной переменной It, это требуется от решения крупной системы двоичных линейных уравнений. По проекту, для решения линейных уравнений можно использовать исключение Гаусса или итерацию, в соответствии с характеристиками LDGC, исключение Гаусса более подходит к декодированию LDGC, поэтому скорость процесса исключения Гаусса прямо влияет на скорость декодирования LDGC.
В процессе определения промежуточной переменной It в соответствии с отношением системы уравнений Gldgct(0:N+d-1,0:L-1)×It=Rt (при стирании канала Gldgct записывается как Ge, Rt записывается как Re, вышеуказанное отношение системы уравнений является Ge×It=Re), для проведенного исключения Гаусса требуется произвести три типа элементарных преобразований над Gldgct (при стирании канала является Ge), как «перестановка строк, сложение строки и перестановка столбцов». В соответствии с принципом линейной алгебры, в целях обеспечения правильности системы уравнений, при проведении элементарного преобразования над Gldgct(Ge), для It и Rt (при стирании канала является Re) нужно проводить следующую соответствующую обработку:
1) перестановка строк, в случае, если проводить перестановку i-й и j-й строк Gldgct(Ge), то для i-го и j-го бита Rt(Re) должно проводить перестановку;
2) сложение строки, в случае, если проводить сложение i-й и j-й строк Gldgct(Ge), то для i-го и j-го бита Rt(Re) должно проводить сложение (сложение по модулю 2);
3) перестановка столбцов, в случае, если проводить перестановку i-го и j-го столбцов Gldgct(Ge), то для i-го и j-го бита It должно проводить перестановку.
Так как окончательный результат требует получения It, а при проведении перестановки столбцов Gldgct(Ge) для элементов в It соответственно проводится перестановка, поэтому нужно записать состояние перестановки It, чтобы использовать в дальнейшем процессе определения обратной перестановки. По проекту, можно проводить запись состояния перестановки It с помощью одного массива. A Rt не является окончательными требуемыми данными, можно прямо обрабатывать их без необходимости записи состояния обработки.
Так как эти отношения преобразования являются строго соответствующими, а также сложность исключения Гаусса главным образом выражается в обработке над Gldgct(Ge), в дальнейшем ради удобства описания всякое элементарное преобразование над Gldgct(Ge), соответственная обработка над It и Rt(Re) должны быть строго выполнены в соответствии с вышеуказанными тремя состояниями. Для выделения главного, в дальнейшем иногда будет упрощаться описание об обработке It и Rt(Re).
Как правило, сложность (объем вычисления) осуществления исключения Гаусса главным образом выражается в операции «сложение строки» матрицы. Так как все элементы Gldgct происходят из поля GF(2), поэтому операция сложения двух строк в Gldgct(Ge) является операцией «сложение по модулю 2», например:
содержание i-й строки row_i является: (1,0,0,0,0,1,0,1);
содержание j-й строки row_j является: (1,1,0,0,0,1,1,1).
При проведении исключения Гаусса выполняется операция исключения row_j с применением row_i, т.е. эквивалентна:
row_j=row_i+row_j=
(1,0,0,0,0,1,0,1)+(1,1,0,0,0,1,1,1)=(0,1,0,0,0,0,1,0),
где «+» обозначает сложение в поле GF(2) (сложение по модулю 2).
Вышеуказанные примеры показывают, что если все элементы в Gldgct происходят из поля GF(2), то значение элемента только ограничено в 0 и 1, если прямо сохранять эти элементы 0 и 1, значит то, что каждый элемент бита занимает один блок памяти или одно процессорное слово (обычно занимает 32 битов), то при более большой длине кода Gldgct(Ge) требует от огромного пространства памяти; а также операция сложения строк требует от проведения сложения по модулю 2 над каждым элементом, расход времени является большим.
Раскрытие изобретения
Настоящее изобретения предназначено для решения такой технической проблемы, как преодолеть недостатки в действующей технике, предоставлять способ и устройство декодирования кода порождающей матрицы с низкой плотностью, предназначенное для экономии пространства памяти, занятой порождающей матрицей LDGC, а также для повышения скорости операции.
Для решения вышеуказанных проблем настоящее изобретение предоставляет способ декодирования кода порождающей матрицы с низкой плотностью для принятой последовательности битов информации, переданных после кодирования LDGC, проводится декодирование, данный способ включает в себя следующее содержание:
S1: в принятой последовательности кодовых слов R заполнять известные биты в количестве L-K, а также вычеркивать символы кодового слова в R, стертые каналом, получается Re;
S2: из транспонированной матрицы Gldgct порождающей матрицы LDGC вычеркивать строки, соответствующие символам кодового слова, стертым каналом, получается Ge; в данном процессе, процессорные слова в количестве WNum используются для поочередного хранения полных или частичных матричных элементов с одинаковыми положениями во всех строках Ge, каждое процессорное слово хранит матричный элемент в количестве WWid Ge;
S3: по отношению Ge×It=Re определяется It;
S4: по отношению Gldgct(0:L-1,0:L-1)×It=st определяется st, а также из st вычеркивать вышеуказанные заполненные известные биты в количестве L-K, и исходная информационная последовательность битов K получается;
вышеуказанная Gldgct является матрицей поля GF(2) строки N+L-K и столбца L, WWid является шириной процессорного слова, WNum=ceil(P/WWid), P является количеством матричных элементов, хранящихся одним битом процессорного слова, во всех строках Ge;
причем способ декодирования осуществляют декодером.
Кроме того, в шаге S3 определять It с применением исключения Гаусса; а также в процессе исключения Гаусса, для матричных элементов, хранящихся одним битом процессорного слова, во всех строках Ge, осуществляется сложение строк соответствующих строк с помощью операции XOR бита процессорного слова, соответствующего двум строкам в Ge.
Кроме того, квадратичная матрица, которой соответствуют первые L строки Gldgct, является нижней треугольной матрицей.
Шаг S3 включает в себя следующие подшаги:
S31: проводить перестановку столбцов над Ge и генерировать 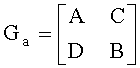 , в т.ч. А является нижней треугольной матрицей М-го порядка, а также записывать соответствующее отношение по перестановке столбцов Ge и Ga.
, в т.ч. А является нижней треугольной матрицей М-го порядка, а также записывать соответствующее отношение по перестановке столбцов Ge и Ga.
S32: по отношению 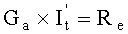 определяется
определяется 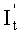 , а также по вышеуказанному соответствующему отношению по перестановке столбцов проводить обратную перестановку строк над
, а также по вышеуказанному соответствующему отношению по перестановке столбцов проводить обратную перестановку строк над 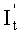 и получать It;
и получать It;
где Р является количеством столбцов матриц С и В, процессорное слово используется для поочередного хранения матричных элементов во всех строках С и В, все биты каждого процессорного слова поочередно хранят матричные элементы в количестве WWid С и В.
Кроме того, M=L-XL, XL является количеством битов, стертых каналом в символах первых L кодовых слов R; P=XL.
Кроме того, допустим, что XsetL является множеством номеров символов вычеркнутых кодовых слов в первых L символах кодовых слов R после заполнения известных битов в количестве L-K, количество номеров в данном множестве составляет XL;
В шаге S31, столбцы в Ge, номер которых принадлежат к XsetL, перемещаются к самой правой стороне Ge, свободные места соответствующих столбцов поочередно заполнены столбцами, дальнейшие номера которых не принадлежат к XsetL, и определять Ga.
Настоящее изобретение еще представляет одно устройство декодирования кода порождающей матрицы с низкой плотностью, данное устройство содержится в декодере и включает в себя: блок заполнения и стирания, блок исключения Гаусса, блок генерации информационной последовательности, в т.ч.:
блок заполнения и стирания предназначен для того, чтобы заполнять известные биты в количестве L-K в принятой последовательности кодовых слов R, а также вычеркивать символы кодового слова, стертые каналом, генерировать и выводить Re; из транспонированной матрицы Gldgct порождающей матрицы LDGC вычеркивать строки, соответствующие символам кодового слова, стертым каналом, генерировать и выводить Ge; в данном процессе, процессорные слова в количестве WNum используются для поочередного хранения полных или частичных матричных элементов с одинаковыми положениями во всех строках Ge; каждое процессорное слово хранит матричные элементы в количестве WWid Ge;
блок исключения Гаусса предназначен для того, чтобы проводить исключение Гаусса над Ge в соответствии с отношением Ge×It=Re, определять и выводить It;
блок генерации информационной последовательности предназначен для того, чтобы принимать It, выведенную блоком исключения Гаусса; в соответствии с отношением Gldgct(0:L-1,0:L-1)×It=st получать st, а также из st вычеркивать известные биты в количестве L-K, и после того выводить исходную информационную последовательность битов K.
Вышеуказанная Gldgct является матрицей поля GF(2) строки N+L-K и столбца L, WWid является шириной процессорного слова, WNum=ceil(P/WWid), P является количеством матричных элементов, хранящих одним битом процессорного слова, во всех строках Ge.
Кроме того, блок исключения Гаусса определяет It с применением исключения Гаусса; а также в процессе исключения Гаусса, для матричных элементов, хранящихся одним битом процессорного слова, во всех строках Ge, осуществляет сложение строк соответствующих строк с помощью операции XOR биты процессорного слова, соответствующего двум строкам в Ge.
Кроме того, квадратичная матрица, которой соответствуют первые L строки Gldgct, является нижней треугольной матрицей.
Устройство еще включает в себя блок перестановки столбцов, предназначен для проведения перестановки столбцов над Ge, выведенной блоком заполнения и стирания, и для генерирования 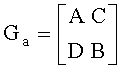 , в т.ч. А является нижней треугольной матрицей М-го порядка, а также для вывода информации о соответствующем отношении по перестановке столбцов Ge и Ga;
, в т.ч. А является нижней треугольной матрицей М-го порядка, а также для вывода информации о соответствующем отношении по перестановке столбцов Ge и Ga;
блок исключения Гаусса по отношению  определяет
определяет 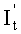 , а также по информации о соответствующем отношении по перестановке столбцов, выведенной блоком перестановки столбцов, проводит обратную перестановку строк над
, а также по информации о соответствующем отношении по перестановке столбцов, выведенной блоком перестановки столбцов, проводит обратную перестановку строк над 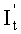 , получает и выводит It;
, получает и выводит It;
где Р является количеством столбцов матриц С и В, процессорное слово используется для поочередного хранения матричных элементов во всех строках С и В, все биты каждого процессорного слова поочередно хранят матричные элементы в количестве WWid С и В.
Кроме того, M=L-XL, XL является количеством битов, стертых каналом в символах первых L кодовых слов R; Р=XL.
Кроме того, допустим, что XsetL является множеством номеров символов вычеркнутых кодовых слов в первых L символах кодовых слов R после заполнения известных битов в количестве L-K, количество номеров в данном множестве составляет XL;
блок перестановки столбцов перемещает столбцы в Ge, номер которых принадлежит к XsetL к самой правой стороне Ge, свободные места соответствующих столбцов поочередно заполнены столбцами, дальнейшие номера которых не принадлежат к XsetL, и определять Ga.
Применяя представленный способ декодирования LDGC в настоящем изобретении, в полном объеме используя характеристики порождающей матрицы LDGC и параллельной обработкой процессором много битов, применяя одно «слово» процессора (сокращенно как процессорное слово) для хранения и выражения элементов в количестве «ширины слова процессора» декодирования порождающей матрицы LDGC, сравнивая со структурой памяти и способом выражения данных прямого хранения элементов порождающей матрицы LDGC, настоящее изобретение снизит расходы памяти декодера в большой степени, а также ускорит скорость декодирования, тем самым LDGC может более гибко использоваться в системе коммуникации высокой скорости.
Краткое описание чертежей
Фиг.1 является схемой транспонированной порождающей матрицы LDGC Gldgct;
Фиг.2 является технологической схемой способа декодирования кода порождающей матрицы с низкой плотностью;
Фиг.3 является схемой проведения обработки стирания порождающей матрицы в соответствии с состоянием стирания принятой последовательности Rt кодовых слов;
Фиг.4 является технологической схемой способа декодирования кода порождающей матрицы с низкой плотностью в первом примере осуществления настоящего изобретения;
Фиг.5 является технологической схемой способа декодирования кода порождающей матрицы с низкой плотностью во втором примере осуществления настоящего изобретения;
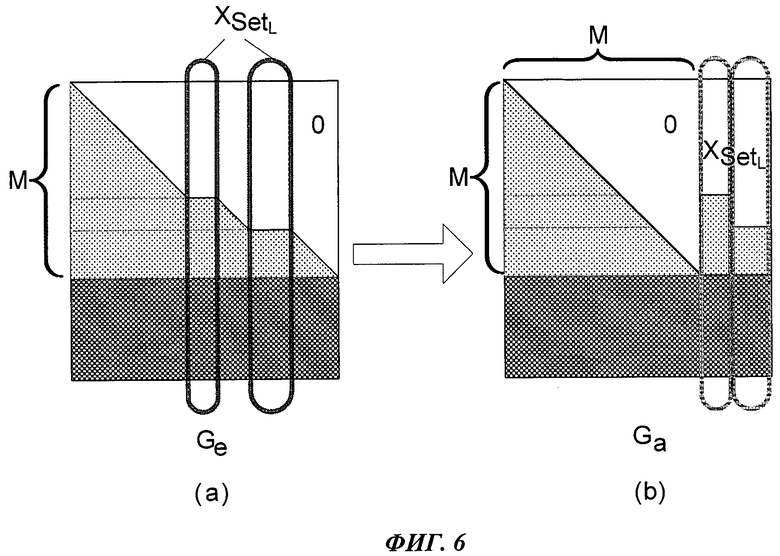
Фиг.6 является схемой перестановки столбцов над порождающей матрицей стирания Ge;
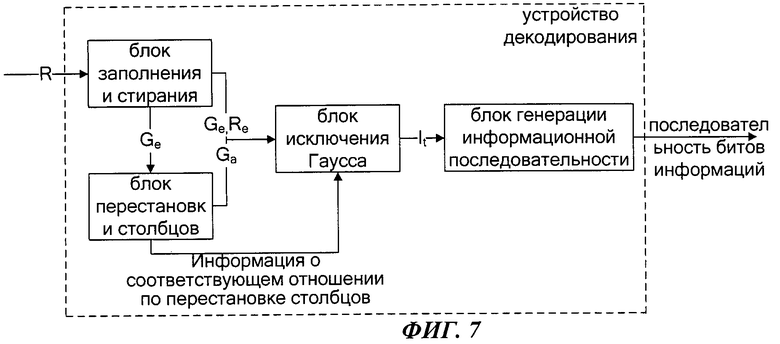
Фиг.7 является схемой устройства декодирования кода порождающей матрицы с низкой плотностью в примере осуществления настоящего изобретения.
Осуществление изобретения
Из вышеуказанного очевидно, что матричные элементы порождающей матрицы LDGC (включая Gstruct или Grandom) только состоят из 0 и 1, а также операция сложения строк, которой касается исключения Гаусса, является сложением по модулю 2; поэтому можно только использовать один бит для хранения и выражения одного матричного элемента, а также использовать побитовое исключающее ИЛИ (т.е. XOR) для замены сложения по модулю 2 всех матричных элементов, быстро осуществляется операция сложения строк порождающей матрицы LDGC.
Например:
содержание i-й строки row_i выражается как: 10000101;
содержание j-й строки row_j выражается как: 11000111;
сложение содержания i-й строки и j-й строки эквивалентно:
row_j=row_i⊕row_i=10000101⊕11000111=01000010.
Вышеуказанное «⊕» обозначает операцию с битами-XOR.
В дальнейшем, с учетом приложенных схем и примеров осуществления проводится подробное описание настоящего изобретения, стоит отметить то, что настоящее изобретение только обратит внимание на способ осуществления программного или программно-аппаратного декодера.
Фиг.4 является технологической схемой способа декодирования кода порождающей матрицы с низкой плотностью в первом примере осуществления настоящего изобретения; данный пример осуществления является способом декодирования общго назначения для структурированной и неструктурированной порождающей матрицы LDGC (Gstruct и Grandom). Как показано на фиг.4, данный способ включает в себя следующие шаги:
401: на соответственном месте принятой последовательности кодовых слов Rt, заполнять последовательность известных битов длительностью d=L-K, при этом вычеркивать символы кодовых слов, стертые каналом, и получается Re;
где K является длительностью битов исходной информации, L является длительностью кодирования заполненных битов исходной информации.
Допустим, что символы в количестве XT, заполненные последовательностью известных битов в формуляре R=(r0, r1,…… rN+d-1)T:{ri, rj,…, rp…rx}, стираются каналом; где символы в количестве XL в первых L символах {ri, rj,…, rp} стираются каналом; то Xset={i, j,…, р,…, х}; XsetL={i, j,… p}.
402: в соответствии с состоянием стирания принятой последовательности кодовых слов Rt, проводится обработка стирания (вычеркивания) над Gldgct, и получается порождающая матрица стирания Ge; где каждая строка Ge выражается в виде процессорного слова (сокращенно как процессорное слово) в количестве WNum, конечно, каждая строка Gldgct также может быть выражена в виде процессорного слова в количестве WNum.
Допустим, что Xset={i, j,…, р,…, х}; XsetL={i, j,… p}, соответственно стирать {i-ю, j-ю, …, р-ю, …, х-ю} строку в Gldgct, то получается Ge.
Так как каждая строка Ge(Gldgct) включает в себя элементы в количестве L, поэтому WNum=ceil(L/WWid); WWid является шириной процессорного слова (в обычном случае представляет собой 8, 16, 32, 64, измеряется в битах); т.е. одно процессорное слово используется для поочередного хранения и выражения непрерывных элементов в количестве WWid в Ge (Gldgct).
В случае, если L не является целым кратным WWid, последнее процессорное слово по каждой строке включает в себя последние элементы в количестве mod(L,WWid), для остальных битов в количестве Z=WWid-mod(L,WWid) данных процессорных слов можно обнулить.
Вышеуказанное ceil обозначает округление вверх, mod обозначает операцию определения модуля.
Окончательно, двумерный массив можно использоваться для выражения Ge(Gldgct), один элемент в двумерном массиве является одним процессорным словом. Общее количество элементов данного двумерного массива составляет: (N+d-XT)×WNum; XT обозначает количество строк стирания. Отсюда следует, что при применении вышеуказанного способа выражения матрицы в настоящем изобретении можно экономить пространство памяти в большом объеме.
Например, ширина процессорного слова WWid=32, каждая строка Ge(Gldgct) включает в себя элементы в количестве L=2000, поэтому нужно применять процессорные слова в количестве ceil(2000/32)=63 для выражения каждой строки Ge(Gldgct); так как 2000 не является целым кратным 32, mod(2000,32)=16, поэтому последнее процессорное слово только обладает 16 действительными битами, остальные биты в количестве 32-16=16 данного процессорного слова бессмысленны, можно обнулить.
403: в соответствии с отношением системы уравнений Ge×It=Re решается система уравнений и определяется промежуточная переменная It.
В процессе определения промежуточной переменной It с применением исключения Гаусса, команда XOR процессора используется для выполнения касающейся операции «сложения строк»; поэтому одна целая операция сложения строк может быть заменена операцией XOR процессорных слов в количестве WNum, т.е. проводится параллельная обработка операции сложения строк, параллельное измерение составляет WWid, чрезвычайно повышать скорость операции «сложения строк».
404: в соответствии с отношением системы уравнений Gldgct(0:L-1,0:L-1)×It=st определяется st, а также из st вычеркивать вышеуказанные заполненные известные биты в количестве d, получается исходная информационная последовательность m битов К и декодирование LDGC выполняется.
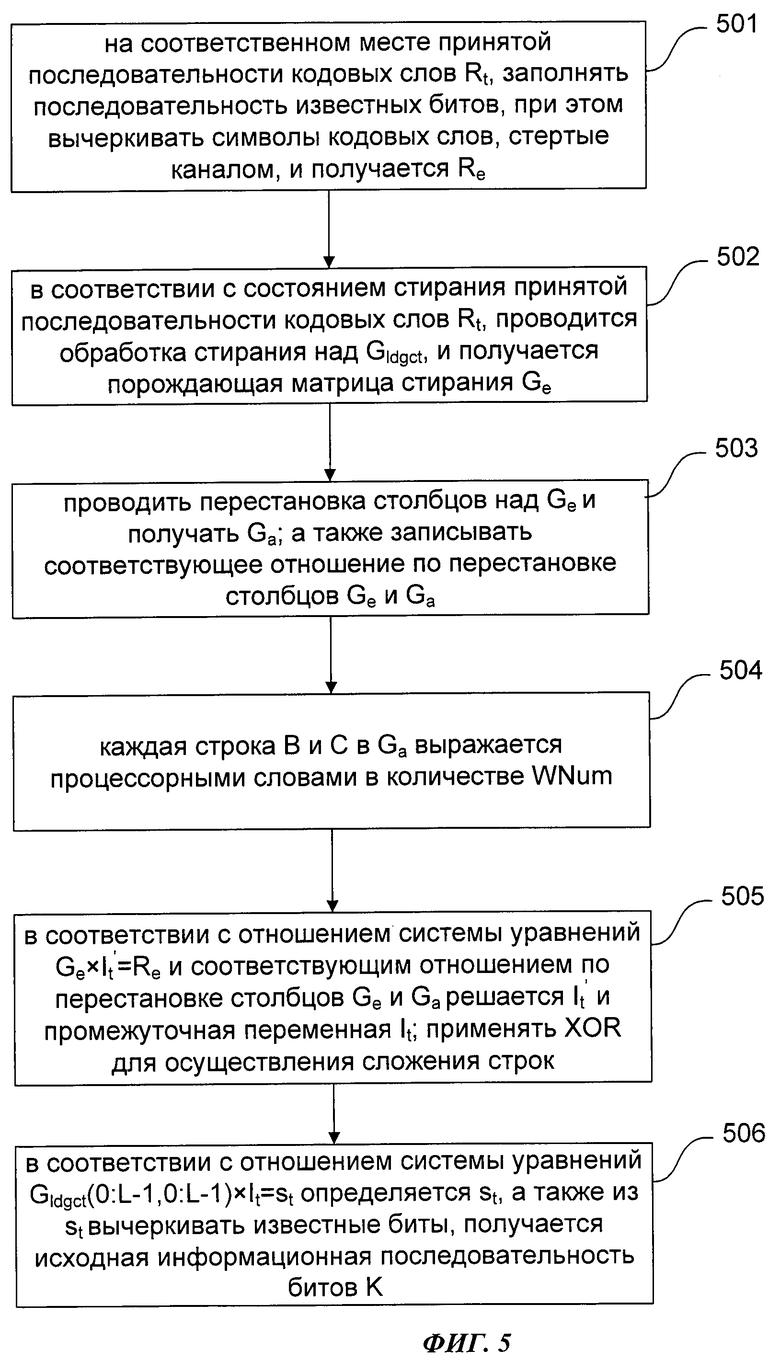
Фиг.5 является технологической схемой способа декодирования кода порождающей матрицы с низкой плотностью во втором примере осуществления настоящего изобретения; данный пример осуществления является способом декодирования для структурированной порождающей матрицы LDGC (Gstruct), процессорное слово может только использоваться для хранения частичных элементов каждой строки в Gstruct после обработки стирания, перестановки столбцов. Как показано на фиг.5, данный способ включает в себя следующие шаги:
501: на соответственном месте принятой последовательности кодовых слов Rt, заполнять последовательность известных битов длительностью d=L-K, при этом вычеркивать символы кодовых слов, стертые каналом, и получать Re;
где K является длительностью битов исходной информации, L является длительностью кодирования заполненных битов исходной информации.
Допустим, что символы в количестве XT, заполненные последовательностью известных битов в формуляре R=(r0, r1,…… rN+d-1)T:{ri, rj,…, rp…rx}, стираются каналом; где символы в количестве XL в первых L символах {ri, rj,…, rp} стираются каналом; то Xset={i, j,…, р,…, х}; XsetL={i, j,… p}.
502: в соответствии с состоянием стирания принятой последовательности кодовых слов Rt, проводится обработка стирания (вычеркивания) над Gldgct, и получается порождающая матрица стирания Ge.
Допустим, что Xset={i, j,…, p,…, х}; XsetL={i, j,… p}, соответственно стирать {i-ю, j-ю, …, p-ю, …, х-ю} строку в Gldgct, то получается Ge.
503: проводить перестановку столбцов над порождающей матрицей стирания Ge для того, чтобы матрица М-порядка вершиной (0, 0) становилась нижней треугольной матрицей, переставленная матрица Ge записывается как порождающая матрица перестановки Ga; а также записывать соответствующее отношение по перестановке столбцов Ge и Ga для проведения обратной операции порожденного 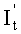 от соответствующей операции перестановки над It в процессе вышеуказанной перестановки столбцов
от соответствующей операции перестановки над It в процессе вышеуказанной перестановки столбцов
Фиг.6 является схемой проведения перестановки столбцов над порождающей матрицей стирания Ge.
В частности, для получения нижней треугольной матрицы, перемещают столбцы в Ge, номер которых принадлежат к XsetL к самой правой стороне Ge, свободные места соответствующих столбцов поочередно заполнены столбцами, дальнейшие номера которых не принадлежат к XsetL, и получают порождающую матрицу перестановки:
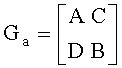 ,
,
где матрица А является квадратичной матрицей М-порядка, все элементы на диагоналях которой являются ненулевыми элементами, отличающимися строгими нижними треугольниками; матрица С - матрица размером M×(L-M); матрица D - матрица размером (N-K-(XT-XL))×М; матрица В - матрица размером (N-K-(XT-XL))(L-M). Вышеуказанное М=L-XL.
504: каждая строка В и С в Ga выражается процессорными словами в количестве WNum.
Из-за того, что длина каждой строки В и С составляет XsetL, допустим, что ширина процессорного слова составляет WWid, то:
WNum=ceil(XsetL/WWid).
В случае, если XsetL не является целым кратным WWid, последнее процессорное слово по каждой строке включает в себя последние элементы в количестве mod(XsetL,WWid); для остальных битов в количестве Z=WWid-mod(XsetL,WWid) данные процессорных слов можно обнулить.
Поэтому двумерный массив отдельно используется для выражения В и С, один элемент в двумерном массиве является одним процессорным словом. Общее количество элементов двумерного массива, которому соответствует матрица С, составляет: M×WNum; общее количество элементов двумерного массива, которому соответствует матрица В, составляет: (N-K-(XT-XL))×WNum.
Например, длина строки В и С составляет XsetL=200; допустим, что ширина процессорного слова WWid=32, то:
WNum=ceil(XsetL/WWid)=ceil(200/32)=7; т.е. хранение и выражение каждой строки В и С должны быть выполнены 7 процессорными словами.
Потому что 200 не является целым кратным 32, mod(XsetL,WWid)=mod(200,32)=8, поэтому последнее процессорное слово только содержит 8 действительных битов, остальные биты в количестве 32-8=24 данного процессорного слова бессмысленны, можно обнулить.
Поэтому матрица С может быть сохранена и выражена двумерными массивами с общим количеством элементов М×7, матрица В может быть сохранена и выражена с помощью двумерными массивами с общим количеством элементов (N-K-(XT-XL))×7; относительно действующей техники, матрица С выражается двумерными массивами с общим количеством элементов М×200, матрица В выражается двумерными массивами с общим количеством элементов (N-K-(XT-XL))×200, тем самым огромное пространство для хранения сэкономлено.
Стоит отметить то, что ненулевые элементы в матрицах А и D могут быть непосредственно вычислены по формуле, определенной структурированной порождающей матрицей при кодировании, поэтому в действительности А и D не требуется хранение, а в процессе исключения А и D только нужно непосредственно вычислить и получать положение ненулевых элементов по формуле, определенной структурированной порождающей матрицей при кодировании, затем в соответствии с положениями этих ненулевых элементов проводится «сложение строки». Конечно, также можно использовать одинаковый способ для хранения и выражения А и D. А можно рассмотреть В и С как случайные редкие матрицы, поэтому операция сложения строки над ними только является последовательными сложениями соответствующего элемента. Одно процессорное слово используется для выражения конструкции данных с элементами в количестве WWid, данный способ позволяет оптимизировать обрабатывающую сложение строк способность программного обеспечения.
505: в соответствии с отношением системы уравнений 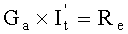 решается система уравнений и определяется промежуточная переменная
решается система уравнений и определяется промежуточная переменная 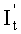 ; а также в соответствии с отношением перестановки от It до
; а также в соответствии с отношением перестановки от It до 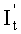 (т.е. отношение перестановки столбцов от Ge до Ga) проводится обратная перестановка, т.е. по
(т.е. отношение перестановки столбцов от Ge до Ga) проводится обратная перестановка, т.е. по 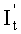 определяется It.
определяется It.
В процессе определения промежуточной переменной 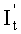 с применением исключения Гаусса, команда XOR процессора используется для выполнения касающейся матрицы В и С операции «сложения строк»; поэтому одна целая операция сложения строк может быть замена операцией XOR процессорных слов в количестве WNum, т.е. проводится параллельная обработка операции сложения строк, параллельное измерение составляет WWid, чрезвычайно повышать скорость операции «сложения строк».
с применением исключения Гаусса, команда XOR процессора используется для выполнения касающейся матрицы В и С операции «сложения строк»; поэтому одна целая операция сложения строк может быть замена операцией XOR процессорных слов в количестве WNum, т.е. проводится параллельная обработка операции сложения строк, параллельное измерение составляет WWid, чрезвычайно повышать скорость операции «сложения строк».
506: в соответствии с отношением системы уравнений Gldgct(0:L-1,0:L-1)×It=st определяется st, а также из st вычеркивать вышеуказанные заполненные известные биты в количестве d, получается исходная информационная последовательность m битов K и декодирование LDGC выполняется.
Фиг.7 является схемой устройства декодирования кода порождающей матрицы с низкой плотностью в примере осуществления настоящего изобретения. Как показано на фиг.7, данное устройство включает в себя: блок заполнения и стирания, блок перестановки столбцов, блок исключения Гаусса, блок генерации информационной последовательности, в т.ч.:
блок заполнения и стирания предназначен для того, чтобы заполнять известные биты в количестве d=L-K в принятой последовательности кодовых слов R, а также вычеркивать символы кодового слова, стертые каналом, генерировать и выводить Re; из транспонированной матрицы Gldgct порождающей матрицы LDGC вычеркивать строки, соответствующие символам кодового слова, стертым каналом, генерировать и выводить Ge.
В данном процессе, для структурированной и неструктурированной порождающей матрицы LDGC, блок заполнения и стирания использует процессорное слова в количестве WNum для поочередного хранения полных или частичных матричных элементов с одинаковыми положениями во всех строках Ge; каждое процессорное слово хранит матричные элементы в количестве WWid Ge; WWid является шириной процессорного слова, WNum=ceil(Len/WWid). Len обозначает количество элементов в одной строке, для выражения которых должно применяться процессорное слово.
Блок перестановки столбцов предназначен для проведения перестановки столбцов Ge, выведенной блоком заполнения и стирания, для того, чтобы матрица М-го порядка А, вершина которой является элементом 0-го столбца и 0-й стройки в Ge, стала нижней треугольной матрицей, для генерирования и вывода  , а также для вывода информации о соответствующем отношении по перестановке столбцов Ge и Ga;
, а также для вывода информации о соответствующем отношении по перестановке столбцов Ge и Ga;
M=L-XL, XL является количеством битов, стертых каналом в символах первых L кодовых слов R.
Блок перестановки столбцов может перемещать столбцы в Ge, номер которых принадлежит к XsetL к самой правой стороне Ge, свободные места соответствующих столбцов поочередно заполнены столбцами, дальнейшие номера которых не принадлежат к XsetL, и определять Ga. Для неструктурированной порождающей матрицы LDGC данный блок является выборочным.
Блок исключения Гаусса предназначен для того, чтобы проводить исключение Гаусса над Ge, выведенной блоком заполнения и стирания в соответствии с отношением Ge×It=Re, определять и выводить It; или проводить исключение Гаусса над Ga, выведенной блоком перестановки столбцов в соответствии с отношением 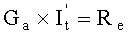 , определять
, определять 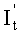 а также по информации о соответствующем отношении по перестановке столбцов, выведенной блоком перестановки столбцов, проводить обратную перестановку строк над
а также по информации о соответствующем отношении по перестановке столбцов, выведенной блоком перестановки столбцов, проводить обратную перестановку строк над  , получать и выводить It.
, получать и выводить It.
Блок генерации информационной последовательности предназначен для того, чтобы принимать It, выведенную блоком исключения Гаусса; в соответствии с отношением Gldgct(0:L-1,0:L-1)×It=st получать st, а также из st вычеркивать известные биты в количестве d, и после того выводить исходную информационную последовательность битов K.
Из вышеуказанного следует, что для порождающей матрицы LDGC применение представленного способа и устройства декодирования в настоящем изобретении позволяет ускорить обработку исключения Гаусса.
В соответствии с основным принципом настоящего изобретения, у вышеуказанных примеров осуществления есть много видов преобразований.
Для порождающих матриц LDGC с другими формами, например, первые L строки являются верхней треугольной матрицей, после того как преобразуют их в нижнюю треугольную матрицу, можно применять способ декодирования в настоящем изобретении.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ И УСТРОЙСТВО ДЛЯ ДЕКОДИРОВАНИЯ КОДА С ГЕНЕРАТОРНОЙ МАТРИЦЕЙ НИЗКОЙ ПЛОТНОСТИ | 2008 |
|
RU2461963C2 |
| Способ передачи сообщений с использованием стохастических помехоустойчивых кодов | 2022 |
|
RU2804323C1 |
| ПЕРЕСТАНОВОЧНЫЙ ДЕКОДЕР С СИСТЕМОЙ БЫСТРЫХ МАТРИЧНЫХ ПРЕОБРАЗОВАНИЙ | 2019 |
|
RU2718224C1 |
| Генератор комбинаций двоичного эквивалентного кода | 2019 |
|
RU2743854C1 |
| Способ мягкого декодирования помехоустойчивого кода | 2019 |
|
RU2725699C1 |
| ДЕКОДЕР С ПОВЫШЕННОЙ КОРРЕКТИРУЮЩЕЙ СПОСОБНОСТЬЮ | 2010 |
|
RU2438252C1 |
| ВЫСОКОСКОРОСТНЫЕ ДЛИННЫЕ LDPC КОДЫ | 2017 |
|
RU2733826C1 |
| ПЕРЕСТАНОВОЧНЫЙ ДЕКОДЕР С ПАМЯТЬЮ | 2017 |
|
RU2672300C2 |
| СПОСОБ ПЕРЕДАЧИ СООБЩЕНИЙ В СИСТЕМАХ С ОБРАТНОЙ СВЯЗЬЮ И ГИБРИДНЫМ АВТОМАТИЧЕСКИМ ЗАПРОСОМ НА ПОВТОРЕНИЕ | 2022 |
|
RU2786023C1 |
| СПОСОБ ДИНАМИЧЕСКОГО УПРАВЛЕНИЯ ПРОПУСКНОЙ СПОСОБНОСТЬЮ КАНАЛА СВЯЗИ НА БАЗЕ КЛАСТЕРНОГО ДЕКОДИРОВАНИЯ ПОЛЯРНЫХ КОДОВ | 2021 |
|
RU2779158C1 |

Изобретение относится к области кодирования и декодирования данных, в частности к способу и устройству декодирования кода порождающей матрицы с низкой плотностью. Для принятой последовательности битов информации, переданных после кодирования LDGC, проводится декодирование, при этом способ включает в себя следующее содержание: S1: в принятой последовательности кодовых слов R заполнять известные биты в количестве L-K, а также вычеркивать символы кодового слова в R, стертые каналом, получается Re; S2: из транспонированной матрицы Gldgct порождающей матрицы LDGC вычеркивать строки, соответствующие символам кодового слова, стертым каналом, получается Ge; S3: по отношению Ge×It=Re определяется It; S4: по отношению Gldgct(0:L-1,0:L-1)×It=st определяется st, а также из st вычеркивать вышеуказанные заполненные известные биты в количестве L-K, и исходная информационная последовательность битов К получается. Технический результат обеспечивает снижение расходов памяти декодера, а также ускорение скорости декодирования, тем самым LDGC более гибко использоваться в системе коммуникации высокой скорости. 2 н. и 8 з.п. ф-лы, 7 ил.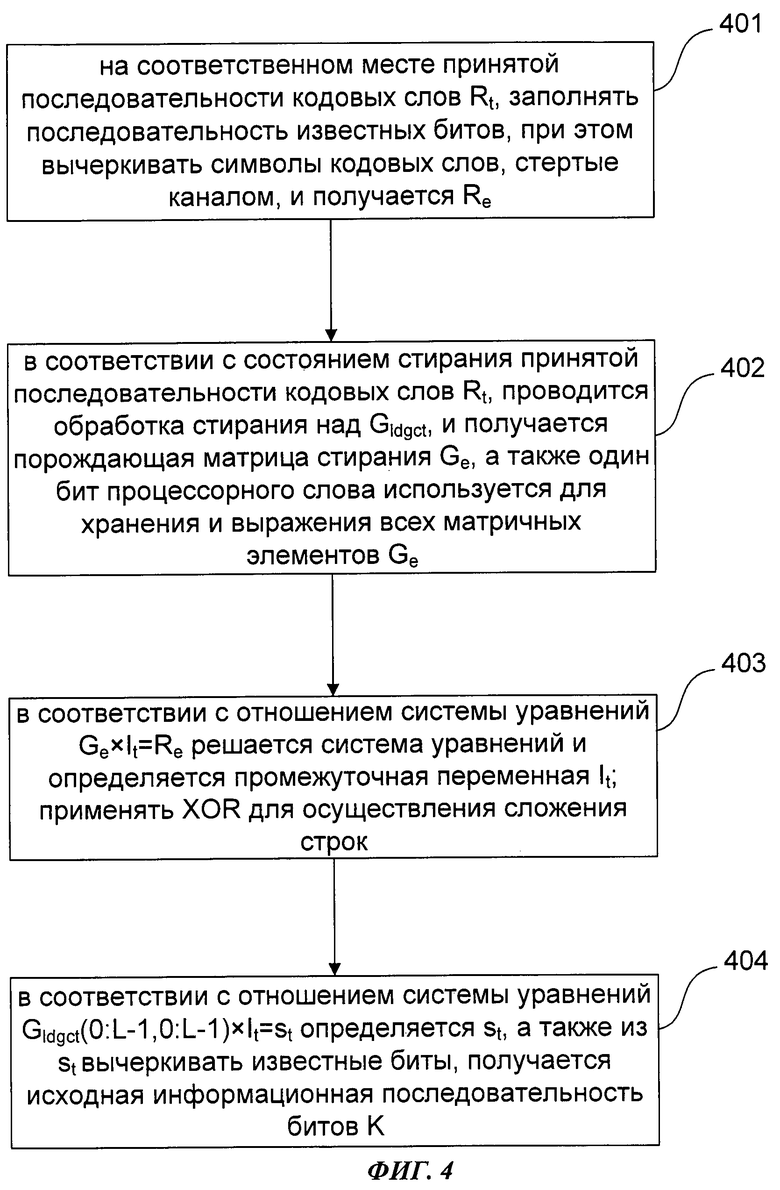
1. Способ декодирования кода порождающей матрицы с низкой плотностью для принятой последовательности битов информации, переданных после кодирования LDGC, проводится декодирование, отличающийся тем, что способ включает в себя следующее:
S1: в принятой последовательности кодовых слов R заполнять известные биты в количестве L-K, а также вычеркивать символы кодового слова в R, стертые каналом, получается Re;
S2: из транспонированной матрицы Gldgct порождающей матрицы LDGC вычеркивать строки, соответствующие символам кодового слова, стертым каналом, получается Ge; в данном процессе, процессорные слова в количестве WNum используются для поочередного хранения полных или частичных матричных элементов с одинаковыми положениями во всех строках Ge, каждое процессорное слово хранит матричный элемент в количестве WWid Ge;
S3: по отношению Ge×It=Re определяется It;
S4: по отношению Cldgct(0:L-1,0:L-1)×It=st определяется st, а также из st вычеркивать указанные заполненные известные биты в количестве L-K, и исходная информационная последовательность битов К получается;
указанное Gldgct является матрицей поля GF(2) строки N+L-K и столбца L, WWid является шириной процессорного слова, WNum=ceil(P/WWid), P является количеством матричных элементов, хранящих одним битом процессорного слова, во всех строках Ge;
причем способ декодирования осуществляют декодером.
2. Способ по п.1, отличающийся тем, что на шаге S3 определять It с применением исключения Гаусса; а также в процессе исключения Гаусса, для матричных элементов, хранящих одним битом процессорного слова, во всех строках Ge, осуществляется сложение строк соответствующих строк с помощью операции XOR биты процессорного слова, соответствующего двум строкам в Ge.
3. Способ по п.1, отличающийся тем, что
указанная квадратичная матрица, которой соответствуют первые L строки Gldgct, является нижней треугольной матрицей;
шаг S3 включает в себя следующие подшаги:
S31: проводить перестановку столбцов над Ge и генерировать 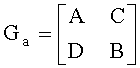 , где А является нижней треугольной матрицей М-го порядка, а также записывать соответствующее отношение по перестановке столбцов Ge и Ga.
, где А является нижней треугольной матрицей М-го порядка, а также записывать соответствующее отношение по перестановке столбцов Ge и Ga.
S32: по отношению 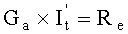 определяется
определяется 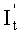 , а также по указанному соответствующему отношению по перестановке столбцов проводить обратную перестановку строк над
, а также по указанному соответствующему отношению по перестановке столбцов проводить обратную перестановку строк над 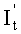 и получать
и получать 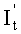 ;
;
где Р является количеством столбцов матриц С и В, указанное процессорное слово используется для поочередного хранения матричных элементов во всех строках С и В, все биты каждого процессорного слова поочередно хранят матричные элементы в количестве WWid С и В.
4. Способ по п.3, отличающийся тем, что M=L-XL, XL является количеством битов, стертых каналом в символах первых L кодовых слов R; P=XL.
5. Способ по п.3, отличающийся тем, что
допустим, что XsetL является множеством номеров символов вычеркнутых кодовых слов в первых L символах кодовых слов R после заполнения известных битов в количестве L-K, количество номеров в данном множестве составляет x1;
на шаге S31, столбцы в Ge, номер которых принадлежат к XsetL, перемещаются к самой правой стороне Ge, свободные места соответствующих столбцов поочередно заполнены столбцами, дальнейшие номера которых не принадлежат к XsetL, и определять Ga.
6. Устройство декодирования кода порождающей матрицы с низкой плотностью, содержащееся в декодере, отличающееся тем, что устройство включает в себя блок заполнения и стирания, блок исключения Гаусса, блок генерации информационной последовательности, причем
указанный блок заполнения и стирания предназначен для того, чтобы заполнять известные биты в количестве L-K в принятой последовательности кодовых слов R, а также вычеркивать символы кодового слова, стертые каналом, генерировать и выводить Re; из транспонированной матрицы Gldgct порождающей матрицы LDGC вычеркивать строки, соответствующие символам кодового слова, стертым каналом, генерировать и выводить Ge; в данном процессе, процессорные слова в количестве WNum используются для поочередного хранения полных или частичных матричных элементов с одинаковыми положениями во всех строках Ge; каждое процессорное слово хранит матричные элементы в количестве WWid Ge;
указанный блок исключения Гаусса предназначен для того, чтобы проводить исключение Гаусса над Ge в соответствии с отношением Ge×It=Re, определять и выводить It;
указанный блок генерации информационной последовательности предназначен для того, чтобы принимать It, выведенную блоком исключения Гаусса; в соответствии с отношением Gldgct(0:L-1,0:L-1)×It=st получать st, а также из st вычеркивать известные биты в количестве L-K, и после того выводить исходную информационную последовательность битов К;
указанное Gldgct является матрицей поля GF(2) строки N+L-K и столбца L, WWid является шириной процессорного слова, WNum=ceil(P/WWid), P является количеством матричных элементов, хранящих одним битом указанного процессорного слова, во всех строках Ge.
7. Устройство по п.6, отличающееся тем, что указанный блок исключения Гаусса определяет It с применением исключения Гаусса; а также в процессе исключения Гаусса, для матричных элементов, хранящих одним битом указанного процессорного слова, во всех строках Ge, осуществляет сложение строк соответствующих строк с помощью операции XOR биты процессорного слова, соответствующего двум строкам в Ge.
8. Устройство по п.6, отличающееся тем, что
указанная квадратичная матрица, которой соответствуют первые L строки Gldgct; является нижней треугольной матрицей;
указанное устройство включает в себя блок перестановки столбцов, предназначенный для проведения перестановки столбцов Ge, выведенный указанным блоком заполнения и стирания, и для генерирования  , где А является нижней треугольной матрицей М-го порядка, а также для вывода информации о соответствующем отношении по перестановке столбцов Ge и Ga;
, где А является нижней треугольной матрицей М-го порядка, а также для вывода информации о соответствующем отношении по перестановке столбцов Ge и Ga;
указанный блок исключения Гаусса по отношению 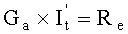 определяет
определяет 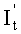 , а также по информации о соответствующем отношении по перестановке столбцов, выведенной блоком перестановки столбцов, проводит обратную перестановку строк над
, а также по информации о соответствующем отношении по перестановке столбцов, выведенной блоком перестановки столбцов, проводит обратную перестановку строк над 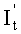 , получает и выводит It;
, получает и выводит It;
где Р является количеством столбцов матриц С и В, указанное процессорное слово используется для поочередного хранения матричных элементов во всех строках С и В, все биты каждого процессорного слова поочередно хранят матричные элементы в количестве WWid С и В.
9. Устройство по п.8, отличающееся тем, что M=L-XL, XL является количеством битов, стертых каналом в символах первых L кодовых слов R; P=XL.
10. Устройство по п.8, отличающееся тем, что
допустим, что XsetL является множеством номеров символов вычеркнутых кодовых слов в первых L символах кодовых слов R после заполнения известных битов в количестве L-K, количество номеров в данном множестве составляет XL;
указанный блок перестановки столбцов перемещает столбцы в Ge, номер которых принадлежат к XsetL к самой правой стороне Ge, свободные места соответствующих столбцов поочередно заполнены столбцами, дальнейшие номера которых не принадлежат к XsetL, и определяет Ga.
| Пломбировальные щипцы | 1923 |
|
SU2006A1 |
| CN 101141131 A, 12.03.2008 | |||
| RU 2006138012 A, 10.05.2008 | |||
| EP 1667328 A1, 07.06.2006 | |||
| US 2005246615 A1, 03.11.2005. | |||
Авторы
Даты
2012-09-20—Публикация
2008-10-14—Подача