Изобретение относится к области передачи дискретных сообщений и может быть использовано для защиты информации стохастическими помехоустойчивыми кодами в каналах связи с помехами.
При передаче сообщений по каналам связи с помехами возможны искажения сигнала, которые на приемной стороне приводят к ошибкам. Одним из основных методов защиты от ошибок является применение помехоустойчивого кодирования, в частности стохастического помехоустойчивого кодирования. Стохастические или случайные коды являются кодами с высокой помехоустойчивостью, но сложным алгоритмом декодирования. Помехоустойчивость стохастических кодов достигает границы Шеннона, однако, очень быстрое возрастание сложности декодирования по экспоненциальному закону в зависимости от длины кода затрудняет их практическое применение. На приемной стороне ошибочные символы стохастического помехоустойчивого кода можно стирать. Тогда декодирование кодов с исправлением ошибок сводится к декодированию кодов с исправлением стираний. Декодирование кодов с исправлением стираний существенно проще, чем декодирование с исправлением ошибок, а по помехоустойчивости не хуже, чем декодирование с исправлением ошибок, а во многих случаях, даже лучше, поскольку число исправляемых стираний примерно вдвое больше, чем число исправляемых ошибок. При этом возможно декодирование с исправлением стираний за пределами минимального кодового расстояния, и доля таких стираний довольно значительна. Декодирование с исправлением стираний можно применять для любых линейных помехоустойчивых кодов, в том числе для линейных стохастических помехоустойчивых кодов, формируемых с использованием двойного линейного стохастического преобразования, обеспечивающего высокую вероятность случайности символов кода. Декодирование линейных стохастических кодов с исправлением стираний сводится к решению системы линейных уравнений относительно значений стертых символов. Система линейных уравнений имеет единственное решение при условии линейной независимости столбцов проверочной матрицы кода, соответствующих позициям стертых символов. При линейной зависимости столбцов выполняется списочное декодирование кода. В списке решений можно выбрать наиболее правдоподобные решения, используя оценки достоверности символов кода. Асимптотически параметры линейных стохастических кодов стремятся к значениям параметров наилучших известных помехоустойчивых кодов. Сложность декодирования возрастает по полиномиальному закону с небольшим показателем степени, равным 2-3.
Известен способ передачи дискретных сообщений с использованием стохастических помехоустойчивых кодов, при котором сначала на передающей стороне исходное сообщение подвергают стохастическому преобразованию и формируют стохастический код, который передают в канале связи, на приемной стороне стохастический код декодируют с исправлением ошибок, выполняют обратное стохастическое преобразование и восстанавливают исходное сообщение (Прокис Д. Цифровая связь. Пер. с англ. / Под ред. Д.Д. Кловского - М.: Радио и связь. - 2000. - с. 332-338).
Недостатком этого способа является чрезмерно большая сложность декодирования кода с исправлением ошибок, что накладывает ограничения на длину стохастического помехоустойчивого кода и число исправляемых кодом ошибок.
Наиболее близким к предлагаемому способу является способ (прототип) передачи дискретных сообщений с использованием стохастических помехоустойчивых кодов, при котором на передающей стороне сначала исходная двоичная информация разбивается на блоки по k бит, каждый из блоков подвергают прямому стохастическому преобразованию, формируют стохастический код, который передают в канале связи, на приемной стороне стирают наименее достоверные символы стохастического кода, исправляют стирания стохастического кода, выполняют обратное стохастическое преобразование и восстанавливают исходное сообщение. (Патент РФ №2292122 Осмоловский С.А. Способ комплексной защиты информации, опубл. 20.01.2007).
Недостатком этого способа является высокая сложность декодирования стохастического кода с исправлением многократных стираний, что ограничивает длину кода и снижает помехоустойчивость передачи.
Целью изобретения является снижение сложности декодирования стохастических кодов с исправлением многократных стираний, что позволяет применять длинные коды, обеспечивающие высокую помехоустойчивость.
Для достижения цели предложен способ декодирования стохастических кодов, при котором на передающей стороне сначала исходную двоичную информацию разбивают на блоки по k бит, каждый из блоков подвергают прямому стохастическому преобразованию, формируют стохастический код, который передают в канале связи, на приемной стороне стирают наименее достоверные символы стохастического кода, исправляют стирания стохастического кода, выполняют обратное стохастическое преобразование и восстанавливают исходное сообщение. Новым является то, что на передающей стороне выполняют двойное стохастическое преобразование исходной информации и формируют линейный стохастический код, а на приемной стороне линейный стохастический код декодируют с исправлением стираний символов. При этом первое стохастическое преобразование заключается в гаммировании исходной информации псевдослучайной последовательностью, а второе стохастическое преобразование представляет собой умножение гаммированной информации на псевдослучайную порождающую матрицу линейного стохастического кода. Причем псевдослучайную порождающую матрицу линейного стохастического кода получают путем генерации элементов матрицы по псевдослучайному закону. При этом на приемной стороне стирания исправляют путем решения системы линейных уравнений относительно неизвестных значений стертых символов линейного стохастического кода. Причем систему линейных уравнений относительно неизвестных значений стертых символов получают при умножении стохастического кода на проверочную матрицу линейного стохастического кода. При этом при равенстве ранга системы линейных уравнений числу стираний символов кода, значения стираний символов определяют однозначно, а при ранге системы меньше числа стираний символов кода выполняют списочное декодирование кода. Причем в списке решений выбирают значения стираний символов, обеспечивающие наибольшее значение суммарной достоверности символов кода.
Рассмотрим реализацию предлагаемого способа. Пусть источник генерирует двоичные информационные символы кода a0,a1,…,ak-1. Первое стохастическое преобразование состоит в гаммировании исходной информации или наложении на исходную информацию псевдослучайной последовательности

 i = 0..k-1,
i = 0..k-1,
где γi - двоичные псевдослучайные символы, генерируемые датчиком случайных чисел. Датчик случайных чисел генерирует равномерно распределенную между 0 и 1 случайную величину random. Генерация псевдослучайного двоичного символа выполняется по закону
random <0,5⇒γi=0, иначе γi=1.
Затем полученную псевдослучайную последовательность подвергают второму стохастическому преобразованию, заключающемуся в умножении гаммированной информации на псевдослучайную порождающую матрицу линейного стохастического кода, размер которой равен k×n. Кодирование стохастического кода запишется в виде C=B×G. Элементы порождающей матрицы  генерируются датчиком случайных чисел. Строки порождающей матрицы являются случайными двоичными последовательностями. Генерируемые случайные последовательности γi и gij являются нелинейными случайными последовательностями, поэтому и стохастический код, формируемый при случайном выборе строк порождающей матрицы, и последующем их суммировании, также является нелинейной случайной последовательностью. Проверочные символы кода получают в виде линейной комбинации информационных символов. Стохастический код является линейным помехоустойчивым кодом и одновременно - нелинейной случайной последовательностью. При случайных информационных символах кода, принимающих с вероятностью 0,5 значения 0 или 1, проверочные символы будут принимать те же значения с вероятностью 0,5, то есть также будут случайными. Поскольку проверочные соотношения кода различаются между собой не менее, чем на 1 случайный символ, то символы кода являются независимыми случайными величинами, то есть не коррелируются.
генерируются датчиком случайных чисел. Строки порождающей матрицы являются случайными двоичными последовательностями. Генерируемые случайные последовательности γi и gij являются нелинейными случайными последовательностями, поэтому и стохастический код, формируемый при случайном выборе строк порождающей матрицы, и последующем их суммировании, также является нелинейной случайной последовательностью. Проверочные символы кода получают в виде линейной комбинации информационных символов. Стохастический код является линейным помехоустойчивым кодом и одновременно - нелинейной случайной последовательностью. При случайных информационных символах кода, принимающих с вероятностью 0,5 значения 0 или 1, проверочные символы будут принимать те же значения с вероятностью 0,5, то есть также будут случайными. Поскольку проверочные соотношения кода различаются между собой не менее, чем на 1 случайный символ, то символы кода являются независимыми случайными величинами, то есть не коррелируются.
Генерация строк порождающей матрицы по псевдослучайному закону может приводить к их линейной зависимости, поэтому для обеспечения линейной независимости строк порождающей матрицы может потребоваться несколько попыток генерации каждой строки. Пусть сгенерировано ƒ линейно независимых строк, тогда вероятность того, что ƒ+1 псевдослучайные строки будут линейно независимы при m-кратной попытке генерации (ƒ+1)-ой строки

Число попыток генерации строки убывает по показательному закону и требуется не слишком большое число попыток m, чтобы с большой вероятностью получить линейно независимые строки. Так, при n=15, ƒ=7, для m=1 получим Рm=0,9961, а для m=2-Рm=0,999985 и так далее.
Псевдослучайную порождающую матрицу можно вычислить заранее, до кодирования стохастического кода, и ее генерация не влияет на сложность кодирования. Сложность кодирования стохастического кода определяется сложностью наложения псевдослучайной последовательности и умножения на порождающую матрицу и имеет порядок Sk=O(n2). Линейный стохастический код C={ci}, i=0…n-1 при не слишком большой скорости кода и достаточно большой блоковой длине п будет иметь минимальное кодовое расстояние, оцениваемое величиной d=n/2.
Код является асимптотически хорошим кодом, поскольку

На приемной стороне будут принятые из канала символы кода F=ƒ0, ƒ1,…, ƒn-1, с оценками их достоверности А=α0, α1…,αn-1, 0≤αi≤1. Код F отличается от переданного кода С на вектор ошибок Е

Синдром ошибок

где Н - проверочная матрица кода. Проверочная матрица кода вычисляется по порождающей матрице кода.
Оценки достоверности символов кода используют для стирания наименее достоверных символов. Символы кода стираются при достоверности меньше некоторого порогового значения αi<αр, i=0…n-1.
Пусть неизвестные значения стертых символов Х=х1,х2,…,xs. Обозначим F1 - код, полученный из F, если значения всех стертых символов принять равными 0, a F2=F-F1=0,…,х1, 0,…,х2,0,…,xs0,… - код, полученный из F, если значения всех нестертых символов равны 0.
Вычислим

вычитая из уравнения (1) уравнение (2) получим
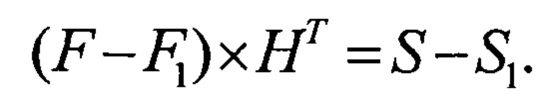
Отсюда 
где S2=S-S1.
Из (3) система линейных уравнений относительно значений стертых символов запишется

где {hkji} - столбцы проверочной матрицы, соответствующие стираниям символов. Таким образом, значения стертых символов получают при решении системы линейных уравнений (4), матрица которой составлена из столбцов проверочной матрицы, соответствующих стертым символам кода.
Система линейных уравнений имеет единственное решение в поле Галуа, если ранг матрицы системы г равен числу неизвестных (r=s). Решения можно получить по формулам Крамера, однако проще их находить по методу исключения Гаусса, приводя матрицу системы при помощи элементарных преобразований к трапециевидной форме. Совместная система линейных уравнений имеет конечное множество решений (>1), если в трапециевидной форме матрицы системы будет меньше, чем s строк, отличных от 0. Тогда, ранг матрицы системы будет меньше числа неизвестных (r<s), при этом некоторым s-r неизвестным можно придавать произвольные значения. Оставшиеся r неизвестных определятся единственным образом. Условие совместности системы линейных уравнений определяется теоремой Кронекера-Капелли о равенстве рангов матриц основной и расширенной системы уравнений.
Конечное множество решений соответствует списочному декодированию кода. При назначении s-r неизвестным произвольных значений список решений будет содержать 2s-r значений стираний. Каждое из значений стертого символа имеет свою достоверность, зависящую от расстояния до правильного значения символа. Суммарная достоверность стертых символов зависит от набора значений стертых символов. В списке решений системы целесообразно выбирать значения стираний, обеспечивающие наибольшую суммарную достоверность стертых символов.
Сложность декодирования определяется сложностью решения системы линейных уравнений и при использовании метода Гаусса оценивается величиной Sd=O(n3).
При стирании всех ошибочных символов оставшиеся безошибочные символы позволяют декодировать кодовое слово, если позициям стертых символов соответствуют линейно независимые столбцы проверочной матрицы кода. При минимальном кодовом расстоянии d любые d-1 столбцов проверочной матрицы линейно независимы и, значит, любые d-1 стираний гарантированно исправляются. Таким образом, в пределах минимального кодового расстояния исправляются все стирания. Долю исправляемых стираний за пределами минимального кодового расстояния определяют, используя оценку случайного кодирования. Некоторые s случайных столбцов проверочной матрицы будут линейно независимы, если s-1 столбцов линейно независимы и все 2s-1 линейных комбинаций этих столбцов проверочной матрицы не равны последнему s столбцу. Число различных комбинаций случайного столбца равно 2n-k. Обозначим Ps - вероятность исправления s стираний, тогда

где начальное условие
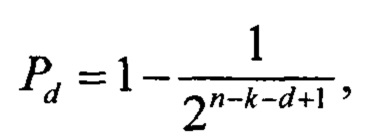
a s=d+1…n-k.
Для больших n увеличение числа стираний на единицу приводит к возрастанию доли неисправимых стираний примерно вдвое.
Например, для двоичного стохастического кода с блоковой длиной 15 и информационной длиной 7, все стирания веса 4 и менее исправляются, доля исправляемых стираний веса 5 примерно равна 0,9375, веса 6 -0,8125, 7 - 0,5625, 8 - 0,0625. Псевдослучайные порождающая и проверочная матрицы этого кода запишутся

Пусть передавался стохастический код B = 100110101111000, а принят код A = 1a130a11al00a8011a41a20aQ, где ai обозначены стирания на i=13,11,10,8,4,2,0 позициях кода. Всего 7 стираний.
Выполним ортогонализацию проверочной матрицы относительно позиций стертых символов по методу Гаусса и выпишем контрольные проверки для восстановления стираний
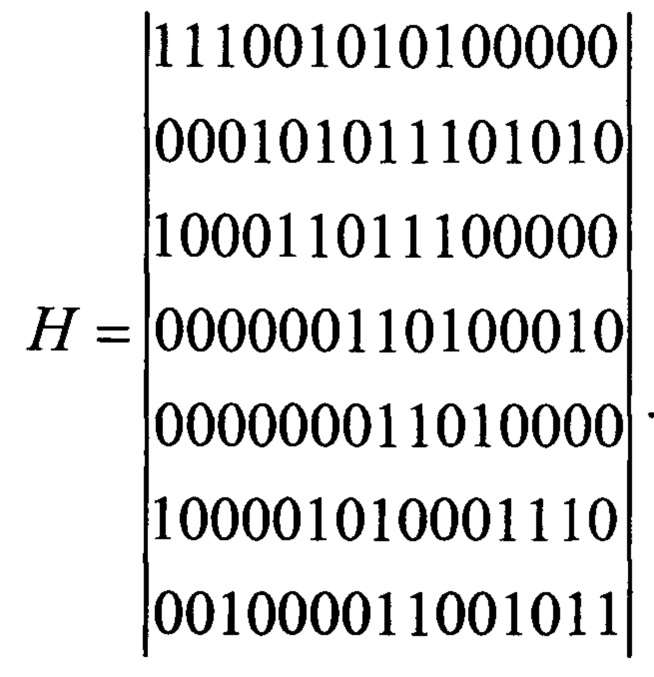
Отсюда значения стертых символов
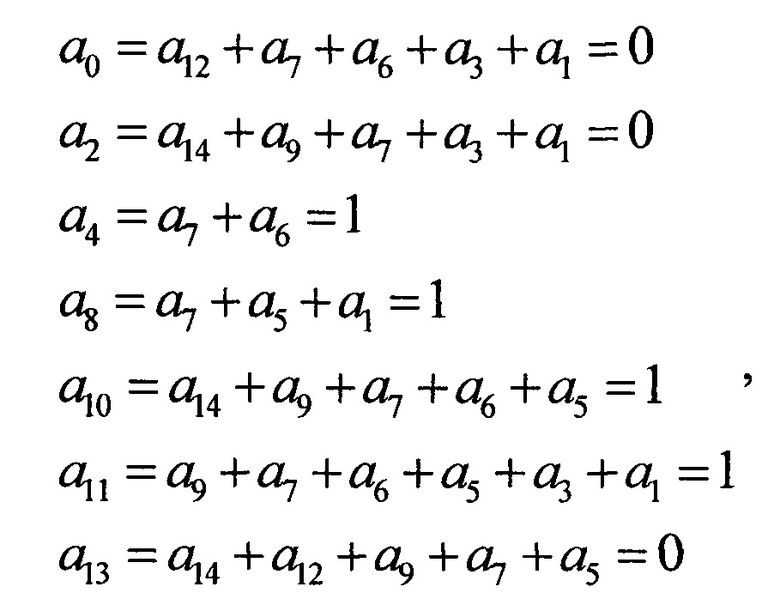
что совпадает с исходным стохастическим кодом.
В примере при небольшом количестве вычислений удалось исправить 7 стираний символов стохастического кода (15,7), что на 3 стирания больше, чем число исправляемых кодом стираний в пределах минимального кодового расстояния.
Таким образом, на приемной стороне стираются наименее достоверные символы коды, в которых наиболее вероятно возникновение ошибок, что обеспечивает высокую помехоустойчивость передачи сообщений. Линейный стохастический код используют для исправления многократных стираний символов. Декодирование с исправлением стираний имеет относительно небольшую сложность реализации, что позволяет использовать код для передачи сообщений достаточно большой длины. Сложность исправления стираний за пределами минимального кодового расстояния кода соизмерима со сложностью исправления стираний в пределах минимального кодового расстояния. Декодирование полностью реализует возможности линейного стохастического помехоустойчивого кода по исправлению стираний, в том числе за пределами минимального кодового расстояния.
Достигаемым техническим результатом предложенного способа является упрощение декодирования стохастического кода с исправлением многократных стираний, что позволяет использовать длинные коды, обеспечивающие более высокую помехоустойчивость.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ мягкого декодирования помехоустойчивого кода | 2019 |
|
RU2725699C1 |
| Способ декодирования линейных помехоустойчивых кодов с исправлением стираний | 2020 |
|
RU2746797C1 |
| Способ мягкого декодирования помехоустойчивого кода | 2023 |
|
RU2812043C1 |
| СПОСОБ КОМПЛЕКСНОЙ ЗАЩИТЫ ИНФОРМАЦИИ | 2005 |
|
RU2292122C1 |
| СПОСОБ ПЕРЕДАЧИ И КОМПЛЕКСНОЙ ЗАЩИТЫ ИНФОРМАЦИИ | 2007 |
|
RU2367007C2 |
| ДЕКОДЕР С ПОВЫШЕННОЙ КОРРЕКТИРУЮЩЕЙ СПОСОБНОСТЬЮ | 2010 |
|
RU2438252C1 |
| СПОСОБ ПЕРЕДАЧИ СООБЩЕНИЙ В СИСТЕМАХ С ОБРАТНОЙ СВЯЗЬЮ И ГИБРИДНЫМ АВТОМАТИЧЕСКИМ ЗАПРОСОМ НА ПОВТОРЕНИЕ | 2022 |
|
RU2786023C1 |
| Способ передачи многоблочных сообщений каскадным кодом [PC (32, 16, 17), БЧХ (31, 16, 7)] | 2020 |
|
RU2755055C1 |
| УНИВЕРСАЛЬНЫЙ СПОСОБ ПЕРЕДАЧИ ИНФОРМАЦИИ С КОНТРОЛИРУЕМЫМИ ПАРАМЕТРАМИ | 2006 |
|
RU2319199C2 |
| Декодер циклического кода | 1988 |
|
SU1599996A1 |
Изобретение относится к области передачи дискретных сообщений и может быть использовано для защиты информации стохастическими помехоустойчивыми кодами в каналах связи с помехами. Техническим результатом является упрощение декодирования стохастического кода с исправлением многократных стираний, что позволяет использовать длинные коды, обеспечивающие более высокую помехоустойчивость. Для этого на передающей стороне сначала исходную двоичную информацию разбивают на блоки по k бит, каждый из блоков подвергают прямому двойному стохастическому преобразованию исходной информации и формируют линейный стохастический код длины n бит, который передают в канале связи. На приемной стороне стирают наименее достоверные символы стохастического кода, исправляют стирания линейного стохастического кода, выполняют обратное стохастическое преобразование и восстанавливают исходное сообщение. При этом первое прямое стохастическое преобразование состоит в гаммировании исходной информации псевдослучайной последовательностью, а второе стохастическое преобразование представляет собой умножение гаммированной информации на псевдослучайную порождающую матрицу линейного стохастического кода размера k×n. 6 з.п. ф-лы.
1. Способ декодирования стохастических кодов, при котором на передающей стороне сначала исходную двоичную информацию разбивают на блоки по k бит, каждый из блоков подвергают прямому стохастическому преобразованию, формируют стохастический код, который передают в канале связи, на приемной стороне стирают наименее достоверные символы стохастического кода, исправляют стирания стохастического кода, выполняют обратное стохастическое преобразование и восстанавливают исходное сообщение, отличающийся тем, что на передающей стороне выполняют двойное стохастическое преобразование исходной информации и формируют линейный стохастический код, а на приемной стороне декодируют линейный стохастический код с исправлением стираний символов.
2. Способ по п. 1, отличающийся тем, что первое стохастическое преобразование заключается в гаммировании исходной информации псевдослучайной последовательностью, а второе стохастическое преобразование представляет собой умножение гаммированной информации на псевдослучайную порождающую матрицу линейного стохастического кода.
3. Способ по п. 2, отличающийся тем, что псевдослучайную порождающую матрицу линейного стохастического кода получают путем генерации элементов матрицы по псевдослучайному закону.
4. Способ по п. 1, отличающийся тем, что на приемной стороне стирания исправляют путем решения системы линейных уравнений относительно неизвестных значений стертых символов линейного стохастического кода.
5. Способ по п. 4, отличающийся тем, что систему линейных уравнений относительно неизвестных значений стертых символов получают при умножении стохастического кода на проверочную матрицу линейного стохастического кода.
6. Способ по п. 4, отличающийся тем, что при равенстве ранга системы линейных уравнений числу стираний символов кода значения стираний символов определяются однозначно, а при ранге системы меньше числа стираний символов кода выполняется списочное декодирование кода.
7. Способ по п. 6, отличающийся тем, что в списке решений выбирают значения стираний символов, обеспечивающие наибольшее значение суммарной достоверности символов кода.
| СПОСОБ КОМПЛЕКСНОЙ ЗАЩИТЫ ИНФОРМАЦИИ | 2005 |
|
RU2292122C1 |
| Способ передачи многоблочных сообщений в комплексах телекодовой связи | 2019 |
|
RU2710911C1 |
| Способ декодирования линейных помехоустойчивых кодов с исправлением стираний | 2020 |
|
RU2746797C1 |
| WO 2000025203 A1, 04.05.2000. | |||
Авторы
Даты
2023-09-28—Публикация
2022-11-23—Подача