Изобретение относится к области техники связи и может быть использовано для мягкого декодирования помехоустойчивого кода в каналах связи с высоким уровнем помех.
Одним из основных направлений повышения помехоустойчивости передачи сообщений в каналах связи различного качества, в том числе низкого качества, является применение помехоустойчивого кодирования. На передающей стороне канала связи исходное сообщение кодируют помехоустойчивым кодом. На приемной стороне помехоустойчивый код декодируют с исправлением ошибок и восстанавливают исходное сообщение. При мягком декодировании помехоустойчивого кода используется дополнительная информация о достоверностях символов, что существенно повышает помехоустойчивость связи, поскольку позволяет исправлять примерно вдвое большее число ошибок по сравнению с жестким декодированием помехоустойчивого кода. Однако, для мягкого декодирования требуется выполнять большой объем вычислений, что значительно усложняет декодирование кода по сравнению с жестким декодированием. Уменьшить сложность мягкого декодирования кода возможно за счет введения стираний наименее достоверных символов и перебора различных вариантов оставшейся части наименее достоверных символов. При этом помехоустойчивость остается на высоком уровне, поскольку число исправляемых стираний в помехоустойчивом коде вдвое больше числа исправляемых ошибок.
Предлагаемый способ мягкого декодирования помехоустойчивого кода является универсальным и может использоваться для многих классов линейных помехоустойчивых кодов: Хемминга, Боуза-Чоудхури-Хоквинхема (БЧХ), Рида-Маллера, Голея, Рида-Соломона и других.
Известен способ мягкого декодирования помехоустойчивого кода, заключающийся в том, что на вход декодирующего устройства поступают n символов принятого помехоустойчивого кода с оценками достоверностей этих символов. В декодирующем устройстве помехоустойчивого кода эти символы сортируют по достоверности, выбирая сначала символы с наибольшей достоверностью, затем символы с меньшей, но следующей по величине достоверностью и так далее, пока не будет набрано n-s наиболее достоверных символов помехоустойчивого кода, где s есть число наименее достоверных символов помехоустойчивого кода. Затем формируют 2s вариантов помехоустойчивого кода, в каждом из которых s наименее достоверных символов помехоустойчивого кода принимают всевозможные двоичные комбинации, начиная с комбинации из множества 0 и заканчивая комбинацией из множества 1, a n-s наиболее достоверных символов помехоустойчивого кода не изменяют. Далее выполняют жесткое декодирование всех 2s вариантов помехоустойчивого кода и корректируют ошибки в каждом из этих вариантов. Затем каждый из 2s вариантов декодированного помехоустойчивого кода сравнивают по расстоянию Хемминга с принятым помехоустойчивым кодом и получают совокупность 2s расстояний Хемминга. На выход декодирующего устройства подается помехоустойчивым код, соответствующий минимальному кодовому расстоянию Хемминга из совокупности 2s расстояний Хемминга. (Кларк Дж., мл. Кейн Дж. Кодирование с исправлением ошибок в системах цифровой связи. - Пер. с англ. - Радио и связь. - 1987. - с. 160-165).
Недостатком этого способа является чрезмерно большая сложность, поскольку жесткое декодирование 2s вариантов помехоустойчивого кода с исправлением ошибок в каждом из вариантов помехоустойчивого кода требует большого числа вычислений.
Наиболее близким к предлагаемому способу является способ (прототип) мягкого декодирования помехоустойчивого кода, заключающийся в том, что на вход декодирующего устройства подают n символов принятого помехоустойчивого кода с оценками достоверностей этих символов. В декодирующем устройстве помехоустойчивого кода сначала в зависимости от качества канала связи, оценивают величину s числа наименее достоверных символов помехоустойчивого кода, чтобы вероятность правильного декодирования помехоустойчивого кода была не менее, чем заданная величина. Затем символы помехоустойчивого кода сортируют по достоверности, выбирая сначала символы с наибольшей достоверностью, затем символы с меньшей, но следующей по величине достоверностью и так далее, пока не будет набрано n-s наиболее достоверных символов помехоустойчивого кода. Далее формируют варианты помехоустойчивого кода, в каждом из которых наименее достоверные символы помехоустойчивого кода принимают всевозможные двоичные комбинации, начиная с комбинации из всех 0 и заканчивая комбинацией из всех 1, а наиболее достоверных символов помехоустойчивого кода остаются неизменными. Затем выполняют жесткое декодирование всех вариантов помехоустойчивого кода и каждый из вариантов декодированного помехоустойчивого кода сравнивают по расстоянию Хемминга с принятым помехоустойчивым кодом и получают совокупность расстояний Хемминга. На выход декодирующего устройства подают помехоустойчивый код, соответствующий минимальному расстоянию Хемминга из совокупности расстояний Хемминга (Патент РФ №2546070 МПК Н03М 13/00 Квашенников В.В., Сосин П.А. Способ мягкого декодирования помехоустойчивого кода. - Приор. 12.11.2013. - Опубл. 10.04.2015.-Бюл. №10).
Недостатком этого способа также является большая сложность, поскольку жесткое декодирование с исправлением ошибок различных вариантов помехоустойчивого кода требует выполнения большого числа вычислений.
Целью изобретения является снижение сложности декодирования за счет того, что часть наименее достоверных символов помехоустойчивого кода стирают и выполняют жесткое декодирование помехоустойчивого кода с исправлением стираний, которое проще, чем декодирование помехоустойчивого кода с исправлением ошибок.
Для достижения цели предложен способ мягкого декодирования помехоустойчивого кода, заключающийся в том, что на вход декодирующего устройства подают n символов принятого помехоустойчивого кода с оценками достоверностей этих символов. В декодирующем устройстве помехоустойчивого кода сначала, в зависимости от качества канала связи, оценивают величину s числа наименее достоверных символов помехоустойчивого кода, чтобы вероятность правильного декодирования помехоустойчивого кода была не менее, чем заданная величина. Затем символы помехоустойчивого кода сортируют по достоверности, выбирая сначала символы с наибольшей достоверностью, затем символы с меньшей, но следующей по величине достоверностью и так далее, пока не будет набрано n-s наиболее достоверных символов помехоустойчивого кода. Далее формируют варианты помехоустойчивого кода, в каждом из которых наименее достоверные символы помехоустойчивого кода принимают всевозможные двоичные комбинации, начиная с комбинации из всех 0 и заканчивая комбинацией из всех 1, а наиболее достоверные символы помехоустойчивого кода остаются неизменными. Затем выполняют жесткое декодирование всех вариантов помехоустойчивого кода, и каждый из вариантов декодированного помехоустойчивого кода сравнивают по расстоянию Хемминга с принятым помехоустойчивым кодом и получают совокупность расстояний Хемминга. На выход декодирующего устройства подают помехоустойчивый код, соответствующий минимальному расстоянию Хемминга из совокупности расстояний Хемминга. Новым является то, что сначала из s наименее достоверных символов помехоустойчивого кода выбирают максимально возможное число t символов, соответствующих линейно независимым столбцам проверочной матрицы помехоустойчивого кода. Эти t символов стирают и формируют 2s-t вариантов помехоустойчивого кода, в которых только s-t наименее достоверных символов помехоустойчивого кода принимают всевозможные двоичные комбинации, начиная с комбинации из всех 0 и заканчивая комбинацией из всех 1. Далее выполняют жесткое декодирование сформированных 2s-t вариантов помехоустойчивого кода с исправлением t стираний. На выход декодирующего устройства подают помехоустойчивый код, соответствующий минимальному расстоянию Хемминга из совокупности 2s-t расстояний Хемминга. При этом для s<d, где d - минимальное кодовое расстояние помехоустойчивого кода, принимают t=s, стирают все наименее достоверные символы помехоустойчивого кода и выполняют только одну попытку жесткого декодирования помехоустойчивого кода с исправлением t стираний. Причем для s≥d число t стертых символов помехоустойчивого кода принимают равным рангу матрицы, состоящей из s столбцов проверочной матрицы помехоустойчивого кода, соответствующих наименее достоверным символам помехоустойчивого кода. При этом жесткое декодирование помехоустойчивого кода с исправлением стираний выполняют путем решения системы линейных уравнений относительно неизвестных значений стертых символов, причем решение системы линейных уравнений относительно неизвестных значений стертых символов осуществляют методом Гаусса исключения неизвестных.
Рассмотрим осуществление предлагаемого способа мягкого декодирования помехоустойчивого кода.
При мягком декодировании помехоустойчивого кода помимо жестких решений о значении каждого символа (0 либо 1) оценивают достоверности символов. Для формирования достоверностей символов можно использовать первичные статистические характеристики канала связи, например амплитуду сигнала на выходе интегратора демодулятора, уровень фонового шума (за пределами полосы частот передачи сигнала), искажения пилот-сигнала по частоте и фазе, отклонения спектра принятого сигнала от ожидаемого спектра и так далее. Для формирования достоверностей символов можно также использовать вторичные статистические характериcтики канала связи в виде дроблений и искажений краев посылок на выходе устройства тактовой цифровой синхронизации. Достоверности символов можно также формировать на выходе декодирующего устройства внутреннего кода каскадного помехоустойчивого кода в зависимости от числа ошибок, корректируемых внутренним кодом. Наиболее достоверными будут символы, полученные при декодировании кодов, в которых не было исправлено ни одной ошибки, менее достоверными - с исправлением одиночной ошибки, затем - двойной ошибки и так далее. Оценки достоверностей символов тогда используют для мягкого декодирования внешнего кода каскадного кода.
Величину s числа наименее достоверных символов помехоустойчивого кода, в которых наиболее вероятно возникновение ошибок, определяют в зависимости от качества канала связи, исходя из условия, чтобы вероятность правильного декодирования помехоустойчивого кода была не менее, чем заданная величина. Основной характеристикой качества каналов связи является средняя вероятность ошибки на бит в канале связи. Для различных каналов связи средняя вероятность ошибки на бит известна. Например, для каналов связи диапазона декаметровых волн (ДКМВ) средняя вероятность ошибки на бит будет не более 5⋅10-2, для каналов связи диапазона метровых волн (MB 1, МВ2) в пределах прямой видимости - не более 10-3, для спутниковых каналов - не более 10-5 и так далее. Вероятность правильного приема помехоустойчивого кода с коррекцией s ошибок в зависимости от средней вероятности ошибки на бит р запишется в виде
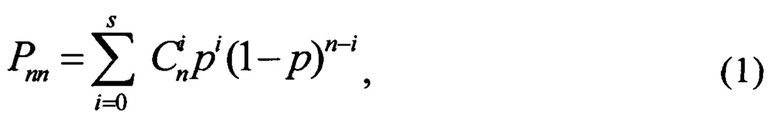
где n - блоковая длина помехоустойчивого кода.
Для системы связи обычно задают требуемое значение вероятности правильного приема помехоустойчивого кода 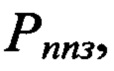 достаточно близкое к 1 (например, 0.99 и более). Число ошибок s, которое должен исправлять помехоустойчивый код, определяют из неравенства
достаточно близкое к 1 (например, 0.99 и более). Число ошибок s, которое должен исправлять помехоустойчивый код, определяют из неравенства
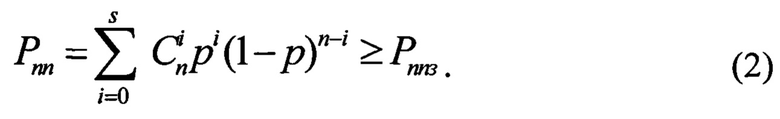
Из нелинейного соотношения (2) выразить величину s в явном виде не представляется возможным, однако можно определить величину s численным методами. Для различных значений s, начиная с 0 с интервалом через 1, по формуле (1) вычисляют вероятности правильного приема помехоустойчивого кода. Значение  при котором впервые выполняется неравенство (2), является оценкой числа наименее достоверных символов помехоустойчивого кода, в которых возможны ошибки.
при котором впервые выполняется неравенство (2), является оценкой числа наименее достоверных символов помехоустойчивого кода, в которых возможны ошибки.
Для жесткого декодирования помехоустойчивого кода минимальное кодовое расстояние связано с числом исправляемых ошибок s формулой

Если полученное из формулы (3) число корректируемых ошибок 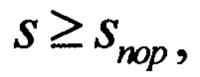 то корректирующая способность жесткого декодирования помехоустойчивого кода не меньше числа ошибок в сообщении, и для правильного приема сообщения достаточно обычного жесткого декодирования кода.
то корректирующая способность жесткого декодирования помехоустойчивого кода не меньше числа ошибок в сообщении, и для правильного приема сообщения достаточно обычного жесткого декодирования кода.
Для 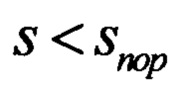 требуется мягкое декодирование помехоустойчивого кода за пределами его минимального кодового расстояния.
требуется мягкое декодирование помехоустойчивого кода за пределами его минимального кодового расстояния.
После определения числа s наименее достоверных символов помехоустойчивого кода, в которых возможны ошибки, символы помехоустойчивого кода сортируют по достоверности, выбирая сначала символы с наибольшей достоверностью, затем символы с меньшей, но следующей по величине достоверностью и так далее, пока не будет набрано n-s наиболее достоверных символов помехоустойчивого кода. Из оставшихся s наименее достоверных символов помехоустойчивого кода выбирают максимально возможное число t символов, соответствующих линейно независимым столбцам проверочной матрицы помехоустойчивого кода.
Проверочную матрицу помехоустойчивого кода записывают в виде

где hi - столбцы проверочной матрицы кода.
Пусть помехоустойчивый код есть A=a0al…an-1 , тогда выполняется равенство

Для s<d принимают t=s, стирают все наименее достоверные символы помехоустойчивого кода и выполняют только одну попытку жесткого декодирования помехоустойчивого кода с исправлением t стираний.
Для s≥d число t стертых символов помехоустойчивого кода будет равно рангу матрицы, состоящей из s столбцов проверочной матрицы помехоустойчивого кода, соответствующих наименее достоверным символам помехоустойчивого кода. Эти t символов стирают, а используя s-t оставшихся символов, формируют 2s-t вариантов помехоустойчивого кода, в которых s-t наименее достоверных символов помехоустойчивого кода принимают всевозможные двоичные комбинации, начиная с комбинации из всех 0 и заканчивая комбинацией из всех 1. Далее выполняют жесткое декодирование сформированных 2s-t вариантов помехоустойчивого кода с исправлением t стираний.
На выход декодирующего устройства подают помехоустойчивый код, соответствующий минимальному расстоянию Хемминга из совокупности 2s-t расстояний Хемминга.
Рассмотрим более подробно жесткое декодирование помехоустойчивого кода с исправлением стираний. Обозначим неизвестные значения стертых символов bj, j∈tj, где j∈tj - множество индексов стертых символов. Тогда (5) перепишется

Правая часть уравнения содержит наиболее достоверные символы помехоустойчивого кода и ее можно вычислить по принятым символам. Таким образом, уравнение (6) представляет собой систему t линейных уравнений относительно неизвестных значений стертых символов bj, j∈tj.
Для жесткого декодирования помехоустойчивого кода с исправлением стираний достаточно решить систему линейных уравнений (6) относительно неизвестных значений стертых символов. Поскольку неизвестным значениям стертых символов соответствуют линейно независимые столбцы проверочной матрицы помехоустойчивого кода, то система (6) совместна и имеет единственное решение. Решение системы линейных уравнений (6) осуществляют, например, методом Гаусса исключения неизвестных. Метод Гаусса включает прямой ход вычислений, при котором за счет перестановок строк системы линейных уравнений (6) и сложения некоторых строк этой системы строят систему линейных уравнений с верхнетреугольной матрицей, а также включает обратный ход вычислений, при котором, начиная с последнего уравнения, выполняют подстановку найденных значений неизвестных в уравнение, которое в системе линейных уравнений (6) стоит выше.
Например, для помехоустойчивого кода Хемминга (15, 11), блоковая длина которого равна n=15, информационная длина кода есть k=11, а минимальное кодовое расстояние равно d=3, проверочная матрица размера 4×15 запишется

Столбцы проверочной матрицы кода Хемминга представляют собой различные ненулевые двоичные комбинации символов. Любые два столбца проверочной матрицы линейно независимы, поэтому любые комбинации двух стираний символов помехоустойчивого кода будут исправляться. Возможно исправление и большего числа стираний, но только, если столбцы проверочной матрицы, соответствующие позициям стертых символов, являются линейно независимыми. В любом случае максимальное число исправляемых стираний равно числу строк проверочной матрицы и не превышает избыточности кода r=n-k=15-11=4.
Пусть качество канала связи характеризуется средней вероятностью ошибки на бит, равной р=5⋅10-2. По формуле (2) при n=15 и s=2 будем иметь 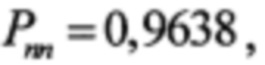 а при s=3 будет
а при s=3 будет 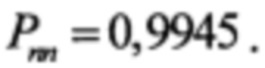 Поэтому, для мягкого декодирования выберем величину s=3, и для обеспечения требуемой помехоустойчивости будем исправлять 3 наименее достоверных символа кода Хемминга. Пусть принятый код Хемминга A=001100111010110. Допустим, множество индексов наименее достоверных символов j∈(1, 8, 10) и A=0b1110011b80b100110. Столбцы проверочной матрицы Н, соответствующие стираниям будут
Поэтому, для мягкого декодирования выберем величину s=3, и для обеспечения требуемой помехоустойчивости будем исправлять 3 наименее достоверных символа кода Хемминга. Пусть принятый код Хемминга A=001100111010110. Допустим, множество индексов наименее достоверных символов j∈(1, 8, 10) и A=0b1110011b80b100110. Столбцы проверочной матрицы Н, соответствующие стираниям будут

Ранг матрицы F равен 2, так как любые два столбца этой матрицы линейно независимы. Поэтому t=2 и потребуется 2s-t=23-2=2 попытки жесткого декодирования помехоустойчивого кода с исправлением стираний. Таким образом, потребуется решить 2 системы линейных уравнений (6) для неизвестных значений стираний, допустим b1 и b8. Для этого выберем, например, 1 и 3 строки матрицы F, в которых возьмем только первые два столбца. Получим систему линейных алгебраических уравнений
b8+b10=1
b8+b10=1⋅
Для b10=0 получим решения b1=1, b8=1, для b10=1 решения будут b1=0,b8=0. Первое решение приводит к коду А=011100111000110, а второе - к коду A=001100110010110. Выбираем второе решение, которое ближе по расстоянию Хемминга к принятому коду.
В данном примере при небольшом объеме вычислений удалось исправить s=3 ошибки. Причем 2 ошибки исправляют за счет стираний, а 1 ошибку - путем перебора различных вариантов.
Обеспечить высокую помехоустойчивость при небольшой сложности мягкого декодирования стало возможным за счет совмещения исправления стираний символов и перебора ошибок на оставшихся местах. Исправление стираний сводится к решению систем линейных уравнений, а поскольку системы линейных уравнений определены над простейшим двоичным полем с двумя элементами 0 и 1, то сложность решения этой системы уравнений, например, по методу Гаусса, невысокая и оценивается примерно квадратом порядка системы линейных алгебраических уравнений. Количество переборов различных вариантов ошибок существенно снижается за счет того, что часть ошибок переводится в стирания символов.
Достигаемым техническим результатом способа мягкого декодирования помехоустойчивого кода является уменьшение сложности при его высокой помехоустойчивости.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ мягкого декодирования помехоустойчивого кода | 2023 |
|
RU2812043C1 |
| Способ передачи сообщений с использованием стохастических помехоустойчивых кодов | 2022 |
|
RU2804323C1 |
| Способ мягкого декодирования помехоустойчивого кода | 2020 |
|
RU2738724C1 |
| Способ декодирования линейных помехоустойчивых кодов с исправлением стираний | 2020 |
|
RU2746797C1 |
| СПОСОБ МЯГКОГО ДЕКОДИРОВАНИЯ ПОМЕХОУСТОЙЧИВОГО КОДА | 2013 |
|
RU2546070C1 |
| Способ передачи многоблочных сообщений каскадным кодом [PC (32, 16, 17), БЧХ (31, 16, 7)] | 2020 |
|
RU2755055C1 |
| СПОСОБ ДЕКОДИРОВАНИЯ ПОМЕХОУСТОЙЧИВЫХ КАСКАДНЫХ КОДОВ ПО НАИБОЛЕЕ ДОСТОВЕРНЫМ СИМВОЛАМ ВНЕШНЕГО КОДА | 2009 |
|
RU2419966C2 |
| СПОСОБ ДЕКОДИРОВАНИЯ БЛОКОВЫХ КОДОВ СО СТИРАНИЯМИ ЭЛЕМЕНТОВ | 2006 |
|
RU2327297C2 |
| Способ передачи многоблочных сообщений в комплексах телекодовой связи | 2018 |
|
RU2669069C1 |
| СПОСОБ ПЕРЕДАЧИ СООБЩЕНИЙ В СИСТЕМАХ С ОБРАТНОЙ СВЯЗЬЮ И ГИБРИДНЫМ АВТОМАТИЧЕСКИМ ЗАПРОСОМ НА ПОВТОРЕНИЕ | 2022 |
|
RU2786023C1 |
Изобретение относится к области связи и может быть использовано для мягкого декодирования помехоустойчивого кода в каналах связи с высоким уровнем помех. Техническим результатом является уменьшение сложности декодирования при его высокой помехоустойчивости. Способ содержит этапы, на которых на вход декодирующего устройства подают n символов принятого помехоустойчивого кода с оценками достоверностей символов, в зависимости от качества канала связи оценивают величину s числа наименее достоверных символов помехоустойчивого кода, чтобы вероятность правильного декодирования помехоустойчивого кода была не менее, чем заданная величина, из s символов выбирают максимально возможное число t символов, соответствующих линейно независимым столбцам проверочной матрицы помехоустойчивого кода, которые стирают и формируют 2s-t вариантов помехоустойчивого кода, в которых s-t наименее достоверных символов помехоустойчивого кода принимают всевозможные двоичные комбинации, начиная с комбинации из всех 0 и заканчивая комбинацией из всех 1, выполняют жесткое декодирование сформированных 2s-t вариантов помехоустойчивого кода с исправлением t стираний. На выход декодирующего устройства подают помехоустойчивый код, соответствующий минимальному расстоянию Хемминга из совокупности 2s-t расстояний Хемминга. 4 з.п. ф-лы.
1. Способ мягкого декодирования помехоустойчивого кода, заключающийся в том, что на вход декодирующего устройства подают n символов принятого помехоустойчивого кода с оценками достоверностей этих символов, в декодирующем устройстве помехоустойчивого кода сначала, в зависимости от качества канала связи, оценивают величину s числа наименее достоверных символов помехоустойчивого кода, чтобы вероятность правильного декодирования помехоустойчивого кода была не менее, чем заданная величина, затем символы помехоустойчивого кода сортируют по достоверности, выбирая сначала символы с наибольшей достоверностью, затем символы с меньшей, но следующей по величине достоверностью и так далее, пока не будет набрано n-s наиболее достоверных символов помехоустойчивого кода, далее формируют варианты помехоустойчивого кода, в каждом из которых наименее достоверные символы помехоустойчивого кода принимают всевозможные двоичные комбинации, начиная с комбинации из всех 0 и заканчивая комбинацией из всех 1, а наиболее достоверные символы помехоустойчивого кода остаются неизменными, затем выполняют жесткое декодирование всех вариантов помехоустойчивого кода, и каждый из вариантов декодированного помехоустойчивого кода сравнивают по расстоянию Хемминга с принятым помехоустойчивым кодом и получают совокупность расстояний Хемминга, на выход декодирующего устройства подают помехоустойчивый код, соответствующий минимальному расстоянию Хемминга из совокупности расстояний Хемминга, отличающийся тем, что сначала из s наименее достоверных символов помехоустойчивого кода выбирают максимально возможное число t символов, соответствующих линейно независимым столбцам проверочной матрицы помехоустойчивого кода, эти t символов стирают и формируют 2s-t вариантов помехоустойчивого кода, в которых только s-t наименее достоверных символов помехоустойчивого кода принимают всевозможные двоичные комбинации, начиная с комбинации из всех 0 и заканчивая комбинацией из всех 1, далее выполняют жесткое декодирование сформированных 2s-t вариантов помехоустойчивого кода с исправлением t стираний и на выход декодирующего устройства подают помехоустойчивый код, соответствующий минимальному расстоянию Хемминга из совокупности 2s-t расстояний Хемминга.
2. Способ по п. 1, отличающийся тем, что для s<d, где d - минимальное кодовое расстояние помехоустойчивого кода, принимают t=s, стирают все наименее достоверные символы помехоустойчивого кода и выполняют только одну попытку жесткого декодирования помехоустойчивого кода с исправлением t стираний.
3. Способ по п. 1, отличающийся тем, что для s≥d число t стертых символов помехоустойчивого кода принимают равным рангу матрицы, состоящей из s столбцов проверочной матрицы помехоустойчивого кода, соответствующих наименее достоверным символам помехоустойчивого кода.
4. Способ по п. 1, отличающийся тем, что жесткое декодирование помехоустойчивого кода с исправлением стираний выполняют путем решения системы линейных уравнений относительно неизвестных значений стертых символов.
5. Способ по п. 4, отличающийся тем, что решение системы линейных уравнений относительно неизвестных значений стертых символов осуществляют методом Гаусса исключения неизвестных.
| СПОСОБ МЯГКОГО ДЕКОДИРОВАНИЯ ПОМЕХОУСТОЙЧИВОГО КОДА | 2013 |
|
RU2546070C1 |
| СПОСОБ ДЕКОДИРОВАНИЯ БЛОКОВЫХ КОДОВ СО СТИРАНИЯМИ ЭЛЕМЕНТОВ | 2006 |
|
RU2327297C2 |
| СПОСОБ МЯГКОГО ДЕКОДИРОВАНИЯ СИСТЕМАТИЧЕСКИХ БЛОКОВЫХ КОДОВ | 2010 |
|
RU2444127C1 |
| СПОСОБ МЯГКОГО ДЕКОДИРОВАНИЯ БЛОКОВЫХ КОДОВ | 2015 |
|
RU2580797C1 |
| US 6654926 B1, 25.11.2003 | |||
| Способ обработки целлюлозных материалов, с целью тонкого измельчения или переведения в коллоидальный раствор | 1923 |
|
SU2005A1 |
Авторы
Даты
2020-07-03—Публикация
2019-08-27—Подача