Предлагаемое изобретение относится к области исследования и освоения околопланетных космических пространств.
Задачей предлагаемого изобретения является расширение возможностей в решении проблем позиционирования в околопланетных космических пространствах различных физических тел (объектов) - наблюдательных и научно-исследовательских станций, телекоммуникационных систем, космических площадок для запуска и посадки космических кораблей и т.п.
Использование этих позиционируемых в околопланетном космическом пространстве физических тел является перспективным направлением в организации глобальной космической радиосвязи, запуска и посадки космических кораблей и в исследованиях околопланетных космических пространств, территорий планет и т.п.
Здесь, в самом начале заявки, необходимо особо подчеркнуть, что, все сказанное в материалах заявки в отношении планет и их околопланетных космических пространствах, будет целиком и полностью справедливым и в отношении возможных естественных спутников планет и их околоспутниковых космических пространств. Поэтому для упрощения записей ссылки на естественные спутники и их околоспутниковые космические пространства в материалах заявки опущены.
Известен способ позиционирования физических тел в околопланетном космическом пространстве, базирующийся на фундаментальных законах И.Ньютона и использующий принцип непрерывного движения позиционируемых физических тел вокруг планеты с определенной скоростью по касательной к воображаемой окружности вокруг планеты в плоскости, проходящей через ее центр. Разгоняют эти физические тела до необходимой скорости с помощью поднявших их на заданную высоту мощных ракет-носителей и мощных ракетных двигателей. При этом с учетом одновременно действующей на эти тела силы притяжения к планете, сообщающей им нормальное ускорение, они не улетают в космос, но и не падают на планету, а движутся с этой скоростью по орбите вокруг планеты, удерживаясь в околопланетном космическом пространстве на заданной высоте в течение длительного времени (например, искусственные спутники, космические корабли, орбитальные станции и т.п.).
Как известно, основоположником этого способа является К.Э.Циолковский, впервые теоретически обосновавший возможность выхода человека в космос с помощью мощных ракет-носителей и ракетных двигателей (несмотря на упреки в нереализуемости этого способа, в т.ч. из-за недопонимания сути реактивного движения и из-за отсутствия необходимых конструктивных решений, специальных материалов и специального топлива), а исполнителями этой возможности являются С.П.Королев и др., реализовавшие ее ценой огромных затрат с привлечением экономики всей страны.
Устройствами для осуществления этого способа являются мощные ракеты-носители и связанные с ними космодромы с их разветвленной инфраструктурой.
Наряду с достоинством, а именно решением проблемы позиционирования физических тел в околопланетном космическом пространстве, этот способ и устройства для его осуществления имеют и существенные, органически присущие им недостатки, обусловленные исключительно используемым при этом способе принципом обязательного непрерывного движения физических тел с определенной скоростью на заданной высоте по орбите вокруг планеты.
Среди недостатков этого способа, кроме отмеченной выше огромной стоимости его реализации, следует особо отметить необходимость использования специальных материалов и специального топлива для мощных ракет-носителей и реактивных двигателей, большую сложность и высокую точность изготовления их и в целом кораблей, а также органически присущие этому способу огромные перегрузки при подъеме и разгоне физических тел (спутников, космических кораблей и т.п.) до необходимых скоростей, отрицательно сказывающиеся на здоровье космонавтов и повышающие вероятность выхода из строя оборудования на этих объектах, и явление невесомости, испытываемое космонавтами при движении космических кораблей по орбите с необходимой скоростью, отрицательно влияющее на здоровье, эффективность работы и сроки пребывания их на орбите.
В связи с этим в настоящей заявке предлагается качественно отличный способ позиционирования физических тел в околопланетном космическом пространстве с устройством для его осуществления.
Он тоже базируется на фундаментальных законах И.Ньютона, но в нем, в отличие от вышеописанного известного способа, физические тела позиционируются в околопланетном космическом пространстве на неподвижной относительно планеты космической опоре в виде самоуравновешивающегося твердого жесткого кольца вокруг планеты с радиусом, большим радиуса планеты, а с массой, значительно меньшей ее массы, и расположенным в плоскости, проходящей через ее центр.
При этом способе подлежащие позиционированию физические тела неподвижны относительно планеты (их не нужно специально разгонять до какой-либо скорости, как это требовалось при вышеописанном известном способе), поэтому затратные мощные ракеты-носители и связанные с ними космодромы с их разветвленной инфраструктурой не нужны, нет перегрузок и явления невесомости, что является большим достоинством по сравнению с известным способом.
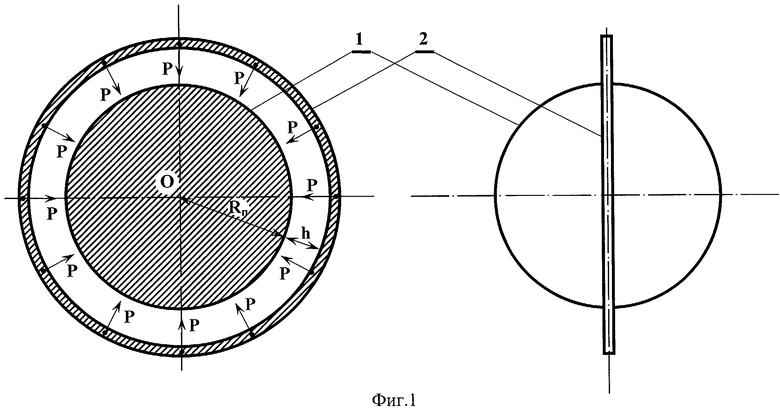
Сущность предлагаемых способа и устройства иллюстрируется чертежом в двух проекциях (фиг.1), где цифрами обозначены:
1 - планета в виде идеального сплошного однородного шара с массой Мп, с радиусом Rп и с центром в точке О;
2 - твердое жесткое кольцо с массой Мк, значительно меньшей массы планеты, с идеальной формой и с одинаковой плотностью по всему контуру, охватывающее планету в плоскости, проходящей через ее центр, и имеющее радиус Rк=Rп+h, больший радиус планеты на величину h.
На чертеже штриховкой на первой проекции показан разрез планеты и кольца вокруг нее в плоскости, проходящей через ее центр, который совпадает с центром кольца.
Покажем механизм самоуравновешивания такого кольца. При этом будем опираться на следующую общеизвестную научную фундаментальную информацию:
1) во-первых, на общеизвестный, широко используемый в физике, продуктивный принцип суперпозиции, согласно которому результирующая сила тяжести, действующая на сложное по форме физическое тело (каковым в нашем случае и является кольцо, охватывающее планету в плоскости, проходящей через ее центр) определяется геометрической (векторной) суммой сил тяжести его элементарных частей (см. учебники по физике для старших классов средней школы и для соответствующих вузов);
2) во-вторых, на то, что сила тяжести, действующая на любую материальную точку с массой m, находящуюся вблизи поверхности планеты, определяется как геометрическая (векторная) сумма силы притяжения планеты (F) и центробежной силы инерции (Q), учитывающей эффект вращения планеты вокруг своей оси:

(см. учебники по физике для старших классов средней школы и для соответствующих вузов или Большую Советскую Энциклопедию. Третье издание. М., Издательство «Советская Энциклопедия». 1976. Том 23, стр.359 и 1974. Том 18, стр.167).
Следует обратить внимание на то, что в формуле (1) не фигурируют силы притяжения других планет, т.к. они пренебрежимо малы по сравнению с силой притяжения F данной планеты.
Следует также сознавать, что геометрическая (векторная) сумма сил F и Q в (1) фактически будет равна разности их модулей, т.к. сила инерции Q направлена противоположно силе притяжения F. Это уменьшает силу тяжести.
Сила притяжения F материальной точки над данной планетой определяется общеизвестной формулой (законом тяготения И.Ньютона)
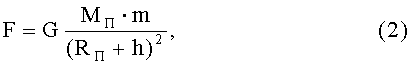
где Мп и Rп - соответственно масса и радиус планеты;
m - масса материальной точки, расположенной на высоте h над поверхностью планеты;
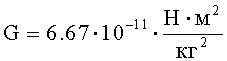 - гравитационная постоянная, численно равная силе, с которой взаимодействуют две материальные точки единичной массы на единичном расстоянии;
- гравитационная постоянная, численно равная силе, с которой взаимодействуют две материальные точки единичной массы на единичном расстоянии;
Сила инерции Q, действующая на материальную точку, определяется формулой
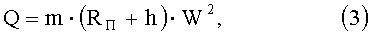
где m - масса материальной точки;
(RП+h) - расстояние от оси планеты до материальной точки;
W - угловая скорость вращения планеты.
К сказанному выше в п.2) следует добавить следующее. Силу тяжести Р, определяемую формулой (1), можно, согласно 2-му закону И.Ньютона, выразить формулой
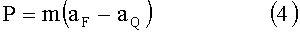
(см., например, учебное пособие «Курс физики» автора Трофимовой Т.И. Издание седьмое. М.: Издательство «Высшая школа». 2003, стр.48).
В формуле (4):
m - масса материальной точки;
a F - ускорение свободного падения материальной точки под действием силы притяжения F;
a Q - ускорение материальной точки, вызванное силой инерции Q.
Это означает, что сила тяжести с учетом силы инерции будет меньше. Следует отметить, что если сила инерции Q будет заметно меньше силы тяготения F (и соответственно ускорение a Q, вызываемое этой силой, заметно меньше ускорения a F свободного падения), то формула (1) и формула (4) запишутся соответственно в виде:


Формулы (5) и (6) часто используют для приближенных расчетов (исключение составляют случаи реализации известного вышеописанного способа, т.е. случаи с искусственными спутниками, для которых P≈0 и соответственно a F-a Q=0, т.к. F=Q и соответственно a F=a Q).
Итак, применим информацию пунктов 1) и 2) к нашему случаю с твердым жестким кольцом, охватывающим планету в плоскости, проходящей через центр планеты, полагая, что центры планет и кольца совпадают.
Согласно п.1), разобьем мысленно кольцо на множество одинаковых элементарных частей (материальных точек) одинаковой массы m.
Согласно п.2), на каждую из этих элементарных частей (материальных точек) в соответствии с формулами (1), (2), (3), (4), (5) и (6) будет действовать сила тяжести Р в направлении к центру планеты в плоскости кольца.
На первой проекции фиг.1 множество этих равных сил тяжести Р в плоскости кольца в направлении к совпадающим центрам кольца и планеты показаны стрелками Р.
Согласно (6), каждую из этих сил тяжести Р удобно выразить формулой
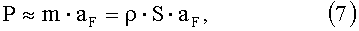
где m=ρ·S - масса каждой элементарной части кольца (материальной точки);
ρ - средняя плотность элементов кольца;
S - площадь поперечного сечения кольца;
a F - ускорение свободного падения элементарной части (материальной точки) кольца, находящейся вблизи поверхности планеты на расстоянии (Rп+h) от центра планеты в плоскости, проходящей через ее центр.
Таким образом, кольцо вокруг планеты оказывается нагруженным множеством равных сил Р, равномерно распределенных по всему контуру кольца и действующих в плоскости кольца по направлению к центру планеты и совпадающему с ним центру кольца.
Из симметрии картины на первой проекции чертежа (фиг.1) следует, что векторная сумма всего множества сил тяжести Р будет равна нулю и, следовательно, кольцо теоретически должно находиться в состоянии равновесия вокруг планеты в плоскости, проходящей через ее центр так, что центр кольца совпадает с центром планеты. Физически это объясняется тем, что, как видно из чертежа (фиг.1), в множестве одинаковых сил тяжести Р, равномерно действующих по всему контуру кольца в его плоскости в направлении к центру планеты (и кольца), для каждой силы тяжести Р той или иной элементарной части кольца существует равная и противоположно направленная ей сила тяжести Р диаметрально противоположной элементарной части кольца, которые, естественно, уравновешивают друг друга.
Этот важный вывод, отражающий главную суть изобретения, можно физически подтвердить еще более наглядно. Мысленно разобьем кольцо на два одинаковых полукольца и определим равнодействующие силы тяжести полуколец по их оси симметрии. Очевидно, что силы тяжести полуколец будут равны по величине и противоположны по знаку. Следовательно, полукольца будут уравновешивать друг друга и кольцо будет находиться в состоянии равновесия.
Этот путь наглядного доказательства равновесия кольца хорош еще и тем, что позволяет определить напряжение сжатия в сечениях стыка полуколец (и вообще в каждом сечении кольца), позволяющее оценить несущую способность конструкции кольца.
Покажем это математически.
В соответствии с (6) равнодействующая сила тяжести одного полукольца, очевидно, будет равна
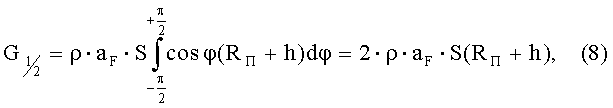
где φ - угловая координата элементарных частей (Rп+h)dφ полукольца, отсчитываемая от оси его симметрии (остальные обозначения прежние).
Сила 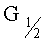 направлена по оси симметрии полукольца, к центру кольца.
направлена по оси симметрии полукольца, к центру кольца.
На другое полукольцо, очевидно, будет действовать равнодействующая сила тяжести - 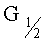 , т.е. равнодействующая сила тяжести другого полукольца, равная и противоположно направленная силе тяжести в (8).
, т.е. равнодействующая сила тяжести другого полукольца, равная и противоположно направленная силе тяжести в (8).
Одно полукольцо уравновешивает другое и, следовательно, кольцо будет находиться в равновесии вокруг планеты.
В сечениях стыка полуколец развивается напряжение сжатия
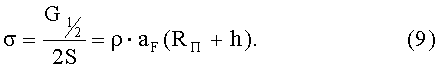
Это напряжение сжатия не зависит от конкретной формы сечения кольца. Очевидно, что такое напряжение будет в каждом сечении кольца.
Формула (9) позволяет оценить несущую способность конструкции кольца. Подставляя в (9) предельные значения σ для различных материалов, можно найти радиус (и диаметр) кольца, способного выдержать распределенные равномерно по его контуру силы тяжести Р. Расчеты показывают, что прочностные свойства существующих специальных высокопрочных материалов достаточны для обеспечения прочности колец вокруг планет (или спутников) с диаметром примерно до (0,5…1,0)*106 м = (500…1000) км, что само по себе немало. Эти размеры будут еще больше по мере появления в перспективе новых высокопрочных материалов, превосходящих существующие по своим свойствам: наука и техника не стоят на месте.
Здесь следует отметить, что приведенные выше предельные размеры кольца получены на основе приближенной формулы (6), в которой не учитывается сила инерции Q, уменьшающая силу тяжести Р элементарных частей кольца.
При расчетах же на основе точной формулы (4), в которой учитывается сила инерции Q, уменьшающая силу тяжести Р элементарных частей кольца, значения размеров кольца будут больше.
Таким образом, твердое жесткое кольцо вокруг планеты с радиусом, большим радиуса планеты и массой, значительно меньшей ее массы, охватывающее планету в плоскости, проходящей через ее центр так, что центры кольца и планеты совпадают, является самоуравновешивающимся устройством, которое будет находиться в состоянии равновесия в «висячем» положении вокруг планеты из-за противонаправленности действия сил тяжести составных частей кольца, находящихся по разные стороны от планеты в плоскости, проходящей через ее центр.
Такое кольцо является основным средством для осуществления предлагаемого изобретения.
Теперь перейдем к некоторым уточнениям, касающимся сделанному ранее выводу об идеальной симметрии картины на фиг.1.
Этот вывод следует считать не окончательным, т.к. он был получен в предположении, что твердое жесткое кольцо имеет одинаковую плотность по всему своему контуру и идеально по форме, а планета является идеальным сплошным однородным шаром.
В действительности же идеальной симметрии не получится, поскольку реальное кольцо невозможно выполнить со строго одинаковой плотностью по всему его контуру и идеальным по форме, а планета не является идеальным сплошным однородным шаром.
По этим причинам на разные мысленно выделенные элементарные части кольца будут действовать разные по величине силы и поэтому результирующая векторная сумма всех этих сил не будет равна нулю. Под действием этой результирующей силы кольцо сместится к планете вплоть до соприкосновения с ней более массивной своей частью, а диаметрально противоположная ей часть кольца максимально отдалится от планеты, как показано на фиг.2.
Этот результат очень важен в практическом отношении, т.к. при этом автоматически возникает доступ к кольцу с поверхности планеты. Поэтому на практике нужно изначально выполнить определенную часть кольца более массивной, чтобы под действием векторной суммы сил тяжести эта часть кольца надежно прижималась к земной поверхности планеты (фиг.2). Для наглядности на первой проекции фиг.2 более массивная часть кольца показана в утолщенном виде, а большие силы тяжести, действующие в этой части кольца, показаны более длинными стрелками Р.
Показанное на фиг.2 положение кольца вокруг планеты, когда оно прижато своей массивной частью к ней и одновременно находится в плоскости, проходящей через ее центр, является положением устойчивого равновесия.
Действительно, если предположить, что кольцо, оставаясь прижатым своей более массивной частью к планете, получило под действием какой-то воображаемой внешней силы Fк ускорение a к и сместилось из положения равновесия в плоскость, не проходящую через центр планеты, как показано пунктиром на второй проекции фиг.2, то в этом случае в векторной сумме действующих на кольцо сил тяжести возникнут составляющие этих сил, возвращающие его в прежнее положение, т.е. в первоначально занимаемую им плоскость, проходящую через центр планеты, что наглядно иллюстрируется показанными на второй проекции фиг.2 стрелками сил тяжести Р, действующих по контуру пунктирного кольца в направлении к центру планеты (кстати, следует заметить, что, согласно второму закону И.Ньютона, для сообщения кольцу какого-то ускорения a к из положения равновесия потребовалось бы, с учетом большой массы кольца Mк, очень большая величина этой упомянутой воображаемой внешней силы Fк=a кMк).
В положении равновесия кольцо будет самоуравновешено вокруг планеты, прижимаясь к ней своей более массивной частью. Для удержания кольца даже большой массы Mк в таком положении вокруг планеты не требуется никаких дополнительных усилий: все обеспечивается мощными силами тяжести.
На таком кольце, как на опоре, можно размещать любые космические объекты, например телекоммуникационные системы для организации глобальной космической радиосвязи, наблюдательные и научно-исследовательские станции с космонавтами, космические площадки для запуска и посадки космических кораблей и т.д. При этом для удобства доставки грузов в любую часть кольца, и особенно в наиболее удаленную от планеты и поэтому самую важную в практическом отношении его часть, кольцо конструктивно должно быть пустотелым с круглым, квадратным (или прямоугольным) поперечным сечением соответствующих размеров (это также позволит уменьшить массу кольца). Для обеспечения необходимой жесткости кольцо должно быть из высокопрочного материала, иметь соответствующую толщину стенок и длину стороны квадрата (или прямоугольника) или диаметра поперечного сечения. Доставку грузов и космонавтов в наиболее удаленную от поверхности планеты часть кольца можно осуществлять транспортом с реактивными или электрическими двигателями внутри кольца. Следует отметить, что усилия по преодолению сил тяжести при доставке этих грузов вдоль кольца будут не намного больше усилий при доставке аналогичных грузов на поверхности планеты. Действительно, вблизи поверхности планеты, где сила тяжести максимальна, угол подъема в кольце относительно поверхности планеты невелик (практически незаметен). По мере удаления от поверхности планеты вдоль кольца угол подъема хотя и увеличивается, но ненамного, причем возрастание усилий из-за этого будет частично компенсироваться уменьшением силы тяжести. Эти силы тяжести будут определяться выражением (6), куда подставляют m, равную массе транспорта с грузом. Что касается возвращения транспорта с грузом на поверхность планеты, то он под действием силы тяжести будет перемещаться по кольцу сам (как говорится, на тормозах).
Космические телекоммуникационные системы на кольце могут не только охватывать радиосвязью территорию планеты, но обеспечивать глобальную космическую радиосвязь на перспективных ультракоротковолновых, сантиметровых, миллиметровых и оптических диапазонах электромагнитных волн.
Космические наблюдательные пункты на кольце очень удобны для исследования как поверхности планеты, так и околопланетного космического пространства и дальнего космоса. Космонавты при работе в них не будут испытывать явление невесомости, а при подъеме на них не будут подвергаться перегрузкам.
Что касается космических площадок для запуска и посадки космических кораблей на кольце в околопланетном космическом пространстве, где силы тяжести меньше, чем на поверхности планеты, то они имеют ряд преимуществ по сравнению с космодромами на поверхности планеты:
- запуск с них космических кораблей может осуществляться проще и дешевле, т.к. при этом в отличие от космодромов на поверхности планеты не потребуются затратные мощные ракеты-носители и большие запасы и расходы дорогостоящего топлива;
- физические усилия космонавтов, находящихся на космических площадках (как и на космических наблюдательных пунктах) будут меньше, чем на поверхности планеты, причем они не будут испытывать типичные для известного способа перегрузки и явление невесомости;
- при запуске и посадке космических кораблей можно использовать скорость самих площадок по касательной вокруг планеты из-за вращения ее вокруг собственной оси: эта скорость при запуске кораблей в направлении вращения планеты будет прибавляться к сообщаемой кораблям скорости, а при посадке кораблей в направлении вращения планеты будет вычитаться из скорости осуществляющих посадку кораблей, что облегчает и удешевляет запуск и посадку (в наибольшей степени это проявится при расположении кольца в плоскости экватора планеты);
- при посадке кораблей вдоль восходящей ветви кольца будет использоваться тормозящая сила тяготения к планете, она будет добавляться к тормозящей силе реактивных двигателей корабля, что облегчит и удешевит посадку.
Таковы в основном отличительные особенности предлагаемых способа и устройства.
К сказанному можно добавить несколько слов о возможной технологии изготовления и подъема кольца вокруг планеты в соответствии с фиг.2. Это можно было бы осуществить в два этапа.
1. Сначала на поверхности планеты по выбранной окружности вокруг нее в плоскости, проходящей через ее центр, выполняется достаточно прочное пустотелое кольцо круглого, квадратного (или прямоугольного) сечения необходимого размера с механизмом сдвига в определенных пределах соседних звеньев кольца (по принципу звено в звене). При этом наиболее массивная часть кольца, в которой будет вход в кольцо, размещается в нужном месте непосредственно на поверхности планеты, а остальная часть - на опорах определенной высоты с учетом рельефа местности. Как только кольцо будет замкнуто вокруг планеты при достаточной жесткости его конструкции, оно, в соответствии с изложенным выше принципом самоуравновешивания, становится самоуравновешивающимся под действием сил тяжести по всему его контуру (фиг.2), и надобность в опорах отпадает.
2. Затем, используя механизм сдвига соседних звеньев кольца, увеличивают его радиус до нужного значения, чтобы получить заданную высоту h над планетой той части кольца, которая согласно фиг.2 диаметрально противоположна его прижатой к планете массивной части.
В заключение следует отметить, что данное предлагаемое изобретение представляет несомненный интерес, расширяет границы познания материального мира и при реализации его в перспективе сулит большие возможности в области исследования и освоения околопланетных космических пространств и дальнего космоса, в области запуска и посадки космических кораблей, в области наблюдений за территориями планет и охвата их глобальной космической радиосвязью в перспективных метровых, сантиметровых, миллиметровых и оптических диапазонах электромагнитных волн.
Изобретения относятся к средствам размещения и перемещения различных объектов в околопланетном космическом пространстве. Способ включает размещение физических тел (объектов) в пространстве около достаточно малой планеты (1) (спутника, астероида и т.п.). Для этого используют неподвижную относительно планеты опору в виде твердого и жесткого кольца (2). Данное кольцо в целом самоуравновешивается силами тяжести его частей, расположенных по разные стороны от планеты (1). Устойчивое положение кольца обеспечивается его смещением от центрально-симметричного (статически неустойчивого) положения относительно планеты до положения, в котором кольцо касается планеты некоторой своей частью. Данная часть кольца (2) может быть выполнена с увеличенной массой на единицу длины. Тем самым обеспечивается доступ к кольцу с поверхности планеты, позволяющий перемещать на опору и возвращать с нее на планету различные грузы. Техническим результатом изобретений является расширение возможностей позиционирования и транспортировки в околопланетном пространстве различных объектов (научно-исследовательских станций, средств наблюдения планеты, телекоммуникационных систем, площадок для запуска и посадки космических кораблей и т.д.). 2 н.п. ф-лы, 2 ил.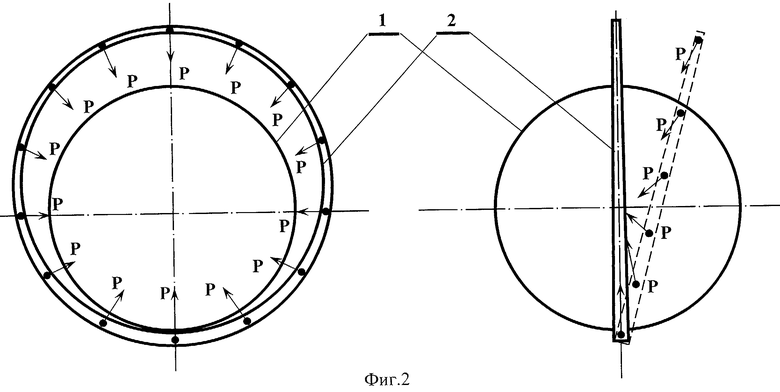
1. Способ позиционирования физических тел в околопланетном космическом пространстве путем размещения их на космической опоре в виде кольца вокруг планеты в указанном околопланетном пространстве в плоскости, проходящей через ее центр, с радиусом, большим радиуса планеты, и массой, значительно меньшей ее массы, отличающийся тем, что в нем используют неподвижное относительно планеты твердое и жесткое кольцо, самоуравновешивающееся силами тяжести частей кольца по разные стороны от планеты, при этом устойчивое положение кольца и доступ к нему с планеты обеспечивают изначальным увеличением массы определенной части кольца, смещающим кольцо в его плоскости относительно центра планеты до прижатия этой более массивной части к планете.
2. Устройство для позиционирования на нем физических тел в околопланетном космическом пространстве, выполненное в виде кольца вокруг планеты в указанном околопланетном пространстве в плоскости, проходящей через ее центр, с радиусом, большим радиуса планеты, и массой, значительно меньшей ее массы, отличающееся тем, что кольцо выполнено неподвижным относительно планеты, твердым, жестким и самоуравновешивающимся силами тяжести частей кольца по разные стороны от планеты, причем устойчивое положение кольца и доступ к нему с планеты обеспечены изначальным увеличением массы определенной части кольца, смещающим кольцо в его плоскости относительно центра планеты до прижатия этой более массивной части к планете.
| Ж.: Техника - молодежи, 6, 1982, с.34-36, с.4 обложки | |||
| Модель космической станции | 1980 |
|
SU1165417A1 |
| Модель орбитальной станции | 1972 |
|
SU548182A1 |
| US 4318517 A, 09.03.1982. | |||
Авторы
Даты
2012-10-10—Публикация
2009-06-23—Подача