Изобретение относится к области радиолокации и может быть использовано в радиолокационных станциях обнаружения и целеуказания (СОЦ), а также в радиолокационных станциях сопровождения для измерения истинного значения радиальной скорости воздушной цели.
Обнаружение воздушных целей в типовых СОЦ происходит следующим образом. Станция имеет антенну, вращающуюся в горизонтальной плоскости с частотой ΩВР. Конструкция антенны такова, что характеристика направленности имеет большую ширину в вертикальной плоскости и малую в горизонтальной плоскости [1, с. 285-286]. Передатчик радиолокационной станции (РЛС) формирует последовательность сверхвысокочастотных импульсов, которая с помощью антенны излучается в пространство. При контакте характеристики направленности антенны (ХНА) и цели появляется отраженный воздушной целью сигнал, который принимается этой же антенной, обрабатывается приемной системой РЛС и направляется в другие системы РЛС. При появлении отметки от цели на экране индикатора делается вывод о наличии цели. Азимут цели принимается равным азимуту антенны в момент приема максимального отраженного сигнала (центра пачки отраженных сигналов), а наклонная дальность до цели определяется по времени задержки отраженного импульса относительно излученного. При дальнейшем вращении антенны ее луч, а соответственно и ХНА покидает место расположения цели, поэтому отраженный сигнал исчезает. Следовательно, информация от цели как и отметка от цели на индикаторе пропадает и появляется только спустя полный оборот антенны в момент следующего облучения воздушной цели. Время, в течение которого информация от цели отсутствует, определяется периодом вращения TВР антенны:

где ΩВР - угловая скорость вращения антенны по азимуту (единицы оборотов в секунду).
При подслеживании (с помощью СОЦ) за воздушной целью по дальности возникает ошибка, определяемая радиальной скоростью Vр полета цели

где t - время от момента облучения до текущего момента времени t.
Такую ошибку называют динамической ошибкой слежения или подслеживания по дальности (ошибкой измерения дальности). Для уменьшения или полного устранения динамической ошибки необходимо как можно точнее измерять радиальную скорость цели и учитывать ее при измерении дальности в последующие контрольные моменты времени tк по формуле

где Dобл - дальность, измеренная РЛС в момент облучения цели (контакта ХНА с целью).
Таким образом, при подслеживании за воздушной целью с помощью СОЦ актуальной задачей является измерение ее радиальной скорости, которая при определенных условиях не может быть в импульсной РЛС вычислена правильно, что связано с неоднозначностью измерений в импульсных радиолокационных системах.
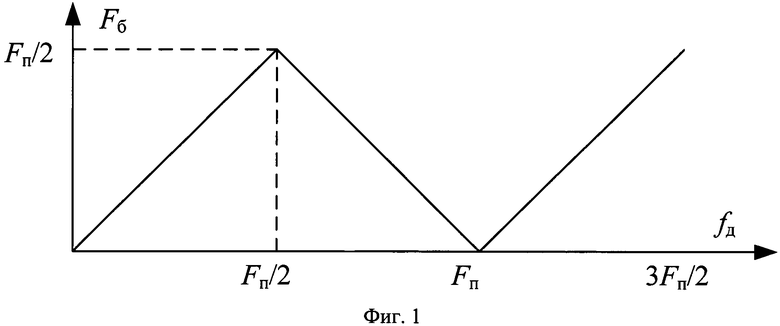
Известны цифровые устройства доплеровской обработки импульсных видеосигналов, обеспечивающие спектральный анализ, когерентную фильтрацию, определение радиальной скорости воздушной или иной цели и направление ее движения (измерение величины частоты Доплера и ее знака) [2, с. 155, рис. 12]. Однако эти устройства при работе на постоянной частоте повторения не обеспечивают возможность прямого однозначного измерения частоты Доплера fд и ее знака, если измеряемая доплеровская частота превышает половину частоты повторения импульсов РЛС Fп/2, где Fп - частота повторения. Причиной этого является проявление известного стробоскопического эффекта. Как известно [3], измерение частоты Доплера эхо-сигнала, отраженного от движущейся цели с помощью когерентно-импульсной РЛС, сопровождается явлением неоднозначности. Данное явление обусловлено тем, что частота биений на выходе фазового детектора в приемнике РЛС однозначно определяет частоту Доплера только в пределах от 0 до половины частоты повторения РЛС (Fп/2) [3, с. 102]. Причем, при частоте Доплера fд, равной Fп/2, частота биений максимальна (фиг. 1).
При превышении частотой Доплера величины Fп/2 частота биений Fб уменьшается. Процесс увеличения и снижения частоты биений в ходе увеличения fд повторяется с периодом, равным частоте повторения РЛС. Таким образом, предел однозначного измерения доплеровской частоты составляет Fп/2.
Известно устройство, обеспечивающее расширение диапазона однозначного определения частоты Доплера до частоты повторения Fп, т.е. в два раза [4]. Принцип действия данного устройства заключается в формировании однополосного импульсного видеосигнала из двухполосного импульсного видеосигнала, поступающего с выхода фазового детектора, путем вырезания (удаления) из его спектра части спектральных линий - четных или нечетных, где нечетные линии соответствуют частотам fд, Fп+fд, 2Fп+fд и т.д., а четные линии соответствуют частотам Fп-fд, 2Fп-fд и т.д. В результате такого вырезания части спектральных линий («прополки» спектра) образуется новый однополосный спектр и соответственно новый однополосный выходной импульсный видеосигнал, обеспечивающий однозначное определение частоты Доплера fд в пределах от 0 до Fп. Однако данное устройство не позволяет однозначно определять радиальную скорость цели, если частота Доплера превышает значение Fп.
Наиболее близким по технической сущности к заявляемому изобретению является способ однозначного измерения радиальной скорости цели в когерентно-импульсной радиолокационной станции, реализованный в зенитной самоходной установке (ЗСУ) 2С6М зенитного пушечно-ракетного комплекса (ЗПРК) 2К22 [5, с. 5-150]. Данный способ аналогично [4] позволяет расширить предел однозначного измерения частоты Доплера до величины Fп, т.е. увеличить интервал однозначного измерения Vp в 2 раза.
Сущность способа [5, с. 5-150] заключается в следующем.
Передающая система СОЦ формирует когерентные зондирующие сверхвысокочастотные (СВЧ) импульсы с частотой повторения Fп, которые с помощью антенно-фидерной системы (АФС) излучаются в пространство [6, с. 76-79], в котором предполагается нахождение целей. Антенна АФС имеет ХНА, широкую в вертикальной плоскости и узкую в горизонтальной плоскости. Данная антенна вращается в горизонтальной плоскости со скоростью в несколько оборотов в секунду. Таким образом, производится поиск воздушных целей в зоне обнаружения СОЦ. Отраженные от воздушной цели радиоимпульсы, несущая частота которых приобретает доплеровскую добавку, принимаются антенной АФС и через резонатор, обеспечивающий электромагнитную совместимость с другими СОЦ, подаются в приемную систему.
В приемной системе отраженные сигналы поступают на разрядник, защищающий элементы приемной системы от мощного импульса передатчика [6, с. 76-79]. Далее отраженные сигналы усиливаются и через фильтр зеркальной частоты, подавляющий помеху по зеркальному каналу приема, подаются на преобразователь частоты, где частота сигнала понижается до промежуточной порядка десятков мегагерц. С выхода преобразователя частоты сигналы подаются на усилитель промежуточной частоты (УПЧ), где усиливаются и подаются на квадратурные фазовые детекторы (ФД) [3, с. 239]. На выходах квадратурных ФД образуются две последовательности импульсов, промодулированных в квадратуре (в двух квадратурных каналах) по амплитуде частотой биений при наличии у цели радиальной скорости. При радиальной скорости цели, соответствующей частоте Доплера, не превышающей Fп/2, частота биений тождественно равна доплеровской частоте Fд [3, с. 69]

где Vp - радиальная скорость цели; λ - длина волны РЛС.
Полученные на выходах ФД последовательности импульсов в квадратуре поступают на устройство однополосной обработки, состоящее из двух фазовращателей и суммирующего устройства [6, с. 105-106].
Как известно [3, с. 96], в спектре сигнала на выходе фазового детектора в случае движущейся цели отсутствуют спектральные линии на частотах, кратных частоте повторения. Данные линии оказываются сдвинутыми в обе стороны от этих значений на доплеровскую добавку. Эти линии получили название верхней боковой (ВБ) и нижней боковой (НБ) составляющих спектра сигнала. Устройство однополосной обработки выделяет из сигнала частоты верхней боковой и нижней боковой составляющих. Частота НБ составляющей (частота биений на выходе ФД) равна Fб, а частота ВБ составляющей равна Fп-Fб. Работа устройства однополосной обработки основана на фазовых различиях сигналов ВБ и НБ составляющих. Анализируя фазовые различия указанных сигналов, устройство однополосной обработки определяет, по какой составляющей необходимо определять частоту Доплера - по ВБ или по НБ. Если скорость цели такова, что доплеровская частота отраженного сигнала меньше Fп/2, то частоте Доплера соответствует НБ составляющая. В противном случае доплеровской частоте соответствует ВБ составляющая. Таким образом, устройство однополосной обработки определяет, в каком интервале находится частота биений: от нуля до Fп/2 или от Fп/2 до Fп.
С выхода устройства однополосной обработки верхняя и нижняя боковые составляющие спектра сигнала поступают на две гребенки узкополосных доплеровских фильтровых каналов. Каждая гребенка включает набор узкополосных доплеровских фильтров (УДФ). Первая гребенка имеет фильтры с 1-го по К-й, а вторая гребенка - с (К+1)-го по 2К-й. Количество К УДФ в гребенке определяется диапазоном измеряемых радиальных скоростей цели и требуемой разрешающей способностью по радиальной скорости.
На первую гребенку подается сигнал НБ составляющей, а на вторую гребенку - сигнал ВБ составляющей. Причем, большему номеру УДФ соответствует большая радиальная скорость цели. Каждый фильтровый канал включает последовательно соединенные УДФ, детектор, интегратор и пороговый элемент. При превышении напряжением на выходе какого-либо z-го УДФ установленной пороговой величины соответствующий z-й пороговый элемент формирует на своем выходе логическую единицу, которая поступает на преобразователь номера канала в код скорости [6, с. 76-79]. Если сигнал логической единицы поступает с первой гребенки, то скорость находится в диапазоне от нуля до Fп/2, а если сигнал логической единицы поступает со второй гребенки, то скорость находится в диапазоне от Fп/2 до Fп. Таким образом, радиальная скорость цели однозначно измеряется в диапазоне от 0 до Fп. Код скорости поступает на интегратор дальности и используется для устранения динамической ошибки измерения дальности до цели.
При очевидных достоинствах способ-прототип [5] не позволяет однозначно определять радиальную скорость цели, если соответствующая ей частота Доплера превышает значение Fп. Иначе говоря, радиальная скорость VP цели может превышать величину, соответствующую частоте Fп. В этом случае радиальная скорость цели будет измерена неверно, т.е. с ошибкой неоднозначности.
В импульсно-доплеровских РЛС частота повторения Fп может достигать сотен кГц. При таких значениях Fп неоднозначность измерения скорости не возникает, так как скорости современных целей ограничены величинами сотен метров в секунду (за исключением гиперзвуковых). Однако в когерентно-импульсных РЛС частота повторения Fп может составлять всего единицы кГц, что позволяет однозначно измерять радиальные скорости целей, летящих не быстрее десятков метров в секунду. Например, при Fп=1 кГц и λ=4 см однозначно измеряются скорости всего лишь до 20 м/с. Для таких РЛС востребован способ, предполагающий устранение возникающей неоднозначности измерений.
Задачей изобретения является разработка способа, позволяющего однозначно измерять радиальную скорость воздушной цели в когерентно-импульсной РЛС при доплеровских частотах, превышающих значение Fп, что обеспечивает уменьшение ошибки подслеживания за воздушной целью по дальности.
Поставленная задача может быть решена на основе использования взаимной корреляционной функции (ВКФ) отраженного и опорного (копии зондирующего) сигналов. Из свойств двумерной корреляционной функции или так называемого тела неопределенности [2, 3] следует, что число горбов (максимумов) в корреляционной функции, являющейся срезом тела неопределенности, зависит от соотношения между доплеровской добавкой сигнала и величиной NFп/2, где N - целое число. Поэтому по числу максимумов во ВКФ можно установить диапазон, в котором находится истинное значение доплеровской частоты отраженного сигнала, а затем определить истинное значение радиальной скорости цели.
Более подробно сущность предлагаемого способа однозначного измерения радиальной скорости цели в когерентно-импульсной радиолокационной станции можно пояснить следующим образом.
Сначала неоднозначную доплеровскую частоту отраженного сигнала fдн измеряют по номеру узкополосного доплеровского фильтра, выходной сигнал которого превышает пороговое значение. Эта операция ничем не отличается от измерения доплеровской частоты типовым фильтровым способом [3]. В дальнейшем же для однозначного определения частоты Доплера предлагается определять, в каком интервале частот от (N-1)Fп/2 до NFп/2 (где N - целое число) находится истинная доплеровская частота (фиг. 1). Другими словами, необходимо установить величину N, для которой истинная доплеровская частота будет верно и однозначно попадать в интервал частот от (N-1)Fп/2 до NFп/2. Для определения величины N и указанного частотного интервала предлагается использовать взаимную корреляционную функцию (ВКФ) отраженного и опорного сигналов. В качестве опорного сигнала в данном случае предполагается использовать зондирующий сигнал, просочившийся в приемный тракт РЛС в соответствующем периоде повторения [7, 8].
Опорный просочившийся в приемную систему зондирующий сигнал на выходе УПЧ математически может быть описан формулой
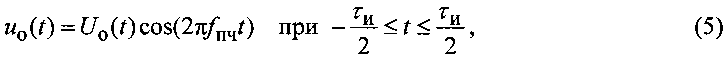
где Uo(t) - закон амплитудной модуляции зондирующего (опорного) сигнала; fпч - промежуточная частота, на которую преобразован в УПЧ зондирующий сигнал; τи - длительность зондирующего импульса.
Пусть отраженный сигнал, прошедший УПЧ, представляет собой радиоимпульс с амплитудной модуляцией, обусловленной отражением от цели, условиями распространения радиоволн и особенностями преобразований в приемном устройстве РЛС, и постоянной частотой заполнения
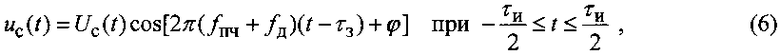
где Uc(t) - закон амплитудной модуляции отраженного сигнала; fд - доплеровская частота отраженного сигнала, зависящая от радиальной скорости цели; τз - временная задержка, обусловленная дальностью цели.
Для получения ВКФ зондирующего и отраженного сигналов предлагается переводить их в цифровую форму и производить все расчеты в процессоре цифровой вычислительной системы (ЦВС), входящей в состав РЛС. Согласно предлагаемому способу отраженные от цели сигналы, снятые с выхода УПЧ, преобразуют с помощью аналого-цифрового преобразователя (АЦП) в цифровую форму. При этом каждый отраженный сигнал дискретизируют с периодом дискретизации Δt, вычисляемым по формуле

где fд макс - максимально возможное значение доплеровской добавки к несущей частоте зондирующего сигнала.
В результате проведенной цифровой дискретизации получают в пределах каждого отраженного сигнала К цифровых дискретных отсчетов, именуемых для краткости дискретами. Число дискретов, приходящихся на один сигнал, будет равно К=τи/Δt.
Гипотеза, лежащая в основе предлагаемого способа, основана на однозначном соответствии между сдвигом сигнала по доплеровской частоте и числом полуволн графического изображения формируемой ВКФ. Как удалось выяснить методом моделирования, имеется объективная возможность по виду формируемой ВКФ определить, при каком значении N истинная доплеровская частота отраженного сигнала будет принадлежать интервалу частот от (N-1)Fп/2 до NFп/2. А это, в свою очередь, позволяет однозначно вычислить истинную радиальную скорость цели.
Однако сформировать ВКФ с нужными свойствами по одному импульсу невозможно. Для обоснования длительности анализируемого отраженного сигнала τс, обеспечивающей получение нужных свойств в ВКФ, обратимся к величине диапазона неоднозначности измерения частоты Доплера, т.е. определим условие, при котором ВКФ имеет хотя бы одну полуволну. Пусть, например, длительность зондирующего радиоимпульса равна τи=3,3 мкс (такую длительность имеет зондирующий импульс СОЦ ЗСУ 2С6М [6, с. 75]). При таких параметрах протяженность диапазона однозначности измерения частоты Доплера, а также протяженность диапазонов неоднозначного измерения доплеровской частоты составляет 0,5/τи=0,15 МГц. Эта величина существенно превышает возможные значения доплеровских частот сигналов реальных целей (при радиальной скорости цели VP=200 м/с и длине волны λ=2 см доплеровская добавка fд=2Vp/λ=20 кГц).
Поскольку граничная частота однозначного измерения частоты Доплера составляет Fп/2, то для получения в графике ВКФ хотя бы одной полуволны, должно выполняться соотношение

откуда длительность сигнала τс, подлежащего корреляционному анализу, должна составлять

Таким образом, длительность используемого при корреляционном анализе сигнала не должна быть меньше периода повторения РЛС Tп, а в условиях стремления к минимальным временным затратам, она должна быть равна Tп. В импульсной РЛС данное условие за счет уменьшения скважности выполнить невозможно. В результате для выполнения условия (9) предлагается в память ЦВС записывать и соединять между собой оцифрованные последовательно принимаемые отраженные сигналы. Сигналы следует в цифровом виде соединять в один протяженный синтезируемый сигнал. Увеличение длительности синтезируемого сигнала необходимо осуществлять до тех пор, пока его значение не достигнет τс=Tп.
Например, в СОЦ ЗСУ 2С6М [6, с. 75] период повторения Tп составляет 133 мкс. Скважность импульсного сигнала равна 40,3. Время накопления 41-го отраженного импульса tн составляет 5,45 мс. При ширине ХНА СОЦ в азимутальной плоскости ΔΘβ=4° и скорости вращения антенны по азимуту Ωβ=1 об/с длительность пачки отраженных сигналов от цели составит около 10 мс, т.е. время накопления сигналов tн приемом пачки отраженных сигналов антенной СОЦ при ее вращении вполне обеспечивается.
Итак, согласно предлагаемому способу для выполнения условия (9) оцифрованные отраженные сигналы в виде цифровых дискретов последовательно запоминают в памяти ЦВС. Операцию запоминания оцифрованных дискретов проводят в течение M периодов повторения, причем число M рассчитывают по формуле M=Λ(Tп/τи), где Λ(*) - функция округления до следующего целого числа. Из оцифрованных дискретов отраженных сигналов M периодов повторения составляют непрерывную последовательность, в которой первому дискрету очередного отраженного сигнала предшествует последний дискрет предыдущего отраженного сигнала. С учетом того, что в пределах одного отраженного сигнала (импульса) получают К дискретов, всего в запоминаемой последовательности получают Х=КМ элементов (дискретов). Из запомненных X дискретов формируют цифровой массив данных M1, выражающий значениями своих элементов амплитудную огибающую M соединенных между собой последовательно принятых отраженных сигналов.
Одновременно с этим зондирующие сигналы, просочившиеся в приемное устройство РЛС, оцифровывают аналогичным образом в этих же M периодах на выходе УПЧ. Аналогично объединяют оцифрованные дискреты M зондирующих сигналов в непрерывную последовательность и создают из них аналогичный цифровой массив данных M2 из X элементов, выражающий значениями своих элементов амплитудную огибающую M соединенных между собой последовательно просочившихся в приемное устройство зондирующих сигналов.
Для запоминания и хранения значений рассчитываемой ВКФ согласно способу создают в памяти ЦВС массив R из (2Х-1) элементов. Каждый элемент массива R будет иметь свой номер j, изменяющийся от 1 до (2Х-1), т.е. массив R будет состоять из j-x элементов rj, предназначенных для запоминания j-x значений взаимной корреляционной функции.
По окончании формирования массивов M1 и M2 с помощью ЦВС производят вычисление j-x элементов rj взаимной корреляционной функции массивов M1 и М2 (ВКФ отраженного и зондирующего синтезированных сигналов) по формуле
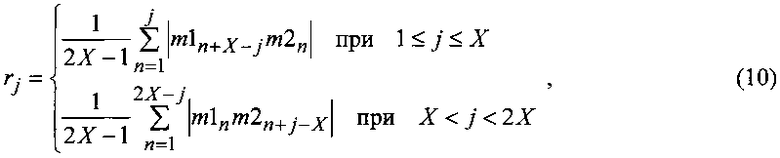
где m1i - значение i-го элемента массива M1; m2i - значение i-го элемента массива M2.
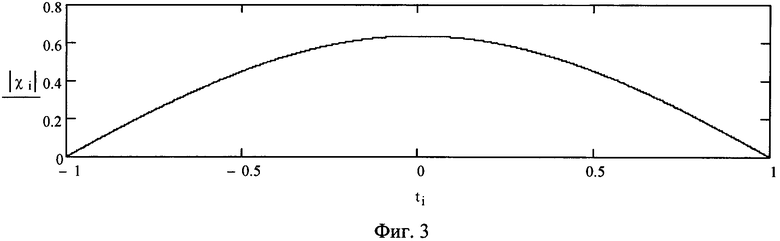
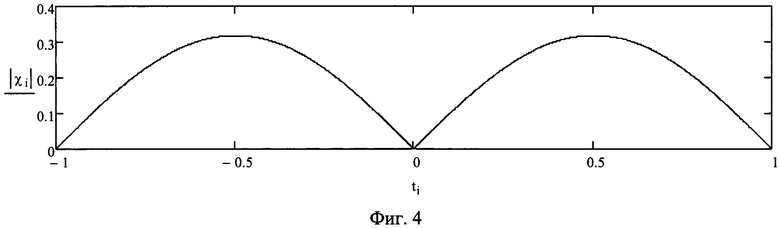
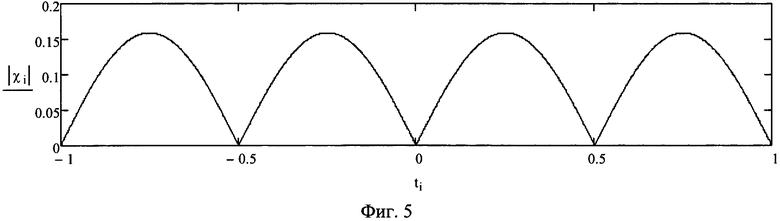
Для удобства проведения дальнейшего анализа в выражении для расчета ВКФ умышленно использован знак модуля, т.е. способ оперирует модулем ВКФ. Далее слово «модуль» для краткости в описании способа не используется. Если по формуле (10) рассчитать всю ВКФ, то ее графическое изображение (вид) будет зависеть от доплеровской добавки отраженного сигнала. Так, если доплеровская добавка равна нулю (т.е. частоты эхо-сигнала и опорного сигнала равны), то ВКФ представляет собой треугольную линейно изменяющуюся функцию [9, с. 108-109], показанную на фиг. 2. Если доплеровская добавка равна 0,5/τи, то график ВКФ представляет собой одну полуволну (фиг. 3). Если доплеровская добавка равна 1/τи, то график ВКФ представляет собой две полуволны (фиг. 4). Если доплеровская добавка равна 2/τи, то график вычисляемой ВКФ представляет собой четыре полуволны (фиг. 5) и т.д.
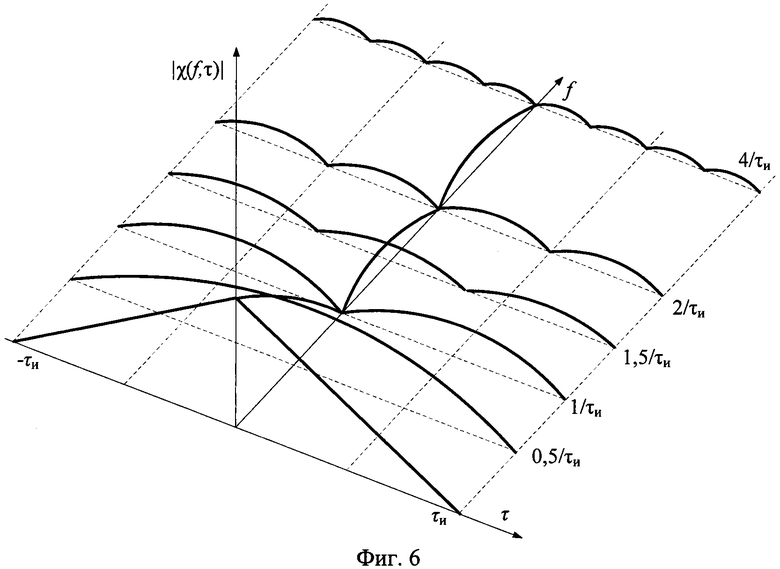
Представленные взаимные корреляционные функции [10] являются сечениями двумерной взаимной корреляционной функции (в координатах «временной сдвиг - частотный сдвиг») плоскостями времени. Вид двумерной взаимной корреляционной функции (двумерной автокорреляционной функции) показан на фиг. 6. Из фиг. 6 видно, что при увеличении величины частотного сдвига между сравниваемыми сигналами функция взаимной корреляции меняет форму, а именно изменяется число ее полуволн. Расстояние между сечениями, в которых функция взаимной корреляции имеет целое число полуволн, составляет 0,5/τи.
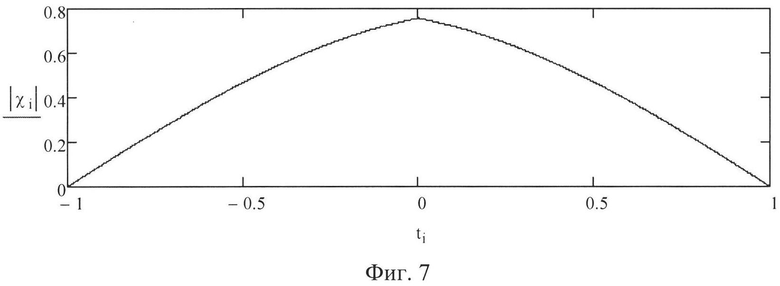
Рассчитанная по формуле (10) ВКФ благодаря использованию знака модуля будет иметь только положительные значения и может иметь большое число локальных экстремумов. Для исключения их из анализа предлагается записанную в цифровой форме в виде элементов массива R ВКФ подвергнуть низкочастотной фильтрации с помощью цифрового низкочастотного фильтра. В результате такой фильтрации выделяют огибающую ВКФ. В выделенной огибающей ВКФ определяют количество ее максимумов N. По числу максимумов N можно принимать решение о нахождении истинной доплеровской частоты отраженного сигнала в том или ином частотном диапазоне. Если график ВКФ имеет одну полуволну, то N=1 и частота Доплера лежит в диапазоне 0<fд<Fп/2. Вид ВКФ при fд=0,4/τс показан на фиг. 7. Если график ВКФ имеет две полуволны, то N=2 и частота Доплера лежит в диапазоне Fп/2<fд<Fп. Вид ВКФ при fд=0,8/τс показан на фиг. 8.
Таким образом, по числу N глобальных максимумов полученной ВКФ на основе выражения

можно определить нижнюю Fн и верхнюю Fв границы диапазона, в котором лежит истинная доплеровская частота отраженного сигнала:
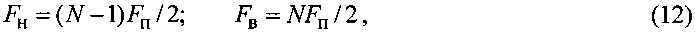
где Fн, Fв - верхняя и нижняя границы частотного диапазона.
Далее к измеренной с помощью гребенки УДФ неоднозначной доплеровской частоте сигнала fдн прибавляют значение нижней границы установленного по числу N доплеровского диапазона Fн=(N-1)Fп/2, в результате чего получают истинную доплеровскую частоту fди отраженного сигнала. Используя значение fди, вычисляют истинную радиальную скорость Vри цели по формуле

Поскольку для вывода на индикатор РЛС используют код скорости цели, то для преемственности согласно способу величину Fн преобразуют в нижнюю границу Vн скоростного диапазона по формуле

Затем величину Vн нижней границы скоростного диапазона преобразуют в код нижней границы скоростного диапазона. На заключительном этапе суммируют код неоднозначной радиальной скорости цели с кодом нижней границы скоростного диапазона и получают код истинного значения радиальной скорости цели, который используется для вывода величины истинной радиальной скорости цели Vри на экран индикатора РЛС.
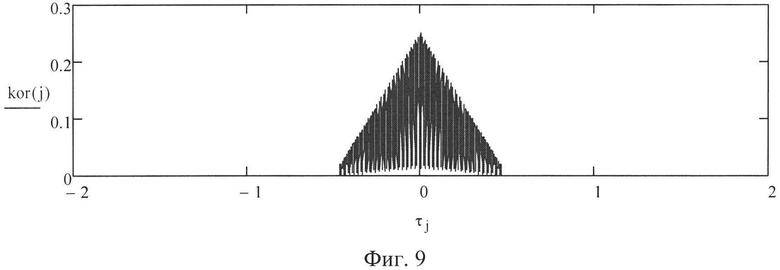
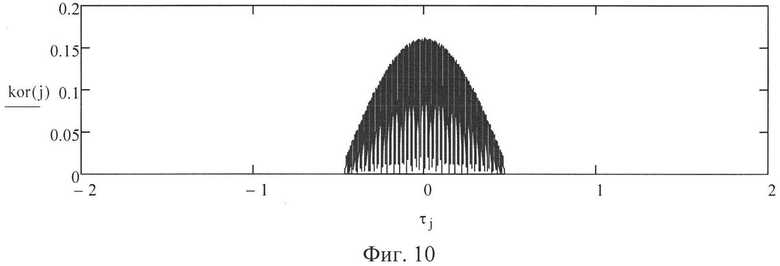
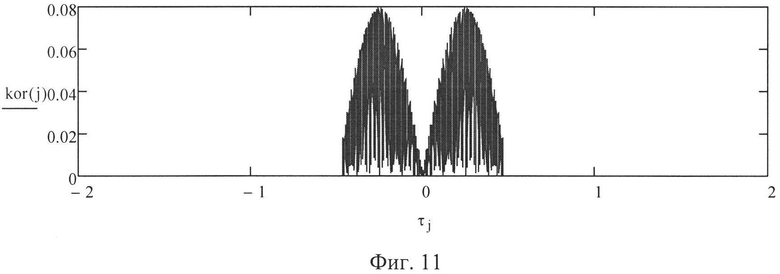
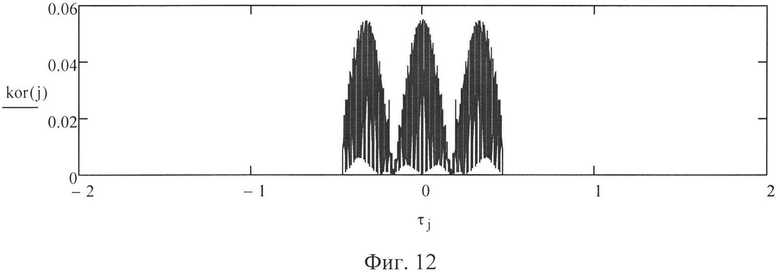
Для проверки приведенных предложений и рассуждений проведено моделирование процесса вычисления ВКФ с исходными данными, типичными для современных РЛС: промежуточная частота Fпч=40 МГц, длительность импульса τи=1 мкс, период повторения Fп=5 кГц, частота излучения - постоянная. В этом случае время накопления tн составляет tн=0,04 с, а длительность синтезируемого протяженного сигнала τс=0,2 мс. Опорный сигнал и отраженный сигнал описывали формулами (5) и (6). Величина каждого j-го элемента ВКФ рассчитывалась по формуле (10). Для нулевой частоты Доплера методом моделирования получена форма ВКФ, показанная на фиг. 9. Для частоты Доплера, равной 2,5 кГц, ВКФ имеет графическую интерпретацию, демонстрируемую фиг. 10. Таким образом, если график ВКФ имеет вид одной полуволны, то принимается решение, что частота Доплера лежит в пределах 0<fд<Fп/2. При доплеровских частотах, равных 5 кГц и 7,5 кГц, ВКФ принимает форму, представленную на фиг. 11 и 12 соответственно. Если ВКФ имеет график в виде двух полуволн, то частота Доплера лежит в пределах Fп/2<fд<Fп, а если ВКФ имеет график в виде трех полуволн, то частота Доплера лежит в пределах Fп<fд<3Fп/2.
Таким образом, использование корреляционной обработки отраженного сигнала позволяет определить интервал, в котором находится истинное значение доплеровской частоты. При этом устраняется неоднозначность измерения частоты Доплера, характерная для когерентно-импульсных РЛС.
В качестве примера рассмотрим процесс измерения радиальной скорости сверхзвуковой цели. Пусть длина волны λ равна 20 см (типичная для СОЦ), частота повторения Fп=5 кГц, радиальная скорость цели Vр=600 м/с. Частота Доплера в этом случае составляет 6 кГц и выходит за пределы интервала неоднозначности (0-5 кГц). Используя известный способ измерения доплеровской частоты, СОЦ определит доплеровскую добавку, равную 1 кГц, что значительно ниже истинного значения. Согласно предлагаемому способу вычисляется ВКФ и определяется, что огибающая ВКФ имеет два максимума (поскольку частота Доплера 6 кГц в соответствии с выражением (10) лежит в пределах от Fп до 2Fп). Следовательно, нижняя граница интервала доплеровских частот сигнала равна Fн=5 кГц. В соответствии с предлагаемым способом производится суммирование доплеровской добавки, измеренной СОЦ известным методом (1 кГц), с величиной нижней границы доплеровского частотного интервала 5 кГц. В результате суммирования получается значение 6 кГц, что соответствует истинному значению доплеровской частоты отраженного от цели сигнала.
Предлагаемый способ осуществляют следующим образом.
С помощью передающей системы СОЦ формируют когерентные зондирующие СВЧ-импульсы с частотой повторения Fп, которые с помощью АФС излучают в пространство. С помощью вращающейся антенны производят поиск целей в зоне обнаружения СОЦ. Отраженные от цели импульсы (радиосигналы), несущая частота которых приобретает доплеровскую добавку, принимают антенной АФС и подают в приемную систему. В приемной системе отраженные сигналы усиливают и через фильтр зеркальной частоты подают на преобразователь частоты, где производят понижение частоты до промежуточной. Далее отраженные сигналы на промежуточной частоте подают на УПЧ, где производится их усиление.
Усиленные сигналы с выхода УПЧ подают на гребенку УДФ и по номеру узкополосного доплеровского фильтра, выходной сигнал которого превышает пороговое значение, определяют неоднозначную доплеровскую частоту отраженного сигнала fдн, а затем преобразуют ее в цифровой код скорости с помощью преобразователя номера канала в код скорости.
Одновременно сигналы, снятые с выхода УПЧ, преобразуют с помощью АЦП в цифровую форму. При этом каждый отраженный сигнал дискретизируют с периодом дискретизации Δt, вычисляемым по формуле (7). В результате в пределах каждого отраженного сигнала получают К цифровых дискретных отсчетов, именуемых для краткости дискретами. Число дискретов, приходящихся на один сигнал, будет равно К=τи/Δt.
Оцифрованные отраженные сигналы в виде цифровых дискретов последовательно запоминают в памяти ЦВС. Операцию запоминания оцифрованных дискретов проводят в течение M периодов повторения, причем число M рассчитывают по формуле M=Λ(Tп/τи), где Λ(*) - функция округления до следующего целого числа. Из оцифрованных дискретов отраженных сигналов M периодов повторения составляют непрерывную последовательность, в которой первому дискрету очередного отраженного сигнала предшествует последний дискрет предыдущего отраженного сигнала. С учетом того, что в пределах одного отраженного сигнала (импульса) получают К дискретов, всего в запоминаемой последовательности получают Х=КМ элементов (дискретов). Из запомненных X дискретов формируют цифровой массив данных M1, выражающий значениями своих элементов амплитудную огибающую M соединенных между собой последовательно принятых отраженных сигналов.
Одновременно с этим зондирующие сигналы, просочившиеся в приемное устройство РЛС, оцифровывают аналогичным образом в этих же M периодах на выходе УПЧ. Аналогично объединяют оцифрованные дискреты M зондирующих сигналов в непрерывную последовательность и создают из них аналогичный цифровой массив данных M2 из X элементов, выражающий значениями своих элементов амплитудную огибающую M плотно соединенных между собой последовательно просочившихся в приемное устройство РЛС зондирующих сигналов.
Для запоминания и хранения значений рассчитываемой ВКФ создают в памяти ЦВС массив R из (2Х-1) элементов. Каждый элемент массива R будет иметь свой номер j, изменяющийся от 1 до (2Х-1), т.е. массив R будет состоять из j-x элементов rj, предназначенных для запоминания j-x значений взаимной корреляционной функции.
По окончании формирования массивов M1 и М2 с помощью ЦВС производят вычисление j-x элементов rj взаимной корреляционной функции массивов M1 и М2 (ВКФ отраженного и зондирующего синтезированных сигналов) по формуле (10).
Записанную в цифровой форме в виде элементов массива R ВКФ подвергают низкочастотной фильтрации с помощью цифрового низкочастотного фильтра. В результате чего выделяют огибающую ВКФ. В выделенной огибающей ВКФ определяют количество ее максимумов N. По количеству максимумов N с помощью выражения (12) определяют нижнюю Fн границу диапазона, в котором лежит истинная доплеровская частота отраженного сигнала. Величину Fн преобразуют в нижнюю границу Vн скоростного диапазона по формуле (14), которую затем преобразуют в код нижней границы скоростного диапазона. В заключение суммируют код неоднозначной радиальной скорости цели Vрн с кодом нижней границы скоростного диапазона и получают код истинного значения радиальной скорости цели.
В предлагаемом способе второй квадратурный ФД, вторая гребенка УДФ и устройство однополосной обработки не используются, так как диапазон однозначного измерения скорости определяется новым способом (по числу максимумов огибающей ВКФ).
Способ однозначного измерения радиальной скорости цели в когерентно-импульсной радиолокационной станции является вполне реализуемым в современных СОЦ, поскольку может быть осуществлен на существующей элементной базе, а также предполагает использование радиолокационной информации, действительно получаемой используемыми в настоящее время СОЦ.
Преимущество предлагаемого способа заключается в обеспечении возможности однозначно измерять радиальную скорость цели в когерентно-импульсной РЛС при доплеровских частотах, превышающих значение Fп, что позволит учитывать динамическую ошибку сопровождения цели при измерении дальности, что, в свою очередь, обеспечит уменьшение ошибки подслеживания за целью по дальности.
Способ может быть рекомендован для реализации в типовых когерентно-импульсных радиолокационных станциях, используемых для предоставления информации о параметрах движения воздушных судов диспетчерским службам аэропортов системы управления воздушным движением.
Источники информации
1. Белоцерковский Г.Б. Основы радиолокации и радиолокационные устройства. М., «Сов. радио», 1975. - 336 с.
2. Ширман Я.Д., Манжос В.Н. «Теория и техника обработки радиолокационной информации на фоне помех», 1981 г., Радио и связь, 416 с.
3. Финкельштейн М.И. Основы радиолокации. Учебник для вузов. М.: Радио и связь, 1983.- 536 с.
4. Цифровое устройство доплеровской обработки квадратурных импульсных видеосигналов. Патент на изобретение №:2155970. Авторы: Офенгейм И.Г., Давыдычев А.В.
5. Зенитная самоходная установка ЗСУ 2С6М. Техническое описание. 2С6М.00.00.000 ТО, 1991, 80 с. (прототип).
6. Изделие 1РЛ144М. Техническое описание. ЦА 1.640.005 ТО, 1991. - 175 с. - прототип.
7. Митрофанов Д.Г. Экспериментальные исследования параметров траекторных нестабильностей полета воздушных объектов. Воронеж. НПФ «САКВОЕЕ» ООО. Сборник докладов XV международной конференции «RLNC-2009». 2009. С. 1536-1547.
8. Митрофанов Д.Г. Исследование отражательных характеристик воздушных объектов в условиях проявления траекторных нестабильностей. Серпухов. Известия института инженерной физики, 2009. №3 (13). С. 37-46.
9. Кук Ч., Бернфельд М. Радиолокационные сигналы. Теория и применение / Перевод с англ. под ред. B.C. Кельзона. М.: Сов. радио, 1971. - 568 с.
10. Марпл мл. С.Л. Цифровой спектральный анализ и его приложения. Пер. с англ. С.И. Хабарова. М.: Мир, 1990. 584 с.


Изобретение относится к области радиолокации и может быть использовано в радиолокационных станциях обнаружения и целеуказания, а также в радиолокационных станциях (РЛС) сопровождения для измерения истинного значения радиальной скорости цели. Достигаемый технический результат - однозначное измерение радиальной скорости воздушной цели в когерентно-импульсной РЛС. Указанный результат достигается на основе использования взаимной корреляционной функции (ВКФ) отраженного и опорного сигналов, при этом по числу максимумов во ВКФ устанавливают диапазон, в котором находится истинное значение доплеровской частоты отраженного сигнала, а затем определяют истинное значение радиальной скорости цели. Для проведения корреляционного анализа отраженных сигналов их сначала переводят в цифровую форму, а затем объединяют в единый синтезированный цифровой сигнал, длительность которого равна периоду повторения импульсов РЛС. После расчета ВКФ синтезированного сигнала ее огибающую пропускают через низкочастотный фильтр и подсчитывают число ее глобальных максимумов N. Это позволяет определить диапазон частот, в котором находится истинная доплеровская частота отраженного сигнала. Преимущество предлагаемого способа заключается в обеспечении возможности однозначного измерения радиальной скорости воздушной цели в когерентно-импульсной РЛС при частотах Доплера, превышающих значение частоты повторения зондирующих сверхвысокочастотных импульсов. 12 ил.
Способ однозначного измерения радиальной скорости цели в когерентно-импульсной радиолокационной станции, включающий формирование в передающей системе когерентных зондирующих сверхвысокочастотных импульсов с частотой повторения Fп и длительностью τи, излучение данных импульсов помощью антенно-фидерной системы в пространство, поиск целей в зоне обнаружения когерентно-импульсной радиолокационной станции с помощью вращающейся антенны, прием антенной отраженных от цели сигналов, передачу отраженных сигналов из антенны в приемную систему, усиление отраженных сигналов, передачу отраженных сигналов через фильтр зеркальной частоты на преобразователь частоты, понижение частоты отраженных сигналов до промежуточной частоты порядка десятков мегагерц, усиление отраженных сигналов на промежуточной частоте в усилителе промежуточной частоты, формирование с помощью фазового детектора последовательности импульсов, промоделированных по амплитуде частотой биений, выделение частоты биений на одном из фильтровых каналов гребенки из Ζ фильтровых каналов, нахождение в гребенке из Ζ фильтровых каналов такого z-го фильтрового канала, в котором сигнал превышает пороговую величину и пороговый элемент вырабатывает сигнал логической единицы, преобразование z-го номера фильтрового канала в код неоднозначной радиальной скорости цели Vрн с помощью преобразователя номера канала в код скорости,
отличающийся тем, что отраженные от цели сигналы на выходе усилителя промежуточной частоты преобразуют с помощью аналого-цифрового преобразователя в цифровую форму, причем каждый сигнал дискретизируют с периодом дискретизации Δt, вычисляемым по формуле Δt=1/(4fпч+4fд макс), где fпч - величина промежуточной частоты, fд макс - максимально возможное значение доплеровской добавки к несущей частоте зондирующего сигнала, получают в пределах каждого отраженного сигнала К цифровых дискретных отсчетов, именуемых для краткости дискретами, причем Κ=τи/Δt, последовательно запоминают в памяти цифровой вычислительной системы оцифрованные дискреты в течение M периодов повторения, причем число M рассчитывают по формуле Μ=Λ(Тп/τи), где Λ(*) - функция округления до следующего целого числа, из оцифрованных дискретов отраженных сигналов M периодов повторения составляют непрерывную последовательность, в которой первому дискрету очередного отраженного сигнала предшествует последний дискрет предыдущего отраженного сигнала, всего в последовательности получают Х=КМ элементов, формируют из них цифровой массив данных M1, выражающий значениями своих элементов амплитудную огибающую M соединенных между собой последовательно принятых отраженных сигналов, одновременно с этим зондирующие сигналы, просочившиеся в приемное устройство радиолокационной станции, оцифровывают аналогичным образом в этих же Μ периодах на выходе усилителя промежуточной частоты, аналогично объединяют оцифрованные дискреты Μ зондирующих сигналов в непрерывную последовательность и создают из них аналогичный цифровой массив данных М2 из X элементов, выражающий значениями своих элементов амплитудную огибающую Μ соединенных между собой последовательно просочившихся в приемное устройство зондирующих сигналов, создают в памяти цифровой вычислительной системы массив R из (2Х-1) элементов rj для запоминания значений взаимной корреляционной функции, по окончании формирования массивов M1 и М2 с помощью цифровой вычислительной системы производят вычисление j-x элементов rj взаимной корреляционной функции массивов M1 и М2 по формуле
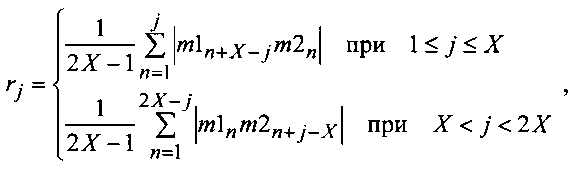
где m1i - значение i-гo элемента массива M1; m2i - значение i-го элемента массива М2, записанную в цифровой форме в виде элементов массива R взаимную корреляционную функцию подвергают низкочастотной фильтрации с помощью цифрового низкочастотного фильтра, в результате чего выделяют огибающую взаимной корреляционной функции, в выделенной огибающей взаимной корреляционной функции определяют количество ее максимумов N, используя найденное количество максимумов N корреляционной функции, определяют нижнюю границу Fн истинного диапазона доплеровской частоты отраженного от цели сигнала по формуле
Fн=(N-1)Fп,
величину Fн преобразуют в нижнюю границу Vн скоростного диапазона по формуле
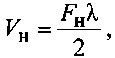
где λ - длина волны излучаемых сигналов, величину Vн нижней границы скоростного диапазона преобразуют в код нижней границы скоростного диапазона, суммируют код неоднозначной радиальной скорости цели с кодом нижней границы скоростного диапазона и получают код истинного значения радиальной скорости цели.
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Техническое описание | |||
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| СПОСОБ ИЗМЕРЕНИЯ СКОРОСТИ ДВИЖЕНИЯ ОБЪЕКТА | 2003 |
|
RU2247395C1 |
| ДОПЛЕРОВСКИЙ ФАЗОМЕТР МНОГОЧАСТОТНЫХ СИГНАЛОВ | 2000 |
|
RU2165627C1 |
| Фазометр доплеровского набега фазы радиоимпульсных сигналов | 1990 |
|
SU1748086A1 |
| US 6147638 A, 14.11.2000 | |||
| US 7119732 B1, 10.10.2006 | |||
| JP 4245422 B2, 25.03.2009. | |||
Авторы
Даты
2016-02-10—Публикация
2014-10-30—Подача