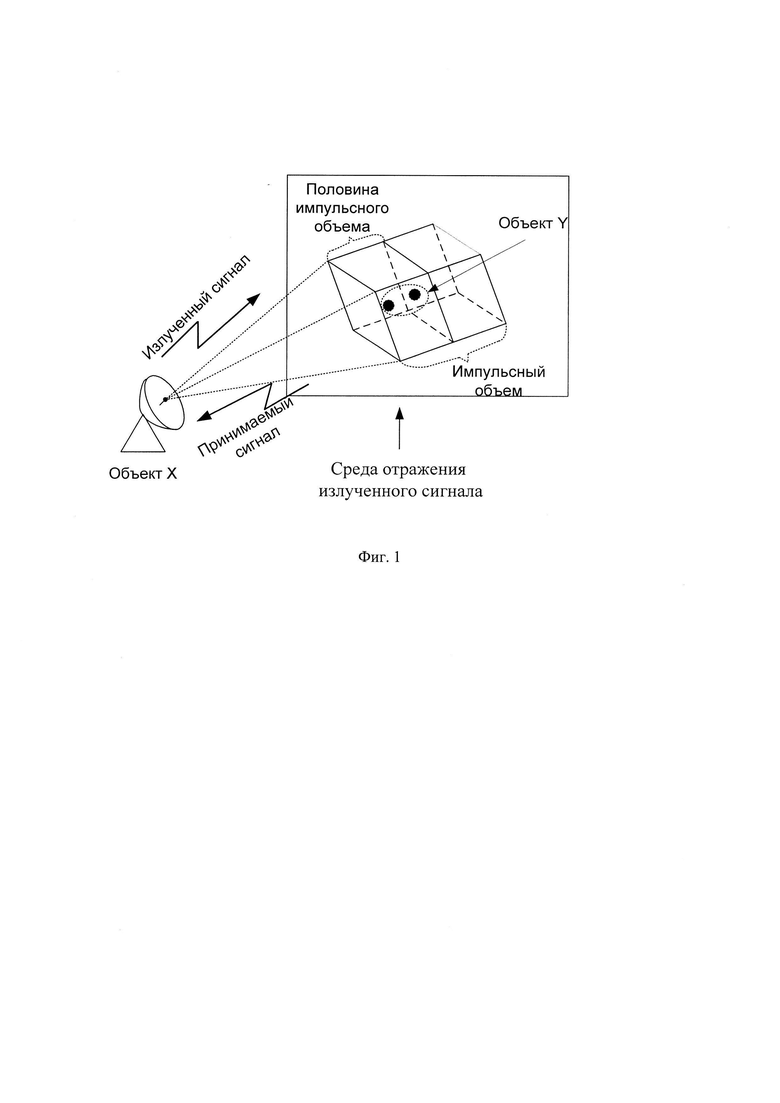
Изобретение относится к теории сверхрелеевского разрешения, восстановления сигналов и предназначено для разрешения отдельных объектов отражающих излученный сигнал радиолокатором по дальности, находящиеся при этом в половине импульсного объема формируемого параметрами излученного сигнала (фиг. 1).
Известен способ разрешения отдельных источников отражения излученного сигнала радиолокатором основанный на инверсной фильтрации [1].
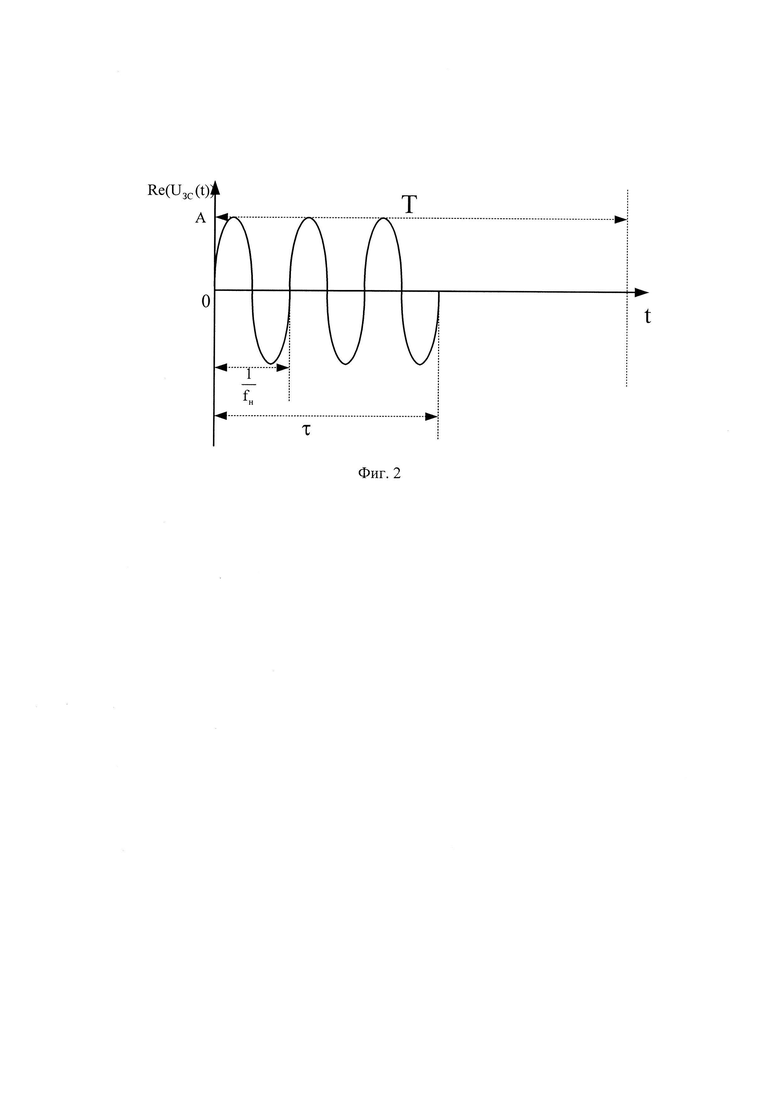
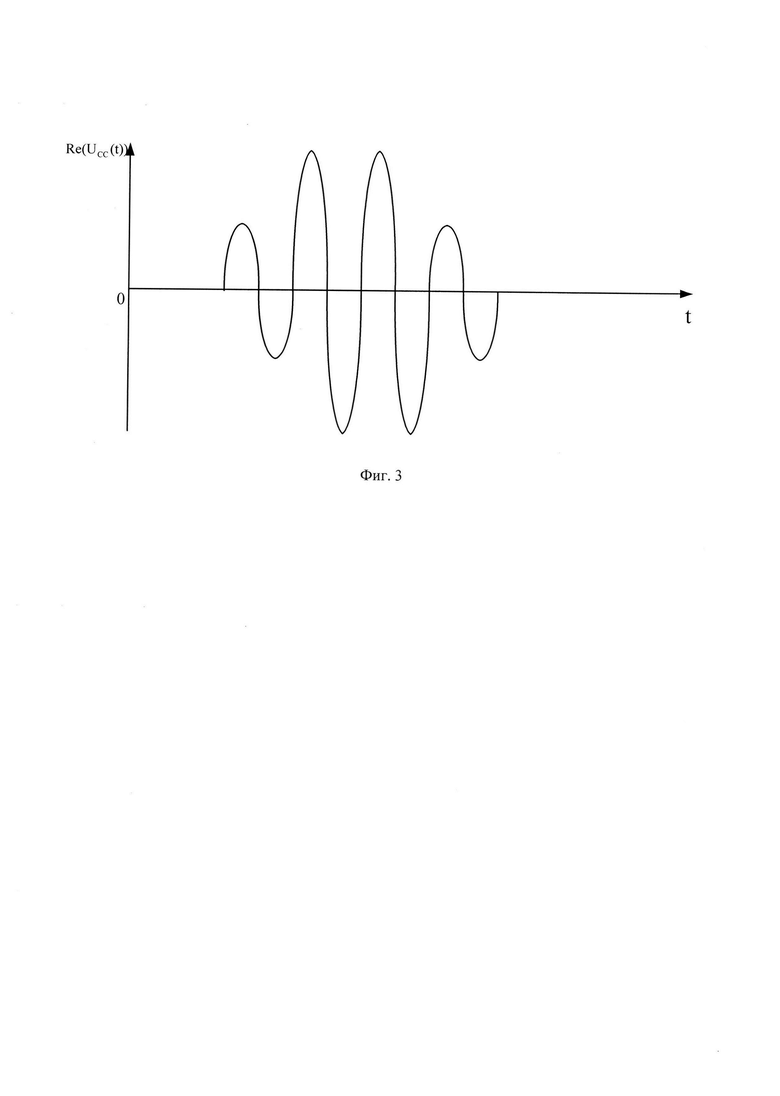
Способ заключается в том, что с помощью приемо-передатчика радиолокатора (объект X) из первой точки пространства излучают в свободное пространство зондирующий сигнал (ЗС) (по умолчанию в комплексном виде) UЗС(t), который представляет собой простой одиночный радиоимпульс (ПОРИ) длительностью τ и амплитудой А на несущей частоте fн, с периодом повторения Т (фиг. 2) (Re - оператор выделения действительной части комплексного сигнала). Объектом Y, представляющим собой L источников отражения ЗС (для примера 2), во второй точке пространства осуществляется отражение ЗС (фиг. 1). В результате на входе приемника радиолокатора (объект X) формируется суммарный сигнал (СС) UCC(t), отраженный от L источников отражения ЗС (фиг. 3).
После прохождения приемника (объекта X) СС оцифровывается при помощи АЦП с частотой дискретизации не менее FД=2⋅fн. Получившийся в результате набор данных, описывающий оцифрованный СС (ОСС), поступает в ЭВМ, где по мере поступления данных с АЦП осуществляют формирование генерального массива данных Uприем ограниченного временным интервалом длительностью Δ. Причем величина Δ равна Т, а число элементов в нем N определяется по формуле
N=Δ⋅Fд,
где Fд - частота дискретизации АЦП.
В результате ОСС представляет собой массив данных Uприемn, где (n=1…N).
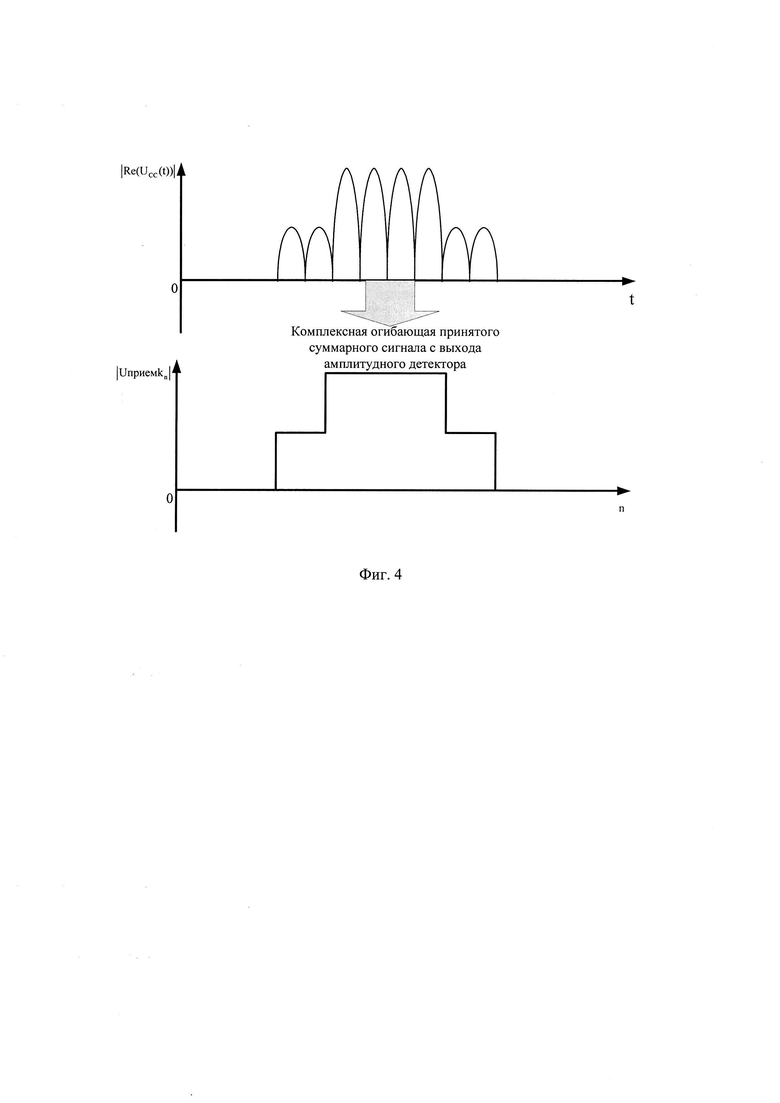
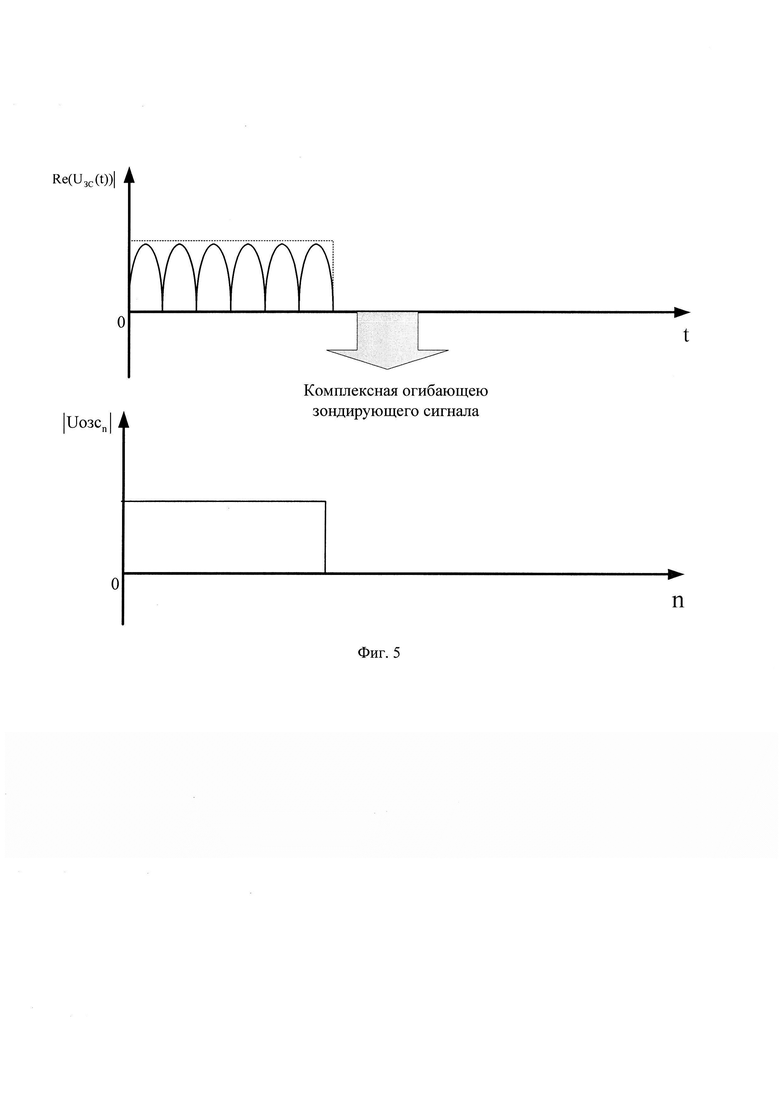
Далее оцифрованный СС (Uприемn) подают на амплитудный детектор, с выхода которого снимают оцифрованную комплексную огибающею принятого суммарного сигнала, значения которой записывают в массив Uприемkn (фиг. 4).
Массив Uприемkn подвергаются корреляционной обработки по формуле
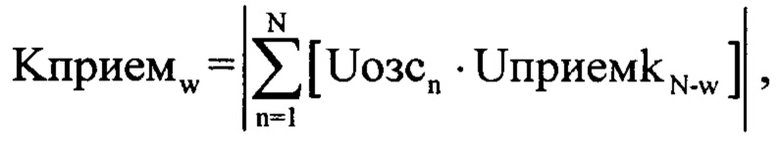
где Uозсn - комплексная огибающая оцифрованного зондирующего сигнала размерностью (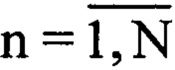 ), a w=1…N (фиг. 5); |…| - модуль.
), a w=1…N (фиг. 5); |…| - модуль.
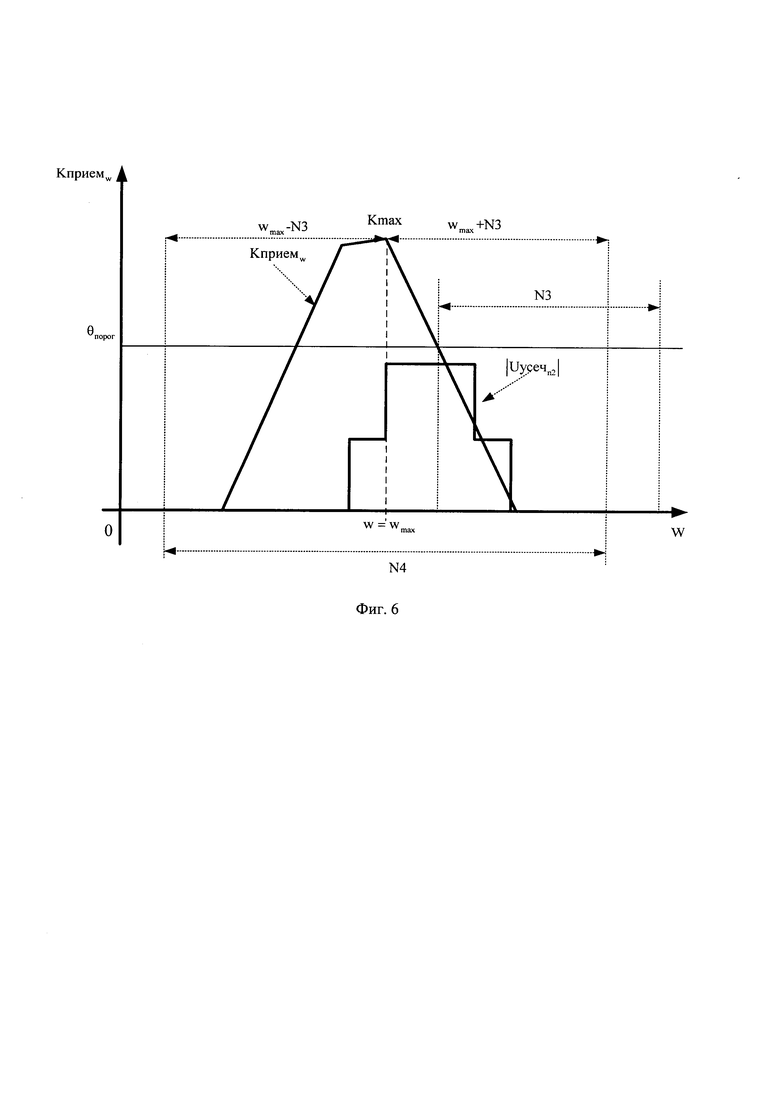
В последующем используют заранее рассчитанное пороговое значение θпорог (зависящее от отношения сигнал/шум) и сравнивают его с каждым значением массива Kприемw. При выполнении условия превышения порога θпорог значениями массива Kприемw и прекращении превышения порога θпорог значениями массива Kприемw в течение интервала N3=FД⋅2⋅τ принимают решение о наличии (обнаружении) в массиве Kприемw ОСС.
После чего определяют максимальное значение Kmax в массиве Kприемw и соответствующее ему значение w=wmax, а затем формируют усеченный массив Kусечw2 длительностью N4=2⋅N3+1(w2=1…N4). Усеченный массив Kусечw2 формируют из элементов массива Kприемw с 1-го по N3-й из отчетов от wmax-N3, а с N3+1-го по N4 из элементов wmax+N3. Полученный массив Kусечw2 записывают в память ЭВМ. После чего формируют усеченный массив Uусечn2 длительностью N4=2⋅N3+1 (n2=1…N4). Усеченный массив Uусечn2 формируют из элементов массива Uприемkn с 1-го по N3-й из отчетов от wmax-N3, а с N3+1-го по N4 из элементов wmax+N3 (фиг. 6).
Параллельно формируют укороченный массив Uозсуn2 состоящий из элементов массива Uозсn с 1-го по N4 (N>>N4).
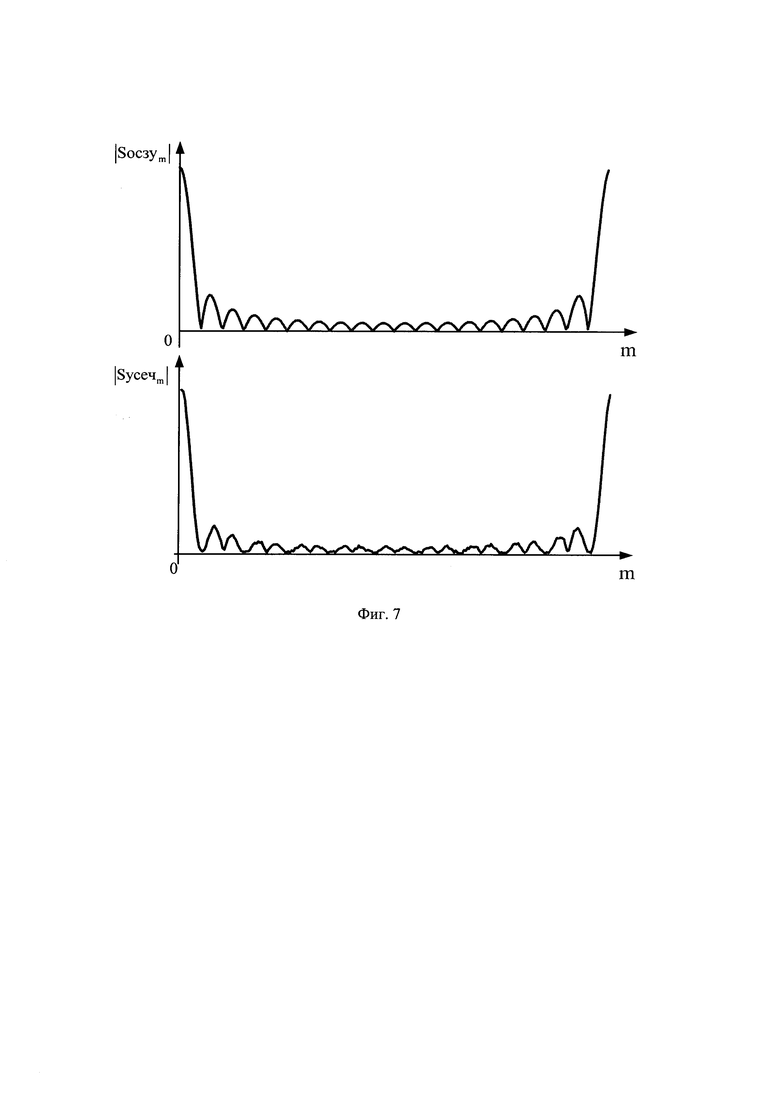
В последующем массивы Uозсуn2 и Uусечn2 подвергают дискретному прямому преобразованию Фурье [2] с использованием формул (фиг. 7):
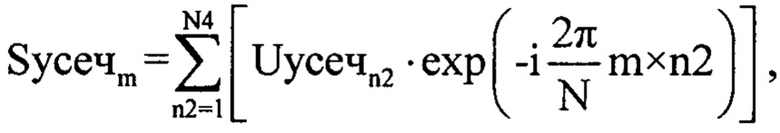
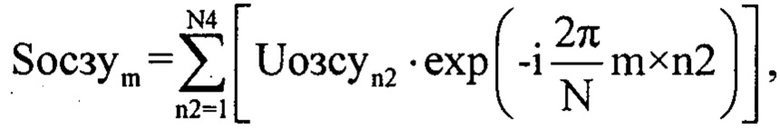
где n2 - номер отчета во временной области, m - номер отчета в частотной области m=1…N4; Syceчm - значение комплексной амплитуды m-го отсчета спектра комплексной огибающей оцифрованного суммарного сигнала для массива Uусечn2; Sосзуm - значение комплексной амплитуды m-го отсчета спектра комплексной огибающей оцифрованного зондирующего сигнала для массива Uозсуn2.
После чего формируют частотную характеристику инверсного фильтра путем деления полученных оцифрованных спектров Syceчm и Sосзуm по формуле:
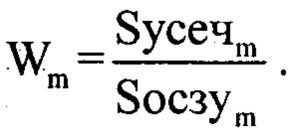
Результат деления представляет собой частотную характеристику инверсного фильтра, который подвергают дискретному обратному преобразованию Фурье [2] по формуле:
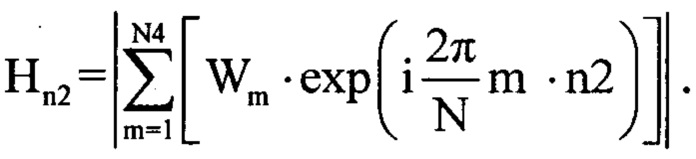
В результате одномерный массив Hn2 будет являться импульсной характеристикой среды отражения излученного сигнала радиолокатором, а ее отклики несут в себе информацию количестве источников отражения ЗС L и их взаимном удаления друг от друга.
Для принятия решения о количестве источников отражения ЗС L и их взаимном удаления друг от друга полученный одномерный массив Hn2 подвергают нормировке по формуле:
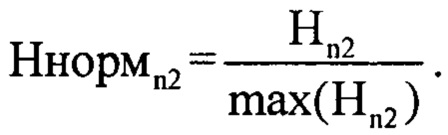
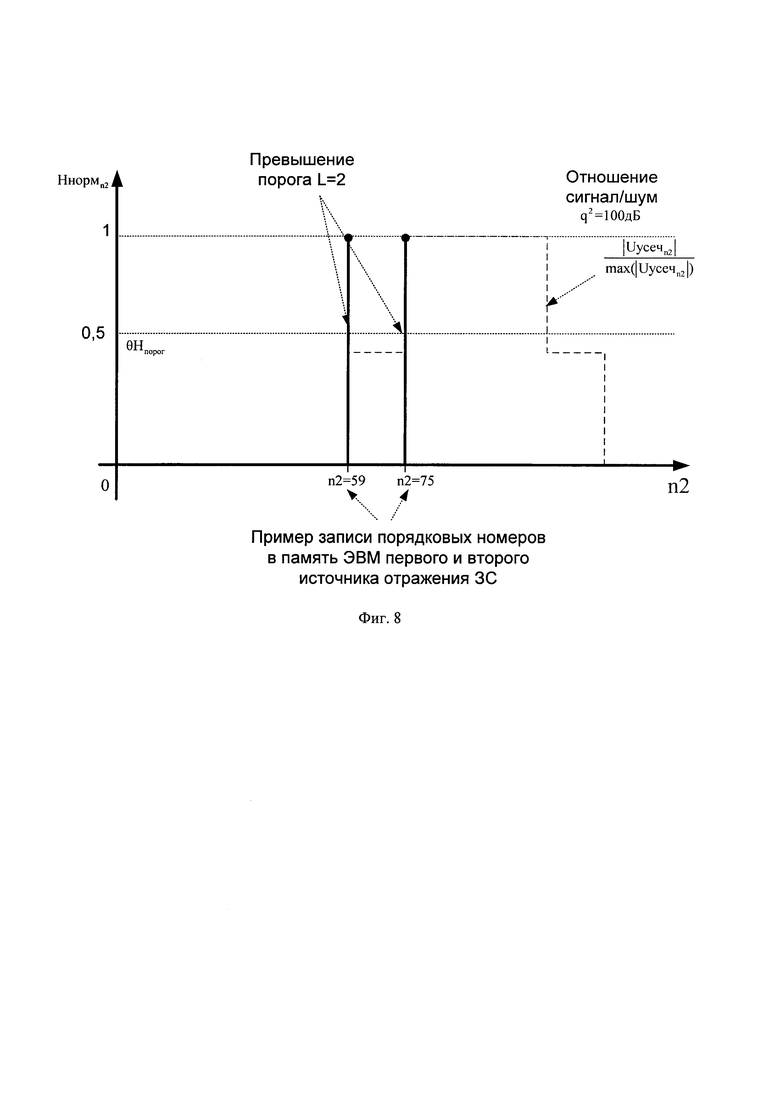
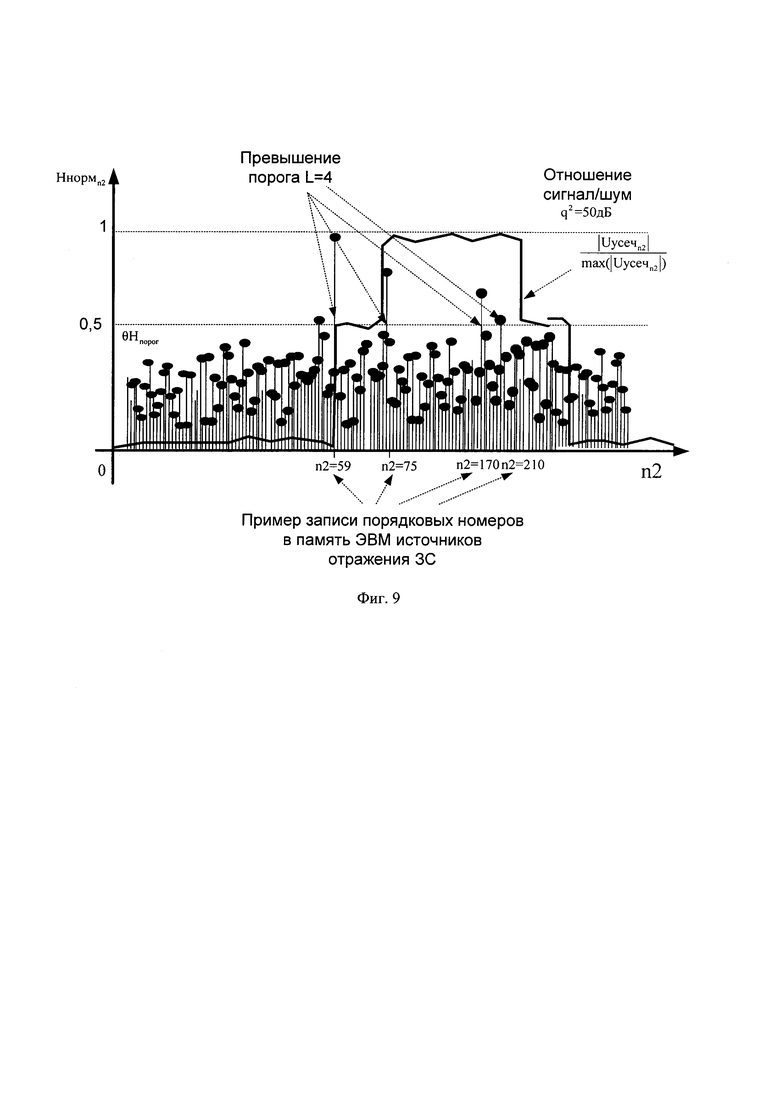
В качестве порогового значения θНпорог (в общем случае определяется вероятностью ложного разрешения F [3]) принимают величину равную 0.5 (для примера) и сравнивают величину θНпорог с каждым значением соответствующего нормированного массива Ннормn2. В случае превышении порога θНпорог значениями массива Ннормn2, количество превышений считается равным L и их порядковые номера pz=n2 записывается в память ЭВМ (фиг. 8).
Для расчета дальности до каждого источника отражения ЗС используют специальную зависимость:
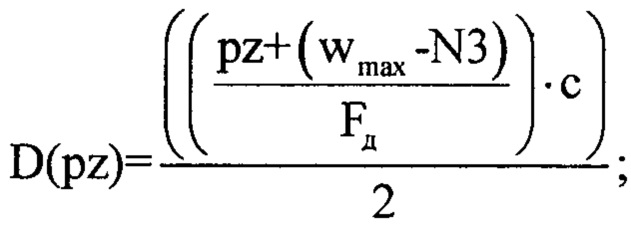
где с - скорость света равная 3⋅108 м/с.
Сущность способа, а именно сущность процесса разрешения источников отражения ЗС L, заключается в делении амплитуд спектров ОСС и ОЗС с последующим обратным дискретным преобразованием Фурье.
Недостатком данного способа разрешения источников отражения ЗС является чрезвычайно слабая устойчивость к шумам различной интенсивности (фиг. 9) (работоспособность сохраняется при отношении сигнал/шум от 50 дБ), так как комплексные амплитуды спектра огибающей ОЗС имею значения близкие к нулю, что после операции деления приводит к нелинейному росту ложных составляющих импульсной характеристике среды отражения излученного сигнала Ннормn2. Данный факт в свою очередь приводит к слабой помехоустойчивости, а как следствие и разрешающей способности данного способа.
Известен Способ повышения разрешающей способности радиолокатора по дальности за счет инверсной фильтрации [4].
Способ заключается в том, что с помощью приемо-передатчика радиолокатора (объект X) из первой точки пространства излучают в свободное пространство зондирующий сигнал (ЗС) UЗС(t), который представляет собой простой одиночный радиоимпульс (ПОРИ) длительностью τ и амплитудой А на несущей частоте fн, с периодом повторения Т (фиг. 2). Объектом Y, представляющим собой L источников отражения (для примера 2) ЗС, во второй точке пространства осуществляется отражение ЗС. В результате на входе приемника радиолокатора (объект X) формируется суммарный сигнал (СС) UCC(t), отраженный от L источников отражения ЗС (фиг. 3).
После прохождения приемника (объекта X) СС оцифровывается при помощи АЦП с частотой дискретизации не менее FД=2⋅fн. Получившийся в результате набор данных, описывающий оцифрованный СС (ОСС), поступает в ЭВМ, где по мере поступления данных с АЦП осуществляют формирование генерального массива данных Uприем ограниченного временным интервалом длительностью Δ. Причем величина Δ равна Т, а число элементов в нем N определяется по формуле
N=Δ⋅Fд,
где Fд - частота дискретизации АЦП.
В результате ОСС представляет собой массив данных Uприемn, где (n=1…N).
Далее оцифрованный СС (Uприемn) подают на амплитудный детектор, с выхода которого снимают оцифрованную комплексную огибающею принятого суммарного сигнала, значения которой записывают в массив Uприемkn (фиг. 4).
Массив Uприемkn подвергаются корреляционной обработки по формуле
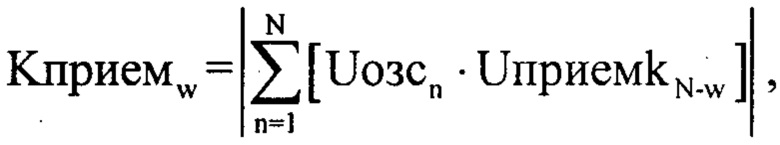
где Uозсn - комплексная огибающая оцифрованного зондирующего сигнала размерностью (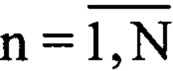 ), a w=1…N (фиг. 5).
), a w=1…N (фиг. 5).
В последующем используют заранее рассчитанное пороговое значение θпорог (зависящее от отношения сигнал/шум) и сравнивают его с каждым значением массива Kприемw. При выполнении условия превышения порога θпорог значениями массива Kприемw и прекращении превышения порога θпорог значениями массива Kприемw в течение интервала N3=FД⋅2⋅τ принимают решение о наличии в массиве Kприемw ОСС.
После чего определяют максимальное значение Kmax в массиве Kприемw и соответствующее ему значение w=wmax, а затем формируют усеченный массив Kусечw2 длительностью N4=2⋅N3+1(w2=1…N4). Усеченный массив Kyceчw2 формируют из элементов массива Kприемw c 1-го по N3-й из отчетов от wmax-N3, а с N3+1-го по N4 из элементов wmax+N3. Полученный массив Kyceчw2 записывают в память ЭВМ. После чего формируют усеченный массив Uусечn2 длительностью N4=2⋅N3+1 (n2=1…N4). Усеченный массив Uусечn2 формируют из элементов массива Uприемkn с 1-го по N3-й из отчетов от wmax-N3, а с N3+1-го по N4 из элементов wmax+N3 (фиг. 6).
Параллельно формируют укороченный массив Uозсуn2 состоящий из элементов массива Uозсn с 1-го по N4 (N>>N4).
В последующем массивы Uозсуn2 и Uусечn2 подвергают дискретному прямому преобразованию Фурье [2] с использованием формул (фиг. 7):
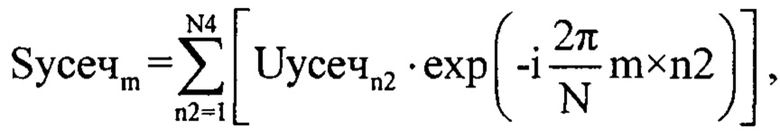
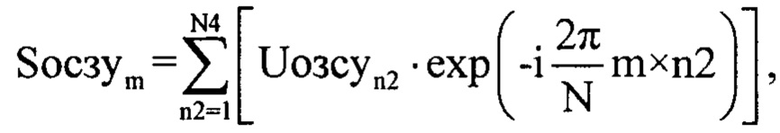
где n2 - номер отчета во временной области, m - номер отчета в частотной области m=1…N4; Syceчm - значение комплексной амплитуды m-го отсчета спектра комплексной огибающей оцифрованного суммарного сигнала для массива Uусечn2; Socзym - значение комплексной амплитуды m-го отсчета спектра комплексной огибающей оцифрованного зондирующего сигнала для массива Uозсуn2.
После чего формируют специальный массив Socзykm элементы которого заполняются по следующему правилу:
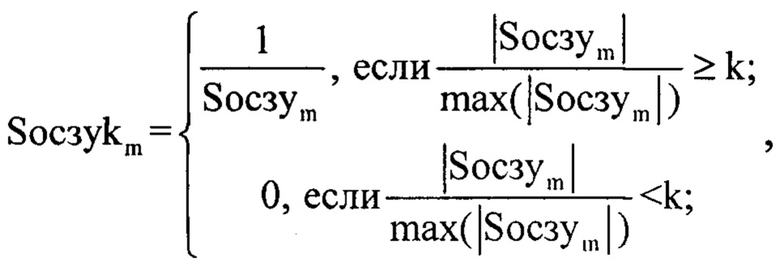
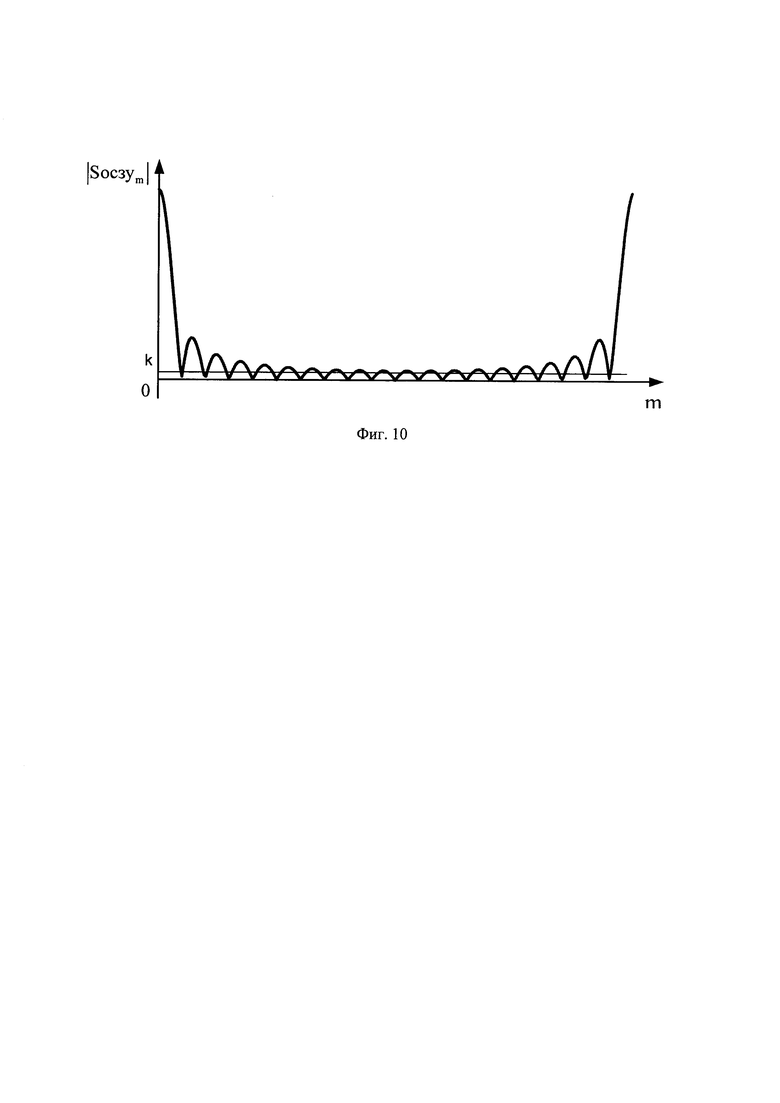
где k - уровень ограничения модуля нормированного спектра комплексной огибающей оцифрованного зондирующего сигнала для массива Uозсуn2(фиг. 10).
Уровень ограничения к выбирается по специальному правилу:
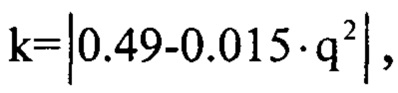
где q2 - отношение сигнал/шум в дБ.
После чего формируют частотную характеристику инверсного фильтра путем умножения полученных оцифрованных спектров Syceчm и Socзykm по формуле:
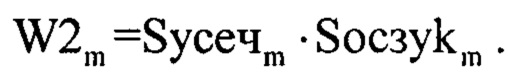
Результат умножения представляет собой модифицированную частотную характеристику инверсного фильтра, который подвергают дискретному обратному преобразованию Фурье [2] по формуле:
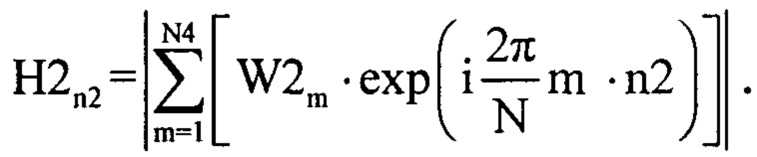
В результате массив H2n2 будет являться сглаженной импульсной характеристикой среды отражения излученного сигнала радиолокатором, а ее отклики несут в себе информацию количестве источников отражения ЗС L и их взаимном удаления друг от друга.
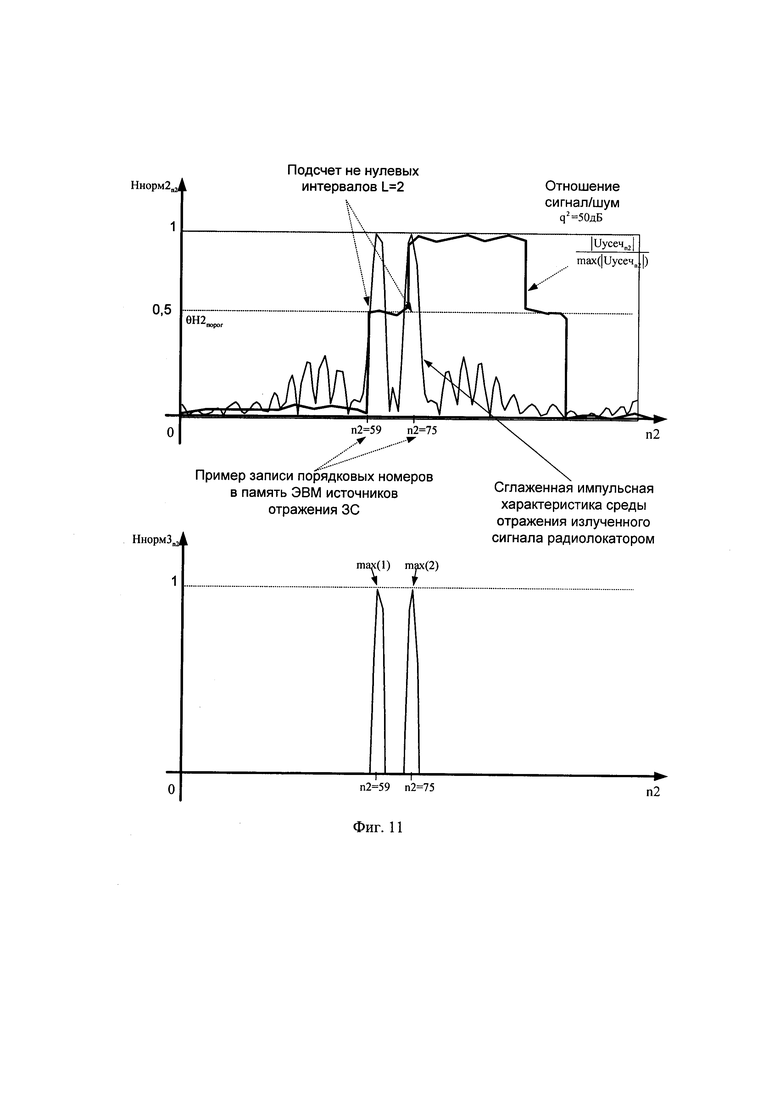
Для принятия решения о количестве источников отражения ЗС L и их взаимном удаления друг от друга полученный массив H2n2 подвергают нормировке по формуле (фиг. 11):
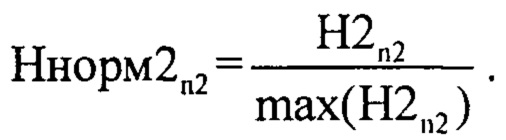
В качестве порогового значения θН2порог (в общем случае определяется вероятностью ложного разрешения F [3]) принимают величину равную 0.5 (для примера) и сравнивают величину θН2порог с каждым значением соответствующего нормированного массива Ннорм2n2, при этом предварительно формируют массив Ннорм3n2 в элементы которого записывают значения массива Ннорм2n2 превысившего порог θН2порог по специальному правилу:

После чего последовательно осуществляют подсчет не нулевых интервалов (которые принимают за L) («число перегибов») значений в массиве Ннорм3n2 по специальному правилу:

где L1 - нулевая переменная, необходимая для последовательного подсчета не нулевых интервалов (которые принимают за L) значений массива Ннорм3n2; пока n2 изменяется от 1 до N4-2 - означает последовательное изменение переменной n2 и далее используется по аналогии для других переменных.
Стоит отметить, что в каждом не нулевом интервале находится максимум и их порядковые номера pz2=n2, которые записываются в память ЭВМ (фиг. 11).
Для расчета дальности до каждого источника отражения ЗС используют специальную зависимость:
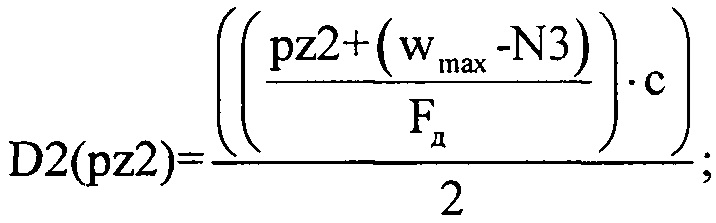
где с - скорость света равная 3⋅108 м/с.
Сущность повышения разрешающей способности данного способа заключается в исключении отдельных значений спектра комплексной огибающей ОЗС ниже некоторого порога. В результате появляется возможность не учитывать значения, комплексной огибающей ОЗС, близкие к нулю, что после операции обращения в Socзykm не приводит к нелинейному росту ложных составляющих импульсной характеристики среды отражения излученного сигнала Ннормn2 (достоверность сохраняется при отношении сигнал/шум от 35 дБ).
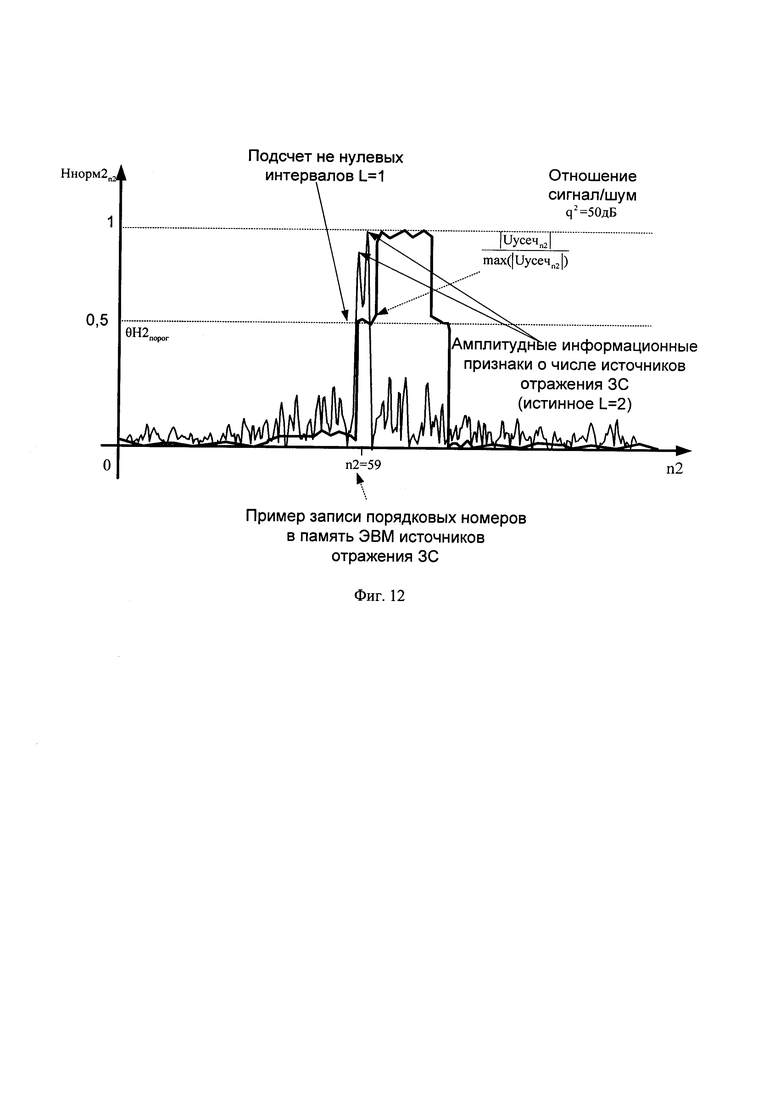
Недостатком данного способа повышение разрешающей способности радиолокатора по дальности является проблема выставления уровня ограничения к (в данном способе правило его выставления предложено авторами на основе эмпирического анализа для известного количества источников отражения ЗС). Уровень ограничения к оптимально может быть выставлен только при известном количестве источников отражения ЗС и их взаимном удалении друг от друга, а при близком расположении источников отражения ЗС (на пример 0.1 Релея интервала разрешения [3]) способ теряет свою разрешающую способность. Этот недостаток возникает из-за грубого подсчета не нулевых интервалов (которые принимают за L) значений в массиве Ннорм3n2, которые не учитывают амплитудные информационные признаки о числе источников отражения ЗС (фиг. 12).
Известен способ обеспечения высокой разрешающей способности радиолокатора по дальности за счет выбора оптимального параметра регуляризации инверсного фильтра [6].
В данном способе для устранения недостатков способа [4] предлагается с помощью приемо-передатчика радиолокатора (объект X) из первой точки пространства излучать в свободное пространство зондирующий сигнал (ЗС) U3C(t), который представляет собой простой одиночный радиоимпульс (ПОРИ) длительностью τ и амплитудой А на несущей частоте fн, с периодом повторения T (фиг. 2). При этом, объектом Y, представляющим собой L источников отражения (для примера 2) ЗС, во второй точке пространства осуществляется отражение ЗС. В результате на входе приемника радиолокатора (объект X) формируется суммарный сигнал (СС) UCC(t), отраженный от L источников отражения ЗС (фиг. 3).
После прохождения приемника (объекта X) СС оцифровывается при помощи АЦП с частотой дискретизации не менее FД=2⋅fн. Получившийся в результате набор данных, описывающий оцифрованный СС (ОСС), поступает в ЭВМ, где по мере поступления данных с АЦП осуществляют формирование генерального массива данных Uприем ограниченного временным интервалом длительностью Δ. Причем величина Δ равна Т, а число элементов в нем N определяется по формуле
N=Δ⋅Fд,
где Fд - частота дискретизации АЦП.
В результате ОСС представляет собой массив данных Uприемn, где (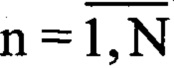 ).
).
Далее оцифрованный СС (Uприемn) подают на амплитудный детектор, с выхода которого снимают оцифрованную комплексную огибающею принятого суммарного сигнала, значения которой записывают в массив Uприемkn (фиг. 4).
Массив Uприемkn подвергаются корреляционной обработки по формуле
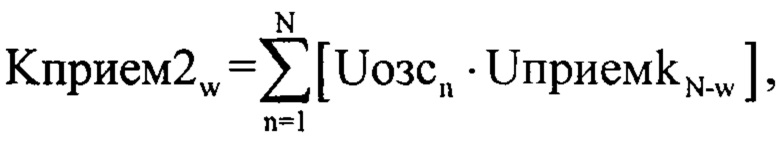
где Uозсn - комплексная огибающая оцифрованного зондирующего сигнала размерностью (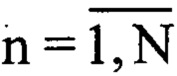 ), a w=1…N (фиг. 5).
), a w=1…N (фиг. 5).
В последующем используют заранее рассчитанное пороговое значение θпорог (зависящее от отношения сигнал/шум) и сравнивают его с каждым значением модуля массива |Kприем2w|. При выполнении условия превышения порога θпорог значениями модуля массива |Kприем2w| и прекращении превышения порога θпорог значениями модуля массива |Kприем2w| в течение интервала N3=FД⋅2⋅τ принимают решение о наличии в массиве Kприем2w ОСС.
После чего определяют максимальное значение Kmax в массиве |Kприемw| и соответствующее ему значение w=wmax, а затем формируют усеченный массив Kусеч2w2 длительностью N4=2⋅N3+1 (w2=1…N4). Усеченный массив Kусеч2w2 формируют из элементов массива Kприем2w с 1-го по N3-й из отчетов от wmax-N3, а с N3+1-го по N4 из элементов wmax+N3. Полученный массив Kyceч2w2 записывают в память ЭВМ. После чего формируют усеченный массив Uусечn2 длительностью N4=2⋅N3+1(n2=1…N4). Усеченный массив Uусечn2 формируют из элементов массива Uприемkn с 1-го по N3-й из отчетов от wmax-N3, а с N3+1-го по N4 из элементов wmax+N3 (фиг. 6).
Параллельно формируют укороченный массив Uозсуn2 состоящий из элементов массива Uозсn с 1-го по N4 (N>>N4).
В последующем массивы Uозсуn2 и Uусечn2 подвергают дискретному прямому преобразованию Фурье [2] с использованием формул (фиг. 7):
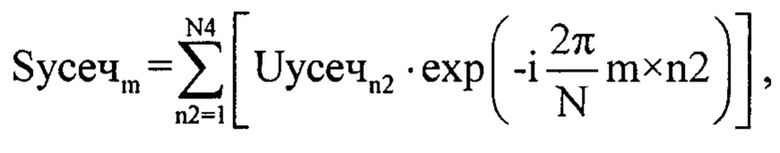
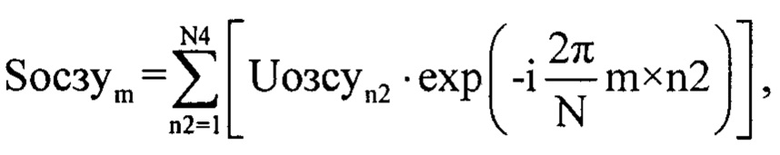
где n2 - номер отчета во временной области, m - номер отчета в частотной области m=1…N4; Syceчm - значение комплексной амплитуды m-го отсчета спектра комплексной огибающей оцифрованного суммарного сигнала для массива Uусечn2; Socзym - значение комплексной амплитуды m-го отсчета спектра комплексной огибающей оцифрованного зондирующего сигнала для массива Uозсуn2.
После чего формируют массив Socзy1m1 (m1=1…floor(N4/2)), где функция floor выполняет операцию округления до целого числа. В элементы данного массива записывают элементы массива |Socзym| с 1-го по floor(N4/2). Далее формируют нулевой массив Socзy2m1, в элементы которого записывают элементы массива |Socзym| с 1-го по floor(N4/2)-1 со сдвигом на один отсчет. К примеру, в 1-й элемент массива Socзy2m1 записывают 0, во второй элемент массива Socзy2m1 записывают 1-й элемент массива |Socзym|, в третий элемент массива Socзy2m1 записывают 2-й элемент массива |Socзym| и т.д. В результате массивы Socзy1m1 и Sосзу2m1 содержат элементы массива |Socзym|.
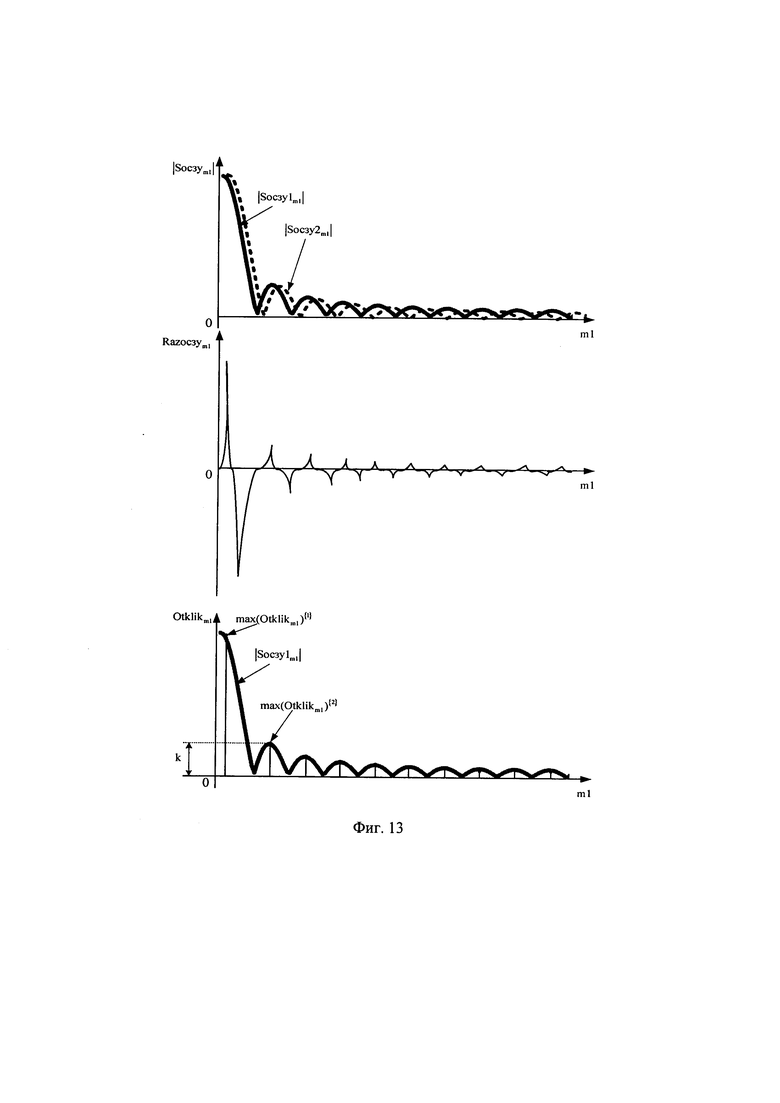
В дальнейшем определяют предел уровня ограничения спектра ОСС по специальному правилу, по которому в начале находят разницу между |Socзy1m1| и |Socзy2m1| по формуле:
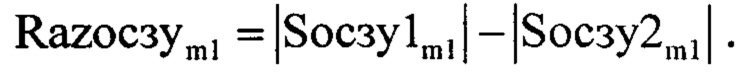
Результат разницы между |Socзy1m1| и |Socзy2m1| записанный в Razocзym1 подвергают процедуре поиска локальных максимумов, для этого формируют массив Otklikm1 в элементы которого записывают результат следующего выражения (фиг. 13):
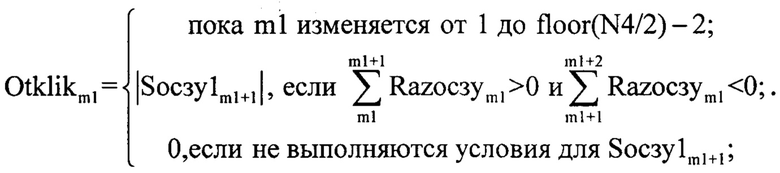
В полученном массиве Otklikm1 определяют второе максимальное значение, max(Otklikm1){2} которое присваивают переменной K (для ПРИ K=0.22),
данное значение и будет предельным при изменении уровня ограничения спектра ОСС k=0…K.
После чего определяют шаг Δk изменения k (для примера 0.01), и формируют двумерный массив SocзykKm,kk, при этом kk=0…K/Δk(kk=0…22).
Сформированный двумерный массив SocзykKm,kk имеет размерность N4 на K/Δk, где N4 количество строк двумерного массива SocзykKm,kk, a K/Δk его количество его столбцов. Элементы массива SocзykKm,kk заполняются по следующему выражению:

После чего формируют двумерный массив W2Km,kk, в строки которого записывают значения частотной характеристики инверсного фильтра, при различном уровне к ограничения спектра оцифрованного СС, путем последовательного перемножения каждого элемента двумерного массива SocзykKm,kk и элементов массива Socзykm по формуле:

Результат умножения представляет собой двумерный массив W2Km,kk в столбцы которого записаны модифицированные частотные характеристики инверсного фильтра при разном k. Далее, двумерный массив W2Km,kk подвергают дискретному обратному преобразованию Фурье [2], предварительно сформировав двумерный массив H2Kn2,kk, для записи в него результата преобразования по формуле:
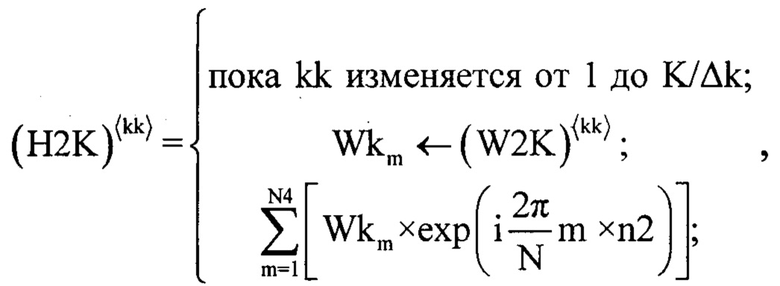
где Wkm - нулевой массив, в элементы которого последовательно записываются столбцы двумерного массива W2Km,kk при изменении kk, а (…)〈…〉 - оператор соответствующий выбору столбца двумерного массива.
В результате, будет получен двумерный массив H2Kn2,kk в столбцы которого записаны комплексные сглаженные импульсные характеристики (при изменении k) среды отражения излученного сигнала радиолокатором, а ее отклики несут в себе информацию о количестве источников отражения ЗС L и их взаимном удаления друг от друга.
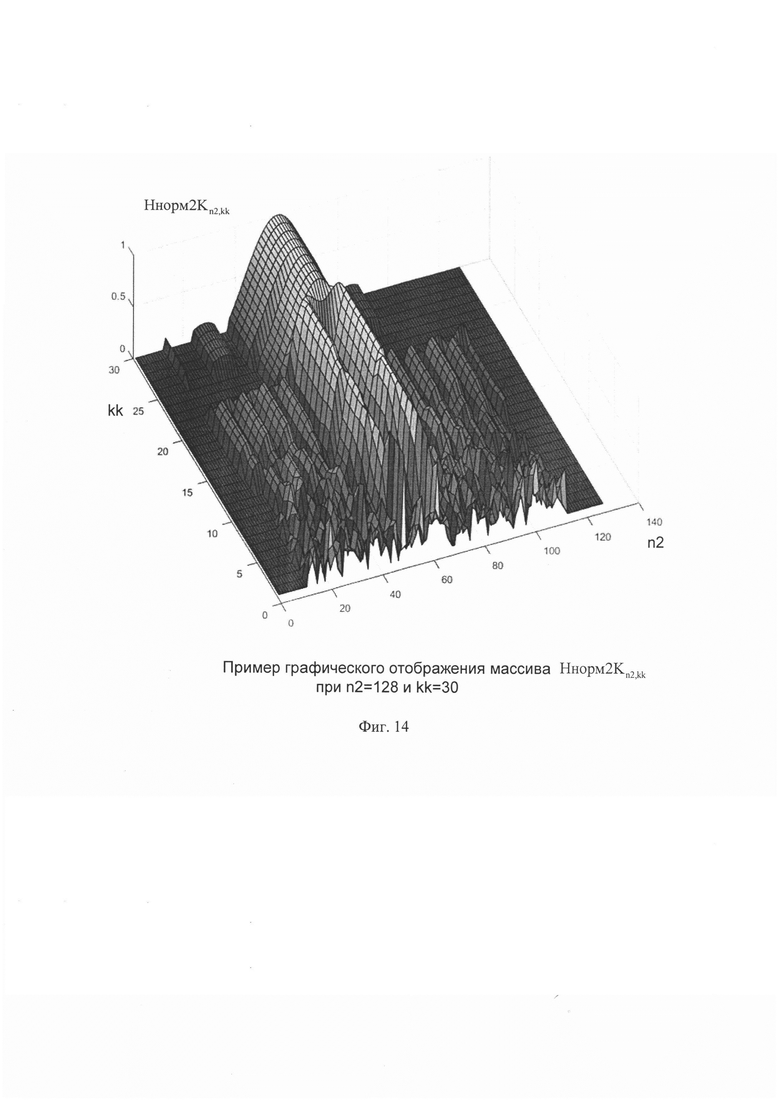
После чего, значения элементов двумерного массива H2Kn2,kk подвергают нормировке, предварительно сформировав двумерный массив Ннорм2Kn2,kk по формуле:
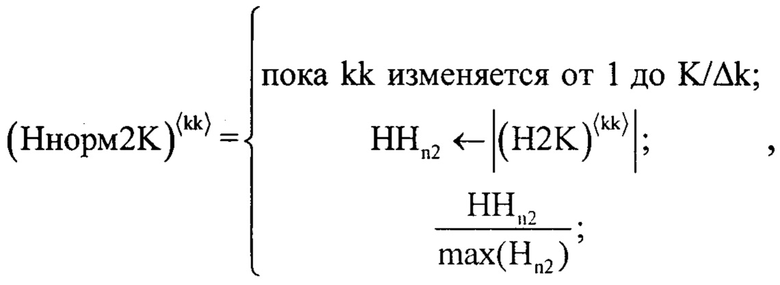
где HHn2 - нулевой массив, в элементы которого последовательно записываются столбцы двумерного массива H2Kn2,kk при изменении kk.
В результате, будет получен двумерный массив Ннорм2Kn2,kk в столбцы которого записаны нормированные сглаженные импульсные характеристики (при изменении k) среды отражения излученного сигнала радиолокатором (фиг. 14).
Формируют двумерный нулевой двумерный массив Ннорм2K2n2,kk, в столбцы которого записывают значения столбцов двумерного массива Ннорм2Kn2,kk сдвинутых на 1 отсчет. К примеру, 2-му элементу первого столбца массива Ннорм2K2n2,1 присваивают 1-й элемент первого столбца массива Ннорм2Kn2,1, 3-му элементу первого столбца массива Ннорм2K2n2,1 присваивают 2-й элемент первого столбца массива Ннорм2Kn2,1, 4-му элементу первого столбца массива Ннорм2K2n2,1 присваивают 3-й элемент первого столбца массива Ннорм2Kn2,1 и т.д., а в N4-му элементу первого столбца массива Ннорм2K2n2,1 присваивают N4-1-й элемент первого столбца массива Ннорм2Kn2,1 и т.д., для каждого kk-го столбца двумерного массива Ннорм2K2n2,kk и двумерного массива Ннорм2Kn2,kk.
В дальнейшем находят разницу между Ннорм2Kn2,kk и Ннорм2K2n2,kk по формуле:
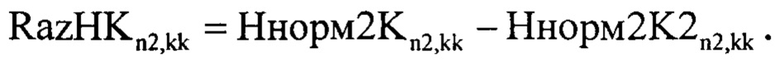
Результат разницы между Ннорм2Kn2,kk и Ннорм2K2n2,kk записанный в RazHKn2,kk подвергают процедуре поиска локальных максимумов, для этого формируют двумерный массив Otk1n2,kk в элементы которого записывают результат следующего выражения:

где M1n2 - нулевой массив, в элементы которого последовательно записываются элементы столбцов двумерного массива RazHKn2,kk при изменении kk; M2n2 - нулевой массив, в элементы которого последовательно записываются элементы столбцов двумерного массива Ннорм2K2n2,kk при изменении kk.
В результате, будет получен двумерный массив Otk1n2,kk (фиг. 15) в столбцы которого записаны локальные максимумы сглаженных импульсных характеристик (при изменении k) среды отражения излученного сигнала радиолокатором, отклики которых несут в себе информацию о количестве источников отражения ЗС L и их взаимном удаления друг от друга.
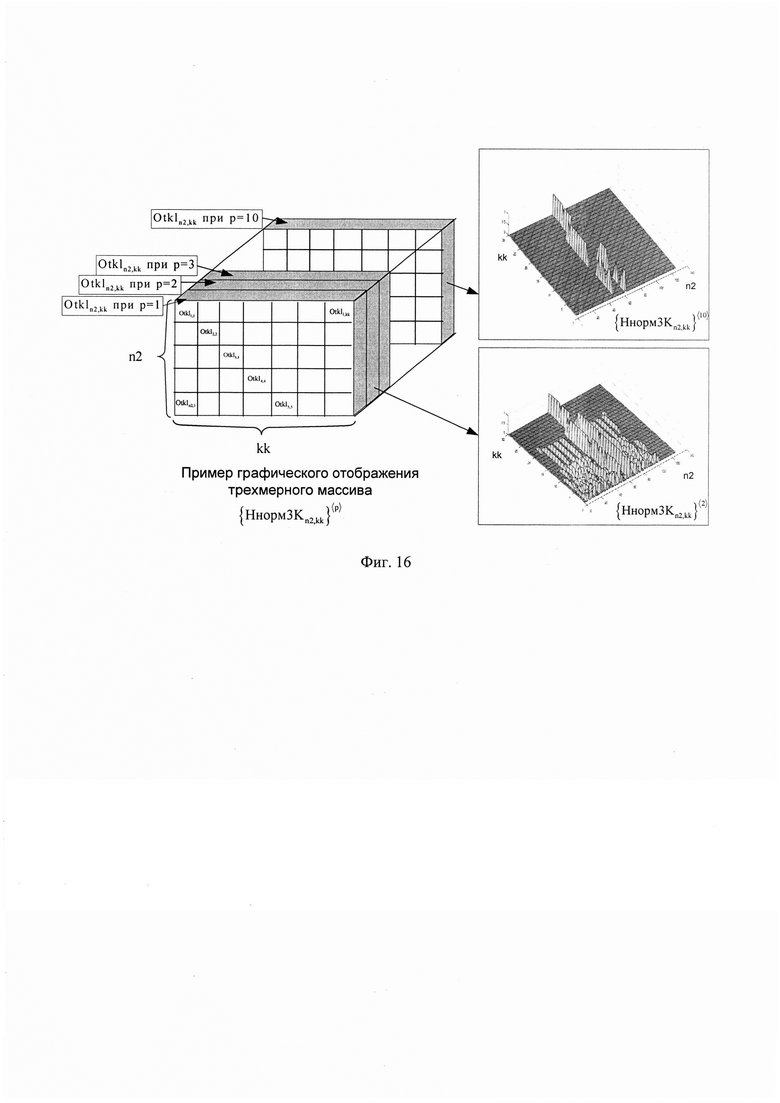
После чего, формируют трехмерный массив {Ннорм3Kn2,kk}〈p〉, где р=0…10. В элементы массива {Ннорм3Kn2,kk}〈p〉 записывают результат пороговой обработки двумерного массива Otk1n2,kk по следующему правилу:

где M3n2 - нулевой массив, в элементы которого последовательно записываются элементы столбцов двумерного массива RazHKn2,kk при изменении kk; {…}〈…〉 - оператор предназначенный для выбора элемента трехмерного массива или присвоения выбранному элементу трехмерного массива некоторого значения.
В результате, будет получен трехмерный массив {Ннорм3K}〈p〉 (фиг. 16) в элементы которого записаны результаты пороговой обработки двумерного массива Otk1n2,kk.
Для замены положительных результатов пороговой обработки двумерного массива Otk1n2,kk в трехмерном массиве {Ннорм3Kn2,kk}〈p〉 на комплексные значения, формируют нулевой трехмерный массив {НкомплKn2,kk}<p>элементы которого заполняются по следующему выражению:

После чего получают комплексную автокорреляционную функцию по выражению (АКФ):
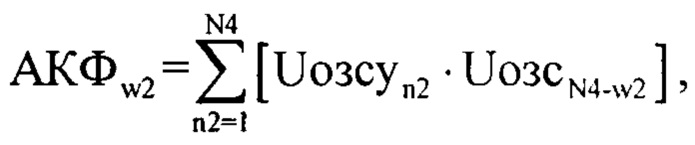
где w2=1…N4 (так как размерность w2=n2, в дальнейшем предложено использовать n2).
Для выбора наиболее правдоподобной импульсной характеристики среды отражения излученного сигнала радиолокатором на основе модифицированного метода наименьших квадратов предложено специальное правило, для реализации которого формируют массив МНКk,р элементы которого заполняются согласно выражению:

где  - математическая операция отражающая свертку двух одномерных массивов.
- математическая операция отражающая свертку двух одномерных массивов.
В результате, будет получен двумерный массив МНКkk,p (фиг. 17) в элементы которого записаны результаты разности корреляционной обработки принятого ОСС и корреляционной функции полученной в результате свертки kk на p вариантов импульсной характеристики среды отражения излученного сигнала радиолокатором с АКФ ОЗС. Поэтому минимум двумерного массива МНКkk,р будет определять значения kk на p в трехмерном массиве {НкомплKn2,kk}〈p〉 отвечающим правдоподобному значению комплексных амплитуд импульсной характеристики среды отражения излученного сигнала радиолокатором и их взаимному положению друг относительно друга.
В результате, определяют значение kk=const и p=const соответствующие минимуму двумерного массива MHКkk,р. После чего, для принятия решения, по выбранным kk и p выбирают правдоподобную импульсную характеристику среды отражения излученного сигнала радиолокатором для этого предварительно формируют массив НМНКn2 элементы которого заполняют согласно следующего выражения:
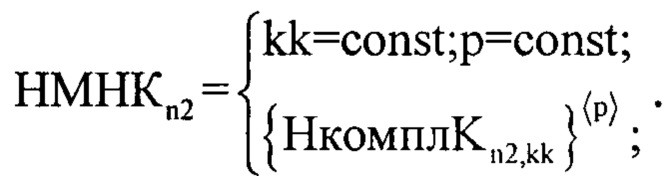
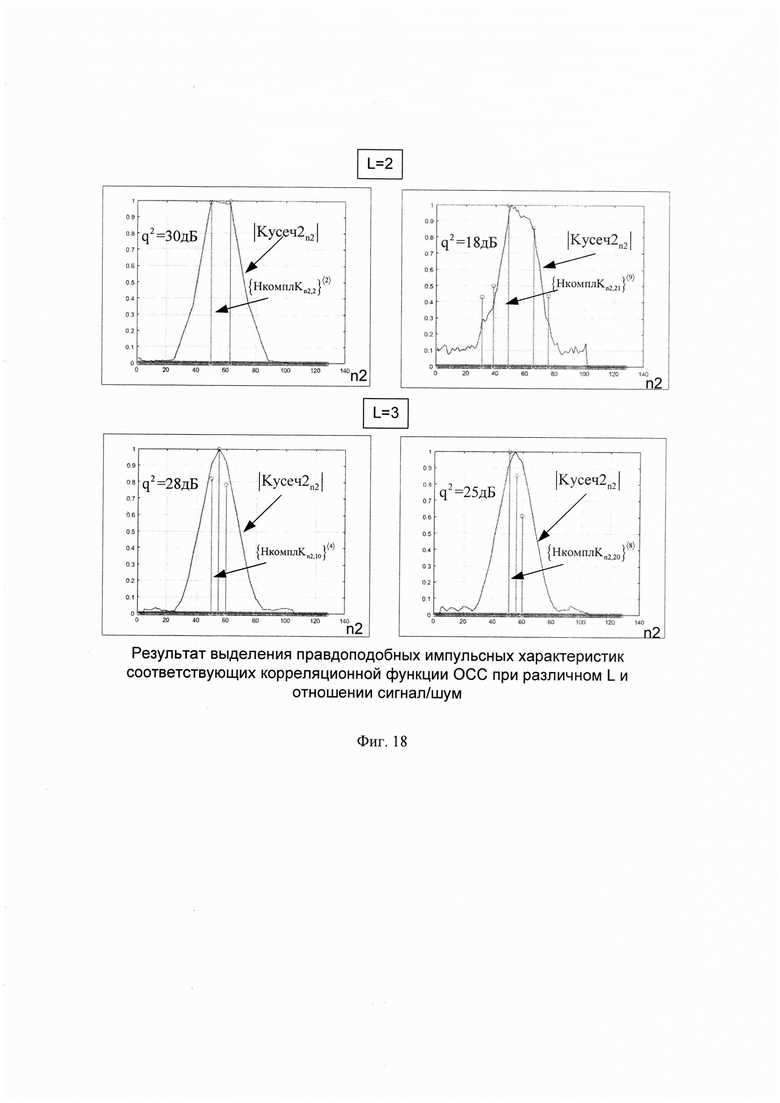
В качестве порогового значения θН3порог (в общем случае определяется вероятностью ложного разрешения F [3]) принимают величину равную 0.5 (для примера) и сравнивают величину θН3порог с каждым значением соответствующего нормированного массива |НМНКn2|. В случае превышении порога θН3порог значениями массива |НМНКn2|, количество превышений считается равным L и их порядковые номера pz3=n2 записывается в память ЭВМ (фиг. 18). Для расчета дальности до каждого источника отражения ЗС используют специальную зависимость:
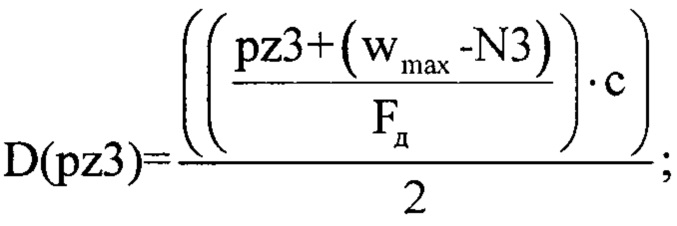
где с - скорость света равная 3⋅108 м/с.
Достоинством данного способа является отсутствие необходимости знать число источников отражения ЗС и их взаимное удаление друг от друга. Предложенный способ легко реализуем и позволяет обеспечить высокую разрешающею способность радиолокатора по дальности при отношении сигнал/шум не менее 27 дБ.
Недостатком данного способа является не эффективное использование априорной информации имеющейся после обнаружения принимаемого сигнала, для реализации дальнейшей процедуры разрешения.
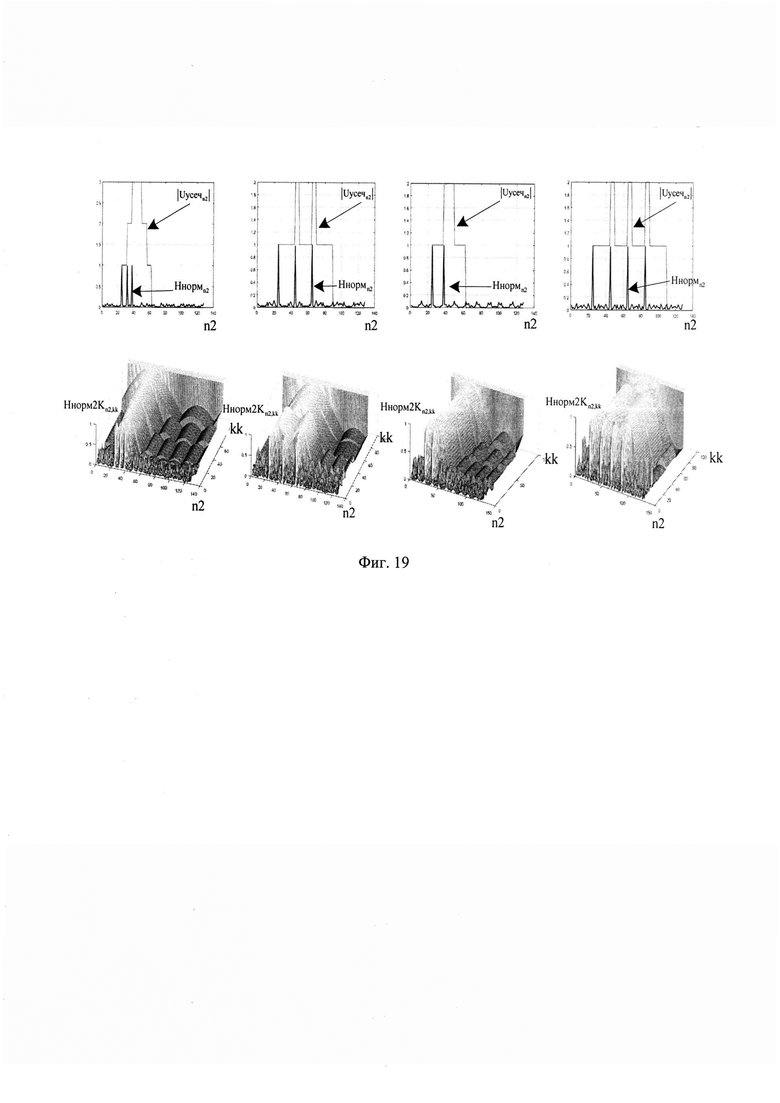
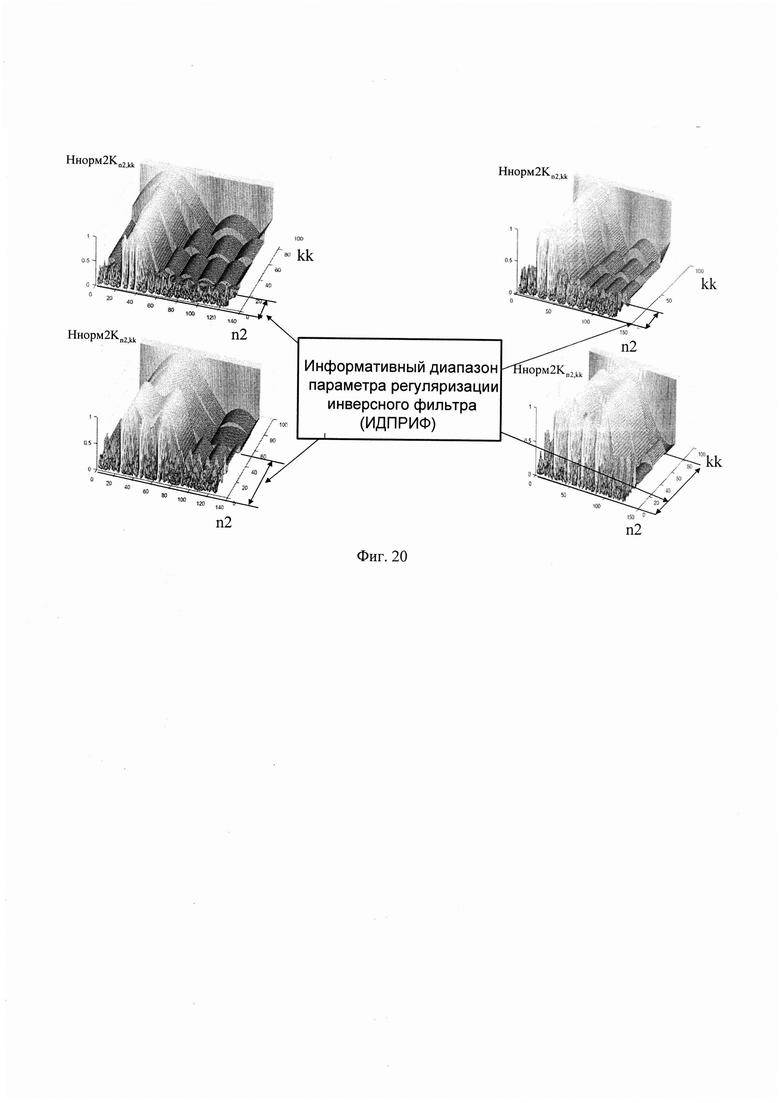
Так, к примеру, при анализе нормированных сглаженных импульсных характеристик (при изменении k) среды отражения излученного сигнала радиолокатором записанных в массив Ннорм2Kn2,kk, в условиях прихода СС отраженного от произвольного числа отражения ЗС видно, что информация о числе разрешаемых сигналов всегда теряется, при некотором уровне регуляризации после которого результат сглажен до одного явного максимума (фиг. 19). Данный эффект приводит к тому, что область возможных вариантов решений расширяется за счет включения информации не несущей практической пользы, приводя к необоснованному увеличению размерности массивов Ннорм2Kn2,kk, МНКkk,p и как следствие к снижению вероятности правильного разрешения отраженных сигналов по дальности, и увеличению требований к вычислительным затратам. Соответственно можно сделать вывод, что все значения ниже данного параметра регуляризации будут обладать полезной информацией о числе разрешаемых сигналов и их можно охарактеризовать, как данные входящие в некоторый информативный диапазон параметра регуляризации инверсного фильтра (ИДПРИФ) (фиг. 20).
Задачей изобретения является адаптивное обеспечение высокой разрешающей способности радиолокатора по дальности за счет оценивания информационного диапазона параметра регуляризации инверсного фильтра, не требующей априорно известной информации о количестве отражений ЗС и их взаимном удалении друг от друга, при отношении сигнал/шум не ниже, чем в способе[6].
Для решения поставленной задачи предлагается применить новый способ оценивания информационного диапазона параметра регуляризации инверсного фильтра. При данном подходе, для принятия решения об ограничении массива Ннорм2Kn2,kk предложено использовать априорно известную информацию, которая получена после обнаружения принимаемого сигнала, заключающаяся в наличии минимум одного сигнала отраженного от источника отражения ЗС.
Операции, выражающие существо предлагаемого способа адаптивного обеспечения высокой разрешающей способности радиолокатора по дальности за счет оценивания информационного диапазона параметра регуляризации инверсного фильтра, могут быть описаны следующей совокупностью последовательных действий:
1) излучение ЗС из первой точки пространства объектом X;
2) отражение ЗС средой отражения второй точкой пространства объектом Y;
3) прием и оцифровка аналого-цифровым преобразователем (АЦП) принимаемого СС;
4) обнаружением принимаемого СС отраженного второй точкой пространства объектом Y;
5) выделение интервала существования принимаемого ОСС;
6) выставление множества уровней ограничения спектра ОСС в пределах установленных специальным правилом;
7) отбор множества сглаженных импульсных характеристик среды отражения излученного ЗС принадлежащих ИДПРИФ, по специальному правилу.
8) выбор оптимального значения амплитуд из множества сглаженных импульсных характеристик среды отражения излученного ЗС радиолокатором и соответствующие им номера отсчетов принадлежащих ИДПРИФ на основе метода наименьших квадратов;
9) принятие решения о количестве источников отражения ЗС на основе пороговой обработки.
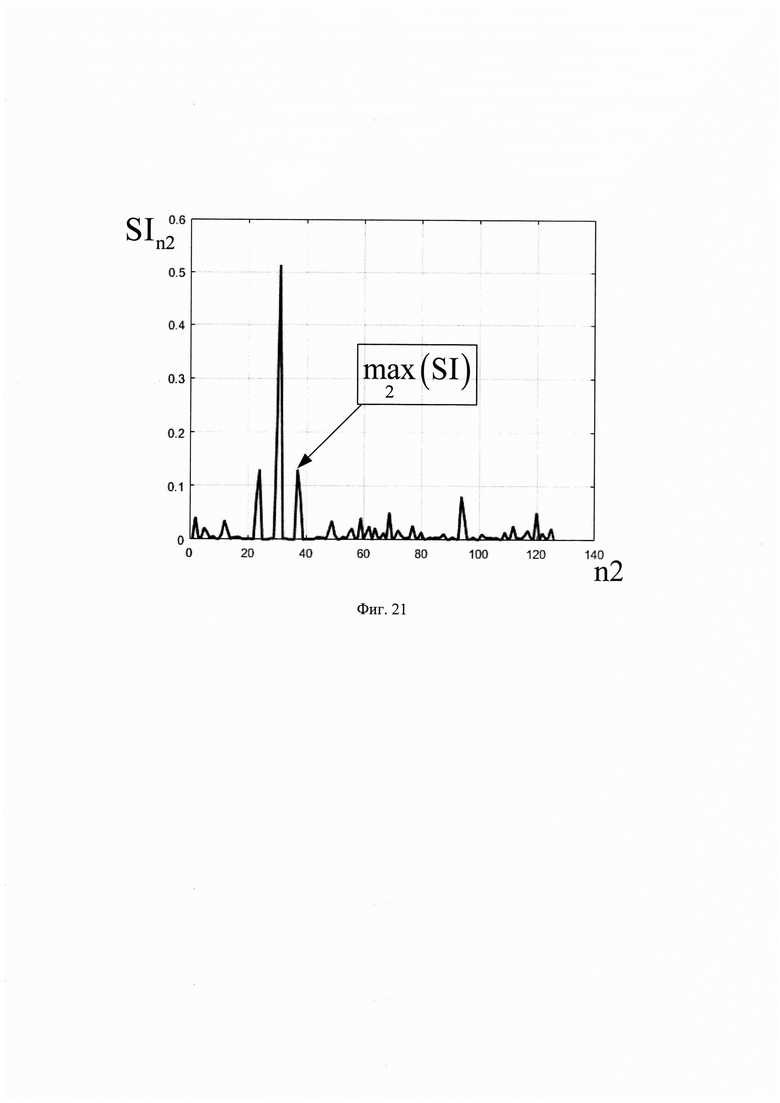
Рассмотрим последовательно процедуру адаптивного обеспечения высокой разрешающей способности радиолокатора по дальности за счет оценивания информационного диапазона параметра регуляризации инверсного фильтра, которая повторяется с пункта 1 по 6-й, как в способе [6] до получения двумерного массива Otk1n2,kk включительно (фиг. 15). После чего формируют информационный вектор, SIn2, учитывающий суммарный вклад локальных максимумов сглаженных импульсных характеристик (при изменении k) среды отражения излученного сигнала радиолокатором в каждом отсчете n2 по следующему правилу:
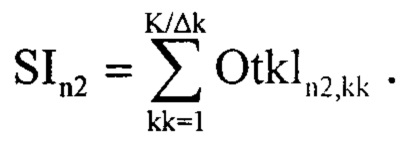
После чего запоминают значение амплитуды второго максимума 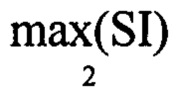 в векторе SIn2 (фиг. 21) и проводят бинаризацию массива Otk1n2,kk по следующему правилу:
в векторе SIn2 (фиг. 21) и проводят бинаризацию массива Otk1n2,kk по следующему правилу:

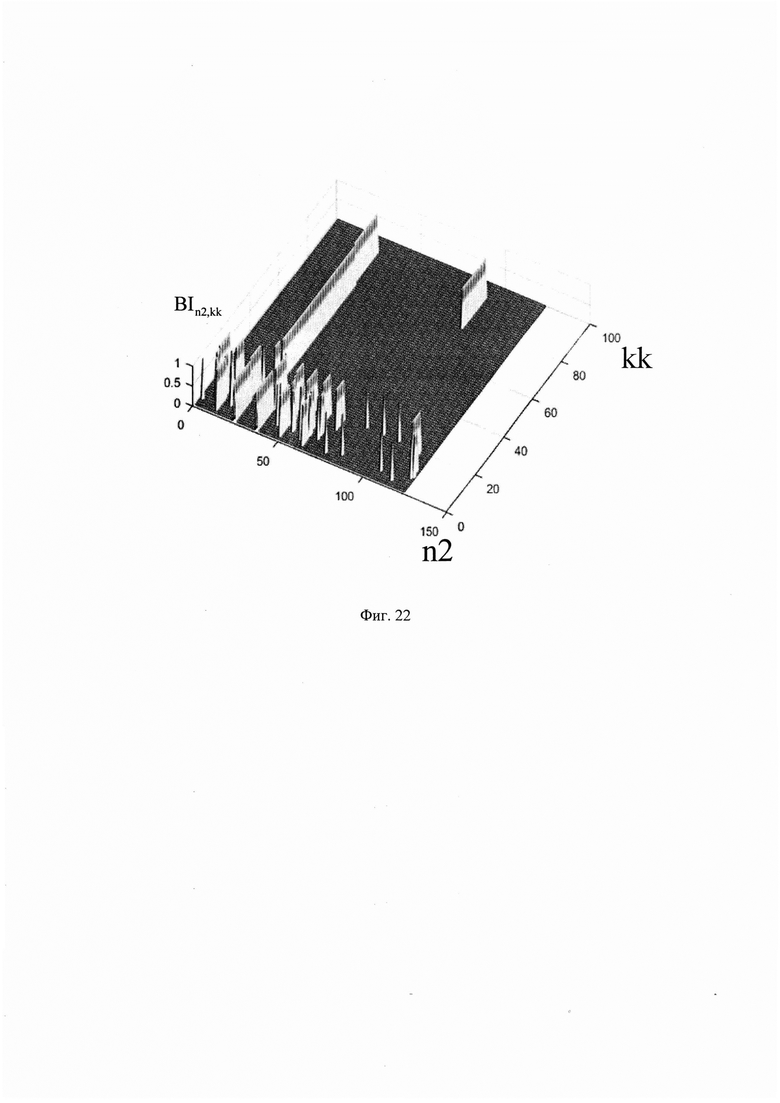
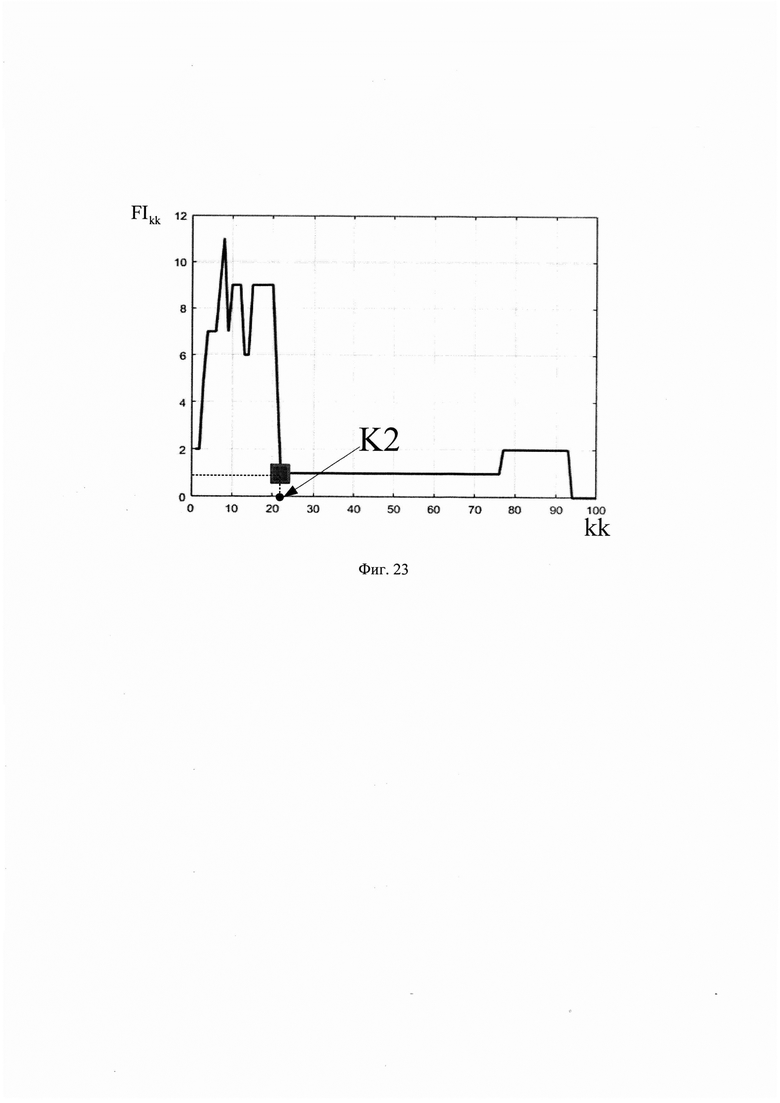
В результате бинаризации будет сформирован массив BIn2,kk (фиг. 22), в котором все значения локальных максимумов сглаженных импульсных характеристик (при изменении k) среды отражения излученного сигнала радиолокатором превысившие пороговое значение 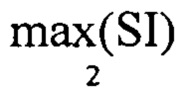 будут равны единицы. Данное условие необходимо, для анализа массива BIn2,kk по параметру kk. Оно наглядно показывает, где всего один отклик, а где несколько, что позволит провести отбор тех сглаженных импульсных характеристик (при изменении к) среды отражения излученного сигнала из массива Ннорм2Kn2,kk, которые несут в себе полезную информацию. Для этого формируют вектор информативности FIkk (фиг. 23) по следующему правилу:
будут равны единицы. Данное условие необходимо, для анализа массива BIn2,kk по параметру kk. Оно наглядно показывает, где всего один отклик, а где несколько, что позволит провести отбор тех сглаженных импульсных характеристик (при изменении к) среды отражения излученного сигнала из массива Ннорм2Kn2,kk, которые несут в себе полезную информацию. Для этого формируют вектор информативности FIkk (фиг. 23) по следующему правилу:
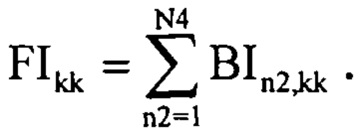
После чего определяют параметр ограничения K2 массива Ннорм2Kn2,kk по специальному правилу, для этого формируют вектор Ikkk согласно следующему выражению:
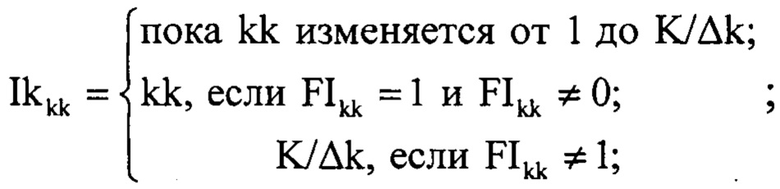
и определяют порядковый номер первого элемента вектора Ikkk равного 1 по формуле:
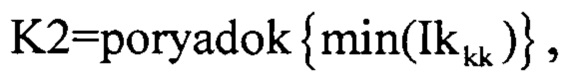
где poryadok{…} - оператор, определяющий порядковый номер первого элемента вектора Ikkk равного 1.
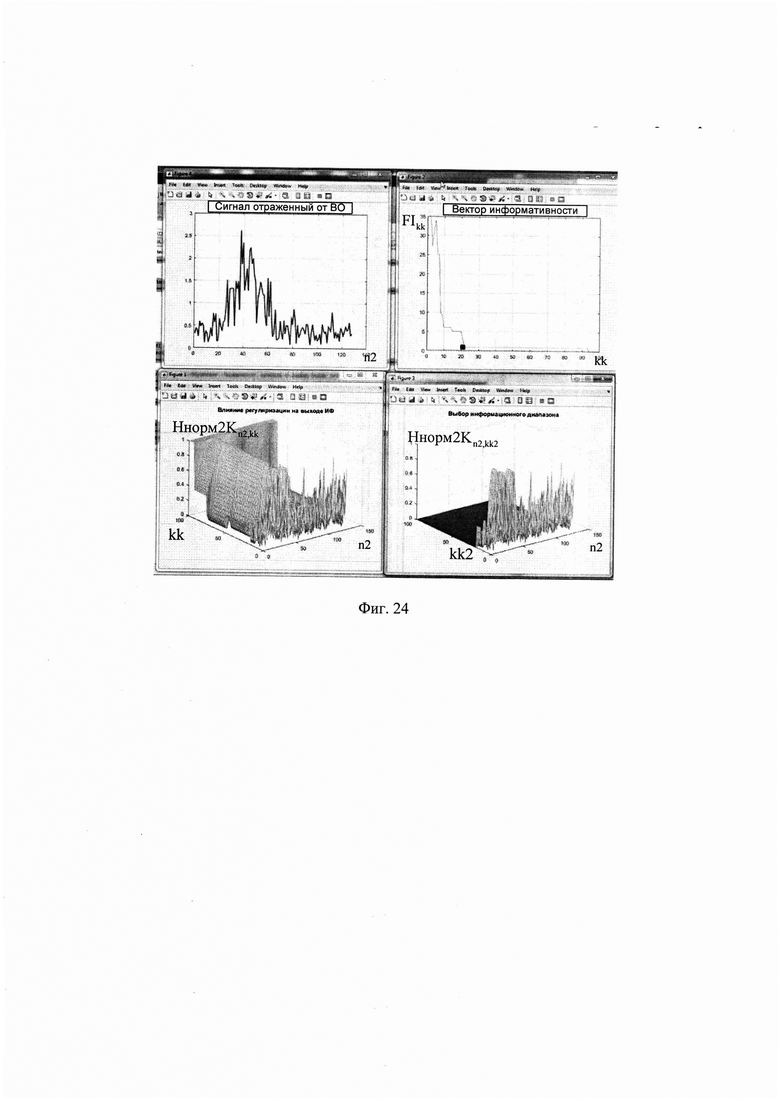
Результатом данных вычислений будет являться значение параметра регуляризации инверсного фильтра, выше которого полезная информация будет отсутствовать (фиг. 24), поэтому в дальнейшем используют массив Otk2n2,kk2, сформированный из массива Otk1n2,kk, но ограниченный по kk2, где kk2=0…K2.
После чего, формируют трехмерный массив {Ннорм3Kn2,kk2}〈р〉, где р=0…10. В элементы массива {Ннорм3Kn2,kk2}〈р〉 записывают результат пороговой обработки двумерного массива Otk2n2,kk2 по следующему правилу:

где M3n2 - нулевой массив, в элементы которого последовательно записываются элементы столбцов двумерного массива RazHKn2,kk2 при изменении kk2; {…}〈…〉 - оператор предназначенный для выбора элемента трехмерного массива или присвоения выбранному элементу трехмерного массива некоторого значения.
В результате, будет получен трехмерный массив {Ннорм3K}〈р〉 в элементы которого записаны результаты пороговой обработки двумерного массива Otk2n2,kk2.
Для замены положительных результатов пороговой обработки двумерного массива Otk2n2,kk2 в трехмерном массиве {Ннорм3Kn2,kk2}〈р〉 на комплексные значения, формируют нулевой трехмерный массив |НкомплKn2,kk2}〈р〉 элементы которого заполняются по следующему выражению:

После чего получают комплексную автокорреляционную функцию по выражению (АКФ):
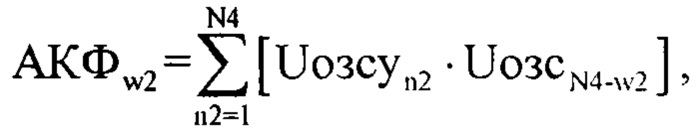
где w2=1…N4 (так как размерность w2=n2, в дальнейшем предложено использовать n2).
Для выбора наиболее правдоподобной импульсной характеристики среды отражения излученного сигнала радиолокатором на основе модифицированного метода наименьших квадратов предложено специальное правило, для реализации которого формируют массив МНКk,p элементы которого заполняются согласно выражению:

где  - математическая операция отражающая свертку двух одномерных массивов.
- математическая операция отражающая свертку двух одномерных массивов.
В результате, будет получен двумерный массив МНКkk2,p, в элементы которого записаны результаты разности корреляционной обработки принятого ОСС и корреляционной функции полученной в результате свертки kk2 на p вариантов импульсной характеристики среды отражения излученного сигнала радиолокатором с АКФ ОЗС. Поэтому минимум двумерного массива МНКkk,p будет определять значения kk2 на p в трехмерном массиве {НкомплKn2,kk2}〈р〉 отвечающим правдоподобному значению комплексных амплитуд импульсной характеристики среды отражения излученного сигнала радиолокатором и их взаимному положению друг относительно друга.
В результате, определяют значение kk2=const и p=const соответствующие минимуму двумерного массива MHKkk2,p. После чего, для принятия решения, по выбранным kk2 и p выбирают правдоподобную импульсную характеристику среды отражения излученного сигнала радиолокатором для этого предварительно формируют массив НМНКn2 элементы которого заполняют согласно следующего выражения:
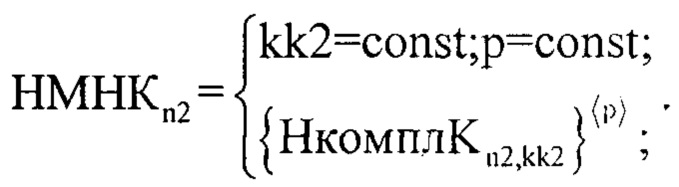
В качестве порогового значения θН3порог (в общем случае определяется вероятностью ложного разрешения F [3]) принимают величину равную 0.5 (для примера) и сравнивают величину θH3порог с каждым значением соответствующего нормированного массива |НМНКn2|. В случае превышении порога θH3порог значениями массива |НМНКn2|, количество превышений считается равным L и их порядковые номера pz3=n2 записывается в память ЭВМ. Для расчета дальности до каждого источника отражения ЗС используют специальную зависимость:
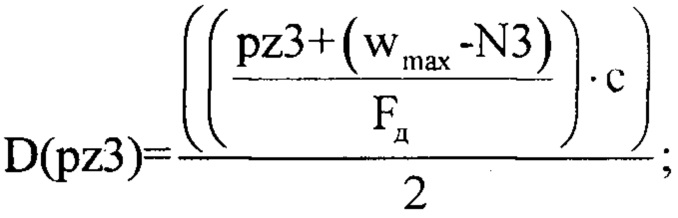
где с - скорость света равная 3⋅108 м/с.
Сущность способа адаптивного обеспечения высокой разрешающей способности радиолокатора по дальности за счет оценивания информационного диапазона параметра регуляризации инверсного фильтра заключается в следующем.
В известном способе [6] для достоверного принятия решения о количестве источников отражения ЗС и их взаимном удалении друг относительно друга по дальности, необходимо использовать последовательный перебор уровней ограничения спектра ОЗС и использовать весь набор сглаженных импульсных характеристик среды отражения излученного ЗС в дальнейшей обработке, что приводит к росту вычислительных затрат и возможному снижению помехоустойчивости.
Для решения указанного недостатка, с целью обеспечения адаптации разрешения по дальности предложено оценивать информационный диапазона параметра регуляризации инверсного фильтра, который будет включать в себя только те сглаженные импульсные характеристики среды отражения излученного ЗС, в которых есть информация о количестве ВО большем чем один.
Из описания способа следует, что в предлагаемом способе нет необходимости знать число источников отражения ЗС и их взаимное удаление друг от друга. Предложенный способ легко реализуем и позволяет обеспечить высокую разрешающею способность радиолокатора по дальности при отношении сигнал/шум не менее 24,6 дБ, за счет ограничения области возможных вариантов решений ИДПРИФ. Положительный технический эффект способа заключается в том, что при выделении ИДПРИФ возможно сокращение вычислительных затрат в среднем на 26% чем в способе [6].
ИСТОЧНИКИ ИНФОРМАЦИИ
1. Введение в контурный анализ. Приложения к обработке изображений и сигналов. Под ред. Я.А. Фурмана. М.: ФИЗМАТЛИТ, 2003. 592.
2. Смоленцев Н.К. Основы теории вейвлетов. Вейвлеты в MATLAB: Издание третье. - М.: Прикладная математика, 2008. - с. 39.
3. Чижов А.А. Сверхрэлеевское разрешение. Т. 1: Классический взгляд на проблему. М.: КРАСАНДР, 2010. - с. 96.
4. Семченков С.М., Печенев Е.А., Абраменков В.В. Повышение разрешающей способности радиолокатора по дальности за счет инверсной фильтрации. // Журнал сибирского федерального института энергетики и технологий. 2018. - 312.
5. Варюхин В.А. Основы теории многоканального анализа, Киев, ВАПВОСВ, 1993. 156.
6. Патент №2756291 (РФ). Способ обеспечения высокой разрешающей способности радиолокатора по дальности за счет выбора оптимального параметра регуляризации инверсного фильтра.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ обеспечения высокой разрешающей способности радиолокатора по дальности за счет выбора оптимального параметра регуляризации инверсного фильтра | 2021 |
|
RU2756291C1 |
| Способ формирования дальностного портрета, получаемого на основе использования сигналов с перестройкой частоты, от импульса к импульсу, за счет построения характеристики изменения радиальной скорости воздушного объекта | 2023 |
|
RU2815730C1 |
| Способ формирования дальностного портрета повышенной информативности на основе использования сигналов с перестройкой частоты от импульса к импульсу | 2023 |
|
RU2808449C1 |
| СПОСОБ ИЗВЛЕЧЕНИЯ ИЗ ДОПЛЕРОВСКИХ ПОРТРЕТОВ ВОЗДУШНЫХ ОБЪЕКТОВ ПРИЗНАКОВ ИДЕНТИФИКАЦИИ С ИСПОЛЬЗОВАНИЕМ МЕТОДА СВЕРХРАЗРЕШЕНИЯ | 2015 |
|
RU2589737C1 |
| Способ оценки пространственного размера воздушной цели по частотной протяженности доплеровского портрета | 2018 |
|
RU2679396C2 |
| Способ селекции реальных воздушных объектов на фоне помех, формируемых имитаторами вторичного излучения, за счет использования мобильного радиолокатора | 2021 |
|
RU2787471C1 |
| СПОСОБ ОДНОЗНАЧНОГО ИЗМЕРЕНИЯ РАДИАЛЬНОЙ СКОРОСТИ ЦЕЛИ В КОГЕРЕНТНО-ИМПУЛЬСНОЙ РАДИОЛОКАЦИОННОЙ СТАНЦИИ | 2014 |
|
RU2574079C1 |
| СПОСОБ ВНЕШНЕГО РАДИОЛОКАЦИОННОГО ВЫЯВЛЕНИЯ ФАКТА НАЛИЧИЯ ТРАЕКТОРНЫХ НЕСТАБИЛЬНОСТЕЙ ПОЛЕТА У ВОЗДУШНОГО ОБЪЕКТА ПО СТРУКТУРЕ ЕГО ИМПУЛЬСНОЙ ХАРАКТЕРИСТИКИ | 2014 |
|
RU2562060C1 |
| СПОСОБ ФОРМИРОВАНИЯ ИМПУЛЬСНОЙ ХАРАКТЕРИСТИКИ ВОЗДУШНОГО ОБЪЕКТА С ПОВЫШЕННОЙ ИНФОРМАТИВНОСТЬЮ НА УЧАСТКАХ ЕГО ПРОСТРАНСТВЕННО-УГЛОВОГО ЗАМИРАНИЯ | 2015 |
|
RU2603694C1 |
| СПОСОБ ПОСТРОЕНИЯ ДВУМЕРНОГО РАДИОЛОКАЦИОННОГО ИЗОБРАЖЕНИЯ ПРЯМОЛИНЕЙНО ЛЕТЯЩЕЙ ЦЕЛИ ПРИ МНОГОЧАСТОТНОМ УЗКОПОЛОСНОМ ЗОНДИРОВАНИИ | 1995 |
|
RU2099743C1 |


Изобретение относится к теории сверхрелеевского разрешения, восстановления сигналов и предназначено для разрешения отдельных объектов, отражающих излученный сигнал радиолокатором по дальности, находящихся при этом в половине импульсного объема, формируемого параметрами излученного сигнала. Техническим результатом является повышение разрешающей способности радиолокатора по дальности, не требующей априорно известной информации о количестве отражений зондирующего сигнала и их взаимном удалении друг от друга. В заявленном способе применяют анализ сглаженной импульсной характеристики среды отражения излученного радиолокатором сигнала. При данном подходе для принятия решения о числе отражений зондирующего сигнала используют процедуру оценивания информационного диапазона параметра регуляризации инверсного фильтра, из которого выбирают наиболее правдоподобное значение амплитуд отраженных сигналов и их взаимное расположение относительно друг друга. Для этого в способе применяют метод наименьших квадратов, а полученный результат подвергают пороговой обработке. Данный способ рекомендуется для помехоустойчивых радиолокационных систем различного назначения. 24 ил.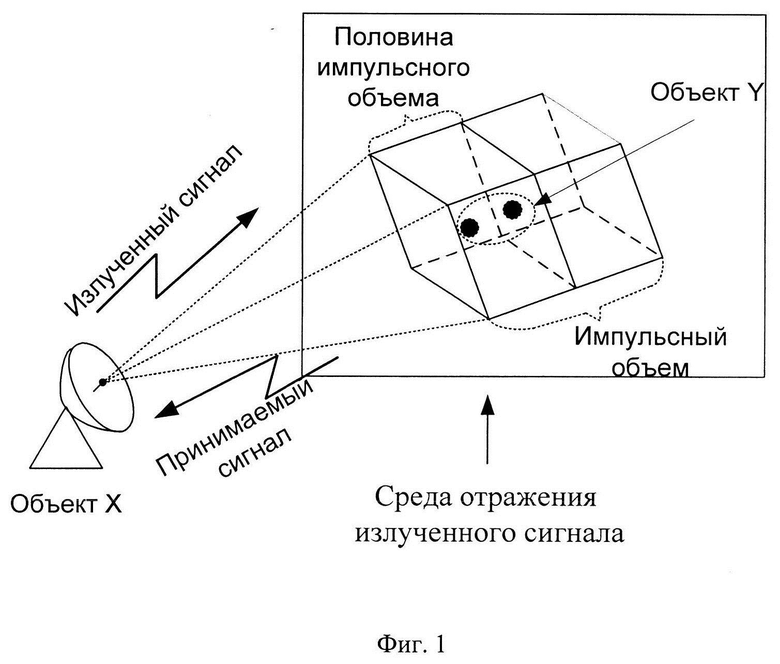
Способ разрешения по дальности источников отражения зондирующих сигналов радиолокатора, заключающийся в том, что с помощью приемопередатчика радиолокатора, называемого объектом X, из первой точки пространства излучают в свободное пространство зондирующий сигнал (ЗС) UЗC(t), который представляет собой простой одиночный радиоимпульс длительностью τ и амплитудой А на несущей частоте fн с периодом повторения Т, во второй точке пространства, называемой объектом Y, представляющей собой L источников отражения зондирующего сигнала, осуществляется отражение зондирующего сигнала, в результате на входе приемника объекта X формируется суммарный сигнал UCC(t), отраженный от L источников отражения зондирующего сигнала, который подают на приемник объекта X, после чего суммарный сигнал оцифровывают при помощи аналого-цифрового преобразователя с частотой дискретизации не менее FД=2⋅fн, получившийся в результате набор данных, описывающий оцифрованный суммарный сигнал, подают в электронно-вычислительную машину, где по мере поступления данных с аналого-цифрового преобразователя осуществляют формирование генерального массива данных Uприем, ограниченного временным интервалом длительностью Δ, причем величину Δ, равную T, и число элементов в нем N определяют по формуле
N=Δ⋅Fд,
где Fд - частота дискретизации аналого-цифрового преобразователя, в результате оцифрованный суммарный сигнал представляет собой массив данных Uприемn, где (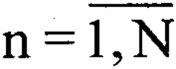 ), который подают на амплитудный детектор, с выхода которого снимают оцифрованную комплексную огибающую принятого суммарного сигнала, значения которой записывают в массив Uприемkn, который подвергают корреляционной обработке по формуле
), который подают на амплитудный детектор, с выхода которого снимают оцифрованную комплексную огибающую принятого суммарного сигнала, значения которой записывают в массив Uприемkn, который подвергают корреляционной обработке по формуле
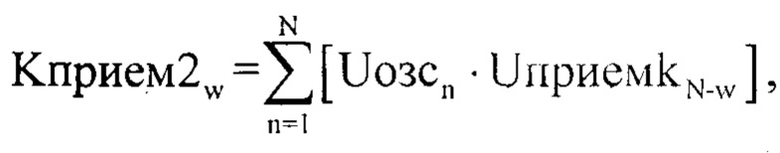
где Uозсn - комплексная огибающая оцифрованного зондирующего сигнала размерностью (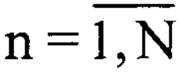 ), a w=1…N, в последующем используют заранее рассчитанное пороговое значение θпорог и сравнивают его с каждым значением модуля массива |Kприем2w|, при выполнении условия превышения порога θпорог значениями модуля массива |Kприем2w| и прекращении превышения порога θпорог значениями модуля массива |Kприем2w| в течение интервала N3=FД⋅2⋅τ принимают решение о наличии в массиве Kприем2w оцифрованного суммарного сигнала, после чего определяют максимальное значение Kmax в массиве |Kприемw| и соответствующее ему значение w=wmax, а затем формируют усеченный массив Kусеч2w2 длительностью N4=2⋅N3+1, где w2=1…N4, который формируют из элементов массива Kприем2w с 1-го по N3-й из отчетов от wmax-N3, а с N3+1-го по N4 из элементов wmax+N3, после чего полученный массив Kусеч2w2 записывают в память электронно-вычислительной машины, далее формируют усеченный массив Uусечn2 длительностью N4=2⋅N3+1, где n2=1…N4, который наполняют из элементов массива Uприемkn с 1-го по N3-й из отчетов от wmax-N3, а с N3+1-го по N4 из элементов wmax+N3, параллельно формируют укороченный массив Uозсуn2, состоящий из элементов массива Uозсn с 1-го по N4, в последующем массивы Uозсуn2 и Uусечn2 подвергают дискретному прямому преобразованию Фурье по формулам
), a w=1…N, в последующем используют заранее рассчитанное пороговое значение θпорог и сравнивают его с каждым значением модуля массива |Kприем2w|, при выполнении условия превышения порога θпорог значениями модуля массива |Kприем2w| и прекращении превышения порога θпорог значениями модуля массива |Kприем2w| в течение интервала N3=FД⋅2⋅τ принимают решение о наличии в массиве Kприем2w оцифрованного суммарного сигнала, после чего определяют максимальное значение Kmax в массиве |Kприемw| и соответствующее ему значение w=wmax, а затем формируют усеченный массив Kусеч2w2 длительностью N4=2⋅N3+1, где w2=1…N4, который формируют из элементов массива Kприем2w с 1-го по N3-й из отчетов от wmax-N3, а с N3+1-го по N4 из элементов wmax+N3, после чего полученный массив Kусеч2w2 записывают в память электронно-вычислительной машины, далее формируют усеченный массив Uусечn2 длительностью N4=2⋅N3+1, где n2=1…N4, который наполняют из элементов массива Uприемkn с 1-го по N3-й из отчетов от wmax-N3, а с N3+1-го по N4 из элементов wmax+N3, параллельно формируют укороченный массив Uозсуn2, состоящий из элементов массива Uозсn с 1-го по N4, в последующем массивы Uозсуn2 и Uусечn2 подвергают дискретному прямому преобразованию Фурье по формулам
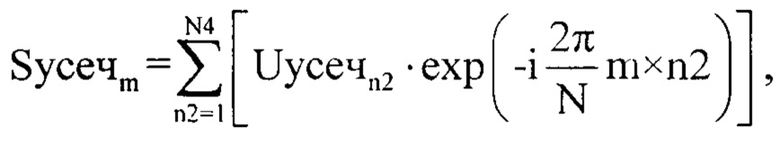
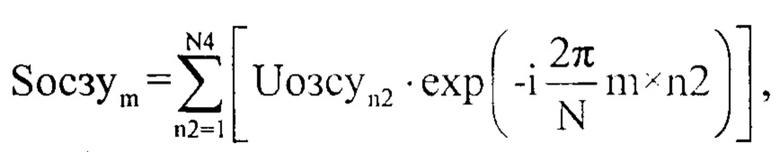
где n2 - номер отчета во временной области, m - номер отчета в частотной области m=1…N4, Syceчm - значение комплексной амплитуды m-го отсчета спектра комплексной огибающей оцифрованного суммарного сигнала для массива Uусечn2, Sосзуm - значение комплексной амплитуды m-го отсчета спектра комплексной огибающей оцифрованного зондирующего сигнала для массива Uозсуn2, после чего формируют массив Sосзу1m1, где m1=1…floor(N4/2), а функция floor выполняет операцию округления до целого числа, в элементы данного массива записывают элементы массива |Sосзуm| с 1-го по floor(N4/2), далее формируют нулевой массив Sосзу2m1, в элементы которого записывают элементы массива |Sосзуm| с 1-го по floor(N4/2)-1 со сдвигом на один отсчет, в дальнейшем определяют предел уровня ограничения спектра оцифрованного суммарного сигнала, для этого находят разницу между |Sосзу1m1| и |Sосзу2m1| по формуле
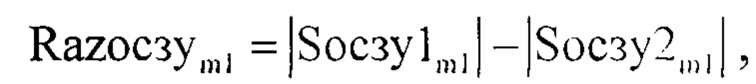
а результат разницы между |Sосзу1m1| и |Sосзу2m1|, записанный в Razосзуm1, подвергают процедуре поиска локальных максимумов, для этого формируют массив Otklikm1, в элементы которого записывают результат по формуле
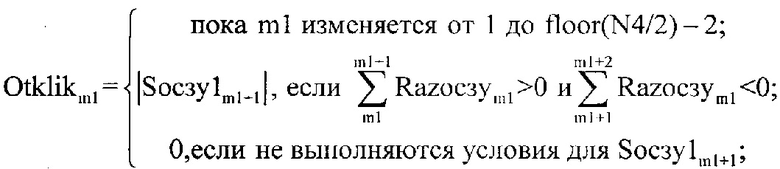
в полученном массиве Otklikm1 определяют второе максимальное значение max(Otklikm1){2}, которое присваивают переменной K, данное значение и будет предельным при изменении уровня ограничения спектра отраженного суммарного сигнала, а k=0…K, после чего определяют шаг Δk изменения k и формируют двумерный массив SосзуkKm,kk, при этом kk=0…K/Δk, а сформированный двумерный массив SосзуkKm,kk имеет размерность N4 на K/Δk, где N4 – количество строк двумерного массива SосзуkKm,kk, а K/Δk – количество его столбцов, элементы массива SосзуkKm,kk заполняют по формуле

после чего формируют двумерный массив W2Km,kk, в строки которого записывают значения частотной характеристики инверсного фильтра при различном уровне k ограничения спектра оцифрованного суммарного сигнала, путем последовательного перемножения каждого элемента двумерного массива SосзуkKm,kk и элементов массива Sосзуkm по формуле
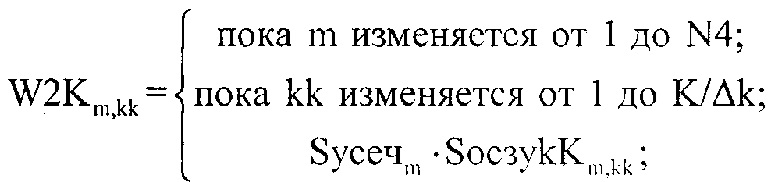
далее двумерный массив W2Km,kk подвергают дискретному обратному преобразованию Фурье, предварительно сформировав двумерный массив H2Kn2,kk, для записи в него результата преобразования по формуле
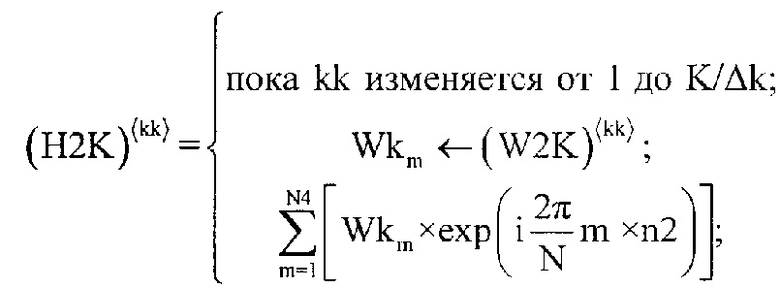
где Wkm - нулевой массив, в элементы которого последовательно записываются столбцы двумерного массива W2Km,kk при изменении kk, а (…)〈…〉 - оператор, соответствующий выбору столбца двумерного массива, после чего значения элементов двумерного массива H2Kn2,kk подвергают нормировке, предварительно сформировав двумерный массив Ннорм2Kn2,kk по формуле
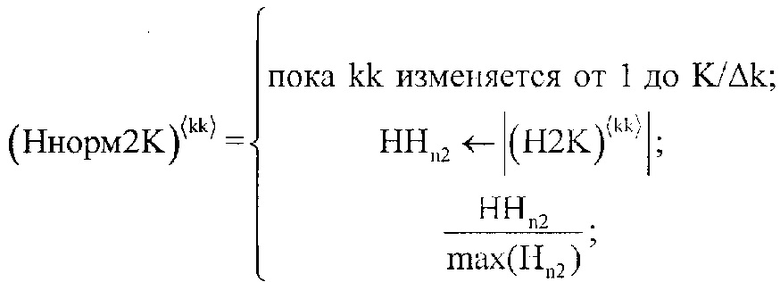
где HHn2 - нулевой массив, в элементы которого последовательно записываются столбцы двумерного массива H2Kn2,kk при изменении kk, далее формируют двумерный нулевой массив Ннорм2K2n2,kk, в столбцы которого записывают значения столбцов двумерного массива Ннорм2Kn2,kk, сдвинутых на 1 отсчет, после чего находят разницу между Ннорм2Kn2,kk и Ннорм2K2n2,kk по формуле
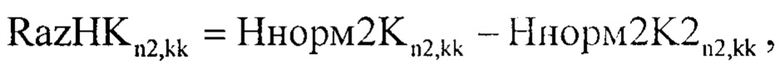
результат разницы между Ннорм2Kn2,kk и Ннорм2K2n2,kk, записанный в RazHKn2,kk, подвергают процедуре поиска локальных максимумов, для этого формируют двумерный массив Otk1n2,kk, в элементы которого записывают результат полученный по формуле

где M1n2 - нулевой массив, в элементы которого последовательно записывают элементы столбцов двумерного массива RazHKn2,kk при изменении kk, M2n2 - нулевой массив, в элементы которого последовательно записывают элементы столбцов двумерного массива Ннорм2K2n2,kk при изменении kk, в результате получают двумерный массив Otk1n2,kk, в столбцы которого записаны локальные максимумы сглаженных импульсных характеристик среды отражения излученного сигнала радиолокатором, отклики которых несут в себе информацию о количестве источников отражения ЗС L и их взаимном удалении друг от друга, отличающийся тем, что формируют вектор SIn2 по следующему правилу:
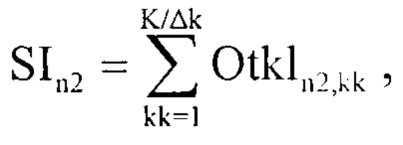
после чего запоминают значение амплитуды второго максимума 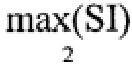 в векторе SIn2 и проводят бинаризацию массива Otk1n2,kk по следующему правилу:
в векторе SIn2 и проводят бинаризацию массива Otk1n2,kk по следующему правилу:

формируют вектор FIkk согласно выражению:
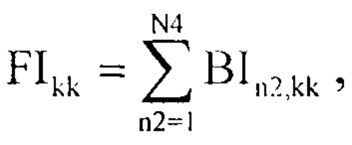
после чего определяют параметр ограничения K2 массива Ннорм2Kn2,kk, для этого формируют вектор Ikkk по следующему правилу:
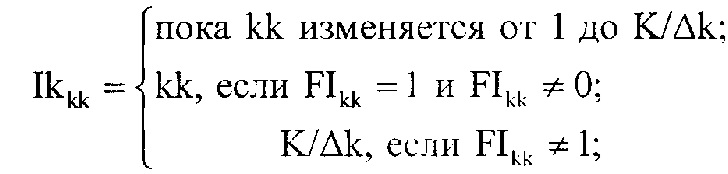
определяют порядковый номер первого элемента вектора Ikkk, равного 1, по формуле:
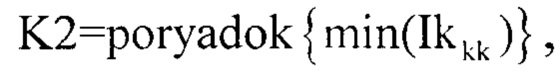
где poryadok{…} - оператор, определяющий порядковый номер первого элемента вектора Ikkk, равного 1, в дальнейшем используют массив Otk2n2,kk2, сформированный из массива Otk1n2,kk, но ограниченный по kk2, где kk2=0…K2, далее формируют трехмерный массив {Ннорм3Kn2,kk2}〈p〉, где р=0…10, в элементы массива {Ннорм3Kn2,kk2}〈p〉 записывают результат пороговой обработки двумерного массива Otk2n2,kk2 по следующему правилу

где M3n2 - нулевой массив, в элементы которого последовательно записываются элементы столбцов двумерного массива RazHKn2,kk2 при изменении kk2, {…}〈…〉 - оператор, предназначенный для выбора элемента трехмерного массива или присвоения выбранному элементу трехмерного массива некоторого значения, в результате получают трехмерный массив {Ннорм3K}〈p〉, в элементы которого записаны результаты пороговой обработки двумерного массива Otk1n2,kk2, после чего формируют нулевой трехмерный массив {НкомплKn2,.kk2}〈p〉, элементы которого заполняются по следующему выражению

далее получают комплексную автокорреляционную функцию по выражению
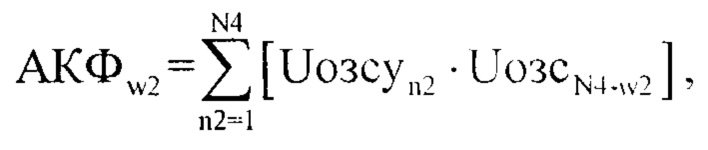
где w2=1…N4, так как размерность w2=n2, в дальнейшем используют только n2, после чего формируют массив МНКk,p, элементы которого заполняются по формуле

где  - математическая операция, отражающая свертку двух одномерных массивов, после чего определяют значения kk2=const и p=const, соответствующие минимуму двумерного массива МНКkk2,p, а затем формируют массив НМНКn2, элементы которого заполняют по формуле
- математическая операция, отражающая свертку двух одномерных массивов, после чего определяют значения kk2=const и p=const, соответствующие минимуму двумерного массива МНКkk2,p, а затем формируют массив НМНКn2, элементы которого заполняют по формуле
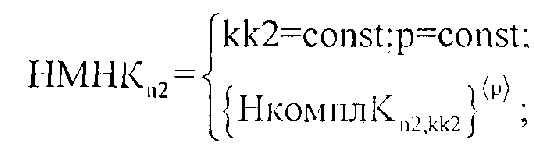
выбирают пороговое значение θН3порог равным 0,5 и сравнивают величину θH3порог с каждым значением соответствующего нормированного массива |НМНКn2|, в случае превышении порога θН3порог значениями массива |НМНКn2| количество превышений считают равным L и их порядковые номера pz3=n2 записывают в память электронно-вычислительной машины, после чего рассчитывают дальность до каждого источника отражения зондирующего сигнала, используя формулу
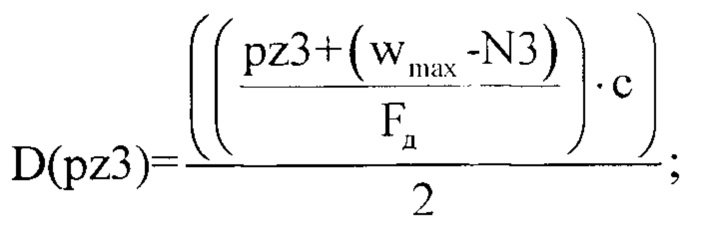
где с - скорость света, равная 3⋅108 м/с.
| Способ обеспечения высокой разрешающей способности радиолокатора по дальности за счет выбора оптимального параметра регуляризации инверсного фильтра | 2021 |
|
RU2756291C1 |
| Способ фильтрации сигналов при обнаружении цели и устройство для его осуществления | 2017 |
|
RU2678822C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ ВОЗДУШНЫХ ОБЪЕКТОВ В ОБЗОРНЫХ РАДИОЛОКАТОРАХ ЗА СЧЕТ ИСПОЛЬЗОВАНИЯ КОГЕРЕНТНЫХ СВОЙСТВ ОТРАЖЕННЫХ СИГНАЛОВ | 2009 |
|
RU2416105C1 |
| СПОСОБ КОМБИНИРОВАННОГО КОДИРОВАНИЯ И ВЫЧИСЛЕНИЯ ЭХО-СИГНАЛОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2011 |
|
RU2516379C2 |
| СЕМЧЕНКОВ C.M., ПЕЧЕНЕВ Е.А., АБРАМЕНКОВ А.В | |||
| Повышение разрешающей способности радиолокатора по дальности за счет инверсной фильтрации // Журнал Сибирского федерального университета | |||
| Серия: Техника и технологии, 2018, Том 11(3), сс | |||
Авторы
Даты
2022-12-07—Публикация
2021-12-06—Подача