Изобретение относится к области оптических способов измерения физических величин с использованием волоконных интерферометров, в том числе для измерения механических и акустических колебаний, а также линий сбора данных на их основе.
Известно «Опросное устройство для волоконно-оптических линий с использованием двух склонов» [Патент US №6778720]. Способ демодуляции сигнала, используемый в данном устройстве, включает вспомогательную модуляцию разности фаз световых волн в интерферометрах гармоническим сигналом, преобразование выходного сигнала фотоприемника, установленного на выходе линии, в последовательность цифровых отсчетов, выбор по пять отсчетов на каждом из двух склонов периодической зависимости сигнала от времени, вычисление по части выбранных отсчетов искомой разности фаз световых волн в интерферометре, вычисление амплитуды вспомогательной модуляции по остальным отсчетам и ее последующую регулировку. Недостатками данного способа являются сложность его реализации, использование в каждом цикле вычислений не менее десяти отсчетов сигнала, необходимость точного поддержания амплитуды вспомогательной модуляции и одинаковости разности плеч всех интерферометров, входящих в линию.
Известен «Четырехступенчатый дискретный способ демодуляции фазовых сдвигов для линий из волоконно-оптических датчиков» [Патент US №6122057]. Способ включает вспомогательную фазовую модуляцию интерферометра гармоническим сигналом, формирование четырех сигналов, являющихся интегралами выходного сигнала фотоприемника в течение разных промежутков времени, преобразование интегральных сигналов в последовательности цифровых отсчетов, вычисление искомой разности фаз световых волн в интерферометре. Недостатками данного способа являются сложность его реализации, необходимость формирования четырех интегральных сигналов, дополнительного вычисления поправочного коэффициента для корректировки вычисленных значений разности фаз.
Известен «Способ и устройство демодуляции выходных сигналов интерферометра повышенной точности», выбранный за прототип [Патент US №6556509]. Способ демодуляции включает модуляцию разности фаз световых волн в интерферометре по гармоническому закону с амплитудой, преобразование периодического сигнала, получаемого с фотоприемника, установленного на выходе интерферометра, (период сигнала равен периоду вспомогательной модуляции) в поток цифровых отсчетов с получением двенадцати отсчетов в течение каждого периода. Отсчеты регистрируются через равные промежутки времени, частота дискретизации в двенадцать раз выше частоты модуляции. Выбор в течение каждого периода сигнала шести отсчетов из двенадцати и вычисление по этим шести отсчетам значения искомой разности фаз один раз за период с использованием формул, полученных для амплитуды модуляции. После чего осуществляют вычисление по оставшимся шести отсчетам амплитуды модуляции, проверка равенства амплитуды значению радиан и корректировка амплитуды.
Недостатками прототипа являются сложность расчетов, сложность реализации способа, необходимость точного поддержания амплитуды вспомогательной гармонической модуляции равной π радиан, требование равенства разностей плеч всех интерферометров при использовании способа для демодуляции сигналов в линии из нескольких интерферометров.
Задачами способа демодуляции являются упрощение вычислений и реализации, исключение требования к определенному значению амплитуды вспомогательной модуляции и равенства разностей длин плеч интерферометров, объединенных в линию.
Для решения поставленной задачи предложено два варианта способа демодуляции сигнала волоконного интерферометра.
Первый вариант способа демодуляции включает модуляцию разности фаз в интерферометре гармоническим сигналом, преобразование сигнала осуществляют с частотой в три раза больше частоты модуляции разности фаз в интерферометре, формируют тройки отсчетов из всех трех отсчетов каждого периода, после чего вычисление искомой разности фаз ведут по каждой тройке по формулам:

где
a=u(0)(C1-C2)+u(1)(C2-C0)+u(2)(C0-C1), b=u(0)(S1-S2)+u(1)(S2-S0)+u(2)(S0-S1),
где u(0), u(1), u(2) - значения отсчетов в тройке, С0=cos[φ(0)], C1=cos[φ(1)], C2=cos[φ(2)] и S0=sin[φ(0)], S1=sin[φ(1)], S2=sin[φ(2)],
где φ(0)=δφmsin[θ0], φ(1)=δφmsin[θ1], φ(2)=δφmsin[θ2],
где δφm - амплитуда модулирующего сигнала, θ0 - фазовая задержка первого отсчета относительно начала периода модуляции, θ1=θ0+2π/3, θ2=θ0 +4π/3. Тройки отсчетов могут быть сформированы из всех трех отсчетов одного периода с пропуском М-1 периодов, где М - целое число >1.
Второй вариант способа демодуляции сигнала волоконного интерферометра включает модуляцию разности фаз в интерферометре гармоническим сигналом, преобразование сигнала осуществляют с частотой в три раза больше частоты модуляции разности фаз в интерферометре, формируют тройки отсчетов, объединяющие каждые три соседних отсчета со сдвигом на один отсчет, затем вычисление искомой разности фаз ведут по каждой тройке по формулам:

где
a=u(0)(C1-C2)+u(1)(C2-C0)+u(2)(C0-C1), b=u(0)(S1-S2)+u(1)(S2-S0)+u(2)(S0-S1),
где u(0), u(1), u(2) - значения отсчетов в тройке, С0=cos[φ(0)], C1=cos[φ(1)], C2=cos[φ(2)] и S0=sin[φ(0)], S1=sin[φ(1)], S2=sin[φ(2)],
где для первой тройки - φ(0)=δφmsin[θ0], φ(1)=δφmsin[θ1], φ(2)=δφmsin[θ2], для второй тройки φ(0)=δφmsin[θ1], φ(1)=δφmsin[θ2], φ(2)=δφmsin[θ0], для третьей тройки φ(0)=δφmsin[θ2], φ(1)=δφmsin[θ0], φ(2)=δφmsin[θ1],
где δφm - амплитуда модулирующего сигнала, θ0 - фазовая задержка первого отсчета относительно начала периода модуляции, θ1=θ0+2π/3, θ2=θ0+4π/3, после чего процесс вычисления фаз повторяют.
Выбор частоты преобразования обусловлен необходимым минимальным количеством отсчетов в течение каждого периода модуляции.
В том случае, когда частота изменения искомой разности фаз мала, целесообразно формировать тройки отсчетов из всех трех отсчетов одного периода с пропуском М-1 периодов, что позволит уменьшить среднее количество данных, обрабатываемых в единицу времени, в М раз, где М - целое число >1.
В том случае, когда частота изменения искомой разности фаз велика, целесообразно формировать тройки отсчетов, объединяющие каждые три соседних отсчета со сдвигом на один отсчет, и использовать разные наборы коэффициентов, чтобы избежать искажения сигнала.
В предлагаемом способе частота преобразования полученного периодического сигнала в последовательность цифровых отсчетов и вычисление каждого значения искомой разности фаз по тройке отсчетов позволяет уменьшить количество данных и упростить расчеты.
Математические формулы, используемые для вычисления искомой разности фаз применимы при произвольной амплитуде модуляции, что упрощает реализацию и снимает требование одинаковой разности плеч всех интерферометров в линии.
Для модуляции разности фаз в интерферометре используем гармонический сигнал

где δφm и fм - амплитуда и частота модулирующего сигнала.
Известно, что напряжение, получаемое с фотоприемника, установленного на выходе двухплечного волоконного интерферометра, при наличии модуляции φ(t) имеет вид

где φС - искомая разность фаз, которую необходимо определить в результате демодуляции, U0 и Um - постоянная составляющая и амплитуда интерференционного сигнала.
Предполагается медленное изменение φС, U0 и Um по сравнению с колебаниями модулирующего сигнала, и в течение одного периода модуляции эти величины можно считать постоянными. Данное условие может быть формально выражено следующими неравенствами:

Преобразуем полученный сигнал (2) в последовательность отсчетов un с частотой дискретизации fd, в три раза превышающей частоту модуляции fd=3·fM,

где n - номер отсчета от начала первого периода модуляции (n=0, 1, 2,…), θ0=2πfМΔt - фазовая задержка первого отсчета относительно начала периода модуляции, tn - момент времени n-го отсчета интерференционного сигнала, φn - значения модулирующего сигнала φ(t) в моменты времени tn.
Для описания формируемых сигналов удобно ввести в рассмотрение значения аргумента модулирующего фазу гармонического колебания (1) в моменты регистрации отсчетов tn

Для вычисления значения искомой разности фаз φC выбираем три отсчета интерференционного сигнала. Это условие определяется тем, что функция (2), описывающая модулированный интерференционный сигнал, имеет три неизвестных параметра, которые исходя из условия (3) полагаются постоянными в течение периода модуляции: искомая разность фаз φС, U0 и Um.
Обозначив тройку отсчетов сигнала в течение одного периода модуляции {u(0), u(1), u(2)} и записав их значения по формуле (4), получим систему уравнений, решение которой приводит к выражениям для искомой разности фаз φC в диапазоне [-π, π]:
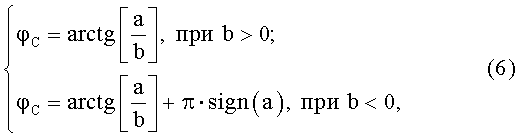
где
a=u(0)(C1-C2)+u(1)(С2-C0)+u(2)(C0-C1), b=u(0)(S1-S2)+u(1)(S2-S0)+u(2)(S0-S1),
где C0=cos[φ(0)], C1=cos[φ(1)], C2=cos[φ(2)] и S0=sin[φ(0)], S1=sin[φ(1)], S2=sin[φ(2)],
где φ(0)=δφmsin[θ0], φ(1)=δφmsin[θ1], φ(2)=δφmsin[θ2].
Тройки отсчетов могут быть сформированы из всех трех отсчетов одного периода, с пропуском М-1 периодов, где М - целое число >1.
Второй вариант способа демодуляции аналогичен первому, но тройки {u(0), u(1), u(2)} формируют из трех соседних отсчетов со сдвигом в каждой последующей тройке на один отсчет.
Формула (6), по которой проводят вычисления значений искомой разности фаз φC, не меняются, но при вычислениях используют три варианта коэффициентов, соответствующих трем разным наборам {φ(0), φ(1), φ(2)}:
для первой тройки {φ(0), φ(1), φ(2)}={δφmsin[θ0], δφmsin[θ1], δφmsin[θ2]},
для второй тройки {φ(0), φ(1), φ(2)}={δφmsin[θ1], δφmsin[θ2], δφmsin[θ0]},
для третьей тройки {φ(0), φ(1), φ(2)}={δφmsin[θ2], δφmsin[θ0], δφmsin[θ1]}.
Каждому из этих трех наборов {φ(0), φ(1), φ(2)} соответствует свой набор коэффициентов {С0, С1, С2, S0, S1, S2}, вычисляемый по тем же формулам: C0=cos[φ(0)], C1=cos[φ(1)], С2=cos[φ(2)] и S0=sin[φ(0)], S1=sin[φ(1)], S2=sin[φ(2)].
После третьей тройки наборы {φ(0), φ(1), φ(2)} и процесс вычисления разности фаз повторяют для 4-й, 5-й и 6-й троек и т.д.
Для реализации способа демодуляции необходимо регистрировать колебания φC(t), вызываемые воздействием на интерферометр в частотном диапазоне, не превышающем полосу 5 кГц и амплитудой не более 1 радиана (например, акустические или вибрационные воздействия).
По первому варианту способа модулируем разность фаз в интерферометре гармоническим сигналом с частотой fM=50 кГц и амплитудой δφm=2 радиана. При этом для максимальной частоты и амплитуды измеряемого сигнала FC=5 кГц неравенства условия (3) принимают вид
fМ/FС=10>>1 и (dφС/dt)=2π·1·5=10π<<2πfМ=100π,
т.е. условия выполняются.
Преобразование полученного периодического сигнала в последовательность цифровых отсчетов производим с частотой fd=3fМ=150 кГц, т.е. в три раза больше, чем частота модуляции. При этом допустим, что сдвиг начального отсчета относительно начала периода соответствует фазовому сдвигу θ0=0.2 радиан (т.е. Δt=0.637 мкс).
Пусть в течение некоторого периода модуляции параметры интерференционного сигнала имеют значения U0=1, Um=1, а искомая фаза составляет φC=2 радиана. Тогда, согласно (4) для этого периода будет сформирована тройка отсчетов
{u(0), u(1), u(2)}={0.264, 0.063, 1.995}
Для вычисления искомой разности фаз используем фиксированные коэффициенты:
φ(0)=δφmsin[θ0]=0.397, φ(1)=δφmsin[θ1]=1.499, φ(2)=δφmsin[θ2]=-1.896 радиан;
C0=cos[φ(0)]=0.922, C1=cos[φ(1)]=0.072, C2=cos[φ(2)]=-0.32;
S0=sin[φ(0)]=0.387, S1=sin[φ(1)]=0.997, S2=sin[φ(2)]=-0.948.
В результате расчета по формуле (6) для указанной тройки получим:
a=u(0)(C1-C2)+u(1)(С2-C0)+u(2)(C0-C1)=0.264 (0.072+0.32)+0.063 (-0.32-0.922)+
1.995 (0.922-0.072)=1.721;
b=u(0)(S1-S2)+u(1)(S2-S0)+u(2)(S0-S1)=0.264 (0.997+0.948)+0.063 (-0.948-0.387)+
1.995 (0.387-0.997)=-0.788;
a/b=-2.185; arctg(a/b)=-1.42;
φС=arctg(a/b)+π=2 радиана.
Таким образом, получили правильное значение искомой разности фаз φC.
Данный пример иллюстрирует вычисление искомой разности фаз φC и в случае формирования троек из отсчетов каждого периода, и в случае формирования троек из всех отсчетов одного периода с пропуском М-1 периодов, где М - целое число >1, например при М=2 пропускаем каждый второй период.
Во втором варианте способа все действия выполняем аналогично первому, но формируем тройки отсчетов, объединяющие каждые три соседних отсчета со сдвигом на один отсчет. Например, пусть в течение некоторых двух периодов модуляции параметры интерференционного сигнала имеют значения U0=1, Um=1, а искомая фаза составляет φC=2 радиана. Тогда, согласно (4) для этих двух периодов будут зафиксированы следующие значения отсчетов
0.264; 0.063; 1.995; 0.264; 0.063; 1.995.
По этому набору отсчетов будут сформированы четыре тройки отсчетов:
первая {u(0), u(1), u(2)}={0.264, 0.063, 1.995}
вторая {u(0), u(1), u(2)}={0.063, 1.995, 0.264}
третья {u(0), u(1), u(2)}={1.995, 0.264, 0.063}
четвертая {u(0), u(1), u(2)}={0.264, 0.063, 1.995}
При вычислении искомой разности фаз используем три набора фиксированных коэффициентов. Для первой (4-й, 7-й и т.д.) тройки:
φ(0)=δφmsin[θ0]=0.397, φ(1)=δφmsin[θ1]=1.499, φ(2)=δφmsin[θ2]=-1.896 радиан;
C0=cos[φ(0)]=0.922, C1=cos[φ(1)]=0.072, C2=cos[φ(2)]=-0.32;
S0=sin[φ(0)]=0.387, S1=sin[φ(l)]=0.997, S2=sin[φ(2)]=-0.948.
Для второй (5-й, 8-й и т.д.) тройки:
φ(0)=δφmsin[θ1]=1.499, φ(1)=δφmsin[θ2]=-1.896, φ(2)=δφmsin[θ0]=0.397 радиан;
C0=cos[φ(0)]=0.072, C1=cos[φ(1)]=-0.32, C2=cos[φ(2)]=0.922;
S0=sin[φ(0)]=0.997, S1=sin[φ(1)]=-0.948, S2=sin[φ(2)]=0.387.
Для третьей (6-й, 9-й и т.д.) тройки:
φ(0)=δφmsin[θ1]=1.499, φ(1)=δφmsin[θ2]=0.397, φ(2)=δφmsin[θ0]=-1.896 радиан;
C0=cos[φ(0)]=-0.32, C1=cos[φ(1)]=0.922, С2=cos[φ(2)]=0.072;
S0=sin[φ(0)]=-0.948, S1=sin[φ(1)]=0.387, S2=sin[φ(2)]=0.997.
Расчет коэффициентов а и b по формулам
a=u(0)(C1-C2)+u(1)(С2-C0)+u(2)(C0-C1); b=u(0)(S1-S2)+u(1)(S2-S0)+u(2)(S0-S1); для каждой тройки даст следующие результаты.
Для первой тройки:
а=0.264(0.072+0.32)+0.063(-0.32-0.922)+1.995(0.922-0.072)=1.721;
b=0.264(0.997+0.948)+0.063(-0.948-0.387)+1.995(0.387-0.997)=-0.788;
Для второй тройки:
a=0.063(-0.32-0.922)+1.995(0.922-0.072)+0.264(0.072+0.32)=1.721;
b=0.063(-0.948-0.387)+1.995(0.387-0.997)+0.264(0.997+0.948)=-0.788;
Для третьей тройки:
a=1.995(0.922-0.072)+0.264(0.072+0.32)+0.063(-0.32-0.922)=1.721;
b=1.995(0.387-0.997)+0.264(0.997+0.948)+0.063(-0.948-0.387)=-0.788;
Для четвертой тройки:
а=0.264(0.072+0.32)+0.063(-0.32-0.922)+1.995(0.922-0.072)=1.721;
b=0.264(0.997+0.948)+0.063(-0.948-0.387)+1.995(0.387-0.997)=-0.788;
Соответственно по всем тройкам согласно (6) получим одинаковые значения искомой разности φС=arctg(a/b)+π=2 радиана, т.е. правильное значение искомой фазы.
Пример реализации 2-х вариантов способа демодуляции сигнала волоконного интерферометра демонстрирует упрощение вычисления искомой разности фаз. При вычислении не требуется определенное значение амплитуды вспомогательной модуляции и равенство разностей длин плеч интерферометров, объединенных в линию.
Изобретение относится к области оптических способов измерения физических величин с использованием волоконных интерферометров. Предложены два варианта способа демодуляции сигнала волоконного интерферометра, включающие модуляцию разности фаз в интерферометре гармоническим сигналом, преобразование полученного сигнала в последовательность цифровых отсчетов и вычисление разности фаз. Согласно первому варианту способа преобразование сигнала осуществляют с частотой в три раза больше частоты модуляции разности фаз в интерферометре и формируют тройки отсчетов из всех трех отсчетов каждого периода, после чего производят вычисление искомой разности фаз по каждой тройке. Согласно второму варианту способа тройки формируют из трех соседних отсчетов со сдвигом каждой последующей тройки на один отсчет. Технический результат - упрощение вычислений и реализации, исключение требования к определенному значению амплитуды вспомогательной модуляции и равенства разностей длин плеч интерферометров, объединенных в линию. 2 н. и 1 з.п. ф-лы.
1. Способ демодуляции сигнала волоконного интерферометра, включающий модуляцию разности фаз в интерферометре гармоническим сигналом, преобразование полученного периодического сигнала в последовательность цифровых отсчетов, вычисление искомой разности фаз, отличающийся тем, что преобразование сигнала осуществляют с частотой в три раза больше частоты модуляции разности фаз в интерферометре, формируют тройки отсчетов из всех трех отсчетов каждого периода, после чего вычисление искомой разности фаз ведут по каждой тройке по формулам:

где
a=u(0)(C1-C2)+u(1)(C2-C0)+u(2)(C0-C1), b=u(0)(S1-S2)+u(1)(S2-S0)+u(2)(S0-S1),
где u(0), u(1), u(2) - значения отсчетов в тройке, С0=cos[φ(0)], C1=cos[φ(1)], C2=cos[φ(2)] и S0=sin[φ(0)], S1=sin[φ(1)], S2=sin[φ(2)],
где φ(0)=δφmsin[θ0], φ(1)=δφmsin[θ1], φ(2)=δφmsin[θ2],
где δφm - амплитуда модулирующего сигнала, θ0 - фазовая задержка первого отсчета относительно начала периода модуляции, θ1=θ0+2π/3, θ2=θ0+4π/3.
2. Способ по п.1 отличающийся тем, что формируют тройки отсчетов из всех трех отсчетов одного периода, с пропуском М-1 периодов, где М - целое число >1.
3. Способ демодуляции сигнала волоконного интерферометра, включающий модуляцию разности фаз в интерферометре гармоническим сигналом, преобразование полученного периодического сигнала в последовательность цифровых отсчетов, вычисление искомой разности фаз, отличающийся тем, что преобразование сигнала осуществляют с частотой в три раза больше частоты модуляции разности фаз в интерферометре, формируют тройки отсчетов, объединяющие каждые три соседних отсчета со сдвигом на один отсчет, затем вычисление искомой разности фаз ведут по каждой тройке по формулам:

где
a=u(0)(C1-C2)+u(1)(C2-C0)+u(2)(C0-C1), b=u(0)(S1-S2)+u(1)(S2-S0)+u(2)(S0-S1),
где u(0), u(1), u(2) - значения отсчетов в тройке, С0=cos[φ(0)], C1=cos[φ(1)], C2=cos[φ(2)] и S0=sin[φ(0)], S1=sin[φ(1)], S2=sin[φ(2)],
где для первой тройки - φ(0)=δφmsin[θ0], φ(1)=δφmsin[θ1], φ(2)=δφmsin[θ2], для второй тройки φ(0)=δφmsin[θ1], φ(1)=δφmsin[θ2], φ(2)=δφmsin[θ0], для третьей тройки φ(0)=δφmsin[θ2], φ(1)=δφmsin[θ0], φ(2)=δφmsin[θ1],
где δφm - амплитуда модулирующего сигнала, θ0 - фазовая задержка первого отсчета относительно начала периода модуляции, θ1=θ0+2π/3, θ2=θ0+4π/3, после чего процесс вычисления фаз повторяют.
| СПОСОБ ДЕМОДУЛЯЦИИ СИГНАЛОВ ОТНОСИТЕЛЬНОЙ ФАЗОВОЙ МОДУЛЯЦИИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2009 |
|
RU2408996C2 |
| СПОСОБ ДЕМОДУЛЯЦИИ СИГНАЛОВ С ОТНОСИТЕЛЬНОЙ ФАЗОВОЙ МОДУЛЯЦИЕЙ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1995 |
|
RU2099892C1 |
| Демодулятор сигналов с фазоразностной модуляцией второго порядка | 1982 |
|
SU1053321A1 |
| US 6556509 B1, 29.04.2003. | |||
Авторы
Даты
2012-12-20—Публикация
2011-05-13—Подача