Изобретение относится к вычислительной технике и может быть использовано для тестирования вычислительных систем, функционирующих в системе остаточных классов.
Известно устройство для обнаружения, локализации и исправления ошибок в системе остаточных классов (Патент RU 2301442, G06F 011/08, G06N 003/06, 2007), содержащее нейронные сеть конечного кольца для формирования остатков по контрольным модулям системы остаточных классов, нейронные сети конечного кольца для вычисления синдрома ошибок, нейронные сети конечного кольца для исправления ошибок, блока памяти и логических элементов.
Однако данное устройство обладает следующими недостатками: низким быстродействием, вызванным высокой логической глубиной (количество последовательно соединенных нейронных сетей конечного кольца), большими аппаратными затратами и жесткими условиями, накладываемыми на абсолютную надежность каналов по избыточным модулям. Наиболее близкой по технической сущности к заявленному устройству является адаптивная параллельно-конвейерная нейронная сеть для коррекции ошибок (Патент RU 2279131, G06 №3/04, 2005 г.), которая содержит блок нейронной сети конечного кольца формирования цифр в представлении обобщенной позиционной системе счисления; блок обнаружения ошибок, блок реконфигурации и локализации ошибок и блок исправления ошибок.
Недостатками известного устройства являются сложность, которая объясняется наличием большого количества нейронных сетей конечного кольца и низкое быстродействие, которое пропорционально количеству модулей системы остаточных классов.
Целью настоящего изобретения являются упрощение устройства и повышение быстродействия.
Поставленная цель достигается тем, что устройство содержит: входной регистр 2, содержащий разрядные регистры 2-1, 2-2, …, 2-n+r для временного хранения контролируемого числа, представленного по модулям p1, p2, …, pn+r; схему формирования проекций числа А по основаниям pi (i=[1,n+r]) 3, (число Ai, полученное из А зачеркиванием цифры αi называется проекцией числа А по основанию pi); блоки памяти 4, содержащие элементы памяти 4-1, 4-2, …, 4-n+r для хранения констант по модулям pi; сумматор 5 для суммирования произведения разрядных констант и соответствующих цифр разрядов числа; блок анализа на равенство, больше или меньше рабочего диапазона 6; триггер 9 для запуска и остановки счетчика проекций 10; блок логических элементов «И» 7, содержащий элементы «И» 7-1, 7-2, …, 7-n+r для локализации неисправного канала pi; входные шины 1 для подачи контролируемого числа А, схему формирования проекций константы, соответствующей рабочему диапазону 11; блок хранения констант рабочего диапазона 12, состоящий из элементов 12n+1, 12n+r; сумматор 13; шину 8, сигнализирующую о неисправности pi канала; шину сигнала «ошибка не установлена» 14 и шину 15 для подключения разрядов константы, соответствующей рабочему диапазону; шину 16 «переполнение диапазона и ошибка», сигнализирующую о переполнении рабочего диапазона и появлении ошибки.
Рассмотрим метод определения ошибки числа и номера неисправного канала системы остаточных классов, обладающий высоким быстродействием и низкими аппаратными затратами.
Суть метода основана на использовании Китайской теоремы об остатках числа, которая связывает позиционное число А с его представлением в остатках (α1, α2, …, αn), где α1 - наименьшие неотрицательные остатки числа по модулям p1, p2, …,pn. При этом используется нестандартный подход, который отличается от классического тем, что используются не абсолютные числа, а их относительные величины.
Кроме того, решение практически любой задачи управления требует сравнения в необходимый момент времени состояния управляемых объектов с заданными состояниями, соответствующими алгоритму функционирования систем. Целью сравнения является обнаружение факта совпадения или несовпадения значений величин, равенства или неравенства чисел, больших или меньших некоторых значений. Конкретное выполнение операции сравнения может определяться аппаратным или программным способом.
С целью упрощения определения переполнения динамического диапазона и исправления ошибок рассмотрим приближенный метод, который позволяет абсолютно правильно реализовать основные классы процедур принятия решений.
Суть приближенного метода сравнения модулярных чисел основана на использовании относительной величины анализируемых чисел к полному диапазону, определенному Китайской теоремой об остатках, которая связывает позиционное число А с его представлением в остатках (α1, α2, …, αn), где αi - наименьшие неотрицательные вычеты числа, относительно модулей системы остаточных классов р1, р2, …, pn следующим выражением
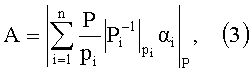
где 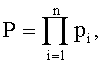 pi - модули СОК,
pi - модули СОК, 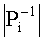 - мультипликативная инверсия Pi относительно pi,и
- мультипликативная инверсия Pi относительно pi,и 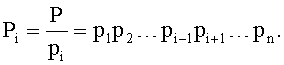
Если (3) разделить на константу Р, соответствующую выбранному диапазону чисел, то получим приближенное значение

где  - константы выбранной системы, а αi - разряды числа, представленного в СОК, при этом значение каждой суммы будет в интервале [0,1). Конечный результат суммы определяется после суммирования и отбрасывания целой части числа с сохранением дробной части суммы. Дробная часть может быть записана также как Amod1, потому что A=A+Amod1. Количество разрядов дробной части числа определяется максимально возможной разностью между соседними числами. При необходимости точного сравнения необходимо вычислить значение (4), которое является эквивалентом преобразования из СОК в позиционную систему счисления. Для решения поставленной задач достаточно знать приблизительное значение используемого числа А по отношению к динамическому диапазону Р, которое выполняется достаточно просто, но при этом верно определяется соотношение А=Р, А>Р или А<Р.
- константы выбранной системы, а αi - разряды числа, представленного в СОК, при этом значение каждой суммы будет в интервале [0,1). Конечный результат суммы определяется после суммирования и отбрасывания целой части числа с сохранением дробной части суммы. Дробная часть может быть записана также как Amod1, потому что A=A+Amod1. Количество разрядов дробной части числа определяется максимально возможной разностью между соседними числами. При необходимости точного сравнения необходимо вычислить значение (4), которое является эквивалентом преобразования из СОК в позиционную систему счисления. Для решения поставленной задач достаточно знать приблизительное значение используемого числа А по отношению к динамическому диапазону Р, которое выполняется достаточно просто, но при этом верно определяется соотношение А=Р, А>Р или А<Р.
Для определения ошибки, переполнения и локализации неисправного pi канала используются избыточные СОК, имеющие n-рабочих r-контрольных оснований, при этом избыточный диапазон для двух избыточных модулей Ризб=Р·pn+1·pn+2, где Р=М - рабочий диапазон. Известно, что для практического применения достаточно иметь два избыточных основания, то есть r=2, при этом система гарантировано обнаруживает появления одновременно двух ошибок и одну ошибку исправляет. Если значения 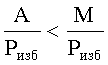 , тогда число безошибочное. Аналогично определяется и переполнение диапазона представляемых чисел. Локализация неисправного канала осуществляется путем анализа относительных значений проекций числа к pi. В результате анализа выявляется правильная проекция Ai числа А, которая определяет неисправный pi канал.
, тогда число безошибочное. Аналогично определяется и переполнение диапазона представляемых чисел. Локализация неисправного канала осуществляется путем анализа относительных значений проекций числа к pi. В результате анализа выявляется правильная проекция Ai числа А, которая определяет неисправный pi канал.
Конечный процесс обнаружения переполнения динамического диапазона, ошибки и неисправного вычислительно pi канала может быть представлен в виде обобщенного алгоритма:
1. Вычисление относительных значений 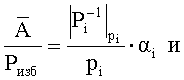
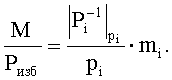 Если
Если 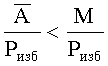 , тогда ошибки нет, если
, тогда ошибки нет, если 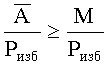 есть ошибка и переполнения динамического диапазона и тогда перейдем к шагу 2.
есть ошибка и переполнения динамического диапазона и тогда перейдем к шагу 2.
2. Вычисление относительных значений проекций  и Mi, если
и Mi, если 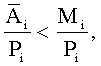 то в разряде i нет ошибки, если
то в разряде i нет ошибки, если 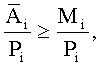 то в данном разряде есть ошибка, которая фиксируется на выходе устройства. На этом процесс заканчивается.
то в данном разряде есть ошибка, которая фиксируется на выходе устройства. На этом процесс заканчивается.
Принцип обнаружения переполнения динамического диапазона, определения ошибки и локализации неисправного канала покажем на примере. Предположим необходимо реализовать функциональный блок для реализации перечисленных функций вычислительной системы, функционирующей в СОК. Пусть набор модулей pi, на которых основаны каналы вычислительной системы, равны: р1=2, р2=3, р3=5, р4=7. Выберем модули p1=2, p2=3 рабочими, а р3=5, р4=7 контрольными, тогда полный диапазон будет равен Ризб=2·3·5·7=210, а рабочий Р=М=2·3=6. Допустим правильный результат равен А=(1,0,3,3), а искаженный 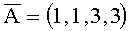 , то есть во втором разряде возникла ошибка, вместо цифры 0 появилась цифра 1, а М=(0,0,1,6).
, то есть во втором разряде возникла ошибка, вместо цифры 0 появилась цифра 1, а М=(0,0,1,6).
Для определения переполнения динамического диапазона и ошибки вычислим относительные значения  и
и 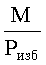 , представленные в СОК, и сравним их результаты. Для этого необходимо найти
, представленные в СОК, и сравним их результаты. Для этого необходимо найти 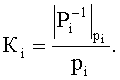 Как показано в примере 1 K1=0.5; K2≈0.333, К3=0.6, K4=0.571. Тогда
Как показано в примере 1 K1=0.5; K2≈0.333, К3=0.6, K4=0.571. Тогда
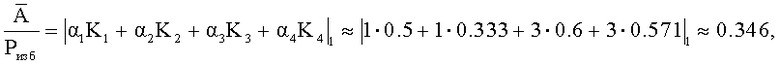
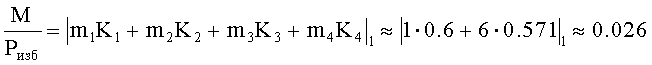
Сравним результаты: 0.346>0.026 и мы можем заключить, что 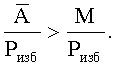 Этим неравенством установлено наличие ошибки и переполнение динамического диапазона. Для локализации ошибочного канала найдем относительные значения проекции чисел
Этим неравенством установлено наличие ошибки и переполнение динамического диапазона. Для локализации ошибочного канала найдем относительные значения проекции чисел 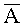 и М к Pi по каждому из оснований путем зачеркивания цифр αi и mi по основаниям pi, где Pi, диапазон чисел, соответствующий i-проекции.
и М к Pi по каждому из оснований путем зачеркивания цифр αi и mi по основаниям pi, где Pi, диапазон чисел, соответствующий i-проекции.
По основанию р1=2
Для систем с основаниями р2=3, р3=5, р4=7 получим
P1=p2p3p4=105, тогда 
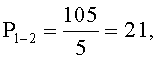
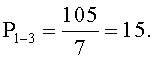
Вычислим: 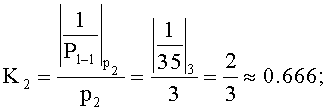

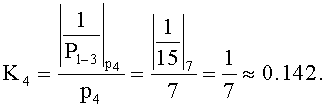
Тогда 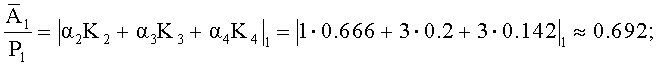
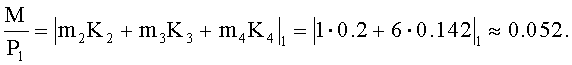
Сравним 0.692>0.052, тогда 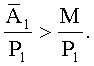
По основанию р2=3
Для систем с основаниями р1=2, р3=5, р4=7 получим
Р2=70, тогда P2-1=35, P2-3=14, P2-4=10.
Вычислим: 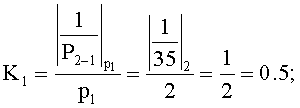
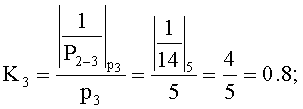

Тогда 

Сравним 0.042<0.084, тогда 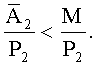
По основанию р3=5
Для систем с основаниями p1=2, p2=3, р4=7 получим
P3=42, тогда Р3-1=21, Р3-2=14, P3-4=6.
Вычислим: 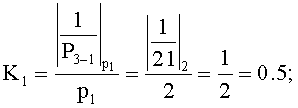


Тогда 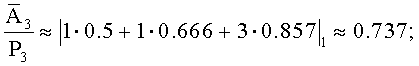
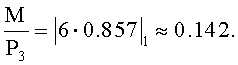
Сравним 0.737>0.142, тогда 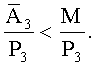
По основанию р4=7
Для систем с основаниями p1=2, p2=3, р3=5 получим
P4=30, тогда P4-1=15, P4-2=10, P4-3=6.
Вычислим: 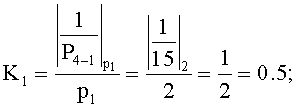

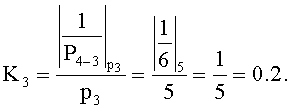
Тогда 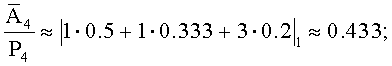
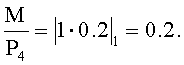
Сравним, тогда 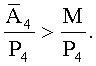
0.433>0.2
Итак все результаты сравнении 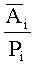 и
и 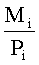 показывают, что только по основанию p2=3 относительное значение проекций числа
показывают, что только по основанию p2=3 относительное значение проекций числа 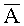 меньше, чем относительное значение константы Mi. Следовательно, ошибка произошла в канале по основанию р2.
меньше, чем относительное значение константы Mi. Следовательно, ошибка произошла в канале по основанию р2.
Рассмотрим работу устройства обнаружения переполнения динамического диапазона, определения ошибки и локализации неисправного вычислительного канала в системах, функционирующих в системе остаточных классов, которые предназначены для оперативного определения вышеизложенных функций. Схема приведена на чертеже.
Контролируемое число А по шинам 1 поступает на входные регистры 2 по соответствующим модулям: p1-регистр 2-1, р2-регистр 2-2, …, pn+r-регистр 2-n+r, а результаты в виде сигналов появляются на выходах устройства: шина 14 «ошибка не установлена»; шина 16 «переполнение диапазона и ошибка» и выходных шинах 8 «неисправный pi» канал. По шине 15 константа М, соответствующая рабочему диапазону, по избыточным модулям поступает на вход схемы формирования проекций константы М 11. В начале работы устройства поступившие сигналы на вход схемы формирования проекций числа А по основания pi и на вход схемы формирования проекции константы М по избыточным модулям напрямую проходят на блоки памяти 4 и 12 по соответствующим модулям р1, р2, …, pn и pn+1, …, pn+r. Выходные сигналы схем формирования проекций являются адресами входных блоков памяти 4 и 12, элементам которых приписываются значение произведений Kiαi и Kimi, соответственно, 4-1, 4-2, … 4-n+r и 12-n+1, …, 12-n+r. Из элементов памяти выбранные значения в виде произведений Kiαi и Kimi поступают на вход сумматоров, соответственно, 5 и 13, где проходит их суммирования по mod1, т.е. отбрасываются целые части чисел. Полученные в виде дробных значений суммы поступают на входы блока анализа на равенство больше или меньше. Если результат сумматора 5 меньше, чем результат сумматора 13, то в блоке 6 формируется сигнал «ошибка не установлена» шина 14 и процесс заканчивается. Если результат сумматора 5 больше или равен результату сумматора 13, то формируется сигнал «переполнение диапазона и ошибка», который поступают на первые входы элементов «И» и вход «s» триггера 9 и переводит его в единичное состояние, выходной сигнал которого запускает счетчик проекции 10. Сигнал с первого выхода счетчика поступает на входы схем формирования проекций 3 и 11. По этому сигналу формируется первая проекция числа 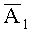 и М1, выходные сигналы которых являются адресными входами блоков 4 и 12, в элементах которых содержатся произведения Kiαi и Kimi, где Ki уже новые константы, соответствующие первой проекции. Выходные сигналы блоков памяти суммируются в сумматорах 5 и 13, результаты которых анализируются в схеме анализа 6. Если результат сумматора 5 меньше, чем результат сумматора 13, то формируется сигнал, равный единице, который поступает на все первые входы элементов «И», а на вторые входы элементов «И» поступают сигналы с выхода блока проекции 3, который соответствует первой проекции. Выходной сигнал появляется по шине 8 того элемента «И», у которого на оба входа одновременно поступают сигналы, выходной сигнал которого является индикатором неисправного канала. После анализа первой проекции счетчик проекции 10 формирует следующую проекцию и процесс контроля осуществляется аналогично. После формирования всех проекций сигнал с выхода блока проекции 3, соответствующий последней проекции, поступает на вход «R» триггера 9, выключает счетчик 10, который устанавливает в нулевое состояние. На этом процесс контроля прекращается, а устройство переходит в исходное состояние. Счетчик имеет емкость, равную n+r. После выполнения n+r проекций счетчик проекций 10 формирует сигнал окончания процесса контроля.
и М1, выходные сигналы которых являются адресными входами блоков 4 и 12, в элементах которых содержатся произведения Kiαi и Kimi, где Ki уже новые константы, соответствующие первой проекции. Выходные сигналы блоков памяти суммируются в сумматорах 5 и 13, результаты которых анализируются в схеме анализа 6. Если результат сумматора 5 меньше, чем результат сумматора 13, то формируется сигнал, равный единице, который поступает на все первые входы элементов «И», а на вторые входы элементов «И» поступают сигналы с выхода блока проекции 3, который соответствует первой проекции. Выходной сигнал появляется по шине 8 того элемента «И», у которого на оба входа одновременно поступают сигналы, выходной сигнал которого является индикатором неисправного канала. После анализа первой проекции счетчик проекции 10 формирует следующую проекцию и процесс контроля осуществляется аналогично. После формирования всех проекций сигнал с выхода блока проекции 3, соответствующий последней проекции, поступает на вход «R» триггера 9, выключает счетчик 10, который устанавливает в нулевое состояние. На этом процесс контроля прекращается, а устройство переходит в исходное состояние. Счетчик имеет емкость, равную n+r. После выполнения n+r проекций счетчик проекций 10 формирует сигнал окончания процесса контроля.
Предложенное устройство имеет лучшие как временные так и технические характеристики, которые определяют диапазон обрабатываемых данных. В известных устройствах диапазоны обрабатываемых данных определяются произведением модулей 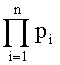 , а в предложенном устройство определяется интервалом [0,1), а точность определяется разностью между соседними целыми значениями чисел (например 1 и 2), которые должны быть ниже максимально выраженной разницы ошибки. Это обстоятельство позволяется отбросить часть младших значащих разрядов дроби. Кроме того, старшие нулевые разряды можно отбросить, так как в описанных выше механизмах сравнения нас интересуют условия «больше»; «равно» или «меньше» без указания конкретной величины, на сколько больше или меньше. Разработанное устройство является лучшим на настоящее время и может быть применено в вычислительных системах, функционирующих в СОК.
, а в предложенном устройство определяется интервалом [0,1), а точность определяется разностью между соседними целыми значениями чисел (например 1 и 2), которые должны быть ниже максимально выраженной разницы ошибки. Это обстоятельство позволяется отбросить часть младших значащих разрядов дроби. Кроме того, старшие нулевые разряды можно отбросить, так как в описанных выше механизмах сравнения нас интересуют условия «больше»; «равно» или «меньше» без указания конкретной величины, на сколько больше или меньше. Разработанное устройство является лучшим на настоящее время и может быть применено в вычислительных системах, функционирующих в СОК.
| название | год | авторы | номер документа |
|---|---|---|---|
| НЕЙРОННАЯ СЕТЬ ДЛЯ ОБНАРУЖЕНИЯ, ЛОКАЛИЗАЦИИ И ИСПРАВЛЕНИЯ ОШИБОК В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2005 |
|
RU2301442C2 |
| Устройство обнаружения и коррекции ошибки модулярного кода | 2017 |
|
RU2653257C1 |
| АДАПТИВНАЯ ПАРАЛЛЕЛЬНО-КОНВЕЙЕРНАЯ НЕЙРОННАЯ СЕТЬ ДЛЯ КОРРЕКЦИИ ОШИБОК | 2003 |
|
RU2279131C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ОБНАРУЖЕНИЯ ОШИБОК В СИММЕТРИЧНОЙ СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2007 |
|
RU2374678C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ДЕЛЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2005 |
|
RU2305312C2 |
| Система распределенного хранения данных | 2021 |
|
RU2780148C1 |
| НЕЙРОННАЯ СЕТЬ С ПОРОГОВОЙ (k, t) СТРУКТУРОЙ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2008 |
|
RU2380751C1 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ЗНАКА МОДУЛЯРНОГО ЧИСЛА | 2011 |
|
RU2503995C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ РАСШИРЕНИЯ КОРТЕЖА ЧИСЛОВОЙ СИСТЕМЫ ВЫЧЕТОВ | 2003 |
|
RU2256226C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ КОРРЕКЦИИ ОШИБОК В МОДУЛЯРНЫХ НЕЙРОКОМПЬЮТЕРАХ | 2003 |
|
RU2256213C2 |
Изобретение относится к вычислительной технике и может быть использовано при диагностике вычислительных систем для обнаружения переполнения динамического диапазона, определения ошибки и локализации неисправного канала в ЭВМ, функционирующих в системе остаточных классов. Техническим результатом является повышение скорости определения функциональных характеристик и сокращения аппаратурных затрат. Устройство содержит входные регистры, схемы формирования проекций, блоки памяти, сумматоры, схему анализа, логические элементы «И», триггер, счетчик проекций. 1 ил.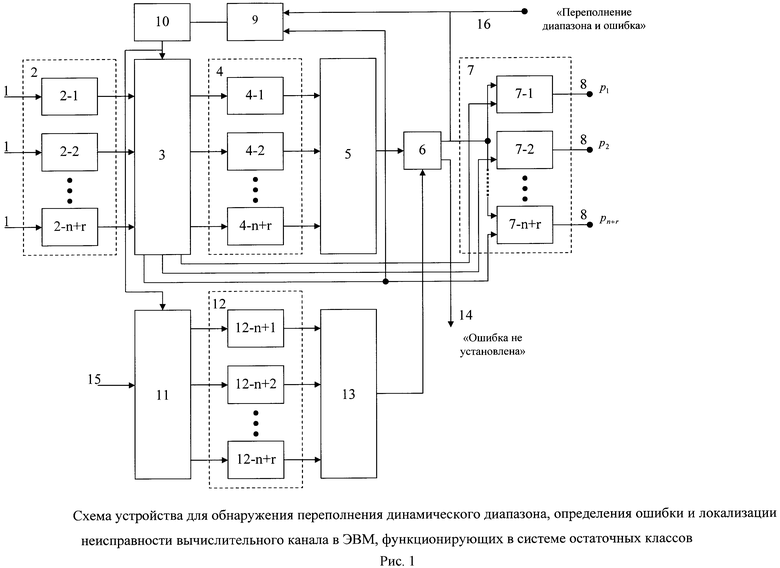
Устройство для обнаружения переполнения динамического диапазона, определения ошибки и локализации неисправности вычислительного канала в ЭВМ, функционирующих в системе остаточных классов, содержащее входные регистры, схемы формирования проекций, логические элементы, отличающееся тем, что в него включены блоки памяти для хранения значений Kiαi и Kimi, сумматоры и схема анализа, при этом контролируемое число и число, соответствующее полному диапазону с выходов входных регистров и по шине поступают на входы схем формирования проекций, выходы которых являются адресными входами блоков памяти, выходы которых соединены со входами сумматоров, а выходы сумматоров соединены со схемой анализа, выходы которой сигнализируют об отсутствии ошибки или наличии переполнения диапазона и ошибки и соединены со входом «S» триггера, один из выходов которого соединен со входом счетчика, выходы которого соединены со входами схем формирования проекций, а второй выход схемы анализа, сигнализирующий об отсутствии ошибки, соединен с первыми входами элементов «И», вторые входы которых подключены к соответствующим выходам схем формирования 1-го номера проекции, а выход последней проекции соединен со входом «R» триггера и выходы элементов «И» и выходы «Переполнение диапазона и ошибка» и «Ошибка не установлена» являются выходами устройства.
| АДАПТИВНАЯ ПАРАЛЛЕЛЬНО-КОНВЕЙЕРНАЯ НЕЙРОННАЯ СЕТЬ ДЛЯ КОРРЕКЦИИ ОШИБОК | 2003 |
|
RU2279131C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ОБНАРУЖЕНИЯ, ЛОКАЛИЗАЦИИ И ИСПРАВЛЕНИЯ ОШИБОК В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2005 |
|
RU2301442C2 |
| US 2009006509 A1, 01.01.2009 | |||
| JP 59060653 A, 06.04.1984 | |||
| JP 63286026 A, 22.11.1988. | |||
Авторы
Даты
2013-05-27—Публикация
2011-11-10—Подача