УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ УГЛОВОГО ОТКЛОНЕНИЯ ОСИ ЛАЗЕРНОГО ПУЧКА ОТ НОМИНАЛЬНОГО ПОЛОЖЕНИЯ Российский патент 2013 года по МПК G01B11/26 

Изобретение относится к области оптического приборостроения, точнее - к оптическим призменным системам, предназначенным для определения углового отклонения оси лазерного пучка от номинального положения.

Оптические оси приемного и передающего каналов лазерных систем должны быть выставлены с необходимой точностью. В некоторых случаях это удается обеспечить на стадии заводской юстировки. К таким системам относятся малогабаритные оптические дальномеры, лазерные системы видения. Они отличаются сравнительно невысокими требованиями по юстировки осей каналов - погрешности выставки могут достигать нескольких угловых минут.

Для целого ряда современных локационных систем выдвигаются очень высокие требования по точности юстировки приемо-передающих каналов - погрешности их взаимной выставки не должны превышать нескольких угловых секунд. Как правило, такие системы имеют значительные габариты, вес, они могут быть подвержены воздействию внешних механических вибраций и температурным уводам элементов конструкции. Требования по точности юстировки каналов таких систем могут быть выполнены только с использованием систем автоюстировки (САЮ).

Принцип организации подобной САЮ заключается в следующем. Часть пучка излучения рабочего лазера передающего канала на выходе системы формирования с помощью призменной системы (ПС) заводится в приемный канал, меняя направление распространения в точности на обратное. Отведенный пучок в приемном канале является репером пространственного положения оси диаграммы направленности излучения рабочего лазера, сформированного в передающем канале. В приемном канале измеряется его угловое рассогласование с осью приемного канала, которое в реальном масштабе времени отрабатывается корректирующими элементами оптической системы.

В большинстве случаев в приемный канал целесообразно отводить пучок излучения не рабочего лазера, а дополнительного маркерного источника излучения, имеющего гораздо меньшую мощность и поперечные размеры. Предварительно его ось выставляется на входе оптической системы передающего канала относительно оси пучка излучения рабочего лазера с высокой точностью.

Как видно, погрешности определения углового рассогласования определяются погрешностью переноса пучка, поэтому ПС в такой САЮ играет ключевую роль. Схемы их построения должны быть обоснованы с учетом условий функционирования, а точностные характеристики каждой схемы должны быть тщательно исследованы.

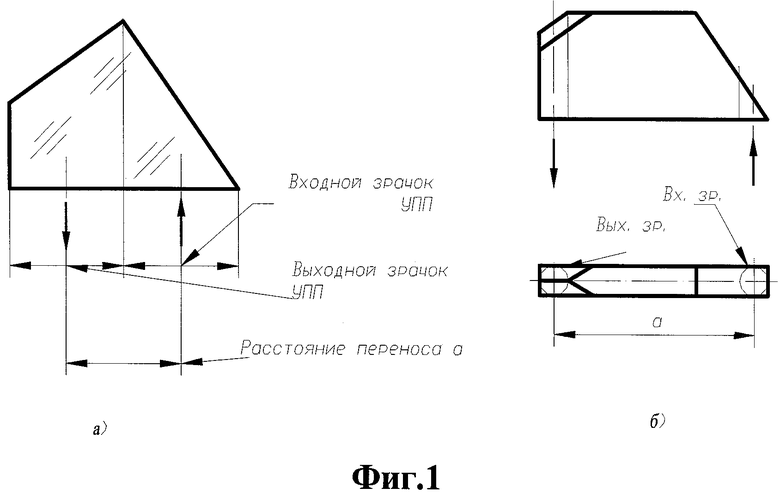
Известно, что уголковый отражатель с двугранными углами между отражающими гранями, равными 90°, является идеальным световозвращателем [Барышников Н.В., Карасик В.Е., Степанов P.O. Исследование отражательных характеристик тетраэдрических световозвращателей в ИК диапазоне. Вестник МГТУ им. Н.Э.Баумана. Сер. «Приборостроение», 2010. №1, С.3-16]. Он отражает падающее на него излучение точно в обратном направлении (см. фиг.1a). Матрица М_УО его действия имеет следующий вид:

$${М}_{УО}=\left(\begin{array}{ccc}-1& 0& 0\\ 0& -1& 0\\ 0& 0& -1\end{array}\right)\left(1\right)$$

Теоретически - это идеальный вариант ПС. Однако расстояние а переноса оси пучка излучения минимально и оно ограничено конструктивными параметрами уголкового отражателя и технологическими возможностями его изготовления.

Модификация конструкции уголкового отражателя - УО с разнесенными входным и выходным зрачками (см. фиг.1б) обеспечивает несколько большие значения расстояния переноса a - до 100…200 мм. На этом возможности уголкового отражателя ограничиваются.

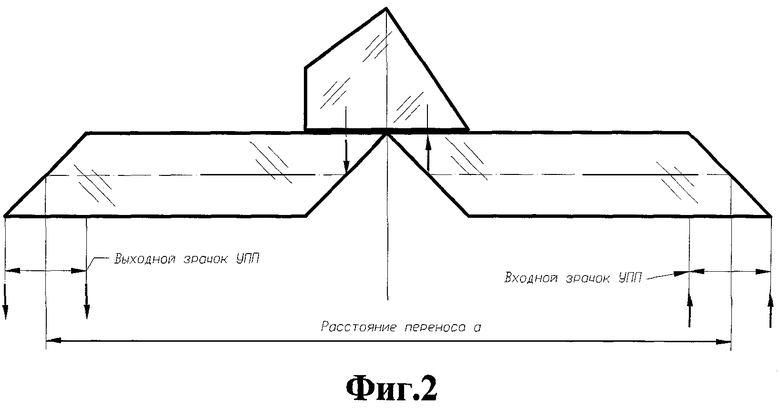
Известно устройство для определения углового отклонения оси лазерного пучка от номинального положения (см. фиг.2), которое является ближайшим аналогом и включает призменную систему, содержащую оптически связанные ромб призму 1, уголковый отражатель и ромб-призму 2 (Н.В. Барышников, В.В. Карачунский, В.И. Козинцев А.С. Румянцев, Д.В. Худяков, Использование методов полунатурного моделирования для исследования характеристик системы автоюстировки Тезисы докладов IV НТК «Радиооптические технологии в приборостроении», Сочи, 2006 г., с.105-108). Эта система обеспечивает большие значения расстояния переноса a.

Идеально изготовленная ромб-призма осуществляет поперечное смещение оси падающего пучка, не меняя его направления. Матрица ее действия М_РП имеет следующий вид:

$${М}_{РП}=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)$$

Действие рассматриваемой ПС можно описать матрицей M:

$$М={М}_{РП2}\cdot {М}_{УО}\cdot {М}_{РП1}=\left(\begin{array}{ccc}-1& 0& 0\\ 0& -1& 0\\ 0& 0& -1\end{array}\right)=\text{}{М}_{УО}$$

Нетрудно заметить, что матрица M соответствует матрице уголкового отражателя (1).

Каждая из трех оптических деталей схемы при малых собственных угловых смещениях идеально переносит ось пучка, поэтому такая система инвариантна к механическим вибрациям и температурным уводам механических оправ. На качество переноса могут повлиять только собственные температурные деформации уголкового отражателя и ромб-призм, а также погрешности их изготовления.

Для увеличения расстояния переноса a в схему ПС можно включить дополнительные ромб-призмы. Их максимальное количество определяется только светопропусканием призменной системы, а также массогабаритными ограничениями.

Однако существует принципиальный недостаток рассмотренных выше схем. Он связан с тем, что элементы конструкции ПС могут располагаются на выходе формирующей оптической системы передающего канала, в сечении пучка высокоэнергетического рабочего лазера. Это обстоятельство вызывает многочисленные проблемы, связанные с защитой конструкции самой ПС от излучения рабочего лазера, а также с нарушениями пространственной структуры формируемого пучка рабочего лазера, вызванные его экранированием.

Технический результат, достигаемый при реализации предлагаемого изобретения, заключается в обеспечении возможности определения углового отклонения оси лазерного пучка от номинального положения при использовании высокоэнергетического лазера и с одновременным уменьшением экранирования сечения его пучка в условиях внешних механических воздействий, приводящих к угловым уводам призм призменной системы.

Указанный технический результат достигается за счет того, что в устройстве для определения углового отклонения оси лазерного пучка от номинального положения, содержащем призменную систему, указанная призменная система включает первую пару пентапризм, содержащую первую и вторую пентапризмы, главные сечения которых расположены в одной плоскости Р, оптический клин, склеенный с первой отражающей гранью первой пентапризмы и выполненный так, что его выходная грань параллельна входной грани первой пентапризмы, причем поверхность склейки имеет светоделительное покрытие, вторую пару пентапризм, содержащую третью и четвертую пентапризмы, главные сечения которых расположены в одной плоскости Р', при этом входная грань третьей пентапризмы расположена за выходной гранью оптического клина и параллельна ей, плоскости Р и Р' расположены под углом 2φ друг к другу, а вторая и четвертая пентапризмы оптически связаны с объективом, в фокальной плоскости которого расположен координатно-чувствительный фотоприемник, выход которого связан со входом микропроцессора.

При этом микропроцессор может быть выполнен с возможностью вычисления углового отклонения θ_Z, θ_Y оси контролируемого пучка от номинального положения на входе первой пентапризмы по формулам:

θ_z=(-θ_y1sinφ+θ_z1cosφ+θ_y2sinφ+θ_z2cosφ)/2cosφ,

θ_y=(θ_y2sinφ+θ_z2cosφ+θ_y1sinφ-θ_z1cosφ)/2sinφ,

где θ_y1; θ_z1 - угловое отклонение от номинального положения оси лазерного пучка, прошедшего первую и вторую пентапризмы;

θ_y2; θ_z2 - угловое отклонение от номинального, положения оси лазерного пучка, прошедшего первую, третью и четвертую пентапризмы.

В предлагаемом устройстве за счет того, что вместо системы призм в виде моноблока, как в ближайшем аналоге, используются отдельные пентапризмы, обеспечивается уменьшение экранирования сечения его пучка. При этом оптические свойства пентапризм позволяет создать призменную систему, обеспечивающую определение углового отклонения оси лазерного пучка от номинального положения в условиях внешних механических воздействий, приводящих к угловым уводам призм призменной системы.

Изобретение более подробно описывается с помощью чертежей.

На фиг.1а, 1б показана призменная система на основе уголкового отражателя.

На фиг.2 показана призменная система ближайшего аналога на основе уголкового отражателя и двух ромб-призм.

На фиг.3 показано расположение призменной системы устройства для определения углового отклонения оси лазерного пучка от номинального положения в локационной станции.

На фиг.4 показана схема, иллюстрирующая определение углового отклонение от номинального положения оси лазерного пучка с помощью координатно-чувствительного фотоприемника при отсутствии угловых уводов призм призменной системы.

На фиг.5 показана призменная система предлагаемого устройства на основе двух пар пентапризм.

На фиг.6 показано расположение системы координат XYZ и связанной с ней нормали $$\overline{N}$$ по отношению к входной грани пентапризмы.

На фиг.4 показана схема, иллюстрирующая определение углового отклонение от номинального положения оси лазерного пучка с помощью координатно-чувствительного фотоприемника при отсутствии угловых уводов призм призменной системы.

Система координат XYZ связана с оптической осью системы, образованной объективом и координатно-чувствительным, например, матричным фотоприемником, расположенным в его фокальной плоскости. Центр координат O совпадает с нулевым чувствительным элементом матричного фотоприемника. При этом обычно в качестве нулевого элемента используется элемент, расположенный в центре матрицы чувствительных элементов. Ось OX выбранной системы координат XYZ совпадает с оптической осью системы, образованной объективом и матричным фотоприемником, расположенным в его фокальной плоскости, и проходит через кардинальные точки объектива и нулевой элемент матричного фотоприемника.

Таким образом, для того, чтобы определить угловой отклонение оси пучка по двум координатам, надо измерить линейные координаты Z1 и Y1 зарегистрированного на матричном фотоприемнике, расположенном в фокальной плоскости объектива, пятна распределения от контролируемого пучка излучения лазера. При этом угловое отклонение θ_Y в плоскости XOY может быть определено из математического выражения

tg(θ_Y)=Y1/f',

где f' - фокусное расстояние объектива.

Аналогично, угловое отклонение θ_Z в плоскости XOZ (на фиг.4 не показано) может быть определено из математического выражения

tg(θ_Z)=Z1/f'.

При этом, как правило, измеряемые угловые отклонения малы, они составляют несколько угловых секунд. Поэтому тангенсом можно пренебречь, т.е. использовать следующие выражения:

θ_Y=Y1/f', θ_Z=Z1/f'

На фиг.5 показана призменная система предлагаемого устройства на основе двух пар пентапризм.

Как известно, пентапризма изменяет в пространстве вектор направления падающего на нее пучка на 90 градусов по одной оси, причем этот угол инвариантен к малым угловым уводом самой пентапризмы. Используя пару пентапризм, можно обеспечить обратное отражение излучения лазера и измерение в приемном канале углового отклонения, но только по одной оси.

Для измерения угловых отклонений по двум осям в условиях внешних механических воздействий, приводящим к угловым уводам самих призм, предлагается устройство, которое содержит призменную систему, включающую первую пару пентапризм, содержащую первую 1 и вторую 2 пентапризмы. Главные сечения этих пентапризм расположены в одной плоскости Р. Вторая пара пентапризм содержит третью 3 и четвертую 4 пентапризмы, главные сечения которых расположены в одной плоскости Р'. Плоскости Р и Р' расположены под углом 2φ друг к другу. Разделение лазерного пучка между парами призм осуществляется с помощью оптического клина 5, имеющего тот же показатель преломления, что и первая 1 пентапризма, и склеенного с первой отражающей гранью первой 1 пентапризмы, причем поверхность склейки 6 имеет светоделительное полуотражающее покрытие, а выходная грань клина параллельна входной грани первой 1 пентапризмы. Входная грань третьей 3 пентапризмы расположена за выходной гранью оптического клина 5 и параллельна ей. На выходе второй 2 и четвертой 4 пентапризм расположен объектив 7, в фокальной плоскости которого расположен координатно-чувствительный фотоприемник 8, выход которого связан со входом микропроцессора 9.

При этом микропроцессор выполнен с возможностью вычисления углового отклонения θ_Z, θ_Y оси контролируемого пучка от номинального положения на входе первой 1 пентапризмы по формулам:

θ_z=(-θ_y1sinφ+θ_z1cosφ+θ_y2sinφ+θ_z2cosφ)/2cosφ,

θ_y=(θ_y2sinφ+θ_z2cosφ+θ_y1sinφ-θ_z1cosφ)/2sinφ,

где θ_y1; θ_z1 - угловое отклонение от номинального положения оси лазерного пучка, прошедшего первую 1 и вторую 2 пентапризмы;

θ_y2, θ_z2 - угловое отклонение от номинального положения оси лазерного пучка, прошедшего первую 1, третью 3 и четвертую 4 пентапризмы.

Проследим преобразование такой призменной системой вектора $${\overrightarrow{L}}_0$$ луча, характеризующего направление пучка лазерного излучения на входе в призменную систему, т.е. на выходе передающего канала локационной системы.

Свяжем с оптической осью объектива приемного канала систему координат X₀Y₀Z₀. Ось OX₀ направим по оптической оси объектива приемного канала.

В этой же системе координат будем в дальнейшем определять направление вектора $${\overrightarrow{L}}_{np}$$ , характеризующего направление пучка излучения лазера на входе объектива приемного канала системы. Вектор $${\overrightarrow{L}}_0$$ в системе координат X₀Y₀Z₀ выражается следующим образом:

$${\overrightarrow{L}}_0=\left(\begin{array}{c}-1\\ {\theta }_y\\ {\theta }_z\end{array}\right),\left(5\right)$$

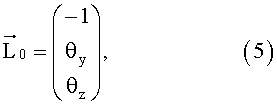
где θ_y и θ_z - углы отклонения оси излучения лазера от идеального направления, вызванные разъюстировками системы. Именно эти углы необходимо измерить в приемном канале.

Получим несколько общих выражений для матриц преобразования пентапризмы. Эти выражения в дальнейшем будем использовать для описания преобразования вектора $$\overrightarrow{L}$$ направления оси излучения лазера парой пентапризм, пространственное положение каждой из которых имеет отступления от идеального.

Рассмотрим систему координат XYZ (см. фиг.6) и связанную с ней нормаль 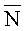$$\overline{N}$$ к входной грани пентапризмы.

1. Матрицы П' и П'' действия идеальной пентапризмы соответственно в прямом и в обратном ходе, записанные в приведенной системе координат, определяются известным образом [Вычислительная оптика: Справочник / М.М. Русинов, А.П. Грамматин, П.Д. Иванов и др. Под общ. ред. М.М. Русинова. - Л.: Машиностроение. Ленинградское отд-ние, 1984, с.110] как:

$$П\text{'}=\left(\begin{array}{ccc}0& 0& -1\\ 0& 1& 0\\ 1& 0& 0\end{array}\right),П\text{'}\text{'}\left(\begin{array}{ccc}0& 0& 1\\ 0& 1& 0\\ -1& 0& 0\end{array}\right)\left(6\right)$$

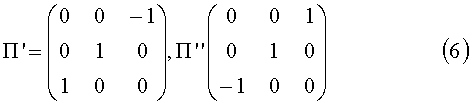
Нестабильность пространственного положения пентапризмы приводит к повороту вектора $$\overline{N}$$ в рассматриваемой системе координат. Будем считать, что повороты происходят в следующей последовательности:

- вокруг оси OZ на угол α;

- вокруг новой оси OY' на угол β;

- вокруг новой оси OX'' на угол γ.

Соответствующие этим поворотам матрицы преобразования имеют следующий вид [Вычислительная оптика: Справочник / М.М. Русинов, А.П. Грамматин, П.Д. Иванов и др. Под общ. ред. М.М. Русинова. - Л.: Машиностроение. Ленинградское отд-ние, 1984, с.121]:

$$M_z=\left(\begin{array}{ccc}\cos \alpha & -\sin \alpha & 0\\ \sin \alpha & \cos \alpha & 0\\ 0& 0& 1\end{array}\right);M_y=\left(\begin{array}{ccc}\cos \beta & 0& -\sin \beta \\ 0& 1& 0\\ \sin \beta & 0& \cos \beta \end{array}\right);M_x=\left(\begin{array}{ccc}1& 0& 0\\ 0& \cos \gamma & \sin \gamma \\ 0& -\sin \gamma & \cos \gamma \end{array}\right)(7)$$

Действие всех трех поворотов на произвольный вектор $$\overline{N}$$ описывается матрицей M:

$$M=M_x\cdot M_y\cdot M_z\left(8\right)$$

Пусть $$\overrightarrow{L}$$ - вектор падающего на пентапризму луча, записанный в системе координат XYZ. Тогда вектор $$\overrightarrow{L}\text{'}$$ луча, преобразованного пентапризмой, пространственное положение которой имеет отступления от номинального, можно определить следующим образом:

$$\overrightarrow{L}\text{'}=\left(M\cdot П\text{'}\cdot M^{-1}\right)\cdot \overrightarrow{L}=T\cdot \overrightarrow{L},\left(9\right)$$

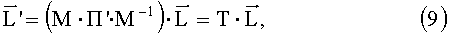
где: T=M·П'·М^-1;

Будем считать, что углы поворота α, β, γ в схеме малы. Тогда с точностью до членов второго порядка малости по углам поворота, с учетом (7) и (8) можно записать выражения для M и M^-1:

$$M=\left(\begin{array}{ccc}1& -\sin \alpha & -\sin \beta \\ \sin \alpha & 1& \sin \gamma \\ \sin \beta & -\sin \gamma & 1\end{array}\right)=\left(\begin{array}{ccc}1& -\alpha & -\beta \\ \alpha & 1& \gamma \\ \beta & -\gamma & 1\end{array}\right)$$ ,

$$M^{-1}=\left(\begin{array}{ccc}1& \sin \alpha & \sin \beta \\ -\sin \alpha & 1& -\sin \gamma \\ -\sin \beta & \sin \gamma & 1\end{array}\right)=\left(\begin{array}{ccc}1& \alpha & \beta \\ -\alpha & 1& -\gamma \\ -\beta & \gamma & 1\end{array}\right)$$ .

Отсюда следует, что

$$T=M\cdot П\text{'}\cdot M^{-1}=\left(\begin{array}{ccc}0& -\alpha -\gamma & -1\\ -\alpha +\gamma & 1& -\alpha -\gamma \\ 1& \alpha -\gamma & 0\end{array}\right)\left(10\right)$$

С учетом (9) и (10), на выходе из пентапризмы направление вектора $$\overrightarrow{L}\text{'}$$ будет определяться:

$$\overrightarrow{L}\text{'}=\left(\begin{array}{c}0\\ \alpha -\gamma \\ -1\end{array}\right)\left(11\right)$$

Этот вектор лежит в плоскости XOZ (т.е. перпендикулярен нормали луча на входе в пентапризму) и угол между осью OZ и этим лучом равен α-γ.

Используя полученные выражения, можно описать преобразование излучения лазера парой пентапризм, например, первой 1 и второй 2 пентапризмами, каждая из которых имеет свои случайные отклонения от номинального положения.

Вектор $${\overrightarrow{L}}_0$$ (5) записан в системе координат X₀Y₀Z₀. Запишем вектор $${\overrightarrow{L}}_1$$ , соответствующий вектору $${\overrightarrow{L}}_0$$ , но уже в системе координат X₁Y₁Z₁, связанной с первой 1 пентапризмой первой пары пентапризм. Для этого используем известное выражение (7) для матрицы M_φ разворота системы координат вокруг оси OX на угол φ:

$$\begin{array}{l}{\overrightarrow{L}}_1=M_{\phi }\cdot {\overrightarrow{L}}_0=\left(\begin{array}{ccc}1& 0& 0\\ 0& \cos \phi & \sin \phi \\ 0& -\sin \phi & \cos \phi \end{array}\right)\cdot \left(\begin{array}{c}-1\\ {\theta }_y\\ {\theta }_z\end{array}\right)=\\ =\left(\begin{array}{c}-1\\ \cos \phi \cdot {\theta }_y+\sin \phi \cdot {\theta }_z\\ -\sin \phi \cdot {\theta }_y+\cos \phi \cdot {\theta }_z\end{array}\right)=\left(\begin{array}{c}-1\\ {\theta }_y^{\text{'}}\\ {\theta }_z^{\text{'}}\end{array}\right)\left(12\right)\end{array}$$

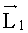
В системе координат X₁Y₁Z₁ вектор луча $${\overrightarrow{L}}_1^{\text{'}}$$ на выходе первой 1 пентапризмы с учетом (10) и (11) находим следующим образом:

$${\overrightarrow{L}}_1^{\text{'}}=T_1\cdot {\overrightarrow{L}}_1=\left(\begin{array}{ccc}0& -{\alpha }_1-{\gamma }_1& -1\\ -{\alpha }_1+{\gamma }_1& 1& -{\alpha }_1-{\gamma }_1\\ 1& {\alpha }_1-{\gamma }_1& 0\end{array}\right)\left(\begin{array}{c}-1\\ {\theta }_y^{\text{'}}\\ {\theta }_z^{\text{'}}\end{array}\right)=\left(\begin{array}{c}-{\theta }_z^{\text{'}}\\ -{\alpha }_1-{\gamma }_1+{\theta }_y^{\text{'}}\\ -1\end{array}\right)$$

где: α₁, γ₁ - углы разворота первой призмы:

$$T_1=\left(\begin{array}{ccc}0& -{\alpha }_1-{\gamma }_1& -1\\ -{\alpha }_1+{\gamma }_1& 1& -{\alpha }_1-{\gamma }_1\\ 1& {\alpha }_1-{\gamma }_1& 0\end{array}\right)$$ .

Свяжем со второй 2 пентапризмой систему координат X₂Y₂Z₂ (см. рисунок 3a), ориентированную относительно самой призмы так же, как система координат X₁Y₁Z₁ ориентирована относительно первой 1 пентапризмы. Преобразуем вектор 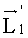$${\overrightarrow{L}}_1^{\text{'}}$$ в вектор $${\overrightarrow{L}}_2$$ , записанный в системе координат X₂Y₂Z₂:

$${\overrightarrow{L}}_2=\left(\begin{array}{c}-1\\ {\alpha }_1-{\gamma }_1+{\theta }_y^{\text{'}}\\ {\theta }_z^{\text{'}}\end{array}\right)$$

Преобразование вектора $${\overrightarrow{L}}_2$$ второй пентапризмой можно записать как:

$$\begin{array}{l}\overrightarrow{L_2^{\text{'}}}=T_2\cdot \overrightarrow{L_2}=\left(\begin{array}{ccc}0& -{\alpha }_2-{\gamma }_2& -1\\ -{\alpha }_2+{\gamma }_2& 1& -{\alpha }_3-{\gamma }_2\\ 1& {\alpha }_2-{\gamma }_2& 0\end{array}\right)\left(\begin{array}{c}-1\\ {\alpha }_1-{\gamma }_1+{\theta }_y^{\text{'}}\\ {\theta }_z^{\text{'}}\end{array}\right)=\\ =\left(\begin{array}{c}-{\theta }_z^{\text{'}}\\ \left({\alpha }_1-{\gamma }_1\right)+\left({\alpha }_2-{\gamma }_2\right)+{\theta }_y^{\text{'}}\\ -1\end{array}\right)\end{array}$$

где: α₂, γ₂ - углы разворота второй призмы;

$$T_2=\left(\begin{array}{ccc}0& -{\alpha }_2-{\gamma }_2& -1\\ -{\alpha }_2+{\gamma }_2& 1& -{\alpha }_2-{\gamma }_2\\ 1& {\alpha }_2-{\gamma }_2& 0\end{array}\right)$$ .

Запишем этот вектор в системе координат X₁Y₁Z₁ (см. рисунок 3a):

$${\overrightarrow{L}}_2^{\text{'}\ast }=\left(\begin{array}{c}1\\ \left({\alpha }_1-{\gamma }_1\right)+\left({\alpha }_2-{\gamma }_2\right)+{\theta }_y^{\text{'}}\\ -{\theta }_z^{\text{'}}\end{array}\right)\left(13\right)$$

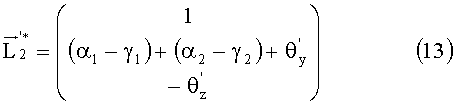
И, наконец, запишем его в системе координат X₀Y₀Z₀, используя матрицу разворота вокруг оси OX (7) на угол -φ. Таким образом, получаем искомый вектор $${\overrightarrow{L}}_{np}$$ луча на входе в приемную систему, записанный в системе координат X₀Y₀Z₀:

$$\begin{array}{l}\overrightarrow{L_{np}}=M_{\left(-\varphi \right)}{\overrightarrow{L}}_2^{\text{'}\ast }=\left(\begin{array}{ccc}1& 0& 0\\ 0& \cos \left(-\varphi \right)& \sin \left(-\varphi \right)\\ 0& -\sin \left(-\varphi \right)& \cos \left(-\varphi \right)\end{array}\right)\cdot \left(\begin{array}{c}1\\ \omega +{\theta }_y^{\text{'}}\\ -{\theta }_z^{\text{'}}\end{array}\right)=\\ =\left(\begin{array}{c}1\\ \left(\omega +{\theta }_y^{\text{'}}\right)\cos \varphi +{\theta }_z^{\text{'}}\cdot \sin \varphi \\ \left(\omega +{\theta }_y^{\text{'}}\right)\sin \varphi -{\theta }_z^{\text{'}}\cdot \cos \varphi \end{array}\right)=\left(\begin{array}{c}1\\ {\theta }_{ynp}\\ -{\theta }_{znp}\end{array}\right)\left(14\right)\end{array}$$

где ω=(α₁-γ₁)+(α₂-γ₂).

Анализируя выражение (14), можно заключить, что прямые измерения угловых отклонений θ_ynp и θ_znp вектора $${\overrightarrow{L}}_{np}$$ на выходе пары пентапризм не позволяют определить искомые угловые отклонения θ_y и θ_z вектора $${\overrightarrow{L}}_0$$ , т.к. в выражении для θ_ynp и θ_znp присутствуют углы α₁, γ₁, α₂, γ₂ отклонения пентапризм от номинального положения.

Обратим внимание, что в выражении (13) присутствует 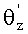$${\theta }_z^{\text{'}}$$ , на которую не влияют случайные возмущения (см. (12)). Используя это выражение, можно найти искомые значения θ_y и θ для луча на выходе передающего канала по следующей методике:

2. В системе координат X₀Y₀Z₀ измеряются угловые отклонения θ_ynp и θ_znp вектора 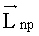$${\overrightarrow{L}}_{np}$$ , характеризующего направление оси пучка излучения лазера на выходе второй пентапризмы 2.

3. Эти значения пересчитываются в систему координат X₁X₁Z₁ с учетом разворота на угол φ, аналогично выражению (12). Получаем вектор $${\overrightarrow{L}}_2^{\text{'}}{}^{\ast }$$ . Как следует из выражений (13) и (12), значение $${\theta }_z^{\text{'}}$$ этого вектора определяется для первой пары пентапризм 1 и 2 следующим образом:

$${\theta }_z^{\text{'}}=-{\theta }_{y1}\sin \varphi +{\theta }_{z1}\cos \varphi ={\theta }_{z1}^{\text{'}}\left(15\right)$$

Проделаем аналогичные преобразования для второй пары пентапризм, т.е. для третьей 3 и четвертой 4 пентапризм. Учтем, что для этой пары угол φ имеет отрицательное значение. В результате получаем выражение для $${\theta }_{z2}^{\text{'}}$$ :

$${\theta }_{z2}^{\text{'}}={\theta }_{y2}\sin \varphi +{\theta }_{z2}\cos \varphi \left(16\right)$$

3. Имея эти два измерения, определяем искомые значения θ_y и θ_z:

$${\theta }_z=\left({\theta }_{z1}^{\text{'}}+{\theta }_{z2}^{\text{'}}\right)/2\cos \varphi$$ $${\theta }_y=\left({\theta }_{z2}^{\text{'}}-{\theta }_{z1}^{\text{'}}\right)/2\sin \varphi$$

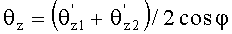
Или, с учетом (15) и (16):

$${\theta }_z=\left(-{\theta }_{y1}\sin \varphi +{\theta }_{z1}\cos \varphi +{\theta }_{y2}\sin \varphi +{\theta }_{z2}\cos \varphi \right)/2\cos \varphi (17)$$

θ_y=(θ_y2sinφ+θ_z2cosφ+θ_y1sinφ-θ_z1cosφ)/2sinφ

Таким образом, полученные выражения (17) показывают, что предлагаемое устройство для определения углового отклонения оси лазерного пучка от номинального положения, содержащее призменную систему, построенную на основе двух пар пентапризм, обеспечивает определение углового отклонения оси лазерного пучка от номинального положения в условиях внешних механических воздействий, приводящих к угловым уводам призм призменной системы. Важно отметить, что при использовании в системе высокоэнергетического рабочего лазера предложенная призменная система позволяет уменьшить и даже практически исключить экранирование сечения его пучка.

Устройство содержит призменную систему, включающую первую пару пентапризм, содержащую первую и вторую пентапризмы, главные сечения которых расположены в одной плоскости Р, оптический клин, склеенный с первой отражающей гранью первой пентапризмы и выполненный так, что его выходная грань параллельна входной грани первой пентапризмы, причем поверхность склейки имеет светоделительное покрытие, вторую пару пентапризм, содержащую третью и четвертую пентапризмы, главные сечения которых расположены в одной плоскости Р'. Входная грань третьей пентапризмы расположена за выходной гранью оптического клина и параллельна ей. Плоскости Р и Р' расположены под углом 2φ друг к другу. Вторая и четвертая пентапризмы оптически связаны с объективом, в фокальной плоскости которого расположен координатно-чувствительный фотоприемник, выход которого связан со входом микропроцессора. Технический результат - определение углового отклонения оси лазерного пучка при использовании высокоэнергетического лазера с одновременным уменьшением экранирования сечения его пучка в условиях внешних механических воздействий, приводящих к угловым уводам призм призменной системы. 1 з.п. ф-лы, 6 ил.

1. Устройство для определения углового отклонения оси лазерного пучка от номинального положения, содержащее призменную систему, включающую первую пару пентапризм, содержащую первую и вторую пентапризмы, главные сечения которых расположены в одной плоскости Р, оптический клин, склеенный с первой отражающей гранью первой пентапризмы и выполненный так, что его выходная грань параллельна входной грани первой пентапризмы, причем поверхность склейки имеет светоделительное покрытие, вторую пару пентапризм, содержащую третью и четвертую пентапризмы, главные сечения которых расположены в одной плоскости Р', при этом входная грань третьей пентапризмы расположена за выходной гранью оптического клина и параллельна ей, плоскости Р и Р' расположены под углом 2φ друг к другу, а вторая и четвертая пентапризмы оптически связаны с объективом, в фокальной плоскости которого расположен координатно-чувствительный фотоприемник, выход которого связан со входом микропроцессора.

2. Устройство по п.1, отличающееся тем, что микропроцессор выполнен с возможностью вычисления углового отклонения θ_Z, θ_Y оси контролируемого пучка от номинального положения на входе первой пентапризмы по формулам:
θ_z=(-θ_y1sinφ+θ_z1cosφ+θ_y2sinφ+θ_z2cosφ)/2cosφ,
θ_y=(θ_y2sinφ+θ_z2cosφ+θ_y1sinφ-θ_z1cosφ)/2sinφ,
где θ_y1; θ_z1 - угловое отклонение от номинального положения оси лазерного пучка, прошедшего первую и вторую пентапризмы;
θ_y2; θ_z2 - угловое отклонение от номинального положения оси лазерного пучка, прошедшего первую, третью и четвертую пентапризмы.