Изобретение относится к области космонавтики, а именно к определению параметров орбиты космического объекта (КО), например, космического мусора, бортовыми средствами космического аппарата (КА).
Изобретение может быть использовано при обеспечении безопасности полетов КА путем обнаружения и точного определения средствами бортового комплекса параметров движения потенциально опасных КО, оценки динамики сближений КА и КО и определения необходимости выработки импульса корректирующего маневра уклонения КА от КО.
Известен «Способ определения параметров орбиты космического аппарата» патент RU №2150414, опубликовано 10.06.2000 - (Д1), заключающийся в выполнении измерений траекторных параметров, передаче на комплекс управления совокупности измеренных значений траекторных параметров с последующим их накоплением и обработкой по методу наименьших квадратов. Причем после окончания итерационного процесса исключают отдельные аномальные значения, корректируют точность измерений обрабатываемых траекторных параметров, после чего циклически повторяют обработку до ее завершения и получения оптимальной оценки орбитальных параметров движения КА в зоне измерений выполненного сеанса связи. Основным недостатком способа является низкая оперативность траекторных измерений параметров космического объекта и, следовательно, расчета орбитальных данных из-за ограничения зон радиовидимости объекта наземными средствами и циклического повторения обработки вычислений.
Известен «Параллактический способ определения координат объекта» патент RU №2027144, опубликовано 20.01.1995 - (Д2), основанный на применении бинокулярной системы оптических датчиков, разнесенных на базовое расстояние относительно друг друга и имеющих параллельные оптические оси. Технические средства, реализующие данный способ, описаны в источниках информации: «Распознавание в системах автоконтроля» / Шибанов Г.П., М.: Машиностроение, 1973, с.176-188 - (Д3); «Голографическое опознавание образов» / Василенко Г.И., М.: Советское радио, 1977, рис.4.21, с.282-283 - (Д4). Данный способ позволяет на основе измеренного параллактического смещения треков прохождения космических объектов, зафиксированных в ПЗС-матрицах (ПЗС-приборы с зарядовой связью) осуществлять определение расстояний - Δr (фиг.1) между космическим аппаратом и космическим объектом и угла - β (фиг.2, фиг.3) между плоскостью движения космического аппарата и направлением от космического аппарата до космического объекта. Основным недостатком способа является сравнительно низкое быстродействие при определении орбитальных параметров в связи с использованием вычислительных алгоритмов, связанных с необходимостью проведения итерационных расчетов при решении краевых задач.
Наиболее близким по совокупности существенных признаков к изобретению является способ, описанный в научном журнале «Американского Института Аэронавтики и Астронавтики» (US) в публикации Mark Psiaki «Autonomous orbit determination for two spacecraft from relative position measurements)) за номером AIAA-98-4560, опубликовано 10.08.1998 - (Д5), его адрес в Интернете http://arc.aiaa.org/doi/abs/10.2514/6.1998-4560. В данном способе используют измерения расстояния и бокового смещения космического аппарата относительно второго космического аппарата, определение расстояний между которыми осуществляют с помощью лазерных дальномеров. По совокупности существенных признаков этот способ выбран в качестве прототипа к изобретению. Основным недостатком, ограничивающим применение данного способа, является обязательное наличие средств лазерной локации на обоих космических объектах.
В изобретении данная проблема решена применением бинокулярной системы оптических датчиков, располагаемых на борту КА.
Сущность изобретения заключается в вычислении параметров орбиты космического объекта: фокального параметра - P(ti), истинной аномалии - ϑ(ti), эксцентриситета - e(ti) и наклонения орбиты - iко космического объекта в момент времени ti в соответствии с полученными аналитическим методом математическими зависимостями. При этом расчеты проводятся по полученным аналитическим формулам без использования итерационных вычислительных процессов. Исходной информацией являются определения абсолютной величины и ориентации вектора, соединяющего центр масс управляемого КА и положение КО.
Также сущность заявленного способа определения параметров орбиты космического объекта заключается в определении на борту космического аппарата в моменты времени ti, где i=1, 2, 3, …, значений радиус-вектора, соединяющего центр Земли с местоположением космического аппарата - rка(ti), значений широты подспутниковых точек космического аппарата - φка(ti), значений расстояния между космическим аппаратом и космическим объектом - Δr(ti), значений угла между плоскостью движения космического аппарата и направлением от космического аппарата до космического объекта β(ti), при этом дополнительно определяют в моменты времени ti бортовыми оптическими датчиками угол между направлением от космического аппарата до космического объекта и местным горизонтом, лежащим в плоскости, образованной положениями космического аппарата, космического объекта и центром Земли - θ(ti), вычисляют значения радиус-вектора - rко(ti) космического объекта, соединяющего центр Земли с положением космического объекта в момент времени ti и угловое расстояние между текущими положениями космического аппарата и космического объекта в момент времени ti - δr(ti) в соответствии с математическими зависимостями:
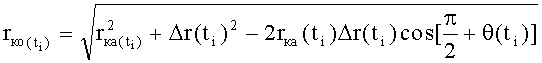
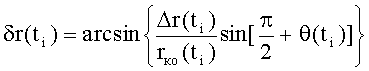
где:
rкa(ti) - радиус-вектор космического аппарата, соединяющий центр Земли с положением космического аппарата в момент времени ti;
Δr(ti) - расстояние между центрами масс космического аппарата и космического объекта в момент времени ti;
θ(ti) - угол между направлением от космического аппарата до космического объекта и местным горизонтом, лежащим в плоскости, образованной положениями космического аппарата, космического объекта и центром Земли в момент времени ti;
δr(ti) - угловое расстояние между текущими положениями космического аппарата и космического объекта в момент времени ti,
вычисляют угловое расстояние между положениями космического объекта - Δν(ti, ti+1) для двух следующих друг за другом моментов времени измерений ti и ti+1 по формуле:
Δν(ti,ti+1)=arccos[cosσ(ti)cosδr(ti+1)-sinσ(ti)sinδr(ti+1)cosα(ti)],
где:
σ(ti)=arccos[cosδr(ti)cosδrка(ti)-sinδr(ti)sinδrка(ti)cosβ(ti)];
α(ti)=π-β(ti+1)-δ(ti);
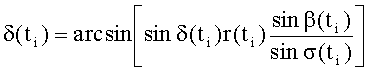
σ(ti) - угловое расстояние между положением космического аппарата в момент времени ti+1 и космического объекта в момент времени ti;
δr(ti) - угловое расстояние между текущими положениями космического аппарата и космического объекта в момент времени ti;
δrкa(ti) - угловое расстояние между положениями космического аппарата в моменты времени ti и ti+1;
β(ti) - угол между плоскостью движения космического аппарата и направлением от космического аппарата до космического объекта в момент времени ti;
α(ti) - угол между плоскостью, образованной положениями космического аппарата и космического объекта в момент времени ti+1, и плоскостью, образованной положениями космического аппарата в момент времени ti+1 и космического объекта в момент времени ti;
β(ri+1)- угол между плоскостью движения космического аппарата и направлением от космического аппарата до космического объекта в момент времени ti+1;
δ(ti) - угол между плоскостью движения космического аппарата и плоскостью, образованной положениями космического аппарата в момент времени ti+1 и космического объекта в момент времени ti,
вычисляют параметры орбиты космического объекта: фокальный параметр - P(ti), истинную аномалию - ϑ(ti), эксцентриситет - e(ti) и наклонение орбиты - iко в момент времени ti в соответствии с математическими зависимостями:
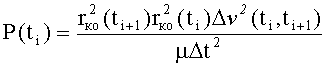 ,
,
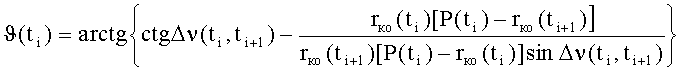
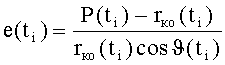
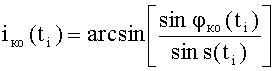
где:
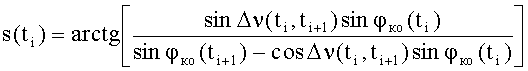
φко(ti)=arcsin[sinj(ti)sin(δz(ti)+δr(ti))];
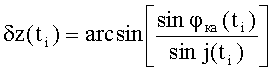
j(ti)=arccos[cosε(ti)cosφка(ti)];
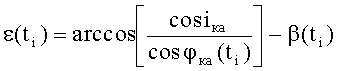
rко(ti+1) - радиус-вектор космического объекта, соединяющий центр Земли с положением космического объекта в момент времени ti+1;
rко(ti) - радиус-вектор космического объекта, соединяющий центр Земли с положением космического объекта в момент времени ti;
µ - произведение гравитационной постоянной на массу Земли;
Δt=ti+1-ti;
Δν(ti, ti+1) - угловое расстояние между положениями космического объекта для двух следующих друг за другом моментов времени измерений ti и ti+1;
s(ti) - дуга, лежащая в плоскости движения космического объекта и соединяющая его положение в момент времени ti и в ближайший момент времени прохождения экватора;
φко(ti) - широта подспутниковой точки космического объекта в момент времени ti;
φко(ti+1) - широта подспутниковой точки космического объекта в момент времени ti+1;
j(ti) - наклонение «условной» орбиты, проходящей через широты подспутниковых точек космического аппарата и космического объекта в момент времени ti;
δz(ti) - дуга, лежащая в плоскости «условной» орбиты с наклонением j(ti) и соединяющая подспутниковую точку космического аппарата в момент времени ti и плоскость экватора;
δr(ti) - угловое расстояние между текущими положениями космического аппарата и космического объекта в момент времени ti;
φка(ti) - широта подспутниковой точки космического аппарата в момент времени ti;
ε(ti) - курсовой угол для плоскости условной орбиты, проходящей через широты подспутниковых точек космического аппарата, космического объекта и центр Земли в момент времени ti;
iкa - наклонение орбиты космического аппарата;
β(ti) - угол между плоскостью движения космического аппарата и направлением от космического аппарата до космического объекта в момент времени ti.
Техническим результатом изобретения является повышение оперативности определения орбит движения КО за счет осуществления на борту КА обработки обнаруженных с помощью бинокулярной системы оптических датчиков и экспонированных ПЗС-матрицами в моменты времени ti и ti+1 изображений КО, получения при этом соответствующих моментам времени ti и ti+1 необходимых измеренных углов и осуществления безытерационного вычисления параметров орбиты КО с использованием предложенных математических зависимостей.
Указанный технический результат достигается тем, что в заявленном способе определения параметров орбиты космического объекта, заключающимся в определении на борту космического аппарата в моменты времени ti, где, где i=1, 2, 3, …, значений радиус-вектора, соединяющего центр Земли с местоположением космического аппарата - rка(ti), значений широты подспутниковых точек космического аппарата -φка(ti), значений расстояния между космическим аппаратом и космическим объектом - Δr(ti), значений угла между плоскостью движения космического аппарата и направлением от космического аппарата до космического объекта - β(ti), при этом определяют в моменты времени ti бортовыми оптическими датчиками угол между направлением от космического аппарата до космического объекта и местным горизонтом, лежащим в плоскости, образованной положениями космического аппарата, космического объекта и центром Земли - θ(ti), вычисляют значения радиус-вектора - rко(ti) космического объекта, соединяющего центр Земли с положением космического объекта в момент времени ti и угловое расстояние между текущими положениями космического аппарата и космического объекта в момент времени ti - δr(ti) в соответствии с математическими зависимостями:
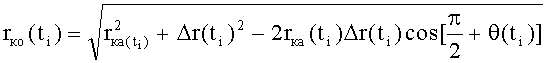
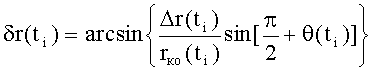
где:
rка(ti) - радиус-вектор космического аппарата, соединяющий центр Земли с положением космического аппарата в момент времени ti;
Δr(ti) - расстояние между центрами масс космического аппарата и космического объекта в момент времени ti;
θ(ti) - угол между направлением от космического аппарата до космического объекта и местным горизонтом, лежащим в плоскости, образованной положениями космического аппарата, космического объекта и центром Земли в момент времени ti;
δr(ti) - угловое расстояние между текущими положениями космического аппарата и космического объекта в момент времени ti,
вычисляют угловое расстояние между положениями космического объекта - Δν(ti, ti+1) для двух следующих друг за другом моментов времени измерений ti и ti+1 по формуле:
Δν(ti,ti+1)=arccos[cosσ(ti)cosδr(ti+1)-sinσ(ti)sinδr(ti+1)cosα(ti)],
где:
σ(ti)=arccos[cosδr(ti)cosδrка(ti)-sinδr(ti)sinδrка(ti)cosβ(ti)];
α(ti)=π-β(ti+1)-δ(ti);
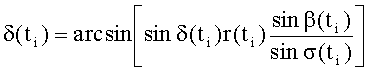
σ(ti) - угловое расстояние между положением космического аппарата в момент времени ti+1 и космического объекта в момент времени ti;
δr(ti) - угловое расстояние между текущими положениями космического аппарата и космического объекта в момент времени ti;
δrкa(ti) - угловое расстояние между положениями космического аппарата в моменты времени ti и ti+1;
β(ti) - угол между плоскостью движения космического аппарата и направлением от космического аппарата до космического объекта в момент времени ti;
α(ti) - угол между плоскостью, образованной положениями космического аппарата и космического объекта в момент времени ti+1, и плоскостью, образованной положениями космического аппарата в момент времени ti+1 и космического объекта в момент времени ti;
β(ti+1) - угол между плоскостью движения космического аппарата и направлением от космического аппарата до космического объекта в момент времени ti+1;
δ(ti) - угол между плоскостью движения космического аппарата и плоскостью, образованной положениями космического аппарата в момент времени ti+1 и космического объекта в момент времени ti,
вычисляют параметры орбиты космического объекта: фокальный параметр - P(ti), истинную аномалию - ϑ(ti), эксцентриситет - e(ti) и наклонение орбиты - iко в момент времени ti в соответствии с математическими зависимостями:
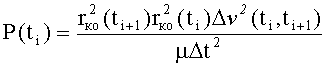 ,
,
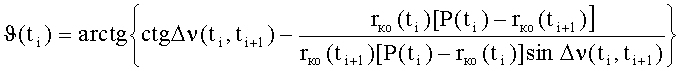
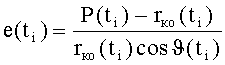
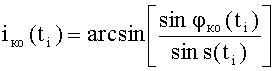
где:
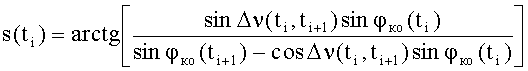
φко(ti)=arcsin[sinj(ti)sin(δz(ti)+δr(ti))];
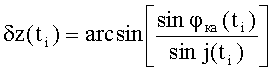
j(ti)=arccos[cosε(ti)cosφка(ti)];
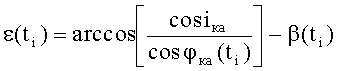
rко(ti+1) - радиус-вектор космического объекта, соединяющий центр Земли с положением космического объекта в момент времени ti+1;
rко(ti) - радиус-вектор космического объекта, соединяющий центр Земли с положением космического объекта в момент времени ti;
µ - произведение гравитационной постоянной на массу Земли;
Δt=ti+1-ti;
Δν(ti, ti+1) - угловое расстояние между положениями космического объекта для двух следующих друг за другом моментов времени измерений ti и ti+1;
s(ti) - дуга, лежащая в плоскости движения космического объекта и соединяющая его положение в момент времени ti и в ближайший момент времени прохождения экватора;
φко(ti) - широта подспутниковой точки космического объекта в момент времени ti;
φко(ti+1) - широта подспутниковой точки космического объекта в момент времени ti+1;
j(ti) - наклонение «условной» орбиты, проходящей через широты подспутниковых точек космического аппарата и космического объекта в момент времени ti;
δz(ti) - дуга, лежащая в плоскости «условной» орбиты с наклонением j(ti) и соединяющая подспутниковую точку космического аппарата в момент времени ti и плоскость экватора;
δr(ti) - угловое расстояние между текущими положениями космического аппарата и космического объекта в момент времени ti;
φка(ti) - широта подспутниковой точки космического аппарата в момент времени ti;
ε(ti) - курсовой угол для плоскости условной орбиты, проходящей через широты подспутниковых точек космического аппарата, космического объекта и центр Земли в момент времени ti;
iка - наклонение орбиты космического аппарата;
β(ti) - угол между плоскостью движения космического аппарата и направлением от космического аппарата до космического объекта в момент времени ti.
Заявленный способ определения параметров орбиты космического объекта поясняется следующими фигурами:
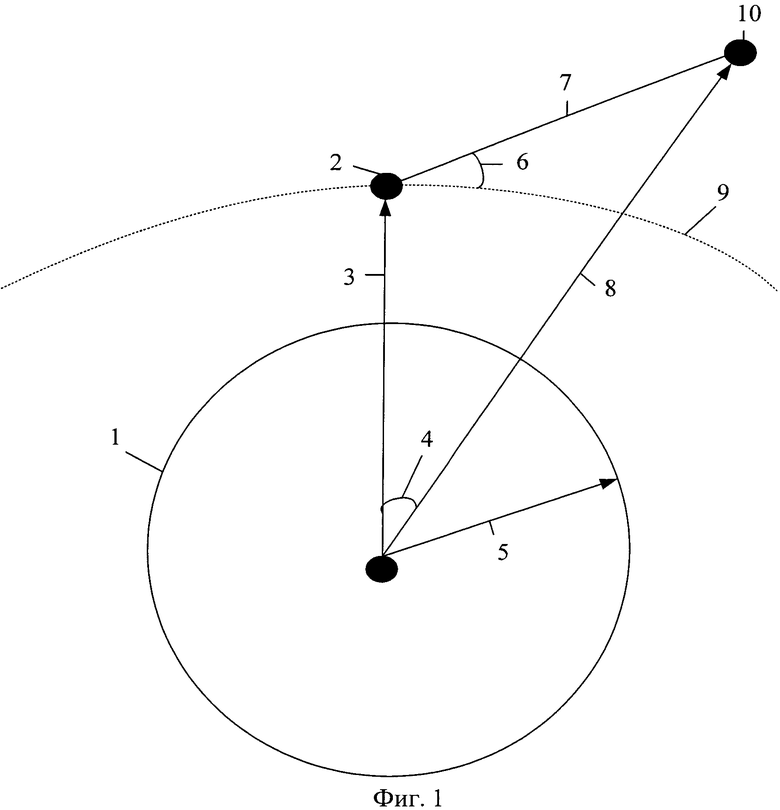
- на фигуре 1 приведено относительное расположение КА и КО,
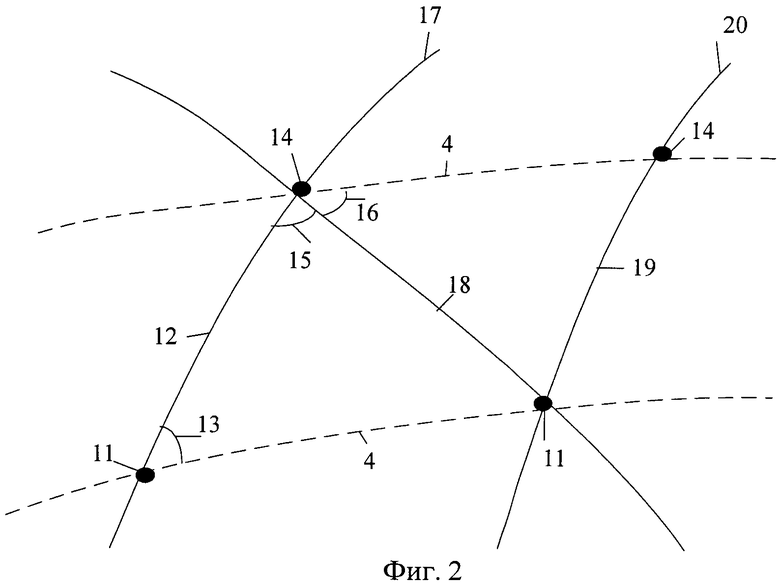
- на фигуре 2 представлено относительное расположение плоскостей движения КА и КО,
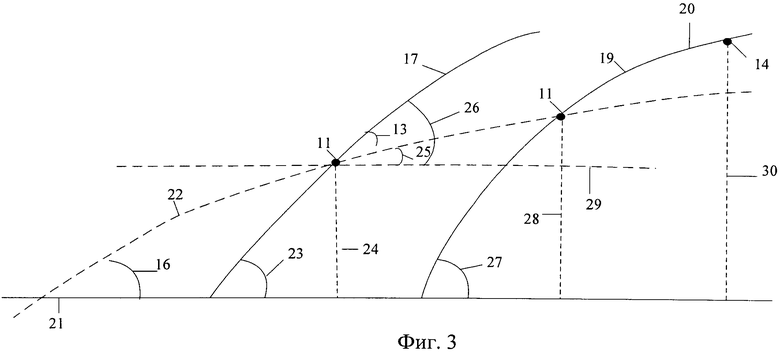
- на фигуре 3 представлены трассы движения КА и КО.
На фиг.1-фиг.3 и в тексте приняты следующие обозначения:
1 - поверхность Земли,
2 - КА,
3 - радиус-вектор космического аппарата, соединяющий начало координат (центр Земли) с положением КА на его траектории - rка,
4 - угловое расстояние между текущими положениями космического аппарата и космического объекта - δr,
5 - радиус Земли - R,
6 - угол между направлением от КА до КО и местным горизонтом, лежащим в плоскости, образованной положениями КА, КО и центром Земли - θ,
7 - расстояние между центрами масс космического аппарата и космического объекта - Δr,
8 - радиус - вектор космического объекта, соединяющий начало координат (центр Земли) с положением КО - rко,
9 - местный горизонт,
10 - КО,
11 - момент времени измерений ti, предшествующий моменту времени измерений ti+1;
12 - угловое расстояние между положениями космического аппарата в моменты времени ti и ti+1 - δrка,
13 - угол между плоскостью движения КА и направлением от КА до KO - β,
14 - момент времени измерений ti+1, следующий за моментом времени измерений ti;
15 - угол между плоскостью движения космического аппарата и плоскостью образованной положениями космического аппарата в момент времени ti+1 и космического объекта в момент времени ti - δ,
16 - угол между плоскостью большого круга, образованной положениями космического аппарата и космического объекта в момент времени ti+1, и плоскостью большого круга, образованной положениями космического аппарата в момент времени ti+1 и космического объекта в момент времени ti - α,
17 - траектория полета КА,
18 - угловое расстояние между положением космического аппарата и космического объекта - σ,
19 - угловое расстояние между положениями космического объекта в моменты времени ti и ti+1 - Δν,
20 - траектория полета КО,
21 - плоскость экватора, проходящая через центр Земли перпендикулярно оси ее вращения;
22 - угловое расстояние между положением космического аппарата в момент времени ti и плоскостью экватора, лежащее в плоскости условной орбиты образованной положениями КА и КО в момент времени ti и центром Земли - δZ,
23 - наклонение орбиты КА - iка,
24 - широта подспутниковой точки КА в момент времени ti - φка,
25 - курсовой угол для плоскости условной орбиты, проходящей через широты подспутниковых точек космического аппарата, космического объекта и центр Земли в момент времени ti - ε(ti),
26 - курсовой угол между проекцией вектора скорости КА на местный горизонт и местной параллелью в момент времени ti - ε(ti),
27 - наклонение орбиты космического объекта - iко,
28 - широта подспутниковой точки КО в момент времени ti - φко(ti),
29 - местная параллель на широте подспутниковой точки КА в момент времени ti,
30 - широта подспутниковой точки КО в момент времени ti+1 - φко(ti+1).
Покажем возможность осуществления изобретения, т.е. возможность его промышленного применения.
При осуществления изобретения с наземных пунктов управления ежесуточно во время сеанса связи на борт космического аппарата производится запись командно-программной информации, содержащей данные о его текущих орбитальных параметрах на момент сеанса связи («Бортовые системы управления космическими аппаратами»: Учебное пособие / Бровкин А.Г., Бурдыгов Б.Г., Гордийко С.В. и др., под редакцией Сырова А.С. М.: Изд-во МАИ-ПРИНТ, 2010, с.45-47, 56-61, 80-98)- (Д6). Далее происходит регистрация космических объектов бортовыми оптическими датчиками, представляющими собой бинокулярную систему разнесенных друг относительно друга оптических датчиков и имеющих параллельные оптические оси (Д3, Д4). На основе измеренного параллактического смещения треков прохождения космических объектов, зафиксированных на ПЗС-матрицах в моменты времени ti и ti+1, производится определение по методике (Д2) расстояния между центрами масс космического аппарата и космического объекта (Δr), а также угла β между плоскостью движения космического аппарата и направлением от космического аппарата до космического объекта (Д6). Затем бортовыми оптическими датчиками и исполнительными органами системы стабилизации и ориентации космического аппарата, описанными в (Д6, с.80-98) определяют угол θ (фиг.1, позиция 6) между направлением от космического аппарата до космического объекта и местным горизонтом, лежащим в плоскости, образованной положениями КА, КО и центром Земли. Далее по вышеприведенным формулам определяют параметры орбиты космического объекта.
Процедуры и технология ежесуточной записи командно-программной информации, содержащей данные о текущих орбитальных параметрах КА на момент сеанса связи, показаны в (Д6, с.45-47).
Регистрация космических объектов, а также состав и технические возможности бортовых оптических датчиков приведены в (Д6, с.56-61).
Реализация бинокулярной системы разнесенных друг относительно друга оптических датчиков и имеющих параллельные оптические оси, описана в (Д3, Д4).
Способ измерений параллактического смещения треков прохождения космических объектов, зафиксированных на ПЗС-матрицах, а также измерение расстояний между центрами масс космического аппарата и космического объекта Δr и углов β между плоскостью движения космического аппарата и направлениями от космического аппарата до космического объекта производится по методикам, приведенных в (Д2 и Д3).
Взаимодействие бортовых оптических датчиков и исполнительных органов системы стабилизации и ориентации космического аппарата описано в (Д6, с.80-98) дает возможность определить угол - θ между направлением от космического аппарата до космического объекта и местным горизонтом, лежащим в плоскости, образованной положениями КА, КО и центром Земли.
Возможность осуществления итерационного вычислительного бортового алгоритма, уточняющего орбитальные параметры космического объекта и прогнозирующего минимальное расстояние между космическим аппаратом и космическим объектом, показана в источниках информации: «Наведение в космосе» / Ричард Беттин. - М.: Машиностроение, 1966 - (Д7), «Введение в теорию полета искусственных спутников земли» / Эльясберг П.Е. - М.: Наука, 1965 - (Д8).
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ АЛЬБЕДО ЗЕМНОЙ ПОВЕРХНОСТИ | 2013 |
|
RU2547894C2 |
| СПОСОБ УПРАВЛЕНИЯ ДВИЖЕНИЕМ КОСМИЧЕСКОГО АППАРАТА ПРИ ПОСАДКЕ В ЗАДАННУЮ ОБЛАСТЬ ПОВЕРХНОСТИ ПЛАНЕТЫ | 2014 |
|
RU2590775C2 |
| СПОСОБ УПРАВЛЕНИЯ КОСМИЧЕСКИМ АППАРАТОМ ПРИ ЕГО СПУСКЕ С ОРБИТЫ ИСКУССТВЕННОГО СПУТНИКА ЗЕМЛИ | 2014 |
|
RU2561490C1 |
| Способ управления наземным антенным комплексом для обеспечения приема и передачи информации в тракте связи с космическим аппаратом на квази-геостационарной орбите и система управления для его осуществления | 2021 |
|
RU2769770C1 |
| Способ ограничения засорения эксплуатируемых областей околоземного космического пространства | 2017 |
|
RU2665156C1 |
| ПЛАНШЕТ ДЛЯ ВЫБОРА ОБЪЕКТОВ НАБЛЮДЕНИЯ С ОРБИТАЛЬНОГО КОСМИЧЕСКОГО АППАРАТА | 2006 |
|
RU2341773C2 |
| СПОСОБ УПРАВЛЕНИЯ ДВИЖЕНИЕМ КОСМИЧЕСКОГО АППАРАТА НА АКТИВНОМ УЧАСТКЕ ЕГО ВЫВЕДЕНИЯ НА ОРБИТУ ИСКУССТВЕННОГО СПУТНИКА ПЛАНЕТЫ | 2015 |
|
RU2596004C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ АЛЬБЕДО ЗЕМНОЙ ПОВЕРХНОСТИ | 2013 |
|
RU2547169C2 |
| УСТРОЙСТВО ДЛЯ ВЫБОРА ОБЪЕКТОВ НАБЛЮДЕНИЯ С ОРБИТАЛЬНОГО КОСМИЧЕСКОГО АППАРАТА | 2006 |
|
RU2346241C2 |
| СПОСОБ МОНИТОРИНГОВОЙ КОЛЛОКАЦИИ НА ГЕОСТАЦИОНАРНОЙ ОРБИТЕ | 2013 |
|
RU2558959C2 |
Изобретение относится к способам определения орбит космических объектов (КО), например космического мусора, бортовыми средствами космического аппарата (КА). Способ заключается в вычислении фокального параметра, истинной аномалии, эксцентриситета и наклонения орбиты интересующего КО по аналитическим формулам, основанным на законах кеплеровского движения. Вычисления ведутся без использования итерационных процедур, на базе определения в последовательные моменты времени расстояний между КО и КА и некоторых углов. Эти исходные данные получают обработкой на борту КА изображений КО, получаемых с помощью бинокулярной системы оптических датчиков и ПЗС-матриц. Техническим результатом изобретения является повышение оперативности определения орбит КО на борту КА и тем самым - безопасности полетов КА. 3 ил.
Способ определения параметров орбиты космического объекта, заключающийся в определении на борту космического аппарата в моменты времени ti, где i=1, 2, 3, …, значений радиус-вектора rка(ti), соединяющего центр Земли с местоположением космического аппарата, значений широты φкa(ti) подспутниковых точек космического аппарата, значений расстояния Δr(ti) между космическим аппаратом и космическим объектом, значений угла β(ti) между плоскостью движения космического аппарата и направлением от космического аппарата до космического объекта, отличающийся тем, что определяют в моменты времени ti бортовыми оптическими датчиками угол θ(ti) между направлением от космического аппарата до космического объекта и местным горизонтом, лежащий в плоскости, образованной положениями космического аппарата, космического объекта и центром Земли, вычисляют значения радиус-вектора rко(ti) космического объекта, соединяющего центр Земли с положением космического объекта в момент времени ti, и угловое расстояние δr(ti) между текущими положениями космического аппарата и космического объекта в момент времени ti в соответствии с математическими зависимостями:
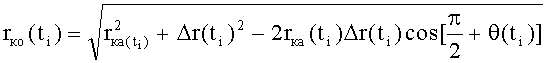 ,
,
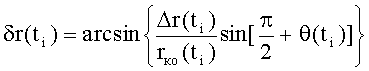 ,
,
где:
rка(ti) - радиус-вектор космического аппарата, соединяющий центр Земли с положением космического аппарата в момент времени ti;
Δr(ti) - расстояние между центрами масс космического аппарата и космического объекта в момент времени ti;
θ(ti) - угол между направлением от космического аппарата до космического объекта и местным горизонтом, лежащий в плоскости, образованной положениями космического аппарата, космического объекта и центром Земли в момент времени ti;
δr(ti) - угловое расстояние между текущими положениями космического аппарата и космического объекта в момент времени ti,
вычисляют угловое расстояние Δv(ti, ti+1) между положениями космического объекта для двух следующих друг за другом моментов времени измерений ti и ti+1 по формуле:
Δv(ti, ti+1)=arccos[cosσ(ti)cosδr(ti+1)-sinσ(ti)sinδr(ti+1)cosα(ti)],
где:
σ(ti)=arccos[cosδr(ti)cosδrка(ti)-sinδr(ti)sinδrка(ti)cosβ(ti)];
α(ti)=π-β(ti+1)-δ(ti);
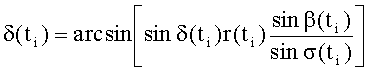 ;
;
σ(ti) - угловое расстояние между положением космического аппарата в момент времени ti+1 и космического объекта в момент времени ti;
δr(ti) - угловое расстояние между текущими положениями космического аппарата и космического объекта в момент времени ti;
δrка(ti) - угловое расстояние между положениями космического аппарата в моменты времени ti и ti+1;
β(ti) - угол между плоскостью движения космического аппарата и направлением от космического аппарата до космического объекта в момент времени ti;
α(ti) - угол между плоскостью, образованной положениями космического аппарата и космического объекта в момент времени ti+1, и плоскостью, образованной положениями космического аппарата в момент времени ti+1 и космического объекта в момент времени ti;
β(ti+1) - угол между плоскостью движения космического аппарата и направлением от космического аппарата до космического объекта в момент времени ti+1;
δ(ti) - угол между плоскостью движения космического аппарата и плоскостью, образованной положениями космического аппарата в момент времени ti+1 и космического объекта в момент времени ti,
вычисляют параметры орбиты космического объекта: фокальный параметр P(ti), истинную аномалию ϑ(ti), эксцентриситет e(ti) и наклонение орбиты iко в момент времени ti в соответствии с математическими зависимостями:
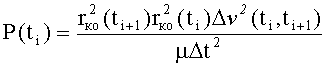 ,
,
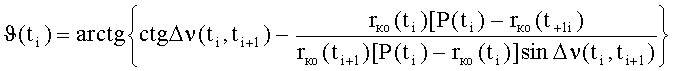 ,
,
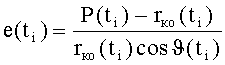 ,
,
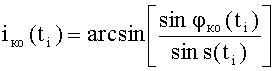 ,
,
где:
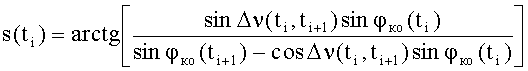 ;
;
φко(ti)=arcsin[sinj(ti)sin(δz(ti)+δr(ti))];
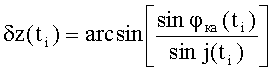 ;
;
j(ti)=arccos[cosε(ti)cosφка(ti)];
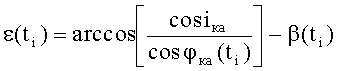 ;
;
rко(i+1) - радиус-вектор космического объекта, соединяющий центр Земли с положением космического объекта в момент времени ti+1;
rко(ti) - радиус-вектор космического объекта, соединяющий центр Земли с положением космического объекта в момент времени ti;
µ - произведение гравитационной постоянной на массу Земли;
Δt=ti+1-ti;
Δv(ti, ti+1) - угловое расстояние между положениями космического объекта для двух следующих друг за другом моментов времени измерений ti и ti+1;
s(ti) - дуга, лежащая в плоскости движения космического объекта и соединяющая его положение в момент времени ti и в ближайший момент времени прохождения экватора;
φко(ti) - широта подспутниковой точки космического объекта в момент времени ti;
φко(ti+1) - широта подспутниковой точки космического объекта в момент времени ti+1;
j(ti) - наклонение «условной» орбиты, проходящей через широты подспутниковых точек космического аппарата и космического объекта в момент времени ti;
δz(ti) - дуга, лежащая в плоскости «условной» орбиты с наклонением j(ti) и соединяющая подспутниковую точку космического аппарата в момент времени ti и плоскость экватора;
δr(ti) - угловое расстояние между текущими положениями космического аппарата и космического объекта в момент времени ti;
φка(ti) - широта подспутниковой точки космического аппарата в момент времени ti;
ε(ti) - курсовой угол для плоскости условной орбиты, проходящей через широты подспутниковых точек космического аппарата, космического объекта и центр Земли в момент времени ti;
iка - наклонение орбиты космического аппарата;
β(ti) - угол между плоскостью движения космического аппарата и направлением от космического аппарата до космического объекта в момент времени ti.
| MARK PSIAKI | |||
| Autonomous Orbit Determination for two Spacecraft from Relative Position Measurements | |||
| Дорожная спиртовая кухня | 1918 |
|
SU98A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ОРБИТЫ КОСМИЧЕСКОГО АППАРАТА | 1999 |
|
RU2150414C1 |
| ПАРАЛЛАКТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ОБЪЕКТА | 1984 |
|
RU2027144C1 |
| JP 61169784 A, 31.07.1986 | |||
| ФЕРРИТОВЫЙ МОНОКРИСТАЛЛИЧЕСКИЙ МАТЕРИАЛ | 1984 |
|
RU1167997C |
| US 6085128 A1, 04.07.2000 | |||
Авторы
Даты
2014-10-20—Публикация
2013-07-16—Подача