Изобретение относится к космонавтике, в частности к управлению спуском космического аппарата (КА) в атмосфере планеты, использующее управляемое аэродинамическое торможение и обеспечивающее минимизацию конечной скорости космического аппарата.
Известен способ управления спуском космического аппарата в атмосфере планеты, использующий управляемое аэродинамическое торможение и обеспечивающий снижение конечной скорости космического аппарата, описанный в книге - Иванов Н.М., Мартынов А.И. «Движение космических летательных аппаратов в атмосферах планет». М.: Наука, 1985, стр.168-173 - [1]. Указанный способ заключается в управлении аэродинамическим торможением путем изменения угла крена γ космического аппарата. При этом движение космического аппарата осуществляется с постоянным значением угла атаки, соответствующим максимальному балансировочному аэродинамическому качеству. Способ предусматривает одноразовое переключение угла крена γ с величины, равной π рад, на нулевое значение, что соответствует переключению эффективного аэродинамического качества с минимального значения (-K) на максимальное (+K).
Недостаток данного способа заключается в том, что он не предусматривает управление углом атаки космического аппарата α. Это существенно уменьшает возможности гашения скорости, поскольку увеличение угла атаки α приводит к возрастанию интенсивности аэродинамического торможения космического аппарата.
Наиболее близким по технической сущности к заявляемому способу управления спуском космического аппарата в атмосфере планеты, использующему управляемое аэродинамическое торможение и обеспечивающему снижение конечной скорости космического аппарата, является способ, описанный в книге - Иванов Н.М., Мартынов А.И. «Управление движением космических аппаратов в атмосфере Марса». Москва, «Наука», Главная редакция физико-математической литературы, 1977, стр.192-213 - [2], который выбран прототипом. Указанный способ заключается в двухпараметрическом управлении углами крена и атаки космического аппарата. Вход космического аппарата в атмосферу планеты осуществляется с углом крена γ=π рад и углом атаки α, соответствующим максимальному значению балансировочного аэродинамического качества. На начальном этапе полета осуществляется переключение угла крена γ на нулевое значение. После достижения углом наклона вектора скорости к местному горизонту нулевого значения угол крена γ определяется из условия обеспечения полета космического аппарата по изовысотному участку (участку с постоянной высотой). Затем осуществляется переключение угла крена γ на нулевое значение, обеспечивающее движение космического аппарата по рикошетирующей траектории с увеличением высоты полета. На этом участке происходит увеличение угла атаки α от значения, соответствующего максимуму аэродинамического коэффициента подъемной силы, до значения, соответствующего максимуму аэродинамического коэффициента лобового сопротивления.
Недостатки данного способа заключаются в том, что при его осуществлении не полностью реализуются резервы управления космическим аппаратом по эффективному гашению его скорости. Это обусловлено следующими факторами. Во-первых, отсутствует обоснование оптимальности момента переключения угла крена со значения π рад на ноль рад по критерию минимизации конечной скорости. При этом момент переключения значительно влияет на динамику торможения КА на последующих участках полета. Во-вторых, использование изовысотных участков укорачивает общую продолжительность траекторий спуска и тем самым снижает эффективность торможения КА в атмосфере. В-третьих, управление углом атаки происходит на достаточно коротком участке: в начале этого участка, например, при спуске в атмосфере Марса скорость полета составляет около 1 км/с, а высота - менее 10 км. Вместе с тем, более раннее управление углом атаки также позволяет повысить интенсивность гашения скорости за счет увеличения аэродинамического сопротивления КА.
Техническим результатом предлагаемого способа управления спуском КА в атмосфере планеты является снижение конечной скорости при вводе в действие системы мягкой посадки за счет рационального управления углами крена и атаки. Это дает возможность сократить расход топлива на осуществление мягкой посадки КА на поверхность планеты. Применение предлагаемого способа в зависимости от проектно-баллистических характеристик космического аппарата, граничных условий и параметров планеты назначения позволяет снизить расход топлива ~ на 10-20% по сравнению с использованием способа-прототипа.
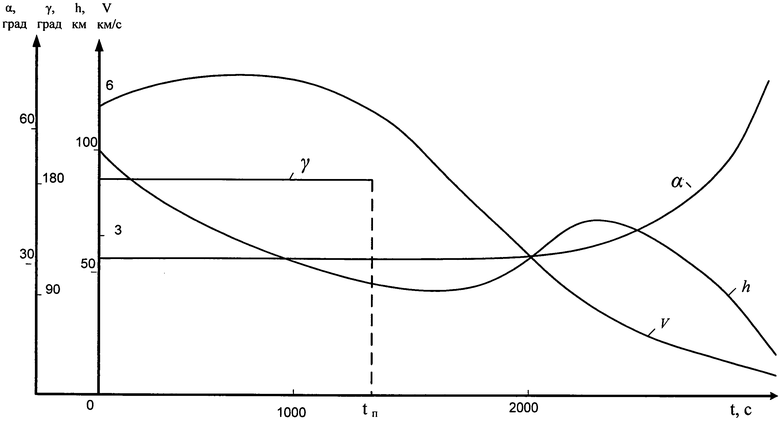
Сущность изобретения заключается в использовании рациональных программ управления углами крена и атаки, обеспечивающих минимизацию конечной скорости полета КА. Это достигается введением новых фрагментов управления по сравнению с прототипом. Во-первых, выбором рациональных условий переключения угла крена со значения π на ноль рад: переключение осуществляется в момент, когда скорость КА становится меньше скорости его входа в атмосферу планеты. Как известно, скорость КА на начальном участке полета в атмосфере увеличивается, так как аппарат движется в направлении условного перицентра оскулирующей орбиты, а плотность атмосферы еще сравнительно мала и не оказывает значительное влияние на торможение КА. Затем, при достижении КА плотных слоев атмосферы его скорость начинает уменьшаться и в определенный момент времени снижается до скорости входа в атмосферу. Именно в этот момент необходимо осуществлять переключение угла крена с π на ноль рад и переводить КА на траекторию движения с максимальным аэродинамическим качеством. При более раннем переключении угла γ (при скорости полета КА, большей скорости входа в атмосферу) возникающая подъемная сила может привести к вылету КА из атмосферы и к невыполнению основной задачи космической миссии - посадке аппарата в заданном районе поверхности планеты. Более позднее переключение угла крена γ приводит к уменьшению продолжительности траектории спуска и, следовательно, к снижению интенсивности торможения КА. Во-вторых, благоприятным фактором повышения эффективности снижения конечной скорости является более раннее, по сравнению с прототипом, начало управления углом атаки α. После перевода КА на режим полета с γ=0 рад реализуется продолжительная рикошетирующая траектория, где скорость полета КА монотонно уменьшается. При достижении максимальной высоты рикошета, например ~50-60 км в условиях снижения в атмосфере Марса и ~200-250 км при снижении в атмосфере Юпитера, происходит увеличение угла атаки и, следовательно, более интенсивное торможение КА. Такое условие начала управления по углу α является рациональным по следующим причинам: более раннее изменение угла α (до завершения набора максимальной высоты) приводит к уменьшению максимальной высоты рикошета, к снижению продолжительности полета и к уменьшению интегрального воздействия сопротивления атмосферы на КА. При более позднем введении управления по углу α (при снижении высоты полета КА) аппарат, как правило, не успевает погасить скорость в конце траектории спуска до минимально возможного значения.
Также сущность заявленного способа управления спуском космического аппарата в атмосфере планеты заключается в его пространственной ориентации и управлении аэродинамическим торможением, стабилизации космического аппарата при входе в атмосферу планеты по углу крена γ, равному около π рад, и углу атаки α, обеспечивающему максимальное аэродинамическое качество космического аппарата, определении текущих значений скорости, плотности атмосферы и высоты полета космического аппарата, установлении угла крена γ равным около 0 рад в процессе торможения космического аппарата в атмосфере планеты, в осуществлении движения космического аппарата в атмосфере планеты с последующим вводом в действие системы мягкой посадки космического аппарата, при этом устанавливают угол крена γ космического аппарата, равный около 0 рад, обеспечивающий движение космического аппарата по рикошетирующей траектории с увеличением высоты полета, в процессе торможения космического аппарата в атмосфере планеты при выполнении условия:
Vi<Vвх,
где: Vi - текущее значение скорости движения космического аппарата в процессе его торможения в атмосфере планеты;
Vвх - скорость входа космического аппарата в атмосферу планеты,
осуществляют дальнейшее движение космического аппарата по рикошетирующей траектории
и при выполнении условия:
hi<hmax,
где: hi - текущее значение высоты полета космического аппарата в атмосфере планеты;
hmax - максимальное значение высоты полета космического аппарата при его движении по рикошетирующей траектории,
устанавливают значение угла атаки α космического аппарата в соответствии с математическим выражением:
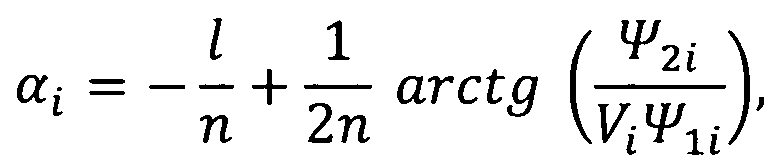 ,
,
где:
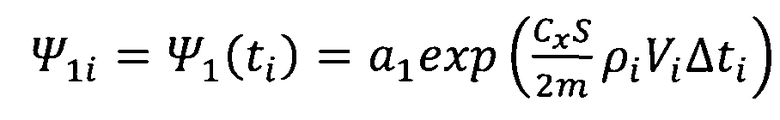 ;
; 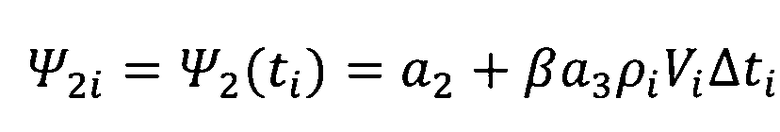 ;
;
αi - угол атаки α космического аппарата в моменты времени ti;
Vi - текущее значение скорости космического аппарата в моменты времени ti;
ρi - плотность атмосферы планеты в моменты времени ti;
Δti - интервалы времени между последующими измерениями, i=1, 2, 3, …;
Cx - аэродинамический коэффициент лобового сопротивления космического аппарата;
S - площадь миделева сечения космического аппарата;
m - масса космического аппарата;
β - логарифмический коэффициент изменения плотности атмосферы от высоты;
l, n - постоянные коэффициенты при аппроксимации зависимостей аэродинамических коэффициентов от угла атаки космического аппарата к аналитическому виду;
a1, a2, a3 - постоянные коэффициенты, полученные при интегрировании дифференциальных уравнений сопряженных переменных,
по достижении углом атаки α космического аппарата величины α*, соответствующей максимальному значению его аэродинамического коэффициента лобового сопротивления, осуществляют полет с этим значением угла атаки α* до ввода в действие системы мягкой посадки.
Заявленный способ управления спуском космического аппарата в атмосфере планеты поясняется чертежом, на котором приведены зависимости скорости V, высоты полета h космического аппарата, его углов крена γ и атаки α от времени движения в атмосфере Марса t при минимизации конечной скорости.
Кроме того, на чертеже и в тексте принято следующее обозначение: tп - момент переключения угла крена с π рад на 0 рад.
Согласно работе [2], стр.194 аэродинамические коэффициенты лобового сопротивления и подъемной силы с высокой степенью точности могут быть аппроксимированы следующими аналитическими зависимостями:
Cx=Cx0+Asin2(nα+l),
Cy=Cy0+Asin(nα+l)cos(nα+l).
В частности, при использовании формы космического аппарата типа несущий корпус: Cx0=0,2; Cy0=-0,1; A=2,3; n=1,125; l=5,625°.
Для других типов форм могут быть использованы аналогичные зависимости при других значениях коэффициентов - [2], стр.194.
Техническим результатом изобретения является уменьшение потребных энергетических затрат на осуществление космических миссий по исследованию планет Солнечной системы и, следовательно, увеличение доли полезной нагрузки в общем весовом балансе космического аппарата.
Указанный технический результат достигается за счет установки на борту спускаемых аппаратов системы управления аэродинамическим качеством и отработки рациональных программ управления углами крена и атаки КА, а именно за счет того, что в способе управления спуском космического аппарата в атмосфере планеты, выбранном прототипом и заключающемся в пространственной ориентации КА и управлении его аэродинамическим торможением, стабилизации космического аппарата при входе в атмосферу планеты по углу крена γ, равному около π рад, и углу атаки α, обеспечивающему максимальное аэродинамическое качество космического аппарата, определении текущих значений скорости, плотности атмосферы и высоты полета космического аппарата, установлении угла крена γ равным около 0 рад в процессе торможения космического аппарата в атмосфере планеты, в осуществлении движения космического аппарата в атмосфере планеты с последующим вводом в действие системы мягкой посадки космического аппарата, дополнительно устанавливают угол крена γ космического аппарата, равный около 0 рад, обеспечивающий движение космического аппарата по рикошетирующей траектории с увеличением высоты полета, в процессе торможения космического аппарата в атмосфере планеты при выполнении условия:
Vi<Vвх,
где: Vi - текущее значение скорости движения космического аппарата в процессе его торможения в атмосфере планеты;
Vвх - скорость входа космического аппарата в атмосферу планеты,
осуществляют дальнейшее движение космического аппарата по рикошетирующей траектории
и при выполнении условия:
hi<hmax,
где: hi - текущее значение высоты полета космического аппарата в атмосфере планеты;
hmax - максимальное значение высоты полета космического аппарата при его движении по рикошетирующей траектории,
устанавливают значение угла атаки α космического аппарата в соответствии с математическим выражением:
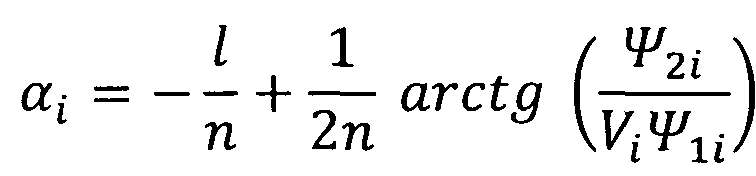 ,
,
где:
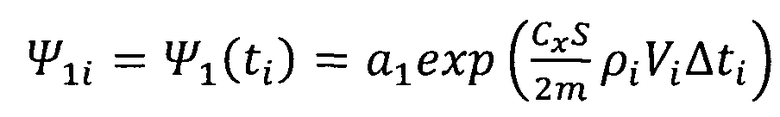 ;
; 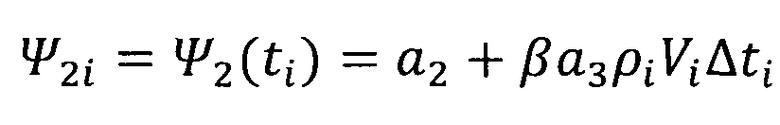 ;
;
αi - угол атаки α космического аппарата в моменты времени ti;
Vi - текущее значение скорости космического аппарата в моменты времени ti;
ρi - плотность атмосферы планеты в моменты времени ti;
Δti - интервалы времени между последующими измерениями, i=1, 2, 3, …;
Cx - аэродинамический коэффициент лобового сопротивления космического аппарата;
S - площадь миделева сечения космического аппарата;
m - масса космического аппарата;
β - логарифмический коэффициент изменения плотности атмосферы от высоты;
l, n - постоянные коэффициенты при аппроксимации зависимостей аэродинамических коэффициентов от угла атаки космического аппарата к аналитическому виду;
a1, a2, a3 - постоянные коэффициенты, полученные при интегрировании дифференциальных уравнений сопряженных переменных, по достижении углом атаки α космического аппарата величины α*, соответствующей максимальному значению его аэродинамического коэффициента лобового сопротивления, осуществляют полет с этим значением угла атаки α* до ввода в действие системы мягкой посадки.
Покажем возможность осуществления изобретения, т.е. возможность его промышленного применения. Особенностью ведения космической деятельности во многих странах мира является активизация изучения планет Солнечной системы. В рамках Федеральной космической программы 2016-2025 гг. предусмотрены работы по созданию космических комплексов для исследования Марса, Венеры, Юпитера, Меркурия, в том числе по проектированию спускаемых аппаратов. При этом, одной из важнейших проблем является разработка ключевых технологий управления, обеспечивающих снижение массово-энергетических затрат на всех участках межпланетных перелетов. Успешное решение этой проблемы во многом обеспечивается при размещении на борту спускаемых аппаратов систем управления аэродинамическим торможением, использующих принципы управления углами крена и атаки, изложенные в предлагаемом изобретении.
Что касается технических средств, обеспечивающих управление аэродинамическим качеством КА, то есть управление его углами крена и атаки, то они известны - см., например, работы [1], стр.37, [2], стр.57, 270, а также работу «Навигационное обеспечение полета орбитального комплекса «САЛЮТ-6» - «СОЮЗ» - «ПРОГРЕС»», ответственные редакторы Б.Н. Петров, И.К. Бажинов, Москва, «Наука», 1985, глава 1 - [3].
Примечания.
1. Заявитель поместил в Приложении к материалам заявки обоснование использованного им (в описании и формуле изобретения) математического выражения для расчета угла атаки КА на его конечном участке спуска в атмосфере планеты, чтобы излишне не перегружать описание изобретения. Однако если Экспертиза сочтет целесообразным, заявитель не будет возражать на его включение в состав описания.
2. Согласно п.2.3.1 Руководства по экспертизе заявок на изобретения от 25.07.2011 г. использование в формуле изобретения признака «около» при характеристике значений числовых параметров допустимо.
3. Заявитель в материалах заявки использовал два тождественных термина «переключают» значение угла крена γ КА (используемое при описании аналогов) и «устанавливают» значение угла крена γ КА (в формуле изобретения), как, по его мнению, более предпочтительное. При этом полагая, что единство терминологии в данном случае не нарушено.
Приложение. Относится к заявке на изобретение «Способ управления спуском космического аппарата в атмосфере планеты» (использующий управляемое аэродинамическое торможение и обеспечивающий минимизацию конечной скорости космического аппарата (примечание Заявителя)).
Вывод используемых математических зависимостей для расчета угла атаки на конечном участке спуска космического аппарата (КА) в атмосфере планеты.
Движение КА в атмосфере планеты согласно работам [1, 2] описывается системой дифференциальных уравнений в скоростной системе координат с учетом влияния гравитационных, аэродинамических, центробежных и кориолисовых сил в предположении центральности поля тяготения:
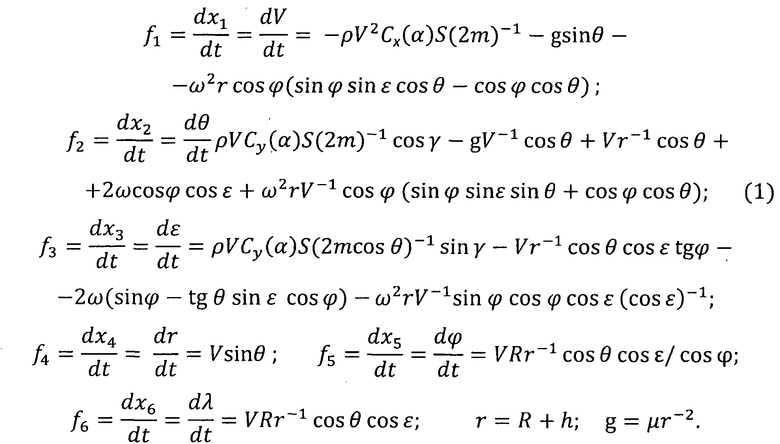
Здесь V - скорость КА, θ - угол наклона вектора скорости к местному горизонту, ε - курсовой угол, r - радиус-вектор, соединяющий центр планеты и положение КА, λ и φ - долгота и широта подспутниковых точек КА соответственно, m - масса КА, t - время, ρ - плотность атмосферы, Cx и Cy - аэродинамические коэффициенты лобового сопротивления и подъемной силы соответственно, R - радиус планеты, h - высота полета, g - ускорение силы тяжести, µ - произведение постоянной притяжения на массу планеты, S - площадь миделева сечения.
Значения управляющих параметров α и γ могут изменяться в пределах:
0≤α≤αmax, -π≤γ≤π.
Преобразуем исходные уравнения (1) с учетом введения допущений, ранее применяемых в ряде отечественных и зарубежных работ, в частности в работах [1, 2]:
h<<R, ρ=ρ0exp(-βh), Fк+Fц<<Fгр<<Fа,
где ρ0 - плотность атмосферы на поверхности Марса, β - логарифмический коэффициент изменения плотности атмосферы от высоты, Fк, Fц, Fгр, Fа - кориолисова, центробежная, гравитационная и аэродинамическая силы соответственно.
Будем рассматривать только конечный участок спуска КА, начинающийся с момента достижения аппаратом максимальной высоты после полета по рикошетирующей траектории и завершающийся моментом ввода в действие системы мягкой посадки.
Используя указанные допущения, рассматривая движение КА в плоскости входа в атмосферу и учитывая, что на конечном участке осуществляется спуск аппарата с нулевым углом крена, преобразуем систему уравнений к виду:
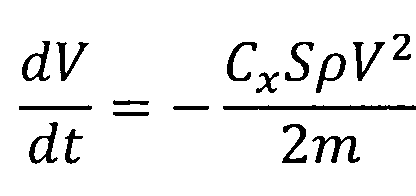 ,
, 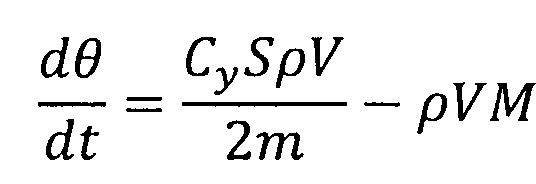 ,
, 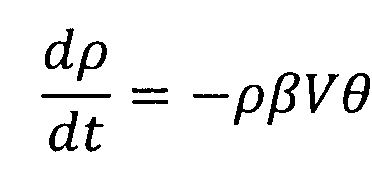 ,
,
где M - кусочно-постоянная функция, согласно работам [1, 2].
Решение задачи поиска оптимального управления КА при обеспечении минимальной конечной скорости проводилось с использованием принципа максимума Понтрягина. Запишем гамильтониан H и сопряженные переменные Ψi:
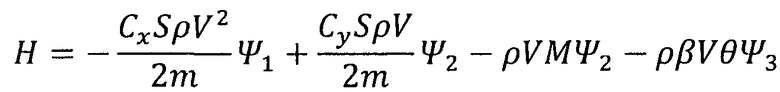 ,
,
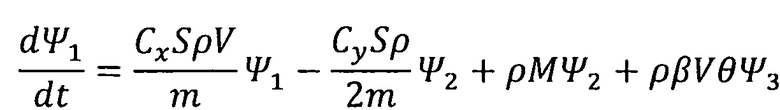 ,
,
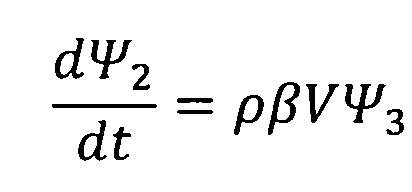 ,
, 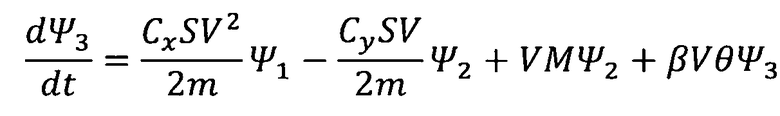 .
.
Сопоставляя уравнения для расчета функций H, Ψ1, Ψ3 преобразуем формулы для сопряженных переменных следующим образом:
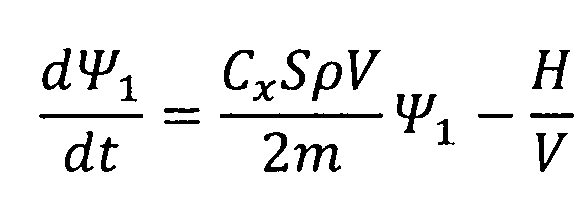 ,
, 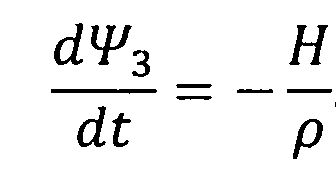 .
.
Из условия трансверсальности в конечной точке траектории полета КА следует, что
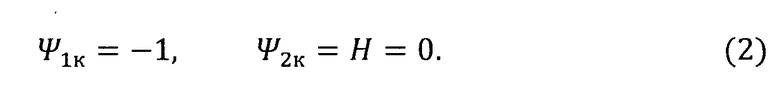
Учитывая, что гамильтониан не зависит в явном виде от времени полета, правомерно записать уравнение:
H≡0.
Это позволяет представить зависимости для расчета сопряженных переменных в виде:
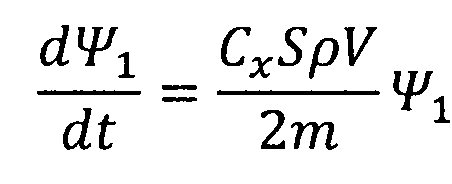 ,
, 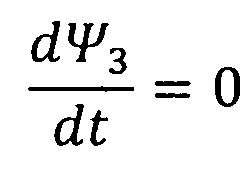 .
.
Интегрируя эти уравнения с учетом формул (2), получим:
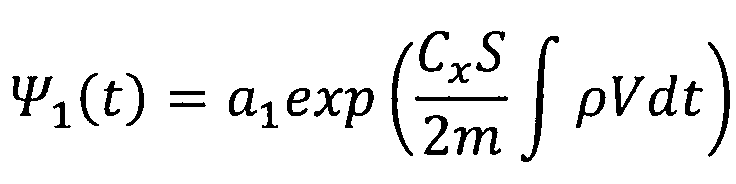 ,
,
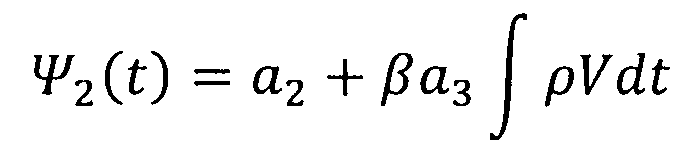 , Ψ3(t)=a3=const.
, Ψ3(t)=a3=const.
При условии непрерывного измерения текущих значений скорости полета Vi и плотности атмосферы ρi сопряженные переменные с высокой степенью точности в моменты измерений ti могут быть вычислены по формулам:
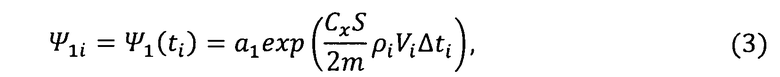
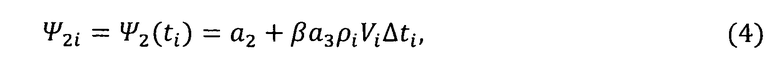
где Δti - интервалы времени между последующими измерениями.
Анализ зависимостей для расчетов сопряженных переменных с учетом равенства нулю гамильтониана показал, что Ψ1(t) является отрицательной монотонно возрастающей функцией, достигающей в конечной точке траектории величины, равной -1; Ψ2(t) - положительная монотонно убывающая функция, достигающая в конечной точке траектории величины, равной нулю; Ψ3(t) - является постоянной функцией, имеющей отрицательное значение.
Определим оптимальный закон управления углом атаки из условия достижения экстремума гамильтониана:
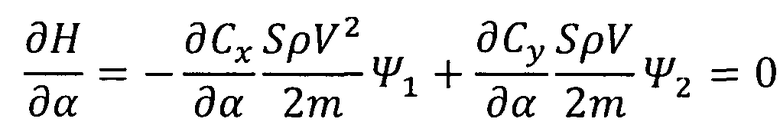 .
.
Решая это уравнение, получим:

Учитывая описанный характер изменения сопряженных переменных Ψ1 и Ψ2, приходим к выводу, что выражение ∂Cx/∂Cy имеет отрицательное значение на всем заключительном участке полета. Это соответствует монотонному увеличению угла атаки: в этом случае ∂Сx>0, а ∂Cy<0. Причем, интенсивность изменения угла атаки увеличивается в связи с монотонным уменьшением скорости полета КА.
Согласно работам [1, 2] аэродинамические коэффициенты лобового сопротивления и подъемной силы с высокой степенью точности могут быть аппроксимированы следующими аналитическими зависимостями:
Cx=Cx0+Asin2(nα+l),
Cy=Cy0+Asin(nα+l)cos(nα+l).
Для спускаемых аппаратов типа несущий корпус Cx0=0,2; Cy0=-0,1; A=2,3; n=1,125; l=5,625°.
С учетом этих зависимостей формула (5) преобразуется к следующему виду:
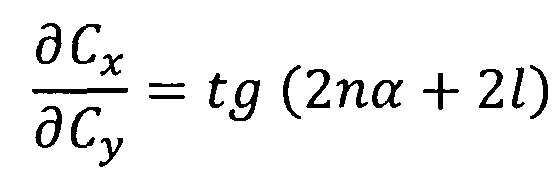 .
.
Тогда уравнение для определения текущих значений углов атаки в моменты проведения измерений параметров КА запишется следующим образом:
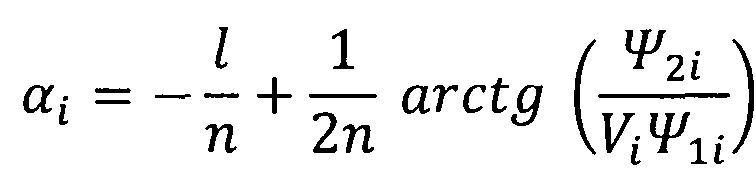 ,
,
где переменные Ψ1i и Ψ2i рассчитываются по формулам (3), (4). Анализ этого уравнения показал, что угол атаки α на рассматриваемом участке полета КА монотонно возрастает от α≈45÷50° до α≈70÷85°, что соответствует максимальному значению аэродинамического коэффициента лобового сопротивления.
Источники информации
1. Иванов Н.М., Мартынов А.И. «Движение космических летательных аппаратов в атмосферах планет». М.: «Наука», 1985, стр.168-173.
2. Н.М. Иванов, А.И. Мартынов «Управление движением космических аппаратов в атмосфере Марса». Москва, «Наука», Главная редакция физико-математической литературы, 1977, стр.159-169.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ УПРАВЛЕНИЯ СПУСКОМ КОСМИЧЕСКОГО АППАРАТА В АТМОСФЕРЕ ПЛАНЕТЫ | 2013 |
|
RU2537192C1 |
| СПОСОБ УПРАВЛЕНИЯ ВЫВЕДЕНИЕМ КОСМИЧЕСКОГО АППАРАТА НА ОРБИТУ ИСКУССТВЕННОГО СПУТНИКА ПЛАНЕТЫ | 2012 |
|
RU2520629C1 |
| СПОСОБ УПРАВЛЕНИЯ СПУСКОМ КОСМИЧЕСКОГО АППАРАТА В АТМОСФЕРЕ ПЛАНЕТ | 2012 |
|
RU2493059C1 |
| СПОСОБ УПРАВЛЕНИЯ ДВИЖЕНИЕМ КОСМИЧЕСКОГО АППАРАТА ПРИ ПОСАДКЕ В ЗАДАННУЮ ОБЛАСТЬ ПОВЕРХНОСТИ ПЛАНЕТЫ | 2014 |
|
RU2590775C2 |
| СПОСОБ УПРАВЛЕНИЯ КОСМИЧЕСКИМ АППАРАТОМ ПРИ ЕГО ВЫВЕДЕНИИ НА ОРБИТУ ИСКУССТВЕННОГО СПУТНИКА ПЛАНЕТЫ | 2014 |
|
RU2575556C2 |
| СПОСОБ УПРАВЛЕНИЯ КОСМИЧЕСКИМ АППАРАТОМ С ИСПОЛЬЗОВАНИЕМ АЭРОДИНАМИЧЕСКОГО КАЧЕСТВА ПРИ СПУСКЕ В АТМОСФЕРЕ | 2014 |
|
RU2552770C1 |
| СПОСОБ УПРАВЛЕНИЯ КОСМИЧЕСКИМ АППАРАТОМ ПРИ ЕГО ВЫВЕДЕНИИ НА ОРБИТУ ИСКУССТВЕННОГО СПУТНИКА ПЛАНЕТЫ | 2014 |
|
RU2573695C1 |
| СПОСОБ УПРАВЛЕНИЯ ДВИЖЕНИЕМ КОСМИЧЕСКОГО АППАРАТА НА АКТИВНОМ УЧАСТКЕ ЕГО ВЫВЕДЕНИЯ НА ОРБИТУ ИСКУССТВЕННОГО СПУТНИКА ПЛАНЕТЫ | 2015 |
|
RU2596004C2 |
| КОСМИЧЕСКИЙ АППАРАТ ДЛЯ СПУСКА В АТМОСФЕРЕ ПЛАНЕТЫ И СПОСОБ СПУСКА КОСМИЧЕСКОГО АППАРАТА В АТМОСФЕРЕ ПЛАНЕТЫ | 1994 |
|
RU2083448C1 |
| КОСМИЧЕСКИЙ АППАРАТ ДЛЯ СПУСКА В АТМОСФЕРЕ ПЛАНЕТЫ И СПОСОБ ЕГО СПУСКА В АТМОСФЕРЕ ПЛАНЕТЫ (ВАРИАНТЫ) | 2001 |
|
RU2213682C2 |
Изобретение относится к управлению спуском космического аппарата (КА) в атмосфере планеты путем регулирования его аэродинамического качества (АК). На начальном участке полета скорость КА в атмосфере увеличивается (КА движется к условному перицентру орбиты). Плотность атмосферы еще мала и не вызывает значительного торможения КА. При достижении КА плотных слоев атмосферы его скорость начинает уменьшаться, и в момент достижения ею скорости входа в атмосферу переключают угол крена (γ) со значения γ=π на γ=0. Этим маневром обеспечивают перевод КА на траекторию движения с максимальным АК. В режиме полета с γ=0 реализуют продолжительную рикошетирующую траекторию, на которой скорость КА монотонно уменьшается. При достижении максимальной высоты рикошета происходит увеличение угла атаки КА и, следовательно, более интенсивное торможение КА. Техническим результатом изобретения является снижение конечной скорости КА при вводе системы мягкой посадки и сокращение тем самым расхода топлива на осуществление мягкой посадки КА. 1 ил.
Способ управления спуском космического аппарата в атмосфере планеты, заключающийся в его пространственной ориентации и управлении аэродинамическим торможением, стабилизации космического аппарата при входе в атмосферу планеты по углу крена γ, равному около π рад, и углу атаки α, обеспечивающему максимальное аэродинамическое качество космического аппарата, определении текущих значений скорости, плотности атмосферы и высоты полета космического аппарата, установлении угла крена γ равным около 0 рад в процессе торможения космического аппарата в атмосфере планеты, в осуществлении движения космического аппарата в атмосфере планеты с последующим вводом в действие системы мягкой посадки космического аппарата, отличающийся тем, что устанавливают угол крена γ космического аппарата равным около 0 рад, обеспечивающим движение космического аппарата по рикошетирующей траектории с увеличением высоты полета, в процессе торможения космического аппарата в атмосфере планеты при выполнении условия:
Vi<Vвх,
где: Vi - текущее значение скорости движения космического аппарата в процессе его торможения в атмосфере планеты,
Vвх - скорость входа космического аппарата в атмосферу планеты,
осуществляют дальнейшее движение космического аппарата по рикошетирующей траектории
и при выполнении условия:
hi<hmax,
где: hi - текущее значение высоты полета космического аппарата в атмосфере планеты,
hmax - максимальное значение высоты полета космического аппарата при его движении по рикошетирующей траектории,
устанавливают значение угла атаки α космического аппарата в соответствии с математическим выражением:
 ,
,
где:
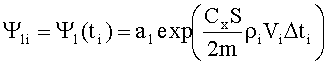 ;
; 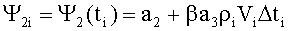 ,
,
αi - угол атаки α космического аппарата в моменты времени ti,
Vi - текущее значение скорости космического аппарата в моменты времени ti,
ρi - плотность атмосферы планеты в моменты времени ti,
Δti - интервалы времени между последующими измерениями, i=1, 2, 3, ...,
Cx - аэродинамический коэффициент лобового сопротивления космического аппарата,
S - площадь миделева сечения космического аппарата,
m - масса космического аппарата;
β - логарифмический коэффициент изменения плотности атмосферы с высотой,
l, n - постоянные коэффициенты при аппроксимации зависимостей аэродинамических коэффициентов от угла атаки космического аппарата в аналитическом виде,
a1, a2, a3 - постоянные коэффициенты, полученные при интегрировании дифференциальных уравнений сопряженных переменных,
и по достижении углом атаки α космического аппарата величины α*, соответствующей максимальному значению его аэродинамического коэффициента лобового сопротивления, осуществляют полет с этим значением угла атаки α* до ввода в действие системы мягкой посадки.
| Н.М | |||
| ИВАНОВ, А.И | |||
| МАРТЫНОВ | |||
| Управление движением космических аппаратов в атмосфере Марса | |||
| М | |||
| "Наука" | |||
| Шеститрубный элемент пароперегревателя в жаровых трубках | 1918 |
|
SU1977A1 |
| СПОСОБ УПРАВЛЕНИЯ СПУСКОМ КОСМИЧЕСКОГО АППАРАТА В АТМОСФЕРЕ ПЛАНЕТ | 2012 |
|
RU2493059C1 |
| КОСМИЧЕСКИЙ АППАРАТ ДЛЯ СПУСКА В АТМОСФЕРЕ ПЛАНЕТЫ И СПОСОБ СПУСКА КОСМИЧЕСКОГО АППАРАТА В АТМОСФЕРЕ ПЛАНЕТЫ | 1994 |
|
RU2083448C1 |
| КОСМИЧЕСКИЙ АППАРАТ ДЛЯ СПУСКА В АТМОСФЕРЕ ПЛАНЕТЫ И СПОСОБ ЕГО СПУСКА В АТМОСФЕРЕ ПЛАНЕТЫ (ВАРИАНТЫ) | 2001 |
|
RU2213682C2 |
| US 3276722 A, 04.10.1966; | |||
| US 6398166 B1, 04.06.2002 | |||
| US 20060226295 A1, 12.10.2006 | |||
Авторы
Даты
2014-12-27—Публикация
2013-09-27—Подача