МЕХАТРОННО-МОДУЛЬНЫЙ РОБОТ И СПОСОБ МНОГОАЛЬТЕРНАТИВНОЙ ОПТИМИЗАЦИИ МОДУЛЕЙ АВТОМАТИЗАЦИИ СТРУКТУРНОГО СИНТЕЗА ДЛЯ ЕГО СОЗДАНИЯ Российский патент 2015 года по МПК G05B19/00 

Изобретение относится к машиностроению, а именно к робототехнике, и может быть использовано при создании мехатронно-модульных роботов.

Одним из важнейших и перспективных направлений развития современной робототехники связано с разработкой нового класса устройств - многозвенных мехатронно-модульных роботов с адаптивной структурой. Структурный синтез при проектировании реконфигурируемых мехатронно-модульных роботов рассматривается как одновременное, автоматизированное решение двух задач выбора: порядка блочно -модульной сборки и варианта настройки априорно периодического закона изменения обобщенных координат (y, z), определяющего алгоритм управления движением.

Известен способ многоальтернативной оптимизации моделей автоматизации структурного синтеза мехатронно-модульных роботов, заключающийся в проведении синтеза структуры многоинвариантной модели мехатронно-модульных роботов, и последующей фиксации полученных оптимальных решений (И.М.Макаров, В.М.Лохин, С.В.Манько, М.П.Романов, М.В.Кадочников. ИТ, "Технологии обработки знаний в задачах управления автономными мехатронно-модульными реконфигурируемыми роботами" приложение к "Информационные технологии" №8, М., "Новые технологии", 2010, стр.3-7, рис.14-прототип).

Указанный способ многоальтернативной оптимизации моделей автоматизации структурного синтеза мехатронно-модульных роботов заключается в создании конкретных модулей и запоминании конкретных положений отдельных модулей для решения целевых задач.

Недостатками данного способа является его значительная сложность, низкая эффективность ориентации в окружающей среде реконфигурируемых мехатронных устройств, преимущественно мехатронно-модульных роботов.

Задачей предложенного технического решения является устранение указанных недостатков и создание мехатронно-модульного робота и способа многоальтернативной оптимизации моделей автоматизации структурного синтеза мехатронно-модульных роботов для его создания, применение которых позволит ускорить процесс синтеза, а также повысит эффективность ориентации в окружающей среде и надежность работы создаваемых мехатронных устройств, преимущественно мехатронно-модульных роботов.

Решение поставленной задачи достигается тем, что предложенный мехатронно-модульный робот согласно изобретению состоит как минимум из двух сопряженных между собой тождественных модулей, предпочтительно двух и более, первичного и вновь с ним сопрягаемого/ых, имеющих интерфейсные площадки для стыковки, причем количество модулей, объединяемых в упомянутый робот, определено из соотношения: n=1, N, где: n - количество модулей, объединяемых в один робот, определено из соотношения n=1+х1+2x2+4x3+8x4, где: х1,х4=1,0 - количество интерфейсных площадок на модуле, N≤16 - предельное количество модулей, которые могут быть объединены в один робот, при этом сопряжение каждого нового модуля с ранее собранным/и осуществлено вдоль выбранного направления и обеспечено стыковкой его первой интерфейсной площадки с одной из свободных на любых других элементах конструкции, занимающих ближайшее крайнее положение в том или ином ряду, причем интерфейсные площадки каждого модуля выполнены с возможностью стыковки с аналогичными площадками по крайней мере в четырех диаметрально противоположных направлениях, при этом альтернативные переменные для алгоритмов управления синтезированной мехатронно-модульной конструкцией для описания параметров периодического закона движения выбраны из следующего соотношения:

Angle=А+Bsin(ωt+φ),

где: A - значение обобщенной координаты, относительно которой происходит периодическое движение; B - амплитуда периодического колебания обобщенной координаты, причем суммарная величина |A|+|B| не превышает максимально допустимого отклонения обобщенной координаты модуля; φ - смещение фазы периодического движения.

В варианте исполнения мехатронно-модульного робота для оптимизационного структурного синтеза выбирают значения

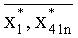
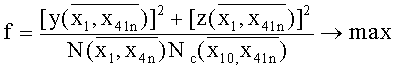
альтернативных переменных $$\overline{x_1^{*},x_{41n}^{*}}$$ , обеспечивающих максимальное значение функции:

$$f=\frac{{[y(\overline{x_1,x_{41n}})]}^2+{[z(\overline{x_1,x_{41n}})]}^2}{N(\overline{x_1,x_{4n}})N{\text{}}_c(\overline{x_{\mathrm{10,}}{x}_{41n}})}\to \max$$

при ограничениях n=1, N

$$|A_1(\overline{x_{\mathrm{10,}}{x}_{12n}})+B_1(\overline{x_{14n},x_{17n}})|\le y^{\max }$$ ,

$$|A_2(\overline{x_{\mathrm{26,}}{x}_{29n}})+B_2(\overline{x_{30n},x_{33n}})|\le z^{\max }$$

$$\overline{x_{\mathrm{1,}}{x}_{41n}}=\{\begin{array}{l}\mathrm{1,}\\ 0.\end{array}$$

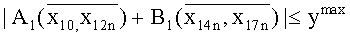
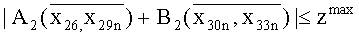
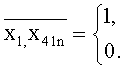
где: y^max, z^max - максимально допустимые отклонения обобщенной координаты модуля относительно ее нулевого значения.

Для создания предложенного мехатронно-модульного робота предложен способ, в котором при проведении синтеза структуры многоинвариантной модели мехатронно-модульных роботов и последующем фиксировании полученных оптимальных решений, рассматривают множество проектных элементов и вводят соответствующие альтернативные переменные путем представления дискретных чисел, соответствующих этим элементам, в двоичном исчислении, после чего обозначают количество модулей, объединяемых в один робот, преимущественно без четко выраженной структуры, и обеспечивают сопряжение каждого нового модуля с ранее собранными вдоль выбранного направления и стыковку его первой интерфейсной площадки с одной из свободных на любых других элементах конструкции, занимающих ближайшее крайнее положение в том или ином ряду, после чего вводят альтернативные переменные для описания параметров периодического закона следующим образом:

Angle=А+Bsin(ωt+φ),

где: A - значение обобщенной координаты, относительно которой происходит периодическое движение;

B - амплитуда периодического колебания обобщенной координаты; суммарная величина |A|+|B| не должна превышать максимально допустимого отклонения обобщенной координаты модуля;

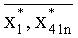
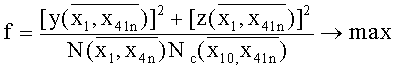
φ - смещение фазы периодического движения, при этом настройкой параметров этого закона определяют алгоритмы управления, синтезируемой мехатронно-модульной конструкции, причем для оптимизационного структурного синтеза выбирают значения альтернативных переменных $$\overline{x_1^{*},x_{41n}^{*}}$$ , обеспечивающих максимальное значение функции:

$$f=\frac{{[y(\overline{x_1,x_{41n}})]}^2+{[z(\overline{x_1,x_{41n}})]}^2}{N(\overline{x_1,x_{4n}})N{\text{}}_c(\overline{x_{\mathrm{10,}}{x}_{41n}})}\to \max$$

при ограничениях n=1, N

$$|A_1(\overline{x_{\mathrm{10,}}{x}_{12n}})+B_1(\overline{x_{14n},x_{17n}})|\le y^{\max }$$ ,

$$|A_2(\overline{x_{\mathrm{26,}}{x}_{29n}})+B_2(\overline{x_{30n},x_{33n}})|\le z^{\max }$$

$$\overline{x_{\mathrm{1,}}{x}_{41n}}=\{\begin{array}{l}\mathrm{1,}\\ 0.\end{array}$$

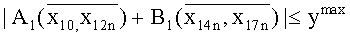
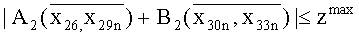
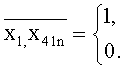
где: y^max, z^max - максимально допустимые отклонения обобщенной координаты модуля относительно ее нулевого значения, причем для нахождения максимального значения функции f используют рандомизированный алгоритм многоальтернативной оптимизации, который дополняют еще одним уровнем в рамках управляемого роя частиц.

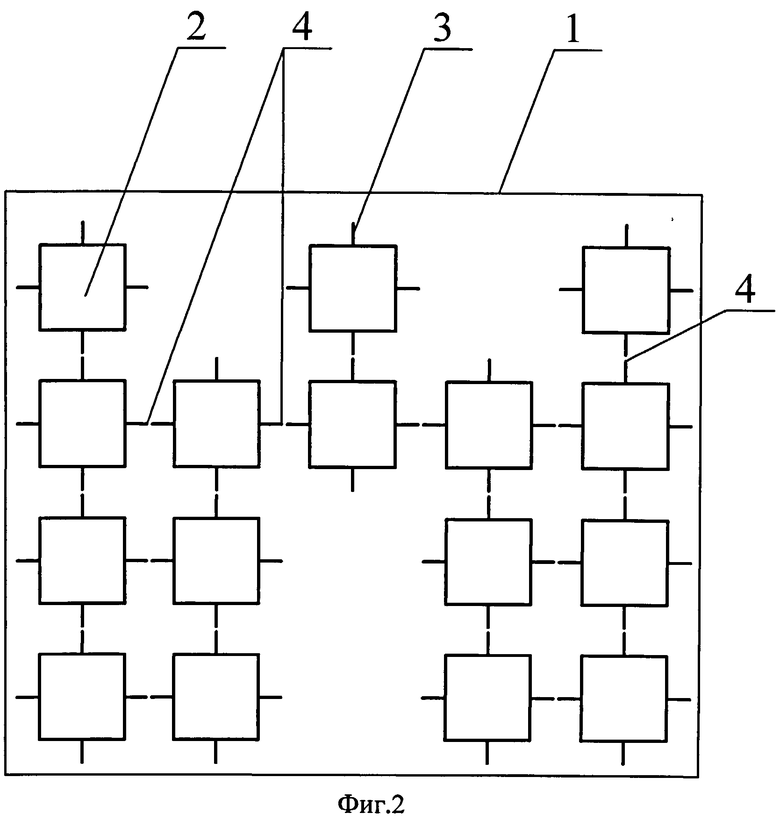
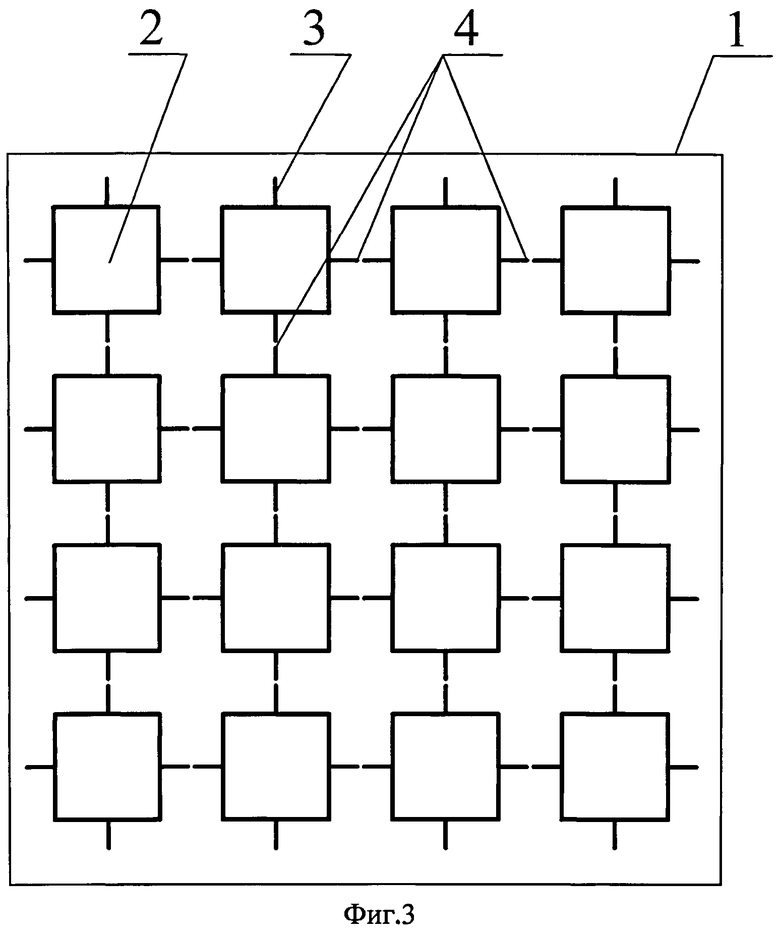
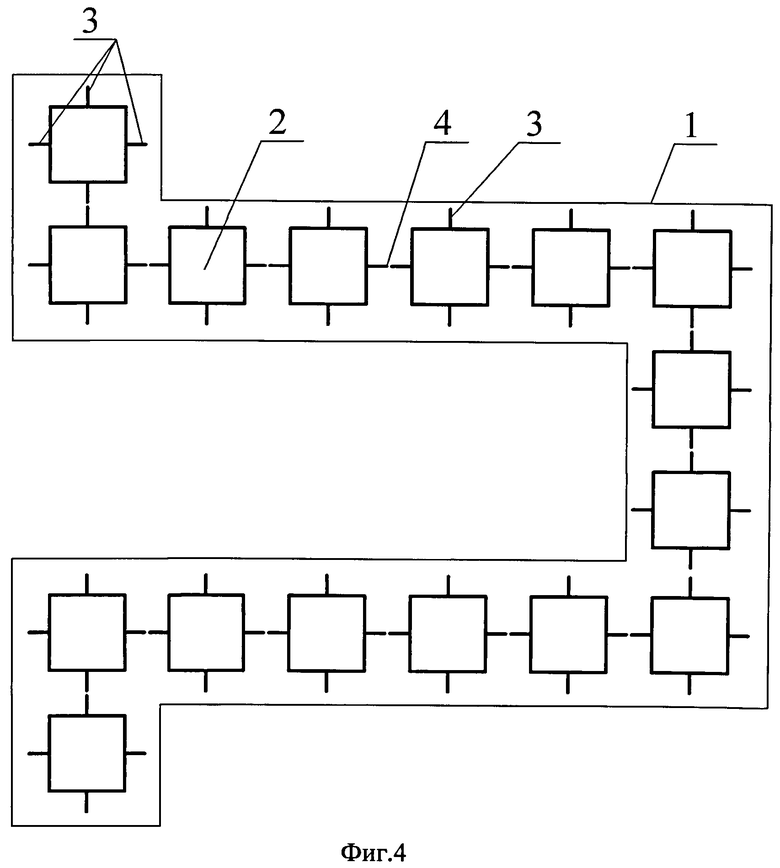
Сущность изобретения иллюстрируется чертежами, где на фиг.1 показаны отдельные мехатронно-модульные роботы со свободными интерфейсными площадками, на фиг.2 - мехатронно-модульный робот, состоящий из нескольких модулей, соединенных между собой по свободным интерфейсным площадкам и образующий фигуру в виде многоугольника, на фиг.3 - мехатронно-модульный робот, состоящий из нескольких модулей, соединенных между собой по свободным интерфейсным площадкам и образующий фигуру в виде квадрата, на фиг.4 - мехатронно-модульный робот, состоящий из нескольких модулей, соединенных между собой по свободным интерфейсным площадкам и образующий фигуру в виде прямоугольника.

Мехатронно-модульный робот 1 состоит как минимум из двух сопряженных между собой модулей 2, предпочтительно двух и более. Сопряжение каждого нового модуля 2 с ранее собранным/и осуществлено вдоль выбранного направления и обеспечено стыковкой его первой свободной интерфейсной площадки 3 с одной из свободных аналогичных площадок 3 на любых других элементах конструкции, занимающих ближайшее крайнее положение в том или ином ряду. Несвободная интерфейсная площадка 4 образована за счет стыковки между собой двух свободных интерфейсных площадок 3.

Предложенный мехатронно-модульный робот функционирует следующим образом.

Произвольно выбирается модуль 2 со свободной интерфейсной площадкой 3 и стыкуется с любым произвольно выбранным модулем 2 с аналогичной свободной интерфейсной площадкой 3. При стыковке между собой двух свободных интерфейсных площадок 3 образуется несвободная интерфейсная площадка 4. Дальнейшее присоединение свободных модулей 2 к образованному модулю, состоящему из двух соединенных между собой модулей 2, происходит вдоль выбранного направления с образованием требуемой конечной структуры мехатронно-модульного робота.

Предложенный способ по созданию мехатронно-модульного робота может быть реализован следующим образом.

Рассматривают множество проектных элементов и вводят соответствующие альтернативные переменные путем представления дискретных чисел, соответствующих этим элементам, в двоичном исчислении.

Обозначают количество модулей 2, объединяемых в один мехатронно-модульный робот 1, без четко выраженной структуры, 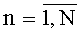$$n=\overline{\mathrm{1,}N}$$ . Тогда в двоичном исчислении получают при N≤16, где: N - количество сторон, n - количество возможный итераций.

n=1+х₁+2х₂+4x₃+8х₄,

где 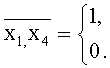$$\overline{x_{\mathrm{1,}}{x}_4}=\{\begin{array}{l}\mathrm{1,}\\ 0.\end{array}$$

При блочно-модульной сборке робота 1 полагают, что сопряжение каждого нового модуля 2 с ранее собранными осуществляется вдоль выбранного направления и обеспечивается стыковкой его первой свободной интерфейсной площадки 3 с одной из свободных аналогичных интерфейсных площадок 3 на любых других модулях 2 как элементах конструкции, занимающих ближайшее крайнее положение в том или ином ряду.

Выделяют этот алгоритм преимущественно как Асб. Описание порядка сборки приводят к указанию направления и места крепления очередного элемента с использованием алгоритма Асб.

В направлении для стыковки n-го модуля ncт принимают четыре значения n_cm=1 - север, n_cm=2 - восток, n_cm=3 - юг, n_cm=4 - запад и представляют через альтернативные переменные:

n_cm.n=1+x_5n+2x_6n,

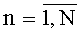
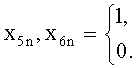
где $$n=\overline{\mathrm{1,}N}$$ , $$x_{5n},x_{6n}=\{\begin{array}{l}\mathrm{1,}\\ 0.\end{array}$$

Номер площадки, выбираемой для стыковки n-го модуля в двоичном исчислении, записывают в следующем виде:

n_cm.n=1+x_7n+2x_8n+4x_9n,

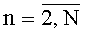
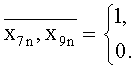
где $$n=\overline{\mathrm{2,}N}$$ , $$\overline{x_{7n},x_{9n}}=\{\begin{array}{l}\mathrm{1,}\\ 0.\end{array}$$

Альтернативные переменные для описания параметров

периодического закона вводят следующим образом:

Angle=A+Bsin(ωt+φ),

где: A - значение обобщенной координаты, относительно которой происходит периодическое движение;

B - амплитуда периодического колебания обобщенной координаты; суммарная величина |A|+|B| не должна превышать максимально допустимого отклонения обобщенной координаты модуля;

φ - смещение фазы периодического движения.

Настройкой параметров этого закона определяют алгоритмы управления, синтезируемой мехатронно-модульной конструкции. Указанные параметры характеризуются дискретными значениями, имеющими соответствующие численные номера в пределах N≤16.

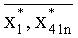
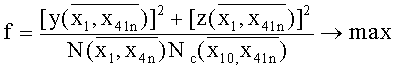
Затем для оптимизационного структурного синтеза выбирают значения альтернативных переменных $$\overline{x_1^{*},x_{41n}^{*}}$$ , обеспечивающих максимальное значение функции:

$$f=\frac{{[y(\overline{x_1,x_{41n}})]}^2+{[z(\overline{x_1,x_{41n}})]}^2}{N(\overline{x_1,x_{4n}})N{\text{}}_c(\overline{x_{\mathrm{10,}}{x}_{41n}})}\to \max$$

при ограничениях n=1, N

$$|A_1(\overline{x_{\mathrm{10,}}{x}_{12n}})+B_1(\overline{x_{14n},x_{17n}})|\le y^{\max }$$ ,

$$|A_2(\overline{x_{\mathrm{26,}}{x}_{29n}})+B_2(\overline{x_{30n},x_{33n}})|\le z^{\max }$$

$$\overline{x_{\mathrm{1,}}{x}_{41n}}=\{\begin{array}{l}\mathrm{1,}\\ 0.\end{array}$$

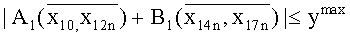
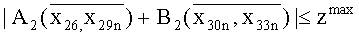
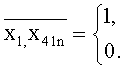
где y^max, z_max - максимально допустимые отклонения обобщенной координаты модуля относительно ее нулевого значения.

Для нахождения максимального значения функции fдачи, используют рандомизированной алгоритм многоальтернативной оптимизации, который дополняют еще одним уровнем в рамках управляемого роя частиц.

Для синхронизации процедуры метода роя частиц и вариационной процедуры многоальтернативной оптимизации на каждом шаге управляют выбором частицы для обновления скорости изменения координат, которую осуществляют с использованием рандомизированной схемы. С этой целью вводят случайную дискретную величину m, которая принимает значение m=1, М с вероятностью pn. На первом шаге получают:

$$p_n^1=\frac{1}{N}{\forall }_n=\overline{\mathrm{1,}N}$$ .

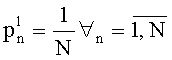
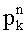
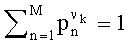
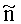
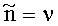
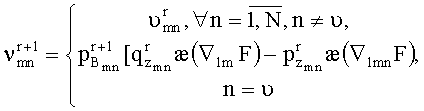
Далее изменение значений $$p_k^n$$ при условии $${\displaystyle {\sum }_{n=1}^M{p}_n^{{\nu }_k}=1}$$ осуществляют следующим образом. Определяют значение случайной величины $$\tilde{n}$$ . Пусть $$\tilde{n}=\nu$$ . Тогда скорости изменения координат на (k+1)-м шаге вычисляются:

$${\nu }_{mn}^{r+1}=\{\begin{array}{c}{\upsilon }_{mn}^r,\forall n=\overline{\mathrm{1,}N},n\ne \upsilon ,\\ p_{B_{mn}}^{r+1}[q_{z_{mn}}^r\text{æ}\left({\nabla }_{1m}F\right)-p_{z_{mn}}^r\text{æ}\left({\nabla }_{1mn}F\right),\\ n=\upsilon \end{array}$$

а значение вероятностей p_n:

$$p_n^{k+1}=\{\begin{array}{c}\frac{p_n^k}{1+{\epsilon }^{k+1}}{\forall }_n=\overline{\mathrm{1,}N},n\ne \nu ,\\ \frac{p_n^k+{\epsilon }^{k+1}}{1+{\epsilon }^{k+1}},n=\nu .\end{array}$$

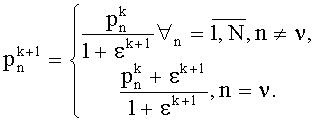
При этом величина ε>0 определяет степень рекордности движения ν-й частицы в направлении к экстремуму оптимизируемой функции.

Использование предложенного технического решения позволит проводить синтез структуры многоинвариантной модели мехатронно-модульных роботов с последующим фиксированием полученных оптимальных решений с последующем повышением количества возможных итераций мехатронно-модульного робота при значительном сокращении времени синтеза.

Изобретение относится к машиностроению, а именно к робототехнике, и может быть использовано при создании мехатронно-модульных роботов. Технический результат заключается в повышении эффективности ориентации в окружающей среде реконфигурируемых мехатронных устройств, преимущественно мехатронно-модульных роботов. Мехатронно-модульный робот состоит как минимум из двух сопряженных между собой модулей, предпочтительно двух и более, первичного и вновь с ним сопрягаемого/ых, при этом сопряжение каждого нового модуля с ранее собранным/и осуществлено вдоль выбранного направления и обеспечено стыковкой его первой интерфейсной площадки с одной из свободных на любых других элементах конструкции, занимающих ближайшее крайнее положение в том или ином ряду. 2 н. и 1 з.п. ф-лы, 4 ил.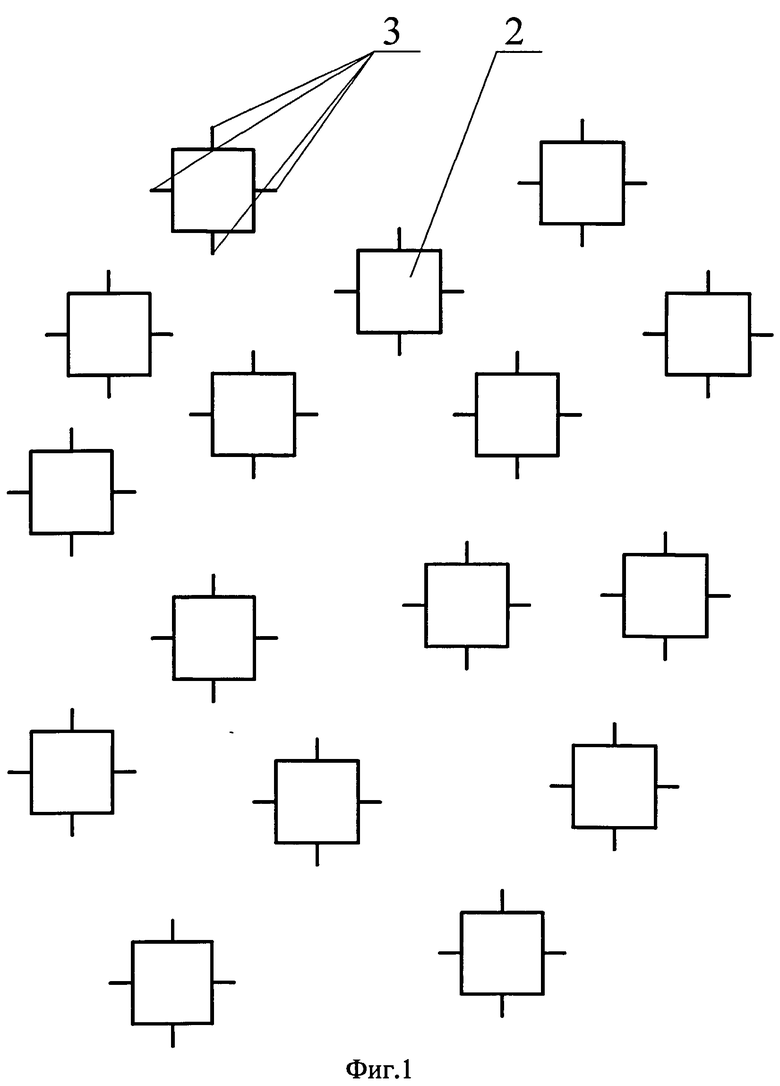

1. Мехатронно-модульный робот, характеризующийся тем, что он состоит как минимум из двух сопряженных между собой тождественных модулей, предпочтительно двух и более, первичного и вновь с ним сопрягаемого/ых, имеющих интерфейсные площадки для стыковки, причем количество модулей, объединяемых в упомянутый робот, определено из соотношения: n=1, N, где: n - количество модулей, объединяемых в один робот, определено из соотношения n=1+х1+2x2+4x3+8x4, где: x1, х4=1,0 - количество интерфейсных площадок на модуле, N≤16 - предельное количество модулей, которые могут быть объединены в один робот, при этом сопряжение каждого нового модуля с ранее собранным/и осуществлено вдоль выбранного направления и обеспечено стыковкой его первой интерфейсной площадки с одной из свободных на любых других элементах конструкции, занимающих ближайшее крайнее положение в том или ином ряду, причем интерфейсные площадки каждого модуля выполнены с возможностью стыковки с аналогичными площадками по крайней мере в четырех диаметрально противоположных направлениях, при этом альтернативные переменные для алгоритмов управления синтезированной мехатронно-модульной конструкцией для описания параметров периодического закона движения выбраны из следующего соотношения:
Angle=А+Bsin(ωt+φ),
где: A - значение обобщенной координаты, относительно которой происходит периодическое движение; B - амплитуда периодического колебания обобщенной координаты, причем суммарная величина |A|+|B| не превышает максимально допустимого отклонения обобщенной координаты модуля; φ - смещение фазы периодического движения.

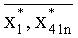
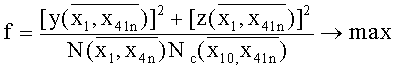
2. Мехатронно-модульный робот по п.1, отличающийся тем, что для оптимизационного структурного синтеза, выбраны значения альтернативных переменных $$\overline{x_1^{*},x_{41n}^{*}}$$ , обеспечивающих максимальное значение функции:
$$f=\frac{{[y(\overline{x_1,x_{41n}})]}^2+{[z(\overline{x_1,x_{41n}})]}^2}{N(\overline{x_1,x_{4n}})N{\text{}}_c(\overline{x_{\mathrm{10,}}{x}_{41n}})}\to \max$$
при ограничениях n=1, N
$$|A_1(\overline{x_{\mathrm{10,}}{x}_{12n}})+B_1(\overline{x_{14n},x_{17n}})|\le y^{\max }$$ ,
$$|A_2(\overline{x_{\mathrm{26,}}{x}_{29n}})+B_2(\overline{x_{30n},x_{33n}})|\le z^{\max }$$
$$\overline{x_{\mathrm{1,}}{x}_{41n}}=\{\begin{array}{l}\mathrm{1,}\\ 0.\end{array}$$
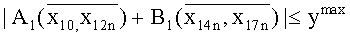
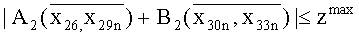
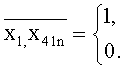
где: y^max, z^max - максимально допустимые отклонения обобщенной координаты модуля относительно ее нулевого значения.

3. Способ создания мехатронно-модульного робота по п.1, характеризующийся тем, что при проведении синтеза структуры многоинвариантной модели мехатронно-модульных роботов и последующем фиксировании полученных оптимальных решений рассматривают множество проектных элементов и вводят соответствующие альтернативные переменные путем представления дискретных чисел, соответствующих этим элементам, в двоичном исчислении, после чего обозначают количество модулей, объединяемых в один робот, преимущественно без четко выраженной структуры, и обеспечивают сопряжение каждого нового модуля с ранее собранными вдоль выбранного направления и стыковку его первой интерфейсной площадки с одной из свободных на любых других элементах конструкции, занимающих ближайшее крайнее положение в том или ином ряду, причем интерфейсные площадки каждого модуля выполняют с возможностью стыковки с аналогичными площадками по крайней мере в четырех диаметрально противоположных направлениях, после чего вводят альтернативные переменные для описания параметров периодического закона движения следующим образом:
Angle=А+Bsin(ωt+φ),
где: A - значение обобщенной координаты, относительно которой происходит периодическое движение; B - амплитуда периодического колебания обобщенной координаты; причем суммарная величина |A|+|B| не превышает максимально допустимого отклонения обобщенной координаты модуля; φ - смещение фазы периодического движения; при этом настройкой параметров этого закона определяют алгоритмы управления, синтезируемой мехатронно-модульной конструкции, причем для оптимизационного структурного синтеза выбирают значения альтернативных переменных 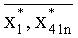$$\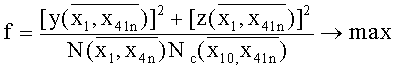overline{x_1^{*},x_{41n}^{*}}$$ , обеспечивающих максимальное значение функции:
$$f=\frac{{[y(\overline{x_1,x_{41n}})]}^2+{[z(\overline{x_1,x_{41n}})]}^2}{N(\overline{x_1,x_{4n}})N{\text{}}_c(\overline{x_{\mathrm{10,}}{x}_{41n}})}\to \max$$
при ограничениях n=1, N
$$|A_1(\overline{x_{\mathrm{10,}}{x}_{12n}})+B_1(\overline{x_{14n},x_{17n}})|\le y^{\max }$$ ,
$$|A_2(\overline{x_{\mathrm{26,}}{x}_{29n}})+B_2(\overline{x_{30n},x_{33n}})|\le z^{\max }$$
$$\overline{x_{\mathrm{1,}}{x}_{41n}}=\{\begin{array}{l}\mathrm{1,}\\ 0.\end{array}$$
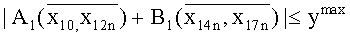
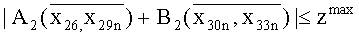
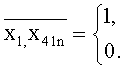
где: y^max, z^max - максимально допустимые отклонения обобщенной координаты модуля относительно ее нулевого значения, причем для нахождения максимального значения функции f используют рандомизированныой алгоритм многоальтернативной оптимизации, который дополняют еще одним уровнем в рамках управляемого роя частиц.