Изобретение относится к области исследований, в ходе которых оценивается работоспособность армированных и подвергающихся воздействию нагрузки изделий при их проектировании, а также в процессе эксплуатации.
Известны традиционные в инженерной практике и курсе «Сопротивления материалов» способы определения механической работоспособности по условиям прочности и жесткости [1, 2].
Условия прочности:
σmax≤[σ],
τmax≤[τ],
где σmax, τmax - действующие максимальные нормальные и касательные напряжения;
[σ], [τ] - допускаемые нормальные и касательные напряжения.
Условия жесткости:
Δl≤[Δl],
Δφ≤[Δφ],
где Δl, Δφ - действующие максимальные удлинение, угол закручивания;
[Δl], [Δφ] - допускаемые удлинение, угол закручивания.
По результатам расчета действующих напряжений строятся эпюры - графики изменения напряжений и деформаций по длине или сечению изделия. Действующие максимальные напряжения и удлинения (углы закручивания) определяются из эпюр. На эпюрах наглядно представлены изменения напряжений и удлинений (углов закручивания) и определены их максимальные значения.
Известен способ оценки механической работоспособности по полям напряжений и деформаций (ближайший аналог [2]). Этот способ основан на сопоставлении действующих максимальных напряжений и деформаций в изделии с допускаемыми значениями напряжений и деформаций.
Недостатками такой оценки работоспособности является то, что величина допускаемых напряжений условна и назначается на основе опыта эксплуатации деталей машин различного назначения. Допускаемые напряжения не являются нормативной характеристикой материала детали. Кроме того, оценка является детерминированной и не учитывает разброс максимальных и предельных напряжений.
Предлагаемый способ решает задачу оценки механической работоспособности изделий путем построения полей вероятностей безотказной работы (ВБР) на основе статистического массива экспериментальных данных и известного подхода к оценке прочностной надежности [3-5].
Оценка прочностной надежности изделия заключается в том, что изделие или его элемент имеет определенную прочность, при превышении которой наступает потеря его работоспособности - разрушение. С одной стороны, факторы, определяющие прочность элементов изделия, являются случайными переменными, а следовательно, и прочность будет случайной переменной. С другой стороны, напряжение, возникающее в элементе изделия, зависит от многих переменных (упругих, деформационных, дилатометрических характеристик и др.), обладающих изменчивостью или рассеиванием. Причинами рассеяния являются различия в структуре материала образца, степень его дефектности, различие в размерах, точность определения измеряемых характеристик, стабильность условий испытания и т.д. Это приводит к тому, что напряжения в элементе также становятся случайными переменными. Нормальное распределение случайных величин применяется в тех случаях, когда они зависят от большого числа независимых воздействий.
Рассмотрим определение вероятности безотказной работы при нормальном распределении предельных и эквивалентных напряжениях. Нормальное распределение является наиболее часто используемой статистической моделью.
Таким образом, для оценки надежности по критерию прочности необходимо определить вероятность того, что прочность изделия или его элемента больше, чем расчетные напряжения [3-5].
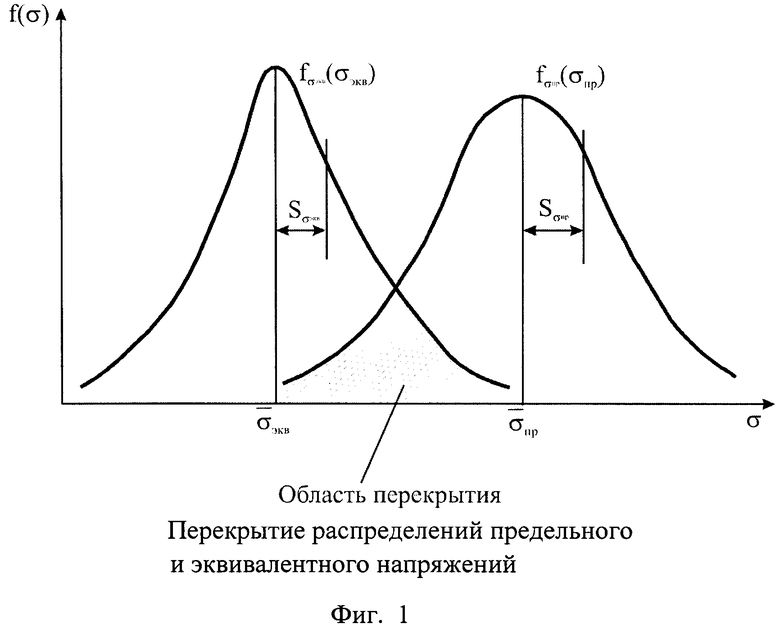
На фиг. 1 показано перекрытие распределений эквивалентных напряжений в опасной точке изделия ƒσ(σэкв) со средним значением 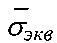 и средним квадратическим отклонением Sσэкв, а также предела текучести ƒσ(σпр) со средним значением
и средним квадратическим отклонением Sσэкв, а также предела текучести ƒσ(σпр) со средним значением 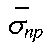 и средним квадратическим отклонением Sσпр.
и средним квадратическим отклонением Sσпр.
Обозначим новую случайную величину
y=σпр-σэкв,
тогда вероятность безотказной работы R(t) можно представить в виде
R(t)=P(y>0).
Случайная величина у имеет нормальное распределение с математическим ожиданием
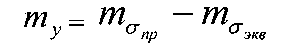
и средним квадратическим отклонением
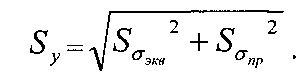
Вероятность безотказной работы, выраженную через y, можно записать
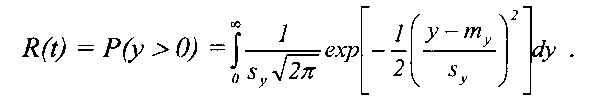
Выражая вероятность безотказной работы R(t) через нормированную функцию нормального распределения, имеем
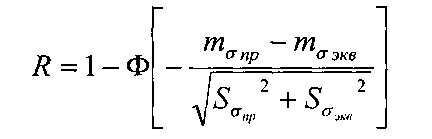
где 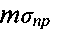 - математическое ожидание предельных напряжений (предела текучести, максимальной прочности при растяжении);
- математическое ожидание предельных напряжений (предела текучести, максимальной прочности при растяжении); 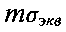 - математическое ожидание эквивалентного напряжения;
- математическое ожидание эквивалентного напряжения; 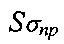 - среднее квадратическое отклонение предельных напряжений;
- среднее квадратическое отклонение предельных напряжений; 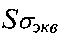 - среднее квадратическое отклонение эквивалентного напряжения.
- среднее квадратическое отклонение эквивалентного напряжения.
Среднее значение случайной величины является оценкой математического ожидания, т.е.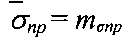 , а
, а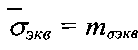 .
.
В том случае, когда предельные и эквивалентные напряжения имеют другие законы распределения, разработаны модели для определения вероятности безотказной работы [4].
Если предельные и эквивалентные напряжения распределены по экспоненциальному закону, вероятность безотказной работы определяется
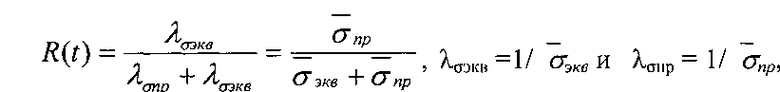
где 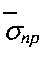 - среднее значение предельного напряжения;
- среднее значение предельного напряжения;
σэкв - среднее значение эквивалентного напряжения.
В том случае, когда предельные и эквивалентные напряжения имеют гамма-распределение с параметрами m, λ и n, µ соответственно, вероятность безотказной работы определяется
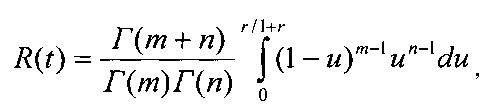
где r=µ/λ.
Если предельные и эквивалентные напряжения имеют распределение Вейбулла с параметрами βσпр, θσпр, σпр0 и βσэкв, θσэкв, σэкв0, то вероятность безотказной работы определяется
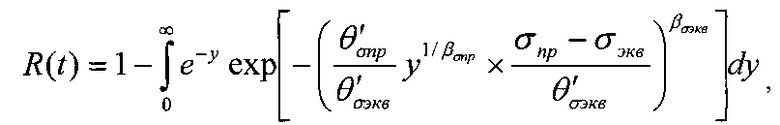
где 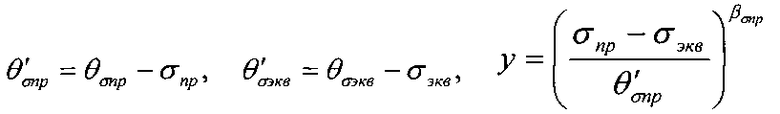
σпр0, σэкв0 - минимальные значения предельных и эквивалентных напряжений.
Условие работоспособности по критерию прочности с учетом времени эксплуатации и температурной зависимости, предельных и расчетных напряжений при детерминированном подходе можно записать:
σэкв(t,T°)<σпр(t,T°),
где σэкв(t,T°) - эквивалентные напряжения в опасной точке изделия,
σпр(t,T°) - предельные напряжения (пределы прочности, текучести, выносливости и т.д.).
Это условие работоспособности может рассматриваться как отдельно для старения материала при одной температуре и учете температурной зависимости предельных и расчетных напряжений исходного материала, так и для учета этих факторов одновременно [6].
Оценкой надежности изделий по критерию прочности с учетом старения материала, а также температурной зависимости предельных и расчетных напряжений служит вероятность того, что предельные напряжения материала изделия или его элемента в момент времени ti или при температуре 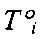 больше, чем расчетные напряжения в тот же момент времени или при той же температуре. Примем в качестве предельных напряжений для материала изделия предел текучести как наиболее часто используемую характеристику в прочностных расчетах.
больше, чем расчетные напряжения в тот же момент времени или при той же температуре. Примем в качестве предельных напряжений для материала изделия предел текучести как наиболее часто используемую характеристику в прочностных расчетах.
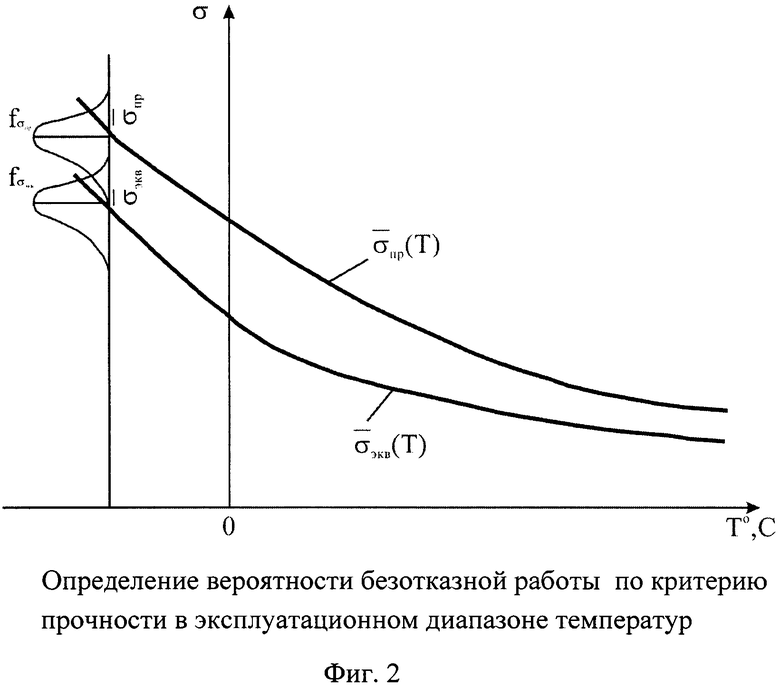
На фиг. 2 показаны температурные зависимости и перекрытие распределений эквивалентных напряжений в опасной точке изделия ƒσ(σэкв) со средним значением σэкв(t,T°) и средним квадратическим отклонением Sσэкв(t,T°), а также предела текучести ƒσ(σm) со средним значением 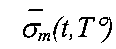 и средним квадратическим отклонением, Som(t,T°).
и средним квадратическим отклонением, Som(t,T°).
Обозначим новую случайную величину yi=σmi(t,T°)-σэквi(t,T°).
Эта случайная величина должна быть положительной, т.е. предел текучести полимерного материала должен быть выше расчетных эквивалентных напряжений. Тогда вероятность безотказной работы элемента в момент времени ti при температуре 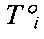 можно представить в виде
можно представить в виде
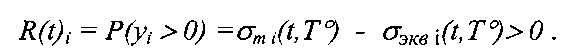
R(t)i=P(yi>0)=σmi(t,T°)-σэквi(t,T°)
Случайная величина yi имеет нормальное распределение с математическим ожиданием
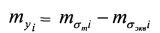
и средним квадратическим отклонением
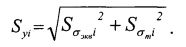
Вероятность безотказной работы, выраженную через yi, можно записать
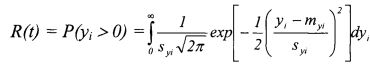
Выражая вероятность безотказной работы R(t) через нормированную функцию нормального распределения, имеем
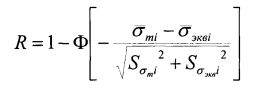
где 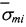 - среднее значение максимальной прочности при растяжении;
- среднее значение максимальной прочности при растяжении;
σэквi - среднее значение эквивалентного напряжения;
Sσэквi - среднее квадратическое отклонение эквивалентного напряжения;
Somi - среднее квадратическое отклонение предела текучести при растяжении.
Выполнены расчеты вероятности безотказной работы на примере трубы, нагруженной внутренним давлением.
При вероятностно-статистическом подходе задаются управляющие параметры (прочностные, упругие, размерные) в соответствии с законом их распределения. Тогда в результате расчета получается вариант напряженно-деформированного состояния (НДС), а проведение ряда аналогичных расчетов - численных экспериментов - дает набор данных о параметрах НДС, поддающихся статистическому анализу.
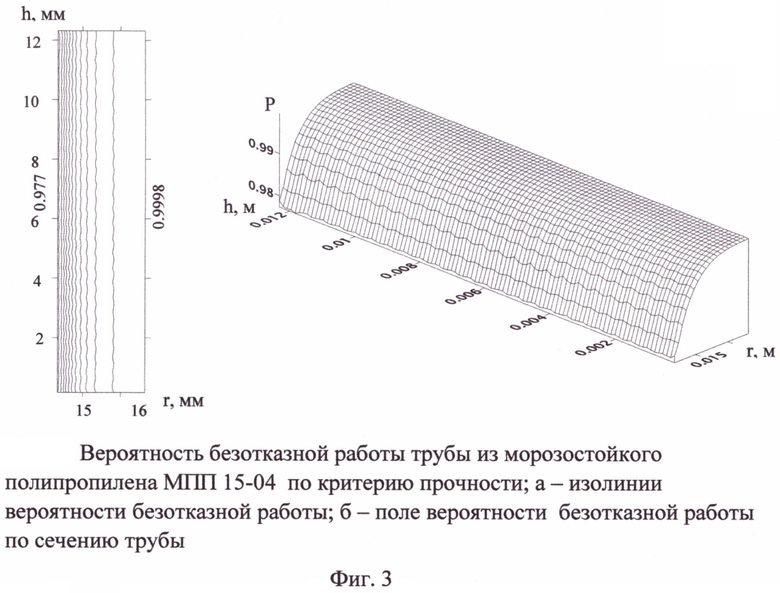
На фиг. 3 показано поле вероятности безотказной работы по объему участка трубы по критерию прочности из МПП 15-04 при температуре 60°C и давлении 1,7 МПа.
На фиг. 4 показано поле вероятностей безотказной работы по объему участка трубы по критерию прочности из МПП 15-04 при температуре 20°C и давлении 4 МПа, выполненной в программном комплексе ANSYS.
Оценка надежности конструкции при рассматриваемом подходе получается в виде вероятности безотказной работы материала во всех точках изделия, что можно представить в виде полей распределения ВБР по всему объему конструкции (фиг. 3 и 4). Видно, что на внутренней стене трубы вероятность безотказной работы уменьшается.
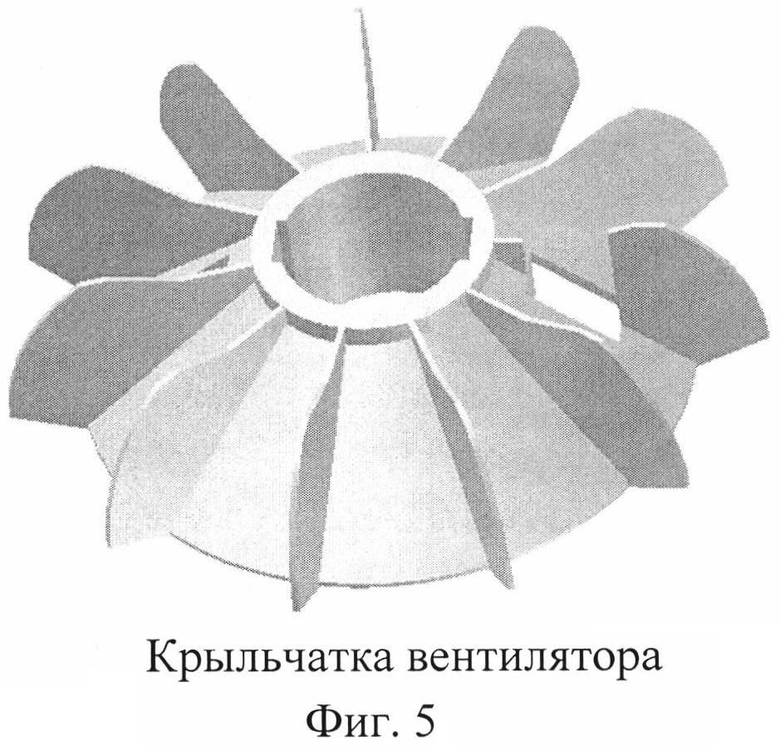
Предлагаемый подход реализован в виде построения поля вероятностей безотказной работы [7] для крыльчатки вентилятора, которая выполнена из полимерного материала. Крыльчатка вентилятора устанавливается на валу электродвигателя серии АИР. На крыльчатке выполнен двусторонний шпоночный паз (фиг. 5). Напряженное состояние в крыльчатке вентилятора возникает за счет исходного натяга при посадке на вал и при эксплуатации электродвигателя при отрицательных температурах.
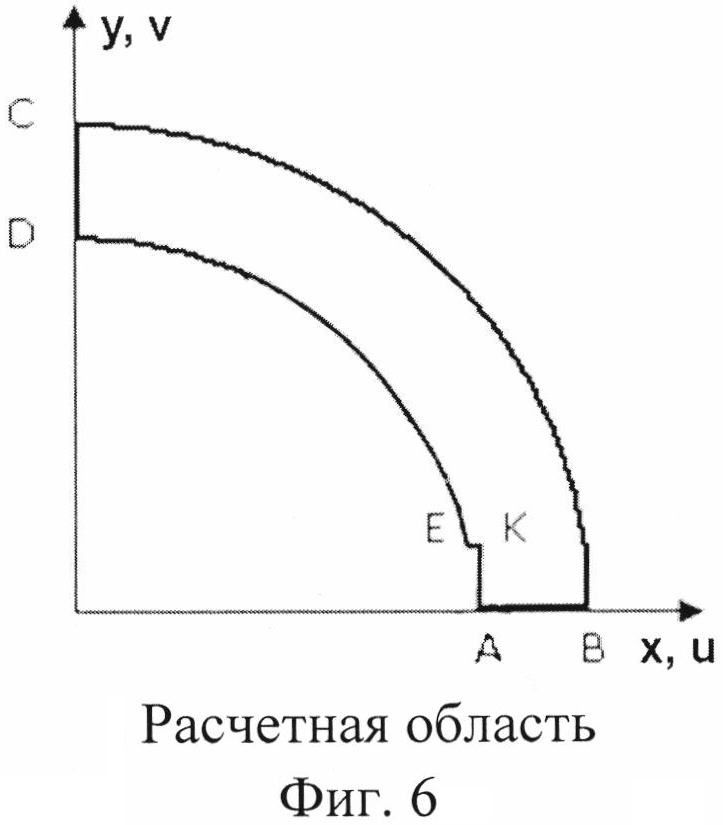
В силу наличия двух взаимно перпендикулярных осей симметрии задачи рассматривается расчетная область, представляющая собой четверть осевого сечения втулки вентилятора, для которой решается плоская задача теории упругости (фиг. 6).
Задача решается с помощью метода конечных элементов. Исходными данными для расчета являются температурные зависимости среднего значения и среднего квадратического отклонения модуля упругости и прочности при растяжении исследуемых материалов и расчетная схема изделия.
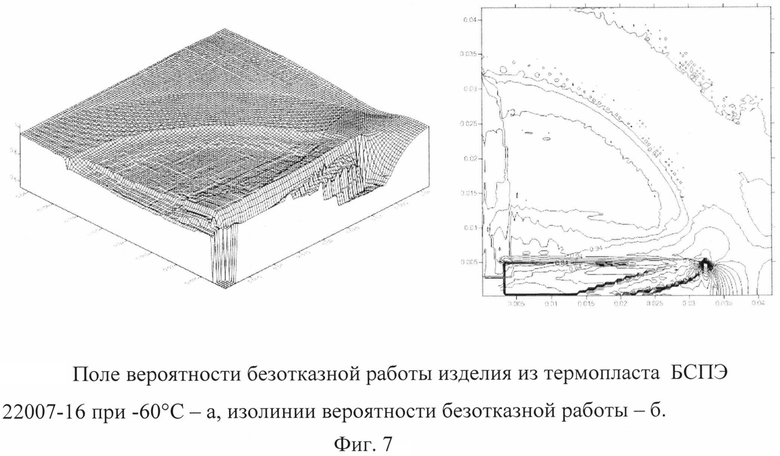
На фиг. 7 наглядно представлены результаты расчетов для материала БСПЭ 22007-16 при температуре, равной -60°C, в виде поля вероятности безотказной работы по поперечному сечению втулки и соответствующих им изолиний. В угловой части паза наблюдается уменьшение значений ВБР, вследствие концентрации напряжений в этой области.
Предлагаемый способ построения полей вероятностей безотказной работы эффективен при выборе материалов и конструктивных решений изделий и конструкций, что позволит выбрать оптимальный вариант.
Источники информации
1. Расчет на прочность деталей машин: Справочник / И.А. Биргер, Б.Ф. Шор, Г.Б. Иосилевич.- 3 изд., перераб. и доп. - М.: Машиностроение, 1979. - 702 с.
2. Пригоровский Н.И. Методы и средства определения полей деформаций и напряжений: Справочник. - М.: Машиностроение, 1983. - 248 с.: ил.
3. Болотин В.В. Методы теории вероятности и теории надежности в расчетах сооружений. - М.: Стройиздат, 1982. - 351 с.
4. Ржаницин А.Р. Теория расчета строительных конструкций на надежность. - М.: Стройиздат, 1978. - 239 с.
5. Капур К., Ламберсон Л. Надежность и проектирование систем. Пер. с англ. / Под ред. И.А.Ушакова. - М.: Мир, 1980. - 604 с.
6. Реутов А.И. Прогнозирование надежности строительных изделий из полимерных материалов: монография / А.И.Реутов. - М.: ООО РИФ «Стройматериалы», 2007. - 184 с.
7. Бочкарева С.А., Люкшин Б.А., Реутов А.И., Дамбаев Ж.., В.А. Удод, Козлова Л.А. Расчет вероятности безотказной работы уплотнительного элемента аварийного клапана высокого давления // «Проблемы механики современных машин», Материалы V Международной конференции, 25-30 июня 2012 г., Улан-Удэ, изд-во ВСГУТУ, 2012, т. 2, с. 69-73.
8. Люкшин Б.А., Реутов А.И., Бочкарева С.А., Попович СИ. Оценка надежности конструкции на основе анализа ее напряженно-деформированного состояния // «Безопасность и живучесть технических систем», Материалы IV Всероссийской конференции, 9-13 октября 2012, г., Красноярск, изд-во ВСГУТУ, 2012, т. 2, с. 69-73.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОЦЕНКИ НИЖНЕЙ ТЕМПЕРАТУРНОЙ ГРАНИЦЫ МЕХАНИЧЕСКОЙ РАБОТОСПОСОБНОСТИ ИЗДЕЛИЙ ИЗ ПОЛИМЕРНЫХ КОМПАУНДОВ | 2015 |
|
RU2599284C1 |
| Способ эксплуатационного контроля технического состояния и прогнозирования ресурса подшипников электродвигателей | 2016 |
|
RU2622493C1 |
| Способ проведения многофакторных эквивалентно-циклических испытаний | 2021 |
|
RU2783770C1 |
| СПОСОБ КРЕПЛЕНИЯ МЕТОК АВТОМАТИЧЕСКОЙ ИДЕНТИФИКАЦИИ НА ЖЕЛЕЗНОДОРОЖНОМ КОЛЕСЕ И ЖЕЛЕЗНОДОРОЖНОЕ КОЛЕСО С ВОЗМОЖНОСТЬЮ АВТОМАТИЧЕСКОЙ ИДЕНТИФИКАЦИИ, ПОЛУЧЕННОЕ ДАННЫМ СПОСОБОМ | 2024 |
|
RU2831954C1 |
| Способ определения остаточного ресурса деталей машин | 2019 |
|
RU2733105C1 |
| СПОСОБ ОЦЕНКИ И ПОДДЕРЖАНИЯ НАДЕЖНОСТИ САМОЛЕТОВ И ИХ СИЛОВЫХ УСТАНОВОК ПРИ ЭКСПЛУАТАЦИИ АВИАЦИОННОЙ ТЕХНИКИ ПО СОСТОЯНИЮ | 1993 |
|
RU2038991C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНОГО ПЕРИОДА ТЕХНИЧЕСКОГО ОБСЛУЖИВАНИЯ СЛОЖНЫХ ТЕХНИЧЕСКИХ СИСТЕМ ПРИ ОГРАНИЧЕННЫХ РЕСУРСАХ | 2009 |
|
RU2436162C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПОВРЕЖДАЕМОСТИ НАГРУЖЕННОГО МАТЕРИАЛА И РЕСУРСА РАБОТОСПОСОБНОСТИ | 1997 |
|
RU2139515C1 |
| СПОСОБ КРЕПЛЕНИЯ МЕТОК АВТОМАТИЧЕСКОЙ ИДЕНТИФИКАЦИИ НА ЖЕЛЕЗНОДОРОЖНОМ КОЛЕСЕ И ЖЕЛЕЗНОДОРОЖНОЕ КОЛЕСО С ВОЗМОЖНОСТЬЮ АВТОМАТИЧЕСКОЙ ИДЕНТИФИКАЦИИ, ПОЛУЧЕННОЕ ДАННЫМ СПОСОБОМ | 2024 |
|
RU2831955C1 |
| СПОСОБ НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ ПРОЧНОСТИ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ | 1991 |
|
RU2006813C1 |
Изобретение относится к области исследований, в ходе которых оценивается работоспособность армированных и подвергающихся воздействию нагрузки изделий при их проектировании, а также в процессе эксплуатации. Сущность: строятся поля вероятностей безотказной работы по объему изделия по критериям прочности или жесткости (предельной деформации), с учетом времени эксплуатации и температурной зависимости. Технический результат: повышение степени оценки механической работоспособности изделий. 7 ил.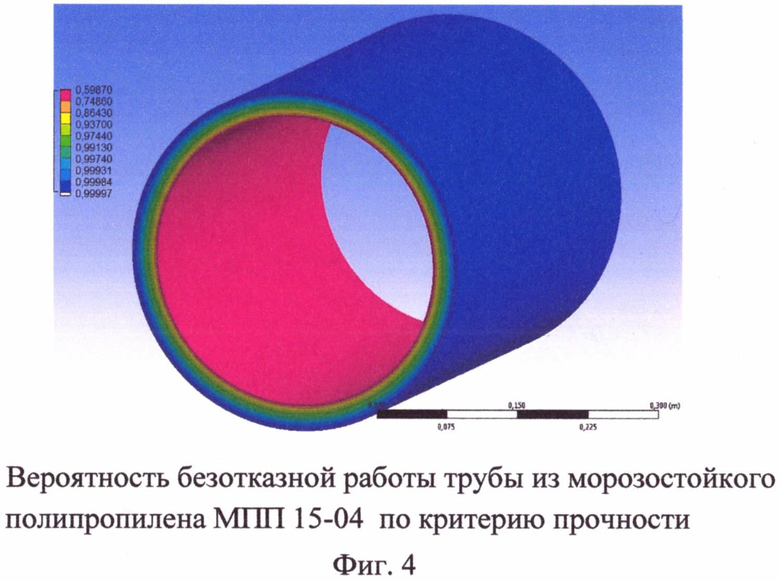
Способ оценки механической работоспособности нагруженных и армированных изделий, отличающийся тем, что строятся поля вероятностей безотказной работы по объему изделия по критериям прочности или жесткости (предельной деформации), с учетом времени эксплуатации и температурной зависимости.
| БОЧКАРЁВА СВЕТЛАНА АЛЕКСЕЕВНА, ОЦЕНКА НАДЕЖНОСТИ КОНСТРУКЦИЙ ИЗ ПОЛИМЕРНЫХ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ С УЧЕТОМ РАЗБРОСА УПРАВЛЯЮЩИХ ПАРАМЕТРОВ, Специальность 01.02.04 Механика деформируемого твердого тела, Автореферат, диссертации на соискание ученой степени кандидата физико-математических наук, Томск 2006 | |||
| Прибор с двумя призмами | 1917 |
|
SU27A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПОКАЗАТЕЛЕЙ БЕЗОТКАЗНОСТИ ИЗДЕЛИЯ ПО РЕЗУЛЬТАТАМ НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ | 2005 |
|
RU2301992C2 |
| RU 2008105108 A 20.08.2009 | |||
| US 7603904 B2 20.10.2009. | |||
Авторы
Даты
2015-12-10—Публикация
2013-01-10—Подача