Изобретение относится к навигации, а более конкретно к способам определения наивыгоднейшего пути судна в зависимости от гидрометеорологических факторов.
При выборе наивыгоднейшего пути судна существенное значение имеет учет воздействия на судно гидрометеорологических факторов, которые меняются от сезона к сезону, от рейса к рейсу и даже в течение рейса.
Учет воздействия на судно гидрометеорологических факторов выполняется с учетом климатических условий в районе плавания с использованием карт распределения ветров и течений по океанам типа «Pilot charts», на которых на каждый месяц приводятся сведения о силе и повторяемости ветров, о вероятных путях штормов, об океанских течениях, о вероятности встречи со штормами и льдами, месячных гидрометеорологических карт, содержащих среднестатистические данные о распределении по месяцам ветра, волнения, зыби, повторяемости штормов, туманов и т.д., а также навигационного пособия «Океанские пути мира» («Ocean passages for the World»). При этом выбор наивыгоднейшего пути судна выполняет судоводитель исходя из тактико-технических данных своего судна (Лесков М.М., Баранов Ю.К., Гаврюк М.И. Навигация. М.: Транспорт, 1986, с. 343-344 [1]).
Для учета потери скорости судна также используют аналитические зависимости вида:
ΔV=ah+bh2-chq, где h - высота волны (м), q - курсовой угол волны (рад), a, b, c - коэффициенты, зависящие от типа судна;
ΔV=Vл-V=h(0,745-0,259qB)(1-1,35·10-6 DVл), где h - высота волны (м), qB - курсовой угол волны (град), D - фактическое водоизмещение судна (т), Vл - скорость судна по лагу (уз), высоту волны при этом определяют по эмпирической формуле
h=0,02286W3/2+1,524, где W - скорость ветра (уз) (Лесков М.М., Баранов Ю.К., Гаврюк М.И. Навигация. М.: Транспорт, 1986, с. 344 [1]).
При плавании в шторм выбирают такую скорость, которая бы обеспечивала безопасный режим плавания.
Для приблизительной оценки потери скорости на волнении может быть также использована формула Г. Аертсена (Климатология. Гидрометеоиздат, 1980, стр. 163):
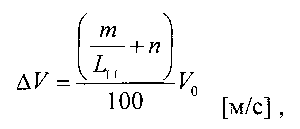
где m и n - эмпирические коэффициенты, выбираемые из таблицы (Климатология. Гидрометеоиздат, 1980);
V0 - скорость полного хода судна на тихой воде;
Lii - длина судна между перпендикулярами.
Климатические (сезонные) пути с учетом гидрометеорологических элементов и потерь скорости судна могут быть также рассчитаны с помощью специальных пособий - «Атласов гидрометеорологических условий плавания судов морского флота» [2], в которых на каждую четверть курсов для указанного типа судна приведены проценты приращения эксплуатационной скорости (положительного и отрицательного) на каждый месяц года и на квадрат, ограниченный 5 градусами широты и долготы. Выбрав с помощью прилагаемой палетки маршрут следования (или проложив его самостоятельно исходя из конкретного рейсового задания), можно снять для каждого квадрата длину плавания S и процент потери скорости ΔV. После этого вычисляется средняя величина потери скорости ΔVcp в процентах и определяется средняя скорость на переходе
ΔVcp=ΔV1S1+ΔV2S2+…+ΔVnSn/(S1+S2+…+Sn);
V=Vo-Vo/100 ΔVср где Vo - скорость судна на спокойной воде.
В ряде случаев судну приходится пересекать районы (зоны), условия плавания в которых резко отличаются, например пересечение «сороковых» штормовых широт, преодоление ледовых полей, плавание в районах постоянного течения и т.д. При этом допускается, что условия плавания в пределах этого выделенного района постоянны, то кратчайший путь определяют по формуле: V1/V2=sinα1/sinα2, при этом если V1>V2, то математическое решение задачи имеет вид sinα2=sinα1 V2/V1; или Δα=tgα ΔV/V, где Δα - изменение угла α1; α1 - начальный угол между линией курса и нормалью к границе зон; α2 - конечный угол между линией курса и нормалью к границе зон, ведущей в точку назначения.
При этом задача решается методом последовательных приближений или графически до тех пор, пока полученное значение угла не приведет в точку назначения (Лесков М.М., Баранов Ю.К., Гаврюк М.И. Навигация. М.: Транспорт, 1986, с. 345 [1]).
Однако на практике зоны нельзя разделить четкой прямолинейной границей, а следовательно, полученные решения являются приближенными.
Кроме того, конкретная гидрометеорологическая обстановка часто отличается от среднестатистической.
Известен также способ выбора наивыгоднейшего оптимального пути в зависимости от гидрометеорологической обстановки, который включает расчет на основе среднестатистических данных о гидрометеорологической обстановке климатического пути судна, который в дальнейшем является «осью» для расчета оптимального пути. За основу расчета может быть также взята дуга большого круга. При этом, имея трех или пятисуточный прогноз волнения, рассчитываются величины ветроволновых потерь для различных курсов на первые, вторые, третьи сутки плавания. С помощью ЭВМ перебирается большое количество вариантов, концы суточных плаваний соединяют кривой линией - изохроной. Некоторая из точек изохроны, построенной на конец третьих суток, окажется ближе к пункту прихода. Курс судна располагают так, чтобы выйти в эту ближайшую точку. С получением нового прогноза вычисления повторяются (Лесков М.М., Баранов Ю.К., Гаврюк М.И. Навигация. М.: Транспорт, 1986, с. 346-347 [1]).
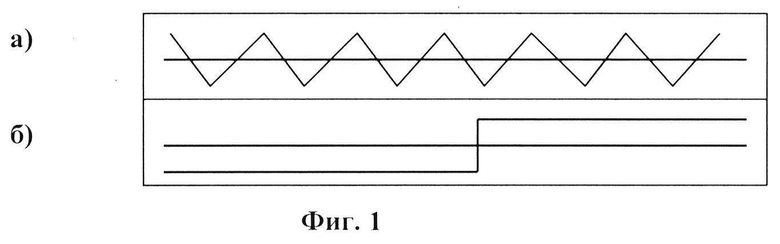
Однако реальные пространственно-временные распределения гидрометеорологических условий представляют собой сложную пятнистую структуру со свойствами динамического хаоса, которая носит название "перемежаемости". Пятна квазиоднородных значений гидрометеорологических характеристик имеют чрезвычайно нерегулярные (извилистые) геометрические очертания, различные площади. Единственной устойчивой их характеристикой является функция распределения числа пятен по площади. Она является степенным распределением - больших пятен мало (максимальное - одно), а малых много. Эта особенность пространственно-временного распределения гидрометеорологических характеристик снижает требования к гидрометеорологической информации, обеспечивающей принятие решений на обеспечение безопасности судовождения.
С другой стороны, при принятии решения эффективность решения задачи с учетом гидрометеоусловий определяется, в конечном счете, возможностью выполнения этой задачи в реальных погодных условиях. Задача решается, если существуют благоприятные условия среды на пространственно-временном интервале, необходимом для ее выполнения. Такое понимание возможности выполнения задачи требует достаточно детального описания пространственно-временной изменчивости геопространственных полей. В настоящее время для этой цели используют вероятностные (статистические) параметры, например, среднеквадратическое отклонение гидрометеорологических характеристик. Однако эти параметры не позволяют описать перемежаемость, так как это "интегральные" характеристики изменчивости, которые не характеризуют структуру пятнистости погодных условий. Например, на фиг. 1 приведены графики двух функций (а, б), имеющих одинаковые дисперсии на рассматриваемом интервале, но разную локальную изменчивость. На фиг. 2 приведены примеры различных пространственных распределений благоприятных условий, имеющих одну суммарную площадь (вероятность) по всему району, но различную локальную по меньшим масштабам. Эти примеры свидетельствуют о необходимости обеспечения процедуры принятия решений информацией, описывающей локальный характер пространственно-временной изменчивости в распределении геопространственных полей. Значимость учета при гидрометеорологическом обеспечении пространственно-временной перемежаемости гидрометеорологических характеристик можно продемонстрировать на примере следующей схематичной задачи, для решения которой будем использовать математический аппарат теории геометрических вероятностей (Кендал М., Моран Л. Геометрические вероятности. - М: Наука, 1972. - 192 с. [3]).
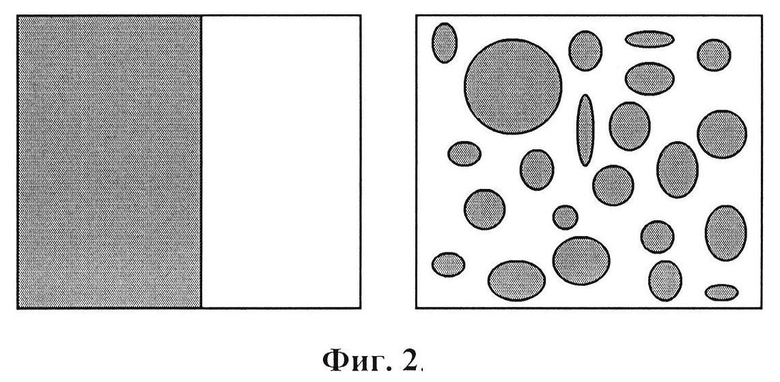
Пусть в районе, пересекаемом судном, имеются зоны с неблагоприятными гидрометеорологическими условиями (фиг. 3). В этом районе по траектории A→В длиной L движется судно. При этом в благоприятных условиях эффективность решения им задачи перехода по кратчайшему пути равна единице, а в неблагоприятных - минус единице. Тогда оценкой потерь в эффективности решения задачи может служить величина χ, равная отношению суммарной длины траектории судна, проходящей через области с неблагоприятными условиями к общей длине траектории L. Следовательно, χ характеризует относительную величину потерь в эффективности действий судна.
В качестве конкретного параметра будем использовать математическое ожидание 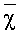
Схема решения задачи оценки потерь следующая: оценим χ по известному закону распределения зон с неблагоприятными условиями. Приведем формальную постановку и решение задачи.
Пусть в трехмерном пространственно-временном единичном объеме V0(x, y, t), где x, y - пространственные координаты, а t - время, задана функция γ(x, y, t), характеризующая степень неблагоприятности гидрометеорологических условий решения задачи в точке (x, y, t) объема V0.
Пусть известен некоторый критический уровень γ0, разделяющий условия на благоприятные γ>γ0 и неблагоприятные γ≤γ0. И пусть области с γ≤γ0 будут несвязными.
Положим, что число областей N с менее благоприятными условиями, имеющих объем V, больший некоторого объема ν, будет описываться выражением

где ν0(γ0) - максимальный объем среди всех объемов с неблагоприятными условиями.
Из (1) следует, что общее число областей с объемами νε≤ν≤ν0 равно

Теперь для простоты предположим, что области с неблагоприятными условиями являются шарами, и они распределены в V0 таким образом, что среднее число центров шаров в любом меньшем объеме равно λ, то есть распределение центров шаров является случайным пуассоновским процессом.
В этом случае, на основании (1) и (2) вероятность F того, что случайно пересеченный судном шар имеет объем V, меньший или равный ν, будет равна

Отсюда легко получить выражение для плотности распределения объемов пересекаемых шаров

Пересечение прямолинейной траектории судна с шаром является хордой. Центры шаров диаметра r, которые могут пересекаться прямолинейной траекторией, должны лежать в цилиндре объемом πr2.
Вероятность того, что траектория судна пересечет заданный шар, возрастает вместе с размером шара. Среднее число шаров 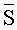
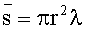

Учитывая, что средняя длина пересечения равна 2/3r, запишем математическое ожидание сумм пересечений траектории с шарами

где φ(r) - плотность распределения диаметров шаров, r0 - диаметр шара с объемом ν0.
Из (4) получим явное выражение для φ(r)

Подставляя (7) в (6) и интегрируя, получим

Очевидно, что для приближенной оценки потерь в эффективности достаточно оценить величину 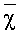
Традиционные показатели ветроволнового режима, такие как повторяемость штормовых (неблагоприятных) условий, недостаточны для адекватного планирования сложных морских транспортных операций. Для обеспечения безопасности и повышения эффективности операций по буксировке или транспортировке крупных объектов, оценки времени ожидания благоприятных условий, планирования перехода, выбора пунктов штормового отстоя, выбора скорости перехода и соответственно состава сил и средств для той или иной морской транспортной операции требуется знать характеристики окон погоды. К числу основных характеристик окон погоды относятся число окон погоды заданной непрерывной продолжительности той или иной обеспеченности, среднее и максимальное время ожидания окна погоды заданной обеспеченности в заданный месяц или сезон.
Для получения статистических оценок характеристик окон погоды лучше всего использовать результаты реанализа полей ветра и волнения за продолжительный период времени длительностью несколько десятков лет. Реализация такого подхода затруднена ввиду недостатка данных реанализа.
Известно несколько подходов к моделированию штормов и окон погоды по волновым условиям (Матушевский Г.В., Надеев В.В. Статистические закономерности распределения характеристик устойчивости ветрового волнения. Метеорология и гидрология, №9. 1987, с. 70-76 [4]; Надеев В.В. Имитационное моделирование рядов ветрового волнения для определения продолжительности штормовых циклов. // Сб. Проблемы исследования и математического моделирования ветрового волнения. Под общей редакцией проф. Давидана И.Н. СПб.: Гидрометеоиздат, 1995, 432 с. [5]; Рожков В.Α., Лопатухин Л.И., Лавренов И.В., Дымов В.И., Бухановский А.В. Моделирование штормового волнения. // Изв. РАН. Физ. атмосферы и океана. 2000, т.36, №5, с. 689-699 [6]), например, вероятностная модель волнения, основанная на теории периодически коррелированного случайного процесса (ПКСП) [6]. Эта модель позволяет генерировать ансамбль временных рядов среднемесячных значений высот волн в ПКСП приближении, которые в дальнейшем используются как переменный во времени уровень z, на который накладывается модель штормов и окон погоды в виде импульсного случайного процесса. Построение и реализация такого подхода требуют детального вероятностного анализа режима штормового волнения и вызывают затруднения при практической реализации.
Задачей заявляемого технического решения является повышение достоверности определения оптимального пути судна на маршруте в зависимости от гидрометеорологических условий.
Поставленная задача решается за счет того, что в способе определения наивыгоднейшего оптимального пути судна в зависимости от гидрометеорологической обстановки, определяемой по гидрометеорологическим параметрам, получаемым от внешних и судовых источников гидрометеорологической информации, включающем расчет на основе среднестатистических данных о гидрометеорологической обстановке климатического пути судна, который в дальнейшем является «осью» для расчета оптимального пути, а за основу расчета может быть также взята дуга большого круга, получают от внешних источников трех- или пятисуточный прогноз волнения, рассчитывают величины ветроволновых потерь скорости судна для различных курсов на первые, вторые, третьи сутки плавания, посредством ЭВМ перебирают большое количество вариантов, концы суточных плаваний соединяют кривой линией - изохроной, при этом некоторая из точек изохроны, построенной на конец третьих суток, окажется ближе к пункту прихода, при этом курс судна располагают так, чтобы выйти в эту ближайшую точку, с получением нового прогноза вычисления повторяют, отличающемся тем, что дополнительно выполняют оценку ветроволновых потерь скорости судна по величине χ, равной отношению суммарной длины траектории судна, проходящей через области с неблагоприятными условиями к общей длине траектории L, по маршруту следования судна определяют цикличность штормов и функции распределения их количества и непрерывной продолжительности путем построения имитационной модели штормов и окон погоды.
Способ поясняется чертежами.
Фиг. 1. Графики двух функций (а, б), имеющих одинаковые дисперсии на всем рассматриваемом интервале, но разную локальную изменчивость.
Фиг. 2. Примеры различных пространственных распределений благоприятных условий, имеющих одну суммарную площадь (вероятность) по всему району, но различную локальную по меньшим масштабам.
Фиг. 3. Зоны с неблагоприятными гидрометеорологическими условиями. Траектория А→В длиной L, по которой движется судно из точки А в точку В.
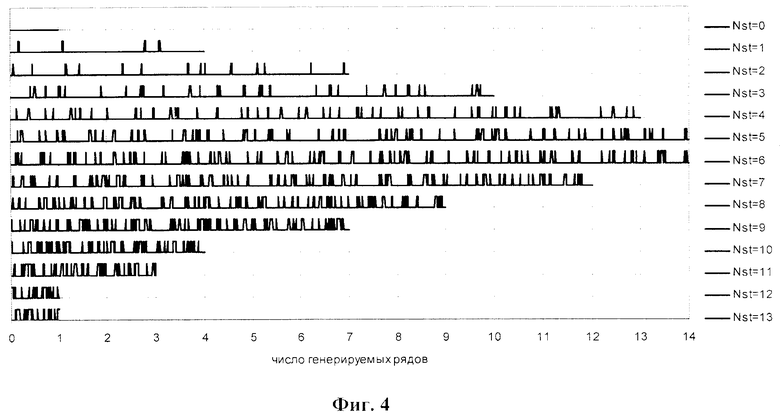
Фиг. 4. Результаты имитации 100 рядов штормов и окон погоды при повторяемости штормовых условий 12,5%.
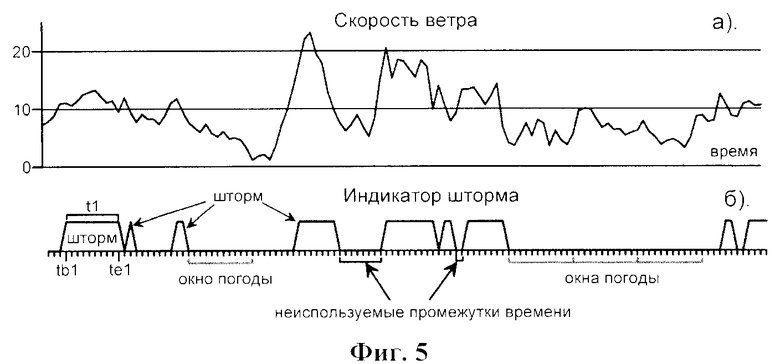
Фиг. 5. Временной ход скорости ветра (а) и временная развертка штормов и окон погоды (б), соответствующая шторму скоростью более 10 м/с.
Сущность способа заключается в следующем.
Перед выходом в море и в процессе плавания по маршруту посредством судовой аппаратуры приема и обработки метеорологической спутниковой информации, включающей комплекс программно-аппаратных средств обработки и представления гидрометеорологической информации и обеспечивающей прием APT, WEFAX, HRPT сигналов от среднеорбитальных метеорологических ИСЗ в диапазоне 137-138 МГц и от 1690 до 1710 МГц, получают параметры гидрометеорологических характеристик по маршруту движения.
Комплекс программно-аппаратных средств обработки и представления гидрометеорологической информации представляет собой специализированное автоматизированное рабочее место, созданное на базе приборов управления, индикации и специального программного обеспечения, работает в режиме локальной вычислительной сети и состоит из пульта автоматизированной системы «Гидрометеонаблюдатель», входящего в состав комплекса средств измерений гидрометеорологических параметров и обеспечивающего прием, обработку, отображение и архивацию гидрометеорологической информации, поступающей от судовой метеостанции и гидрологического блока, пульта автоматизированной системы «Метеоспутник», обеспечивающего прием и обработку метеорологической информации, поступающей от метеорологических космических аппаратов, пульта автоматизированной системы «Метеорадиолокация», входящего в состав судового метеорадиолокатора и обеспечивающего прием и обработку радиолокационной информации, пульта автоматизированной системы «Метеосвязь», обеспечивающего обработку данных, поступающих по радио и проводным каналам от береговых гидрометеорологических центров, пульта автоматизированной системы «Прогноз», обеспечивающего обобщение всех метеорологических данных, включая архивную гидрометеорологическую информацию, формирование прогностической информации. Пульты всех автоматизированных систем через общую информационную шину соединены с ЭВМ, которая также соединена с судовыми средствами навигации и судовождения, включая электронную картографическую навигационную информационную систему (ЭКНИС).
Для организации процесса обмена информацией в средства программного обеспечения включены программные средства для организации каналов обмена информацией для приема и передачи внутри вычислительной сети объемных файлов информации и карт распределения метеопараметров в кодах HDF5, FM-94 BUFR, FM-20 (RADOB), для ввода географических карт местности и/или иной информации для формирования электронных карт районов плавания из различных источников, включая Интернет и аэрологическую информацию. Технические средства обслуживают как проводные, так и любые иные линии связи, включая спутниковые. На случай невозможности организации автоматического ввода географической и аэрологической информации имеются средства ее ручного ввода.
В ЭВМ на основе полученных гидрометеорологических данных выполняется расчет климатического пути судна, который в дальнейшем является «осью» для расчета оптимального пути, а за основу расчета может быть также взята дуга большого круга. При этом получают от внешних источников трех или пятисуточный прогноз волнения, рассчитывают величины ветроволновых потерь скорости судна для различных курсов на первые, вторые, третьи сутки плавания, посредством ЭВМ перебирают большое количество вариантов, концы суточных плаваний соединяют кривой линией - изохроной, при этом некоторая из точек изохроны, построенной на конец третьих суток, окажется ближе к пункту прихода, при этом курс судна располагают так, чтобы выйти в эту ближайшую точку, с получением нового прогноза вычисления повторяются. Посредством ЭВМ также выполняют оценку ветроволновых потерь скорости судна по величине χ, равной отношению суммарной длины траектории судна, проходящей через области с неблагоприятными условиями к общей длине траектории L в соответствии с зависимостями (1-8).
По маршруту следования судна также определяют цикличность штормов и функции распределения их количества и непрерывной продолжительности путем построения имитационной модели штормов и окон погоды.
Для этого в качестве исходных данных о состоянии природной среды достаточно иметь сведения об интегральной повторяемости штормов, которые приведены в многочисленных пособиях по режиму ветра и волнения и которые хранятся в электронном виде в ПЗУ системы «Прогноз». Для построения модели используются сведения о статистических связях повторяемости штормов со средними значениями количества штормов и их непрерывной продолжительности, а также статистические связи между функциями распределения числа штормов и их непрерывной продолжительности со средними значениями количества штормов и их непрерывной продолжительности.
Для подготовки массива данных о ветре может быть использована спектрально-параметрическая модель волнения ААНИИ (Надеев В.В. Имитационное моделирование рядов ветрового волнения для определения продолжительности штормовых циклов.// Сб. Проблемы исследования и математического моделирования ветрового волнения. Под общей редакцией проф. Давидана И.Н. СПб.: Гидрометеоиздат, 1995, 432 с. [5]). Модель верифицирована, рекомендована для применения Центральной методической комиссией Росгидромета и используется в практике ГМЦ РФ.
Поле ветра рассчитывается с использованием этой модели по архиву полей приземного давления Европейского центра среднесрочных прогнозов погоды (ECMWF). Расчет выполняется с временным шагом Δt 6 часов и пространственным шагом 2.5° для каждого узла расчетной области за период 25-30 лет с учетом среднего положения кромки льда (для северных морей). Для оценки статистических характеристик ветрового режима выбирают 8-10 расчетных точек в зависимости от продолжительности перехода и количества пересекаемых морей при переходе.
На первом этапе выполняется оценка среднемесячной повторяемости набора штормовых условий (критическая скорость ветра V более 10, 11, …23 м/с) для выбранных расчетных точек за период 25-30 лет.
Затем для градаций повторяемости штормовых условий (40-50, 30-40, 20-30, 15-20, 10-15, 5-7, 1-5%) выбирают группы месяцев для каждой расчетной точки и соответствующего значения критической скорости ветра V. Для периодов времени, в которые отмечалась выбранная градация повторяемости штормовых условий, для каждого года за период 25-30 лет рассчитывается число штормов и непрерывная продолжительность штормов. По этим данным рассчитываются средние значения непрерывной продолжительности и количество штормов (в месяц) для выбранных градаций повторяемости штормов, а также функции их распределения.
Связь между средней непрерывной продолжительностью шторма τ и вероятностью штормовых условий Ρ определяется по формуле

В формуле (9) средняя непрерывная продолжительность шторма измеряется в часах, вероятность шторма Ρ - в долях единицы. При вероятности шторма 0.1% средняя непрерывная продолжительность шторма составляет 6 часов, что соответствует дискретности использованных 4-х срочных результатов реанализа. При вероятности шторма 50% средняя непрерывная продолжительность шторма составляет 33 часа. Средняя квадратическая невязка полученной оценки τ составляет 1.5 часа, максимальное отклонение от «фактической» средней непрерывной продолжительности не превышает 5 часов.
Среднее число штормов N за период продолжительностью Τ часов при известной средней непрерывной продолжительности шторма τ оценивается по формуле

В формуле (10) Τ и τ измеряются в часах, Ρ - в долях единицы.
При анализе периодов продолжительностью 1 месяц, при вероятности шторма Ρ, равной 0.1%, среднее число штормов в месяц составляет 0.1. То есть за 1 месяц шторм будет наблюдаться 1 раз в 10 лет. При возрастании вероятности шторма до 50% среднее число штормов достигает 11 в месяц.
Далее строятся эмпирические кривые плотности распределения числа штормов, полученные для 8-ми точек маршрута перехода.
Для аппроксимации эмпирической функции распределения числа штормов n используется модифицированная функция распределения Вейбулла, имеющая для плотности распределения f(n) и интегральной функции распределения F(n) вид
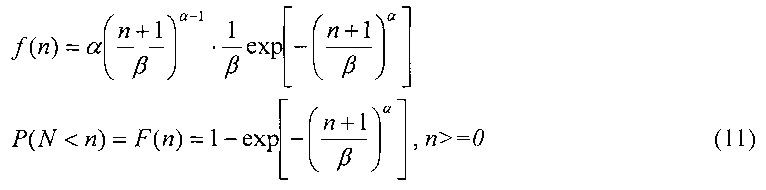
Параметры распределения Вейбулла α и β связаны со средним и дисперсией числа штормов соотношениями
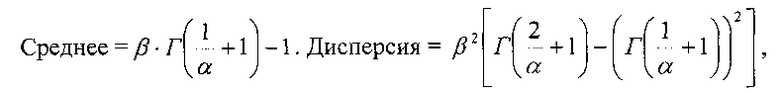
где Г(х) - гамма функция.
Эмпирическая функция распределения непрерывной продолжительности штормов удовлетворительно аппроксимируется модифицированной экспоненциальной функцией распределения с одним параметром λ.
Плотность распределения f(t) и интегральная функция F(t) модифицированного экспоненциального распределения непрерывной продолжительности штормов t при дискретности временного ряда Δt имеют вид
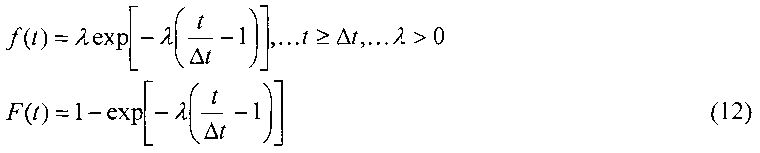
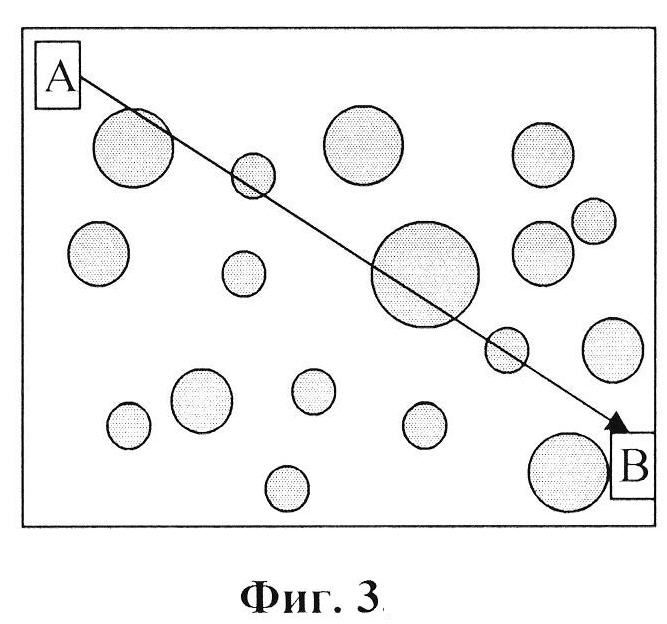
При этом параметр экспоненциального распределения λ связан со средней непрерывной продолжительностью шторма τ и дискретностью ряда Δt соотношением
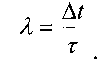
Таким образом, используя модифицированное однопараметрическое экспоненциальное распределение, определив по данным о повторяемости штормовых условий с применением (10) среднюю непрерывную продолжительность шторма, можно рассчитать функцию распределения непрерывной продолжительности штормов.
Задачей имитационного моделирования является генерация значительного числа временных рядов заданной продолжительности, например сезон или месяц, на которых должно быть специальным образом распределено разное число временных промежутков разной непрерывной продолжительности, которые представляют собой штормовые периоды. Это должно быть сделано так, чтобы:
интегральная повторяемость штормовых условий (за 30-100 лет) соответствовала бы заданной повторяемости штормовых условий;
число штормов, определенное по совокупности генерируемых рядов, подчинялось бы выбранному закону распределения;
распределение непрерывной продолжительности штормов для каждого из генерируемых рядов подчинялась бы выбранному закону распределения.
По сведениям об интегральной повторяемости штормовых условий Ρ оценивается среднее число штормов и с использованием нормального распределения (при вероятности штормовых условий выше 20%) или распределения Вейбулла определяется число рядов (лет) m с тем или иным количеством штормов n. Предположим, нам нужно сгенерировать M временных рядов, тогда число лет m с числом штормов n определяется по формуле

где квадратные скобки обозначают оператор взятия целой части от действительного числа.
На следующем шаге задается непрерывная продолжительность штормов t для каждого шторма генерируемого ряда. Если требуется сгенерировать ряд с одним штормом, его продолжительность принимается равной средней непрерывной продолжительности. Если требуется сгенерировать ряды с двумя и более штормами, предварительно рассчитывается продолжительность каждого из n штормов. Для этого с помощью выбранной аналитической функции распределения непрерывной продолжительности штормов F(t) (12) оценивается вероятность превышения непрерывной продолжительности шторма p(T>t)=1-F(t). Нумеруя дискретный ряд i в порядке уменьшения непрерывной продолжительности штормов t, можно, задавая число штормов генерируемого ряда n, рассчитать число штормов к той или иной продолжительности ti

После определения числа лет с тем или иным количеством штормов m(n) и числа штормов с той или иной непрерывной продолжительностью k(t, n) производится собственно генерация временных рядов. При отсутствии шторма каждый член временного ряда принимает значение, равное нулю. В других случаях допускается, что сроки начала штормов в течение месяца (сезона) подчиняются закону равномерного распределения, то есть равновероятны. Естественным ограничением при этом является лишь условие непересечения двух штормовых периодов. Время начала tb и окончания te шторма связаны с непрерывной продолжительностью шторма t соотношением: te=tb+t/Δt-1.
По существу собственно имитационная модель основана на использовании генератора случайных чисел в диапазоне от первого до последнего номера члена генерируемого ряда для задания срока начала шторма. Окончание шторма определяется с учетом полученных оценок непрерывной продолжительности каждого из штормов. Значениям членов ряда на полученном участке присваивается значение, например единица, что является признаком шторма. Если период нового шторма пересекается с периодом любого из ранее размещенных на временном отрезке штормов, срок начала шторма рассчитывается вновь с использованием того же генератора случайных чисел, если после 100 генераций случайных чисел это условие не выполняется, шторм «размещается» в любом месте временной последовательности.
Построенная таким образом имитационная модель штормов и окон погоды, для применения которой достаточно знать повторяемость штормовых условий, позволяет генерировать временные ряды штормов и окон погоды, совокупность которых отражает характерные особенности ветрового режима, включая повторяемость штормов и функции распределения их количества и непрерывной продолжительности. Модель может быть использована для любых акваторий океана, поскольку функции распределения числа штормов и их непрерывной продолжительности являются производными от повторяемости штормовых условий. Модель пригодна для расчета статистических характеристик окон погоды при планировании сложных морских транспортных операций.
На фиг. 4 в качестве иллюстрации приведены результаты имитации штормов и окон погоды для повторяемости штормовых условий 12.5%, путем анализа данных о 1034 штормах на акватории Норвежского, Баренцева и Белого морей.
На фиг. 5 приведен пример временного хода скорости ветра (а) и соответствующая ему временная развертка штормов и окон погоды (б). Обычно под окном погоды понимают промежуток времени любой продолжительности, в пределах которого скорость ветра меньше заданной. Для выполнения транспортных и других морских операций имеют значение только те окна погоды, продолжительность которых позволяет выполнить запланированную операцию или ее этап с соответствующими ограничениями по скорости ветра. Поэтому под окнами погоды принимаются окна погоды заданной непрерывной продолжительности. Если непрерывная продолжительность благоприятных условий больше заданной непрерывной продолжительности операции в целое число раз, то именно это число принимается за число окон погоды в рассматриваемый промежуток времени.
При заданной непрерывной продолжительности окна погоды на фиг. 5 выделяются 9 штормов и 4 окна погоды.
Реализация предлагаемого способа определения наивыгоднейшего оптимального пути судна в зависимости от гидрометеорологической обстановки технической трудности не представляет, так как способ может быть реализован с использованием штатного судового оборудования и серийно выпускаемых вычислительных средств.
Источники информации
1. Лесков М.М., Баранов Ю.К., Гаврюк М.И. Навигация. М.: Транспорт, 1986, с. 343-347.
2. Атлас гидрометеорологических условий плавания судов морского флота. - Л.: УГС ВМФ, 1966. - 176 с.
3. Кендал М., Моран Л. Геометрические вероятности. - М.: Наука, 1972. - 192 с.
4. Матушевский Г.В., Надеев В.В. Статистические закономерности распределения характеристик устойчивости ветрового волнения. Метеорология и гидрология, №9. 1987, с. 70-76.
5. Надеев В.В. Имитационное моделирование рядов ветрового волнения для определения продолжительности штормовых циклов.// Сб. Проблемы исследования и математического моделирования ветрового волнения. Под общей редакцией проф. Давидана И.Н. СПб.: Гидрометеоиздат, 1995, 432 с.
6. Рожков В.Α., Лопатухин Л.И., Лавренов И.В., Дымов В.И., Бухановский А.В. Моделирование штормового волнения. // Изв. РАН. Физ. атмосферы и океана. 2000, т.36, №5, с. 689-699.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ построения предварительной прокладки маршрута автономного необитаемого подводного аппарата | 2018 |
|
RU2672840C1 |
| СПОСОБ ПРОГНОЗА ШТОРМОВЫХ ПОДЪЕМОВ УРОВНЯ ВОДЫ | 2014 |
|
RU2583063C1 |
| Способ генерации предварительной прокладки пути судна и устройство для его реализации | 2021 |
|
RU2782617C1 |
| СПОСОБ КОНТРОЛЯ И ОБЕСПЕЧЕНИЯ БЕЗОПАСНОСТИ ШТОРМОВОГО ПЛАВАНИЯ СУДНА | 2023 |
|
RU2813122C1 |
| СПОСОБ АВТОМАТИЧЕСКОЙ ПРОВОДКИ СУДОВ | 2005 |
|
RU2277495C1 |
| Носовая оконечность быстроходного надводного корабля или относительно тихоходного гражданского судна повышенной штормовой мореходности и ледовой проходимости в автономном плавании | 2015 |
|
RU2607136C2 |
| Каботажное пассажирское судно | 2016 |
|
RU2653906C1 |
| Кормовая оконечность стабилизированного для штормового плавания корабля | 2015 |
|
RU2607135C2 |
| КОРАБЛЬ ГИДРОГРАФИЧЕСКОЙ И ПАТРУЛЬНОЙ СЛУЖБЫ | 2010 |
|
RU2459738C2 |
| СПОСОБ АВТОМАТИЧЕСКОЙ ПРОВОДКИ СУДНА | 2012 |
|
RU2501708C1 |
Нахождение наивыгоднейшего пути судна на основе гидрометеорологической обстановки, определяемой по параметрам с внешних источников. Вычисление пути базируется на среднестатистических данных о гидрометеорологической обстановке на климатическом пути судна, который в дальнейшем является его «осью», за основу расчета может быть также взята дуга большого круга. От внешних источников получают трех- или пятисуточный прогноз волнения моря. Проводят расчет величины ветроволновых потерь скорости судна для различных курсов на первые, вторые, третьи сутки плавания; посредством ЭВМ перебирают варианты его движения. Концы суточных плаваний соединяют кривой линией - изохроной, курс судна располагают так, чтобы выйти в ближайшую к пункту назначения точку изохроны. С получением нового прогноза вычисления повторяют. Дополнительно определяют ветроволновые потери скорости судна по величине χ, равной отношению суммарной длины траектории судна, проходящей через области с неблагоприятными условиями, к общей длине траектории L. По маршруту следования судна на основе имитационной модели штормов и окон погоды с использованием штатных средств судовождения также вычисляют цикличность штормов и функции распределения их количества и непрерывной продолжительности. Технический результат - повышение достоверности определения оптимального пути судна на маршруте в зависимости от гидрометеорологических условий. 5 ил.
Способ определения наивыгоднейшего оптимального пути судна в зависимости от гидрометеорологической обстановки, определяемой по гидрометеорологическим параметрам, получаемым от внешних источников, включающий расчет на основе среднестатистических данных о гидрометеорологической обстановке климатического пути судна, который в дальнейшем является «осью» для расчета оптимального пути, а за основу расчета может быть также взята дуга большого круга, при этом получают от внешних источников трех- или пятисуточный прогноз волнения, рассчитывают величины ветроволновых потерь скорости судна для различных курсов на первые, вторые, третьи сутки плавания, посредством ЭВМ перебирают большое количество вариантов, концы суточных плаваний соединяют кривой линией - изохроной, при этом некоторая из точек изохроны, построенной на конец третьих суток, окажется ближе к пункту прихода, при этом курс судна располагают так, чтобы выйти в эту ближайшую точку, с получением нового прогноза вычисления повторяют, отличающийся тем, что дополнительно выполняют оценку ветроволновых потерь скорости судна по величине χ, равной отношению суммарной длины траектории судна, проходящей через области с неблагоприятными условиями к общей длине траектории L, по маршруту следования судна определяют цикличность штормов и функции распределения их количества и непрерывной продолжительности путем построения имитационной модели штормов и окон погоды.
| СПОСОБ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ КУРСОМ СУДНА И СИСТЕМА АВТОРУЛЕВОГО ДЛЯ РЕАЛИЗАЦИИ СПОСОБА | 2004 |
|
RU2282884C2 |
| Устройство для определения положения судна | 1987 |
|
SU1532432A1 |
| НАВИГАЦИОННЫЙ КОМПЛЕКС ВЫСОКОСКОРОСТНЫХ СУДОВ | 2004 |
|
RU2260191C1 |
| СПОСОБ АВТОМАТИЧЕСКОЙ ПРОВОДКИ СУДНА | 2012 |
|
RU2501708C1 |
Авторы
Даты
2015-12-10—Публикация
2014-07-04—Подача