Изобретение относится к области вычислительной техники.
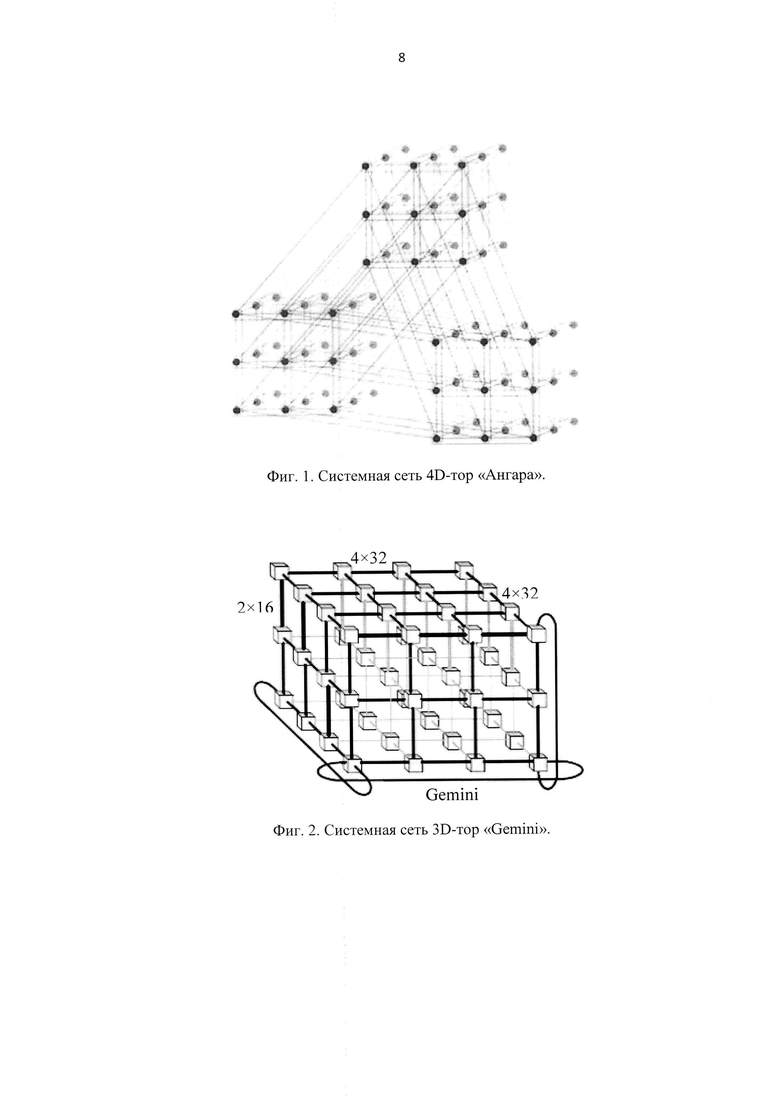
Известно построение системных сетей современных высокопроизводительных параллельных МВС (суперкомпьютеров) в виде многомерных торов (Дмитрий Макагон, Евгений Сыромятников. Сети для суперкомпьютеров. // Открытые системы. 2011. №07). Сети с топологией торов представляют собою решетки, у которых в каждом измерении, кроме связей между соседними узлами, имеются связи между крайними узлами, таким образом, в каждом измерении образуется кольцевой канал передачи данных (далее кольцо). Сеть «Ангара», например, имеет топологию 4-мерного (4D) тора (Михеев В.А. и др. Реализация высокоскоростной сети для суперкомпьютерных систем: проблемы, результаты, развитие. // URL: http://2013.nscf.ru/TesisAll/Section%201/12 2761 SimonovAS S1.pdf). На фиг. 1 изображена эта сеть с 3-мя узлами в каждом измерении (3×3×3×3).
В качестве прототипа выбрана сеть «Gemini» (The Gemini System Interconnect ALVERSON R., ROWETH D. AND KAPLAN L. The Gemini System Interconnect // 18th IEEE Symposium on High Performance Interconnects. 2009. P. 3-87.). В конкретном 3-мерном решении, представленном на фиг. 2, измерения X и Y включают по 32 узла, которые связывают 4 дуплексных кольца, а измерение Ζ соответственно 16 узлов и 2 дуплексных кольца (дуплексное кольцо представляет собою пару встречных симплексных колец). Многомерные торы применяются в первую очередь для сокращения времени доставки пакетов по системной сети и повышения ее пропускной способности за счет пространственного распараллеливания при сравнительно невысокой сложности сетевых узлов.
Недостатком топологии, примененной в прототипе, является неоптимальность использования множества колец. В каждом измерении все кольца имеют одинаковую топологию (последовательность соединения узлов). Использование колец с разной топологией открывает возможность существенного уменьшения времени доставки сообщений и повышения пропускной способности множества колец каждого измерения. Целью изобретения является повышение быстродействия системной сети многомерного тора.
Технический результат заключается в повышение быстродействия тора за счет сокращения времени передачи пакетов по кольцам отдельных измерений. Время передачи по отдельному кольцу складывается из времен доставки пакетов по кольцу и времени ожидания передачи в это кольцо. Время доставки по дуплексному кольцу может быть уменьшено за счет сокращения его диаметра (расстояния между узлами в кольце измерения). Время ожидания передачи в дуплексное кольцо (нахождения в очереди к нему) может быть уменьшено за счет повышения его пропускной способности.
Технический результат достигается тем, что каждая пара кольцевых каналов передачи сообщений любого измерения образует мультикольцо, в котором первое кольцо образовано последовательным соединением коммутаторов всех узлов данного измерения, то есть соответствующий порт коммутатора i-го узла каждого кольца соединен с соответствующим портом коммутатора (i+1)-го узла, а второе кольцо образовано хордовыми связями с шагом p для данного кольца, то есть соответствующий данному кольцу порт коммутатора i-го узла соединен с соответствующими данному кольцу портом коммутатора (i+p)-го узла, где Ν - количество узлов в данном измерении тора, 0≤i≤Ν, Ν≥4, p≥2 и номер следующего узла вычисляется по modN, при этом коммутатор узла для этой пары колец имеет функции передачи сообщений как по своему кольцу, так и функции перекрестной передачи из одного кольца в другое.
Кольцевые каналы передачи сообщений являются симплексными, и коммутатор передает сообщения в направлении возрастания номеров узлов.
Кольцевые каналы передачи сообщений являются дуплексными, и коммутатор может передавать сообщения по любому симплексному кольцу любого дуплексного кольца как в направлении возрастания номеров узлов, так и в направлении убывания номеров узлов.
Техническая сущность и принцип действия предложенной сети поясняются следующими иллюстрациями.
Фиг. 1. Системная сеть 4D-тор «Ангара».
Фиг. 2. Системная сеть 3D-тор «Gemini».
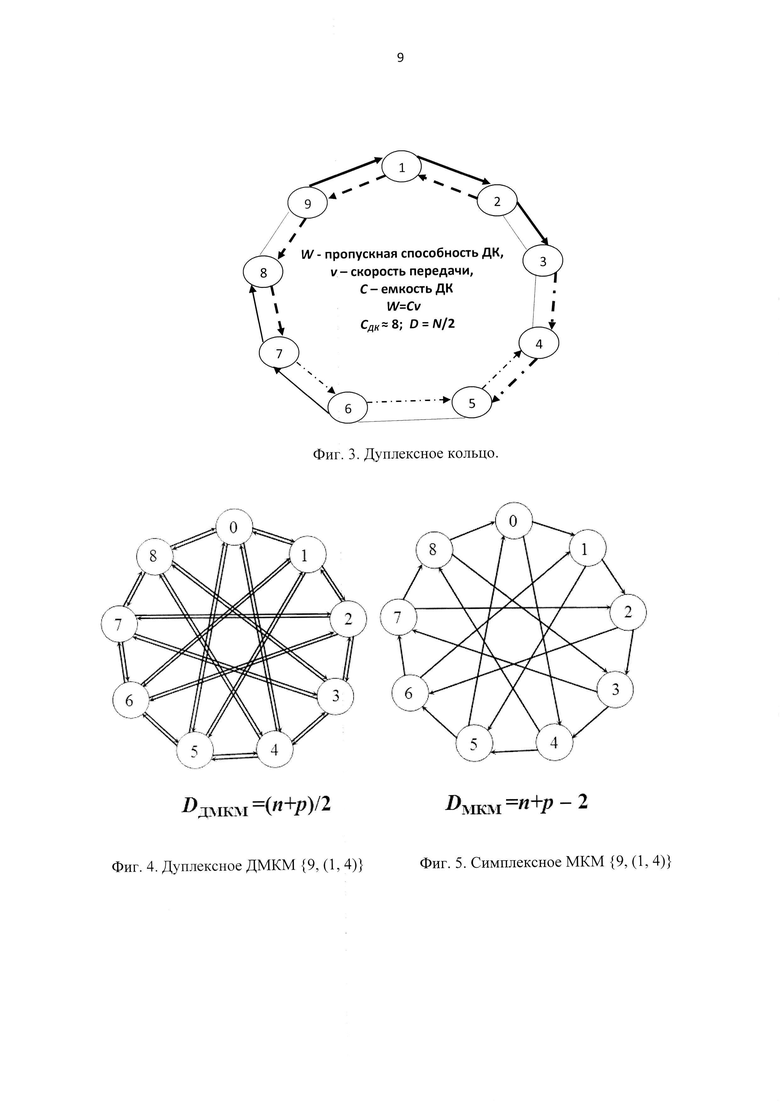
Фиг. 3. Дуплексное кольцо.
Фиг. 4. Дуплексное ДМКМ {9, (1, 4)}.
Фиг. 5. Симплексное МКМ {9, (1, 4)}.
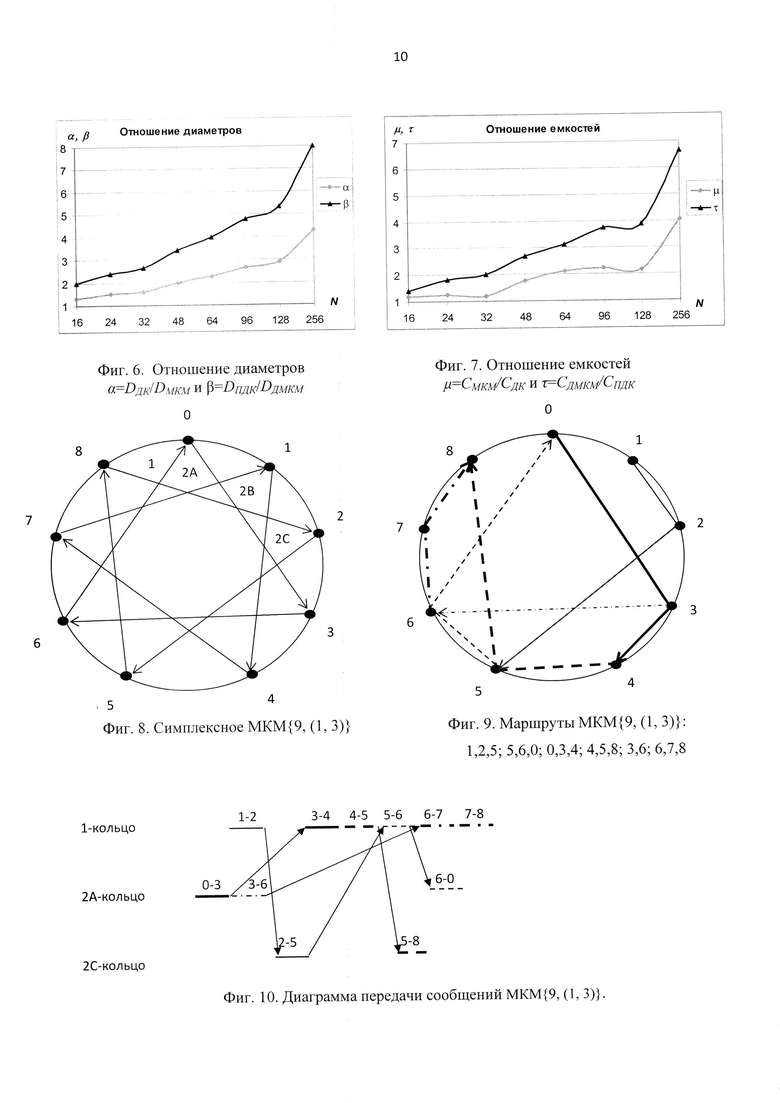
Фиг. 6. Отношения диаметров α=DДК/DМКМ и β=DПДК/DДМКМ
Фиг. 7. Отношения емкостей µ=СМКМ/СДК и τ=СДМКМ/СПДК
Фиг. 8. Симплексное МКМ {9, (1, 3)}.
Фиг. 9. Маршруты МКМ {9, (1, 3)}: 1, 2, 5; 5, 6, 0; 0, 3, 4; 4, 5, 8; 3, 6; 6, 7, 8.
Фиг. 10. Диаграмма передачи сообщений МКМ {9, (1, 3)}.
Опишем предложенную системную сеть.
Для начала рассмотрим работу дуплексного кольца (ДК), которое является непременным элементом любого измерения известных торов, фиг. 3.
В описании предположим сегментированную передачу сообщений (пакетов), хотя в предлагаемой сети могут быть использованы разные методы доступа к каналу (в частности, вставка регистра). При сегментированной передаче в кольце перемещается постоянное число сегментов (выделенных, например, синхрометками) со скоростью ν, в кольце помещается целое число сегментов. Абонент-источник «помещает» готовый к выдаче пакет длины сегмента в проходящий мимо него свободный сегмент; и абонент-приемник забирает пакет из кольца, очищая сегмент для последующего использования другими источниками. Таким образом, сегмент за один проход по кольцу может быть использован многократно. Среднее число пакетов, перенесенное сегментами за один проход (при постоянной готовности абонентов к выдаче) называется его емкостью С (этот параметр также характеризует среднее число параллельных передач в одном сегменте). Последовательность узлов, через которые проходит пакет от источника до приемника, называется маршрутом. Среди возможных маршрутов между источником и приемником есть минимальный. Самый длинный маршрут из множества всех минимальных маршрутов в кольце - есть его диаметр D. Пропускная способность W определяется как произведение Cv. На фиг. 3 изображено дуплексное кольцо (ДК), состоящее из двух встречных симплексных колец, и указаны его основные параметры. Разными линиями показаны маршруты передач, выполняемые в одном сегменте каждого симплексного кольца: по внешнему кольцу 9→3 (9, 1, 2, 3); 3→5 (3, 4, 5); 6→8 (6, 7, 8), по внутреннему кольцу 2→7 (2, 1, 9, 8, 7); 7→4 (7, 6, 5, 4).
Для построения системной сети многомерного тора с хордовыми связями предлагается в каждом измерении из сгруппированных пар колец образовывать минимальные коммутируемые мультикольца (МКМ), одно из которых применительно к дуплексным каналам представлено на фиг. 4. Маршрут в таком мультикольце может начинаться и заканчиваться в одном кольце или быть перекоммутирован в другое и там завершиться. Коммутируемые мультикольца были введены в статье Алленов А.В., Подлазов B.C. Пропускная способность набора кольцевых каналов II. Кольцевые коммутаторы // Автоматика и телемеханика. 1996. №4. С. 162-172.
Дуплексное минимальное коммутируемое мультикольцо (ДМКМ) с N узлами, перенумерованными целыми числами из [0, N-1], состоит из двух дуплексных колец: одно с шагом S=±1, а другое с шагом S=±p, где 0≤i≤Ν, N≥4, p≥2, знак «+» означает соединение и передачу по симплексному кольцу в направлении возрастания номеров узлов, а знак «-» означает соединение и передачу по симплексному кольцу в направлении убывания номеров узлов. Номер j-го узла, подсоединенного в кольце к i-му узлу, определяется по формуле j=(i+S)modN. Будем обозначать такое минимальное коммутируемое мультикольцо в виде {N, (1, p)}. На фиг. 4 приведено дуплексное ДМКМ {9, (1, 4)}, а на фиг. 5 симплексное МКМ {9, (1, 4)}, которое является однонаправленной частью ДМКМ {9, (1, 4)}. В МКМ в пары группируются симплексные кольца, а в ДМКМ - дуплексные кольца.
Коммутаторы узлов позволяют передавать сообщения во всех заданных выше направлениях по любому симплексному кольцу.
Вариантом системной сети многомерного тора с хордовыми связями, также повышающим быстродействие сети, является сеть, полностью построенная на МКМ в каждом измерении. Такую сеть, например, можно организовать, если каждое дуплексное кольцо (ДК) прототипа заменить на МКМ.
На фиг. 4 и фиг. 5 приведены вычисленные значения диаметров для этих топологий (в предположении, что число узлов N=np), которые показывают преимущество их использования в многомерных торах по сравнению с топологиями, имеющей одинаковые кольца: повышение быстродействия происходит не за счет увеличения числа колец, а за счет изменения топологии, число входов сетевых коммутаторов не меняется, а изменяется вид связей и алгоритм коммутации в узлах.
Аналитические выкладки и имитационное моделирование показали (Подлазов B.C. Повышение характеристик многомерных торов. Управление большими системами // 2014. Вып. 51. С. 60-81), что в практически важном диапазоне 16≤N≤64 имеет место, во-первых, уменьшение диаметра МКМ в 1,3÷2,3 раза и диаметра ДМКМ - в 2÷4 раза, и, во-вторых, увеличение пропускной способности МКМ в 1,2÷2,1 раза и пропускной способности ДМКМ - в 1,4÷3,1 раза по сравнению с обычным ДК и парой дуплексных колец (ПДК) соответственно. Графики отношений диаметров α=DДК/DМКМ и β=DПДК/DДΜΚΜ приведены на фиг. 6, а графики отношений пропускной способности, определяемые емкостью С мультиколец, µ=СМКМ/СДК и τ=СДМКМ/СПДК приведены на фиг. 7, где С приводятся для тех р, при которых они достигают максимума.
Покажем возможность реализации данного изобретения на примере работы МКМ {9, (1, 3)}. Первое полное кольцо этой МКМ помечено цифрой 1, второе хордовое кольцо в данном случае состоит из 3-х миниколец 2А, 2В и 2С, фиг. 8. На МКМ заданы несколько маршрутов передачи: 1, 2, 5; 5, 6, 0; 0, 3, 4; 4, 5, 8; 3, 6; 6, 7, 8, изображенных на фиг. 9 разными линиями. Они представлены в виде дуг, по которым должна осуществляться передача сообщений. На фиг. 10 изображена возможная диаграмма передачи сообщений для заданных маршрутов в этом МКМ. Диаграмма представлена в виде отрезков, пара цифр над которыми указывает дугу маршрута, по которой осуществляется передача, стрелки означают переход с одного кольца на другое. Все мультикольца предлагаемого многомерного тора работают аналогично. При использовании мультиколец ДМКМ передача сообщений в них осуществляется с учетом использования двух встречных МКМ и возможности передачи сообщений из одного в другое. В приведенном примере все маршруты осуществляются параллельно за один проход сегментов по каждому кольцу.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ организации оптимальных отказоустойчивых многомерных торов на основе малопортовых маршрутизаторов и разветвителей дуплексных каналов | 2020 |
|
RU2753147C1 |
| Способ организации системной сети в виде неблокируемого самомаршрутизируемого трехмерного р-ичного мультикольца | 2018 |
|
RU2703351C1 |
| СПОСОБ ПОСТРОЕНИЯ НЕБЛОКИРУЕМОГО САМОМАРШРУТИЗИРУЕМОГО РАСШИРЕННОГО КОММУТАТОРА | 2009 |
|
RU2435295C2 |
| Способ организации системной сети в виде отказоустойчивого неблокируемого трехмерного разреженного р-ичного гиперкуба | 2019 |
|
RU2720553C1 |
| МУЛЬТИПРОЦЕССОРНАЯ СИСТЕМА | 2015 |
|
RU2614926C2 |
| ОБОБЩЕННЫЕ НЕБЛОКИРУЕМЫЕ ДВУХКАСКАДНЫЕ СЕТИ КЛОЗА | 2014 |
|
RU2580100C2 |
| СЕТЬ С ТОПОЛОГИЕЙ РАСШИРЕННОГО ОБОБЩЕННОГО ГИПЕРКУБА | 2013 |
|
RU2556458C2 |
| Способ построения коммутируемых управляющих сетей с топологией квазиполного орграфа | 2023 |
|
RU2815332C1 |
| НЕКООРДИНИРОВАННАЯ БЕСПРОВОДНАЯ МНОГОПОЛЬЗОВАТЕЛЬСКАЯ СИСТЕМА С ПИКОЯЧЕЙКАМИ СО СКАЧКООБРАЗНЫМ ИЗМЕНЕНИЕМ ЧАСТОТЫ | 1998 |
|
RU2201034C2 |
| ВЫЧИСЛИТЕЛЬНАЯ СЕТЬ ВЫСОКОПРОИЗВОДИТЕЛЬНОЙ ВЫЧИСЛИТЕЛЬНОЙ СИСТЕМЫ | 2020 |
|
RU2754605C1 |
Изобретение относится к вычислительной технике, в частности к построению системных сетей для суперкомпьютеров в виде многомерных торов. Технический результат изобретения заключается в возможности существенного уменьшения времени доставки сообщений за счет сокращения диаметра сети (расстояния между узлами в каждом измерении тора) и уменьшения времени ожидания передачи (нахождения в очереди для передачи по сети). В системной сети передачи сообщений в сгруппированных попарно кольцах любого измерения первое кольцо образовано последовательным соединением коммутаторов всех узлов данного измерения, а второе кольцо образовано хордовыми связями с шагом p для данного кольца, то есть соответствующий данному кольцу порт коммутатора i-го узла соединен с соответствующим данному кольцу портом коммутатора (i+p)-го узла, при этом коммутатор узла для этой пары колец имеет функции передачи сообщений как по своему кольцу, так и функции перекрестной передачи из одного кольца в другое. Причем улучшение характеристик может быть достигнуто не только преобразованием пар дуплексных колец в дуплексные мультикольца, но и при замене дуплексных колец на симплексные мультикольца. 1 н. и 2 з.п. ф-лы, 10 ил.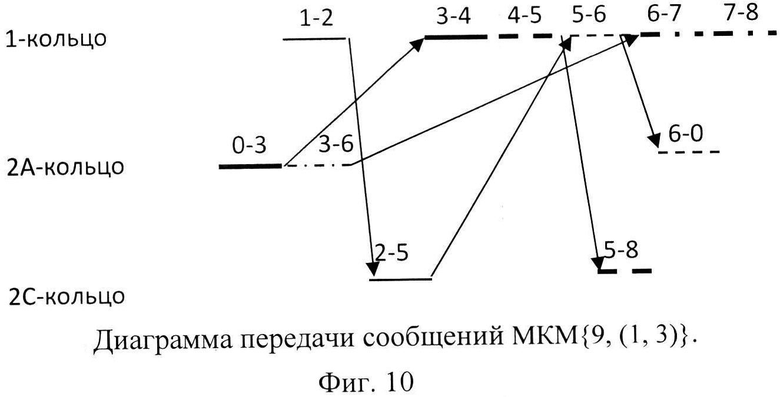
1. Системная сеть передачи сообщений многомерного тора с хордовыми связями, характеризующаяся тем, что каждая пара кольцевых каналов передачи сообщений любого измерения образует мультикольцо, в котором первое кольцо образовано последовательным соединением коммутаторов всех узлов данного измерения, то есть соответствующий порт коммутатора i-го узла каждого кольца соединен с соответствующим портом коммутатора (i+1)-го узла, а второе кольцо образовано хордовыми связями с шагом р для данного кольца, то есть соответствующий данному кольцу порт коммутатора i-го узла соединен с соответствующим данному кольцу портом коммутатора (i+p)-го узла, где N - количество узлов в данном измерении тора, 0≤i≤N, N≥4, р≥2 и номер следующего узла вычисляется по modN, при этом коммутатор узла для этой пары колец имеет функции передачи сообщений как по своему кольцу, так и функции перекрестной передачи из одного кольца в другое.
2. Системная сеть передачи сообщений по п. 1, характеризующаяся тем, что кольцевые каналы передачи сообщений являются симплексными и коммутатор передает сообщения в направлении возрастания номеров узлов.
3. Системная сеть передачи сообщений по п. 1, характеризующаяся тем, что кольцевые каналы передачи сообщений являются дуплексными и коммутатор может передавать сообщения по любому симплексному кольцу любого дуплексного кольца как в направлении возрастания номеров узлов, так и в направлении убывания номеров узлов.
| В.Г.ХОРОШЕВСКИЙ РАСПРЕДЕЛЕННЫЕ ВЫЧИСЛИТЕЛЬНЫЕ СИСТЕМЫ С ПРОГРАММИРУЕМОЙ СТРУКТУРОЙ | |||
| ВЕСТНИК СИБГУТИ | |||
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Видоизменение прибора с двумя приемами для рассматривания проекционные увеличенных и удаленных от зрителя стереограмм | 1919 |
|
SU28A1 |
| М.Ф.КАРАВАЙ, В.С.ПОДЛАЗОВ | |||
| ПОВЫШЕНИЕ БЫСТРОДЕЙСТВИЯ МНОГОМЕРНЫХ ТОРОВ | |||
| ПРОГРАММНЫЕ СИСТЕМЫ: ТЕОРИЯ И ПРИЛОЖЕНИЯ | |||
| Видоизменение пишущей машины для тюркско-арабского шрифта | 1923 |
|
SU25A1 |
Авторы
Даты
2016-06-10—Публикация
2015-02-27—Подача