Изобретение относится к машиностроению, а именно к выполнению измерений геометрических параметров, таких как координаты центра и/или радиус кривизны цилиндрических поверхностей деталей.
Известен способ определения радиуса отверстия, по которому в исследуемом сечении выбирают параллельные хорды с заданным расстоянием между ними и определяют радиус с учетом длин хорд; длину одной из хорд выбирают в качестве базовой, измеряют длину второй хорды и при определении радиуса учитывают разность хорд (пат. РФ №2005990; МПК G01B 5/08; опубл. 15.01.1994).
Измерения по данному способу, как правило, выполняются стальной линейкой, поэтому способ годится для измерения и контроля неответственных поверхностей деталей с достаточно широкими допусками.
Известен способ определения диаметра и радиуса поверхности по результатам измерения элементов окружности, включающих измерение угла между касательными и высоты сегмента или размера хорды и высоты сегмента и расчет диаметра по математическим зависимостям (Кутай А.К. Справочник по производственному контролю в машиностроении. Л.: Машиностроение. - 1974, стр. 563-565).
Измерения данным способом проводят приборами седлообразного типа, представляющими собой корпус с выполненными на нем опорными элементами, измерительным наконечником и отсчетным устройством (пат. РФ №95096; МПК G01B 5/213; опубл. 10.06.2010).
Данные способ и устройства применяют, как правило, для измерения крупногабаритных деталей. При этом отсутствует необходимость в базировании измеряемого изделия, так как измерительный прибор устанавливается непосредственно на измеряемую поверхность.
Применяемое в указанном способе устройство имеет недостаток - узкие технологические возможности, ограничивающие его применение в основном в тяжелом машиностроении. Кроме этого, данный способ не позволяет определить координаты центра радиуса, что также ограничивает область применения способа.
Наиболее близким к заявляемому является способ измерения поверхности изделия на координатно-измерительной машине, включающий определение координат центра сферического наконечника радиусом R измерительной головки при каждом его касании с поверхностью изделия и вычисление координат точек касания сферического наконечника с поверхностью изделия, с дополнительным определением координат центра сферического наконечника радиусом r≠R, при условии его касания с поверхностью изделия в точках, идентичных точкам касания с поверхностью изделия сферического наконечника радиусом R при условии расположения центра сферического наконечника радиусом r на минимальном расстоянии от центра сферического наконечника радиусом R, при этом вычисление координат точек касания с поверхностью изделия осуществляют по найденным координатам центров обоих наконечников (пат. №2336492; МПК G01B 5/004, G01B 5/20; опубл. 20.10.2008).
Данный способ позволяет определить координаты точек поверхности с точностью, достаточной для большинства деталей машиностроения. В случае базирования измеряемой детали по конструкторским базам способ обеспечивает определение геометрических параметров и показателей точности. Однако выполнение измерений различных параметров требует каждый раз своего базирования. Это требует наличия нескольких специальных приспособлений. Однако при измерении на координатно-измерительной машине целесообразно измерить максимальное количество параметров при неизменном положении детали, при ее произвольном или частичном базировании. При произвольном базировании деталь лишается всех степеней свободы по поверхностям, не являющимся конструкторскими базами. При частичном базировании деталь лишается нескольких степеней свободы по поверхностям, являющимся конструкторскими базами, а остальных степеней свободы прочими поверхностями.
Технической задачей, на которую направлено заявляемое изобретение, является определение относительного положения центров цилиндрических участков детали и значений радиусов этих участков при произвольном базировании или частичном базировании по конструкторским базам.
Указанная задача решается тем, что в способе измерения поверхности изделия на координатно-измерительной машине, включающем определение координат центра сферического наконечника радиусом RH измерительной головки при каждом его касании с поверхностью изделия и вычисление координат точек касания сферического наконечника с поверхностью изделия, измерения выполняют не менее чем в трех точках радиусного участка, для которых определяют координаты центра сферического наконечника Xi и Yi, вычисляют координаты центра B (xb; yb) и радиус Rb этого участка, после чего выполняют измерения поверхностей конструкторских баз, не совпадающих с измерительными базами, и находят их характерные точки C (xc; yc) и D (xd; yd), по которым строят конструкторскую систему координат, начало которой смещено относительно начала измерительной системы координат на величины xc и yc, а ее оси повернуты на угол α, в конструкторской системе координат определяют положение центра B радиусного участка относительно характерных точек конструкторских баз C и D по следующим зависимостям:
Lx=|(xa-xc)cosα+(ya-yc)sinα|;
Ly=|-(xa-xc)sinα+(ya-yc)cosα|;
Kx=|((xa-xc)cosα+(ya-yc)sinα)-((xb-xc)cosα+(yb-yc)sinα)|;
Ky=|(-(xa-xc)sinα+(ya-yc)cosα)-(-(xb-xc)sinα+(yb-yc)cosα)|;
где LX, LY, KX, KY - линейные размеры положения центра радиусного участка относительно характерных точек конструкторских баз, причем угол α определяют решением оптимизационной задачи F→min, целевая функция F которой представляет собой сумму отклонений tx, ty, px, py указанных выше размеров от их значений LXcep, LYcep, KXcep, KYcep, соответствующих серединам полей допусков:
F=tx+ty+px+py,
tx=|LXcep-LX|;
ty=|LYcep-LY|;
px=|KXcep-KX|;
py=|KYcep-KY|.
Выполнение способа измерения координат центра и радиуса цилиндрических участков, включающего определение координат центра сферического наконечника радиусом RH измерительной головки при каждом его касании с поверхностью изделия, осуществляемого не менее чем в трех точках каждого участка, с определением координат центра сферического наконечника Xi и Yi, вычислением координат центра B (xb; yb) и радиуса радиусного участка, в сочетании с выполнением измерений поверхностей конструкторских баз, не совпадающих с измерительными базами, нахождением их характерных точек C (xc; yc) и D (xd; yd), построением конструкторской системы координат, начало которой смещено относительно начала измерительной системы координат на величины xc и yc, а ее оси повернуты на угол α, и определением в конструкторской системе координат положения центра B радиусного участка относительно характерных точек конструкторских баз C и D по приведенным зависимостям позволит определить относительное положение центра радиусного участка относительно конструкторских баз при произвольном или частичном базировании детали.
Заявителю не известны способы измерения координат центра и радиуса цилиндрических участков, и заявленная совокупность существенных признаков не вытекает явным образом из современного уровня техники, что подтверждает соответствие заявляемого технического решения условию «новизна».
Заявляемое техническое решение поясняется чертежами, где:
фиг. 1 - схема расположения детали и измерительного наконечника при измерении, где 1 - сферический наконечник измерительной головки; 2 - измеряемое изделие; 3 - измеряемый радиусный участок детали; 4 - поверхность конструкторской базы, не совпадающая с измерительной; 5 - измерительная оснастка;
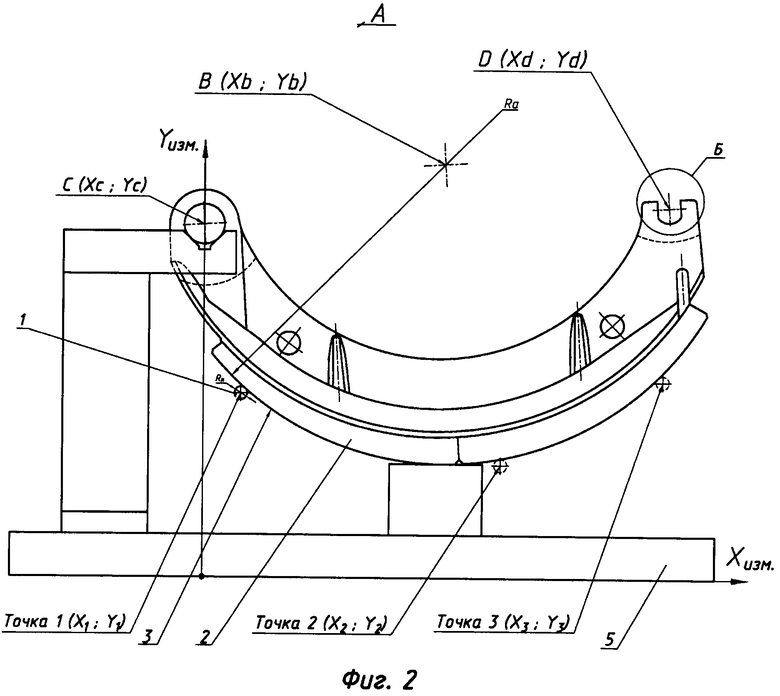
фиг. 2 - вид A на фиг. 1;
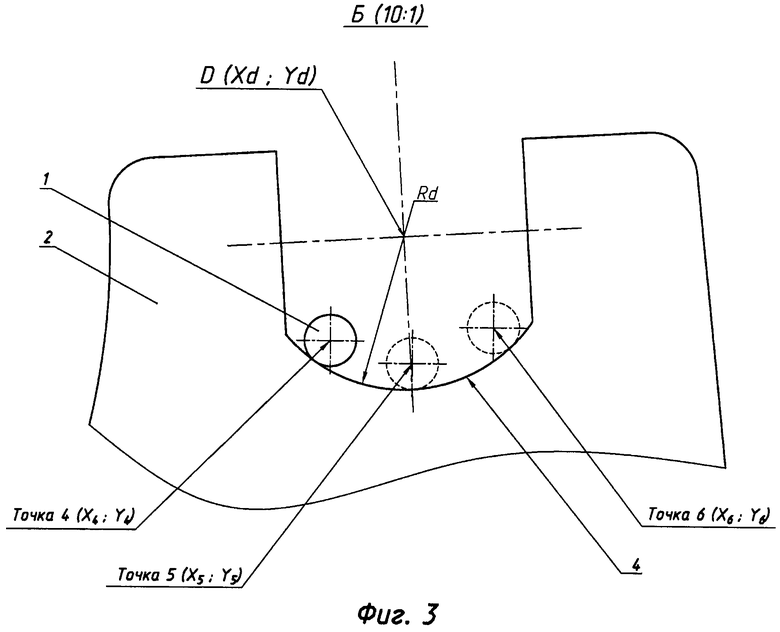
фиг. 3 - выносной элемент Б на фиг. 2;
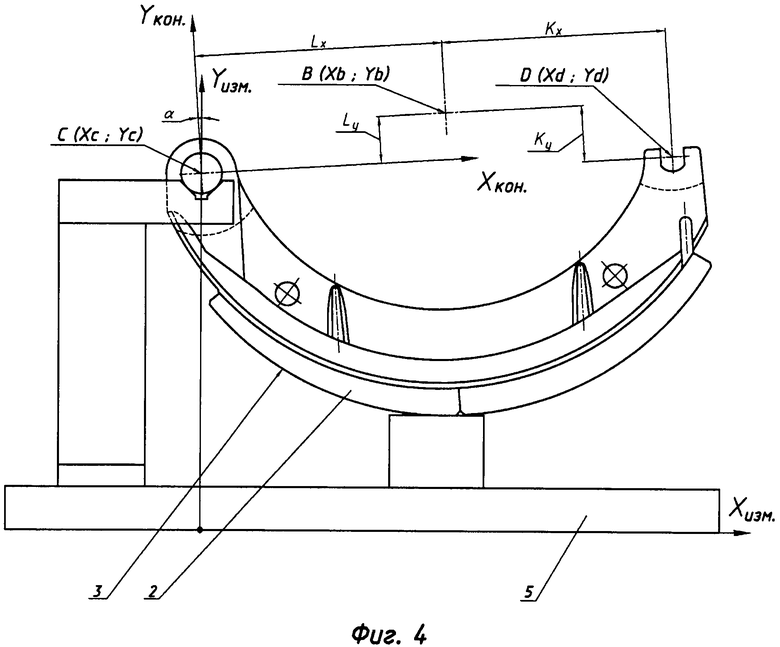
фиг. 4 - расчетная схема преобразования систем координат и определения относительного положения центра радиусного участка;
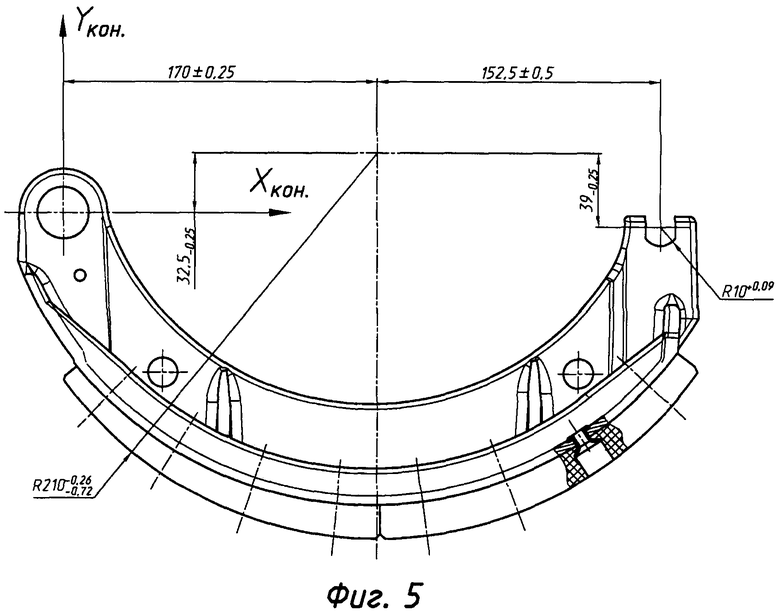
фиг. 5 - параметры радиусного участка детали колодки тормоза.
Способ измерения координат центра и радиуса цилиндрических участков деталей включает определение координат центра сферического наконечника 1 радиусом RH измерительной головки при каждом его касании с поверхностью изделия 2, установленного в измерительной оснастке 5. Измерения выполняют не менее чем в трех точках радиусного участка 3, для которых определяют координаты центра сферического наконечника Xi и Yi. Вычисляют координаты центра B (xb; yb) и радиус Rb радиусного участка 3 в измерительной системе координат Xизм., Yизм.. После чего выполняют измерения поверхностей 4 конструкторских баз, не совпадающих с измерительными базами, и находят характерные точки конструкторских баз C (xc; yc) и D (xd; yd). По характерным точкам строят конструкторскую систему координат Xкон., Yкон., начало которой смещено относительно начала измерительной системы координат на величины xc и yc, а ее оси повернуты на угол α. В конструкторской системе координат определяют положение центра B радиусного участка относительно характерных точек конструкторских баз C и D по следующим зависимостям:
Lx=|(xa-xc)cosα+(ya-yc)sinα|;
Ly=|-(xa-xc)sinα+(ya-yc)cosα|;
Kx=|((xa-xc)cosα+(ya-yc)sinα)-((xb-xc)cosα+(yb-yc)sinα)|;
Ky=|(-(xa-xc)sinα+(ya-yc)cosα)-(-(xb-xc)sinα+(yb-yc)cosα)|;
где LX, LY, KX, KY - линейные размеры положения центра радиусного участка относительно характерных точек конструкторских баз.
Угол α определяют решением оптимизационной задачи F→min, целевая функция F которой представляет собой сумму отклонений tx, ty, px, py указанных выше размеров от их значений LXcep, LYcep, KXcep, KYcep, соответствующих серединам полей допусков:
F=tx+ty+px+py,
tx=|LXcep-LX|;
ty=|LYcep-LY|;
px=|KXcep-KX|;
py=|KYcep-KY|,
где LXcep, LYcep, KXcep, KYcep - середины полей допусков соответствующих линейных контрольных размеров в конструкторской системе координат:
LXcep - середина поля допуска линейного контрольного размера CB по оси абсцисс;
LYcep - середина поля допуска линейного контрольного размера CB по оси ординат;
KХсер - середина поля допуска линейного контрольного размера BD по оси абсцисс;
KYcep - середина поля допуска линейного контрольного размера BD по оси ординат.
Ограничения целевой функции принимают вид:
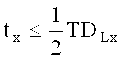
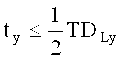
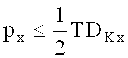
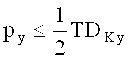
где TDLx; TDLy; TDKx; TDKy - соответствующие допуски на линейные контрольные размеры.
Результатом оптимизации целевой функции является найденный угол поворота системы координат, после чего определяют координаты центров окружностей B, D. Далее вычисляют линейные размеры изделия, подлежащие контролю, и определяют их принадлежность соответствующим полям допусков.
Анализ известных технических решений в данной области показал, что предложенный способ измерения координат центра и радиуса цилиндрических участков имеет признаки, которые отсутствуют в аналогах, а их использование в заявляемой совокупности существенных признаков позволяет получить новый технический результат.
Использование способа рассмотрим на примере измерения радиусного участка колодки тормоза автомобиля КАМАЗ. Измеряемые показатели - расстояния до центра радиусного участка 170±0,25; 32,5-0,25; 152,5±0,5; 39-0,25 и величина радиуса 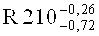
Колодку тормоза с фрикционной накладкой в сборе базировали по одной конструкторской базе - отверстию ⌀28+0,062, в котором разместили оправку с минимальным зазором, установленную на призмы. Второй конструкторской базой является паз с радиусным участком R10+0,09, расположенный на противоположной стороне колодки. Однако из соображений максимизации числа измеряемых показателей при неизменном базировании детали в качестве второй базы выбрана измеряемая поверхность с радиусом 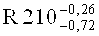
В измерительной системе координат измерили координаты шести точек наружной цилиндрической поверхности, описываемой окружностью с центром в точке B (xb; yb). Для трех (из шести) наиболее удаленных друг от друга точек определили координаты центра B (167,78; 289,5) и радиус Rb=209,49 мм окружности, описывающей наружную цилиндрическую поверхность. Полученный радиус принадлежит полю допуска на размер. Для остальных трех (из шести) точек проверили принадлежность значений радиусов, проведенных в эти точки из центра B (167,78; 289,5), полю допуска на размер. Измерили также в измерительной системе координат поверхность конструкторской базы, не являющейся измерительной, для которой определили координаты трех точек цилиндрической поверхности, описываемой окружностью с центром в точке D (12,6; 569,48), и радиус Rd=10,01 мм окружности, описывающей эту поверхность. Полученный радиус Rd принадлежит полю допуска на размер. Для контроля качества изготовления колодки тормоза с фрикционной накладкой в сборе необходимо проверить принадлежность полям соответствующих допусков линейных размеров колодки Lx, Ly, Kx, Ky, указанных в конструкторской системе координат, отличной от измерительной. Для этого осуществили параллельный перенос системы координат в точку C (0; 247,0) - центр окружности ⌀28+0,062, являющейся конструкторской базой, совпадающей с измерительной. В новой системе координат получили центры окружностей B (167,78; 42,5), D (12,6; 322,48), C (0; 0). Для перехода в конструкторскую систему координат необходимо оси координат повернуть на некоторый угол α, который заранее неизвестен. Для определения угла поворота системы координат и вычисления контрольных линейных размеров колодки составили оптимизационную задачу. Целевая функция - это функция от угла поворота α. F=F(α). Функция F приняла вид:
F=tx+ty+px+py;
F→min,
где
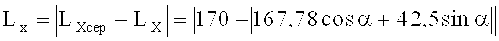
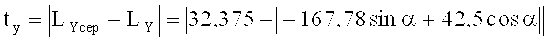
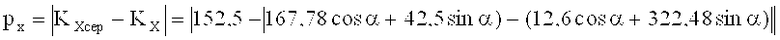
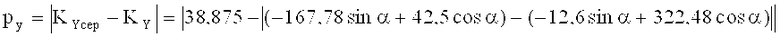
То есть
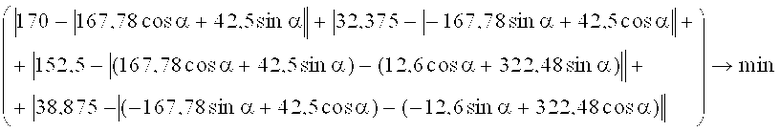
Ограничения целевой функции F:
поля допусков на линейные размеры Lx, Ly, Kx, Ky имеют следующие значения:
TDLx=0,5;
TDLy=0,25;
TDKx=1,0;
TDKy=0,25.
Разности середин полей допусков линейных размеров и вычисляемых линейных размеров, являющихся в свою очередь функциями от α, должны быть меньше или равны половинам соответствующих допусков на размер:
tx≤0,25; ty≤0,125; px≤0,5; py≤0,125.
Таким образом, определяется угол α, при котором выполняются все четыре условия годности детали, и контролируемые размеры находятся как можно ближе к серединам полей допусков.
После оптимизации целевой функции получили результаты:
α=3,39°; F=0,66; tx=0,001; ty=0,12; px=0,414; py=0,125.
Для найденного угла поворота α=3,39° вычисленные линейные размеры колодки принимают значения:
LX=170,001 (контрольное значение 170±0,25);
LY=32,495 (контрольное значение 32,5-0,25);
KX=152,664 (контрольное значение 152,5±0,5);
KY=39,000 (контрольное значение 39-0,25).
Таким образом, приведенный выше пример подтверждает, что предложенный способ измерения координат центра и радиуса цилиндрических участков обеспечивает возможность измерения указанных показателей с высокой степенью точности, вполне достаточной для мониторинга качества изготовления изделия по показателям геометрической точности.
| название | год | авторы | номер документа |
|---|---|---|---|
| СИСТЕМА И СПОСОБ МОДЕЛИРОВАНИЯ И КАЛИБРОВКИ УСТРОЙСТВА ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЯ | 2014 |
|
RU2677562C2 |
| Способ управления положением модели в аэродинамической трубе | 2017 |
|
RU2660225C1 |
| СПОСОБ УМЕНЬШЕНИЯ УГЛА АТАКИ НЕСУЩЕГО ВИНТА НА ПРЕДПОСАДОЧНЫХ МАНЕВРАХ ОДНОВИНТОВОГО ВЕРТОЛЕТА (ВАРИАНТЫ) | 2014 |
|
RU2539621C1 |
| РАЗНОСТНО-ДАЛЬНОМЕРНЫЙ СПОСОБ ПЕЛЕНГОВАНИЯ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЯ | 2006 |
|
RU2325666C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕНТРА ОТВЕРСТИЯ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2017 |
|
RU2667666C1 |
| МАГНИТОМЕХАНИЧЕСКИЙ ТЕСЛАМЕТР | 2002 |
|
RU2232399C2 |
| МНОГОЛУЧЕВАЯ НЕАПЛАНАТИЧЕСКАЯ ГИБРИДНАЯ ЗЕРКАЛЬНАЯ АНТЕННА | 2001 |
|
RU2181519C1 |
| РАЗНОСТНО-ДАЛЬНОМЕРНЫЙ СПОСОБ ПЕЛЕНГОВАНИЯ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЯ И РЕАЛИЗУЮЩЕЕ ЕГО УСТРОЙСТВО | 2003 |
|
RU2258242C2 |
| СТЕНД ДЛЯ ИЗМЕРЕНИЯ МАССЫ, КООРДИНАТ ЦЕНТРА МАСС И МОМЕНТОВ ИНЕРЦИИ ИЗДЕЛИЯ | 2012 |
|
RU2506551C2 |
| РАЗНОСТНО-ДАЛЬНОМЕРНЫЙ СПОСОБ ПЕЛЕНГОВАНИЯ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЯ И РЕАЛИЗУЮЩЕЕ ЕГО УСТРОЙСТВО | 2000 |
|
RU2204145C2 |
Изобретение относится к средствам для измерения координат центра и радиуса цилиндрических участков деталей. Данный способ включает в себя определение координат центра сферического наконечника радиусом Rн измерительной головки при каждом его касании с поверхностью изделия. Измерения выполняют не менее чем в трех точках радиусного участка, для которых определяют координаты центра сферического наконечника Xi и Yi. Вычисляют координаты центра B (xb; yb) и радиус Rb радиусного участка в измерительной системе координат Xизм., Yизм.. После чего выполняют измерения поверхностей конструкторских баз, не совпадающих с измерительными базами, и находят характерные точки конструкторских баз C (xc; yc) и D (xd; yd). По характерным точкам строят конструкторскую систему координат Xкон., Xкон., начало которой смещено относительно начала измерительной системы координат на величины xc и yc, а ее оси повернуты на угол α. В конструкторской системе координат определяют положение центра B радиусного участка относительно характерных точек конструкторских баз C и D по следующим зависимостям: Lx=|(xa-xc)cosα+(ya-yc)sinα|; Ly=|-(xa-xc)sinα+(ya-yc)cosα|; Kx=|((xa-xc)cosα+(ya-yc)sinα)-((xb-xc)cosα+(yb-yc)sinα)|; Ky=|(-(xa-xc)sinα+(ya-yc)cosα)-(-(xb-xc)sinα+(yb-yc)cosα)|; где LX, LY, KX, KY - линейные размеры положения центра радиусного участка относительно характерных точек конструкторских баз. Угол α определяют решением оптимизационной задачи F→min, целевая функция F которой представляет собой сумму отклонений tx, ty, px, py указанных выше расстояний от их значений LXcep, LYcep, KXсер, KYcep, соответствующих серединам полей допусков: F=tx+ty+px+py, tx=|LXcep-LX|; ty=|LYcep-Ly|; px=|KXcep-KX|; py=|KYcep-KY|, где LXcep, LYcep, KXcep, KYcep - середины полей допусков соответствующих линейных контрольных размеров в конструкторской системе координат: LXcep - середина поля допуска линейного контрольного размера CB по оси абсцисс; LYcep - середина поля допуска линейного контрольного размера CB по оси ординат; KXcep - середина поля допуска линейного контрольного размера BD по оси абсцисс; KYcep - середина поля допуска линейного контрольного размера BD по оси ординат. Была решена задача определения относительного положения центров цилиндрических участков детали и значений радиусов этих участков при произвольном или частичном базировании по конструкторским базам. Данное изобретение позволяет определять координаты центра и радиуса цилиндрических участков деталей при произвольном базировании по конструкторским базам. 5 ил.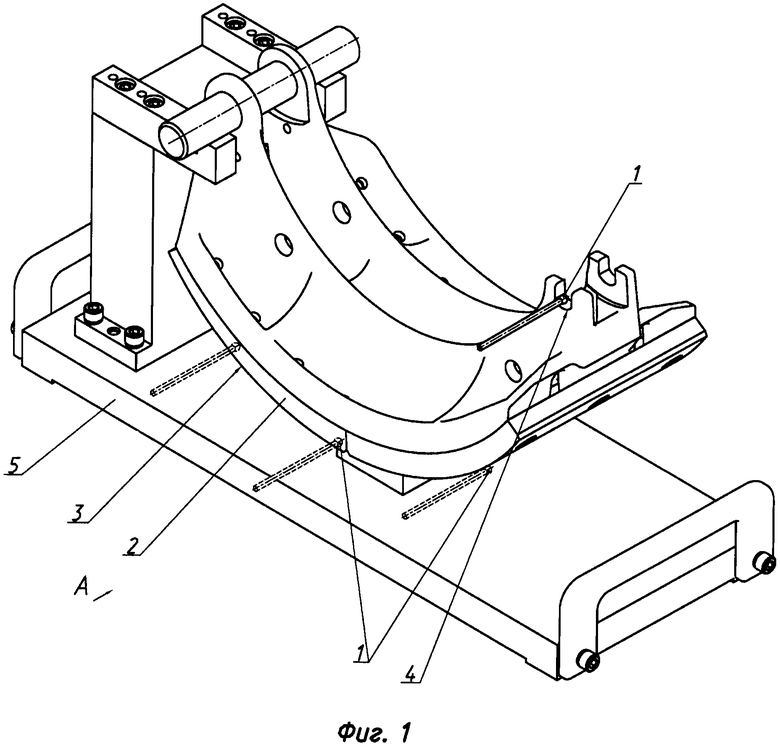
Способ измерения координат центра и радиуса цилиндрических участков деталей, включающий определение координат центра сферического наконечника радиусом Rн измерительной головки при каждом его касании с поверхностью изделия, отличающийся тем, что измерения выполняют не менее чем в трех точках радиусного участка, для которых определяют координаты центра сферического наконечника Xi и Yi, вычисляют координаты центра В(хb; уb) и радиус Rb этого участка, после чего выполняют измерения поверхностей конструкторских баз, не совпадающих с измерительными базами, и находят характерные точки С(xс; yс) и D(xd; yd) конструкторских баз, по которым строят конструкторскую систему координат, начало которой смещено относительно начала измерительной системы координат на величины xс и yс, а ее оси повернуты на угол α, в конструкторской системе координат определяют положение центра В радиусного участка относительно характерных точек конструкторских баз С и D по следующим зависимостям:
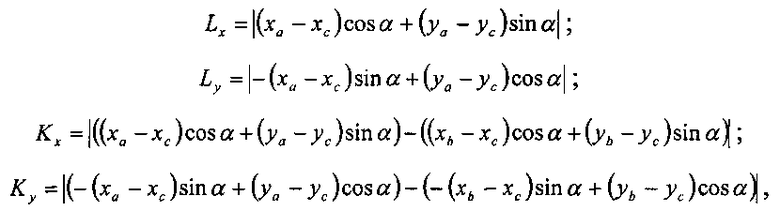
где LX, LY, КX, KY - линейные размеры положения центра радиусного участка относительно характерных точек конструкторских баз, причем угол α определяют решением оптимизационной задачи F→min, целевая функция F которой представляет собой сумму отклонений tx, ty, рx, рy указанных выше размеров от их значений LXcep>LYceр, КXсер, КYсер, соответствующих серединам полей допусков:
F=tx+ty+px+py,
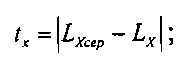
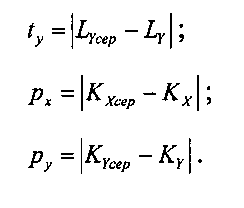
| СПОСОБ РАЗМЕРНОГО КОНТРОЛЯ ПОВЕРХНОСТЕЙ ДЕТАЛЕЙ, ИМЕЮЩИХ КРУГЛЫЕ СЕЧЕНИЯ | 2007 |
|
RU2348006C1 |
| СПОСОБ КОНТРОЛЯ ПАРАМЕТРОВ ТОЧНОСТИ ТОРЦЕВЫХ ПОВЕРХНОСТЕЙ ДЕТАЛЕЙ ТИПА "ТЕЛО ВРАЩЕНИЯ" | 2011 |
|
RU2471145C1 |
| Способ измерения диаметров цилиндрических поверхностей деталей | 1986 |
|
SU1612203A1 |
| СПОСОБ КОНТРОЛЯ ФОРМЫ И ДИАМЕТРОВ ВНУТРЕННИХ СЕЧЕНИЙ КРУПНОГАБАРИТНЫХ ЦИЛИНДРИЧЕСКИХ ДЕТАЛЕЙ | 2000 |
|
RU2166729C1 |
| US 20050155242 A1 21.07.2005. | |||
Авторы
Даты
2016-04-20—Публикация
2014-12-30—Подача