Изобретение относится к электротехнической технике, а именно к изготовлению секционированных проходных изоляторов.
Известно, что пробивная напряженность поверхности диэлектрика в вакууме возрастает с уменьшением толщины испытуемого на электрическую прочность образца. Указанное положение находит свое отражение в конструкциях высоковольтных изоляторов, применяемых в высоковольтных трансформаторах, ускорительной технике и т.д. [1].
С целью повышения электрической прочности изоляторов последние делят на множество секций проводящими градиентными кольцами. При этом применяют цилиндрическую или дисковую форму элементов секций. Высоту секций в этих конструкциях изоляторов определяют, как правило, исходя из большого объема экспериментальных исследований, что связано со значительным расходом времени и материалов, идущих на изготовление испытуемых образцов изоляторных секций. Кроме того, полученный при исследованиях результат не гарантирует создания конструкции секционированного изолятора с оптимальными габаритами.
Известен способ выбора высоты диэлектрического кольца в секционированном изоляторе по графику зависимости поверхностного пробивного напряжения изоляционного материала от толщины испытуемого образца [2]. Этот способ заключается в том, что набор образцов из одинакового изоляционного материала разной толщины подвергают испытанию на электрическую прочность поверхности в какой-либо среде, строят зависимость пробивного напряжения от толщины образца, определяют на этой зависимости точку изменения наклона кривой и толщину изоляционного кольца секционированного изолятора выбирают такой, чтобы она не превышала толщины образца, при которой снятая зависимость меняет свой наклон.
Известный способ не позволяет выбрать для проходного изолятора конкретную толщину диэлектрического кольца в секции, которая обеспечила бы получение максимальных пробивных градиентов при заданной высоте изолятора.
Оптимальная толщина диэлектрика в секционированных изоляторах зависит от толщины градиентных прокладок, материала диэлектрика и конструктивных особенностей изолятора. Поэтому для каждой конкретной конструкции проходного изолятора должна быть определена конкретная оптимальная толщина секционного кольца, а следовательно, и количество колец в конструкции.
Наиболее близким к заявляемому является способ определения оптимального числа секций секционированного изолятора [3].
Способ-прототип заключается в том, что известным способом определяют среднюю пробивную напряженность Ei изоляционного слоя высотой H и среднюю пробивную напряженность En набора из n произвольных, но равных по толщине изоляционных слоев, разделенных градиентными прокладками толщиной b, причем высота набора должна равняться H, после чего определяют оптимальное количество секций по формуле
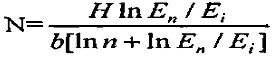
где N - оптимальное количество секций в изоляторе;
H - высота изолятора;
b - толщина градиентной прокладки;
Ei - средняя пробивная напряженность не секционированного слоя высотой H;
En - средняя пробивная напряженность произвольно секционированного слоя высотой H;
n - количество изоляционных слоев, произвольных и равных по толщине в наборе высотой H.
Следует отметить, что выбор толщины градиентного кольца диктуется условиями эксплуатации всего изолятора, технологией его сборки. В частности, при определении b учитывают электрическую прочность среды, окружающей изолятор, требования к механической прочности кольца.
Недостатком способа-прототипа является низкая точность определения оптимального числа секций в изоляторе, что не позволяет при заданной высоте изолятора H и заданной толщине градиентной прокладки b получить максимально возможное пробивное напряжение для указанных габаритов изолятора. Кроме того, способ-прототип достаточно сложен и требует для своего воплощения, особенно для изоляторов с большими габаритами, изготовления испытательного стенда со сверхвысоким источником напряжения, что не всегда возможно воплотить в жизнь.
Техническая задача, поставленная в рамках настоящего изобретения, заключается в том, чтобы упростить способ и повысить точность определения оптимального количества секций в изоляторе, что позволит получить максимальное значение пробивного напряжения для заданных габаритов изолятора.
Поставленная задача решается тем, что в способе определения оптимального числа секций N секционированного изолятора заданной высоты H, выполненного в виде чередующихся кольцевых, дисковых или цилиндрических элементов из изоляционного материала и прокладок из проводящего материала заданной толщины b, предварительно снимают зависимость пробивного напряжения U по поверхности диэлектрика, помещенного в вакуум, от толщины диэлектрика d, аналитическое описание которой представляют в виде степенной функции U=kdα, и, используя полученные при снятии зависимости пробивного напряжения по поверхности диэлектрика от его толщины экспериментальные данные, определяют коэффициенты k и α в упомянутой функции, после чего находят оптимальное количество секции в изоляторе по выражению 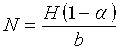
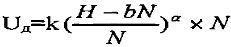
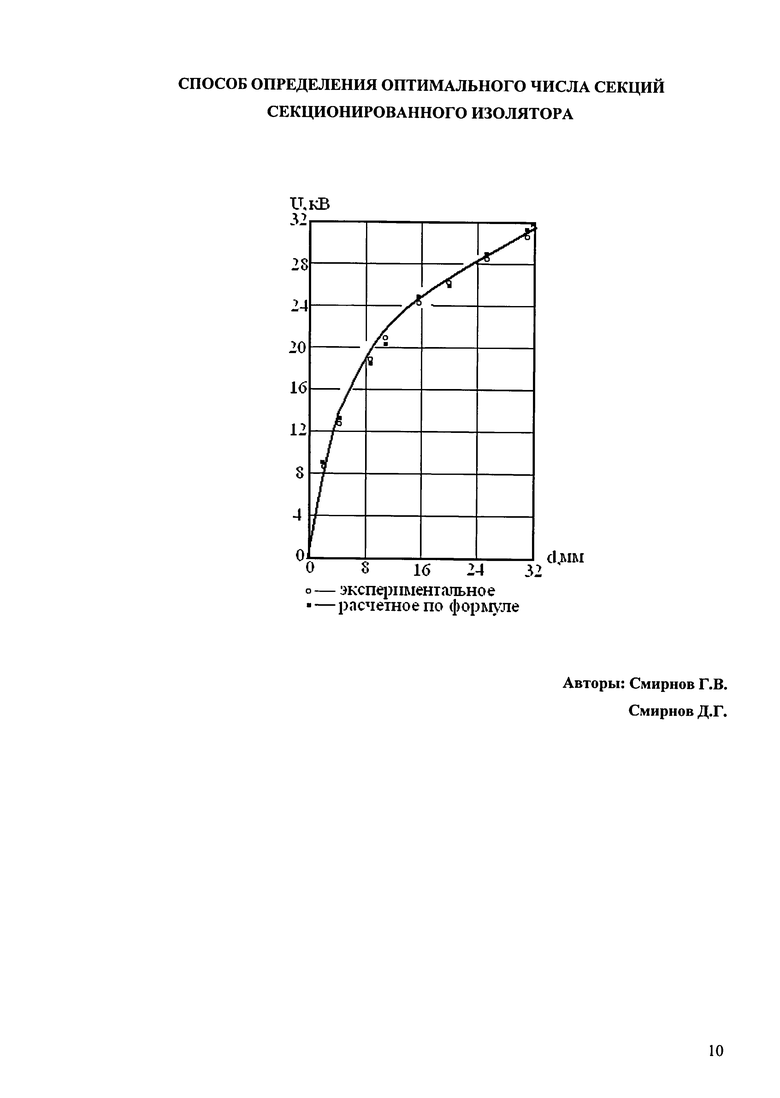
На чертеже представлена зависимость пробивного напряжения поверхности пирексовых колец от их толщины.
Сущность изобретения заключается в следующем. Пробивное напряжение поверхности любого диэлектрика в любой среде, и, в частности, в вакууме достаточно точно можно описать в виде степенной функции, имеющей вид

Выражение 1 для секционированного изолятора, имеющего n секций, можно переписать в виде:
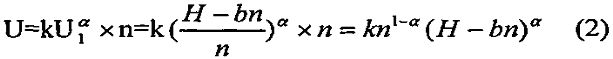
где U1 - пробивное напряжение одной секции толщиной d1, 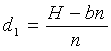
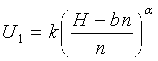
Для определения оптимального числа секций в секционированном изоляторе найдем максимум значения U. Для этого продифференцируем выражение 2 и приравняем значение производной к 0.
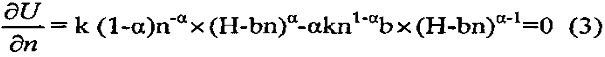
Преобразовав выражение (3), получим:
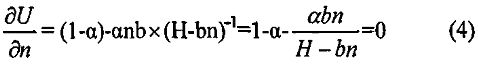
Из уравнения (4) после преобразования получим:

Из выражения (5) следует:

Коэффициенты k и α в выражении (1) для каждого конкретного случая можно рассчитать методом наименьших квадратов, используя экспериментальные значения, полученные при снятии зависимости пробивного напряжения U от толщины диэлектрика d.
Рассмотрим определение указанных коэффициентов на примере пирексовых колец, помещенных в вакуум. Экспериментальные значения пробивных напряжений U пирексовых колец от их толщины d приведены в таблице 1 и отображены на чертеже кружками.

Для упрощения нахождения коэффициентов k и α в формуле 1 линеаризуем уравнение, для чего прологарифмируем указанное выражение и получим:
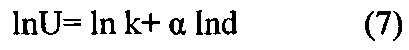
Введем обозначения y=lnU, b0=lnk, x=lnd. С учетом введенных обозначений уравнение 7 можно записать в виде:
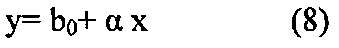
Коэффициенты b0 и α в уравнении (8) с использованием метода наименьших квадратов могут быть определены по выражениям (9) и (10), взятым из работы [4].
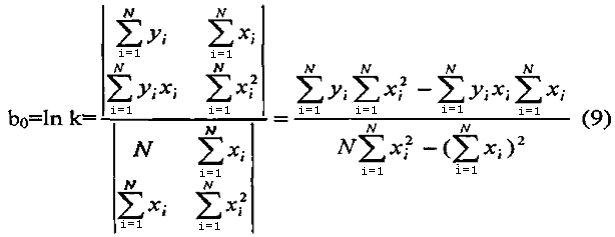
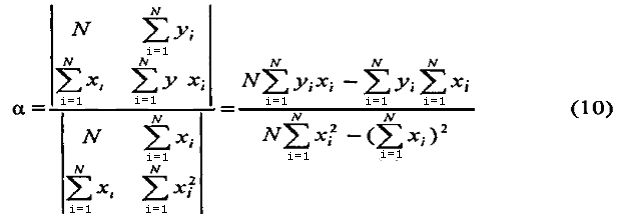
Для расчета численных значений коэффициентов b0 и α используем таблицу 2.
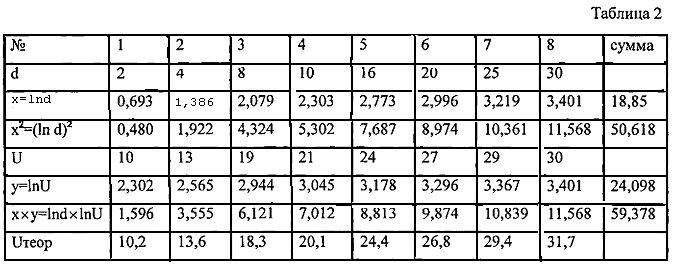
Подставив численные значения в формулы (9) и (10), получим:
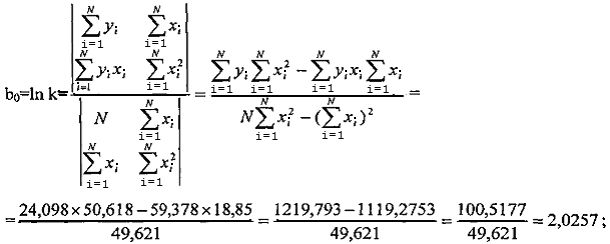
проведя потенцирование, получим:
k=7,648
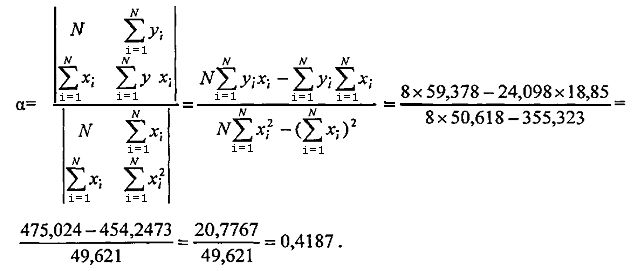
Окончательный вид уравнения (1) после подстановки в него численных значений k=7,648 и α=0,4187 примет вид:
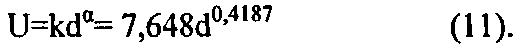
На чертеже черными квадратиками обозначены расчетные значения напряжения из пирексовых колец, определяемого по выражению (11). Как следует из чертежа, расчетные значения пробивного напряжения от толщины изолятора по формуле (11) практически полностью совпадают с экспериментальными значениями, т.е. адекватно описывают эксперимент.
Примером конкретного осуществления заявляемого способа является расчет оптимального количества секций в секционированном изоляторе высотой H=300 мм и толщиной b=3 мм по формуле (6):
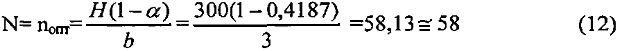
Толщина одной секции d1 будет равна:
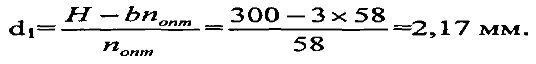
Предельно допустимое напряжение такого секционированного изолятора определим по формуле (2):
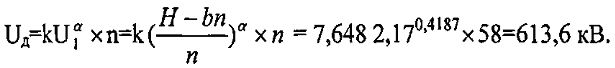
Рассчитанное предельное значение напряжения Uд=613,6 кВ указывает на то, что данный изолятор может быть использован в установках, рабочее напряжение которых не превышает напряжение Uд.
Для наглядности в таблице 3 приведены значения пробивного напряжения секционированного изолятора высотой H=300 мм и толщиной градиентной прокладки b=3 мм при различном количестве секций n в нем. Расчет производили по формуле (2) с использованием выражения (11). Из таблицы 3 наглядно видно, что при дроблении изолятора на секции пробивное напряжение всей конструкции изолятора имеет максимальное значение при оптимальном количестве секций N=nопт=58.

Сравним полученное значение пробивного напряжения с пробивным напряжением такого же по габаритам изолятора, но выполненного по способу-прототипу. Для сравнения возьмем цифры из примера конкретного выполнения, приведенные в [3].
Определим оптимальное число секций по выражению, приведенному в способе-прототипе:
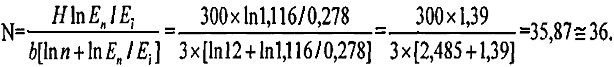
Толщина dспрот одной секции изолятора, выполненного по способу-прототипу, будет равна:
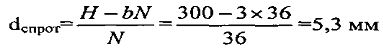
Величина пробивного напряжения секционированного изолятора, выполненного по способу-прототипу, будет равна:
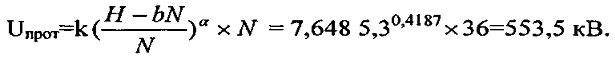
На фиг. 1 способа-прототипа [3] изображен слой изолятора высотой H (например, H=300 мм); на фиг. 2 способа-прототипа [3] - набор произвольных и равных по толщине изоляционных слоев количеством n (например, n=12) общей толщиной H, толщина разделяющих градиентных прокладок равна b (например, b=3 мм); на фиг. 3 способа-прототипа [3] - секционированный изолятор высотой H (например, H=300 мм). Способ-прототип осуществляют следующим образом. Определяют с помощью известных устройств (делителя напряжения, осциллографа или киловольтметра) среднюю пробивную напряженность изоляционного слоя 1 высотой H (например, Ei=l кВ/см) (см. способ-прототип, фиг. 1). Затем также измеряют среднюю пробивную напряженность набора произвольных и равных по толщине изоляционных слоев (см. способ-прототип, фиг. 2), например, для набора высотой H=300 мм, состоящего из двенадцати пирексовых колец, разделенных градиентными прокладками 2 толщиной b=3 мм; En=3,8 кВ/см. Набор расположен между высоковольтными электродом 3 и заземленным фланцем 4. Измеренные Ei, En подставляют в формулу, по которой определяют оптимальное количество секций:
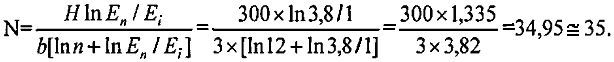
Если подставить цифры, следующие из способа-прототипа: N=35; dпрот=5,57; N=35 секций, в формулу (2), то получим Uпрот=549,5 кВ. Как следует из приведенных цифр, заявляемый способ, по сравнению со способом-прототипом, позволяет повысить пробивное напряжение приведенного в примере изолятора высотой H=300 мм и толщиной градиентной прокладки b=3 мм на 11,7%.
Таким образом, заявляемый способ по сравнению со способом-прототипом имеет более высокую точность определения оптимального числа секций в изоляторе, что позволяет при заданной высоте изолятора H и заданной толщине градиентной прокладки b получить максимально возможное пробивное напряжение для указанных габаритов изолятора. Кроме того, заявляемый способ, по сравнению со способом-прототипом, достаточно прост и не требует для своего воплощения, особенно для изоляторов с большими габаритами, изготовления испытательного стенда со сверхвысоким источником напряжения, что не всегда возможно воплотить в жизнь. В частности, в рассмотренных нами примерах для реализации заявляемого способа достаточно того, чтобы экспериментальная высоковольтная установка позволяла получать напряжение, не превышающее 30÷35 кВ. Тогда как для реализации способа-прототипа, необходимо, как это следует из таблицы 3, чтобы экспериментальная установка имела возможность экспериментировать при напряжениях 450÷500 кВ, что более чем на порядок выше напряжения, необходимого для реализации заявляемого способа.
Предлагаемый способ позволяет, не меняя габаритов изолятора, путем определения оптимального количества секций повысить его электрическую прочность не менее чем на 11,7%. Кроме того, при заданном рабочем напряжении изолятора выбором оптимального количества его секций можно добиться сокращения габаритов и уменьшения стоимости изолятора.
Источники информации
1. Патент США №2082474, опубл. 1937.
2. Раховский В.Н. Физические основы электрического тока в вакууме. М.: «Наука», 1970, с. 57.
3. А.с. 758266. Способ определения оптимального числа секций секционированного изолятора / Смирнов Г.В., Кассиров Г.М., Планкин Ю.В. - Опубл. в БИ 23.08.80, №31 (прототип).
4. Смирнов Г.В., Смирнов Д.Г. Моделирование и оптимизация технологических процессов РЭС: Учебное пособие. - Томск: Издательство Томского государственного университета систем управления и радиоэлектроники, 2007. - C. 66-67.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНОГО КОЛИЧЕСТВА СЕКЦИЙ СЕКЦИОНИРОВАННОГО ИЗОЛЯТОРА | 2014 |
|
RU2584543C1 |
| ПРОХОДНОЙ СЕКЦИОНИРОВАННЫЙ ИЗОЛЯТОР | 2015 |
|
RU2592870C1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ ПРОХОДНОГО ВАКУУМНОГО ИЗОЛЯТОРА ВЫСОКОГО НАПРЯЖЕНИЯ | 2015 |
|
RU2593827C1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ ПРОХОДНОГО ВАКУУМНОГО ИЗОЛЯТОРА ВЫСОКОГО НАПРЯЖЕНИЯ | 2014 |
|
RU2557064C1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ ПРОХОДНОГО ВАКУУМНОГО ИЗОЛЯТОРА ВЫСОКОГО НАПРЯЖЕНИЯ | 2014 |
|
RU2556879C1 |
| Способ определения оптимального числа секций секционированного изолятора | 1984 |
|
SU1552235A1 |
| Проходной секционированный изолятор | 1977 |
|
SU636687A1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ ПРОХОДНОГО ВАКУУМНОГО ИЗОЛЯТОРА ВЫСОКОГО НАПРЯЖЕНИЯ | 2014 |
|
RU2560965C1 |
| Проходной секционированный изолятор | 1989 |
|
SU1760561A1 |
| СПОСОБ ИЗОЛИРОВКИ ПАЗОВ МАГНИТНЫХ СЕРДЕЧНИКОВ СТАТОРОВ ЭЛЕКТРОДВИГАТЕЛЕЙ | 2012 |
|
RU2532541C2 |
Изобретение относится к изготовлению секционированных проходных изоляторов. В способе определения оптимального числа секций N секционированного изолятора заданной высоты H, выполненного в виде чередующихся кольцевых, дисковых или цилиндрических элементов из изоляционного материала и прокладок из проводящего материала заданной толщины b, предварительно снимают зависимость пробивного напряжения U по поверхности диэлектрика, помещенного в вакуум, от толщины диэлектрика d, аналитическое описание которой представляют в виде степенной функции U=kdα, и, используя полученные при снятии зависимости пробивного напряжения по поверхности диэлектрика от его толщины экспериментальные данные, определяют коэффициенты k и α в упомянутой функции. Заявляемый способ имеет более высокую точность определения оптимального числа секций в изоляторе, что позволяет при заданной высоте изолятора H и заданной толщине градиентной прокладки b получить максимально возможное пробивное напряжение для указанных габаритов изолятора. 1 ил., 3 табл.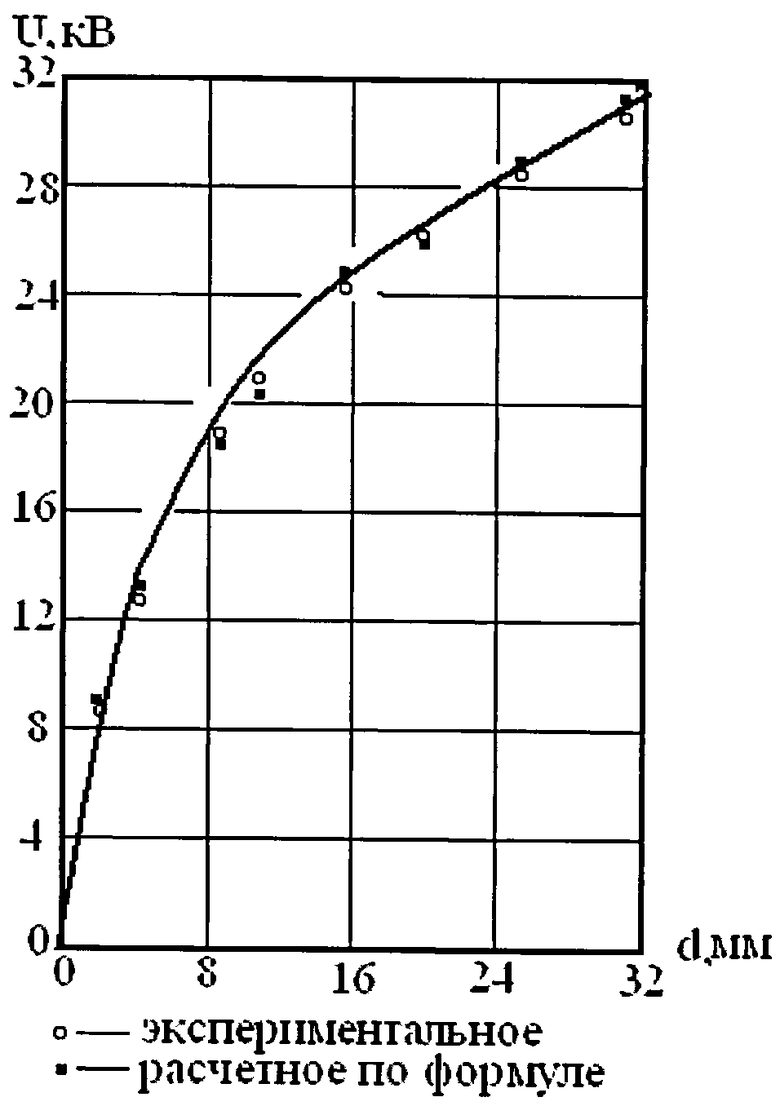
Способ определения оптимального числа секций N секционированного изолятора заданной высоты H, выполненного в виде чередующихся кольцевых, дисковых или цилиндрических элементов из изоляционного материала и прокладок из проводящего материала заданной толщины b, отличающийся тем, что снимают зависимость пробивного напряжения U по поверхности диэлектрика, помещенного в вакуум, от толщины диэлектрика d, аналитическое описание которой представляют в виде степенной функции U=kdα, и, используя полученные при снятии зависимости пробивного напряжения по поверхности диэлектрика от его толщины экспериментальные данные, определяют коэффициенты k и α в упомянутой функции, после чего находят оптимальное количество секций в изоляторе по выражению 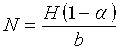 , после чего определяют уровень предельного максимального напряжения Uд изолятора по уравнению
, после чего определяют уровень предельного максимального напряжения Uд изолятора по уравнению
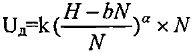
| SU758266 A, 23.08.1980 | |||
| Способ определения оптимального числа секций секционированного изолятора | 1984 |
|
SU1552235A1 |
| US4459430 A, 10.07.1984 | |||
| US3801725 A, 02.04.1974. | |||
Авторы
Даты
2016-04-20—Публикация
2014-09-15—Подача