Изобретение относится к области метрологии, а именно к способу определения гравитационной постоянной при форме взаимодействующих тел, отличной от шаровой.
Известен способ измерения гравитационной постоянной при шаровой форме взаимодействующих тел [1] (Патент РФ №2364896 на изобретение. Способ измерения гравитационной постоянной // Приоритет изобретения 31.07.08). Способ заключается в том, что при всех позициях притягивающих тел измеряют периоды и амплитуды колебаний крутильных весов, рассчитывают моменты притяжения рабочего тела, определяют гравитационную постоянную либо по системе двух дифференциальных уравнений движения, либо по аналитическим формулам, полученным с учетом теории нелинейных колебаний. Способ применим только при шаровых формах взаимодействующих тел. Более сложные варианты не рассматриваются.
Наиболее близким по своей сущности к заявляемому способу является способ определения гравитационной постоянной [2] (Сагитов М.У., Милюков В.К., Монахов Е.А., Назаренко B.C., Таджитдинов К.Г. Новое определение кавендишевой гравитационной постоянной // ДАН СССР, 1979, т. 245, №3, с. 567-569), в котором измеряются периоды и амплитуды колебаний крутильных весов при размещении цилиндрических притягивающих тел на четырех позициях, расположенных на линии равновесия весов на различных расстояниях от их оси вращения. Моменты притяжения цилиндрическими притягивающими телами коромысла прямоугольного сечения, его цилиндрических концов и цилиндрических грузов находят шестикратным интегрированием. Все требуемые технические характеристики даны в [3] (Е.А. Монахов. Дифференциальный метод измерения гравитационной постоянной, уточнение масс и средней плотности Земли, Луны и планет. Кандидатская диссертация, ГАИШ, 1979). Приведены измеренные значения периодов и амплитуд колебаний, а также полученные значения гравитационной постоянной. Утверждается, что моменты притяжения в ближней и дальней позициях определены с точностью 10-5, которая обеспечила погрешность при определении G на уровне 10-4. Предполагалось, что моменты остаются постоянными при разных углах отклонения весов. Нелинейность момента притяжения не учитывалась. Однако погрешность при амплитуде 18 мрад в первой позиции достигала 1800 ppm, во второй 1500 ppm, в третьей 1200 ppm, а в дальней четвертой - 800 ppm.
Недостаток такого способа заключается в том, что при форме взаимодействующих тел, отличной от шаровой, отсутствие аналитических формул моментов притяжения существенно осложняет определение гравитационной постоянной. Классический вариант динамического метода, заключающийся в измерении периодов и амплитуд колебаний, трансформирован в прототипе в прецизионные измерения углового отклонения φ, его первой и второй производных. Эти дополнительные измерения привели к усложнению систем индикации. Дифференциальные уравнения колебаний преобразованы в системы алгебраических уравнений, в которые вносились свои постоянные значения гравитационной жесткости при ближнем и дальнем положении притягивающих тел. Нелинейность моментов притяжения не учитывалась. Периоды и амплитуды колебаний были тщательно измерены, но при определении гравитационной постоянной так и не использовались. Это привело к неоправданному усложнению методики, исключению значительной части имеющихся в эксперименте данных, получению недостоверного результата. Заявленное значение гравитационной постоянной не согласуется с проведенными результатами измерений.
Задачей изобретения является уточнение значения гравитационной постоянной в уже проведенных экспериментах, где использовались тела усложненной формы.
Поставленная задача достигается тем, что оригинальная система взаимодействующих тел преобразуется в модельную, в которой коромысло с прямоугольным сечением и его цилиндрические концы заменены на тонкие стержни, а все цилиндрические тела - на шаровые. При этом требуется добиться полной адекватности реальной и модельной систем.
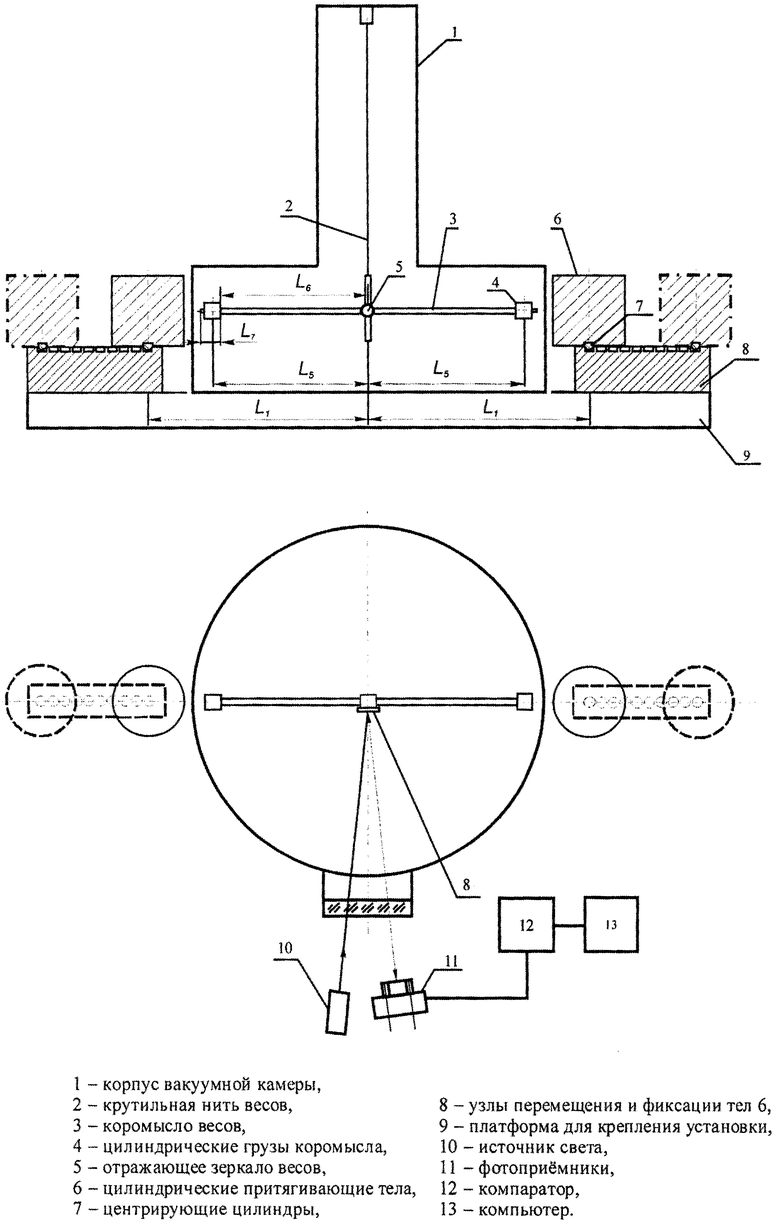
Способ поясняется чертежом, где 1 - корпус вакуумной камеры, 2 - крутильная нить весов, 3 - коромысло весов с плечами прямоугольного сечения длиной L6 и цилиндрическими концами длиной L7, 4 - цилиндрические грузы коромысла массой m1, 5 - отражающее зеркало весов, 6 - цилиндрические притягивающие тела массой М, 7 - центрирующие цилиндры, 8 - узлы для перемещения и фиксации притягивающих тел 6, 9 - платформа для крепления установки, 10 - источник света, 11 - фотоприемники, 12 - компаратор, 13 - компьютер, L5 - расстояние от оси вращения до центра масс грузов коромысла, Li (i=1, 2, 3, 4) - расстояние от оси вращения до центра масс притягивающих цилиндров.
Внутри вакуумной камеры 1 размещают крутильные весы, в которых на крутильной нити 2 крепится рабочее тело весов, включающее коромысло 3 с цилиндрическими грузами 4 на концах и отражающее зеркало 5. Цилиндрические притягивающие тела 6, снабженные центрирующими цилиндрами 7, фиксируются на круглых отверстиях узлов 8, которые устанавливаются на жесткой платформе 9. Узлы 8 содержат дополнительные линейки для подхвата и перемещения тел с одного отверстия неподвижной линейки на соседнее с помощью электропривода. Источник света 10 направляет на зеркало весов 5 через стеклянное окно камеры 1 луч света, который после отражения от зеркала выходит обратно и проходит мимо двух фотоприемников 11. С них колоколообразные импульсы подаются на компаратор 12. При определенной амплитуде сигнала компаратор опрокидывается. Его импульсы с крутыми фронтами поступают на входной порт компьютера 13, который завершает при этом измерение интервала времени, фиксирует его и начинает измерение нового. Последний восьмой интервал компьютер привязывает к реальному времени. После окончания измерений на данной позиции компьютер формирует сигнал на включение электропривода и задает время, в течение которого он не может быть выключен. Выключение двигателей осуществляется кнопочными выключателями после окончания заданного в программе времени и возвращения узлов перемещения в первоначальное положение. Для предотвращения аварийной ситуации в случае сбоя в системе управления предусмотрены концевые выключатели, обесточивающие привод до сброса притягивающих тел с узлов 8.
При отклонении весов на угол φ на рабочее тело воздействует упругая сила закрученной нити 2 и момент притяжения цилиндрических притягивающих тел 6, который в первом приближении пропорционален φ. Такой момент уменьшает период колебаний весов. При увеличении расстояния цилиндрических тел от оси вращения момент притяжения уменьшается, а период колебаний приближается к нормальному значению. По величине момента притяжения можно определить значение гравитационной постоянной. Такие операции удается провести при шаровой форме всех взаимодействующих тел. При усложнении их формы задача становится чрезвычайно трудной. В этом случае по значениям Li, М, m1, m2 шестикратным интегрированием определяют моменты притяжения. На эту операцию затрачивается солидное время даже при использовании самых современных вычислительных средств. Затем аналогичные моменты притяжения определяют в упрощенной модельной системе, в которой коромысло с цилиндрическими концами заменено на два тонких стержня, а все остальные участвующие во взаимодействии тела на шаровые. При этом подбираются такие значения Lim, при которых достигается равенство моментов притяжения в реальной и модельной системах при малых значениях φ. На всех позициях Lim>Li. После этого находятся все возможные комбинации Gij по имеющейся программе, разработанной для шаровой формы взаимодействующих тел. Такая методика оказалась вполне эффективной при анализе эксперимента [2], где максимальная амплитуда колебаний не превышала 18 мрад. При этом сохранялась удовлетворительная адекватность модельной системы реальной при любой величине φ. При φ=18 мрад погрешность момента притяжения в модельной системе при расположении притягивающих тел в ближней к весам позиции составила величину 4.04-10-5, в дальней она уменьшилась до 6.13-10-6. Моменты притяжения в модельной системе были меньше, чем в реальной. Для более точного совпадения реальных и модельных моментов притяжения последние были умножены на член 1+kiφ2, где i - номер позиции, на которой установлены притягивающие тела. Массив этих коэффициентов составил следующий ряд: k1=0.126494, k2=0.099346, k3=0.055091, k4=0.019228. Они были введены в программу для определения Gij, что снизило погрешность до уровня 1·10-6.
В [3] момент инерции рабочего тела весов J=21483.64 г·см2. С учетом вытесненного воздуха масса цилиндрических притягивающих тел диаметром 18.0012 см и высотой 19.9531 см М=39756.452 г. Масса цилиндрических грузов коромысла длиной 1.63905 см и диаметром 1.6415 см с осевым отверстием диаметром 0.3015 см m1=29.9198 г. Масса всего коромысла шириной 0.3906 см, высотой 0.4071 и длиной плеч L6=16.92935 см mk=24.93909 г. С учетом объема прямоугольной части коромысла и его концов диаметром 0.3 см найдем, что масса прямоугольной части m2=23.9091 г, масса цилиндрического тела длиной 2(L6+L7) m3=11.65826 г, масса цилиндрического тела длиной 2L6 m4=10.62826 г. Центр масс грузов находился на расстоянии L5=17.748875 см от оси вращения весов. Центры масс притягивающих цилиндров располагались на четырех расстояниях L1=28.99845, L2=30.99860, L3=33.99805, L4=38.99795 см. При этом модельные расстояния на четырех позициях имели величину: Llm=29.970037, L2m=31.810130, L3m=34.632626, L4m=39.453571 см.
Модельная система позволила определить значения гравитационной постоянной во всех возможных комбинациях позиций притягивающих тел. В табл. 1 приведены усредненные по шести сериям измерений периоды и амплитуды колебаний с учетом перемещающихся кареток, а также значения Gij при различных комбинациях позиций ni и nj. В столбце 7 приведены Gij с учетом вклада кареток, в столбцах 8 и 9 - при уменьшении расстояния до притягивающих тел в реальной системе на 190 и 217 мкм. Для уравнивания всех значений Gij в столбце 10 следует уменьшить среднее значение периодов колебаний в третьей позиции на 12.6 мс, а в четвертой позиции - увеличить на 43.2 мс. В итоге получим
G=(6.6729±0.0008)-10-11 Нм2/кг2.
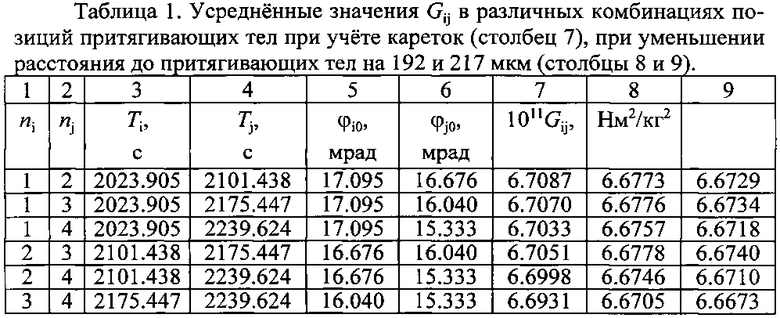
Влияние нелинейности на погрешность расчета Gij показано в табл. 2. В ней при различных комбинациях позиций ni и nj приведены усредненные по шести сериям измерений значения Gij при указанной в табл. 6 амплитуде (столбец 6), а также при ее уменьшении в 10 и 100 раз (столбцы 7 и 8). В столбце 5 приведены значения Gij без учета корректирующих коэффициентов ki (столбец 5).
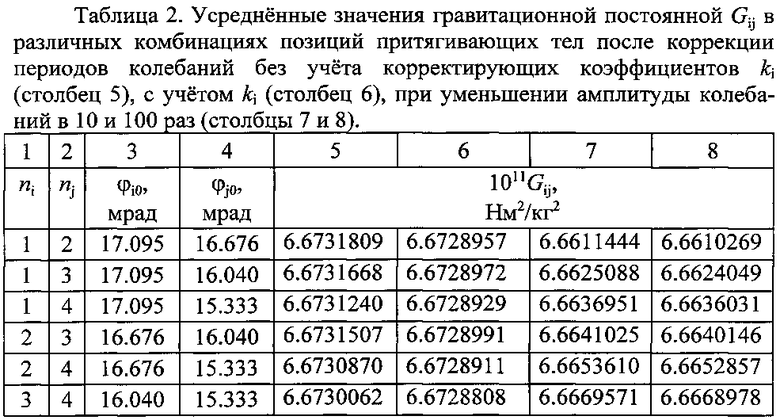
Использованные при окончательных расчетах моменты притяжения всего рабочего тела весов Ki, а также в отдельности грузов коромысла K1i, прямоугольной части коромысла K2i и его цилиндрических концов K3i на всех четырех позициях при L1=28.97675, L2=30.97690, L3=33.97635, L4=38.97625 см приведены в табл. 3. Соответствующие им моменты притяжения в модельной системе Kmi, K1mi, K2mi, K3mi, при L1m=29.950275, L2m=31.789977, L3m=34.611974, L4m=39.432431 см приведены в табл. 4. Эти моменты лежат в основе реализации предложенного способа. Видно, что для уравнивания моментов в реальной и модельной системах следует использовать массив корректирующих коэффициентов.
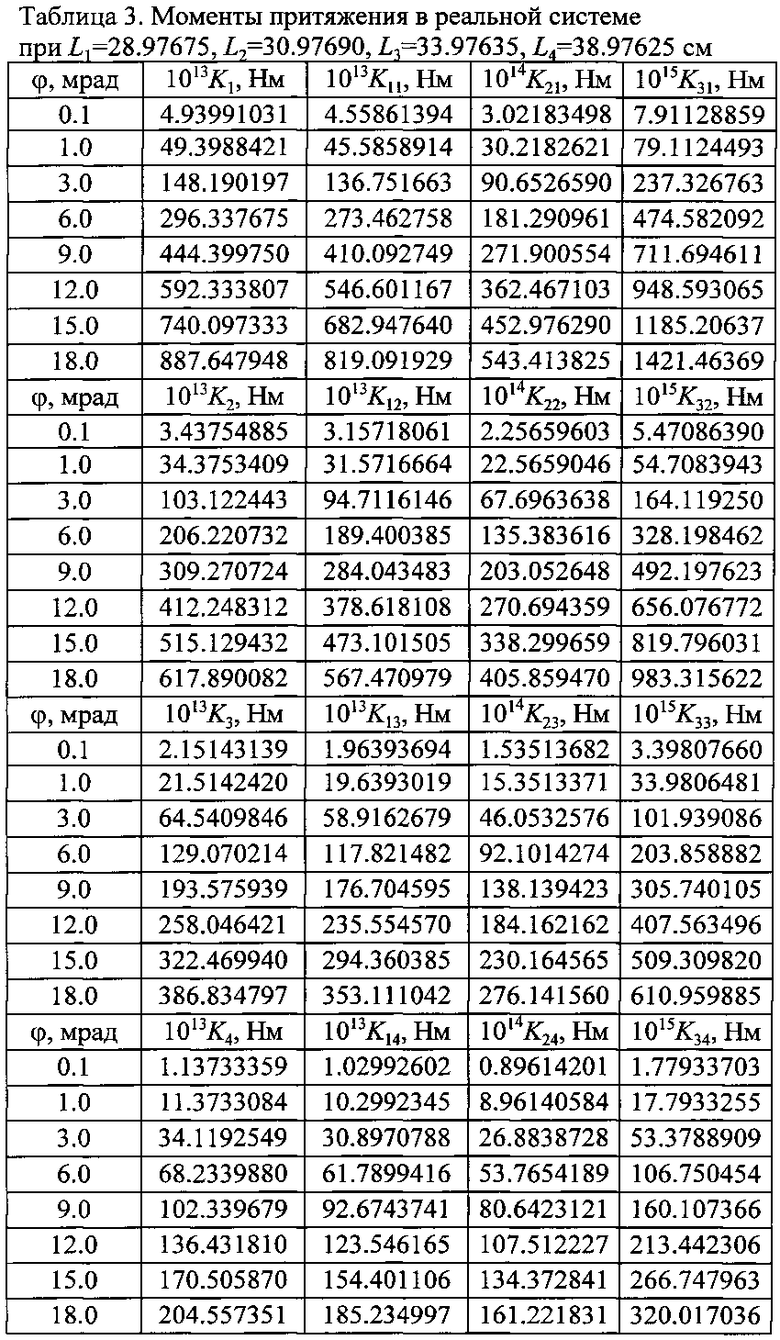
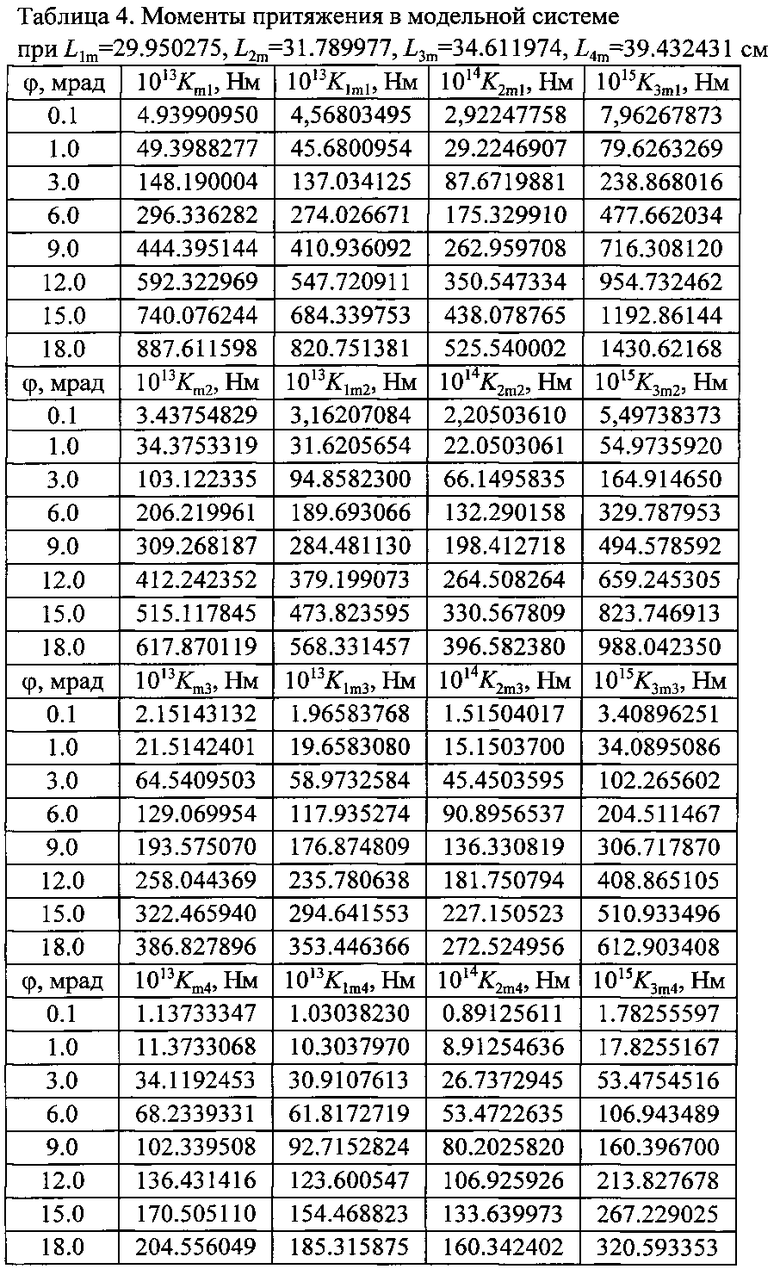
Детально рассмотрим вопрос, получили ли авторы прототипа хотя бы недостоверное значение G14=(6.6745±0.0008)-10-11 Нм2/кг2. Скорее всего им это достигнуть не удалось. Разработанная ими методика могла привести к желаемому результату только в случае преодоления ряда сложнейших барьеров. Кроме периодов и амплитуд колебаний предстояло одновременно получить значения углов отклонений и их двух производных. Эту задачу они успешно решили ценой существенного усложнения конструкции установки и методики измерений. Была предложена и оригинальная методика дальнейших операций, не базирующаяся на теории нелинейных колебаний. Необходимо было определить моменты притяжения хотя бы в двух наиболее ценных позициях 1 и 4. Авторы утверждают, что они были осуществлены при фиксированном угле отклонения. Следовало, конечно, для учета нелинейности провести подобные операции при нескольких углах отклонения весов, однако имевшиеся в то время средства вычислений это не позволяли. Но принципиальную проблему вызывали перемещающиеся вместе с притягивающими телами каретки. Определять моменты притяжения без учета кареток бессмысленно. Учесть их вклад невозможно, поскольку неизвестна их масса, а также геометрия. Эту проблему удалось решить только введением поправки в периоды колебаний весов. При положении кареток в 1, 2, 3 и 4 позициях периоды весов имели значения 2316.9967, 2317.0480, 2317.5864, 2318.9207 с. Наличие кареток при сохранении величины периода в четвертой позиции вело к уменьшению периода колебаний в 1, 2 и 3 позициях на 1.924, 1.8727, 1.3343 с. Поэтому в первом приближении следует просто увеличить значения периодов в соответствующих позициях на указанные поправки. Однако при дополнительном учете периодов колебаний в трех первых позициях при наличии притягивающих тел их периоды увеличены только на 1.280, 1.394, 1.102 с умножением поправок на отношение кубов периодов при наличии притягивающих тел и без них. Если не вводить в периоды поправку на наличие перемещающихся кареток, то в комбинации позиций 1 и 4 G14=(6.7496±0.0008)-10-11 Нм2/кг2. Авторы прототипа корректировку периодов не осуществляли и нигде их не использовали.
Теперь проанализируем, удалось ли на базе предложенного способа получить новый технических результат. Табл. 1 его наглядно демонстрирует. Вместо одного заявленного в прототипе недостоверного результата получены шесть новых значений гравитационной постоянной во всех возможных комбинациях позиций притягивающих тел. Поскольку в прототипе содержится только одно значение G14 в комбинации позиций 1 и 4, определим отличие нашего результата от прототипа, выраженное в единицах ppm. В данной комбинации при указанных в прототипе параметрах оно составляет 4315 ppm. После устранения обнаруженных погрешностей различие снизилось до 240 ppm. При определении гравитационной постоянной следует не допускать погрешность свыше 10 ppm.
Для проверки предложенного способа были проведены контрольные эксперименты на нашей установке. Использовались крутильные весы с периодом колебаний 1574.384 с, в которых масса грузов на концах коромысла - 9.7180 г, масса всего коромысла - 3.93095 г, расстояние от оси вращения до центра масс грузов -11.5056 см, длина плеч коромысла - 10.875 см. Массы цилиндрических притягивающих тел с учетом вытесненного воздуха - 5368.785 г, расстояния от оси вращения весов до центров масс цилиндрических тел - 18.7730, 21.4526 и 31.13070 см. Измерения проведены на амплитудах 32 и 88 мрад. Получены стандартные значения Gij, что дополнительно подтвердило достоверность предложенного способа.
В чем же состоит смысл данного способа. Он основан, прежде всего, на принципиально новом физическом подходе к решению этой сложнейшей проблемы. Основная его суть заключается в преобразовании исходной системы любой сложности, практически не предоставляющей никаких шансов для определения гравитационной постоянной, в упрощенную модельную. Такая цель была намечена и успешно достигнута в связи с тем, что для нее уже имелось полное обеспечение на базе специальной программы на языке Borland С. Такое преобразование кроме авторов заявки никто предложить не может, поскольку даже анализ упрощенной модельной системы пока никто не осуществлял.
В модельной системе при определении гравитационной постоянной применяются две независимых методики. Одна из них базируется на численном решении уравнений движения, другая - на теории нелинейных колебаний. Момент сил притяжения K1mi в позиции i между шаровыми грузами массой m1, укрепленными на концах коромысла, и двумя притягивающими телами массой М
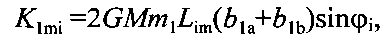
где 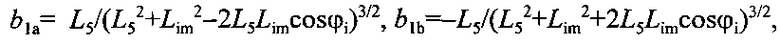
L5, Lim - расстояния от оси вращения до центра масс шарового груза и притягивающего шара; М - разность масс притягивающего шара и вытесненного им воздуха; φi - угол отклонения коромысла от положения равновесия в позиции i.
Момент силы притяжения коромысла с плечами прямоугольного сечения двумя телами массой М
где 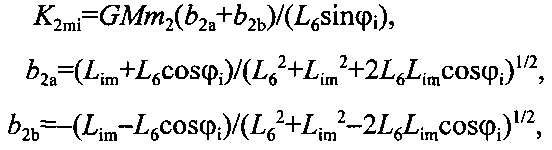
m2 - масса прямоугольной части коромысла, L6 - длина его плеч.
Момент притяжения цилиндрических концов коромысла K3 двумя телами массой М
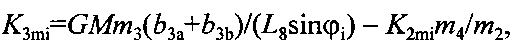
где L8=L6+L7, m3 - масса цилиндрического тела длиной 2L8,
m4 - масса цилиндрического тела длиной 2L6,
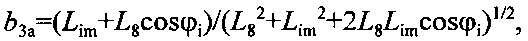
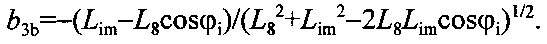
Полный момент Kmi=Klmi+K2mi-K3mi.
В методике 1 методом Рунге-Кутты определяют величину половины периода ангармонических колебаний весов в позициях i и j интегрированием двух дифференциальных уравнений движения:
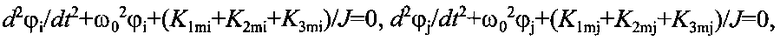
где J - момент инерции рабочего тела, ω0=2π/T0 - частота колебаний при отсутствии притягивающих тел, φi и φj - углы отклонения весов от положения равновесия. Численные интегрирования проводят при двух значениях G=G0(1±k), где G0 - стандартное значение G. При положительном и отрицательном значениях k в позициях i и j вычисляют разность обратных квадратов половин периодов колебаний τ1 и τ2. С учетом экспериментальной разности обратных квадратов периодов колебаний τехр гравитационную постоянную G определяют по формуле:
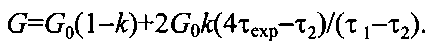
Методика 2 предусматривает операции по аналитическим формулам. Моменты сил притяжения раскладывают в ряд по степеням угла отклонения весов φ. Теория нелинейных колебаний изложена в работе: Кузнецов А.И., Карагиоз О.В., Измайлов В.П. Частота ангармонических колебаний осциллятора при учете нелинейных членов седьмого порядка // Измерительная техника. - 2005, 9, 11-13.
При разложении в ряд по степеням φ с учетом пятой степени
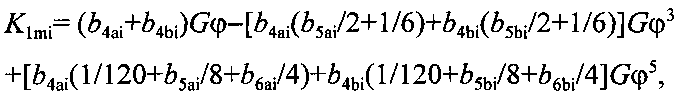
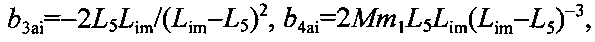
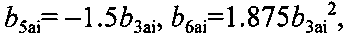
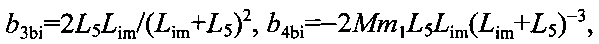
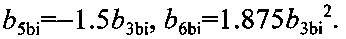
Гравитационная постоянная выражается соотношением:
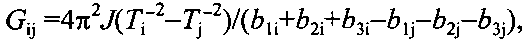 где
где
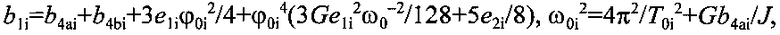
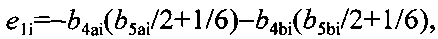
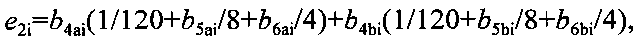
φ0i - амплитуда колебаний, член b2i учитывает вклад всех участков коромысла, каждое плечо которого разделено на n равных отрезков массой m2/2n, расположенных на расстояниях L6(k-0.5)/n от оси вращения, к изменяется в пределах от 1 до n, член b3i учитывает вклад всех участков коромысла, каждое плечо которого разделено на n равных отрезков массой (m3-m4)/2n, расположенных на расстояниях L6+L7(k-0.5)/n.
В итоге проведенных исследований получены следующие основные технические результаты:
- учтено влияние кареток на периоды колебаний крутильных весов при наличии притягивающих тел,
- при заявленных в прототипе позициях притягивающих тел определены моменты притяжения коромысла и его грузов притягивающими цилиндрическими телами на всех четырех позициях при различных углах φ,
- осуществлено преобразование реальных систем в модельные,
- после обнаружения зависимости Gij от комбинации позиций и устранения ее в модельной системе путем уменьшения расстояния до первой позиции на 192 мкм проведены дополнительные вычисления моментов притяжения в реальной системе при уменьшении расстояний до притягивающих цилиндрических тел на 190 мкм,
- моменты притяжения в завершающем варианте позиций получены методом линейной экстраполяции при уменьшения расстояния до первой позиции на 217 мкм,
- на базе модельной системы во всех комбинациях позиций притягивающих тел определены новые значения Gij, принципиально отличающиеся от заявленного в прототипе результата,
- показана невозможность проведения операций по оригинальной методике авторов прототипа из-за большого вклада перемещающихся кареток в момент притяжения, оценить который не представляется возможным, огромной погрешности в определении положения притягивающих тел в ближней к весам позиции, низком уровне вычислительной техники тех уже давних времен, чрезвычайно затрудняющих даже приближенные вычисления моментов притяжения, игнорировании нелинейности колебательной системы,
- на базе модельной системы, учитывающей влияние нелинейных членов высокого порядка, осуществлен анализ факторов, который привел к получению завышенных значений Gij,
- после получения уточненного положения притягивающих тел с погрешностью не более 1 мкм получено достоверное значение G=(6.6729±0.0008)-10-11 Нм2/кг2, представляющее интерес в том числе и для международной организации CODATA,
- для практической реализации способа на базе имеющейся у нас программы разработан ее усложненный вариант, позволяющий проводить все необходимые дополнительные операции в прототипе,
- показано, что предложенный способ при наличии протоколов измерений может принести новые ценные технические результаты даже в случае полного физического уничтожения установки.
Полученные технические результаты являются следствием непосредственных действий материальных средств над материальными объектами. Использовались все имевшиеся технические средства: весы, микрометры, частотомеры и другие вспомогательные устройства. Ценность и достоверность результатов измерений целесообразно проверять рядом последовательных операций с получением значения гравитационной постоянной. Такой возможности в то время не было. Поэтому реальную ценность случайно сохранившихся данных удается оценить впервые только сейчас с привлечением мощного дополнительного средства - компьютера, а также уникальной методики по преобразованию сложной системы в упрощенную и специальной программы. Получение в конечном итоге разумного значения гравитационной постоянной свидетельствует как об удовлетворительном состоянии сохранившихся данных, так и ценности предложенного способа. При проведении операций в модельной системе данные уточняются, очевидные промахи ликвидируются. Так, например, в [3] ошибочно представлено расстояние от оси вращения весов до центра масс грузов коромысла L5. По длине плеча L6 и длине груза коромысла удалось уточнить эту величину. Она занижена на 4.2 мкм, что должно привести к деформации коромысла. Моменты притяжения определены после устранения замеченной погрешности. А вот учесть погрешность в определении расстояний от оси вращения до центров притягивающих тел удалось только после операций в модельной системе. Пришлось уменьшить данные расстояния на 217 мкм, базируясь на независимости гравитационной постоянной от комбинации позиций притягивающих тел. Расстояния были измерены без разработки специальной методики и представлены с точностью до 100 мкм. Реальная погрешность в два раза превысила заявленную точность. Оценить погрешность и установить более точные значения расстояний до притягивающих тел удалось только теперь.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения гравитационной постоянной | 2016 |
|
RU2644437C1 |
| Способ определения гравитационной постоянной с добавлением периода колебаний при отсутствии кареток | 2019 |
|
RU2714518C2 |
| Способ определения гравитационной постоянной с учётом вклада кареток в моменты притяжения | 2018 |
|
RU2691622C2 |
| СПОСОБ ИЗМЕРЕНИЯ ГРАВИТАЦИОННОЙ ПОСТОЯННОЙ | 2015 |
|
RU2633804C2 |
| СПОСОБ ИЗМЕРЕНИЯ ГРАВИТАЦИОННОЙ ПОСТОЯННОЙ | 2015 |
|
RU2633000C2 |
| СПОСОБ ИЗМЕРЕНИЯ ГРАВИТАЦИОННОЙ ПОСТОЯННОЙ | 2008 |
|
RU2364896C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГИСТЕРЕЗИСНЫХ ПОТЕРЬ МАЯТНИКОВЫМ ТРИБОМЕТРОМ | 2014 |
|
RU2559120C1 |
| Способ определения гравитационной постоянной | 1974 |
|
SU492837A1 |
| Вакуумированные крутильные весы | 1976 |
|
SU569989A1 |
| Способ определения гистерезисных потерь крутильной системой | 2015 |
|
RU2614647C1 |
Изобретение относится к способам определения гравитационной постоянной. При реализации предложенного способа реальную систему взаимодействующих тел, имеющих сложную форму, заменяют модельной системой тел, закрепленных на тонком стержне и имеющих форму шара. Далее определяют значения гравитационной постоянной для всех возможных комбинаций позиций взаимодействующих тел модельной системы. Для этого измеряют период и амплитуду колебаний тел модельной системы и рассчитывают значение гравитационной постоянной по известной формуле. В случае выявления зависимости гравитационной постоянной от комбинации позиций, данную зависимость устраняют путем подбора положения притягивающихся тел в ближней позиции, после чего продолжают измерения в новой модельной системе. Экспериментальные данные считают достоверными, если во всех комбинациях позиций было получено значение, близкое к стандартному. Техническим результатом заявленного изобретения является возможность определения гравитационной постоянной для тел сложной формы. 1 ил.
Способ определения гравитационной постоянной при форме взаимодействующих тел, отличной от шаровой, в котором при всех позициях притягивающих тел измеряют периоды и амплитуды колебаний крутильных весов, а также массы, размеры, положение всех взаимодействующих тел, по которым рассчитывают моменты притяжения рабочего тела весов притягивающими телами и момент его инерции вокруг вертикальной оси, дополнительно измеряют влияние средств перемещения притягивающих тел на период колебаний весов, определяют гравитационную постоянную по системе двух дифференциальных уравнений движения, отличающийся тем, что с целью определения гравитационной постоянной на базе теории нелинейных колебаний преобразуют реальную систему в модельную, в которой с сохранением масс всех тел коромысло, на котором укреплены шаровые грузы, заменено на тонкие стержни, заменяющие центральные плечи с прямоугольным сечением и его цилиндрические концы, а притягивающие тела имеют шаровую форму, рассчитывают моменты притяжения в реальной системе при заданных положениях взаимодействующих тел, определяют положение модельных тел, обеспечивающих аналогичные моменты притяжения при малой амплитуде, сохраняют достигнутое равенство во всем диапазоне колебаний введением массивов корректирующих коэффициентов, уточняют периоды колебаний в каждой позиции с учетом влияния перемещающихся кареток, после чего определяют гравитационную постоянную во всех возможных комбинациях позиций притягивающих тел с использованием модельной системы, при обнаружении зависимости гравитационной постоянной от комбинаций позиций устраняют ее подбором положения притягивающих тел в ближней позиции с сохранением расстояний между всеми позициями, после устранения такой зависимости проводят новые вычисления моментов притяжения в оригинальной системе во всех позициях с учетом скорректированного положения в первой позиции, после чего возвращаются в уже новую модельную систему, если в ней сохранится зависимость гравитационной постоянной от комбинации позиций, получают на базе уже проведенных вычислений новые моменты притяжения в реальной системе методом линейной интерполяции или экстраполяции, после этого в очередной раз возвращаются в следующую модельную систему, при этом считают окончательный результат и экспериментальные данные достоверными, если во всех комбинациях позиций получается близкое к стандартному значение гравитационной постоянной без коррекции в модельной системе положения притягивающих тел, на завершающей стадии уравнивают все возможные комбинации гравитационной постоянной коррекцией периодов колебаний.
| В.М | |||
| Шахпаронов "Определение численного значения гравитационной постоянной при сложной форме взаимодействующих тел "// Вестник МГУ | |||
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| Физика | |||
| Астрономия | |||
| Способ защиты переносных электрических установок от опасностей, связанных с заземлением одной из фаз | 1924 |
|
SU2014A1 |
| В.М | |||
| Шахпаронов, В.П | |||
| Измайлова, О.В | |||
| Карагиоз "Измерения гравитационной постоянной при наличии неравновестных потоков разреженного газа"// Материалы доклада по прецизионной физике и | |||
Авторы
Даты
2016-04-20—Публикация
2015-03-27—Подача