Изобретение относится к области метрологии, а именно к способу определения гравитационной постоянной при форме взаимодействующих тел, отличной от шаровой.
Известен способ измерения гравитационной постоянной при шаровой форме взаимодействующих тел [1] (Патент РФ №2364896 на изобретение. Способ измерения гравитационной постоянной // Приоритет изобретения 31.07.08). Способ заключается в том, что при всех позициях притягивающих тел измеряют периоды и амплитуды колебаний крутильных весов, рассчитывают моменты притяжения рабочего тела, определяют гравитационную постоянную либо по системе двух дифференциальных уравнений движения, либо по аналитическим формулам, полученным с учетом теории нелинейных колебаний. Способ применим только при шаровых формах взаимодействующих тел. Более сложные варианты не рассматриваются.
Близким по своей сущности к заявляемому способу является способ определения гравитационной постоянной [2] (Сагитов М.У., Милюков В.К., Монахов Е.А., Назаренко B.C., Таджитдинов К.Г. Новое определение кавендишевой гравитационной постоянной // ДАН СССР, 1979, т. 245, №3, с. 567-569), в котором измеряются периоды и амплитуды колебаний крутильных весов при размещении цилиндрических притягивающих тел на четырех позициях, расположенных на линии равновесия весов на различных расстояниях от их оси вращения. Моменты притяжения цилиндрическими притягивающими телами коромысла прямоугольного сечения, его цилиндрических концов и цилиндрических грузов находят шестикратным интегрированием. Все требуемые технические характеристики даны в [3] (Е.А. Монахов. Дифференциальный метод измерения гравитационной постоянной, уточнение масс и средней плотности Земли, Луны и планет. Кандидатская диссертация, ГАИШ, 1979). Приведены измеренные значения периодов и амплитуд колебаний, а также полученные значения гравитационной постоянной. Утверждается, что моменты притяжения в ближней и дальней позициях определены с точностью 10-5, которая обеспечила погрешность при определении G на уровне 10-4. Предполагалось, что моменты остаются постоянными при разных углах отклонения весов. Нелинейность момента притяжения не учитывалась.
Недостаток такого способа заключается в том, что при форме взаимодействующих тел, отличной от шаровой, отсутствие аналитических формул моментов притяжения существенно осложняет определение гравитационной постоянной. Классический вариант динамического метода, заключающийся в измерении периодов и амплитуд колебаний, трансформирован в прототипе в прецизионные измерения углового отклонения ϕ, его первой и второй производных. Эти дополнительные измерения привели к усложнению систем индикации. Дифференциальные уравнения колебаний преобразованы в системы алгебраических уравнений, в которые вносились постоянные значения гравитационной жесткости при ближнем и дальнем положениях притягивающих тел. Периоды и амплитуды колебаний были тщательно измерены, но при определении гравитационной постоянной так и не использовались. Это привело к неоправданному усложнению методики, исключению значительной части имеющихся в эксперименте данных, получению недостоверного результата. Заявленное значение гравитационной постоянной не согласуется с проведенными результатами измерений.
Более близким по своей сущности к заявляемому способу является способ определения гравитационной постоянной [4] (Патент РФ №2581765 на изобретение. Способ определения гравитационной постоянной // Приоритет изобретения 27.03.2015). В нем непригодная для расчетов оригинальная система [2] заменена на модельную, что привело, наконец, к получению численного значения гравитационной постоянной. В процессе решения удалось установить истинное значение расстояний между взаимодействующими массами с точностью 1 мкм, которое экспериментально было получено с погрешностью 217 мкм. Строго учтено влияние перемещающихся кареток, которые затруднили проведение расчетов. Лишь после этого на базе адаптированной к данному эксперименту программы для расчета гравитационной постоянной при шаровой форме взаимодействующих тел были проведены окончательные расчеты. Они подтвердили ценность и достоверность данных, полученных в работе [2].
Недостаток предложенного метода состоит только в потребности создания упрощенной модельной системы. Она затрудняет понимание всего процесса в целом. Кроме того, даже появляются альтернативные предложения по ее совершенствованию. Отметим, что способ обеспечит достижение поставленной цели даже в самом неудачном варианте модельной системы. Возникает вопрос, можно ли получить требуемый результат более простым и понятным способом, не допускающим какого-либо дальнейшего творчества.
Задачей изобретения является уточнение значения гравитационной постоянной в уже проведенных работах, где использовались тела усложненной формы, без дополнительных экспериментов.
Поставленная задача достигается тем, что после проведения чрезвычайно трудоемких расчетов моментов притяжения на всех позициях притягивающих тел при различных углах отклонения в диапазоне от 0.1 до 18 мрад создается аналитическая формула для моментов притяжения. Она содержит два параметра, позволяющих учесть члены при первой и третьей степенях угла отклонения. Член при пятой степени в работе [2] не требуется, но в случае необходимости можно учесть члены пятого и даже седьмого порядка.
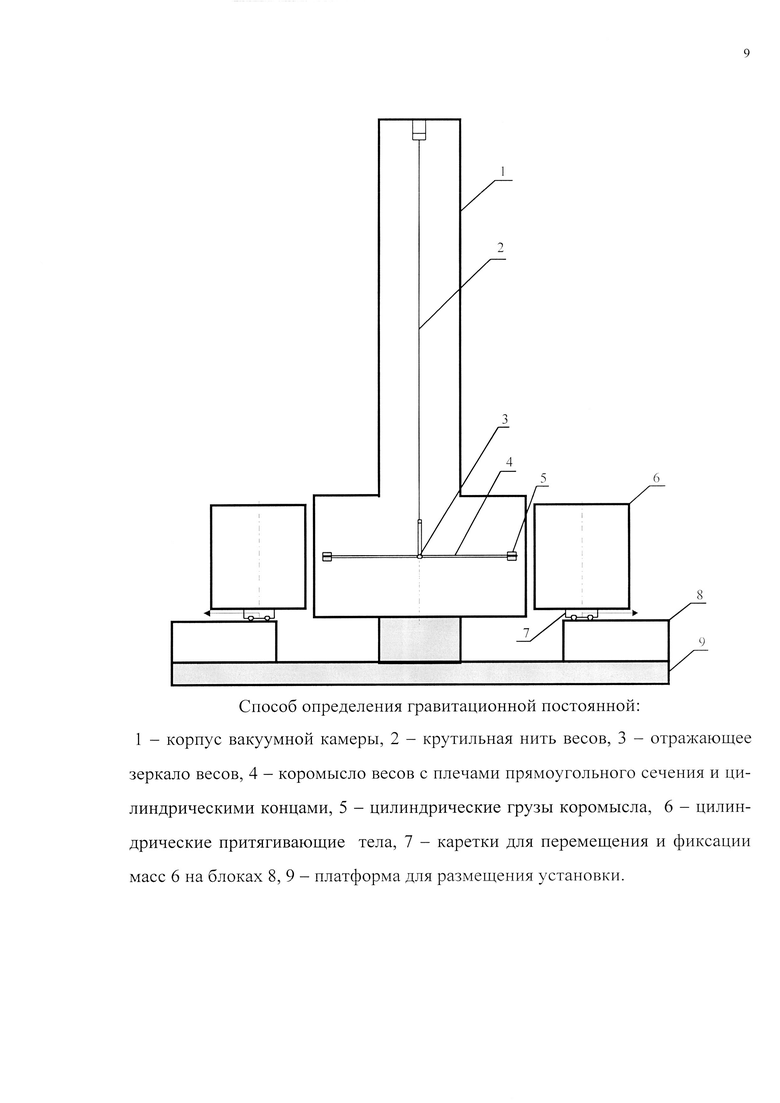
Способ поясняется чертежом (фиг.), где 1 - корпус вакуумной камеры, 2 - крутильная нить весов, 3 - отражающее зеркало весов, 4 - коромысло весов с плечами прямоугольного сечения длиной L6 и цилиндрическими концами длиной L7, 5 - цилиндрические грузы коромысла массой m1, 6 - цилиндрические притягивающие тела массой М, 7 - каретки для перемещения и фиксации в четырех положениях на блоках 8 масс 6, 9 - платформа для размещения установки.
Внутри вакуумной камеры 1 размещают крутильные весы, в которых на крутильной нити 2 крепится рабочее тело весов, включающее коромысло 4 с цилиндрическими грузами 5 на концах и отражающее зеркало 3. Зеркало 3 обеспечивает измерение амплитуд и периодов колебаний весов. Цилиндрические притягивающие тела 6 перемещаются с помощью кареток 7 вдоль линии равновесия весов и фиксируются на блоке 8 в четырех позициях. На платформе 9 размещается вся установка.
При отклонении весов на угол ϕ на рабочее тело воздействует упругая сила закрученной нити 2 и момент притяжения цилиндрических притягивающих тел 6, который в первом приближении пропорционален ϕ. Такой момент уменьшает период колебаний весов. По величине момента притяжения можно определить значение гравитационной постоянной. Такие операции удается провести при шаровой форме всех взаимодействующих тел. При усложнении их формы задача становится чрезвычайно трудной. В этом случае по значениям Li, M, m1, m2 шестикратным интегрированием определяют моменты притяжения. На эту операцию затрачивается солидное время даже при использовании самых современных вычислительных средств.
В [2] момент инерции рабочего тела весов J=21483.64 г⋅см2. С учетом вытесненного воздуха масса цилиндрических притягивающих тел диаметром 18.0012 см и высотой 19.9531 см M=39756.452 г. Масса цилиндрических грузов коромысла длиной 1.63905 см и диаметром 1.6415 см с осевым отверстием диаметром 0.3015 см m1=29.9198 г. Масса всего коромысла шириной 0.3906 см, высотой 0.4071 и длиной плеч L6=16.92935 см mk=24.93909 г. С учетом объема прямоугольной части коромысла и его концов диаметром 0.3 см найдем, что масса прямоугольной части m2=23.9091 г, масса цилиндрического тела длиной 2(L6+L7)m3=11.65826 г, масса цилиндрического тела длиной 2L6 m4=10.62826 г. Центр масс грузов находился на расстоянии L5=17.748875 см от оси вращения весов. Центры масс притягивающих цилиндров располагались на четырех расстояниях L1=28.99845, L2=30.99860, L3=33.99805, L4=38.99795 см.
Использованные при окончательных расчетах моменты притяжения всего рабочего тела весов Ki на всех четырех позициях при L1=28.97675, L2=30.97690, L3=33.97635, L4=38.97625 см приведены в табл. 1.
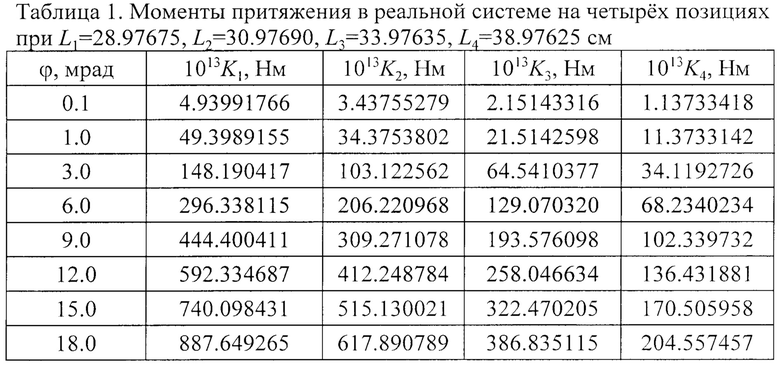
При определении гравитационной постоянной применяются две независимые методики. Одна из них базируется на численном решении уравнений движения, другая - на теории нелинейных колебаний.
В методике 1 определяют величину половины периода ангармонических колебаний весов в позициях i и j интегрированием двух дифференциальных уравнений движения:
d2ϕi/dt2+ω02ϕi+Ki/J=0,
d2ϕj/dt2+ω02ϕj+Kj/J=0,
где J - момент инерции рабочего тела, ω0=2π/T0 - частота колебаний при отсутствии притягивающих тел, ϕi и ϕj - углы отклонения весов от положения равновесия. Численные интегрирования проводят при двух значениях G=G0(1±k), где G0 - стандартное значение G. При положительном и отрицательном значениях k в позициях i и j вычисляют разность обратных квадратов половин периодов колебаний τ1 и τ2. С учетом экспериментальной разности обратных квадратов периодов колебаний τехр гравитационную постоянную G определяют по формуле:
G=G0(1-k)+2G0k(4τexp-τ2)/(τ1-τ2).
Методика 2 предусматривает операции по аналитическим формулам. С учетом членов третьего порядка момент сил притяжения в позиции i между рабочим телом весов и двумя цилиндрическими притягивающими телами массой M
Ki=aiϕi-biϕi3.
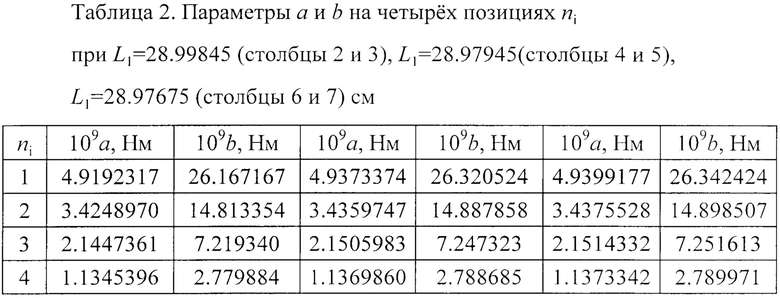
Члены более высокого порядка в данном случае не потребовались. В случае необходимости следует добавить члены пятого и даже седьмого порядка, которые теория нелинейных колебаний позволяет учесть. Параметры a и b подобраны минимизацией суммы квадратов разностей Ki по данным табл. 1 и по приведенной формуле. Параметры a и b в четырех позициях ni при различных L1 даны в табл. 2.
Гравитационная постоянная
Gij=4π2JG0(Ti-2-Tj-2)/(qi-qj),
где qi=ai-0.75biϕ0i2, qj=aj-0.75bjϕ0j2, ϕ0i, ϕ0j - амплитуды колебаний.
Формула для расчета значений Gij сильно упрощена, поскольку основные расчеты уже были проведены при определении коэффициентов ai и bi, а также aj и bj.
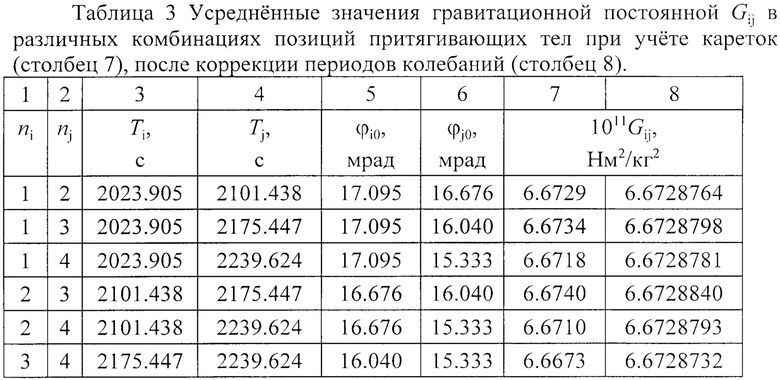
В табл. 3 приведены усредненные по шести сериям измерений периоды и амплитуды колебаний с учетом перемещающихся кареток, а также значений Gij при различных комбинациях позиций ni и nj. Для уравнивания всех значений Gij в столбце 8 следует уменьшить среднее значение периодов колебаний в третьей позиции на 12.7 мс, а в четвертой позиции - увеличить на 42 мс. В итоге получим
G=(6.6729±0.0008)⋅10-11 Н⋅м2/кг2.
В итоге проведенных исследований получены следующие основные технические результаты:
- осуществлено преобразование численных значений моментов притяжения при различных значениях расстояния L1, полученных шестикратным интегрированием с погрешностью менее 100 ppm, в аналитические формулы, обеспечивающие численные расчеты,
- во всех комбинациях четырех позиций притягивающих тел с учетом влияние перемещающихся кареток на периоды колебаний весов в процессе измерений гравитационной постоянной определены новые значения Gij, принципиально отличающиеся от заявленного в [2] результата, но строго совпадающие с данными патента [4],
- в итоге после выявления уточненного значения L1 с погрешностью не более 1 мкм вновь получено достоверное значение гравитационной постоянной G=(6.6729±0.0008)⋅10-11 Н⋅м2/кг2,
- наличие двух независимых методик определения гравитационной постоянной свидетельствует об отсутствии ошибок при их реализации, но не обеспечивает доказательство достоверности расчетов моментов притяжения,
- полученное значение гравитационной постоянной косвенно свидетельствует о достоверности расчетов моментов притяжения, для практической реализации способа на базе имеющейся у нас программы разработан ее модифицированный вариант, позволяющий проводить все необходимые операции в прототипе,
- показано, что предложенный способ при наличии протоколов измерений также может принести новые ценные технические результаты даже в случае полного физического уничтожения установки на базе уже имеющихся значений периодов, амплитуд колебаний и других технических характеристик без проведения каких-либо дополнительных измерений.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ГРАВИТАЦИОННОЙ ПОСТОЯННОЙ | 2015 |
|
RU2581765C1 |
| Способ определения гравитационной постоянной с учётом вклада кареток в моменты притяжения | 2018 |
|
RU2691622C2 |
| Способ определения гравитационной постоянной с добавлением периода колебаний при отсутствии кареток | 2019 |
|
RU2714518C2 |
| СПОСОБ ИЗМЕРЕНИЯ ГРАВИТАЦИОННОЙ ПОСТОЯННОЙ | 2015 |
|
RU2633804C2 |
| СПОСОБ ИЗМЕРЕНИЯ ГРАВИТАЦИОННОЙ ПОСТОЯННОЙ | 2015 |
|
RU2633000C2 |
| СПОСОБ ИЗМЕРЕНИЯ ГРАВИТАЦИОННОЙ ПОСТОЯННОЙ | 2008 |
|
RU2364896C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГИСТЕРЕЗИСНЫХ ПОТЕРЬ МАЯТНИКОВЫМ ТРИБОМЕТРОМ | 2014 |
|
RU2559120C1 |
| Способ определения гистерезисных потерь крутильной системой | 2015 |
|
RU2614647C1 |
| Вакуумированные крутильные весы | 1976 |
|
SU569989A1 |
| Способ определения гравитационной постоянной | 1974 |
|
SU492837A1 |
Изобретение относится к способам определения гравитационной постоянной и может быть использовано для определения гравитационной постоянной при форме взаимодействующих тел, отличной от шаровой. Сущность: при всех позициях притягивающих тел измеряют периоды и амплитуды колебаний крутильных весов, а также массы, размеры, положение всех взаимодействующих тел, по которым рассчитывают моменты притяжения рабочего тела весов притягивающими телами и момент его инерции вокруг вертикальной оси. Дополнительно измеряют влияние средств перемещения притягивающих тел на период колебаний весов. Определяют гравитационную постоянную по системе двух дифференциальных уравнений движения. При этом с целью определения гравитационной постоянной на базе численных значений моментов притяжения рабочего тела весов притягивающими телами при различных фиксированных значениях углов отклонения вместо модельных систем, обеспечивающих расчеты по аналитическим формулам с сохранением периодов и амплитуд колебаний весов, находят аналитические выражения для моментов притяжения при заданных положениях взаимодействующих тел, содержащие коэффициенты при первой и третьей степенях угла отклонения весов. Причем в случае необходимости добавляют более высокие степени. После этого определяют численные значения гравитационной постоянной по двум независимым методикам, адаптированным к конкретному эксперименту введением массивов коэффициентов на всех позициях при различных степенях угла отклонения весов. При обнаружении зависимости гравитационной постоянной от комбинаций позиций устраняют ее подбором положения притягивающих тел в ближней позиции с сохранением расстояний между всеми позициями. При этом считают окончательный результат и экспериментальные данные достоверными, если во всех комбинациях позиций получается близкое к стандартному значение гравитационной постоянной. На завершающей стадии уравнивают все возможные комбинации гравитационной постоянной коррекцией периодов колебаний. Технический результат: уточнение значения гравитационной постоянной в уже проведенных работах, где использовались тела усложненной формы, без дополнительных экспериментов. 1 ил.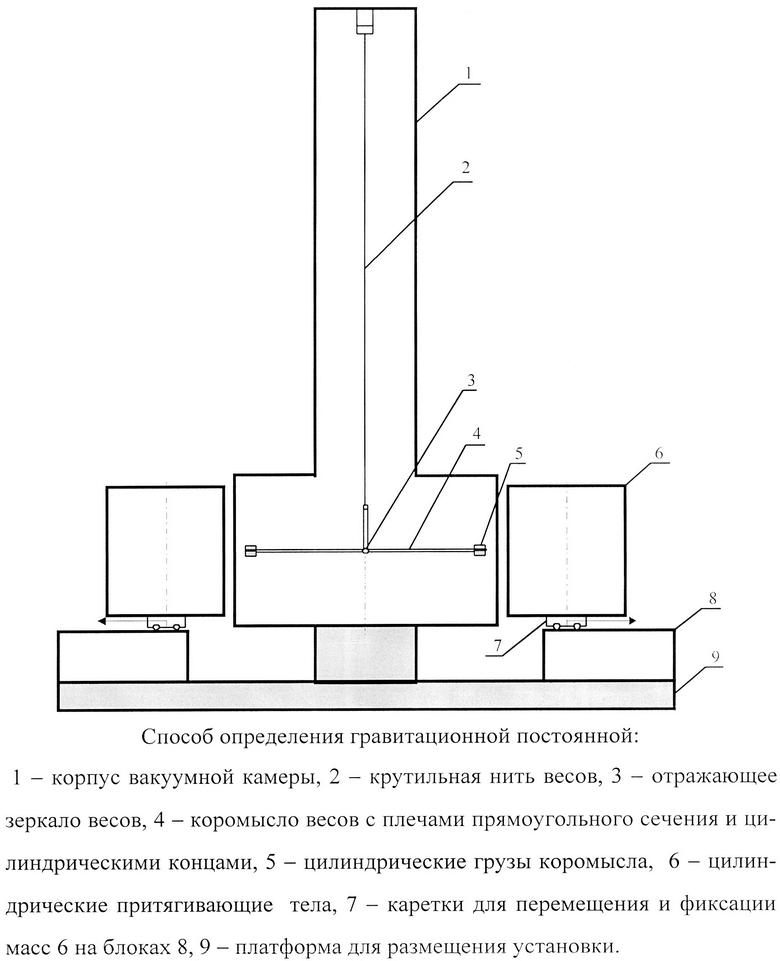
Способ определения гравитационной постоянной при форме взаимодействующих тел, отличной от шаровой, в котором при всех позициях притягивающих тел измеряют периоды и амплитуды колебаний крутильных весов, а также массы, размеры, положение всех взаимодействующих тел, по которым рассчитывают моменты притяжения рабочего тела весов притягивающими телами и момент его инерции вокруг вертикальной оси, дополнительно измеряют влияние средств перемещения притягивающих тел на период колебаний весов, определяют гравитационную постоянную по системе двух дифференциальных уравнений движения, отличающийся тем, что с целью определения гравитационной постоянной на базе численных значений моментов притяжения рабочего тела весов притягивающими телами при различных фиксированных значениях углов отклонения вместо модельных систем, обеспечивающих расчеты по аналитическим формулам с сохранением периодов и амплитуд колебаний весов, находят аналитические выражения для моментов притяжения при заданных положениях взаимодействующих тел, содержащие коэффициенты при первой и третьей степенях угла отклонения весов, в случае необходимости добавляют более высокие степени, после чего определяют численные значения гравитационной постоянной по двум независимым методикам, адаптированным к конкретному эксперименту введением массивов коэффициентов на всех позициях при различных степенях угла отклонения весов, при обнаружении зависимости гравитационной постоянной от комбинаций позиций устраняют ее подбором положения притягивающих тел в ближней позиции с сохранением расстояний между всеми позициями, при этом считают окончательный результат и экспериментальные данные достоверными, если во всех комбинациях позиций получается близкое к стандартному значение гравитационной постоянной, на завершающей стадии уравнивают все возможные комбинации гравитационной постоянной коррекцией периодов колебаний.
| СПОСОБ ОПРЕДЕЛЕНИЯ ГРАВИТАЦИОННОЙ ПОСТОЯННОЙ | 2015 |
|
RU2581765C1 |
| RU 2011112434 A, 10.10.2012 | |||
| RU 2013135686 A, 10.02.2015. | |||
Авторы
Даты
2018-02-12—Публикация
2016-12-13—Подача