Изобретение относится к области метрологии, а именно к способу определения гравитационной постоянной при форме взаимодействующих тел, отличной от шаровой.
Известен способ измерения гравитационной постоянной при шаровой форме взаимодействующих тел [1] (Патент РФ №2364896 на изобретение. Способ измерения гравитационной постоянной // Приоритет изобретения 31.07.08). Способ заключается в том, что при всех позициях притягивающих тел измеряют периоды и амплитуды колебаний крутильных весов, рассчитывают моменты притяжения рабочего тела, определяют гравитационную постоянную либо по системе двух дифференциальных уравнений движения (методика 1), либо по аналитическим формулам, полученным с учетом теории нелинейных колебаний. Способ применим только при шаровых формах взаимодействующих тел.
Более близким по своей сущности к заявляемому способу является способ определения гравитационной постоянной [2] (Патент РФ №2581765 на изобретение. Способ определения гравитационной постоянной // Приоритет изобретения 27.03.2015). В нем непригодная для расчетов оригинальная система заменена на модельную, что привело к получению численного значения гравитационной постоянной. Учтено влияние перемещающихся кареток на периоды колебаний весов.
Недостаток предложенного метода состоит в сложности процесса преобразования реальной в упрощенную модельную систему.
Наиболее близким по своей сущности к заявляемому способу является способ определения гравитационной постоянной [3] (Карагиоз О.В., Измайлов В.П., Шахпаронов В.М. Патент РФ №2644437. Способ определения гравитационной постоянной. // Приоритет изобретения 13.12.2016. В нем после вычисления моментов притяжения на всех четырех позициях при различных углах отклонения весов создана аналитическая формула для моментов притяжения.
Недостаток данного способа заключается в отсутствии пятой позиции кареток, которая возможно играет роль в уменьшении погрешности вычислений.
Близким по своей сущности к заявляемому способу является также способ определения гравитационной постоянной [4] (Карагиоз О.В., Измайлов В.П., Шахпаронов В.М. Патент РФ №2691622. Способ определения гравитационной постоянной с учетом вклада кареток в моменты притяжения. // Приоритет изобретения 01.08.2018). В нем впервые использована пятая позиция кареток. Вместо внесения поправок в периоды колебаний введены поправки непосредственно в моменты притяжения.
Задачей изобретения является определение значения гравитационной постоянной по способу [3] с добавлением пятой позиции кареток и сравнение результатов в [3], [4] и данной заявке.
Поставленная задача достигается тем, что к измеренным значениям периодов колебаний весов при положении кареток в четырех позициях добавляется пятая позиция, которая отсутствует в протоколах измерений.
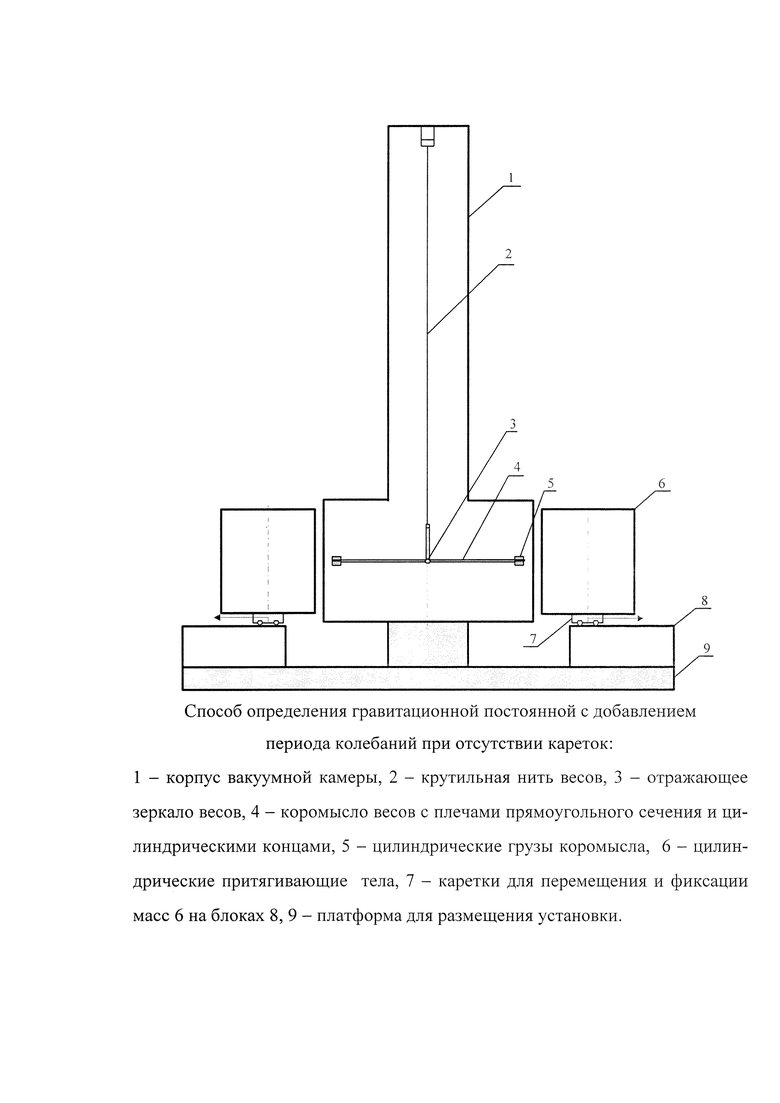
Способ поясняется чертежом (фиг.), где 1 - корпус вакуумной камеры, 2 - крутильная нить весов, 3 - отражающее зеркало весов, 4 - коромысло весов с плечами прямоугольного сечения длиной L6 и цилиндрическими концами длиной L7, 5 - цилиндрические грузы коромысла массой m1, 6 - цилиндрические притягивающие тела массой М, 7 - каретки для перемещения и фиксации в четырех положениях на блоках 8 масс 6, 9 - платформа для размещения установки.
Внутри вакуумной камеры 1 размещают крутильные весы, в которых на крутильной нити 2 крепится рабочее тело весов, включающее коромысло 4 с цилиндрическими грузами 5 на концах и отражающее зеркало 3. Зеркало 3 обеспечивает измерение амплитуд и периодов колебаний весов. Цилиндрические притягивающие тела 6 перемещаются с помощью кареток 7 вдоль линии равновесия весов и фиксируются на блоке 8 в четырех позициях. На платформе 8 размещается вся установка.
При отклонении весов на угол ϕ на рабочее тело воздействует упругая сила закрученной нити 2 и момент притяжения цилиндрических притягивающих тел 6, который в первом приближении пропорционален ϕ. Такой момент уменьшает период колебаний весов. По величине момента притяжения можно определить значение гравитационной постоянной при шаровой форме всех взаимодействующих тел. При отличной от шаровой форме тел вычисления становятся трудоемкими. В этом случае по значениям Li, М, m1, m2 шестикратным интегрированием определяют моменты притяжения.
В [2] момент инерции рабочего тела весов J=21483.64 г⋅см2. С учетом вытесненного воздуха масса цилиндрических притягивающих тел диаметром 18.0012 см и высотой 19.9531 см М=39756.452 г. Масса цилиндрических грузов коромысла длиной 1.63905 см и диаметром 1.6415 см с осевым отверстием диаметром 0.3015 см m1=29.9198 г. Масса всего коромысла шириной 0.3906 см, высотой 0.4071 и длиной плеч L6=16.92935 см mk=24.93909 г. С учетом объема прямоугольной части коромысла и его концов диаметром 0.3 см найдем, что масса прямоугольной части m2=23.9091 г, масса цилиндрического тела длиной 2(L6+L7) m3=11.65826 г, масса цилиндрического тела длиной 2L6 m4=10.62826 г. Центр масс грузов находился на расстоянии L5=17.748875 см от оси вращения весов. Центры масс притягивающих цилиндров располагались на четырех расстояниях L1=28.99845, L2=30.99860, L3=33.99805, L4=38.99795 см.
Использованные при окончательных расчетах моменты притяжения всего рабочего тела весов Ki на всех четырех позициях при L1=28.97675, L2=30.97690, L3=33.97635, L4=38.97625 см приведены в табл. 1.

В [4] показано, что T0=2321.0. Найдем разность периодов колебаний между T0 и T1, Т2, Т3, T4.
2321.0-2316.9967=4.0032
2321.0-2317.0480=3.9520
2321.0-2317.5864=3.4136
2321.0-2318.9207=2.0793
Получим следующий ряд значений: 4.0032, 3.9520, 3.4136, 2.0793 с. Умножим эти разности на отношение кубов периодов колебаний при наличии притягивающих масс и их отсутствии. Получим ряд величин, на которые следует увеличить периоды колебаний.
4.0032(2022.6253/2321.0)3=2.6493
3.9520(2100.1351/2321.0)3=2.9277
3.4136(2174.3469/2321.0)3=2.8066
2.0793(2239.6236/2321.0)3=1.8682
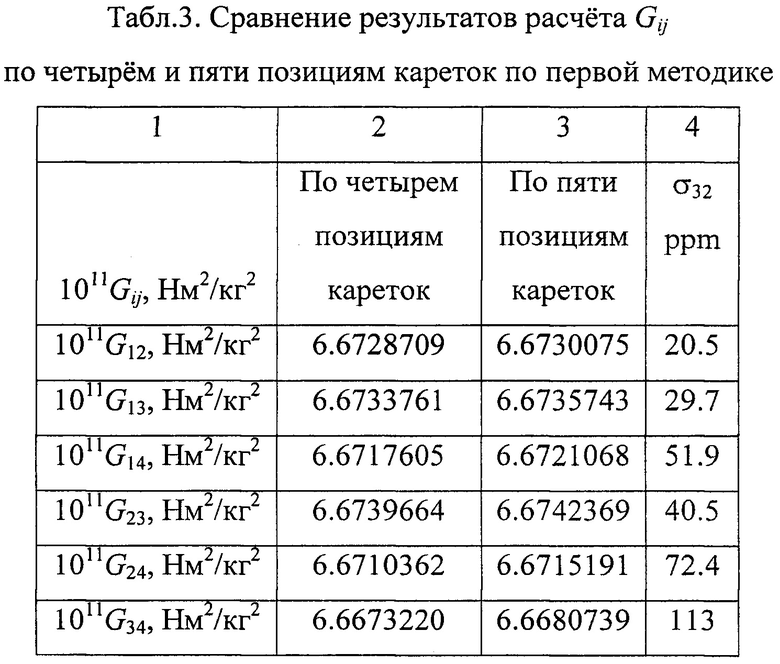
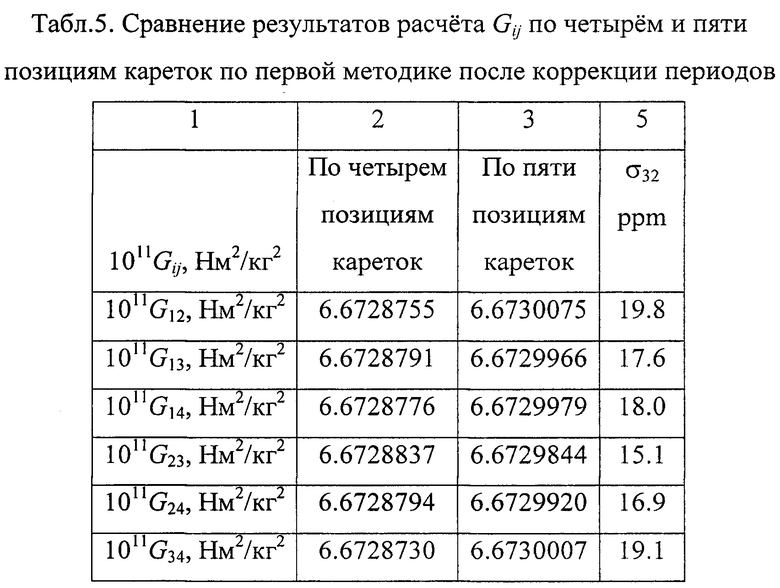
При положении притягивающих тел в первой позиции период должен быть увеличен на 2.6493 с. В остальных позициях периоды колебаний будут увеличены на 2.9277, 2.8066 и 1.8682 с. После ведения поправок вычисление гравитационной постоянной по методике 2 дает результаты, приведенные в 3 столбце табл. 2. Аналогичные вычисления по методике 1 приведены в табл. 3. Полученные значения Gij не существенно отличаются от данных, приведенных в столбцах 2 этих таблиц. Следовательно, погрешность при расчетах Gij мало зависит от наличия дополнительной пятой позиции кареток. Результаты все же изменились, но они стали достовернее. После введения аналогичных поправок в периоды колебаний в третьей и четвертой позициях получим результаты, представленные в табл. 4 и 5.
Анализ показал, что наличие трудно контролируемых неравновесных потоков разреженного газа было основным дестабилизирующим фактором. Для их полного подавления недостаточен даже вакуум порядка 10-6 Па. В данном эксперименте вакуум был хуже примерно на три порядка. Перемещение притягивающих тел вблизи вакуумной камеры, в которой размещены крутильные весы, может не только изменить конвективные потоки, но и изменить неравновесные внутри самой камеры. Переход притягивающих тел на очередную позицию изменял потоки вокруг камеры. Даже если вакуумная камера и притягивающие тела расположены в термостате, такого эффекта не избежать. При проведении данных экспериментов подобных мер предосторожности предпринято не было. Вследствие этого при минимальном и максимальном удалении притягивающих тел ситуация могла существенно различаться. При этом изменялась жесткость, вносимая неравновесными потоками в крутильную систему. Для компенсации дополнительной жесткости пришлось уменьшить расстояния до притягивающих тел на 217 мкм, что увеличило моменты притяжения на четырех позициях в 1.00418, 1.00368, 1.00311, 1.00245 раз. При дополнительной коррекции период колебаний в позиции 3 снижен на 14.6 мс, а в позиции 4 увеличен на 33.6 мс. В прототипе аналогичные величины составляли значения 12.7 и 42.0 мс.


В итоге проведенных исследований получены следующие основные технические результаты:
- показано, что использование дополнительной пятой позиции кареток все же смещает значение гравитационной постоянной после коррекции периодов колебаний примерно на 20 ppm, при этом повышается достоверность вычислений, до коррекции при учете позиции 4 смещение достигает 100 ppm,
- наличие кареток усложняет расчеты, но принципиальных трудностей не создает,
- во всех комбинациях четырех позиций притягивающих тел определены значения Gij, близкие к данным прототипа, получено достоверное значение гравитационной постоянной G=(6.6730±0.0008)⋅10-11 Нм2/кг2,
- совпадение результатов расчетов Gij по независимым вариантам расчета свидетельствует об отсутствии ошибок при их реализации, а также низкой погрешности при расчетах моментов притяжения тела весов цилиндрическими телами на всех четырех позициях,
- различие результатов в [4] и данной заявке, использующих дополнительную пятую позицию кареток, свидетельствует о погрешности измерений периодов колебаний при наличии кареток на четырех позициях,
- выявлен основной дестабилизирующий фактор, обусловленный влиянием неравновесных потоков на периоды колебаний весов вследствие недостаточно высокого вакуума,
- наличие такого фактора приводит к необходимости его компенсации уменьшением расстояний до притягивающих тел на 217 мкм,
- коррекции периодов колебаний в третьей и четвертой позициях на -14.6 и 33.6 мс компенсируют обусловленными неравновесными потоками погрешности при измерении периодов колебаний, когда каретки фиксировались на четырех позициях, в прототипе аналогичные величины составляли -12.7 и 42.0 мс.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения гравитационной постоянной с учётом вклада кареток в моменты притяжения | 2018 |
|
RU2691622C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГРАВИТАЦИОННОЙ ПОСТОЯННОЙ | 2015 |
|
RU2581765C1 |
| Способ определения гравитационной постоянной | 2016 |
|
RU2644437C1 |
| СПОСОБ ИЗМЕРЕНИЯ ГРАВИТАЦИОННОЙ ПОСТОЯННОЙ | 2015 |
|
RU2633000C2 |
| СПОСОБ ИЗМЕРЕНИЯ ГРАВИТАЦИОННОЙ ПОСТОЯННОЙ | 2015 |
|
RU2633804C2 |
| СПОСОБ ИЗМЕРЕНИЯ ГРАВИТАЦИОННОЙ ПОСТОЯННОЙ | 2008 |
|
RU2364896C1 |
| Способ определения гистерезисных потерь крутильной системой | 2015 |
|
RU2614647C1 |
| Способ определения гистерезисных потерь крутильной системой при повышенных температурах | 2018 |
|
RU2680976C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГИСТЕРЕЗИСНЫХ ПОТЕРЬ МАЯТНИКОВЫМ ТРИБОМЕТРОМ | 2014 |
|
RU2559120C1 |
| Крутильные весы | 1977 |
|
SU693323A1 |
Изобретение относится к области метрологии и может быть использовано при определении гравитационной постоянной. Технический эффект, заключающийся в уменьшении погрешности вычислений гравитационной постоянной, достигается за счёт того, что по периодам колебаний весов при четырёх положениях кареток предварительно добавляют пятую позицию кареток, определяют пятый период колебаний при их отсутствии, затем вносят поправки в периоды колебаний весов с использованием пятой позиции, после чего вычисляют гравитационную постоянную при всех комбинациях притягивающих тел по двум независимым методикам, а на завершающей стадии уравнивают все возможные комбинации гравитационной постоянной коррекцией периодов колебаний. 1 ил., 5 табл.
Способ определения гравитационной постоянной при нешаровой форме взаимодействующих тел, в котором при всех позициях притягивающих тел измеряют периоды и амплитуды колебаний весов, а также массы, размеры, положение всех взаимодействующих тел, рассчитывают моменты притяжения тела весов притягивающими телами и момент его инерции, измеряют влияние средств перемещения притягивающих тел на период колебаний весов, определяют гравитационную постоянную по системе двух дифференциальных уравнений движения, отличающийся тем, что по периодам колебаний весов при четырех положениях кареток предварительно определяют дополнительный пятый период колебаний при их отсутствии, затем вносят поправки в периоды колебаний весов с использованием пятой позиции, после чего вычисляют гравитационную постоянную при всех комбинациях притягивающих тел по двум независимым методикам, на завершающей стадии уравнивают все возможные комбинации гравитационной постоянной коррекцией периодов колебаний.
| Способ определения гравитационной постоянной | 2016 |
|
RU2644437C1 |
| Крутильные весы | 1977 |
|
SU693323A1 |
| Вакуумированные крутильные весы | 1976 |
|
SU569989A1 |
| Способ определения вторых производных гравитационного потенциала | 1977 |
|
SU669306A1 |
| US 9341807 B2, 17.05.2016. | |||
Авторы
Даты
2020-02-18—Публикация
2019-07-01—Подача