Изобретение относится к области повышения энергетической эффективности механической передачи за счет оптимизации ее нагрузочного режима.
В классических курсах «Теория машин и механизмов» и «Детали машин» [1, 2] в целях упрощения определения величины фрикционных потерь в элементах механических передач принято допущение о возможности использования в инженерных расчетах простого выражения:

где ηΣ - суммарное значение КПД механической передачи;
n - количество кинематических пар в механической передаче;
Ri - предельное (максимальное) значение КПД соответствующей (i-й) кинематической пары механической передачи.
Неточность расчета КПД как произведения постоянных коэффициентов очевидна, так как при этом не учитывается влияние на КПД нагрузочных, скоростных и температурных режимов, вида и состояния смазки и других условий эксплуатации механической передачи. Во многих случаях такая методика расчета энергетической эффективности механической передачи становится неприемлемой.
Важнейшим фактором, принципиально изменяющим значение КПД, является нагрузочный режим работы механической передачи, определяемый передаваемым крутящим моментом, который при работе любой машины меняется в широких пределах: от нуля до максимально допустимых значений. Остальные факторы: скоростной и температурный режимы и другие эксплуатационные условия зачастую можно стабилизировать в пределах номинальных значений.
Впервые ревизию упрощенной методики энергетического анализа механической передачи провел Левит Г.А. [3], который представил КПД механической передачи как функцию, зависящую от нагрузочного (мощностного) режима.
Левит Г.А. предложил разделить общие потери в механической передаче на нагрузочные и постоянные:

где NC - суммарные потери мощности;
NH - переменные (нагрузочные) потери мощности (эти потери прямо пропорциональны реализуемой полезной мощности);
NX - постоянные потери мощности, необходимые для совершения холостого хода механической передачи.
Отсюда возникла принципиальная формула КПД механической передачи:

где N - полная мощность на приводном валу.
При выполнении холостого хода КПД механической передачи равен нулю, а близкое к максимальному стабильное значение КПД достигается только при значительной полезной нагрузке. С учетом этой закономерности Левит предложил формулу для расчета текущего значения КПД:

где η - текущее значение КПД механической передачи;
ηΣ - предельное суммарное значение КПД механической передачи, определяемое по традиционной формуле (1).
Однако следует отметить, что гиперболическая зависимость (4) содержит методологическую некорректность, которая заключается в том, что использование отношения мощностей NX/N допустимо только при условии соблюдения равной частоты вращения приводного вала как при холостом ходе, так и при нагрузочном режиме работы механической передачи: ωX=ω=const. В противном случае формула (4) не работает.
Допустим, что приводом механической передачи является электродвигатель с мягкой характеристикой (например, электродвигатель постоянного тока последовательного возбуждения), который имеет механическую характеристику, близкую к режиму постоянной мощности. В этом случае 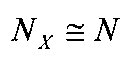 и текущее значение КПД механической передачи, вычисленное по формуле (4), во всем диапазоне нагрузок окажется равным нулю.
и текущее значение КПД механической передачи, вычисленное по формуле (4), во всем диапазоне нагрузок окажется равным нулю.
В связи с этим необходимо внести коррективы в формулу (4), учитывающие условие постоянства скоростного режима, а именно, заменить отношение мощностей отношением моментов:
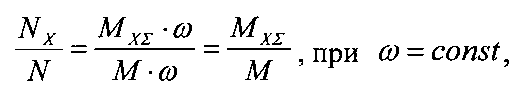
где М - момент на приводном валу;
МХΣ - суммарный момент холостого хода на приводном валу;
ω - заданная частота вращения приводного вала.
Формула (4) в откорректированном виде будет выглядеть следующим образом:
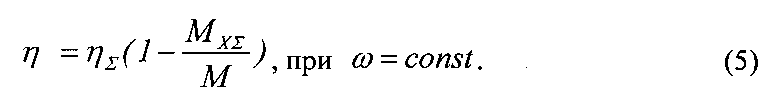
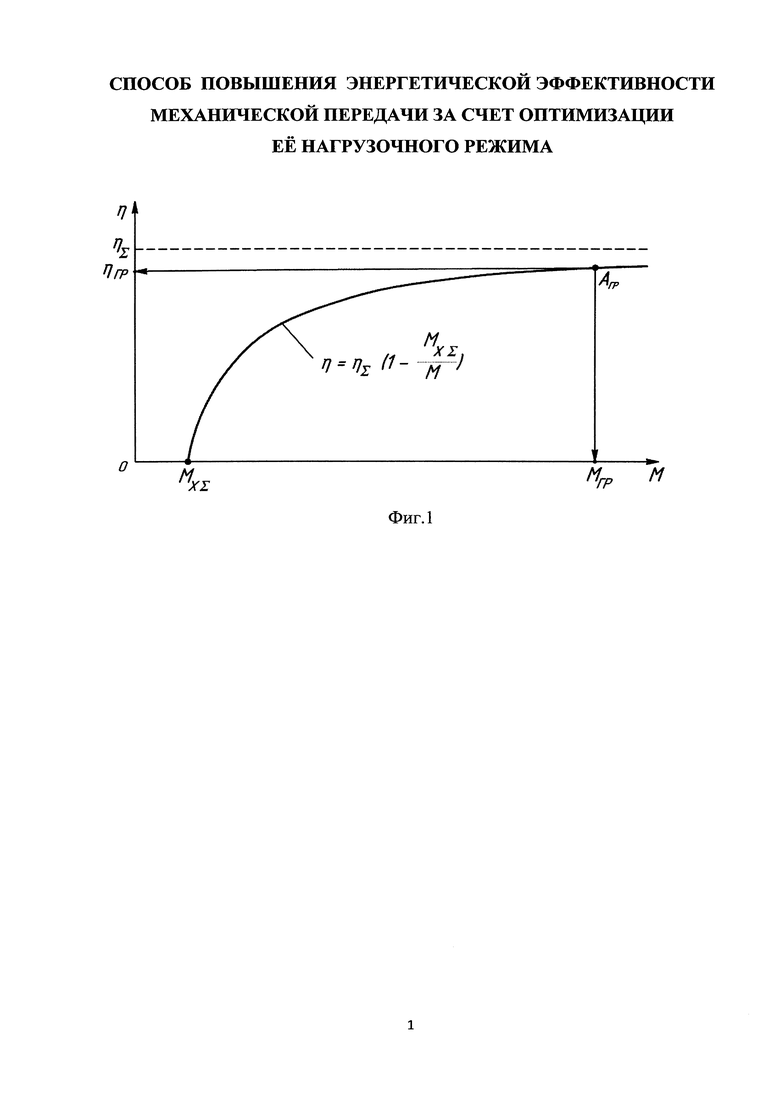
На фиг. 1 зависимость (5) представлена графически.
Поскольку в формуле (5) значения ηΣ и МХΣ - константы, то функция η=f(M) является гиперболой, для которой соблюдаются два очень важных условия:
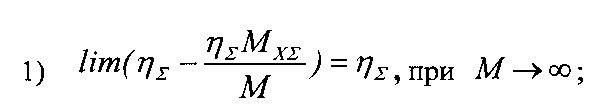
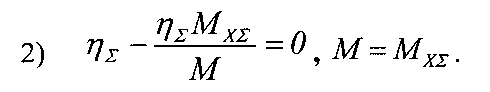
Для данной зависимости характерно то, что по мере увеличения нагрузочного режима вначале текущее значение КПД механической передачи очень существенно изменяется в зависимости от нагрузки и имеет низкие значения, но, достигнув некоего граничного значения (на фиг. 1 точка АГР), приобретает высокие и стабильные значения. Таким образом, для определения энергетически эффективного режима работы механической передачи необходимо установить граничное значение нагрузочного момента МГР на приводном валу, при котором стабилизируется текущее значение КПД механической передачи.
Известен способ, в рамках которого определяется это граничное условие работы механической передачи [4, 5]. Выбираем этот способ в качестве прототипа.
Согласно прототипу граничное условие определяют на основе стабилизации первой производной функциональной зависимости η=f(М). В этом случае граничное значение нагрузочного момента МГР определяют по формуле:
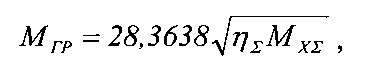
или находят с помощью номограммы. После чего вычисляют граничное значение КПД механической передачи ηГР по формуле:
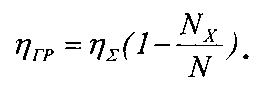
Предлагаемый способ многократно упрощает определение граничного условия работы механической передачи, не снижая качество результата, что способствует широкому внедрению данного способа в инженерную практику. Использование данного способа определения граничного условия допустимо как при проектировании машин, так и в процессе их эксплуатации.
Суть способа заключается в следующем. Принимают условие, что достоверность вычислений предельного значения КПД механической передачи по формуле (3) составляет 90% (что в большинстве случаев соответствует действительности). Таким образом, получают величину граничного значения КПД механической передачи: ηГР=0,9ηΣ. Далее находят граничное значение нагрузочного момента МГР, при котором КПД механической передачи становится стабильным на уровне высоких значений (см. фиг. 1):
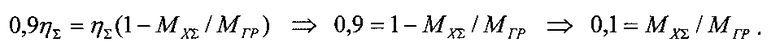
В результате получают соотношение:

Далее экспериментально (путем прокручивания механической передачи за приводной вал) находят значение суммарного момента холостого хода на приводном валу МХΣ и по формуле (6) определяют граничное значение нагрузочного момента МГР на приводном валу. Соответственно, с учетом заданной частоты вращения приводного вала ω определяют минимально необходимую мощность приводного двигателя NДВ, при которой достигается стабилизация величины КПД механической передачи на уровне высоких значений:
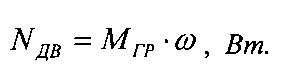
Предлагаемый способ позволяет оперативно решать задачу повышения энергетической эффективности механических передач за счет оптимизации их нагрузочных режимов. Универсальность и простота способа расширяют возможность его применения в инженерной практике как при разработке, так и при эксплуатации машин самого различного назначения.
Литература
1. Артоболевский И.И. Теория машин и механизмов / И.И. Артоболевский. - Москва: Наука, 1988. - 639 с.
2. Решетов Д.Н. Детали машин / Д.Н. Решетов. - Москва: Машиностроение, 1989. - 496 с.
3. Левит Г.А. Расчет потерь на трение в приводах станков / Г.А. Левит // Станки и инструмент. - 1959. - №9. - С. 3-10.
4. Александров И.К. Энергетический анализ механизмов и машин. Теоретическое и экспериментальное обоснование принципов исследования и определения энергетических потерь в механизмах и машинах: монография / И.К. Александров. - Вологда: ВоГТУ, 2012. - 244 с.
5. Александров И.К. Определение потерь в кинематических парах и механических трансмиссиях на основе закона Амонтона-Кулона / И.К. Александров // Вестник машиностроения. - 2010. - №5. - С. 8-15.
Изобретение относится к области испытаний и может быть использовано для повышения энергетической эффективности механической передачи за счет оптимизации ее нагрузочного режима. КПД механической передачи η подчиняется гиперболической зависимости в функции от момента М на приводном валу. По данной зависимости можно определить граничное значение нагрузочного режима, при котором КПД механической передачи становится стабильным на уровне высоких значений. Принимая доверительный интервал вычисления предельного значения КПД механической передачи равным 90%, получаем граничное значение КПД ηГР, равное 0,9 ηΣ. Тогда на основании указанной гиперболической зависимости искомое граничное значение нагрузочного момента МГР на приводном валу механической передачи становится равным: МГР=10 МХΣ. Таким образом, на основе экспериментального определения суммарного момента холостого хода MXΣ на приводном валу механической передачи устанавливают величину минимально необходимого нагрузочного режима, равного МГР, при котором обеспечивается энергетическая эффективность работы механической передачи. После чего вычисляют также минимально необходимую мощность приводного двигателя NДB:NДВ=МГР·ω, где ω - заданная частота вращения приводного вала механической передачи. Технический результат заключается в упрощении процесса измерений, расширении функциональных возможностей. 1 ил.
Способ повышения энергетической эффективности механической передачи за счет оптимизации ее нагрузочного режима путем определения граничного нагрузочного момента на приводном валу, при котором стабилизируется текущее значение КПД механической передачи, отличающийся тем, что доверительный интервал вычисления граничного значения КПД механической передачи 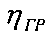 принимают равным 90%, на основании чего получают значение
принимают равным 90%, на основании чего получают значение 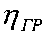 равным 0,9 от предельного суммарного значения КПД механической передачи
равным 0,9 от предельного суммарного значения КПД механической передачи 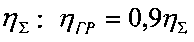 , при этом
, при этом 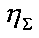 рассчитывают по формуле:
рассчитывают по формуле: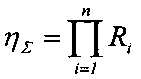 , где n - количество кинематических пар в механической передаче, Ri - предельное (максимальное) значение КПД соответствующей (i-й) кинематической пары механической передачи; затем экспериментально, путем прокручивания механической передачи за приводной вал, определяют значение суммарного момента холостого хода на приводном валу
, где n - количество кинематических пар в механической передаче, Ri - предельное (максимальное) значение КПД соответствующей (i-й) кинематической пары механической передачи; затем экспериментально, путем прокручивания механической передачи за приводной вал, определяют значение суммарного момента холостого хода на приводном валу 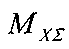 и принимают граничное значение нагрузочного момента
и принимают граничное значение нагрузочного момента 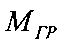 на приводном валу механической передачи равным десяти значениям
на приводном валу механической передачи равным десяти значениям 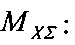
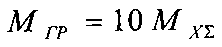 ; путем умножения
; путем умножения 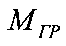 на заданную частоту вращения приводного вала ω механической передачи вычисляют минимально необходимую мощность приводного двигателя
на заданную частоту вращения приводного вала ω механической передачи вычисляют минимально необходимую мощность приводного двигателя 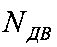 , при которой достигается стабилизация величины КПД механической передачи на уровне высоких значений:
, при которой достигается стабилизация величины КПД механической передачи на уровне высоких значений: 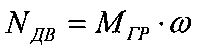 .
.
| Определение потерь в кинематических парах и механических трансмиссиях на основе закона Амонтона-Кулона / И.К | |||
| Александров // Вестник машиностроения | |||
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
| СПОСОБ ЭКСПЕРИМЕНТАЛЬНО-ТЕОРЕТИЧЕСКОГО ОПРЕДЕЛЕНИЯ ФРИКЦИОННЫХ ХАРАКТЕРИСТИК ЭЛЕМЕНТА КИНЕМАТИЧЕСКОЙ ЦЕПИ ДЛЯ ПЕРЕДАЧИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ С УЧЕТОМ ЧАСТОТЫ ВРАЩЕНИЯ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2011 |
|
RU2468352C1 |
| СПОСОБ УПРАВЛЕНИЯ КОМБИНИРОВАННОЙ ЭНЕРГЕТИЧЕСКОЙ УСТАНОВКОЙ | 2009 |
|
RU2424926C1 |
Авторы
Даты
2016-04-27—Публикация
2015-03-20—Подача