ОБЛАСТЬ ТЕХНИКИ
Изобретение относится к машиностроению и приборостроению и может быть использовано в механических устройствах, реализующих дискретные законы движения при непрерывном движении ведущего.
УРОВЕНЬ ТЕХНИКИ
Известны волновые передачи с роликовыми, дисковыми и кулачковыми генераторами волн внутреннего и внешнего деформирования [1, 2].
Наиболее близким техническим решением является шаговая волновая передача [2], которая содержит гибкое колесо, генератор волн и жесткое колесо, состоящее из четырех зубчатых секторов, попарно и диаметрально противоположно расположенных с которыми гибкое колесо последовательно образует двухволновую зубчатую передачу или волновую муфту. При непрерывном вращении генератора волн, обеспечивающее в зоне одной пары зубчатых секторов жесткого колеса волновое зацепление, реализуется вращательное движение выходного звена, при зацеплении гибкого колеса со второй парой зубчатых секторов жесткого колеса, образующих с гибким колесом зубчатую муфту, реализуется режим «выстоя» - выходное звено остается неподвижным. В результате, при непрерывном вращении входного звена имеется дискретный режим вращения выходного звена.
Недостатком данного конструктивного решения является высокие динамические нагрузки и интенсивный износ зубьев при переходе контакта зубьев гибкого колеса с жестким колесом с одной пары секторов на другую, возникающее за счет разности угловых шагов зубчатых венцов секторов жесткого колеса, образующих с гибким колесом волновое зацепление или волновую муфту. В этом случае ударное нагружение гибкого колеса снижает несущую способность и ресурс устройства в целом.
РАСКРЫТИЕ ИЗОБРЕТЕНИЯ
Задачей настоящего изобретения является существенное снижение динамических нагрузок в зонах пересопряжения зубьев гибкого колеса на границах секторов жесткого колеса, снижение износа и повышение долговечности передачи.
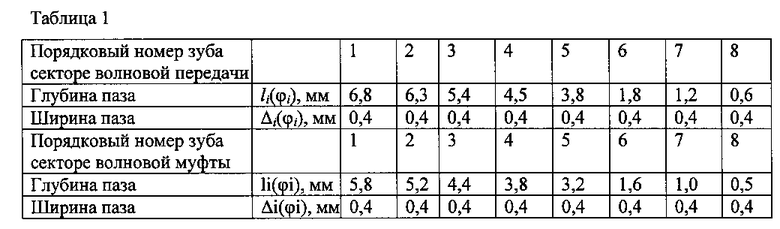
Технический результат достигается тем, что в зонах контакта секторов жесткого зубчатого колеса зубья жесткого колеса выполнены переменной изгибной жесткости за счет системы пазов во впадинах зубьев, геометрия которых (li,(φi), li(φj) - глубина, Δi(φi), Δi(φj) - ширина) определяется законом распределения боковых зазоров в волновом зацеплении и волновой муфте соответственно и обеспечивает распределение нагрузки по зубьям гибкого колеса, гарантирующее безударное сопряжение зубьев гибкого колеса при переходе волны деформации (зоны зацепления) с одного сектора жесткого колеса на другой. Пазы обеспечивают за счет упругой податливости зубьев жесткого колеса выравнивание угловых шагов гибкого колеса и зубчатых секторов жесткого.
Таким образом, волновая передача дискретного движения содержит гибкое колесо, расположенный внутри него генератор волн и жесткое колесо, состоящее из четырех зубчатых секторов из двух пар, одинаковых и диаметрально противоположно расположенных, причем одна пара зубчатых секторов образует с гибким колесом волновую передачу, а другая пара секторов - волновую муфту. При этом в локальных областях относительно граничных линий между секторами жесткого колеса его зубья имеют систему пазов переменной геометрии, расположенных во впадинах между зубьями. Размеры угловых границ φ0i и φ0j локальных областей системы пазов относительно граничных линий между секторами жесткого колеса и переменные геометрические параметры пазов определяются законом распределения боковых зазоров зубьев в волновой передаче и в волновой муфте соответственно, материалом зубьев жесткого колеса и расчетным усилием на зуб жесткого колеса.
Переменные геометрические параметры глубины li(φi) пазов в их системе определены следующими математическими формулами и зависимостями: 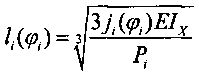 , где: Pi - заданное по условиям эксплуатационного нагружения передачи усилие на i-й зуб жесткого колеса; ji - расчетное упругое перемещение i-го зуба жесткого колеса; Е - модуль упругости материала зубчатого венца жесткого колеса;
, где: Pi - заданное по условиям эксплуатационного нагружения передачи усилие на i-й зуб жесткого колеса; ji - расчетное упругое перемещение i-го зуба жесткого колеса; Е - модуль упругости материала зубчатого венца жесткого колеса; 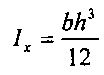 - момент инерции профиля зубчатого венца жесткого колеса, где: b - ширина зубчатого венца, h - высота зубчатого венца. Далее размер ширины пазов по формуле Δi(φi)=р-hi, где р - шаг зубчатого венца жесткого колеса; hi - высота профиля i-го зуба жесткого колеса. При этом расчетное упругое перемещение ji i-го зуба жесткого колеса определяется из условия его равенства с соответствующим боковым зазором в соответствующей паре зубьев по зависимости распределения боковых зазоров от угла поворота φ в волновом зацеплении и волновой муфте соответственно. Указанная зависимость получена в результате автоматизированных вычислительных расчетов математических моделей, базирующихся на положениях классической теории эвольвентного зацепления, для случая волновой передачи и волновой муфты соответственно, при следующих заданных параметрах: числа зубьев жесткого колеса, углов зацепления, половины угла облегания гибкого колеса, модуля зацепления; коэффициентов смещения исходного профиля при нарезании соответствующих зубчатых колес.
- момент инерции профиля зубчатого венца жесткого колеса, где: b - ширина зубчатого венца, h - высота зубчатого венца. Далее размер ширины пазов по формуле Δi(φi)=р-hi, где р - шаг зубчатого венца жесткого колеса; hi - высота профиля i-го зуба жесткого колеса. При этом расчетное упругое перемещение ji i-го зуба жесткого колеса определяется из условия его равенства с соответствующим боковым зазором в соответствующей паре зубьев по зависимости распределения боковых зазоров от угла поворота φ в волновом зацеплении и волновой муфте соответственно. Указанная зависимость получена в результате автоматизированных вычислительных расчетов математических моделей, базирующихся на положениях классической теории эвольвентного зацепления, для случая волновой передачи и волновой муфты соответственно, при следующих заданных параметрах: числа зубьев жесткого колеса, углов зацепления, половины угла облегания гибкого колеса, модуля зацепления; коэффициентов смещения исходного профиля при нарезании соответствующих зубчатых колес.
ПЕРЕЧЕНЬ ФИГУР
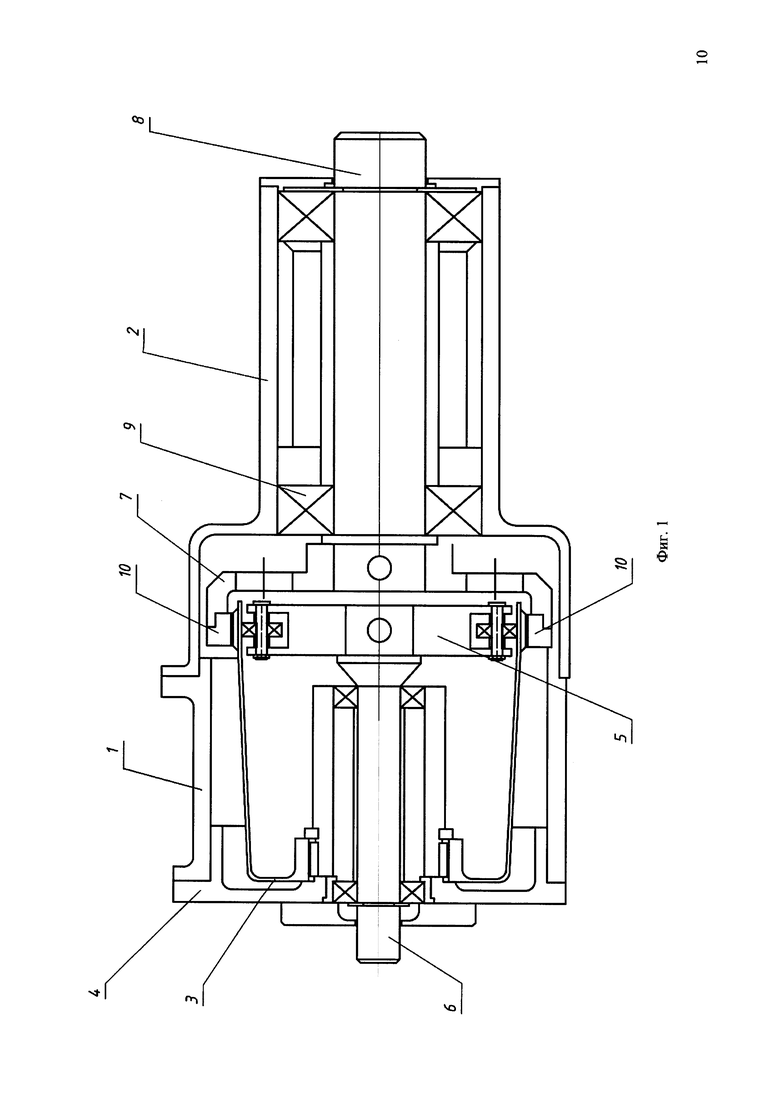
На фиг. 1 показан осевой разрез волновой передачи.
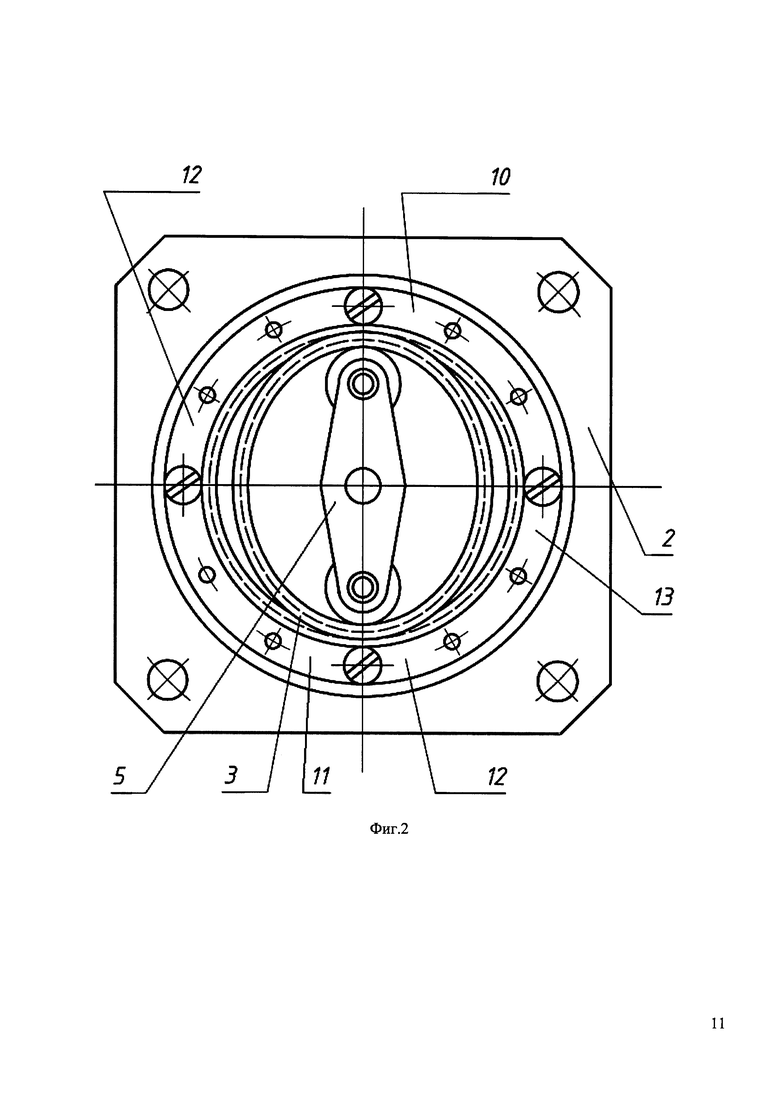
На фиг. 2 показан поперечный разрез волновой передачи.
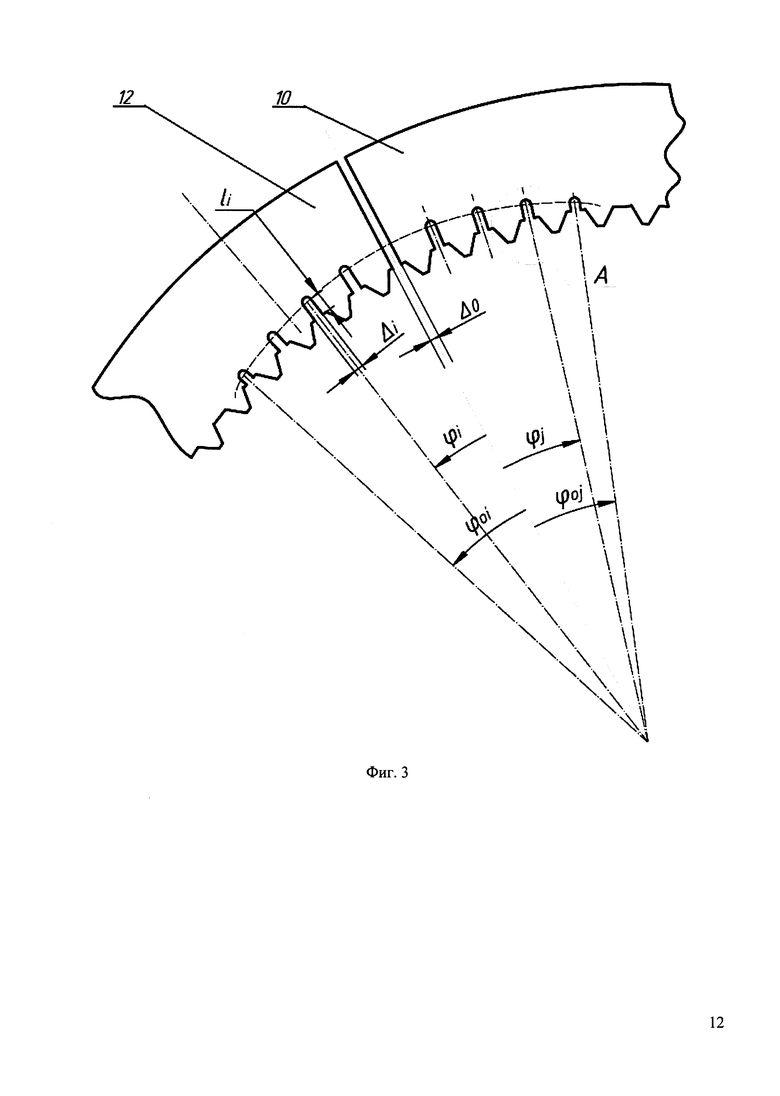
На фиг. 3 показана конструкция соседних зубчатых секторов жесткого колеса.
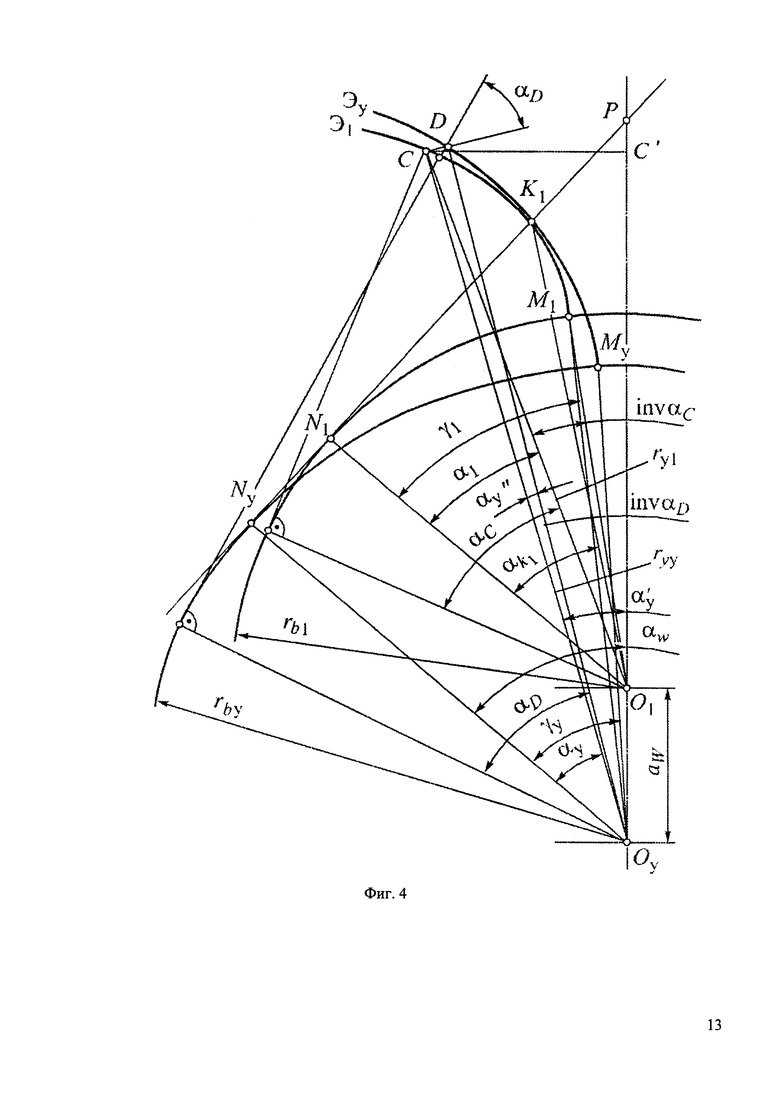
На фиг. 4 показана расчетная схема эвольвентного зацепления для определения боковых зазоров между зубьями гибкого и жесткого колес.
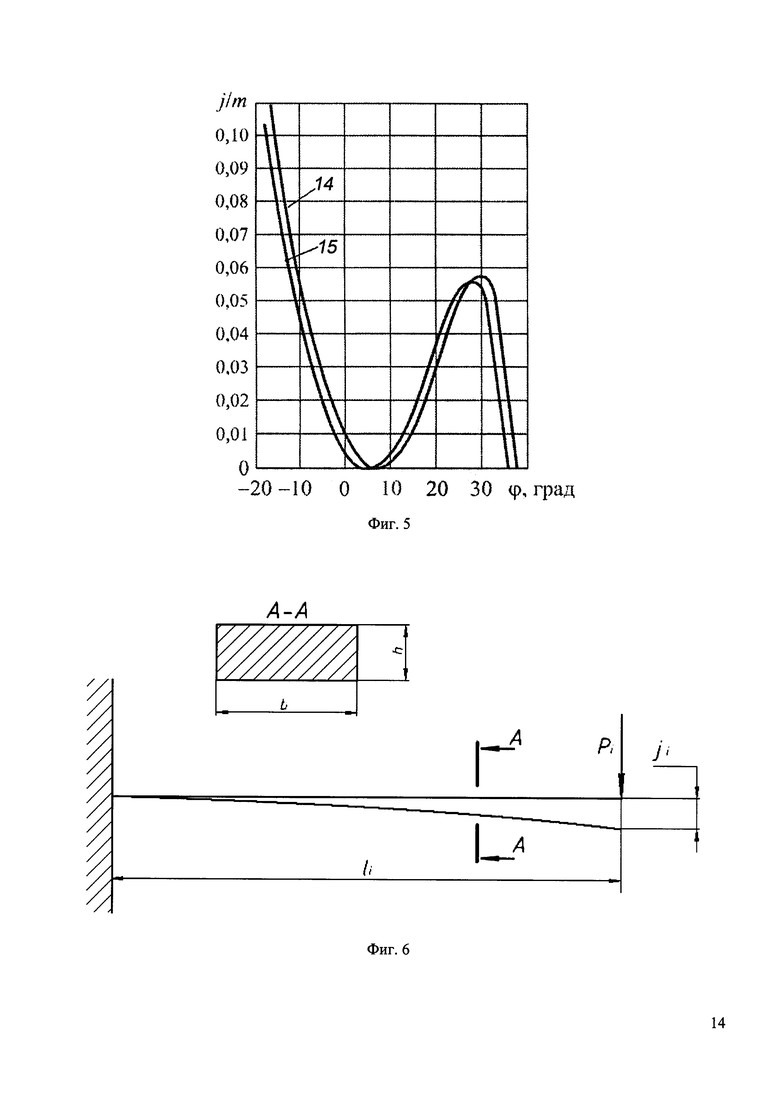
На фиг. 5 представлена зависимость распределения боковых зазоров в волновом зацеплении в виде графика зависимости относительного бокового зазора, удельного по модулю зацепления (j/m), от угла поворота φ.
На фиг. 6 показана расчетная схема определения упругой податливости зубьев жесткого колеса.
ОСУЩЕСТВЛЕНИЕ ИЗОБРЕТЕНИЯ
На фиг. 1 показана волновая передача дискретного движения, осевой разрез. В корпусе 1 и 2 содержится гибкое колесо 3, закрепленное на крышке 4; расположенный внутри колеса 3 генератор волн 5, соединенный с ведущим валом 6, и жесткое колесо 7, являющееся ведомым звеном, жестко соединенное с выходным валом 8, установленным на подшипниках 9 в корпусе 2. Генератор волн 5 (фиг. 2) придает гибкому колесу 3 форму двухвершинного овала. Жесткое колесо 7 выполнено составным из четырех зубчатых секторов. Пара секторов 10 и 11 расположены диаметрально противоположно относительно оси передачи, выполнены одинаковыми и имеют зубчатый венец с угловым шагом, равным угловому шагу зубчатого венца гибкого колеса 3. Другая пара секторов 12 и 13 также расположены диаметрально противоположно относительно оси передачи, выполнены одинаковыми и имеют зубчатый венец с угловым шагом, отличным от углового шага зубчатого венца гибкого колеса 3. Зубчатое колесо 7, в локальных областях сопряжения соседних секторов, имеет систему пазов во впадинах зубьев (фиг. 3). Расстояние Δ0 между секторами жесткого колеса на их общей границе определяется геометрическими параметрами зубьев гибкого и жесткого колес.
Передача работает следующим образом. При вращении генератора волн 5 (фиг. 2) гибкое колесо 3 в зацеплении с секторами 12 и 13 образует двухволновую передачу (осуществляется режим движения выходного звена), а в зацеплении с секторами 10 и 11 - волновую муфту (осуществляется режим «выстоя»), что приведет к дискретному перемещению выходного вала 8. При переходе волны деформации гибкого колеса с одной пары секторов жесткого зубчатого колеса на другую, за счет упругой податливости зубьев жесткого колеса, которая обеспечивается системой пазов во впадинах зубьев (фиг. 3), происходит выравнивание угловых шагов гибкого колеса и зубчатых секторов жесткого. Т.е. гарантируется безударное чередование режимов движения и «выстоя» выходного звена. Методика расчета параметров (li,(φi), Δi(φi)) системы пазов (фиг. 3) базируется на основных положениях классической теории эвольвентного зацепления [3], по которой рассчитываются геометрические параметры волнового зацепления для случая волновой передачи и волновой муфты [4], затем определяется окружной зазор между профилями зубьев гибкого и жесткого колес [5].
Исследование боковых зазоров ведется в обращенном механизме, так как при ведущем жестком колесе рабочими профилями в обращенном механизме будут те же профили, что и в реальном механизме. Значение боковых зазоров определяем по формулам, которые выводятся из рассмотрения геометрии волнового зубчатого зацепления [4]. Расчетные схемы для определения зазоров в зацеплении показаны на фиг. 4. Эвольвенты Э1 и ЭУ, описывающие рабочие профили зубьев колес, касаются друг друга на линии зацепления до точки N1. На участке N1NY линии зацепления эвольвенты пересекаются. Касание рабочих профилей зубьев происходит на рабочем участке линии зацепления. Вне рабочего участка линии зацепления между профилями зубьев будет теоретический зазор. Характер распределения зазоров в зацеплении определяется особенностями расположения эвольвент, описывающих профили зубьев колес. На фиг. 4 точка касания эвольвент находится внутри участка N1P линии зацепления.
Окружной зазор между профилями зубьев определяется по зависимости:

где ryy - радиус произвольной окружности условного колеса, по которой определяется окружной зазор;
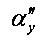 - центральный угол, равный угловому зазору между эвольвентами Э1 и ЭУ по окружности произвольного радиуса ryy.
- центральный угол, равный угловому зазору между эвольвентами Э1 и ЭУ по окружности произвольного радиуса ryy.
Для определения окружного зазора в произвольном угловом положении между эвольвентами Э1 и ЭУ необходимо знать параметры волнового зацепления и исполнительные размеры зубчатых колес. Они определяются геометрическим расчетом исследуемого волнового зацепления [4]. Положением точки С на жестком колесе, в которой определяется зазор, задаемся с помощью текущего значения угловой координаты αk1. Значение αk1 характеризуется отрезком N1K1 на линии зацепления. Вначале задаемся отрезком N1K1, равным нулю, далее с шагом, определяемым требуемой точностью расчета, увеличиваем N1K1, увеличивая тем самым угол αk1:

Значение радиуса ryy (на условном колесе) определяем из рассмотрения треугольника 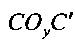 :
: 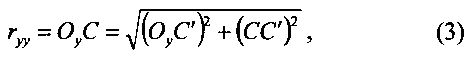
где 
Значениями радиуса ry1 обычно задаются, выбирая расчетные точки в произвольном положении по высоте зуба, но при этом один из расчетов обязательно проводится на окружности вершин при ry1-ra1. Это позволяет проследить все этапы зацепления от входа зубьев в зацепления до их выхода из зацепления, определить величину боковых зазоров в начальный момент входа в зацепление (запас по заклиниванию между вершинами зубьев колес на входе в зацепление). Угол α1 определяется из геометрических свойств эвольвенты:

Угол γ1 развернутости эвольвенты Э1 равен:

Из геометрии на фиг. 4 определяем:

Подставляя (4) и (5) в (3) и после преобразований получаем:
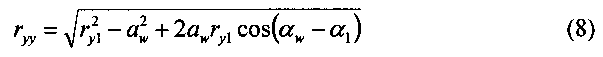
Далее определяем значение центрального угла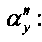
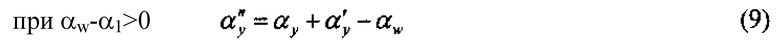
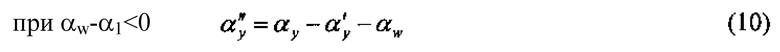
Угол αy определяется из геометрических свойств эвольвенты:

где γy - угол развернутости эвольвенты Эу;
αD - угол профиля эвольвенты Эу в точке D.
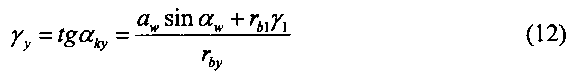

Угол 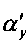 определяем из треугольника
определяем из треугольника 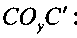

для αw>α1 имеем: 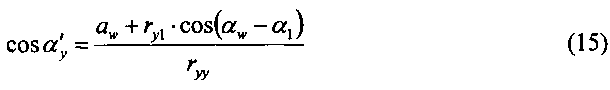
для αw<α1 имеем: 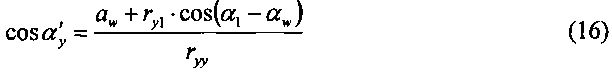
Окончательно, характер распределения величин боковых зазоров между зубьями гибкого и жесткого колес рассчитывается по формуле:

Характер распределения боковых зазоров, рассчитанный по данной методике, иллюстрируется на фиг. 5 (Зависимости бокового зазора по окружностям вершин (14) и по делительной окружности (15) жесткого колеса для волновой зубчатой передачи со следующими геометрическими параметрами: число зубьев жесткого колеса z2=152 (нарезанного долбяком с числом зубьев z0=80), число зубьев сектора волновой передачи =37, число зубьев сектора волновой муфты =39, углом зацепления αw=18°, половиной угла облегания гибкого колеса β=40°, модулем зацепления m=0,3 мм).
Расчетная схема нагружения зубьев жесткого колеса показана на фиг. 6, где обозначены: Pi - усилие на зуб жесткого колеса и ji - его упругое перемещение, связаны известным соотношением:

здесь момент инерции профиля в сечении А-А: 
где: b - ширина зубчатого венца, h высота профиля,
Е - модуль упругости материала.
Приравнивая упругие перемещения и соответствующие боковые зазоры получаем геометрические параметры системы пазов на секторах жесткого колеса:


где: р - шаг зубчатого венца жесткого колеса [3].
Задавая величину ji по известному закону распределения отнормированных (j/m) боковых зазоров j по модулю m (фиг. 5), данная методика расчета геометрических параметров системы пазов позволит не только обеспечить безударное пересопряжение зубьев гибкого и жесткого колес при переходе волны деформации с одного сектора жесткого колеса на другой, но и равномерный закон распределения нагрузок по зубьям гибкого колеса, что еще более повысит его долговечность. В качестве примера в таблице 1 приведены геометрические параметры системы пазов на жестком колесе волновой зубчатой передачи с характером распределения боковых зазоров, приведенных на фиг. 5.
Источники информации
1. Костиков Ю.В., Тимофеев Г.А., Фурсяк Ф.И. Новое в проектировании волновых зубчатых передач // Известия высших учебных заведений. Машиностроение. 2012, №12. С. 42-49
2. Волновая передача. АС СССР №1307127, кл. F16/H 1/00, опубл. 30.04.87 // БИ №16, 1987.
3. Гавриленко В.А. Основы теории эвольвентной зубчатой передачи. - М.: Машиностроение. - 1969. - 432 с.
4. Гавриленко В.А., Скворцова Н.А., Семин Ю.И. и др. Конструкция и геометрический расчет волновых зубчатых передач. Труды МВТУ, 1978, №291, Теория механизмов, вып. 8, - М., С. 22-33.
5. Исследование характера распределения боковых зазоров между рабочими профилями зубьев волновых передач с различными исходными параметрами / Тимофеев Г.А., Барбашов Н.Н. // Известия ВУЗов. Сер. "Машиностроение". - 2014. - №9. - С. 60-66.
| название | год | авторы | номер документа |
|---|---|---|---|
| ЖЕСТКОЕ КОЛЕСО ВОЛНОВОЙ ПЕРЕДАЧИ ДИСКРЕТНОГО ДВИЖЕНИЯ | 2016 |
|
RU2615578C1 |
| Зубчатая передача | 2024 |
|
RU2831817C1 |
| ВОЛНОВАЯ ТОРЦЕВАЯ ПЕРЕДАЧА СО СКРЕЩИВАЮЩИМИСЯ ВАЛАМИ | 1982 |
|
SU1839827A1 |
| Волновой механизм подачи станка ударно-вращательного бурения | 1980 |
|
SU945410A1 |
| ВОЛНОВАЯ ЗУБЧАТАЯ ТОРЦЕВАЯ ПЕРЕДАЧА | 1990 |
|
RU2019760C1 |
| Волновая зубчатая передача | 1977 |
|
SU750182A1 |
| МОТОР-РЕДУКТОР С ИНТЕГРИРОВАННЫМ ПРЕЦЕССИРУЮЩИМ ЗУБЧАТЫМ КОЛЕСОМ (ВАРИАНТЫ) | 2013 |
|
RU2538478C1 |
| Шестеренный насос | 1990 |
|
SU1784747A1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ И СБОРКИ/РАЗБОРКИ ВОЛНОВОЙ ГЕРМЕТИЧНОЙ ПЕРЕДАЧИ И УСТРОЙСТВО ДЛЯ ИХ ОСУЩЕСТВЛЕНИЯ Абрамова В.А. | 2014 |
|
RU2568626C1 |
| Шаговая волновая передача | 1985 |
|
SU1260598A1 |
Изобретение относится к машиностроению и может быть использовано в механических устройствах, реализующих дискретные законы движения при непрерывном движении ведущего. Волновая передача дискретного движения содержит гибкое колесо, расположенный внутри него генератор волн и жесткое колесо, состоящее из четырех зубчатых секторов из двух пар, одинаковых и диаметрально противоположно расположенных. Одна пара зубчатых секторов образует с гибким колесом волновую передачу, а другая пара секторов - волновую муфту. В локальных областях относительно граничных линий между секторами жесткого колеса его зубья имеют систему пазов переменной геометрии, расположенных во впадинах между зубьями. Размеры угловых границ φ0i и φ0j локальных областей системы пазов относительно граничных линий между секторами жесткого колеса и переменные геометрические параметры пазов определяются законом распределения боковых зазоров зубьев в волновой передаче и в волновой муфте соответственно, материалом зубьев жесткого колеса и расчетным усилием на зуб жесткого колеса. Обеспечивается существенное снижение динамических нагрузок в зонах пересопряжения зубьев гибкого колеса на границах секторов жесткого колеса, а также повышение долговечности передачи. 1 з.п. ф-лы, 1 табл., 6 ил.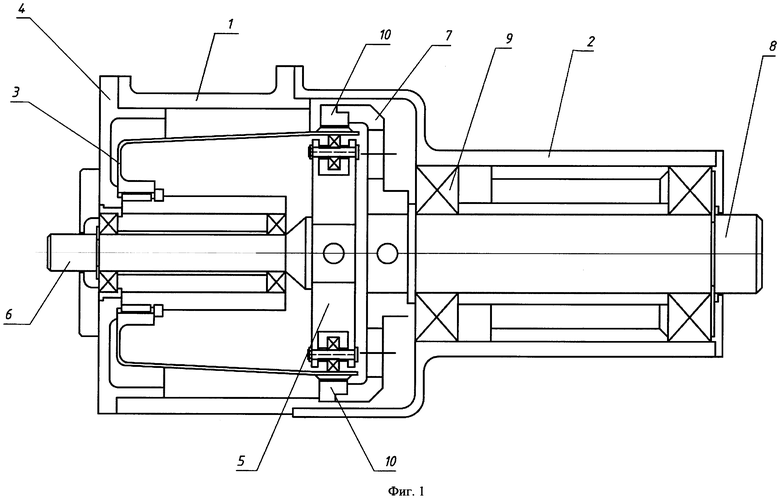
1. Волновая передача дискретного движения, содержащая гибкое колесо, расположенный внутри него генератор волн и жесткое колесо, состоящее из четырех зубчатых секторов из двух пар, одинаковых и диаметрально противоположно расположенных, причем одна пара зубчатых секторов образует с гибким колесом волновую передачу, а другая пара секторов - волновую муфту, отличающаяся тем, что в локальных областях относительно граничных линий между секторами жесткого колеса его зубья имеют систему пазов переменной геометрии, расположенных во впадинах между зубьями, при этом размеры угловых границ φ0i и φ0j локальных областей системы пазов относительно граничных линий между секторами жесткого колеса и переменные геометрические параметры пазов определяются законом распределения боковых зазоров зубьев в волновой передаче и в волновой муфте, соответственно, материалом зубьев жесткого колеса и расчетным усилием на зуб жесткого колеса.
2. Волновая передача по п. 1, отличающаяся тем, что переменные геометрические параметры глубины li(φi) пазов в их системе определены следующими математическими формулами и зависимостями: 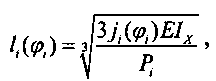 где: Pi - заданное по условиям эксплуатационного нагружения передачи усилие на i-й зуб жесткого колеса; ji - расчетное упругое перемещение i-го зуба жесткого колеса; Е - модуль упругости материала зубчатого венца жесткого колеса;
где: Pi - заданное по условиям эксплуатационного нагружения передачи усилие на i-й зуб жесткого колеса; ji - расчетное упругое перемещение i-го зуба жесткого колеса; Е - модуль упругости материала зубчатого венца жесткого колеса; 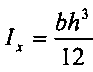 - момент инерции профиля зубчатого венца жесткого колеса, где: b - ширина зубчатого венца, h - высота зубчатого венца; далее размер ширины пазов по формуле Δi(φi)=р-hi, где р - шаг зубчатого венца жесткого колеса; hi - высота профиля i-го зуба жесткого колеса; при этом расчетное упругое перемещение ji i-го зуба жесткого колеса определяется из условия его равенства с соответствующим боковым зазором в соответствующей паре зубьев по зависимости распределения боковых зазоров от угла поворота φ в волновом зацеплении и волновой муфте соответственно, указанная зависимость получена в результате автоматизированных вычислительных расчетов математических моделей, базирующихся на положениях классической теории эвольвентного зацепления, для случая волновой передачи и волновой муфты соответственно, при следующих заданных параметрах: числа зубьев жесткого колеса, углов зацепления, половины угла облегания гибкого колеса, модуля зацепления, коэффициентов смещения исходного профиля при нарезании соответствующих зубчатых колес.
- момент инерции профиля зубчатого венца жесткого колеса, где: b - ширина зубчатого венца, h - высота зубчатого венца; далее размер ширины пазов по формуле Δi(φi)=р-hi, где р - шаг зубчатого венца жесткого колеса; hi - высота профиля i-го зуба жесткого колеса; при этом расчетное упругое перемещение ji i-го зуба жесткого колеса определяется из условия его равенства с соответствующим боковым зазором в соответствующей паре зубьев по зависимости распределения боковых зазоров от угла поворота φ в волновом зацеплении и волновой муфте соответственно, указанная зависимость получена в результате автоматизированных вычислительных расчетов математических моделей, базирующихся на положениях классической теории эвольвентного зацепления, для случая волновой передачи и волновой муфты соответственно, при следующих заданных параметрах: числа зубьев жесткого колеса, углов зацепления, половины угла облегания гибкого колеса, модуля зацепления, коэффициентов смещения исходного профиля при нарезании соответствующих зубчатых колес.
| Волновая передача | 1985 |
|
SU1307127A1 |
| WO 2007115510 A1, 18.10.2007 | |||
| US 4491033 A1, 01.01.1985 | |||
| US 5016491 A1, 21.05.1991. | |||
Авторы
Даты
2016-06-27—Публикация
2015-05-27—Подача