Изобретение относится к технике стрельбы по движущимся целям и может использоваться в системах обнаружения, определения траектории и поражения целей.
Известен способ прицеливания при атаке скоростных целей истребителем по спрямленной траектории, заключающийся в том, что цель сопровождают с помощью бортовых радиолокационных или/и оптических систем и при этом определяют текущие значения векторов ее относительной дальности, скорости и линейного ускорения, прогнозируют вектор дальности упрежденного положения цели на суммарное время выхода истребителя на границу области эффективного применения оружия и полета снаряда, пущенного с границы этой области до встречи с целью, направляют полет истребителя в процессе атаки в точку выхода истребителя на границу области эффективного применения оружия и полета снаряда (RU 2170907 C2).
Известен способ стрельбы управляемым снарядом с лазерной полуактивной головкой самонаведения по движущейся цели, включающий топографическую привязку целеуказателя и огневой позиции к местности, обнаружение цели целеуказателем. В этом способе задают набор вероятных маршрутов движения цели и, после обнаружения цели, выбирают ближайший к измеренным координатам цели маршрут, с учетом которого осуществляют расчет прогнозируемой точки встречи снаряда с целью (RU 2347999 C2).
Известен способ определения точности наведения и сближения снаряда с целью по наблюдаемым параметрам их траекторного движения, в котором с помощью станций сопровождения авиационно-космических объектов в едином базисе измеряют текущие значения векторов дальности до снаряда и цели, вычитают из первого второй и определяют текущее значение вектора дальности до снаряда относительно цели, по измеренным в момент начала наблюдения векторам дальности цели и снаряда определяют значения векторов их скорости, на основе полученных данных прогнозируют траектории их полета до расчетной точки встречи (RU 2355990 C2).
Однако данные известные способы не являются универсальными. Каждый из этих способов имеет свою ограниченную область применения, при выходе за рамки которой расчетная точка встречи или не будет определяться, или будет определяться некорректно.
Технический результат заявленного способа заключается в повышении точности стрельбы артиллерийской установки за счет обеспечения возможности формирования траектории движения снаряда, учитывающей функциональную зависимость движения от начальных условий полета снаряда.
Для этого в способе стрельбы по цели, сопровождаемой радиолокационной системой, и двигающейся по произвольной траектории, описываемой уравнением y=g(t), у∈ℝ3, поражающим снарядом, двигающимся по траектории, описываемой системой обыкновенных дифференциальных уравнений 
Здесь y - вектор, состоящий из 3-х компонент y1, y2, y3, соответствующих положению цели по каждой оси прямоугольной системы координат;
t - время;
g - вектор-функция, состоящая из 3-х компонент gi(t), g2(t), g3(t), описывающих движение цели вдоль каждой оси прямоугольной системы координат,
ℝ3 - 3-мерное Евклидово пространство;
x - вектор фазовых координат снаряда, первые 3 координаты которого описывают положение снаряда по осям прямоугольной системы координат,
х0 - вектор начальных условий движения снаряда,
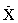
f - вектор-функция, описывающая скорость изменения фазовых координат снаряда,
n - количество координат (длина) вектора фазовых координат снаряда.
Существо заявленного способа состоит в следующем.
Необходимо определить точку встречи цели и поражающего снаряда. Рассматриваемый способ разработан для снарядов, динамика движения которых в процессе полета может явным образом зависеть от начальных условий, например начального угла бросания. Так, начальный угол бросания может оказывать влияние на траекторию штатного снаряда как непосредственно в момент выстрела, так и на всем протяжении полета.
Считаем, что движение снаряда описывается системой обыкновенных нелинейных дифференциальных уравнений, а движение цели известно и описывается гладкими функциями времени:

Фазовый вектор x(t)∈ℝn, описывающий движение снаряда, удовлетворяет системе обыкновенных дифференциальных уравнений:

Часть компонент вектора начальных условий движения снаряда задана, а часть не задана и подлежит определению (например, углы прицеливания):

a∈ℝn-m - заданная часть начальных условий, a z∈ℝm - незаданная часть начальных условий фазового вектора, которая может варьироваться. Знак Т в верхней индексации вектора и матрицы обозначает операцию транспонирования.
Задача состоит в нахождении такого вектора начальных условий z, при котором в некоторый момент времени T траектории x(t) и y(t) пересекутся:

где i=1, 2, 3.
Предположим, что первые 3 координаты фазовых векторов снаряда и цели соответствуют векторам положения этих точек в 3-мерном евклидовом пространстве ℝ3. На вектор z могут быть наложены дополнительные ограничения в форме равенств:


Задача (2)-(5) является классической нелинейной краевой задачей.
При фиксированном векторе Z фазовый вектор-функция x является решением задачи Коши и в каждый момент времени является функцией своих начальных условий. Поэтому, если k+3=m+1, то эта задача сводится к решению системы k+3 нелинейных уравнений (4), (5) относительно m+1 неизвестных (m неизвестных начальных условий плюс время встречи).
Метод Ньютона, применяемый к решению этой системы уравнений, предполагает на каждом шаге вычисление матрицы частных производных фазового вектора решения системы дифференциальных уравнений (2) (матрицы Якоби) по начальным условиям z. Матрица частных производных Н(t) вектор-функции решения этой системы по начальным условиям z 


где Еm×m - единичная матрица размерности m×m, 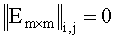

Численное интегрирование системы дифференциальных уравнений (6), (7) одновременно с системой дифференциальных уравнений (2) позволяет организовать итерационный вычислительный процесс метода Ньютона.
Если правая часть дифференциального уравнения, описывающего движение точки 1, явно зависит от вектора начальных условий Z, то задача о точке встречи имеет некоторые специфические особенности. В этом случае дифференциальное уравнение (2) принимает вид:

где x(t)∈ℝn, z∈ℝm, и уравнение в вариациях для матрицы Якоби решения этой системы отличается от уравнения (6).
В любом случае краевая задача о точке встречи сводится к системе нелинейных уравнений относительно вектора z и момента встречи t.

где Ф(z,t)∈ℝk+3, z∈ℝm.
x1(z,t), x2(z,t), x3(z,t) - первые 3 компоненты вектора x(t) - решения системы дифференциальных уравнений (8) с начальными условиями (3).
Далее для решения системы уравнений применяется метод Ньютона (9), при этом (q+1)-й шаг итерационного вычисления имеет вид:

где J(z(q), t(q)) - матрица Якоби вектор-функции Ф:

Jφ(z) - матрица Якоби вектор-функции φ(z), (Jφ(z))i,j=∂φi/∂zj,
0k×1 - нулевой вектор длиной k,
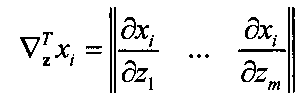 - градиент функции xi по переменным z.
- градиент функции xi по переменным z.
Для вычисления матрицы J(z, t) необходимо иметь выражение для градиента функции xi(z, t) по переменным z, t. Частная производная функции xi(z, t) определяется следующим образом:

где x(t) - решение системы дифференциальных уравнений (8).
Далее вычисляют векторы частных производных вектор-функции x(z, t) по начальным условиям z1, …, zm. Для определенности вычисляют вектор  и формулируют обобщение системы дифференциальных уравнений (6), (7).
и формулируют обобщение системы дифференциальных уравнений (6), (7).
При фиксированных начальных условиях z вектор hi(t) является решением следующей линейной неоднородной системы дифференциальных уравнений:


где х(t) - решение системы дифференциальных уравнений (8) с начальными условиями (2). Через δj обозначен j-й орт.
Для того чтобы найти градиент ∇zxi(z,t) по переменным z1, …, zm надо проинтегрировать m систем линейных неоднородных дифференциальных уравнений на интервале времени [0; t], получив при этом m векторов столбцов hi(t) - решений этих систем в момент времени t. Тогда:

Такие вычисления дают возможность организации итерационного вычислительного процесса метода Ньютона.
На прилагаемой фигуре показана принципиальная блок-схема алгоритма расчета точки встречи.
В блоке 1 осуществляется формирование начального приближения, в блоке 2 - расчет вектор-функции Ф и ее матрицы Якоби J, в блоке 3 - формирование вектора поправки начальных условий траектории снаряда, в блоке 4 осуществляется поправка траектории снаряда, в блоке 5 - расчет невязки, в блоке 6 - проверка того, что траектория снаряда найдена с заданной точностью.
Из физических соображений выбираются начальные условия z(0), удовлетворяющие системе уравнений (5).
Блок 1. Формирование начального приближения.
Интегрируется система дифференциальных уравнений (8) с достаточно малым шагом h по времени:

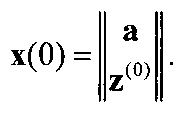
Одновременно интегрируется m систем дифференциальных уравнений:


На каждом шаге интегрирования вычисляется расстояние между снарядом и целью:

Если расстояние на текущем шаге увеличилось по сравнению с предыдущим, то фиксируется конечное время T(0)=t.
Блок 2. Расчет вектор-функции Ф и матрицы Якоби J.
В рассматриваемом блоке производится численное интегрирование систем дифференциальных уравнений на шаге с номером q итерационного процесса, а затем, по результатам интегрирования, формируется вектор-функция Ф(z(q), Т(q)) и ее матрица Якоби J(z(q), T(q)).
Начальные условия (3) системы дифференциальных уравнений (2) заданы и являются входными данными этого блока. Надо численно проинтегрировать на интервале [0; Т(q)] следующие системы дифференциальных уравнений:




Интегрирование можно производить любым известным численным методом, например методом Эйлера.
Блок 3. Формирование вектора поправки начальных условий траектории снаряда.
d=J-1Ф, где d - вектор поправки начальных условий, a J-1 - матрица, обратная матрице J.
Блок 4. Коррекция начальных условий расчетной траектории, проводимая в этом блоке, осуществляется по формуле:

Блок 5. Расчет невязки, осуществляемый по формуле:
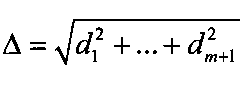 , где d1, d2, …dm+1 - компоненты вектора невязки d.
, где d1, d2, …dm+1 - компоненты вектора невязки d.
Блок 6. Проверка точности.
Проверяется выполнение неравенства:
Δ<ε, где ε - некоторое малое наперед заданное число.
В предложенном способе стрельбы по цели поражающим снарядом определяют точку встречи и момент встречи цели и снаряда, для чего проводится линеаризация траектории снаряда по начальным условиям движения (углам наведения), определяется зависимость движения снаряда от его начальных условий. При этом матрица частных производных вектора положения снаряда по начальным условиям его движения удовлетворяет системе обыкновенных линейных неоднородных дифференциальных уравнений. Для решения возникающей краевой задачи применяется метод Ньютона. Все полученные результаты для системы дифференциальных уравнений описывают движение штатного снаряда.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО МОДЕЛИРОВАНИЯ ФУНКЦИОНИРОВАНИЯ КОРАБЕЛЬНОГО АРТИЛЛЕРИЙСКОГО КОМПЛЕКСА | 2008 |
|
RU2385817C1 |
| КОМПЛЕКСНЫЙ СПОСОБ ОПРЕДЕЛЕНИЯ ТОЧНОСТИ НАВЕДЕНИЯ И СБЛИЖЕНИЯ СНАРЯДА С ЦЕЛЬЮ ПО НАБЛЮДАЕМЫМ ПАРАМЕТРАМ ИХ ТРАЕКТОРНОГО ДВИЖЕНИЯ | 2004 |
|
RU2267090C1 |
| СПОСОБ ПРИЦЕЛИВАНИЯ ПРИ АТАКЕ СКОРОСТНЫХ ЦЕЛЕЙ ИСТРЕБИТЕЛЕМ ПО СПРЯМЛЕННОЙ ТРАЕКТОРИИ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2000 |
|
RU2170907C1 |
| УСТРОЙСТВО УПРАВЛЕНИЯ АРТИЛЛЕРИЙСКИМ ОГНЕМ ПО ДВИЖУЩИМСЯ ЦЕЛЯМ | 1997 |
|
RU2134892C1 |
| СПОСОБ СТРЕЛЬБЫ АРТИЛЛЕРИЙСКИМИ СНАРЯДАМИ С ЗАКРЫТЫХ ОГНЕВЫХ ПОЗИЦИЙ | 2011 |
|
RU2453790C1 |
| СПОСОБ СТРЕЛЬБЫ УПРАВЛЯЕМЫМ АРТИЛЛЕРИЙСКИМ СНАРЯДОМ С ЛАЗЕРНОЙ ПОЛУАКТИВНОЙ ГОЛОВКОЙ САМОНАВЕДЕНИЯ | 2009 |
|
RU2408832C1 |
| УЛУЧШЕННЫЙ СПОСОБ ФОРМИРОВАНИЯ СИГНАЛА УПРАВЛЕНИЯ РАКЕТЫ ПРИ НАВЕДЕНИИ НА МАНЕВРИРУЮЩУЮ ЦЕЛЬ | 2017 |
|
RU2684432C2 |
| СПОСОБ СТРЕЛЬБЫ НЕУПРАВЛЯЕМЫМИ СНАРЯДАМИ С ЗАКРЫТЫХ ОГНЕВЫХ ПОЗИЦИЙ | 2002 |
|
RU2236665C2 |
| СПОСОБ АВТОМАТИЧЕСКОГО ПРИЦЕЛИВАНИЯ ПО ПОДВИЖНОЙ НАЗЕМНОЙ ЦЕЛИ | 2016 |
|
RU2629130C1 |
| СПОСОБ ФОРМИРОВАНИЯ СИГНАЛА УПРАВЛЕНИЯ РАКЕТЫ ПРИ НАВЕДЕНИИ НА МАНЕВРИРУЮЩУЮ ЦЕЛЬ | 2009 |
|
RU2419057C2 |

Изобретение относится к технике стрельбы по двигающимся целям и может использоваться в системах обнаружения и определения траектории полета поражающих целей. Технический результат - повышение точности. Для этого определяют точку встречи и момента встречи цели и снаряда, на основании оценок координат положения цели формируют начальную опорную траекторию движения снаряда и вектор промаха снаряда, осуществляют линеаризацию траектории снаряда в окрестности опорной траектории по углам прицеливания, на основании которой формируют матрицу частных производных вектора положения снаряда по углам прицеливания, которая удовлетворяет системе линейных однородных дифференциальных уравнений; при превышении длины вектора промаха своего максимально возможного допустимого порогового значения с использованием матрицы частных производных осуществляют коррекцию углов прицеливания артиллерийского орудия и повторяют формирование опорной траектории снаряда и вектора промаха, а при отсутствии превышения длины вектора промаха своего максимально возможного допустимого порогового значения осуществляют стрельбу по цели, используя последние величины углов прицеливания. 1 ил.
Способ стрельбы по цели, сопровождаемой радиолокационной системой, двигающейся по произвольной траектории, описываемой уравнением y=g(t), y∈R3, поражающим снарядом, двигающимся по траектории, описываемой системой обыкновенных дифференциальных уравнений 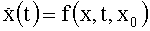
| СПОСОБ СТРЕЛЬБЫ УПРАВЛЯЕМЫМ СНАРЯДОМ С ЛАЗЕРНОЙ ПОЛУАКТИВНОЙ ГОЛОВКОЙ САМОНАВЕДЕНИЯ ПО ДВИЖУЩЕЙСЯ ЦЕЛИ (ВАРИАНТЫ) | 2007 |
|
RU2347999C2 |
| Испаритель | 1928 |
|
SU16211A1 |
| Видоизменение соединительной гайки для пожарных и иных рукавов | 1928 |
|
SU16959A1 |
| СПОСОБ ПРИЦЕЛИВАНИЯ ПРИ АТАКЕ СКОРОСТНЫХ ЦЕЛЕЙ ИСТРЕБИТЕЛЕМ ПО СПРЯМЛЕННОЙ ТРАЕКТОРИИ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2000 |
|
RU2170907C1 |
| Сейдж Э.П., Уайт Ч.С | |||
| Оптимальное управление системами | |||
| -М.: Радио и связь, 1982, стр.81-91 | |||
| Красовский Н.Н Оптимальное управление в обыкновенных динамических системах | |||
| УМН, 1965, том 20, выпуск 3(123), стр.153-174 . | |||
Авторы
Даты
2016-07-27—Публикация
2015-05-14—Подача