Изобретение относится к радиотеплолокации, а именно к радиотеплолокационным системам наблюдения за объектами с помощью радиометра [1, 2].
Радиометрическая система, работающая в миллиметровом или сантиметровом диапазоне длин волн, наблюдает объекты на местности. Объекты излучают тепловое поле X={x{i, j)}, 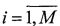 ,
, 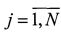 , элементы дискретизации которого x(i, j) имеют смысл интенсивности излучения в i,j-м направлении и рассматриваются в системе угловых координат наблюдателя: θi - по углу места и φj - по азимуту в i,j-x элементах дискретизации с шагом дискретизации Δθ и Δφ соответственно (обычно Δθ=Δφ). Числа M и N определяют размеры поля X в числе элементов дискретизации.
, элементы дискретизации которого x(i, j) имеют смысл интенсивности излучения в i,j-м направлении и рассматриваются в системе угловых координат наблюдателя: θi - по углу места и φj - по азимуту в i,j-x элементах дискретизации с шагом дискретизации Δθ и Δφ соответственно (обычно Δθ=Δφ). Числа M и N определяют размеры поля X в числе элементов дискретизации.
Антенна радиометра построчно сканирует участок местности по азимуту и углу места. При каждом i,j-м положении линии визирования антенны принимаемое поле X усиливается радиометром и после первичной обработки регистрируется в виде напряжения y(i, j). Величина y(i, j) носит интегральный характер по i,j-м элементам дискретизации поля X и подчинена модели измерений в виде свертки:
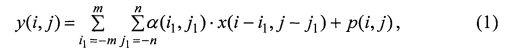
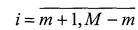 ,
, 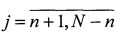 ,
,
где 2m+1 и 2n+1 - ширина диаграммы направленности антенны (ДНА) соответственно по углу места и азимуту (на уровне 0,5 мощности); α(i, j) - коэффициенты аппаратной функции, получаемые экспериментально при наблюдении точечного источника излучения x(i, j)=δ(i, j), имитирующего действие дельта-функции; p(i, j) - шумы аппаратуры в виде белого шума с дисперсией 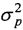 .
.
Совокупность измерений (1) представляет матрицу измерений Y размером M×N. Элементы матрицы Y, расположенные по периметру поля X, заполняются нулями: y(i,j)=0, 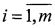 ,
, 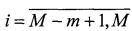 ,
, 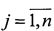 ,
, 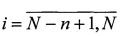 . В результате получается матрица измерений Y={y(i, j)},
. В результате получается матрица измерений Y={y(i, j)}, 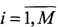 ,
, 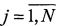 такого же размера, как матрица X. Совокупность P={p(i, j)},
такого же размера, как матрица X. Совокупность P={p(i, j)}, 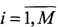 ,
, 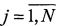 дает матрицу шумов.
дает матрицу шумов.
Задача заключается в восстановлении ненаблюдаемого поля X на основе наблюдений Y. Данная задача относится к классу некорректно поставленных задач и решается известными способами восстановления полей или изображений как в пространственной, так и в частотной областях [3-7].
В качестве прототипа рассматривается способ [3, с. 64-67] восстановления X в частотной области, который заключается в следующем.
1. Наблюдения Y подвергаются дискретному или быстрому преобразованию Фурье (ДПФ или БПФ), в результате чего в области пространственных частот ƒi и ƒj образуется спектральная матрица наблюдений:
Yƒ={yƒ(i, j)}, 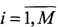 ,
, 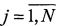 ,
,
где yƒ(i, j)=F[y(i, j)] - Фурье-спектр y(i, j), и в силу свойства преобразования Фурье выполняется равенство:
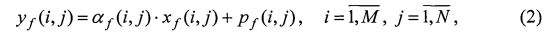
где xƒ(i, j)=F[x(i, j)], pƒ(i, j)=F[p(i, j)] - соответствующие спектры X и P.
2. Заранее составляется матрица коэффициентов ДНА A={a(i, j)}, 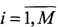 ,
, 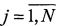 , по углам которой размещаются коэффициенты α(i1, j1),
, по углам которой размещаются коэффициенты α(i1, j1), 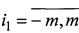 ,
, 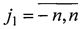 так, чтобы обеспечить пространственную периодичность матрицы А и соответственно функции (2) [8, с. 130]. Остальные элементы матрицы А заполняются нулями. Матрица А подвергается преобразованию Фурье, в результате образуется матрица A={a(i, j)},
так, чтобы обеспечить пространственную периодичность матрицы А и соответственно функции (2) [8, с. 130]. Остальные элементы матрицы А заполняются нулями. Матрица А подвергается преобразованию Фурье, в результате образуется матрица A={a(i, j)}, 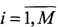 ,
, 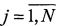 , где a
ƒ(i, j)=F[a(i, j)].
, где a
ƒ(i, j)=F[a(i, j)].
3. Уравнение (2) решается относительно xƒ{i, j). Решением, отвечающим критерию минимума дисперсии ошибки восстановления [3], является оценка 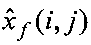 комплексной величины xƒ(i, j), вычисляемая по формуле:
комплексной величины xƒ(i, j), вычисляемая по формуле:
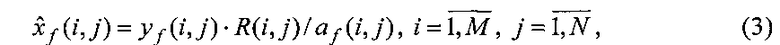
где R(i, j) - множитель, повышающий устойчивость решения за счет подавления действия широкополосного шума pƒ(i, j) на высоких частотах и вычисляемый по формуле:
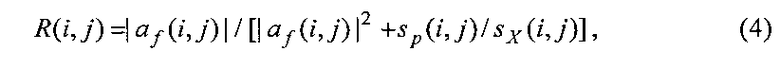
где sp(i, j) и sX(i, j) - значения спектральных плотностей соответственно шумового поля Р и искомого поля X.
Практически операции (3), (4) сводятся к умножению спектра измерений yƒ(i, j) на заранее вычисленную передаточную функцию hƒ(i, j) восстанавливающего фильтра:
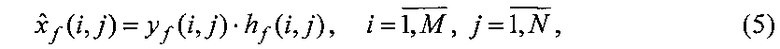
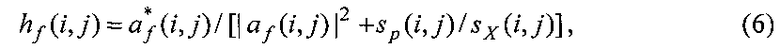
где учтено свойство: 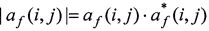 ,
, 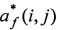 - сопряженная комплексная величина.
- сопряженная комплексная величина.
При отсутствии информации относительно sX(i, j) передаточную функцию (6) целесообразно заменить функцией вида
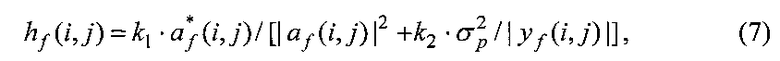
где коэффициенты k1 и k2 подбираются эмпирически.
4. Полученная матрица оценок в спектральной области 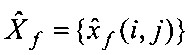 ,
, 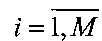 ,
, 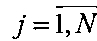 подвергается обратному преобразованию Фурье:
подвергается обратному преобразованию Фурье:
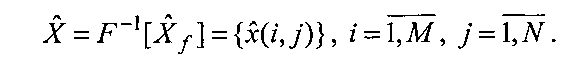
Результатом являются оценки 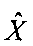 искомого поля изображения X, в составе которого присутствует изображение объектов.
искомого поля изображения X, в составе которого присутствует изображение объектов.
Рассмотренный способ обладает следующим недостатком. При механическом сканировании антенны шаг сканирования по углу места h=k·Δφ при k>1 оказывается больше размера Δθ элемента дискретизации поля X по азимуту, что приводит к несоответствию масштабов по θ и φ. При этом матрица наблюдений становится разреженной 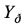 , и число ее строк
, и число ее строк 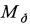 оказывается меньше числа строк искомой матрицы
оказывается меньше числа строк искомой матрицы 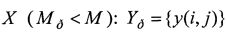 ,
, 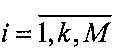 ,
, 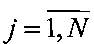 , k>1. Восстанавливать изображение X по разреженной матрице
, k>1. Восстанавливать изображение X по разреженной матрице 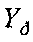 с помощью способа-прототипа невозможно. Попытка заполнить недостающие строки матрицы
с помощью способа-прототипа невозможно. Попытка заполнить недостающие строки матрицы 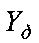 нулями приводит к существенному искажению оценок
нулями приводит к существенному искажению оценок 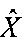 , что затрудняет распознавание изображений объектов.
, что затрудняет распознавание изображений объектов.
Технический результат направлен на восстановление изображений объектов при шаге сканирования по углу места, большем, чем шаг дискретизации искомого поля X, за счет интерполяции недостающих строк в разреженной матрице наблюдений 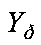 .
.
Технический результат предлагаемого технического решения достигается тем, что способ восстановления изображений объектов по разреженной матрице радиометрических наблюдений заключается в построчном сканировании антенны радиометра по азимуту и углу места с шагом по углу места, большим, чем шаг дискретизации искомого изображения, с последующей обработкой матрицы наблюдений в частотной области, отличающийся тем, что между соседними строками разреженной матрицы наблюдений располагают новые строки по числу недостающих элементов дискретизации угла места, а элементы этих строк получают линейной интерполяцией соответствующих элементов соседних строк исходной матрицы, затем полученную расширенную матрицу подвергают преобразованию Фурье, умножают результат преобразования на передаточную функцию восстанавливающего фильтра, осуществляют обратное преобразование Фурье и получают матрицу восстановленного изображения объектов.
Способ осуществляют следующим образом.
1. При сканировании антенны радиометра с шагом h=kΔφ, k>1, по углу места большим, чем шаг дискретизации Δθ восстанавливаемого изображения X={x(i, j)}, 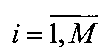 ,
, 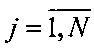 , получают разреженную по строкам матрицу наблюдений
, получают разреженную по строкам матрицу наблюдений 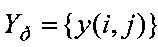 ,
, 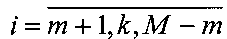 ,
, 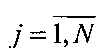 , k>1, элементы которой y(i, j) отвечают модели (1). Элементы матрицы
, k>1, элементы которой y(i, j) отвечают модели (1). Элементы матрицы 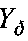 , расположенные по периметру поля X, заполняют нулями:
, расположенные по периметру поля X, заполняют нулями: 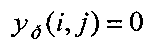 ,
, 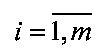 ,
, 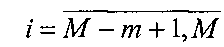
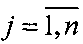 ,
, 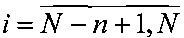 .
.
2. Между соседними строками разреженной матрицы 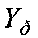 помещают k-1 строк по числу k-1 недостающих элементов дискретизации угла места, а элементы этих строк получают линейной интерполяцией соответствующих элементов соседних i-й и (i+1)-й строк матрицы
помещают k-1 строк по числу k-1 недостающих элементов дискретизации угла места, а элементы этих строк получают линейной интерполяцией соответствующих элементов соседних i-й и (i+1)-й строк матрицы 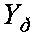 по формуле:
по формуле:
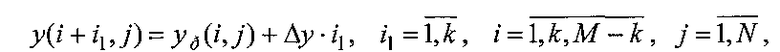
где 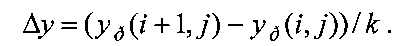
В результате получают расширенную матрицу измерений Y={y(i, j)}, 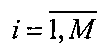 ,
, 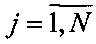 такого же размера, как матрица X.
такого же размера, как матрица X.
3. Расширенную матрицу Y подвергают преобразованию Фурье и получают спектральную матрицу Yƒ={yƒ(i, j)}, 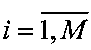 ,
, 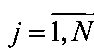 .
.
4. Элементы матрицы Yƒ умножают на передаточную функцию (6) или (7) в соответствии с формулой (5) и получают спектральную матрицу оценок 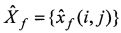 ,
, 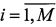 ,
, 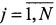 , где
, где 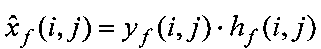 .
.
5. Полученную матрицу 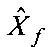 подвергают обратному преобразованию Фурье:
подвергают обратному преобразованию Фурье: 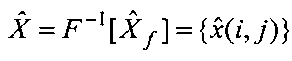 ,
, 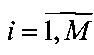 ,
, 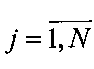 , результатом которого является матрица
, результатом которого является матрица 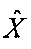 восстановленного изображения объектов в пространственной области.
восстановленного изображения объектов в пространственной области.
Для повышения качества изображения 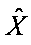 дополнительно может применяться пороговая обработка матрицы
дополнительно может применяться пороговая обработка матрицы 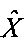 , устраняющая шумовые эффекты, а также итерационные процедуры восстановления [4, 5], повышающие четкость изображения.
, устраняющая шумовые эффекты, а также итерационные процедуры восстановления [4, 5], повышающие четкость изображения.
Экспериментальная часть (результаты моделирования).
На фигуре 1 показано изображение объекта в элементах дискретизации поля X. Антенна с косинусной ДНА шириной 3° по азимуту и углу места (на уровне 0,5 мощности) сканировала искомое поле X с шагом дискретизации Δφ=(1/16)° по азимуту и шагом h=16Δφ=1° по углу места (в 16 элементов дискретизации). Полученное на выходе радиометра изображение объекта в составе разреженной матрицы наблюдения 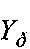 показано на фигуре 2. После интерполяции недостающие строки матрицы
показано на фигуре 2. После интерполяции недостающие строки матрицы 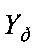 заполнялись по линейному закону, и изображение объекта в составе расширенной матрицы принимало вид, показанный на фигуре 4. Изображение объекта
заполнялись по линейному закону, и изображение объекта в составе расширенной матрицы принимало вид, показанный на фигуре 4. Изображение объекта 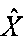 , восстановленное в соответствии с предлагаемым способом, показано на фигуре 3. Для чистоты эксперимента дополнительные процедуры, повышающие качество изображения, не использовались. Применение способа-прототипа в одинаковых условиях показало неудовлетворительные результаты.
, восстановленное в соответствии с предлагаемым способом, показано на фигуре 3. Для чистоты эксперимента дополнительные процедуры, повышающие качество изображения, не использовались. Применение способа-прототипа в одинаковых условиях показало неудовлетворительные результаты.
Таким образом, предлагаемый способ позволяет восстанавливать изображения объектов по разреженной матрице наблюдений.
Литература
1. Николаев А.Г., Перцов С.В. Радиотеплолокация (пассивная радиолокация). М.: Сов. радио, 1964. 335 с.
2. Шарков Е.А. Радиотепловое дистанционное зондирование Земли: физические основы: в 2 т. / Т. 1. М.: ИКИ РАН, 2014. 544 с.
3. Василенко Г.И., Тараторин A.M. Восстановление изображений. М.: Радио и связь, 1986. 304 с.
4. Пирогов Ю.А., Тимановский А.Л. Сверхразрешение в системах пассивного радиовидения миллиметрового диапазона / Радиотехника, 2006. №3. С. 14-19.
5. Цифровая обработка изображений в информационных системах: Учеб. пособие / И.С. Грузман, B.C. Киричук и др. Новосибирск: Изд-во НГТУ, 2002. 352 с.
6. Клочко В.К. Математические методы восстановления и обработки изображений в радиотеплооптоэлектронных системах. Рязань: РГРТУ, 2009. 228 с.
7. Патент RU 2379706 С2. Способ повышения разрешающей способности радиотепловых изображений / В.К. Клочко, В.В. Курилкин, А.А. Куколев, С.А. Львов. Приоритет 28.03.2008. Опубл. 20.01. 2010. Бюл. №2.
8. Гонсалес Р., Вудс Р., Эддинс С. Цифровая обработка изображений в среде MATLAB. М.: Техносфера, 2006. 616 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ДВУХЭТАПНОГО ВОССТАНОВЛЕНИЯ РАДИОТЕПЛОВЫХ ИЗОБРАЖЕНИЙ | 2017 |
|
RU2702228C2 |
| СПОСОБ НАБЛЮДЕНИЯ ЗА ОБЪЕКТАМИ С ПОМОЩЬЮ РАДИОМЕТРА С ДВУМЯ АНТЕННАМИ | 2017 |
|
RU2648270C1 |
| СПОСОБ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЙ ОБЪЕКТОВ В РАДИОМЕТРЕ С ДВУМЯ АНТЕННАМИ | 2017 |
|
RU2646434C1 |
| Способ формирования радиотеплового изображения | 2017 |
|
RU2661491C1 |
| СПОСОБ ФОРМИРОВАНИЯ РАДИОТЕПЛОВОГО ИЗОБРАЖЕНИЯ ОБЪЕКТОВ | 2019 |
|
RU2713731C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ АППАРАТНОЙ ФУНКЦИИ РАДИОМЕТРА | 2016 |
|
RU2622899C1 |
| СПОСОБ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЙ ОБЪЕКТОВ В ДВУХКАНАЛЬНОЙ РАДИОМЕТРИЧЕСКОЙ СИСТЕМЕ | 2016 |
|
RU2612193C1 |
| СПОСОБ ВОССТАНОВЛЕНИЯ ИЗОБРАЖЕНИЙ В ДВУХКАНАЛЬНОЙ СКАНИРУЮЩЕЙ СИСТЕМЕ | 2016 |
|
RU2612323C1 |
| СПОСОБ ПОВЫШЕНИЯ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ РАДИОТЕПЛОВЫХ ИЗОБРАЖЕНИЙ | 2008 |
|
RU2379706C2 |
| СПОСОБ ПОВЫШЕНИЯ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ ИЗОБРАЖЕНИЙ В МНОГОКАНАЛЬНЫХ РТЛС | 2017 |
|
RU2656355C1 |

Изобретение относится к радиотеплолокации, а именно к радиотеплолокационным системам наблюдения за объектами с помощью радиометра со сканирующей по азимуту и углу места антенной. Достигаемый технический результат направлен на восстановление изображений объектов при шаге сканирования антенны радиометра по углу места, большем, чем шаг дискретизации искомого изображения. Указанный результат достигается за счет того, что формируют расширенную матрицу наблюдений путем интерполяции недостающих строк с последующей обработкой расширенной матрицы в частотной области с помощью восстанавливающего фильтра, что позволяет получать неискаженное изображение объектов. 4 ил.
Способ восстановления изображений объектов по разреженной матрице радиометрических наблюдений, заключающийся в построчном сканировании антенны радиометра по азимуту и углу места с шагом по углу места, большим, чем шаг дискретизации искомого изображения, с последующей обработкой матрицы наблюдений в частотной области, отличающийся тем, что между соседними строками разреженной матрицы наблюдений располагают новые строки по числу недостающих элементов дискретизации угла места, а элементы этих строк получают линейной интерполяцией соответствующих элементов соседних строк исходной матрицы, затем полученную расширенную матрицу подвергают преобразованию Фурье, умножают результат преобразования на передаточную функцию восстанавливающего фильтра, осуществляют обратное преобразование Фурье и получают матрицу восстановленного изображения объектов.
| ВАСИЛЕНКО Г.И | |||
| и др | |||
| Восстановление изображения | |||
| Москва, Радио и связь, 1986, с.64-67 | |||
| СПОСОБ НАБЛЮДЕНИЯ ЗА ВОЗДУШНЫМИ ОБЪЕКТАМИ И ПОВЕРХНОСТЬЮ НА БАЗЕ БОРТОВОЙ РЛС | 2005 |
|
RU2292060C1 |
| СПОСОБ ДВУХЭТАПНОГО ВОССТАНОВЛЕНИЯ РАДИОЛОКАЦИОННОГО ИЗОБРАЖЕНИЯ | 2009 |
|
RU2411536C1 |
| СПОСОБ ИЗМЕРЕНИЯ РАДИОМЕТРИЧЕСКИХ КОНТРАСТОВ ЦЕЛЕЙ И РАДИОМЕТР ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2005 |
|
RU2285940C2 |
| US 20130106642 A1, 02.05.2013 | |||
| JP 4977806 B2, 18.07.2012 | |||
| US 20140168007 A1, 19.06.2014. | |||
Авторы
Даты
2016-10-27—Публикация
2015-11-23—Подача