Изобретение относится к наглядным пособиям и может быть использовано при изучении поверхностных явлений.
Известна возможность перехода металл-изолятор при постепенном увеличении расстояния между атомами в объеме металла, что способствует локализации электронов проводимости на этих атомах с резким ростом удельного сопротивления (Mott N.F. (1967). The transition from metal to insulator. Endeavour Vol. 26, p. 155. Займан Дж. (1974) Принципы теории твердого тела, изд. «Мир», Москва, с. 195).
Известен способ демонстрации перехода металл-изолятор, включающий постепенное изменение давления на образец окисла V2O3 с примесью атомов Cr, измерение электропроводности образца и регистрацию порога давления, соответствующего скачку электропроводности ( J. (2010). Fundamentals of the physics of solids. Vol. 3. Springer-Verlag, Berlin Heidelberg, p. 476).
J. (2010). Fundamentals of the physics of solids. Vol. 3. Springer-Verlag, Berlin Heidelberg, p. 476).
Известен метод регистрации переменного поверхностного натяжения твердых тел, впервые предложенный автором (Авт. свид. СССР 178161, МПК G01N 13/00, 08.01.1966, Бюл. №2; Авт. свид. СССР 277399 МПК G01N 13/02, 22.07.1970, Бюл. №24; Электрохимия 1966, том 2, с. 1061; Доклады АН СССР 1969. том 187, с. 601; Electrochimica Acta, 1970, vol. 15, p. 219; книга «Поверхностное натяжение твердых тел и адсорбция», Москва, изд. «Наука», 1976, 400 с.; Успехи физических наук, 2000, том 170, с. 779; J. Solid State Electrochemistry, 2013, vol. 17, p. 1743; Патент РФ 2552116, МПК G01N 13/00, 10.06.2015, Бюл. №16).
Указанный метод позволяет измерить производную поверхностного натяжения электропроводного твердого тела по поверхностной плотности заряда. Данная производная получила название эстанс (estance), которое принято в международной литературе. В указанном методе, называемом методом эстанса, исследуемое электропроводное твердое тело в виде электрода скрепляют с пьезоэлементом и приводят в контакт с ионной жидкостью, например с водным раствором электролита. Через границу исследуемого электрода с раствором пропускают переменный ток заданной частоты и фиксированной амплитуды. Колебания поверхностной плотности заряда исследуемого электрода сопровождаются колебаниями его поверхностного натяжения, которые раскачивают систему электрод-пьезоэлемент в режиме резонанса. При избирательной регистрации колебаний электрода на заданной частоте становится заметным удлинение электрода порядка тысячных долей размера атома, то есть 10-11 см. Отношение малых амплитуд поверхностного натяжения и поверхностной плотности заряда регистрируют как производную поверхностного натяжения твердого тела по поверхностной плотности заряда.
Потенциал исследуемого электрода, измеренный относительно стандартного электрода сравнения, изменяют линейно со временем. Регистрируют осциллограмму зависимости указанной производной от потенциала. Масштаб осциллограммы определяют с помощью эталонного теплового натяжения, создаваемого переменным нагревом поверхности исследуемого электрода. Регистрируемая зависимость эстанс-потенциал содержит сведения о поверхностных явлениях и не подвержена влиянию объемных процессов, а также влиянию макроскопической формы электрода.
Способ демонстрации самоизоляции металла и расщепления его поверхностного заряда не известен.
Перед настоящим изобретением поставлена задача экспериментально показать связь между спонтанным образованием изолирующего покрытия на металле, свободном от окисла, и расщеплением поверхностного заряда металла на две части, разделенные этим изолирующим покрытием.
Поставленная задача решена благодаря тому, что согласно изобретению электрод из исследуемого металла приводят в контакт с ионной жидкостью, на указанном электроде регистрируют зависимости эстанса и плотности электрического тока от потенциала электрода, на зависимости эстанса от потенциала находят ступени в форме экстремума и перегибов, расположенные в том интервале потенциалов, где зависимость плотности электрического тока от потенциала, меняющегося в анодном направлении, не имеет ни экстремума, ни перегибов, оценивают безразмерный наклон зависимости эстанс-потенциал между ступенями эстанса, показывают превосходство максимального абсолютного значения этого наклона над единицей, из указанного превосходства делают вывод о наличии у металла изолирующего покрытия, которое составлено исключительно из атомов металла и электрострикция которого увеличивает абсолютную величину указанного наклона, а отсутствие изменений плотности электрического тока, соответствующих ступеням эстанса, объясняют расщеплением поверхностного заряда металла изолирующим покрытием на внутреннюю и внешнюю части, которые при изменении потенциала поочередно получают приращения заряда с образованием у них взаимно компенсирующих ступеней, причем из указанных частей только внутренняя, ступенчато меняющаяся часть вызывает в изолирующем покрытии электрострикцию, создающую ступени эстанса, тогда как электрический ток обусловлен изменением полного поверхностного заряда, не имеющего ступеней.
Зависимость эстанса от потенциала регистрируют в координатах «модуль эстанса - потенциал». В диапазон изменения потенциала включают область поляризуемости электрода.
В качестве исследуемого металла используют платину. При этом в качестве ионной жидкости используют водный раствор серной кислоты с концентрацией 0.5 моля на литр, зависимости эстанса и плотности электрического тока от потенциала регистрируют в диапазоне потенциала, включающем интервал от +0.8 В до +0.3 В относительно равновесного водородного электрода при изменении потенциала в анодном направлении. В качестве ионной жидкости используют также расплав фторида калия либо фторида натрия.
В качестве исследуемого металла используют медь. При этом в качестве ионной жидкости используют водный раствор фтористого натрия с концентрацией 0.1 моля на литр, зависимости эстанса и плотности электрического тока от потенциала регистрируют в диапазоне потенциала, включающем интервал от -1.8 В до -0.4 В относительно насыщенного каломельного электрода при изменении потенциала в анодном направлении.
Сравнение зависимостей эстанса и электрического тока от потенциала указывает на парадоксальное различие двух физических величин, характеризующих состояние одной и той же поверхности. Согласно осциллограмме эстанса изменение потенциала сопровождается серией резких изменений состояния поверхности, которые выражены крупными ступенями эстанса. Согласно осциллограмме электрического тока никакой серии изменений состояния поверхности при тех же потенциалах нет, что выражено достаточно гладким ходом зависимости электрического тока от потенциала.
Указанная парадоксальность обладает достаточной наглядностью и использована в настоящем изобретении для демонстрации расщепления поверхностного заряда металла изолирующим покрытием, образованным поверхностными атомами металла при дефиците электронов.
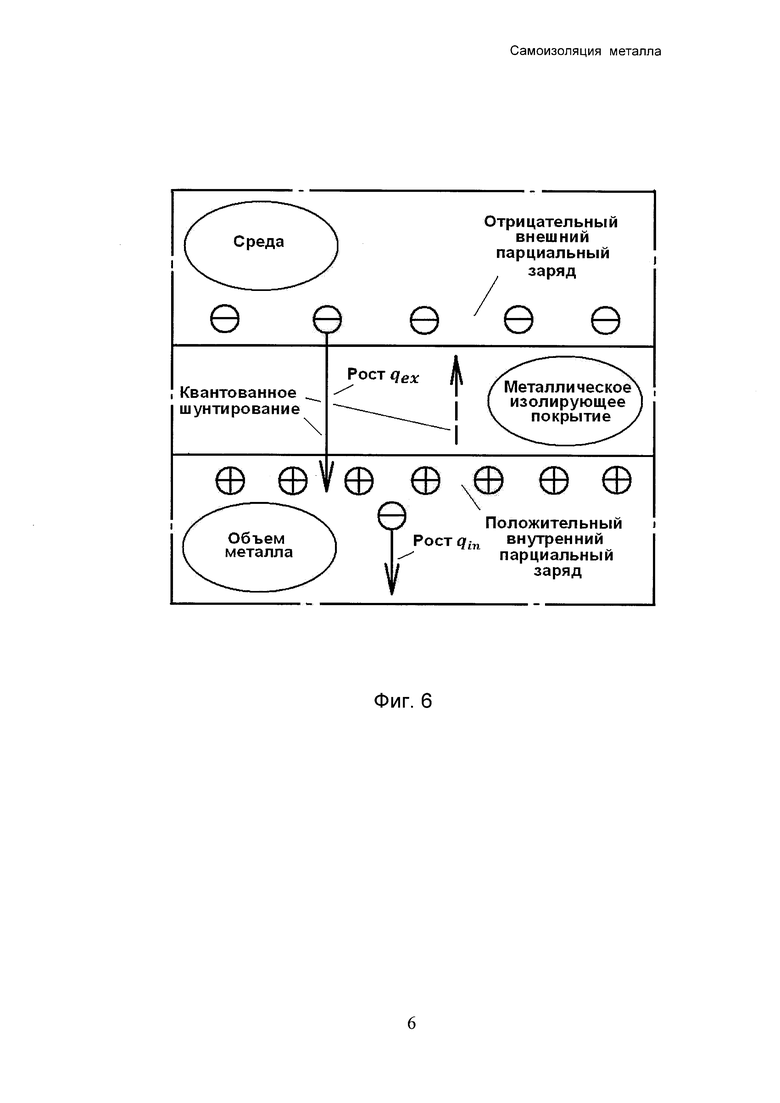
Суммарный избыточный поверхностный заряд металла возникает как реакция на внешнее электрическое поле, создаваемое в данном случае ионами раствора электролита. При этом суммарный поверхностный заряд расщепляется на внутренний парциальный заряд, расположенный под изолирующим покрытием, и внешний парциальный заряд, расположенный над изолирующим покрытием. Часть внешнего электрического поля заканчивается на внешнем парциальном заряде и до изолирующего покрытия не доходит. Остальная часть внешнего электрического поля проходит через изолирующее покрытие и заканчивается на внутреннем парциальном заряде. Таким образом, только внутренний парциальный заряд участвует в создании электрического поля, вызывающего электрострикцию изолирующего покрытия и дающего вклад в изменение поверхностного натяжения твердого тела.
При изменении потенциала суммарный поверхностный заряд монотонно меняется, тогда как внутренний и внешний парциальные заряды получают приращения поочередно, что создает у них взаимно обратные ступени, не затрагивающие суммарного поверхностного заряда. Объяснение парадокса состоит в различии частей заряда, влияющих на изменение эстанса и электрического тока с потенциалом. Ступени эстанса отражают ступенчатую зависимость внутреннего парциального заряда от потенциала. Электрический ток определяется бесступенчатым изменением суммарного поверхностного заряда.
Наряду со ступенями эстанса независимым подтверждением существования собственного изолирующего покрытия, состоящего исключительно из атомов металла, является аномально высокий безразмерный наклон зависимости эстанс-потенциал на участках между ступенями эстанса. Он показывает, что в поверхностном натяжении присутствует значительный вклад электрострикции, которая свойственна диэлектрикам, находящимся в электрическом поле. Создание изолирующего покрытия только атомами металла, без образования окисла, позволяет рассматривать данное явление как самоизоляцию металла.
Использование ионных жидкостей с анионами F- и 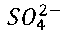 обусловлено отсутствием у этих анионов существенной способности к хемосорбции, что обеспечивает электростатический характер заряжения ионной обкладки двойного электрического слоя на границе твердой и жидкой фаз.
обусловлено отсутствием у этих анионов существенной способности к хемосорбции, что обеспечивает электростатический характер заряжения ионной обкладки двойного электрического слоя на границе твердой и жидкой фаз.
На иллюстрациях показаны:
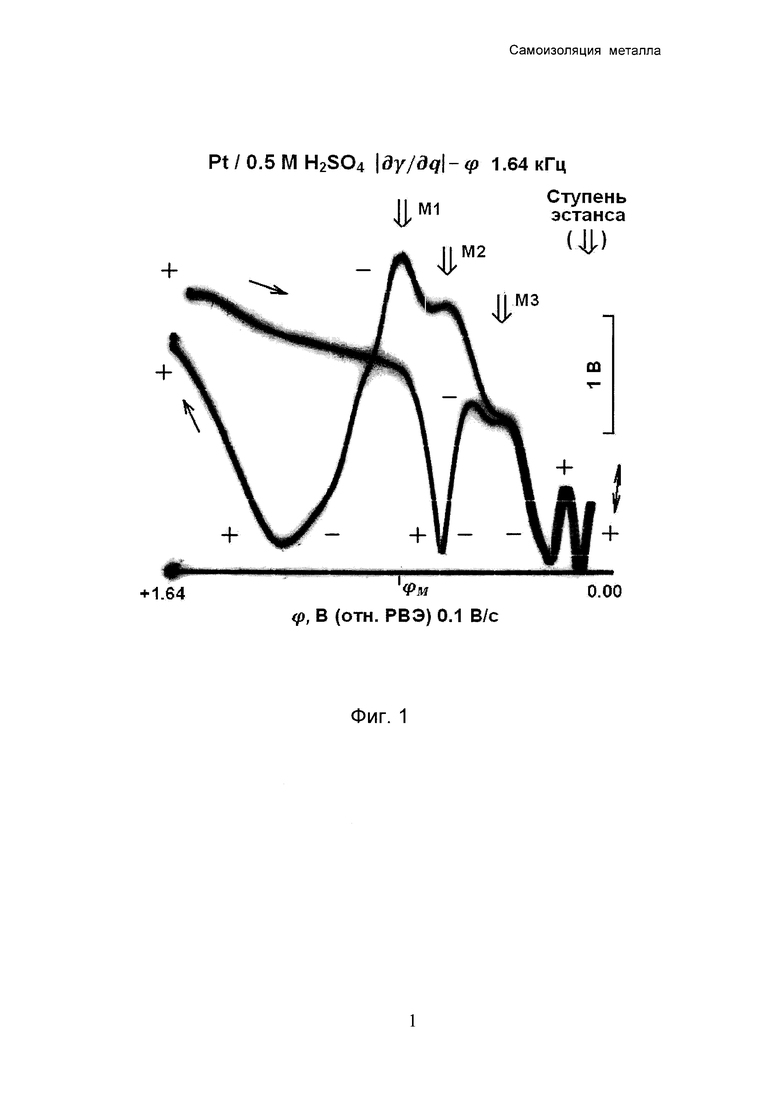
Фиг. 1 - осциллограмма эстанс-потенциал, полученная на платине в катодном и затем анодном направлениях.
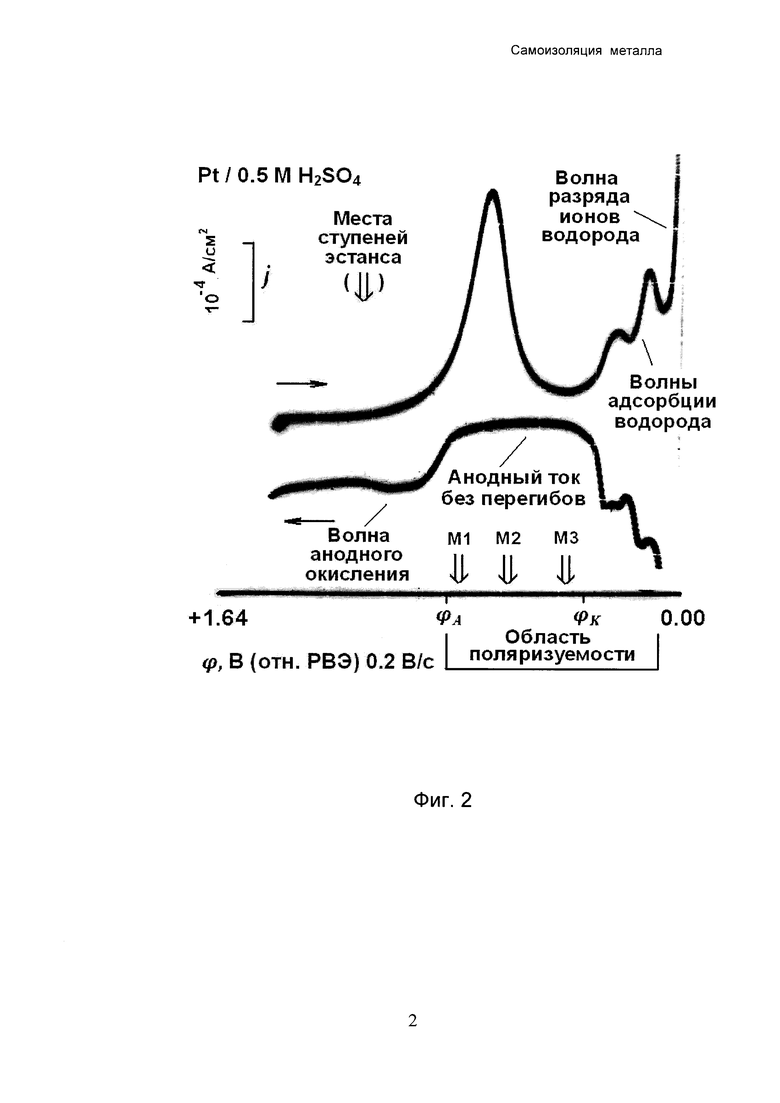
Фиг. 2 - осциллограмма плотность тока-потенциал, полученная на платине в катодном и затем анодном направлениях.
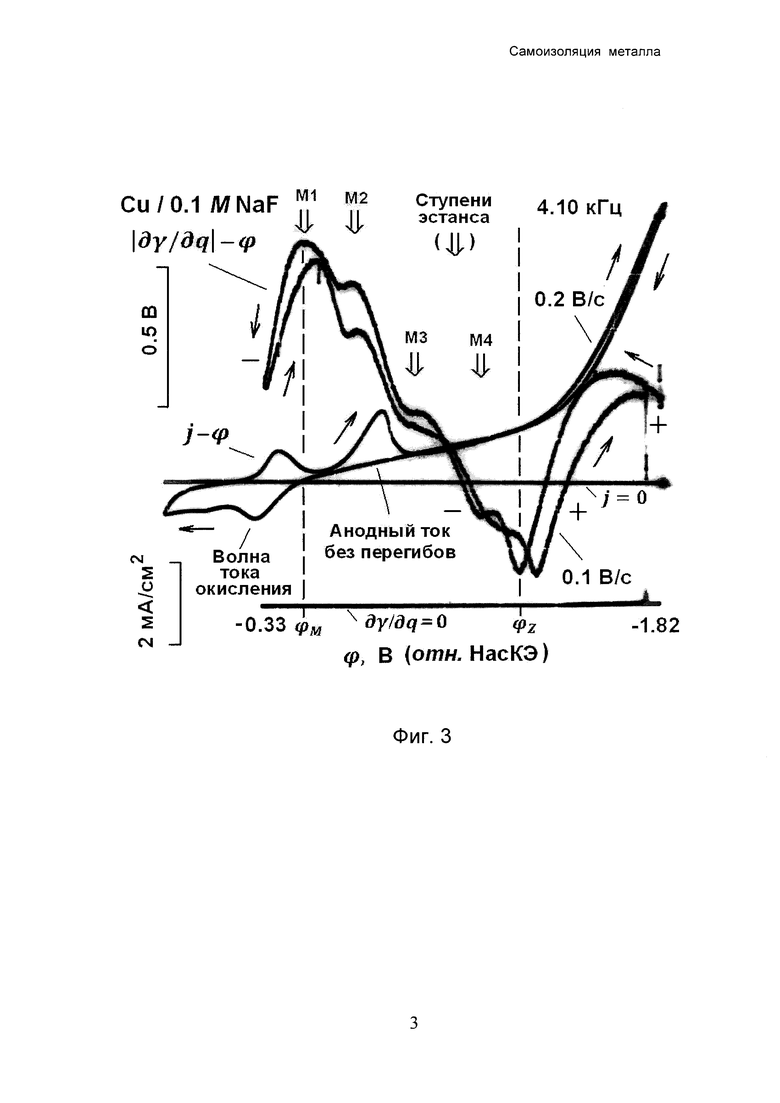
Фиг. 3 - совмещенные осциллограммы эстанс-потенциал и ток-потенциал, полученные на меди в анодном и затем катодном направлениях
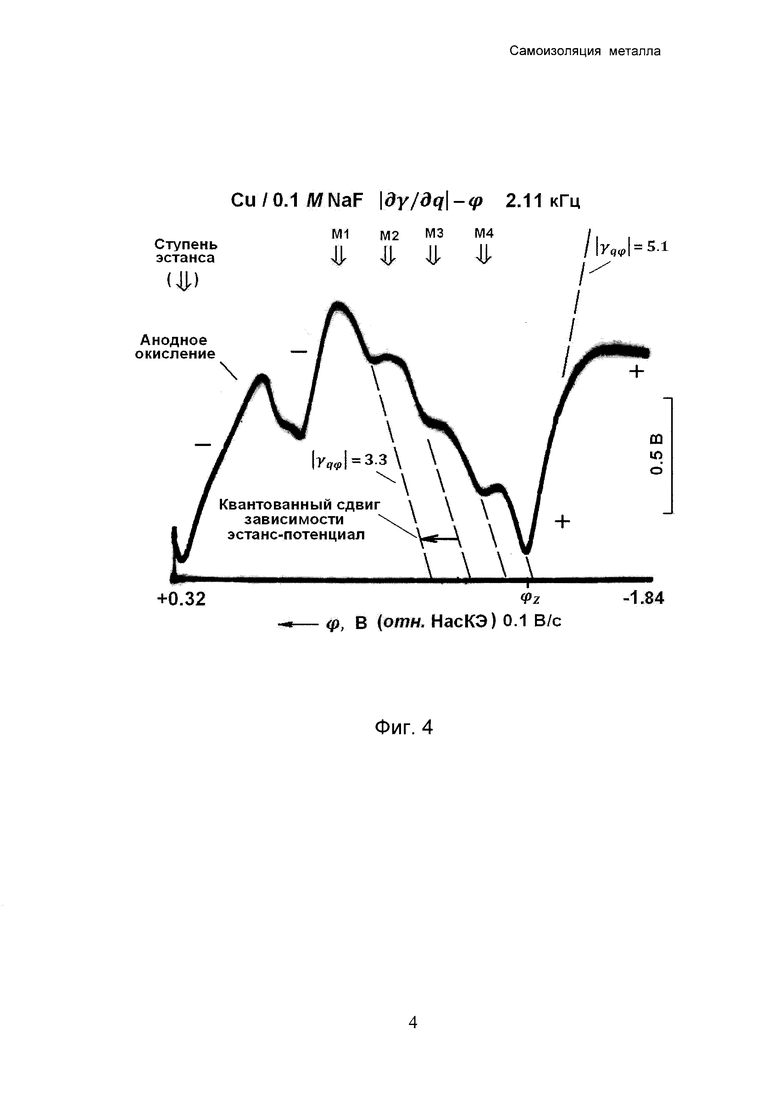
Фиг. 4 - дискретные сдвиги зависимости эстанс-потенциал на меди, обусловленные ступенчатым изменением внутреннего парциального заряда поверхности металла. Безразмерный наклон зависимости эстанс-потенциал приблизительно одинаков до и после каждого сдвига, выраженного ступенью эстанса в области потенциалов, расположенной положительнее нуля эстанса. При прохождении через нуль эстанса в положительном направлении наклон зависимости эстанс-потенциал снижается в полтора раза, но остается значительным.
Фиг. 5 - эквивалентная схема двойного электрического слоя на границе твердого металла с поверхностно-неактивной ионной жидкостью. Емкость Cm изолирующего покрытия замкнута постоянным сопротивлением Rm и прерываемым сопротивлением Ro, моделирующим квантованное шунтирование. Наблюдаемое в некоторых случаях размывание нуля эстанса на осциллограммах 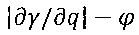 обусловлено снижением Rm. Приведенные графики рассчитаны для указанных параметров эквивалентной схемы, различающихся значениями Rm.
обусловлено снижением Rm. Приведенные графики рассчитаны для указанных параметров эквивалентной схемы, различающихся значениями Rm.
Фиг. 6 - схематический разрез поверхностного слоя металла при положительном суммарном избыточном поверхностном заряде. Увеличение суммарной плотности поверхностного заряда q=qin+qex (сдвиг к более положительным значениям) происходит за счет выхода электронов из поверхностного слоя металла при неподвижности среднего положения положительных ионов металла в узлах кристаллической решетки. Увеличение внешнего и внутреннего парциальных зарядов qex и qin также происходит путем потери ими электронов. Потери показаны, соответственно, длинной и короткой сплошными стрелками. Пунктирная стрелка обозначает обратное шунтирование. Кружки со знаком «минус» обозначают избыточные электроны. Кружки со знаком «плюс» обозначают избыточные ионы металла в его кристаллической решетке.
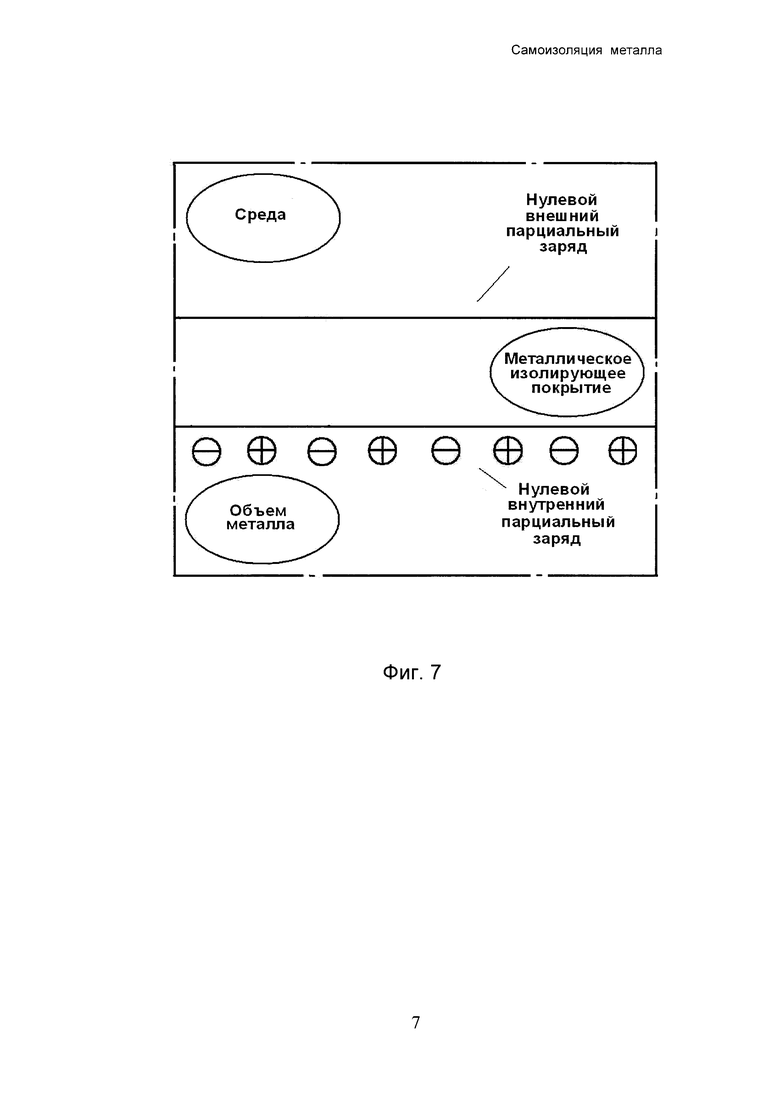
Фиг. 7 - схематический разрез поверхностного слоя металла при нулевом полном избыточном поверхностном заряде. Нулевой внешний парциальный заряд показан без электронного облака, которое соответствует компенсированному по заряду собственному дипольному скачку металла.
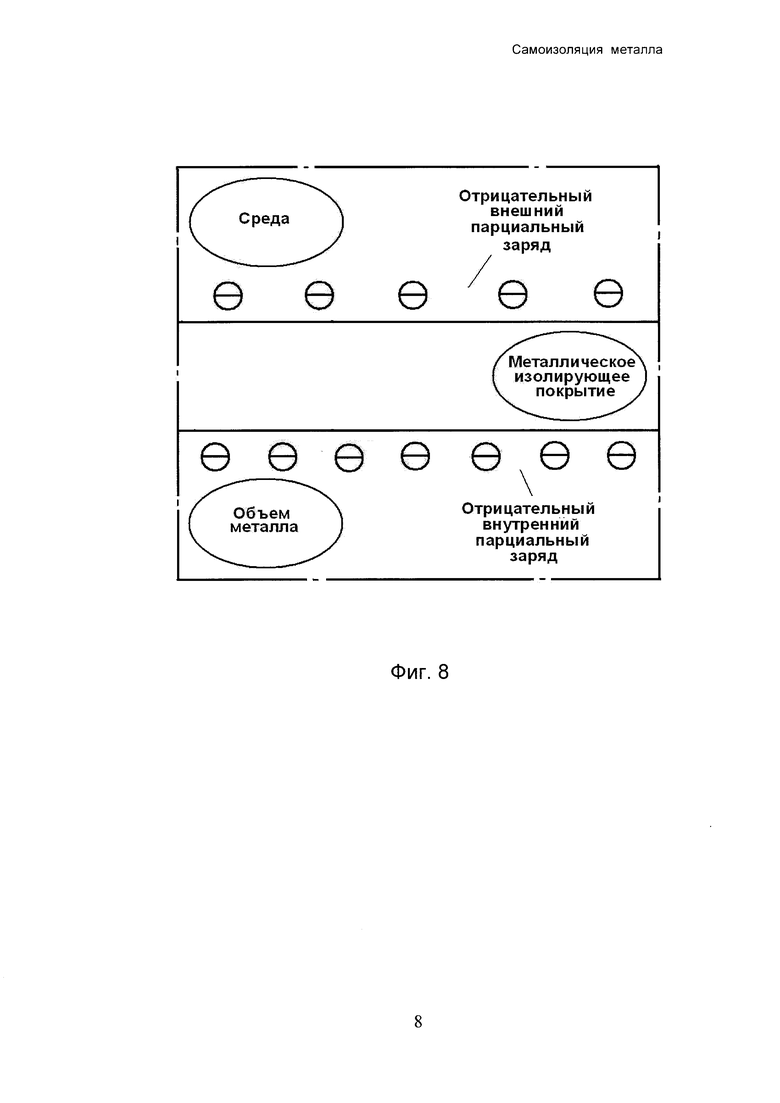
Фиг. 8 - схематический разрез поверхностного слоя металла при отрицательном полном избыточном поверхностном заряде, обе части которого (внутренняя и внешняя) образованы электронами.
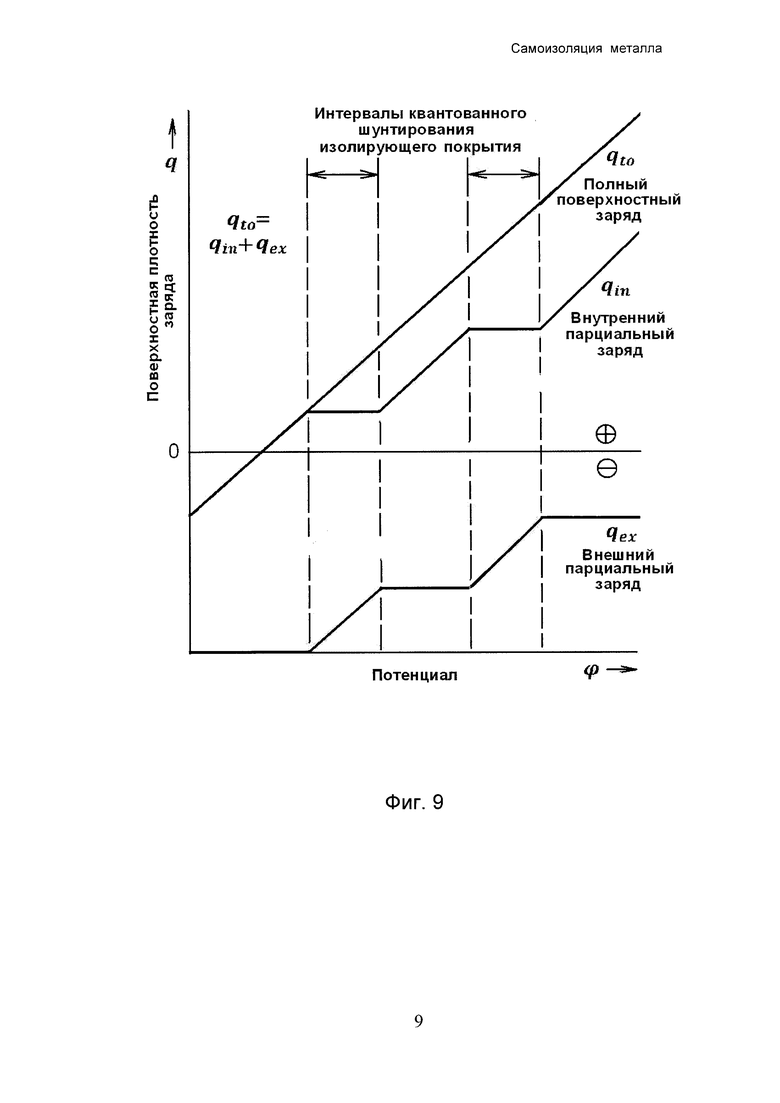
Фиг. 9 - схема образования ступеней внутреннего и внешнего парциальных зарядов, разделенных изолирующим покрытием. Взаимная компенсация ступеней исключает их влияние на суммарный поверхностный заряд.
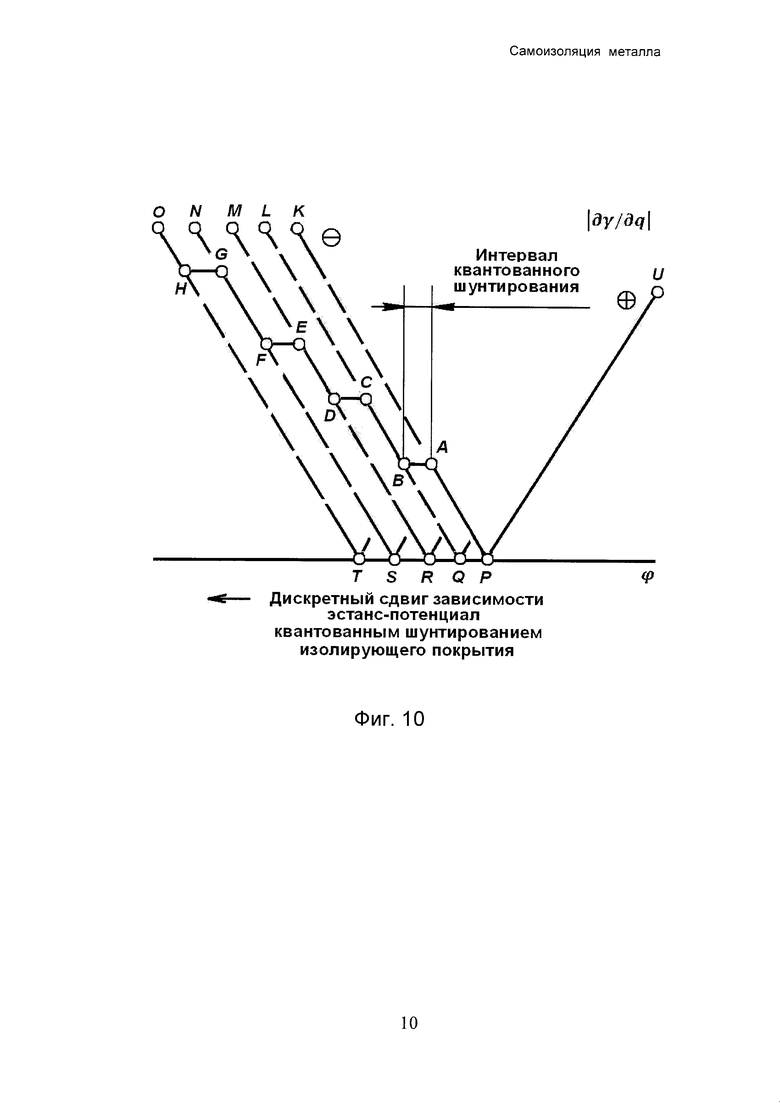
Фиг. 10 - схема формирования ступенчатой зависимости эстанс-потенциал (UPABCDEFGHO) путем повторения ступеней внутреннего парциального заряда.
На иллюстрациях и в описании приняты следующие обозначения:
γ - поверхностное натяжение твердого тела в форме электрода,
q - суммарная поверхностная плотность избыточного заряда электрода,
q=qin+qex,
собственный дипольный скачок металла вклада в избыточный заряд электрода не дает,
qin - внутренний парциальный заряд (часть плотности заряда q, расположенная под изолирующим покрытием),
qex - внешний парциальный заряд (часть плотности заряда q, расположенная над изолирующим покрытием),
φ - потенциал электрода, измеренный относительно электрода сравнения,
ϑ - относительное изменение площади границы раздела электрода с ионной жидкостью при упругой деформации электрода, имеющего с изотропную поликристаллическую поверхность,
∂γ/∂q - эстанс,
 - модуль (абсолютная величина) эстанса,
- модуль (абсолютная величина) эстанса,
φZ - нуль эстанса, то есть потенциал, соответствующий прохождению эстанса через нуль,
γqφ=∂(∂γ/∂q)/∂φ - безразмерный наклон зависимости эстанс-потенциал,
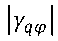 - модуль безразмерного наклона,
- модуль безразмерного наклона,
j - плотность электрического тока через границу электрода с ионной жидкостью,
С=∂q/∂φ - удельная дифференциальная емкость границы электрода с ионной жидкостью (здесь и далее удельные величины отнесены к единице площади границы фаз),
Cs - удельная дифференциальная емкость ионной части двойного слоя,
Cm - удельная дифференциальная емкость металлической части двойного слоя,
Ro - удельное прерываемое сопротивление изолирующего покрытия,
Rm - удельное постоянное сопротивление изолирующего покрытия,
φa - скачок потенциала в двойном электрическом слое на границе фаз,
РВЭ - равновесный водородный электрод,
НКЭ - насыщенный каломельный электрод,
в кГц указана частота колебаний поверхностного натяжения и поверхностной плотности заряда при регистрации эстанса как отношения амплитуд (Δγ и Δq) этих величин, ∂γ/∂q→Δγ/Δq при Δγ, Δq→0.
Ниже приведены два примера использования предложенного способа.
Пример 1. Электрод из платины приводят в контакт с водным раствором серной кислоты с концентрацией 0.5 моля на литр при температуре 20±2°С. На этом электроде регистрируют зависимость модуля эстанса 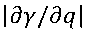 от потенциала φ, измеренного относительно равновесного водородного электрода (РВЭ) в том же растворе. Потенциал φ изменяют со скоростью 0.1 В/с сначала в катодном направлении, от +1.64 В до 0 В, затем в анодном направлении, от 0 В до +1.64 В (Фиг. 1). В тех же границах и в той же последовательности регистрируют зависимость плотности электрического тока j от потенциала φ при скорости изменения потенциала 0.2 В/с (Фиг. 2). Область поляризуемости платинового электрода ограничена волной разряда ионов водорода и волной анодного окисления металла. Данная область входит в указанный диапазон изменения потенциала.
от потенциала φ, измеренного относительно равновесного водородного электрода (РВЭ) в том же растворе. Потенциал φ изменяют со скоростью 0.1 В/с сначала в катодном направлении, от +1.64 В до 0 В, затем в анодном направлении, от 0 В до +1.64 В (Фиг. 1). В тех же границах и в той же последовательности регистрируют зависимость плотности электрического тока j от потенциала φ при скорости изменения потенциала 0.2 В/с (Фиг. 2). Область поляризуемости платинового электрода ограничена волной разряда ионов водорода и волной анодного окисления металла. Данная область входит в указанный диапазон изменения потенциала.
На зависимости эстанса от потенциала находят три ступени: одну ступень М1 в форме экстремума (максимум модуля эстанса) и две ступени М2, М3 в форме перегибов (Фиг. 1). Найденные ступени эстанса расположены в области потенциалов от φK=+0.35 В до φA=+0.83 В, в которой зависимость плотности электрического тока от потенциала, меняющегося в анодном (положительном) направлении, не имеет ни экстремума, ни перегибов (Фиг. 2). Указанная область потенциалов ограничена процессами окисления платины (при φ>φA) и адсорбции водорода (при φ<φK).
Потенциал нулевого заряда платины расположен отрицательнее этой области, которая поэтому соответствует положительному поверхностному заряду металла.
Измеряют безразмерный наклон γqφ=∂(∂γ/∂q)/∂φ зависимости эстанс-потенциал между указанными ступенями эстанса и оценивают его максимальную абсолютную величину. Между ступенями М2 и М3 безразмерный наклон отрицателен и достигает величины ∂(∂γ/∂q)/∂φ=-6.6. Соответственно, абсолютная величина указанного безразмерного наклона достигает значения 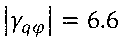 . Отсюда следует неравенство
. Отсюда следует неравенство  , показывающее значительное превосходство максимальной абсолютной величины безразмерного наклона над значением 1. При интерпретации полученного неравенства исходят из уравнения безразмерного наклона
, показывающее значительное превосходство максимальной абсолютной величины безразмерного наклона над значением 1. При интерпретации полученного неравенства исходят из уравнения безразмерного наклона
∂(∂γ/∂q)/∂φ=-1-(∂С/∂ϑ)/С-(∂γ/∂q)(∂C/∂φ)/С,
выведенного в цитированной книге автора. Член -1 отражает вклад электростатического отталкивания вдоль двойного электрического слоя в поверхностное натяжение. Остальные члены описывают более сложные взаимодействия.
Отсутствие перегибов на осциллограмме плотности тока в области ступеней эстанса указывает на малость величины (∂С/∂φ)/С, характеризующей изменение емкостного тока с потенциалом. Кроме того, в окрестности нуля эстанса, где ∂γ/∂q=0, мала величина ∂γ/∂q. Это позволяет в области ступеней эстанса пренебречь последним членом указанного уравнения и пользоваться упрощенным уравнением
∂(∂γ/∂q)/dφ=-1-(∂С/∂ϑ)/С.
Подставляют в это уравнение найденное значение ∂(∂γ/∂q)/∂φ=-6.6 и находят относительную производную дифференциальной емкости по упругой деформации (∂С/∂ϑ)/С=5.6. Отличие этой величины от нуля и, более того, значительность этой величины свидетельствуют о связи ступеней эстанса с электронными процессами в поверхностном слое металла, поскольку на границе твердого металла с ионной жидкостью только металл подвержен упругой деформации. Возможность существенного участия адсорбированных ионов и молекул жидкости в упругой деформации исключена отсутствием изменений электрического тока, которые бы соответствовали наблюдаемым ступеням эстанса.
Из найденной величины (∂С/∂ϑ)/С следует, что в поверхностном слое металла присутствует определенная электрическая емкость Cm, дополняющая электрическую емкость Cs ионной части двойного электрического слоя до общей емкости С,
C=CsCm/(Cs+Cm).
Исходя из существования электрической емкости Cm, обладающей изолирующим зазором, делают вывод о наличии у металла изолирующего покрытия, электрострикция которого увеличивает абсолютную величину безразмерного наклона зависимости эстанс-потенциал в промежутках между ступенями эстанса.
Происхождение ступеней эстанса объясняют расщеплением поверхностного заряда на две части, расположенные по обе стороны от изолирующего покрытия, под ним и над ним - соответственно, внутренний и внешний парциальные заряды.
Учитывая отсутствие изменений плотности электрического тока, соответствующих ступеням эстанса, делают вывод о поочередном приращении указанных частей поверхностного заряда при изменении потенциала, что создает у них взаимно компенсирующие ступени, не влияющие на суммарный поверхностный заряд, изменение которого создает электрический ток.
Из двух частей поверхностного заряда только внутренний парциальный заряд индуцирует электрострикцию изолирующего покрытия, дающую вклад в поверхностное натяжение и в регистрируемый эстанс. В этих условиях зависимость эстанса от потенциала повторяет ступени внутреннего парциального заряда.
Пример 2. Электрод из меди проводят в контакт с водным раствором фтористого натрия с концентрацией 0.1 моля на литр при температуре 20±2°С. Потенциал электрода измеряют относительно насыщенного каломельного электрода (НКЭ). Последовательно снимают осциллограммы модуль эстанса-потенциал,  , и плотность тока-потенциал, j - φ, которые совмещают на одной фотографии при сохранении общего начала отсчета потенциала (Фиг. 3). Потенциал изменяют со скоростью, соответственно, 0.1 В/с и 0.2 В/с, сначала в катодном и затем в анодном направлениях. Зависимость эстанса от потенциала снимают в интервале между -0.33 В и -1.82 В, который включает потенциал нуля эстанса φZ, практически совпадающий с потенциалом нулевого заряда меди. Область положительного поверхностного заряда металла расположена в данном случае при φ>φZ.
, и плотность тока-потенциал, j - φ, которые совмещают на одной фотографии при сохранении общего начала отсчета потенциала (Фиг. 3). Потенциал изменяют со скоростью, соответственно, 0.1 В/с и 0.2 В/с, сначала в катодном и затем в анодном направлениях. Зависимость эстанса от потенциала снимают в интервале между -0.33 В и -1.82 В, который включает потенциал нуля эстанса φZ, практически совпадающий с потенциалом нулевого заряда меди. Область положительного поверхностного заряда металла расположена в данном случае при φ>φZ.
На зависимости эстанса от потенциала, полученной в анодном направлении, находят четыре ступени: одну ступень М1 в форме экстремума (максимум модуля эстанса) и три ступени М2, М3, М4 в форме перегибов (Фиг. 3). Найденные ступени эстанса расположены в области потенциалов от φZ=-1.30 В до φM=-0.48 В, в которой зависимость плотности электрического тока от потенциала, меняющегося в анодном (положительном) направлении, не имеет ни экстремума, ни перегибов.
В пределах интервала φM>φ>φZ ступени эстанса практически полностью обратимы. Некоторое расхождение между прямым и обратным ходом осциллограммы эстанса, наблюдаемое на приведенной иллюстрации (Фиг. 3), обусловлено выходом потенциала развертки за указанные пределы и началом анодного окисления меди при потенциале -0.33 В. На осциллограмме плотности тока окисление меди выражено анодной волной, достигающей при -0.33 В максимума (обращенного вниз).
Измеряют безразмерный наклон γqφ=∂(∂γ/∂q)/∂φ зависимости эстанс-потенциал между указанными ступенями эстанса и оценивают его максимальную абсолютную величину. Между ступенями М2 и М3 безразмерный наклон отрицателен и достигает величины ∂(∂γ/∂q)/∂φ=-3.3. Отсюда следует неравенство 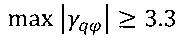 , показывающее значительное превосходство максимальной абсолютной величины безразмерного наклона над значением 1.
, показывающее значительное превосходство максимальной абсолютной величины безразмерного наклона над значением 1.
Интерпретацию полученного неравенства проводят аналогично рассмотренному случаю платины. Приходят к выводу о присутствии изолирующего покрытия, образованного атомами меди и расщепляющего поверхностный заряд металла на две части, которые меняются с потенциалом ступенчато. Показывают, что только внутренняя часть поверхностного заряда вызывает электрострикцию изолирующего покрытия. Появление ступеней эстанса объясняют ступенчатой зависимостью внутренней части поверхностного заряда от потенциала.
Включение изолирующего покрытия в поверхностный слой металла схематически представлено на фиг. 5-7 при нулевом, отрицательном и положительном суммарном поверхностном заряде. Соответствие между ступенями эстанса и внутренней части поверхностного заряда показано на фиг. 8, 9.
Остается загадкой физическая причина квантованного поочередного приращения двух частей поверхностного заряда, разделенных изолирующим покрытием. Однако факт существования такого квантованного процесса подтвержден экспериментально сериями ступеней эстанса, подобными друг другу на различных металлах.

Изобретение может быть использовано для изучения поверхностных явлений. Электрод из исследуемого металла приводят в контакт с ионной жидкостью. Регистрируют эстанс (производная поверхностного натяжения твердого тела по поверхностной плотности заряда) и ток как функции потенциала электрода. Находят ступени эстанса в форме экстремума и перегибов в интервале потенциалов, где зависимость тока от потенциала не имеет ступеней. Оценивают наклон зависимости эстанс-потенциал между ступенями эстанса. Показывают превосходство абсолютного значения этого наклона над единицей, из чего делают вывод о наличии у металла изолирующего покрытия, электрострикция которого дает вклад в поверхностное натяжение твердого тела. Отсутствие изменений тока, соответствующих ступеням эстанса, объясняют расщеплением поверхностного заряда металла изолирующим покрытием на внутреннюю и внешнюю части, имеющие взаимно компенсирующие ступени, причем только внутренняя, ступенчато меняющаяся часть вызывает в изолирующем покрытии электрострикцию, создающую ступени эстанса, тогда как ток обусловлен изменением суммарного заряда, не имеющего ступеней. Изобретение обеспечивает возможность экспериментально показать связь между спонтанным образованием изолирующего покрытия на металле, свободном от окисла, и расщеплением поверхностного заряда металла на две части, разделенные этим изолирующим покрытием. 10 з.п. ф-лы, 10 ил.
1. Способ демонстрации самоизоляции металла и расщепления его поверхностного заряда, отличающийся тем, что электрод из исследуемого металла приводят в контакт с ионной жидкостью, на указанном электроде регистрируют зависимости эстанса и плотности электрического тока от потенциала электрода, на зависимости эстанса от потенциала находят ступени в форме экстремума и перегибов, расположенные в том интервале потенциалов, где зависимость плотности электрического тока от потенциала, меняющегося в анодном направлении, не имеет ни экстремума, ни перегибов, оценивают безразмерный наклон зависимости эстанс-потенциал между ступенями эстанса, показывают превосходство максимального абсолютного значения этого наклона над единицей, из указанного превосходства делают вывод о наличии у металла изолирующего покрытия, которое составлено исключительно из атомов металла и электрострикция которого увеличивает абсолютную величину указанного наклона, а отсутствие изменений плотности электрического тока, соответствующих ступеням эстанса, объясняют расщеплением поверхностного заряда металла изолирующим покрытием на внутреннюю и внешнюю части, которые при изменении потенциала поочередно получают приращения заряда с образованием у них взаимно компенсирующих ступеней, причем из указанных частей только внутренняя, ступенчато меняющаяся часть вызывает в изолирующем покрытии электрострикцию, создающую ступени эстанса, тогда как электрический ток обусловлен изменением полного поверхностного заряда, не имеющего ступеней.
2. Способ по п. 1, отличающийся тем, что зависимость эстанса от потенциала регистрируют в координатах «модуль эстанса - потенциал».
3. Способ по п. 1, отличающийся тем, что в диапазон изменения потенциала включают область поляризуемости электрода.
4. Способ по п. 1, отличающийся тем, что в качестве исследуемого металла используют платину.
5. Способ по п. 4, отличающийся тем, что в качестве ионной жидкости используют водный раствор серной кислоты с концентрацией 0.5 моля на литр, зависимости эстанса и плотности электрического тока от потенциала регистрируют в диапазоне потенциала, включающем интервал от +0.8 В до +0.3 В относительно равновесного водородного электрода при изменении потенциала в анодном направлении.
6. Способ по п. 4, отличающийся тем, что в качестве ионной жидкости используют расплав фторида калия либо фторида натрия.
7. Способ по п. 1, отличающийся тем, что в качестве исследуемого металла используют медь.
8. Способ по п. 7, отличающийся тем, что в качестве ионной жидкости используют водный раствор фтористого натрия с концентрацией 0.1 моля на литр, зависимости эстанса и плотности электрического тока от потенциала регистрируют в диапазоне потенциала, включающем интервал от -1.8 В до -0.4 В относительно насыщенного каломельного электрода при изменении потенциала в анодном направлении.
9. Способ по п. 1, отличающийся тем, что в качестве исследуемого металла используют серебро.
10. Способ по п. 1, отличающийся тем, что в качестве исследуемого металла используют золото.
11. Способ по п. 1, отличающийся тем, что в качестве исследуемого металла используют никель.
| А.Я.Гохштейн | |||
| Метод эстанса, Успехи химии, т.XLIV, вып.11, 1975, 1956-1977 | |||
| СПОСОБ ДЕМОНСТРАЦИИ КВАНТОВЫХ ОСЦИЛЛЯЦИЙ ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ ТВЕРДОГО ТЕЛА | 2013 |
|
RU2552116C2 |
| УСТРОЙСТВО ДЛЯ РЕГИСТРАЦИИ ПЕРЕМЕННОГО ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ ТВЕРДЫХ ТЕЛ (ВАРИАНТЫ) | 2008 |
|
RU2369861C2 |
Авторы
Даты
2016-10-27—Публикация
2015-09-11—Подача