Изобретение относится к наглядным пособиям для изучения структуры электронных зон твердого тела.
Известно, что электрические свойства твердого тела определяются параметрами зон, каждая из которых образуется путем расщепления вырожденного уровня энергии, создаваемого одним из уровней электрона в атоме (Дж. Займан, Принципы теории твердого тела, изд. «Мир», Москва, 1974). На стр. 112 указанной книги процесс образования электронной зоны представлен наглядным образом:
«Возьмем N атомов и разместим их вдали друг от друга. Каждый атом обладает различными уровнями… При сближении атомов атомные функции перекрываются и уровни, ранее N-кратно вырожденные, расщепляются, образуя зоны. Каждому атомному уровню отвечает зона, содержащая N состояний. Можно говорить о 3s-зонах, 4p-зонах и т.д., возникающих из соответствующих атомных уровней.»
Аналогично образование зоны путем расщепления вырожденного уровня электрона описано в других известных руководствах по физике твердого тела. N-кратным вырождением (N-fold degeneracy) уровня именуется совпадение энергий определенного электронного уровня у N одинаковых атомов до их сближения и объединения в твердое тело, состоящее из этих N атомов. Необходимость расщепления следует из принципа Паули (Pauli exclusion principle), согласно которому в квантовой системе два электрона не могут одновременно находиться в одном состоянии. Размещение двух электронов на одном уровне энергии допустимо, если их спины противоположны, что делает состояния этих электронов различными.
В общем виде принцип Паули относится к фермионам (тождественным частицам с полуцелым спином) и равносилен тому, что волновая функция системы одинаковых фермионов должна быть антисимметричной относительно перестановки любых двух фермионов. Совпадение состояний двух или более фермионов обращает такую волновую функцию в нуль и потому в указанной системе невозможно.
В книге С. Hermann, Statistical Physics Including Applications to Condensed Matter, Springer, New York, 2005, page 187:
"FIG. 8.7. In a N atom crystal, to each atomic state corresponds a band that can accommodate 2N times more electrons than the initial state."
В книге J. Solyom, Fundamentals of the Physics of Solids, Vol. 2, Electronic properties, Springer Berlin Heidelberg, 2009, page 140:
"As long as the atoms are far from each other, the same atomic energy levels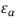 
appear for each atom. For N atoms the levels are at least N-fold degenerate. Electrons occupy these highly degenerate atomic states. When the lattice constant is reduced, the overlap between atomic functions gradually increases, energies become shifted from the atomic values, and the multiple degeneracy is lifted. As shown in Fig 18.21 schematically, the energies form broader and broader bands as the lattice constant decreases."
Согласно первой ссылке (Дж. Займан), число состояний в электронной зоне равно числу N атомов в образце твердого тела. Размер образца произволен и число атомов в нем может быть любым. Отсюда следует, что увеличение размера образца способно привести к беспредельному расщеплению одного атомного уровня энергии, которому соответствует зона.
Ширина W электронной зоны не зависит от числа атомов и ограничена (обычно W≤10 эВ). Поэтому беспредельный рост числа атомов и числа различных состояний равносилен беспредельному уменьшению интервалов энергии между смежными состояниями внутри зоны.
Согласно второй ссылке (С. Hermann), электронная зона способна вместить 2N электронов. Смысл обоих утверждений одинаков, поскольку в одном состоянии могут находиться два электрона с противоположными спинами в соответствии с принципом Паули.
Ввиду аналогии в содержании приведенных трех цитат (авторы Дж. Займан, С. Hermann, J. Solyom) вторая и третья цитаты даны без перевода английского текста и без рисунков.
Число атомов N в образце пропорционально объему V образца, N=nV, где n - число атомов на единицу объема. Число электронов проводимости в образце составляет ZN, где Z - валентность металла. У меди n=8.47⋅1022 см-3 при 20°С и Z=1.
Приближенно (без учета неравномерности распределения состояний) средний интервал ΔE(V) между ближайшими состояниями в электронной зоне может быть оценен по порядку величины отношением W/(2N),
ΔE(V)≈W/(2nV).
Примерами двух образцов разного объема могут служить намотанный на катушку медный провод длиной 1000 м и отрезанный от него кусок длиной 1 м. При сечении провода 1 мм2 расход энергии на операцию реза достаточно мал, не зависит от исходной длины провода и не должен значительно повлиять на состояние меди в куске.
Однако согласно известному представлению, описанному в цитированной литературе, влияние операции реза должно возрастать при увеличении объема образца металла. Так, в примере с катушкой провода при начальном объеме образца меди V0=1000 см3 отделение куска с объемом V1=1 см3 должно увеличить в этом куске средний интервал между ближайшими состояниями в тысячу раз, причем независимо от сечения провода и, соответственно, от расхода энергии на отделение куска:
ΔE(V0)≈10 эВ/(2⋅8.47⋅1022 см-3⋅1000 см3)=5.90⋅10-26 эВ,
ΔE(V1)≈10 эВ/(2⋅8.47⋅1022 см-3⋅1 см3)=5.90⋅10-23 эВ.
Таким образом, известно представление о возможности расщепления одного уровня энергии электрона в отдельном атоме на неограниченное число различающихся по энергии состояний в любой электронной зоне твердого тела, составленного из произвольного числа атомов. Это равносильно измельчению интервалов между состояниями до исчезающе малых величин, практически не доступных измерению (как в приведенном примере с медным проводом). Из известного представления следует, что рельеф электронной зоны металла представляет собой дискретное множество отличающихся по энергии состояний, но не доступен наглядному восприятию из-за неразличимости отдельных состояний.
Экспериментальная проверка известного представления до последнего времени не проведена из-за отсутствия технических средств, обеспечивающих измерение интервалов между ближайшими уровнями энергии в какой-либо зоне твердого тела и сравнение этих интервалов при различных объемах исследуемого образца.
Способы демонстрации рельефа зоны проводимости металла не известны.
Известен и использован в настоящем изобретении метод регистрации переменного поверхностного натяжения твердых тел (метод эстанса), впервые предложенный автором и подробно им описанный (авт. свид. СССР 178161, МПК G01N 13/00, 08.01.1966, Бюл. №2; авт. свид. СССР 277399, МПК G01N 13/02, 22.07.1970, Бюл. №24; Электрохимия, 1966, том 2, с. 1061; Доклады АН СССР, 1969, том 187, с. 601; Electrochimica Acta, 1970, vol. 15, p. 219; книга «Поверхностное натяжение твердых тел и адсорбция», Москва, изд. «Наука», 1976, 400 с.; Успехи физических наук 2000, том 170, с. 779; J. Solid State Electrochemistry 2013, vol. 17, p.1743; патент РФ 2552116, МПК G01N 13/00, 10.06.2015, Бюл. №16; патент РФ 2601921, МПК G09B 23/18, 10.11.2016, Бюл. №31).
Известен также предложенный автором ранее блок электрода, включающий исследуемый электрод, скрепленный с пьезоэлементом и смоченный ионной жидкостью, находящейся в резервуаре (Гохштейн А.Я. «Поверхностное натяжение твердых тел и адсорбция», Москва, изд. «Наука», 1976). Конструкция известного блока электрода не предусматривает возможность изменения объема электрода с сохранением неизменными его контактов с пьезоэлементом и с ионной жидкостью, что является недостатком применительно к настоящему изобретению.
Перед настоящим изобретением поставлены две задачи: 1) обеспечить возможность экспериментальной оценки интервала между ближайшими дискретными уровнями энергии в зоне проводимости металла, получить таким путем данные на образцах различного объема, путем сравнения этих данных продемонстрировать дискретный рельеф зоны проводимости металла, а также независимость этого рельефа от занимаемого металлом объема, 2) обеспечить возможность изменения объема электрода из исследуемого металла при сохранении неизменными контактов электрода с пьезоэлементом и с ионной жидкостью.
Первая из задач, поставленных перед изобретением, решена благодаря тому, что из исследуемого металла изготавливают электроды, различающиеся объемом, превосходящим 1 мм3, приводят каждый электрод в контакт с ионной жидкостью, задают потенциал электрода, регистрируют производную поверхностного натяжения электрода по поверхностной плотности заряда электрода как функцию потенциала электрода, определяют область потенциала, соответствующую положительному заряду электрода, и в этой области у полученной функции находят последовательность ступеней, которую рассматривают как образ последовательности дискретных состояний зоны проводимости металла, на одном и том же интервале потенциала электрода сравнивают числа ступеней, найденные на электродах различного объема, совпадение найденных чисел ступеней интерпретируют как доказательство независимости интервалов между дискретными состояниями зоны проводимости металла от объема, занимаемого этим металлом.
Указанную независимость связывают с пространственным ограничением действия принципа Паули, допускают существование предельного объема, в котором возможно классическое расщепление вырожденных уровней энергии и который заведомо меньше чем 1 мм3, характеризуют указанный предельный объем радиусом равновеликого шара, именуемым радиусом расщепления.
Отмечают превосходство безразмерного наклона указанной функции над единицей, рассматривают это превосходство как признак электрострикции диэлектрического наружного монослоя атомов металла, разделяющего поверхностный заряд на внешний и внутренний заряды, сообщающиеся путем туннельного переноса электронов, ступенчатый вид указанной функции объясняют повторением туннельного переноса при последовательном сближении потенциала электрода с расположенными в виде ряда значениями, соответствующими дискретным состояниям зоны проводимости металла, обращение указанной функции в нуль связывают с приближением потенциала электрода к границе заполнения зоны проводимости.
Указанную функцию регистрируют в виде осциллограмм в координатах
⎢∂γ/∂q⎢-ϕ,
где γ - поверхностное натяжение электрода,
q - поверхностная плотность заряда электрода,
ϕ - потенциал электрода,
развертку потенциала электрода производят в анодном и катодном направлениях в диапазоне потенциала, включающем области восстановленной и окисленной поверхности металла.
Ступени указанной функции выявляют по колебаниям наклона ∂⎢∂γ/∂q⎢/∂ϕ регистрируемой осциллограммы вдоль оси потенциала, которые выражаются в чередовании спадов и подъемов указанного наклона.
Отмечают сходство последовательности ступеней с графиком величины y=⎢sin x⎢, имеющим скачки наклона в минимумах, вследствие чего именно минимумы регистрируемой функции ⎢∂γ/∂q⎢ ставят в соответствие дискретным состояниям зоны проводимости металла, при этом интервалы потенциала между минимумами регистрируемой функции ⎢∂γ/∂q⎢ рассматривают как образ интервалов энергии между дискретными состояниями зоны проводимости.
Отмечают совпадение дугообразной формы указанной функции между ее минимумами в областях восстановленной и окисленной поверхности металла, откуда делают вывод о сохранении туннельного сообщения между внутренним и внешним зарядами при образовании между этими зарядами окисной пленки.
Сравнивают интервалы между минимумами регистрируемой функции ⎢∂γ/∂q⎢ в областях восстановленной и окисленной поверхности металла, находят, что окисление поверхности металла уменьшает интервалы между указанными минимумами, объясняют это тем, что окисление поверхности металла увеличивает относительную долю металла в межфазном скачке потенциала по сравнению с долей ионной жидкости, что меняет масштаб регистрируемого образа состояний зоны проводимости при сохранении самих этих состояний неизменными.
Различимость выделенных ступеней используют для оценки интервала энергии между дискретными состояниями зоны проводимости металла, рассматривают указанную различимость как признак превосходства этого интервала над энергией теплового движения
ΔEb≥kBT,
где ΔEb - интервал энергии между дискретными состояниями зоны проводимости металла,
kB=1.3807⋅10-23 Дж⋅K-1 - постоянная Больцмана,
Т - температура.
Интервал потенциала между ближайшими минимумами регистрируемой величины ⎢∂γ/∂q⎢ используют для оценки радиуса расщепления в поверхностном слое исследуемого металла, применяют формулу
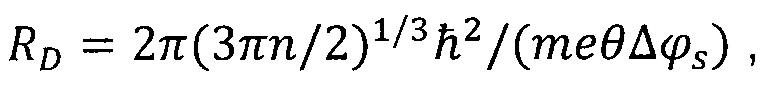
где RD - радиус расщепления, n - численная плотность электронов проводимости в металле,
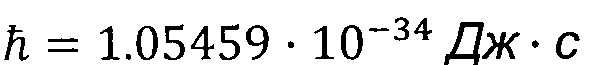- постоянная Планка,
m=0.911⋅10-30 кг - масса электрона,
е=1.60219⋅10-19 Кл - заряд электрона,
Δϕs - интервал потенциала между ближайшими ступенями регистрируемой величины ⎢∂γ/∂q⎢.
θ≥Δϕb/Δϕs - доля металла в межфазном скачке потенциала на границе металла с ионной жидкостью, Δϕb=ΔEb/e, θ≥0.1.
В качестве исследуемых металлов используют медь, платину, кобальт, никель, серебро, золото в монолитном виде и в виде гальванических покрытий.
В качестве ионных жидкостей используют водные растворы гидроокиси калия, фтористого натрия, фтористого калия и серной кислоты, расплавы фтористого натрия и фтористого калия.
При исследовании меди водный раствор гидроокиси калия готовят в концентрации 0.1 моль на литр, потенциал измеряют в шкале насыщенного каломельного электрода, развертками потенциала охватывают диапазон от -1.7 В до +0.3 В, а началом окисления поверхности металла считают потенциал -0.4 В при анодном направлении развертки потенциала в соответствии с волной тока анодного окисления на зависимости тока от потенциала.
У меди на осциллограмме анодного направления выявляют шесть минимумов величины ⎢∂γ/∂q⎢, из которых три минимума расположены в области потенциала, где поверхность меди свободна от окисла, остальные - в области потенциала, где поверхность меди окислена. На осциллограмме катодного направления выявляют три минимума величины ⎢∂γ/∂q⎢, которые ставят в соответствие трем состояниям зоны проводимости в поверхностном слое меди, свободном от окисла.
Используют значения n=8.4⋅1028 м-3, Δϕs=0.3 В, Т=293 K, θ≥0.1 и находят таким путем оценку RD≤1.175⋅10-7 м=1.175⋅10-4 мм=117.5 нм для радиуса расщепления в поверхностном слое меди, свободном от окисла.
Область потенциала, соответствующую окисленной поверхности металла, определяют по развитию гистерезиса величины ⎢∂γ/∂q⎢ в этой области и по волнам анодного тока на осциллограмме зависимости тока от потенциала.
Используют образцы исследуемого металла, различающиеся степенью чистоты в диапазоне от 99.9% до 99.99%, а также толщиной в диапазоне от 10 мкм до 1 мм, независимость числа выделенных ступеней от степени чистоты и толщины образца в указанных диапазонах считают признаком, исключающим определяющее влияние примесей и размера кристаллических зерен на механизм образования выделенных ступеней в указанном диапазоне чистоты исследуемого металла.
Вторая из задач, поставленных перед изобретением, решена благодаря тому, что в известном блоке электрода, включающем исследуемый электрод, скрепленный с пьезоэлементом и смоченный ионной жидкостью, находящейся в резервуаре, исследуемый электрод дополнен монолитно связанным с ним шлейфом, который выполнен с возможностью двукратного сокращения объема исследуемого электрода при сохранении неизменными контактов исследуемого электрода с пьезоэлементом и с ионной жидкостью.
Шлейф выходит из резервуара через отверстие в крышке резервуара и закреплен в этом отверстии пробкой с возможностью укорочения части шлейфа, находящейся вне резервуара. Внутри резервуара шлейф имеет зигзагообразный участок. На зигзагообразном участке шлейфа выполнено сужение. Держатель электрода выполнен в форме бруска с двумя взаимно перпендикулярными отверстиями, в одном из отверстий находится шток, в другом отверстии находится винт с возможностью закрепления электрода
Производную ∂γ/∂q называют эстансом. Сохраняют (для краткости) этот термин и для абсолютного значения ⎢∂γ/∂q⎢ этой величины.
Физической предпосылкой новизны и полезности изобретения является соответствие между дискретными состояниями зоны проводимости металла и ступенями производной поверхностного натяжения металла по поверхностной плотности заряда. Данное соответствие использовано в настоящем изобретении впервые. Это стало возможным благодаря методу эстанса, который ранее был предложен автором изобретения и позволил впервые измерить экспериментально изменение поверхностного натяжения твердых тел, что признано в международной научной литературе. Настоящее изобретение расширяет применения метода эстанса в области образования.
Сделано доступным изображение дискретного рельефа зоны проводимости металла. Найдена возможность следить за рельефом зоны проводимости при изменении объема металла. Наглядно показана независимость рельефа от объема, откуда следует существование предельного объема, ограничивающего расщепление вырожденного уровня энергии.
Описываемый механизм зондирования зоны проводимости металла имеет квантовую природу и использует явление поверхностной самоизоляции металла. Оно обнаружено автором ранее по аномальному безразмерному наклону зависимости «эстанс-потенциал» в окрестности потенциала нулевого заряда металла в электролитической среде при полном отсутствии окисла на поверхности металла. Значительное превосходство указанного наклона над единицей выявляет электрострикцию наружного монослоя атомов металла, что свидетельствует о диэлектрическом состоянии этого монослоя.
Будучи изолятором, наружный монослой металла расщепляет поверхностный заряд металла на две части. Внутренняя часть заряда принадлежит кристаллической решетке и определяется соотношением между электронами и положительными ионами металла. Наружная часть заряда образована электронным облаком над поверхностью кристаллической решетки металла. Обе части заряда сообщаются между собой путем туннельного переноса электрона через изолирующий монослой металла.
Туннельный перенос происходит при равенстве энергий исходного и конечного состояний электрона. Со стороны кристаллической решетки состояние электрона входит в фиксированный набор дискретных состояний зоны проводимости металла. Со стороны среды энергия электрона зависит от скачка потенциала на границе металла со средой. При линейном росте скачка потенциала туннельный перенос электрона совершается только в моменты соответствия этого скачка одному из дискретных состояний зоны проводимости.
В масштабе макроскопического образца металла коллективный туннельный перенос большого числа электронов развивается в окрестностях усредненных дискретных состояний. На осциллограмме эстанс-потенциал этот процесс выражен последовательностью минимумов, которые являются образами дискретных состояний зоны проводимости.
Перемещение электрона от внешнего поверхностного заряда к внутреннему не меняет суммарного поверхностного заряда, который поэтому не обнаруживает отклонений, связанных с туннельным переносом, и меняется практически линейно с потенциалом. Это подтверждается осциллограммой ток-потенциал, достаточно гладкой там, где осциллограмма эстанс-потенциал обнаруживает регулярные колебания с образованием серии минимумов.
Отсутствие реакции тока на процесс туннельного переноса электрона парадоксально. Оно является ключевым эффектом в демонстрации рельефа зоны проводимости путем регистрации переменного поверхностного натяжения твердого тела. Дело в том, что электрострикция изолирующего наружного монослоя атомов металла создается только внутренней частью поверхностного заряда, которая испытывает скачок при туннельном обмене электроном с внешней частью поверхностного заряда. Изменение электрострикции наружного монослоя атомов приводит к регистрируемому изменению поверхностного натяжения. В то же время обмен между частями поверхностного заряда не затрагивает суммарной величины поверхностного заряда и не дает поэтому вклада в электрический ток.
Таким образом, достаточно нетривиальное явление - образование чисто металлического изолирующего поверхностного слоя - позволяет решить другую нетривиальную задачу - прозондировать рельеф зоны проводимости металла.
Существование изолирующего монослоя металла следует из экспериментальных данных эстанса в сочетании с уравнениями электрокапиллярности твердых тел, полученными автором ранее (1969 г.). Применительно к поликристаллическим образцам металлов уравнения имеют вид:
∂γ/∂q=∂ϕ/∂ϑ,
∂γ/∂ϕ=-q-∂q/∂ϑ,
где γ - поверхностное натяжение электропроводного твердого тела,
q - поверхностная плотность заряда,
ϕ - потенциал твердого тела как электрода относительно среды,
ϑ - относительное упругое приращение площади S поверхности твердого тела.
Изменение γ измеряется при ϑ=const. Изменение q измеряется при ϕ=const. Изменение ϕ измеряется при Sq=const, то есть в режиме разомкнутой цепи, гарантирующем постоянство полного заряда твердого тела.
Из уравнений электрокапиллярности твердых тел следует уравнение для безразмерного наклона зависимости эстанс-потенциал:
∂(∂γ/∂q)/∂ϕ=-1-(∂C/∂ϑ)/C-(∂γ/∂q)(∂C/∂ϕ)/C,
где С=∂q/∂ϕ - емкость двойного электрического слоя на границе твердого тела с ионной жидкостью (сокращенно - емкость двойного слоя). В окрестности потенциалов нулевого эстанса (∂γ/∂q=0) и экстремумов емкости (∂C/∂ϕ=0, min С, max С) это уравнение приобретает упрощенную форму:
∂(∂γ/∂q)/∂ϕ=-1-(∂C/∂ϑ)/C,
⎢∂(∂γ/∂q)/∂ϕ⎢=1+(∂C/∂ϑ)/C.
При этом величина (∂C/∂ϑ)/C>0 может быть найдена по наклону
⎢γqϕ⎢=⎢∂(∂γ/∂q)/∂ϕ⎢,
известному из осциллограммы ⎢∂γ/∂q⎢-ϕ.
Емкость С двойного слоя может быть представлена в виде последовательно соединенных емкости Cm металлической части двойного слоя и емкости Cs электролитической части двойного слоя
C=CmCs/(Cm+Cs)=Cs/[1+(Cs/Cm)],
(∂C/∂ϑ)/C<(Cs/Cm)(∂Cm/∂ϑ)/Cm.
С≈Cs, (∂C/∂ϑ)/C<<(∂Cm/∂ϑ)/Cm при Cs<<Cm.
В первом приближении емкость Cm может рассматриваться как емкость плоского конденсатора с эффективными толщиной δm и проницаемостью ∈m прокладки
Cm=∈o∈m/δm,
где ∈o - электрическая постоянная.
При упругой деформации
(∂∈m/∂ϑ)/∈m=(∂Cm/∂ϑ)/Cm+(∂δm/∂ϑ)/δm.
Изменение толщины ограничено эффективным коэффициентом Пуассона ν:
(∂δm/∂ϑ)/δm=-ν/(1-ν),
0≤(∂Cm/∂ϑ)/Cm=(∂∈m/∂ϑ)/∈m-(∂δm/∂ϑ)/δm,
ν≤1/2, 0≤ν/(1-ν)≤1.
Отсюда
(∂δm/∂ϑ)/δm>-1,
(∂∈m/∂ϑ)/∈m>(∂Cm/∂ϑ)/Cm-1>(∂C/∂ϑ)/C-1.
Обычно из опыта ⎢γqϕ⎢≥5, откуда следуют оценки (∂C/∂ϑ)/C≥4 и
(∂∈m/∂ϑ)/∈m≥3,
что является признаком электрострикции металлической части двойного слоя. Независимо от этой оценки изолирующий характер металлической части двойного слоя следует из наблюдаемого повторения туннельных переходов.
Сущность изобретения поясняется следующими чертежами.
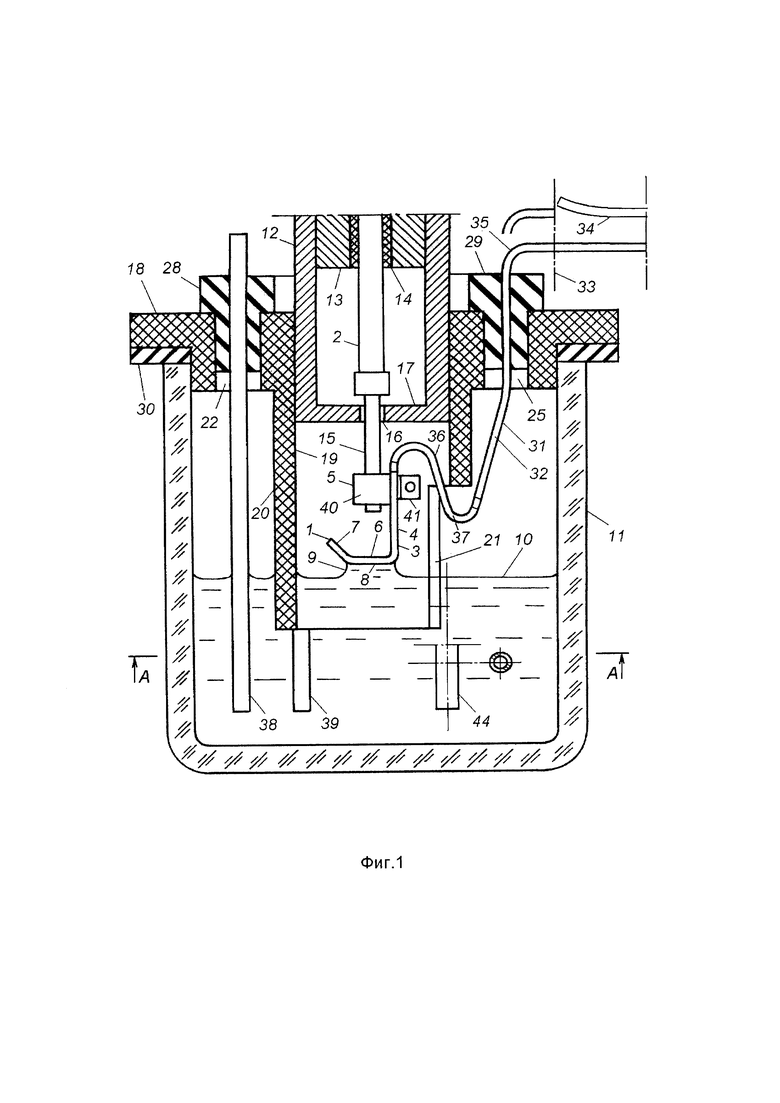
Фиг. 1 - блок электрода, общий вид.
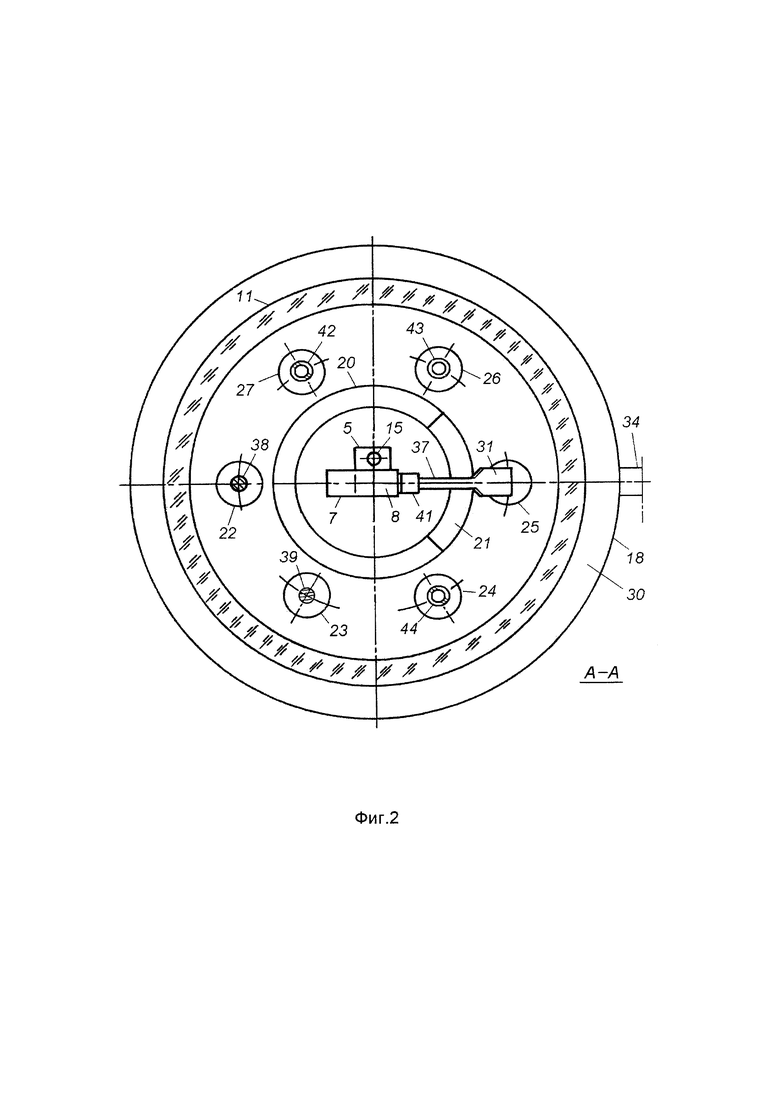
Фиг. 2 - разрез А-А на фиг. 1, вид снизу.
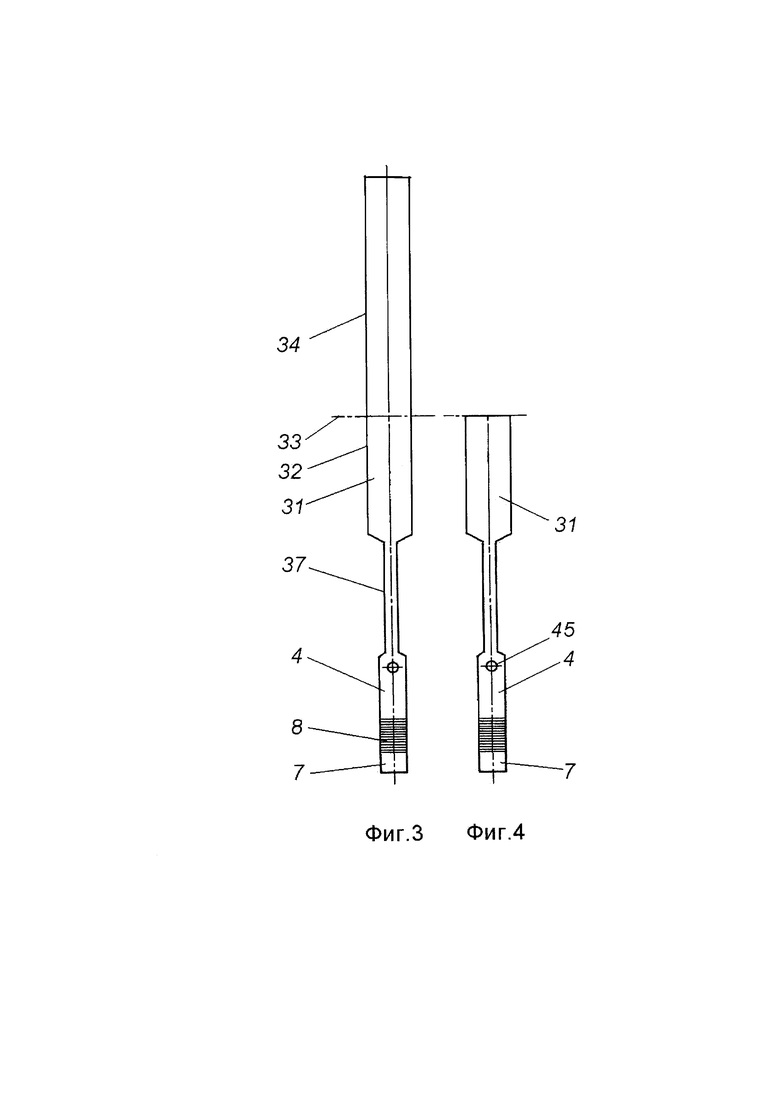
Фиг. 3 - заготовка электрода в форме плоской полосы меди с возможностью отреза части полосы для уменьшения объема исследуемого образца металла.
Фиг. 4 - используемый в качестве электрода остаток полосы меди после разреза полосы и восстановления ее плоской формы.
Фиг. 5 - медный исследуемый электрод со шлейфом, проходящим через отверстие в крышке резервуара (фотография).
Фиг. 6 - зигзагообразный участок шлейфа (фотография).
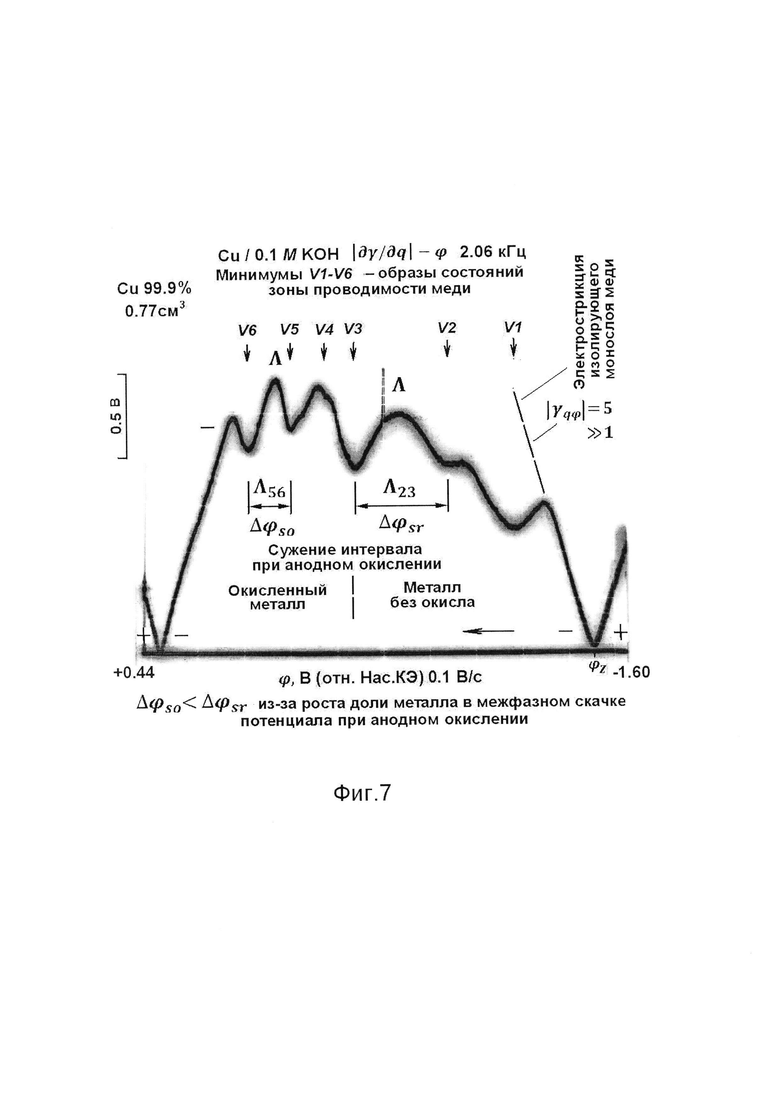
Фиг. 7 - осциллограмма ⎢∂γ/∂q⎢-ϕ на меди 99.9% в водном растворе гидроокиси калия, снятая при анодном направлении развертки потенциала при объеме электрода 0.77 см3 до разреза полосы меди. Концентрация раствора 0.1 моль на литр. Частота заданного переменного тока и регистрируемых колебаний поверхностного натяжения 2.06 кГц. Скорость изменения потенциала 0.1 В/с. Потенциал ϕ исследуемого электрода указан в шкале насыщенного каломельного электрода (Нас.КЭ). Масштаб 0.5 В указан для ⎢∂γ/∂q⎢. Символами V (V1-V6) обозначены минимумы величины ⎢∂γ/∂q⎢, ⎢γqϕ⎢=⎢∂(∂γ/∂q)/∂ϕ⎢ - абсолютная величина безразмерного наклона в координатах ⎢∂γ/∂q⎢-ϕ. Λ - дугообразные участки осциллограммы между минимумами ⎢∂γ/∂q⎢, Λ23>Λ56 - интервалы потенциала между минимумами до и после анодного окисления поверхности меди. Сужение интервала при образовании окисла - эффект изменения масштаба вдоль оси потенциала из-за роста доли θ металла в межфазном скачке потенциала при неизменной величине интервала между состояниями зоны проводимости.
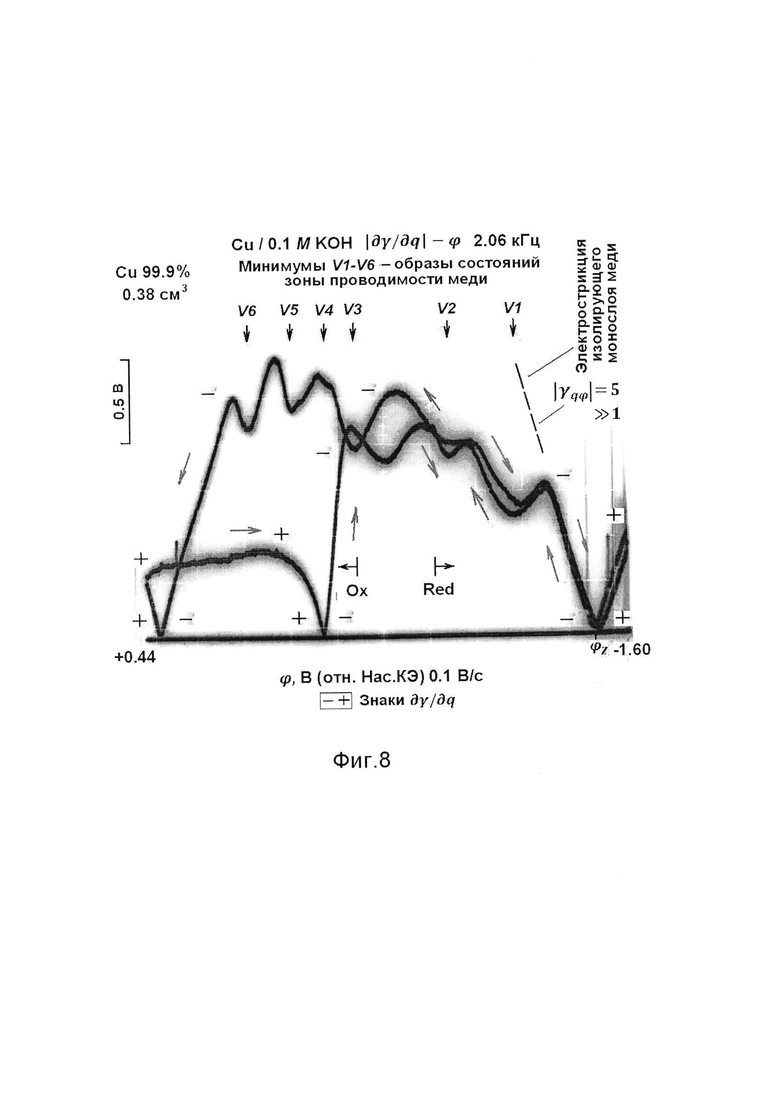
Фиг. 8 - осциллограмма ⎢∂γ/∂q⎢-ϕ в условиях фиг. 7, снятая на первых развертках в катодном и анодном направлениях сразу после разреза полосы меди с уменьшением объема электрода до 0.38 см3. Сохранение всех шести минимумов V1-V6 (фиг. 7) после двукратного уменьшения объема электрода (фиг. 8) показывает независимость интервалов между дискретными состояниями зоны проводимости меди от объема электрода. Стрелки «Ох» и «Red» указывают начало окисления металла при анодном направлении развертки и полное освобождение металла от окисла при катодном направлении развертки.
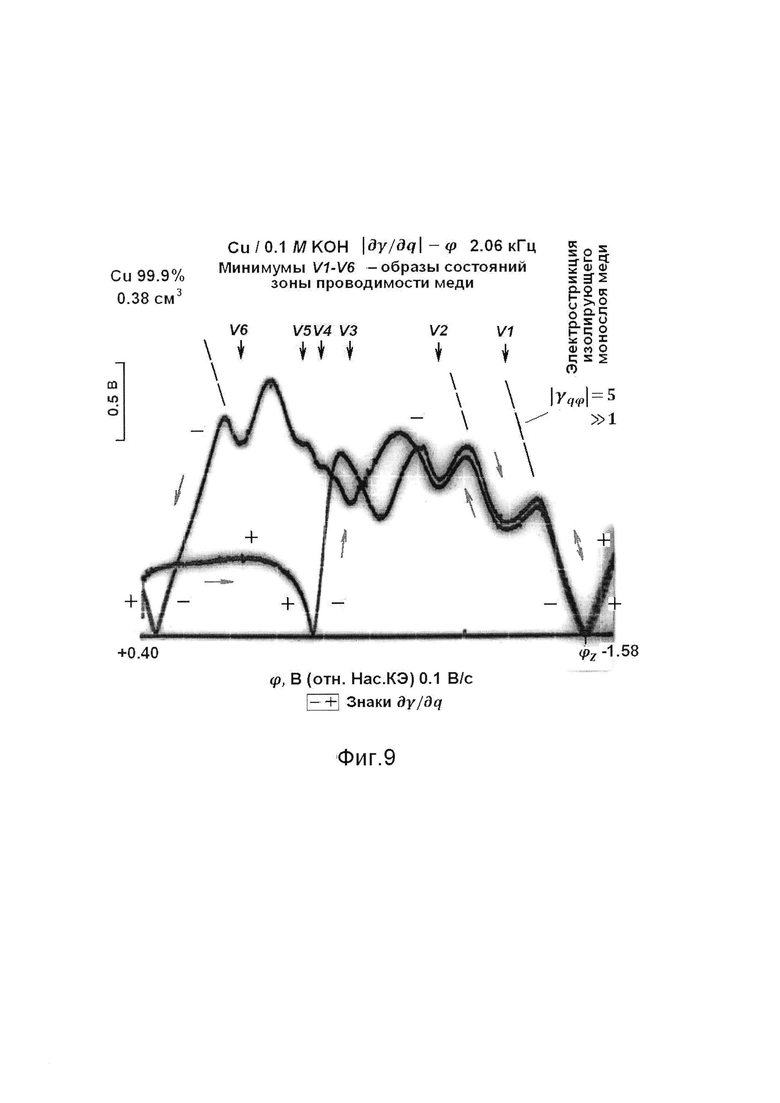
Фиг. 9 - осциллограмма ⎢∂γ/∂q⎢-ϕ на меди в условиях фиг. 8 после повторения 11 циклов разверток.
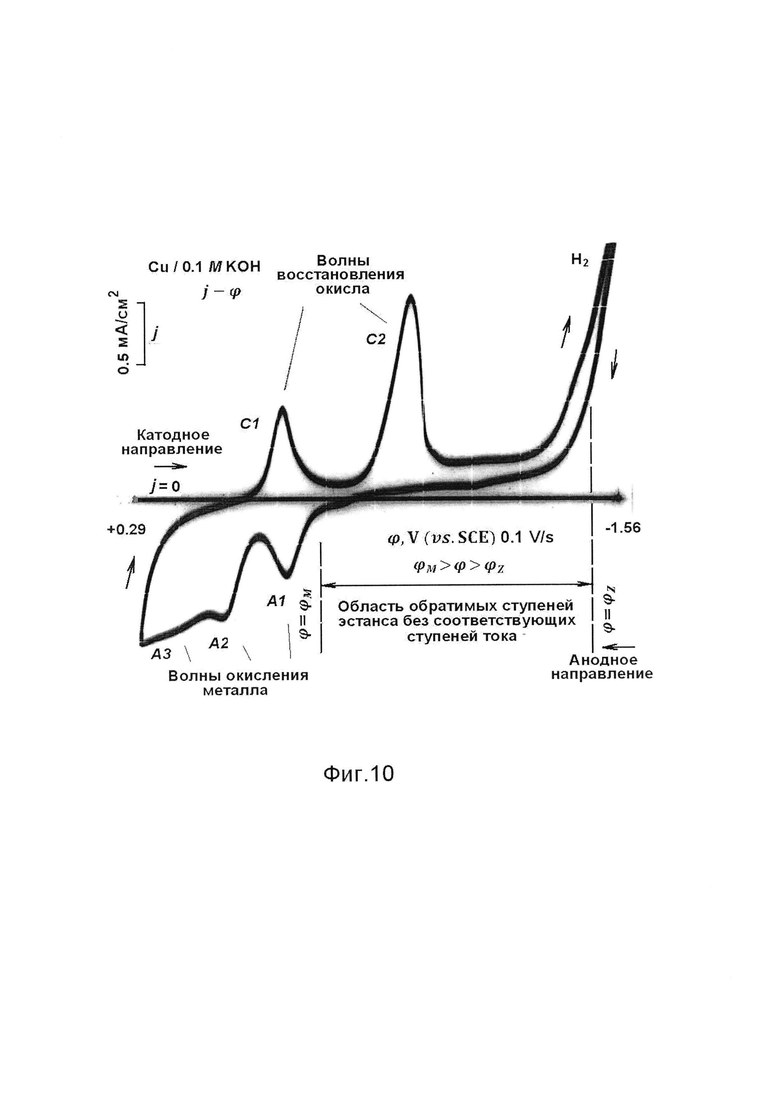
Фиг. 10 - осциллограмма «поверхностная плотность тока - потенциал», j-ϕ, на меди в водном растворе гидроокиси калия в условиях фиг. 9 (наравне с терминами «поверхностная плотность тока» и «поверхностная плотность заряда» в настоящем описании используются их очевидные сокращения: «ток» и «заряд»).
Отсутствие ступеней тока в области потенциала, где возникают минимумы V1, V2, V3 эстанса, объясняют изолирующим свойством наружного монослоя меди, который расщепляет поверхностный заряд на внутреннюю и внешнюю части. Эстанс ∂γ/∂q определяется ступенчато нарастающим внутренним зарядом. Ток j создается изменением суммарного заряда, который нарастает без ступеней, почти линейно при линейном нарастании потенциала развертки.
Волны тока, расходуемого на анодное окисление меди (положительнее потенциала ϕOx=-0.52 В), показывают, что три минимума V4, V5, V6 эстанса находятся в области потенциала, где медь покрыта слоем окисла. Таким образом, присутствие окисла не нарушает механизма образования минимумов эстанса, чем подтверждается связь этого механизма с туннельным переносом электронов.
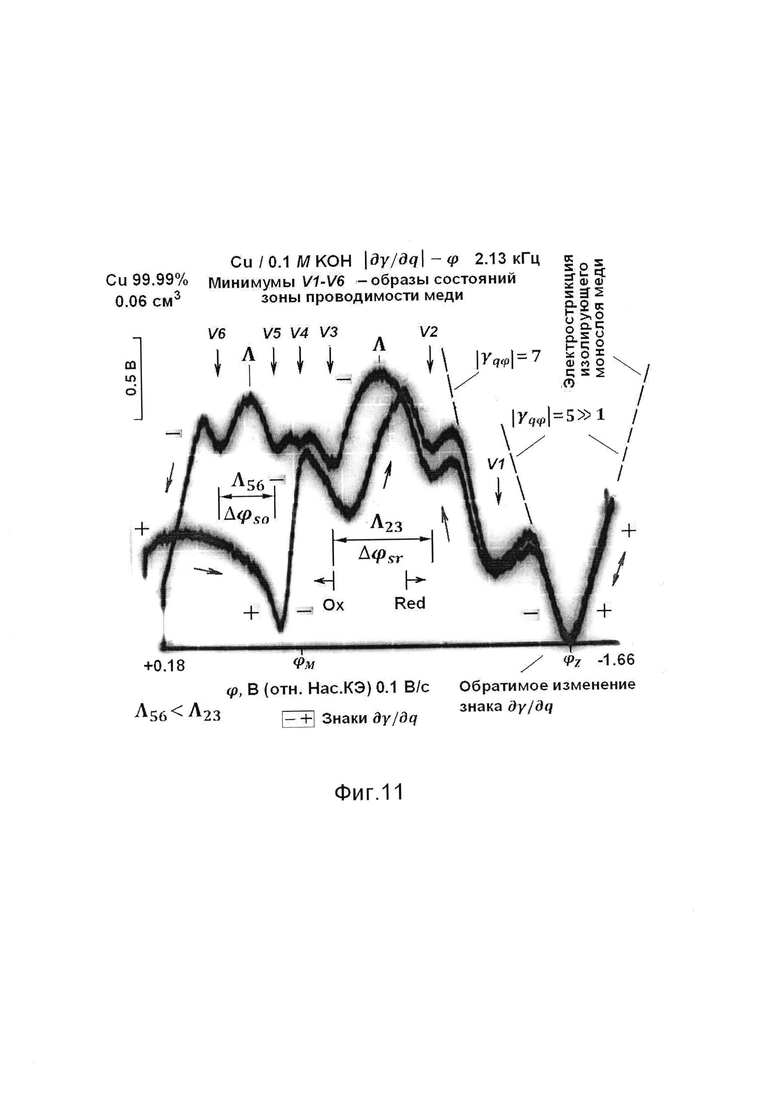
Фиг. 11 - осциллограмма ⎢∂γ/∂q⎢-ϕ на меди 99.99% в водном растворе гидроокиси калия, снятая в катодном и затем анодном направлениях развертки потенциала при объеме электрода 0.08 см3. Сходство с осциллограммами фиг. 7-9, полученными на меди 99.9%, исключает роль каких-либо примесей в происхождении ступенчатого рельефа представленных осциллограмм.
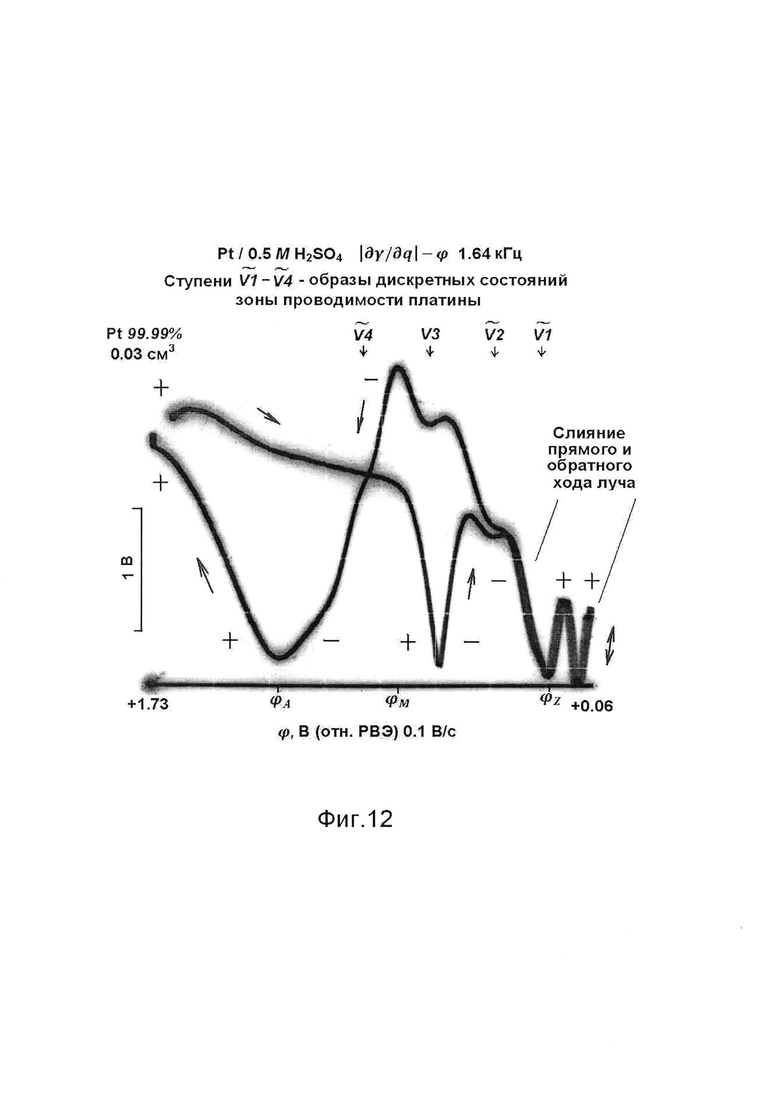
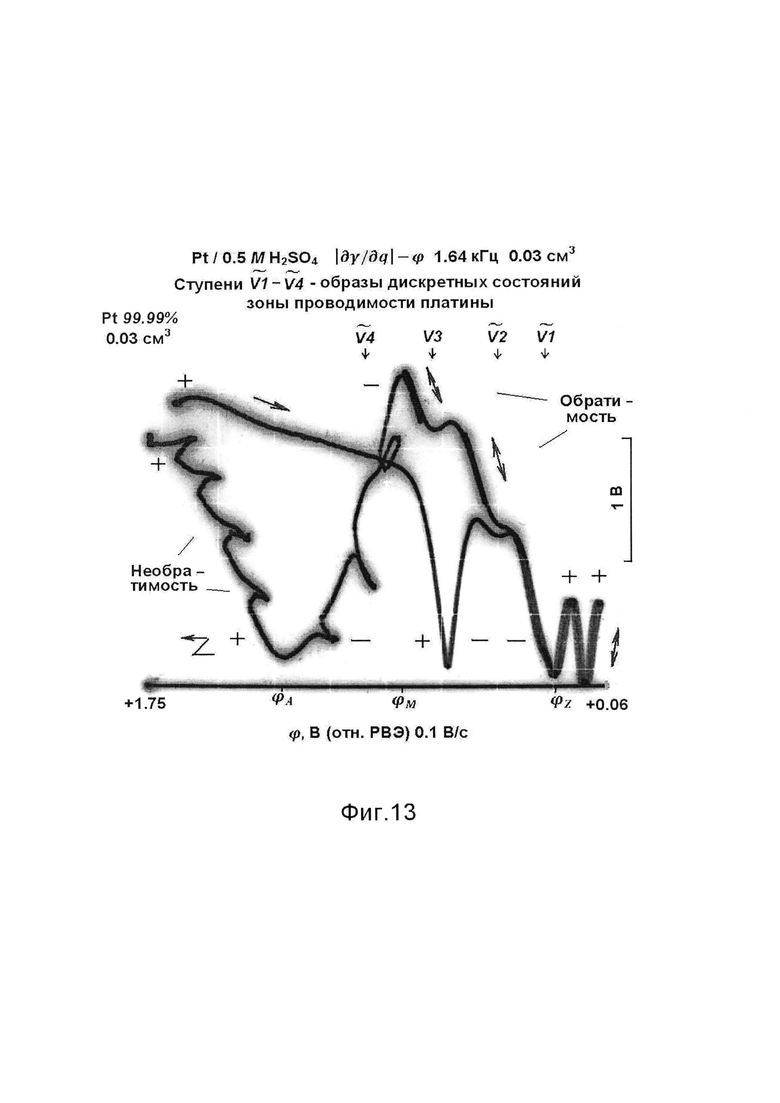
Фиг. 12 - осциллограмма ⎢∂γ/∂q⎢-ϕ на платине 99.99% в водном растворе серной кислоты, электрод фиксированного объема 0.03 см3. Потенциал указан в шкале равновесного водородного электрода (РВЭ). Символ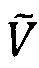 
(V с волной) использован для обозначения ступеней, которые рассматриваются как замаскированные минимумы величины ⎢∂γ/∂q⎢.
Фиг. 13 - осциллограмма в условиях фиг. 12, кроме развертки потенциала в анодном направлении, которая выполнена зигзагообразной для выявления степени обратимости. Слияние прямого и обратного хода луча характеризует обратимость и выделяет область потенциала (от +0.8 В до 0 В), в которой платина свободна от окисла и в которой проявляются три ступени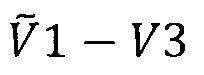 
. Петли гистерезиса (положительнее +0.8 В) - признак анодного окисления платины. Ступень 
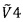искажена нарастающим слоем окисла и потому видна менее четко.
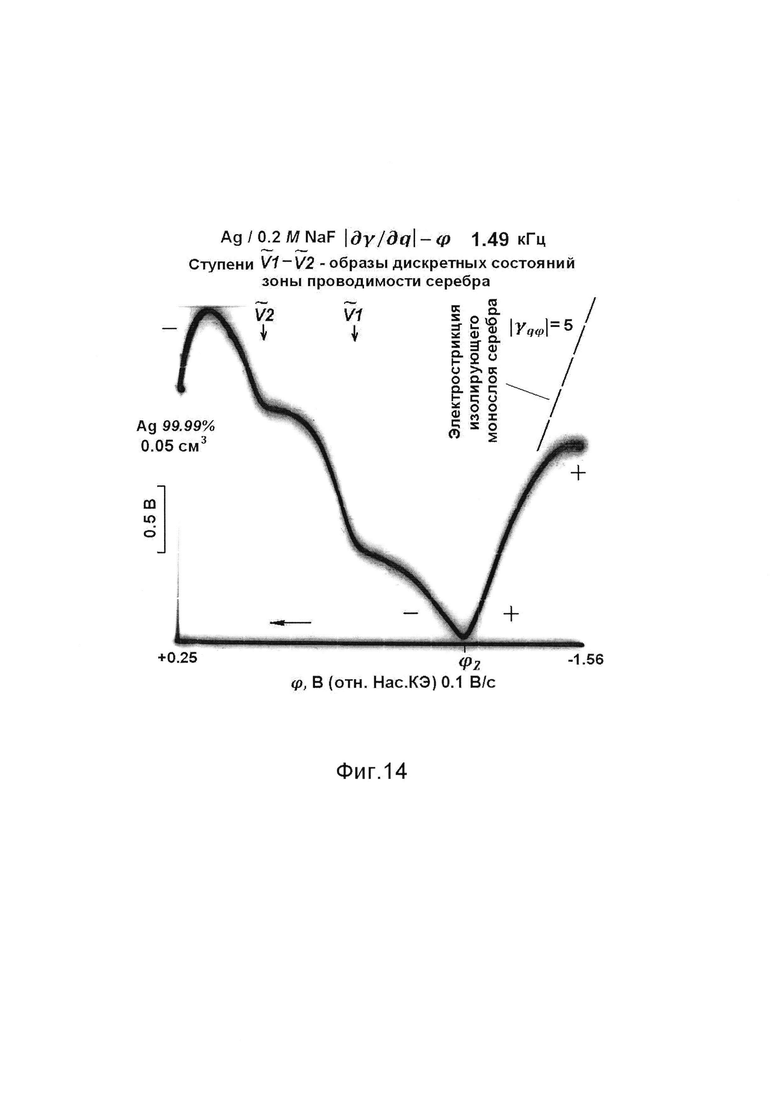
Фиг. 14 - осциллограмма ⎢∂γ/∂q⎢-ϕ на серебре 99.99% в водном растворе фтористого натрия, снятая в анодном направлении развертки потенциала, электрод фиксированного объема 0.08 см3.
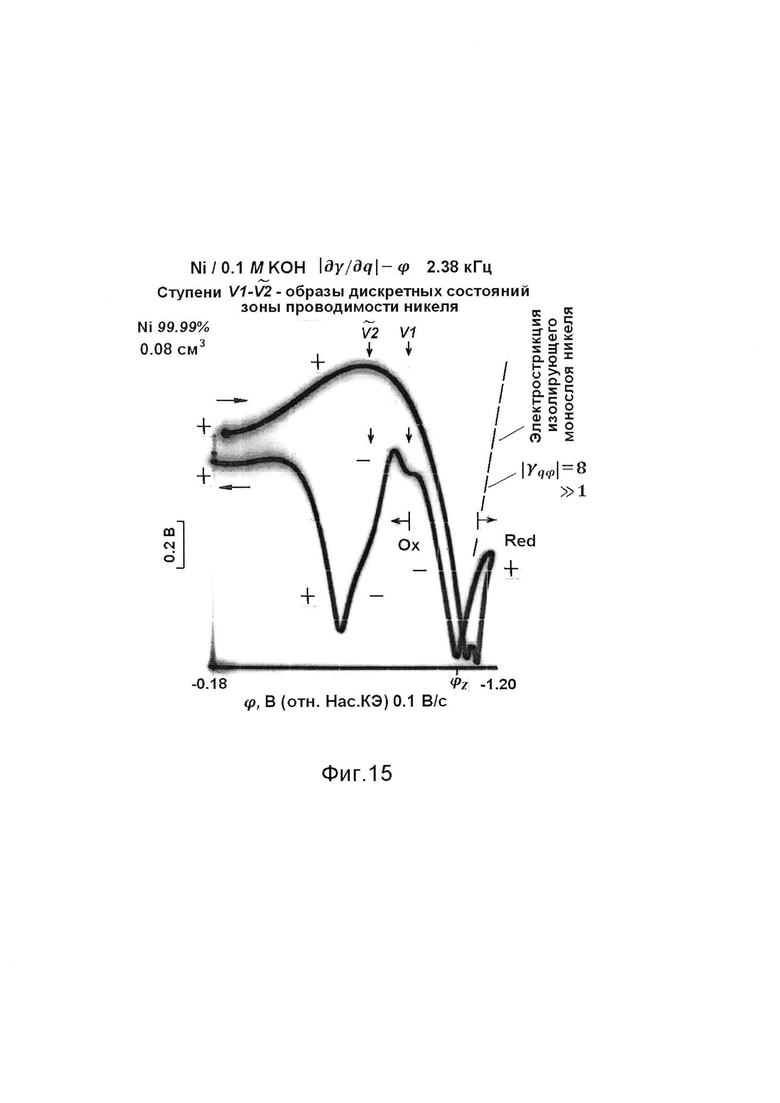
Фиг. 15 - осциллограмма ⎢∂γ/∂q⎢-ϕ на никеле 99.99% в водном растворе гидроокиси калия, снятая в катодном и затем анодном направлениях развертки потенциала при объеме электрода 0.08 см3.
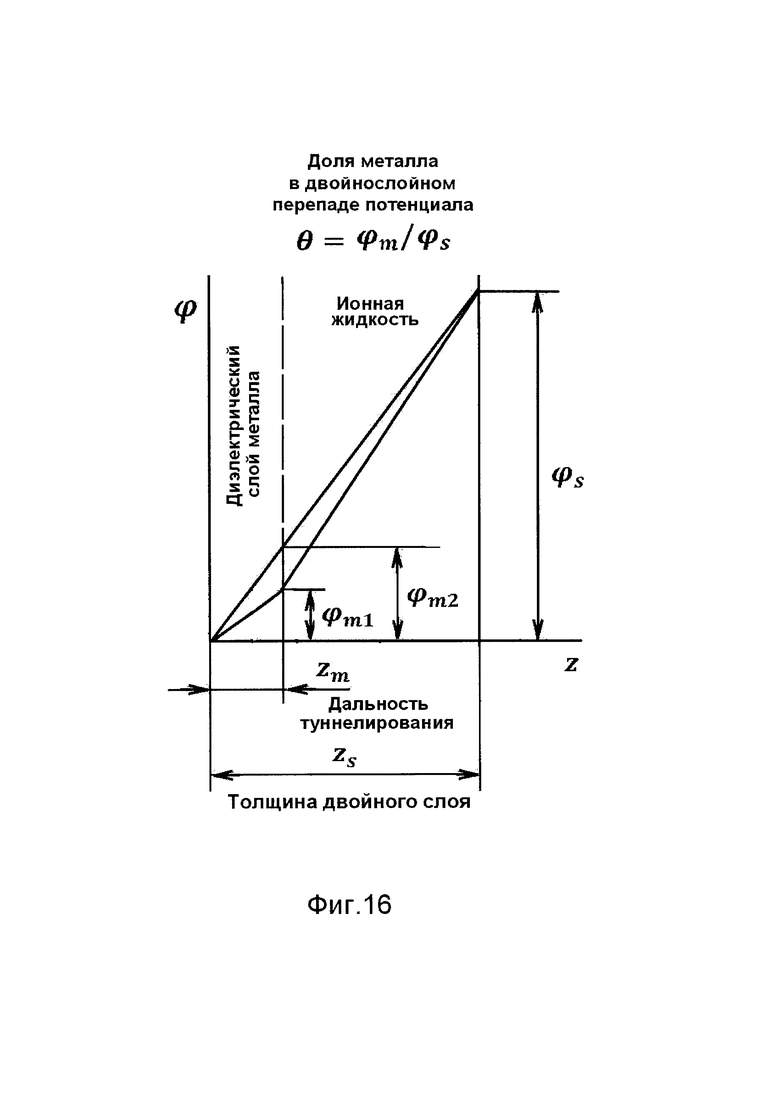
Фиг. 16 - схема распределения потенциала ϕ в двойном слое при различных проницаемостях металлической части двойного слоя, основу которой составляет внешний монослой атомов металла, обладающий свойствами диэлектрика. Толщина zm металлической части совпадает с дальностью туннельного переноса электрона от внешнего заряда к внутреннему, ϕs - перепад потенциала в двойном слое, ϕm - перепад потенциала в металлической части двойного слоя.
Окисление снижает проницаемость металлической части двойного слоя и увеличивает этим перепад ϕm потенциала в металлической части двойного слоя, ϕm1<ϕm2. Кроме того, металлическая часть двойного слоя шунтируется туннельным переносом электрона, что сопровождается периодическим спадом ϕm.
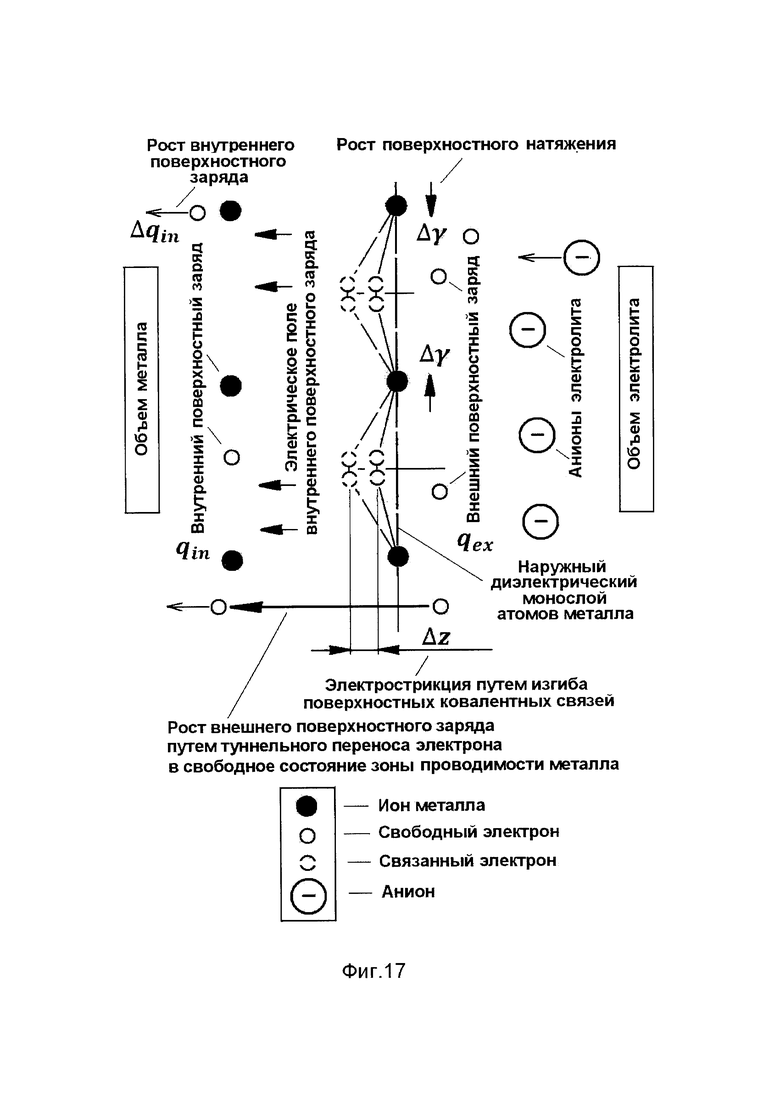
Фиг. 17 - схема электрострикции наружного монослоя атомов металла путем изгиба поверхностных ковалентных связей в электрическом поле внутреннего поверхностного заряда.
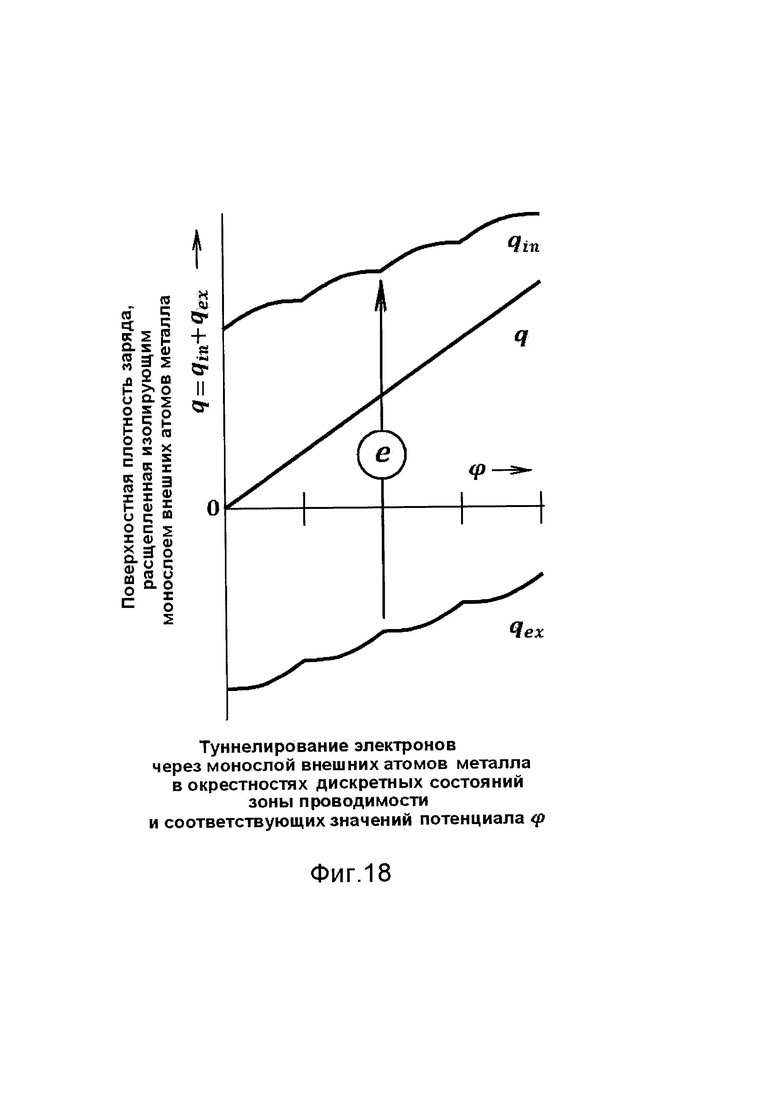
Фиг. 18 - схема поочередного ступенчатого изменения внутреннего и внешнего поверхностных зарядов qin, qex путем туннельного переноса электрона между ними в моменты соответствия потенциала ϕ дискретным состояниям зоны проводимости металла.
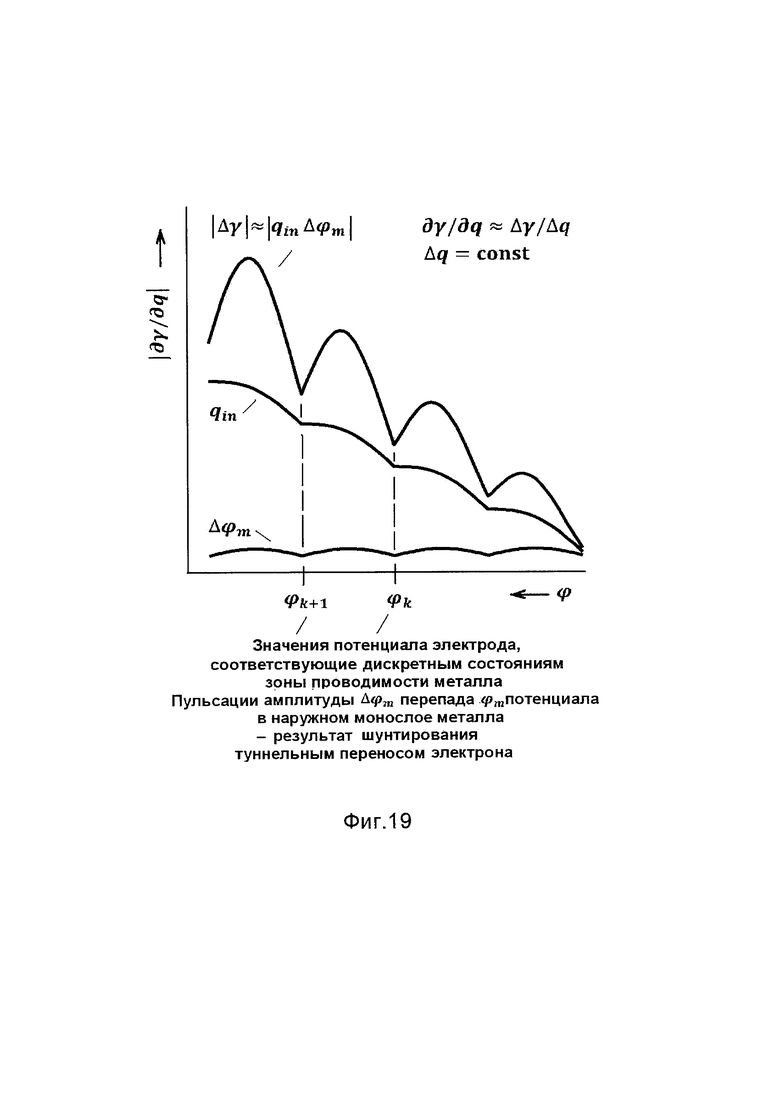
Фиг. 19 - схема образования минимумов абсолютной величины эстанса ⎢∂γ/∂q⎢ при монотонном ступенчатом возрастании внутреннего поверхностного заряда qin. Туннельный перенос электрона через наружный монослой атомов металла периодически шунтирует этот монослой, что выражается в периодическом снижении амплитуды Δϕm перепада ϕm потенциала в наружном монослое. Абсолютная величина эстанса ⎢∂γ/∂q⎢ пропорциональна произведению qinΔϕm и потому повторяет минимумы амплитуды Δϕm колебаний ϕm при пропускании переменного тока.
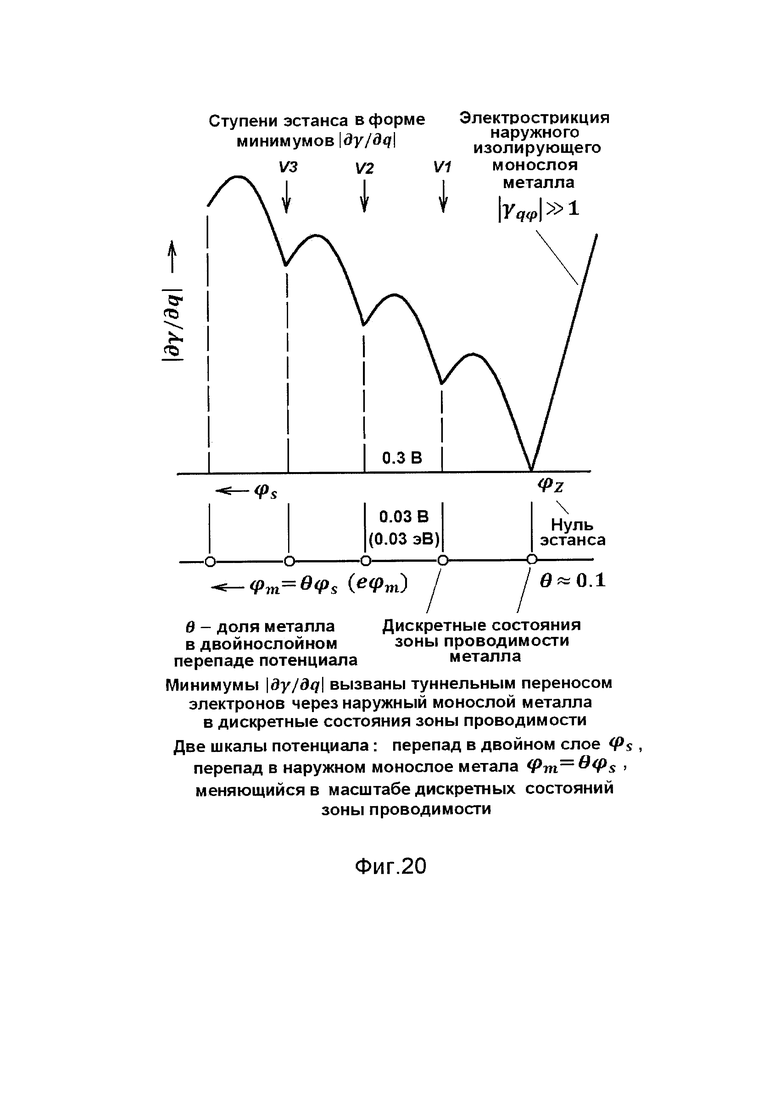
Фиг. 20 - схема перехода от интервала между минимумами эстанса к интервалу между состояниями зоны проводимости металла.
Блок электрода включает исследуемый электрод 1, механически соединенный с пьезоэлементом 2. Электрод имеет форму изогнутой пластины 3. Вертикальная часть 4 пластины скреплена с держателем 5. Горизонтальная часть 6 пластины ограничена бортом 7. Рабочая поверхность 8 горизонтальной части пластины смочена снизу мениском 9 ионной жидкости 10, находящейся в круглом резервуаре 11 из боросиликатного стекла. Пьезоэлемент закреплен в корпусе 12 экрана с помощью втулки 13 и прокладок 14. Держатель соединен с пьезоэлементом посредством штока 15, который проходит с зазором через отверстие 16 в дне 17 корпуса.
Резервуар 11 закрыт фторопластовой крышкой 18, которая имеет центральное отверстие 19, окруженное перегородкой в виде трубы 20 с окном 21. Нижний конец трубы погружен в ионную жидкость. Вокруг трубы в крышке выполнены шесть боковых отверстий 22-27, закрытых эластичными пробками 28, 29. Между резервуаром 11 и крышкой 18 установлено уплотнительное кольцо 30.
Пластина 3 снабжена шлейфом 31, который выполнен из того же материала, что пластина. Шлейф образует с пластиной монолитную полосу 32, причем вдоль этой полосы держатель 5 расположен между шлейфом 31 и смоченной горизонтальной частью 6 пластины. Шлейф выходит из резервуара через отверстие 23 в крышке резервуара и закреплен в этом отверстии пробкой 29 с возможностью укорочения части шлейфа, находящейся вне резервуара. Шлейф может быть разрезан, например, по линии 33 с удалением отрезанной части 34. Такое сокращение размера шлейфа не отражается на положениях мениска 9 и штока 15 и, следовательно, не меняет состояния механических контактов исследуемого электрода с ионной жидкостью и с пьезоэлементом.
Токовывод исследуемого электрода в виде достаточно тонкой проволоки присоединен к выступающей части 35 шлейфа (токовывод на чертеже не показан).
Внутри резервуара шлейф имеет зигзагообразный участок 36. На этом участке шлейфа выполнено сужение 37. Через боковые отверстия крышки резервуара в ионную жидкость опущены вспомогательный электрод 38 и зонд 39.
Держатель электрода изготовлен в форме полимерного бруска 40 с двумя взаимно перпендикулярными отверстиями для штока 15 и винта 41, который служит для закрепления электрода в держателе.
Винт 41 выполнен из алюминия и анодирован для получения изолирующей окисной пленки на его поверхности. Через отверстия 26, 27 в резервуар 11 введены трубка 42 для пропускания инертного газа через ионную жидкость и трубка 43 для выпуска использованного газа. В вертикальной части 4 пластины выполнено отверстие 44 для винта 41.
При работе блока электрода переменный ток заданной частоты проходит через активную поверхность 8 исследуемого электрода 1, ионную жидкость 10 и вспомогательный электрод 38. Прохождение переменного тока сопровождается колебаниями поверхностной плотности заряда исследуемого электрода 1. Заряд влияет на состояние поверхности металла, которое определяет величину поверхностного натяжения. Вызванные переменным зарядом колебания поверхностного натяжения раскачивают исследуемый электрод 1 и через шток 15 передаются пьезоэлементу. Амплитуда напряжения на обкладках пьезолемента пропорциональна амплитуде поверхностного натяжения γ исследуемого электрода. При фиксированной амплитуде поверхностной плотности заряда q переменное напряжение, снимаемое с пьезоэлемента, пропорционально отношению амплитуд Δγ/Δq величин γ и q. При малых амплитудах это отношение практически совпадает с производной ∂γ/∂q. Выпрямление напряжения дает абсолютную величину производной, ⎢∂γ/∂q⎢. Зонд 39 контролирует потенциал ϕ исследуемого электрода 1. Совмещение переменного тока с заданием линейного во времени потенциала исследуемого электрода, достигаемое путем фильтрации, обеспечивает получение осциллограмм в координатах ⎢∂γ/∂q⎢-ϕ.
Механическая система электрод-пьезоэлемент имеет спектр собственных частот. Частоту переменного тока выбирают равной одной из собственных частот механической системы. Это обеспечивает регистрацию переменного поверхностного натяжения в режиме механического резонанса, что повышает чувствительность и избирательность регистрации. Закрепление шлейфа в отверстии крышки резервуара предохраняет спектр собственных частот системы электрод-пьезоэлемент от влияния среза части шлейфа, расположенной вне резервуара.
В демонстрационных опытах в качестве исследуемых металлов используют медь двух разных квалификаций: 99.99% и 99.9%, а также никель, серебро и платину квалификации 99.99%. Ионную жидкость применяют в виде растворов, которые готовят с использованием дважды перегнанной воды и реактивов квалификации «чистый для анализа» (KOH) и «особой чистоты» (NaF, H2SO4). Применяют зонды и вспомогательные электроды из стеклоуглерода (при исследовании меди, никеля и серебра) либо платины. Для удаления кислорода воздуха из растворов используют водород (в случае меди) либо аргон (в случае никеля, серебра, платины). Данная операция необходима при регистрации электрического тока через границу исследуемого металла с раствором. Она не обязательна при регистрации переменного поверхностного натяжения исследуемого металла, которое свободно от влияния тока восстановления кислорода. Это дает возможность упростить постановку основных демонстрационных опытов без ущерба для их точности.
Демонстрацию рельефа зоны проводимости металла проводят в основном на примере меди, которая представляет собой доступный и легко обрабатываемый металл. Используют образцы, различающиеся степенью чистоты: пруток диаметром 2.5 мм из меди 99.99% и лист толщиной 0.5 мм из меди 99.9%. Пруток стачивают до пластины толщиной 0.8 мм. Из листа вырезают полосу меди шириной 6 мм длиной 280 мм, выполняют сужение длиной 40 мм. Наносят на полосу линию 33, которая делит полосу приблизительно на равные по объему части.
Концы изготовленных таким путем пластины и полосы подвергают электрополировке в смеси ортофосфорной кислоты с водой, промывают в воде и отгибают с образованием L-образного электрода из меди 99.99% без шлейфа и L-образного электрода из меди 99.9%. со шлейфом. Путем взвешивания находят объемы этих электродов: 0.06 см3 и 0.77 см3 соответственно.
В демонстрационном опыте вначале используют электрод со шлейфом. Шлейф 31 пропускают через отверстие 25 в крышке резервуара и зажимают в отверстии эластичной пробкой 29. Вертикальную часть 4 пластины электрода крепят к держателю 5 с помощью винта 41 с изолирующим покрытием.
В качестве ионной жидкости применяют водный раствор гидроокиси калия в концентрации 0.1 моля на литр, 0.1 М KOH. Заливают раствор в резервуар через свободное отверстие в крышке до касания раствора с рабочей поверхностью 8 исследуемого электрода. После этого исследуемый электрод смещают вверх с образованием мениска 9 раствора под ним.
Посредством вспомогательного электрода 38 через границу исследуемого электрода с раствором пропускают переменный ток с фиксированной амплитудой 10 мА. Варьируют частоту переменного тока и по максимуму переменного напряжения, генерируемого пьезоэлементом, находят один из резонансов механической системы электрод-пьезоэлемент, имеющий частоту 2.06 кГц. Фиксируют эту частоту.
Линейно изменяют потенциал исследуемого электрода в диапазоне от +0.2 до - 1.7 В относительно насыщенного каломельного электрода (Нас.КЭ) в катодном и анодном направлениях. Снимают осциллограмму в координатах ⎢∂γ/∂q⎢-ϕ (фиг. 7).
От расположенной вне резервуара части шлейфа по линии 33 отрезают ножницами участок 34, что уменьшает объем исследуемого электрода приблизительно вдвое. По возможности без задержки и без промежуточных разверток повторяют регистрацию осциллограмм ⎢∂γ/∂q⎢-ϕ в том же диапазоне потенциала и на той же резонансной частоте (фиг. 8). Сравнивают осциллограммы, полученные непосредственно до (фиг. 7) и после (фиг. 8) двукратного уменьшения объема исследуемого электрода.
Формы обеих осциллограмм практически совпадают. На интервале потенциалов от -1.60 В до +0.44 В воспроизводятся все шесть минимумов V1-V6, соответствующих дискретным состояниям зоны проводимости меди.
На основании проведенного сравнения делают вывод, что в использованных макроскопических образцах меди интервалы энергии между смежными состояниями зоны проводимости не зависят от объема образца.
Многократного повторяют развертки потенциала. Отмечают в качестве сопутствующего обстоятельства, что минимум V4 постепенно деформируется без существенного изменения других наблюдаемых минимумов (фиг. 9). Интерпретируют это как информацию о дрейфе соответствующего состояния зоны проводимости с возможностью его дополнительного расщепления.
В той же системе Cu/ 0.1 М KOH регистрируют осциллограмму j-ϕ зависимости плотности тока от потенциала (фиг. 10). Отмечают отсутствие ступеней плотности тока j, которые бы соответствовали ступеням эстанса ∂γ/∂q. Такое различие рассматривают как дополнительное доказательство существования изолирующего монослоя металла, который расщепляет поверхностный заряд металла на внутреннюю и внешнюю части.
Показывают, что эстанс определяется внутренним зарядом, вызывающим электрострикцию изолирующего монослоя, тогда как ток определяется изменением суммарного заряда.
Поставленный опыт повторяют на электроде с объемом 0.06 см3 из меди 99.99% без шлейфа. Получают осциллограмму ⎢∂γ/∂q⎢-ϕ с воспроизведением тех же шести минимумов, из которых минимум V4 обнаруживает аналогичную деформацию (фиг. 11). Подтверждают этим отсутствие искажений со стороны примесей.
Отсутствие зависимости интервалов между состояниями области проводимости от объема образца металла объясняют существованием радиуса расщепления, то есть предельного размера области металла, в которой согласно принципу Паули может происходить расщепление вырожденного уровня энергии.
Оценку радиуса расщепления производят с использованием интервала между ближайшими минимумами регистрируемой величины ⎢∂γ/∂q⎢. Применяют формулу
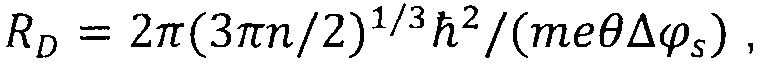
где RD - радиус расщепления,
n - численная плотность электронов проводимости в металле,
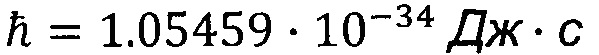- постоянная Планка,
m=0.911⋅10-30 кг - масса электрона,
е=1.60219⋅10-19 Кл - заряд электрона,
Δϕs - интервал потенциала между ближайшими ступенями регистрируемой величины ⎢∂γ/∂q⎢,
θ≥Δϕb/Δϕs - доля металла в межфазном скачке потенциала на границе металла с ионной жидкостью, Δϕb=ΔEb/e, θ≥0.1.
Вывод приведенной формулы исходит из классического представления о расщеплении вырожденного уровня энергии в образце металла произвольной формы. Для куба со стороной L интервал энергии между ближайшими состояниями в окрестности уровня Ферми составляет
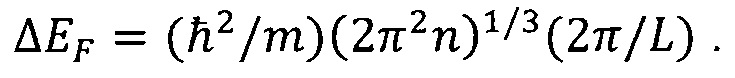
Особенность в том, что согласно описанным опытам область расщепления не совпадает по объему с макроскопическим образцом металла. Ее размер Lmax существенно меньше размера образца и может быть найден из уравнения
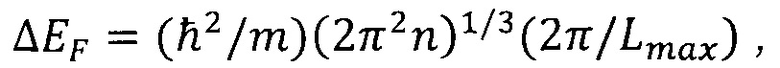
где интервал ΔEF известен из расстояния Δϕs между минимумами величины ⎢∂γ/∂q⎢,
ΔEF=eθΔϕs.
Тогда RD - радиус шара, имеющего объем куба со стороной Lmax,
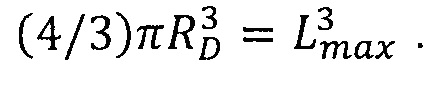
Применительно к случаю меди используют значения n=8.4⋅1028 м-3, Δϕs=0.3 В, Т=293 K, θ≥0.1. Находят таким путем оценку RD≤1.175⋅10-7 м=1.175⋅10-4 мм=117.5 нм для радиуса расщепления в поверхностном слое меди, свободном от окисла.
Изображения рельефа зоны проводимости получают также на других металлах. Регистрируют ступенчатые осциллограммы ⎢∂γ/∂q⎢-ϕ на платине (фиг. 12, 13), серебре (фиг. 14), никеле (фиг. 15). Путем зигзагообразного изменения потенциала находят области обратимого и необратимого изменения поверхностного натяжения металлов в твердом состоянии. Признаком обратимости служит слияние прямого и обратного хода луча (на платине - отрицательнее потенциала +0.8 В).
Обратимость характерна для металла, свободного от окисла. Необратимость обнаруживает себя по петлям гистерезиса и в зависимости от формы петель указывает на различные степени покрытия металла слоем окисла.
На основании осциллограмм меди (фиг. 9, 11) и платины (фиг. 13) делают вывод об обратимости ступеней эстанса и соответствующих им состояний зоны проводимости на металлах, свободных от окисла.
Сохранение ступеней эстанса на окисленной поверхности металла (минимумы V4-V6 на фиг. 9, 11) рассматривают как подтверждение стадии туннельного переноса электрона через наружный монослой атомов металла, поскольку свойствами диэлектрика этот слой обладает и до и после окисления.
Учитывают изменение диэлектрической проницаемости наружного монослоя атомов металла при его соединении с атомами кислорода либо гидроксильными группами, что приводит к увеличению перепада потенциала в нем (от ϕm1 до ϕm2 на схеме фиг. 16). В качестве подтверждения приводят сужение дуги Λ56 на окисленной поверхности по сравнению с дугой Λ23 на свободной от окисла поверхности металла (фиг. 9, 11).
Изменение поверхностного натяжения твердого тела, регистрируемое методом эстанса, отражает в основном процессы, затрагивающие состояние наружного монослоя атомов. Переход наружного монослоя атомов металла в диэлектрическое состояние обусловлен образованием ковалентных связей между этими атомами с образованием поверхностной изолирующей пленки атомной толщины. Локализованные в пленке электроны, участвующие в ковалентных связях, смещаются в электрическом поле внутреннего поверхностного заряда (фиг. 17). Возникающие при этом локальные прогибы пленки увеличивают ее вклад в поверхностное натяжение металла.
Взаимно компенсированный процесс ступенчатого роста внутреннего и внешнего поверхностных зарядов регулируется импульсами туннельного переноса электронов между этими зарядами (фиг. 18).
Ступенчатый рост внешнего и внутреннего поверхностных зарядов является монотонным. В сочетании с пульсирующей амплитудой Δϕm потенциала ϕm он создает минимумы регистрируемой величины ⎢∂γ/∂q⎢ (фиг. 19). Для перехода к интервалам между состояниями зоны проводимости регистрируемые интервалы между минимумами эстанса должны быть умножены на отношение θ перепада ϕm потенциала в металлической части двойного слоя к полному перепаду ϕs потенциала в двойном слое (фиг. 20).
Изобретение относится к наглядным пособиям для изучения структуры электронных зон твердого тела. Из исследуемого металла изготавливают электроды, различающиеся объемом, превосходящим 1 мм3, приводят каждый электрод в контакт с ионной жидкостью, задают потенциал электрода, регистрируют производную поверхностного натяжения электрода по поверхностной плотности заряда электрода как функцию потенциала электрода, определяют область потенциала, соответствующую положительному заряду электрода, и в этой области у полученной функции находят последовательность ступеней, которую рассматривают как образ последовательности дискретных состояний зоны проводимости металла, на одном и том же интервале потенциала электрода сравнивают числа ступеней, найденные на электродах различного объема, совпадение найденных чисел ступеней интерпретируют как признак независимости интервалов между дискретными состояниями зоны проводимости металла от объема, занимаемого этим металлом. Блок электрода включает исследуемый электрод, скрепленный с пьезоэлементом и смоченный ионной жидкостью, находящейся в резервуаре. Исследуемый электрод дополнен монолитно связанным с ним шлейфом, который выполнен с возможностью двукратного сокращения объема исследуемого электрода при сохранении неизменными контактов исследуемого электрода с пьезоэлементом и с ионной жидкостью. 2 н. и 21 з.п. ф-лы, 20 ил.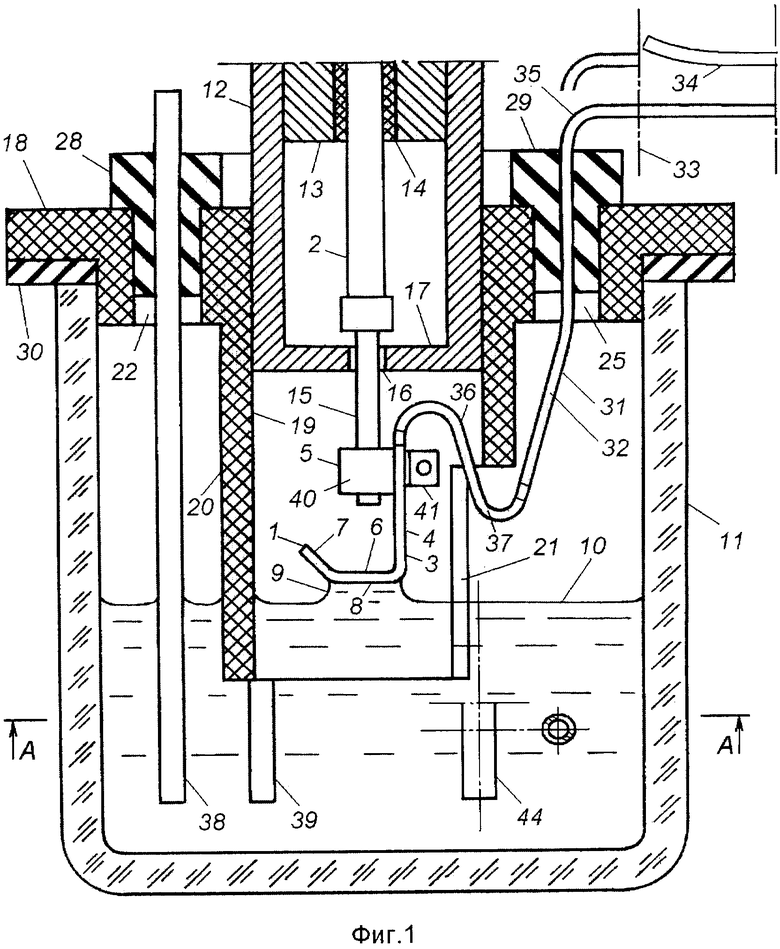
1. Способ демонстрации рельефа зоны проводимости металла, отличающийся тем, что из исследуемого металла изготавливают электроды, различающиеся объемом, превосходящим 1 мм3, приводят каждый электрод в контакт с ионной жидкостью, задают потенциал электрода, регистрируют производную поверхностного натяжения электрода по поверхностной плотности заряда электрода как функцию потенциала электрода, определяют область потенциала, соответствующую положительному заряду электрода, и в этой области у полученной функции находят последовательность ступеней, которую рассматривают как образ последовательности дискретных состояний зоны проводимости металла, на одном и том же интервале потенциала электрода сравнивают числа ступеней, найденные на электродах различного объема, совпадение найденных чисел ступеней интерпретируют как доказательство независимости интервалов между дискретными состояниями зоны проводимости металла от объема, занимаемого этим металлом.
2. Способ по п. 1, отличающийся тем, что указанную независимость связывают с пространственным ограничением действия принципа Паули, допускают существование предельного объема, в котором возможно классическое расщепление вырожденных уровней энергии и который заведомо меньше чем 1 мм3, характеризуют указанный предельный объем радиусом равновеликого шара, именуемым радиусом расщепления.
3. Способ по п. 1, отличающийся тем, что отмечают превосходство безразмерного наклона указанной функции над единицей, рассматривают это превосходство как признак электрострикции диэлектрического наружного монослоя атомов металла, разделяющего поверхностный заряд на внешний и внутренний заряды, сообщающиеся путем туннельного переноса электронов, ступенчатый вид указанной функции объясняют повторением туннельного переноса при последовательном сближении потенциала электрода с расположенными в виде ряда значениями, соответствующими дискретным состояниям зоны проводимости металла.
4. Способ по п. 1, отличающийся тем, что указанную функцию регистрируют в виде осциллограмм в координатах
|∂γ/∂q|-ϕ,
где γ - поверхностное натяжение электрода,
q - поверхностная плотность заряда электрода,
ϕ - потенциал электрода,
развертку потенциала электрода производят в анодном и катодном направлениях в диапазоне потенциала, включающем области восстановленной и окисленной поверхности металла.
5. Способ по п. 4, отличающийся тем, что ступени указанной функции выявляют по колебаниям наклона ∂|∂γ/∂q|/∂ϕ регистрируемой осциллограммы вдоль оси потенциала, которые выражаются в чередовании спадов и подъемов указанного наклона.
6. Способ по п. 1, отличающийся тем, что отмечают сходство последовательности ступеней с графиком величины у=|sin x|, имеющим скачки наклона в минимумах, вследствие чего именно минимумы регистрируемой функции |∂γ/∂q| ставят в соответствие дискретным состояниям зоны проводимости металла, при этом интервалы потенциала между минимумами регистрируемой функции |∂γ/∂q| рассматривают как образ интервалов энергии между дискретными состояниями зоны проводимости.
7. Способ по п. 6, отличающийся тем, что отмечают совпадение дугообразной формы указанной функции между ее минимумами в областях восстановленной и окисленной поверхности металла, откуда делают вывод о сохранении туннельного сообщения между внутренним и внешним зарядами при образовании между этими зарядами окисной пленки.
8. Способ по п. 6, отличающийся тем, что сравнивают интервалы между минимумами регистрируемой функции |∂γ/∂q| в областях восстановленной и окисленной поверхности металла, находят, что окисление поверхности металла уменьшает интервалы между указанными минимумами, объясняют это тем, что окисление поверхности металла увеличивает относительную долю металла в межфазном скачке потенциала по сравнению с долей ионной жидкости, что меняет масштаб регистрируемого образа состояний зоны проводимости при сохранении самих этих состояний неизменными.
9. Способ по п. 1, отличающийся тем, что различимость выделенных ступеней используют для оценки интервала энергии между дискретными состояниями зоны проводимости металла, рассматривают указанную различимость как признак превосходства этого интервала над энергией теплового движения
ΔEb≥kBT,
где ΔEb - интервал энергии между дискретными состояниями зоны проводимости металла,
kB=1.3807⋅10-23 Дж⋅К-1 - постоянная Больцмана,
T - температура.
10. Способ по п. 2, отличающийся тем, что интервал потенциала между ближайшими минимумами регистрируемой величины |∂γ/∂q| используют для оценки радиуса расщепления в поверхностном слое исследуемого металла, применяют формулу
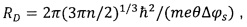
где RD - радиус расщепления, n - численная плотность электронов проводимости в металле,
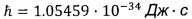- постоянная Планка,
m=0.911⋅10-30 кг - масса электрона,
е=1.60219⋅10-19 Кл - заряд электрона,
θ≥Δϕb/Δϕs - доля металла в межфазном скачке потенциала на границе металла с ионной жидкостью,
Δϕs - интервал потенциала между ближайшими минимумами регистрируемой величины |∂γ/∂q|,
Δϕb=ΔEb/e - интервал потенциала между ближайшими состояниями зоны проводимости, θ≥0.1.
11. Способ по п. 1, отличающийся тем, что в качестве исследуемых металлов используют медь, платину, кобальт, никель, серебро, золото в монолитном виде и в виде гальванических покрытий.
12. Способ по п. 1, отличающийся тем, что в качестве ионных жидкостей используют водные растворы гидроокиси калия, фтористого натрия, фтористого калия и серной кислоты, расплавы фтористого натрия и фтористого калия.
13. Способ по пп. 11, 12, отличающийся тем, что при исследовании меди водный раствор гидроокиси калия готовят в концентрации 0.1 моль на литр, потенциал измеряют в шкале насыщенного каломельного электрода, развертками потенциала охватывают диапазон от -1.7 В до +0.3 В, а началом окисления поверхности металла считают потенциал -0.4 В при анодном направлении развертки потенциала в соответствии с волной тока анодного окисления на зависимости тока от потенциала.
14. Способ по пп. 4, 13, отличающийся тем, что на осциллограмме анодного направления выявляют шесть минимумов величины |∂γ/∂q|, из которых три минимума расположены в области потенциала, где поверхность меди свободна от окисла, остальные - в области потенциала, где поверхность меди окислена.
15. Способ по пп. 4, 13, отличающийся тем, что на осциллограмме катодного направления выявляют три минимума величины |∂γ/∂q|, которые ставят в соответствие трем состояниям зоны проводимости в поверхностном слое меди, свободном от окисла.
16. Способ по пп. 10, 11, отличающийся тем, что используют значения n=8.4⋅1028 м-3, Δϕs=0.3 В, T=293 K, θ≥0.1 и находят таким путем оценку RD≤1.175⋅10-7 м=1.175⋅10-4 мм=117.5 нм для радиуса расщепления в поверхностном слое меди, свободном от окисла.
17. Способ по п. 4, отличающийся тем, что область потенциала, соответствующую окисленной поверхности металла, определяют по развитию гистерезиса величины |∂γ/∂q| в этой области и по волнам анодного тока на осциллограмме зависимости тока от потенциала.
18. Способ по п. 11, отличающийся тем, что используют образцы исследуемого металла, различающиеся степенью чистоты в диапазоне от 99.9% до 99.99%, а также толщиной в диапазоне от 10 мкм до 1 мм, независимость числа выделенных ступеней от степени чистоты и толщины образца в указанных диапазонах считают признаком, исключающим определяющее влияние примесей и размера кристаллических зерен на механизм образования выделенных ступеней в указанном диапазоне чистоты исследуемого металла.
19. Блок электрода, включающий исследуемый электрод, скрепленный с пьезоэлементом и смоченный ионной жидкостью, находящейся в резервуаре, отличающийся тем, что исследуемый электрод дополнен монолитно связанным с ним шлейфом, который выполнен с возможностью двукратного сокращения объема исследуемого электрода при сохранении неизменными контактов исследуемого электрода с пьезоэлементом и с ионной жидкостью.
20. Блок электрода по п. 19, отличающийся тем, что шлейф выходит из резервуара через отверстие в крышке резервуара и закреплен в этом отверстии пробкой с возможностью укорочения части шлейфа, находящейся вне резервуара.
21. Блок электрода по п. 19 отличающийся тем, что внутри резервуара шлейф имеет зигзагообразный участок.
22. Блок электрода по п. 21, отличающийся тем, что на зигзагообразном участке шлейфа выполнено сужение.
23. Блок электрода по п. 19, отличающийся тем, что держатель электрода выполнен в форме бруска с двумя взаимно перпендикулярными отверстиями, в одном из отверстий находится шток, в другом отверстии находится винт с возможностью закрепления электрода.
