Изобретение относится к наглядным пособиям для изучения поверхностных явлений.
Известен метод регистрации переменного поверхностного натяжения твердых тел, впервые предложенный автором и реализованный им в виде ряда устройств (Авт. свид. СССР 178161 МПК G01N 13/00, 08.01.1966, Бюл. №2; авт. свид. СССР 277399 МПК G01N 13/02, 22.07.1970, Бюл. №24; Электрохимия 1966, том 2, с. 1061; Доклады АН СССР 1969, том 187, с. 601; Electrochimica Acta 1970, vol. 15, p. 219; Успехи физических наук 2000, том 170, с. 779).
Данный метод, его теория, приборы и эксперименты подробно описаны в книге: А.Я. Гохштейн, Поверхностное натяжение твердых тел и адсорбция, Москва, изд. «Наука», 1976, 400 с.
До указанных работ изменение поверхностного натяжения твердых тел под влиянием внешних факторов не было доступно измерению из-за малости упругой деформации, составляющей обычно доли размера атома при условии исключения пластического течения.
Прогресс в решении проблемы был достигнут путем генерирования колебаний поверхностного натяжения и их избирательной регистрации. Стало возможным не только зарегистрировать само явление изменения поверхностного натяжения твердого тела, но и расширить условия эксперимента путем введения существенного параметра - частоты, которая может быть выбрана из широкого интервала, практически от нуля (измерения, близкие к статическим) до радиочастот и выше.
Пропускание переменного тока через границу твердого металла с жидким раствором электролита изменяет поверхностную плотность заряда металла, от которой зависит состояние поверхности. Соединение пластины исследуемого металла с пьезоэлементом и подключение этой системы к избирательному усилителю, настроенному на частоту переменного тока, позволяют выделить полезный сигнал, вызванный колебаниями поверхностного натяжения, и измерить амплитуду относительного упругого удлинения порядка 10-11…10-9, что меньше размера атома для исследуемого образца длиной 1 см. При этом остается резерв для дальнейшего повышения чувствительности.
Способ определения масштаба регистрируемого сигнала, также предложенный в указанных работах, состоит в тепловом моделировании поверхностного натяжения твердого тела. Периодический нагрев рабочей стороны пластины создает вблизи поверхности переменное тепловое напряжение, которое служит эталоном и допускает простой пересчет в переменное поверхностное натяжение по выведенным для этого формулам.
Рассматриваемые квантовые осцилляции поверхностного натяжения твердого тела вызваны физическими процессами и не осложнены химическими взаимодействиями.
Способы демонстрации квантовых осцилляций поверхностного натяжения твердого тела ранее не были известны.
Перед настоящим изобретением поставлены две задачи:
1) выявить одинаковые признаки осцилляции поверхностного натяжения у разных металлов в разных средах и тем самым сделать наглядной общность этого явления,
2) показать аналогию между ступенчатым изменением производной поверхностного натяжения твердого тела и ступенчатым изменением плотности состояний электронов в двухмерной квантовой яме.
Квантовая природа наблюдаемых осцилляций поверхностного натяжения твердого тела исключает возможность их объяснения в рамках классической физики, а также возможность отыскания классических аналогов. Отсюда следует нетривиальность задач предлагаемого изобретения.
Поставленные задачи решены благодаря тому, что, согласно изобретению, в качестве твердых тел используют металлы - медь и серебро, изготавливают из них электроды, приводят каждый из электродов в контакт с жидким раствором электролита, осуществляют предварительный электролиз с чередованием анодного окисления и катодного восстановления поверхности металла, после чего на восстановленной поверхности металла регистрируют зависимость производной поверхностного натяжения по поверхностной плотности заряда от потенциала электрода, изготовленного из этого металла, относительно электрода сравнения, сопоставляют указанные зависимости, полученные на меди и серебре, отмечают в качестве их общих признаков участок ступенчатого спада в анодном направлении, созданный колебаниями безразмерного наклона регистрируемой зависимости и включающий по меньшей мере три ступени, разделенные точками перегиба, убывание протяженности ступеней вдоль оси потенциала в анодном направлении, а также аномальную величину безразмерного наклона регистрируемой зависимости, который на указанном участке ступенчатого спада превосходит по абсолютной величине число 2, происхождение наблюдаемых колебаний наклона производной поверхностного натяжения твердого тела объясняют локализацией электронов поверхностной проводимости в двухмерной квантовой яме, что приводит к ступенчатой зависимости плотности состояний этих электронов от потенциала, при этом протяженность ступеней указанной производной поверхностного натяжения вдоль оси потенциала рассматривают как источник информации о расстоянии между дискретными уровнями энергии электронов в двойном электрическом слое и об эффективной массе электронов, отмечают, что наблюдаемые колебания наклона производной поверхностного натяжения твердых тел по поверхностной плотности заряда представляют собой квантовое явление, не имеющее аналога в рамках классической физики.
Возможность наблюдения осцилляции поверхностного натяжения твердых тел обосновывают выполнением условия
kT<eФmin,
где k - постоянная Больцмана,
Т - абсолютная температура,
е - заряд электрона,
Фmin - протяженность наиболее короткой ступени производной поверхностного натяжения вдоль оси потенциала.
Измеренную экспериментально протяженность наиболее короткой ступени производной поверхностного натяжения вдоль оси потенциала используют для оценки эффективной массы электрона в двойном электрическом слое по формуле
m=(ħπ/δ)2/(2eФmin),
где m - эффективная масса электрона,
ħ - постоянная Планка,
δ - толщина металлической секции двойного электрического слоя, равная глубине проникания в металл электрического поля, создаваемого свободными зарядами, поступающими из внешней цепи, и приближенно совпадающая с постоянной кристаллической решетки в объеме металла,
В качестве раствора электролита готовят водный раствор фтористого натрия с концентрацией в пределах от 0.001 до 0.5 моля на литр в диапазоне температур от 10 до 30°C. Используют поликристаллические образцы металлов, их поверхность после предварительного электролиза рассматривают как изотропную,
Регистрируют зависимость производной поверхностного натяжения по поверхностной плотности заряда от потенциала на платине в водном растворе серной кислоты с концентрацией в пределах от 0.001 до 0.1 моля на литр, сравнивают ее с зависимостями, полученными на меди и серебре, и находят общий признак в виде ступенчатого спада указанной зависимости.
Из безразмерного наклона регистрируемой зависимости рассчитывают относительную производную дифференциальной емкости двойного электрического слоя на границе металла с раствором по упругой деформации поверхности металла, используют для этого уравнение

где С - дифференциальная емкость двойного электрического слоя на границе металла с раствором электролита, отнесенная к единице площади поверхности металла,
ϑ - упругая деформация поверхности металла, равная относительному увеличению площади поверхности металла при его упругом растяжении,
φ - потенциал металла относительно электрода сравнения,
γ - поверхностное натяжение твердого металла,
q - поверхностная плотность заряда металла,
∂γ/∂q - производная поверхностного натяжения по поверхностной плотности заряда,
∂(∂γ/∂q)/∂φ - безразмерный наклон регистрируемой зависимости ∂γ/∂q от φ,
(∂С/∂ϑ)/С - относительная производная дифференциальной емкости двойного электрического слоя по упругой деформации поверхности металла,
(∂С/∂φ)/С - относительная производная дифференциальной емкости двойного электрического слоя по потенциалу.
При нулевом значении производной поверхностного натяжения твердого металла по поверхностной плотности заряда используют упрощенное уравнение

выражающее относительную производную дифференциальной емкости двойного электрического слоя по упругой деформации поверхности металла непосредственно через безразмерный наклон регистрируемой зависимости,
Показывают, что в области ступенчатого спада регистрируемой зависимости справедливо неравенство
max(∂С/∂ϑ)/С>1,
объясняют это неравенство аномальным поперечным сжатием поверхностного слоя металла при упругом растяжении в условиях квантовых переходов, показывают более чем двукратное превосходство величины (∂С/∂ϑ)/С над коэффициентом Пуассона для того же металла.
В процессе регистрации производной ∂γ/∂q через границу образца твердого металла с раствором электролита пропускают переменный ток с заданной частотой, на той же частоте избирательно детектируют колебания поверхностного натяжения твердого металла, производную поверхностного натяжения по поверхностной плотности заряда определяют как предел отношения комплексных амплитуд поверхностного натяжения и поверхностной плотности заряда:
∂γ/∂q=lim(Δγ/Δq) при Δq→0,
где Δ - обозначение амплитуды, характеризуемой модулем
|Δ| и фазой arg Δ,
Δγ - амплитуда колебаний поверхностного натяжения, зависящая от потенциала φ,
Δq=ΔJ/(Sω) - амплитуда колебаний поверхностной плотности заряда,
ΔJ - амплитуда колебаний заданного переменного тока, поддерживаемая постоянной при изменении потенциала φ,
S - площадь границы металла с раствором электролита,
ω - угловая частота переменного тока.
Выделяют абсолютную величину производной поверхностного натяжения по поверхностной плотности заряда, которую определяют как предел отношения модулей амплитуд колебаний поверхностного натяжения и поверхностной плотности заряда,
|∂γ/∂q|=lim(|Δγ|/|q|) при Δq→0,
изменение знака указанной производной при прохождении ее через нуль определяют по изменению фазы колебаний поверхностного натяжения, численное значение указанной производной определяют путем сравнения с эталонным значением, полученным путем теплового моделирования переменного поверхностного натяжения твердого тела.
При частоте переменного тока ниже 10 кГц знак производной поверхностного натяжения как функции потенциала восстанавливают путем зеркального отражения графика ее абсолютной величины относительно нулевой линии.
По величине относительной производной дифференциальной емкости двойного электрического слоя по упругой деформации поверхности металла оценивают относительное поперечное сжатие слоя поверхностных атомов металла при упругом растяжении металла вдоль его поверхности, используют неравенство

где δ - толщина металлической секции двойного электрического слоя,
(∂δ/∂ϑ)/δ - относительное поперечное сжатие указанной секции при упругом растяжении металла вдоль его поверхности
∈ - эффективная диэлектрическая проницаемость указанной секции.
Зависимость производной поверхностного натяжения твердого металла по поверхностной плотности заряда от потенциала сравнивают с зависимостью электрического тока от потенциала на той же границе металла с раствором, изменяют потенциал в пределах, достигающих анодной волны тока окисления поверхности металла и катодной волны тока восстановления поверхности металла, указанные волны тока используют для определения интервала значений потенциала, в котором поверхность металла восстановлена.
При изменении потенциала в анодном направлении отмечают отсутствие ступеней тока в диапазоне потенциала, содержащем ступени производной поверхностного натяжения, объясняют этот экспериментальный факт избирательной чувствительностью поверхностного натяжения твердого тела к образованию двухмерной квантовой ямы в металлической секции двойного электрического слоя.
Показывают совпадение экстремума наиболее анодной ступени производной поверхностного натяжения с началом анодной волны тока окисления поверхности металла при изменении потенциала в анодном направлении, объясняют такое совпадение достижением нулевой плотности состояний электронов, участвующих в образовании связи поверхностных атомов металла с его объемом, что приводит к ослаблению этой связи и облегчает соединение поверхностных атомов металла с кислородом, причем в случае благородных и переходных металлов в качестве указанной плотности состояний рассматривают плотность состояний d-электронов в двойном электрическом слое.
Задача предлагаемой диаграммы - наглядно показать причинную связь между осцилляциями поверхностного натяжения твердого тела и дискретностью изменения энергии электронов в двойном электрическом слое. Известных аналогов у предлагаемой диаграммы нет.
Поставленная задача решена благодаря тому, что, согласно изобретению, диаграмма соответствия между осцилляциями поверхностного натяжения твердого тела и плотностью состояний электронов в двойном электрическом слое содержит график производной поверхностного натяжения по поверхностной плотности заряда как функции потенциала с сохранением знака этой функции, потенциал показан изменяющимся справа налево в сторону более положительных значений, что соответствует ступенчатому спаду указанной производной от положительных значений над нулевой линией к отрицательным значениям под нулевой линией, спад включает три подобных по форме ступени, протяженность которых уменьшается от ступени к ступени вплоть до достижения минимума указанной производной, ступени разделены точками перегиба, через которые проведены вертикальные пунктирные линии, под графиком производной поверхностного натяжения в том же диапазоне изменения потенциала представлен график плотности состояний электронов, имеющий вид ступенчатой функции потенциала, которая убывает при изменении потенциала в сторону более положительных значений и достигает нуля при потенциале минимума производной поверхностного натяжения, каждой ступени производной поверхностного натяжения соответствует расположенная под ней ступень плотности состояний.
На диаграмме представлены экспериментальные данные, относящиеся к серебру в водном растворе фтористого натрия, показаны знаки производной поверхностного натяжения серебра по поверхностной плотности заряда и плотности состояний электронов в двойном электрическом слое при изменении потенциала,
∂γ/∂q(φ)>0 при φ<φEO, ∂γ/∂q(φ)<0 при φ>φEO, ρ(φ)≥0,
где φ - потенциал металла,
∂γ/∂q - производная поверхностного натяжения по поверхностной плотности заряда,
ρ - плотность состояний электронов в квантовой яме двойного электрического слоя,
φEO - известное из опыта значение потенциала в точке изменения знака функции ∂γ/∂q (φ),
нулевые линии показаны равенствами
∂γ/∂q=0 и ρ=0,
протяженность ступеней функций ∂γ/∂q (φ) и ρ(φ) возрастает в ряду
|φS1-φS0|<|φS2-φS1|<|φS3-φS2|,
где φS0>φS1>φS2>φS3 - значения потенциала в точках перегиба функции ∂γ/∂q (φ) на границах между ее ступенями, φS0 - значение потенциала в точке минимума функции ∂γ/∂q (φ), интерпретируемое как потенциал нулевой плотности состояний, протяженность наиболее короткой ступени представлена уравнением
|φS1-φS0|=(ħπ/δ)2/(2me),
где ħ - постоянная Планка,
δ - толщина металлической секции двойного электрического слоя,
m - эффективная масса электрона,
е - заряд электрона.
Квантовые осцилляции поверхностного натяжения свойственны многим металлам. Выбор меди и серебра в качестве объекта опытов обусловлен возможностью исключить хемосорбцию в достаточно широком интервале потенциалов.
Предварительный электролиз с чередованием анодного окисления и катодного восстановления поверхности металла приводит к очистке поверхности от посторонних адсорбированных атомов и к ее рекристаллизации с преобладанием одного типа граней. Такая операция делает поверхность более однородной и приближает ее по качеству к поверхности монокристалла.
В отличие от поверхностного натяжения жидкостей поверхностное натяжение твердых тел связано с упругой деформацией. Упругая деформация позволяет провести измерения. Однако главным в указанной связи является влияние упругой деформации на свойства вещества. Сведения об этом влиянии могут быть получены из опыта путем применения известного уравнения электрокапиллярности твердых тел,
∂γ/∂φ=-q-∂q/∂ϑ,
которое ранее было получено автором и подтверждено экспериментально.
Используемые в предлагаемом способе выражения для производной электрической емкости по упругой деформации являются следствиями этого уравнения. Поскольку емкость зависит от расстояния между противоположно заряженными областями, то демонстрируемые опыты дают, в частности, сведения об упругих свойствах металла на его поверхности, которые существенно отличаются от аналогичных свойств в объеме металла. Способность метала к поперечному сжатию при продольном упругом растяжении оказывается на поверхности значительно большей, чем в объеме, где она описывается известным коэффициентом Пуассона. Как и поверхностное натяжение, упругие свойства металла на его поверхности подвержены влиянию квантовых эффектов.
На иллюстрациях показаны: Фиг.1 - Квантовые осцилляции поверхностного натяжения меди в растворе фтористого натрия. Фиг.2 - Квантовые осцилляции поверхностного натяжения серебра в растворе фтористого натрия. Фиг.3 - Графическое преобразование осциллограммы, показанной на фиг.1. Фиг.4 - Графическое преобразование осциллограммы, показанной на фиг.2.
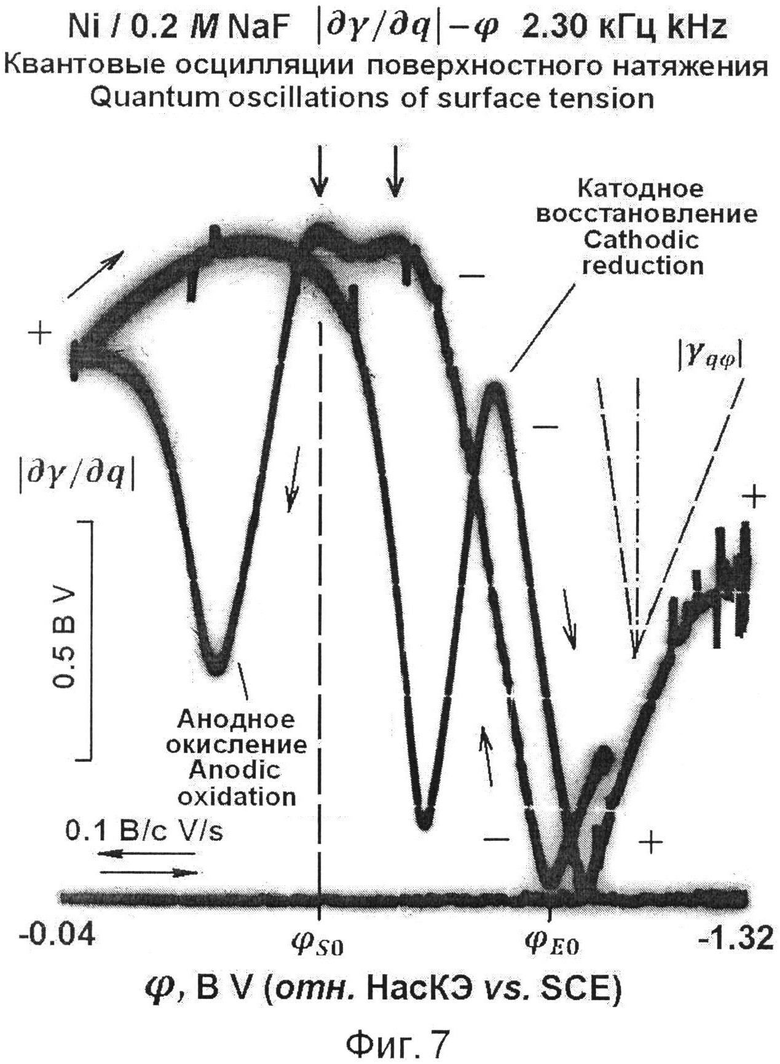
Фиг.5 - Выделение ступеней на зависимости производной поверхностного натяжения по поверхностной плотности заряда от потенциала для серебра в растворе фтористого натрия. Фиг.6 - Квантовые осцилляции поверхностного натяжения платины в растворе серной кислоты. Фиг.7 - Квантовые осцилляции поверхностного натяжения никеля в растворе фтористого натрия. Фиг.8 - Квантовые осцилляции поверхностного натяжения свинца в растворе серной кислоты. Фиг.9 - Фотография L-образного электрода в контакте с раствором при регистрации производной поверхностного натяжения по поверхностной плотности заряда. Фиг.10 - Чертеж L-образного электрода, вид сбоку. Фиг.11 - Вид А на фиг.10. Фиг.12 - Эволюция осциллограммы |∂γ/∂q|-φ в процессе предэлектролиза с чередованием окисления и восстановления поверхности меди (соответственно, развертка потенциала справа налево и слева направо). Фиг.13 - Прямой и обратный ход осциллограммы |∂γ/∂q|-φ на меди после предэлектролиза, показанного на фиг.12; прямой ход воспроизводит осциллограмму фиг.1.
Фиг.14 - Снятые одновременно осциллограммы плотности тока и производной поверхностного натяжения при изменении потенциала, j(φ) и |∂γ/∂q(φ)|, на меди в растворе фтористого натрия. Фиг.15 - диаграмма соответствия между осцилляциями поверхностного натяжения твердого тела и плотностью состояний электронов в двойном электрическом слое.
Температура в опытах 20±2°C. Электроды сравнения - насыщенный каломельный (НасКЭ) и равновесный водородный (РВЭ).
Представленная на фиг.1 осциллограмма получена на L-образном медном электроде в водном растворе 0.1 М NaF. Раствор готовят из фтористого натрия квалификации ОСЧ (особой чистоты) и дважды перегнанной воды. Используют медь квалификации 99.95%. Из листа меди толщиной 0.4 мм вырезают прямоугольную пластину размером (в миллиметрах) 30×6×0.4. Подвергают пластину электрополировке и изгибают в соответствии с чертежами фиг.10, 11. Полученный таким путем L-образный электрод приводят нижней гранью в контакт с раствором (фиг.9). В данном примере площадь контакта составляет 0.6 см2.
Через границу медного электрода с водным раствором пропускают переменный ток с частотой 2.11 кГц и с амплитудой 2 мА, что соответствует амплитуде поверхностной плотности заряда Δq=2.5·10-7 Кл/см2. На той же частоте регистрируют абсолютную величину производной поверхностного натяжения медного электрода по поверхностной плотности заряда (|∂γ/∂q|), как функцию потенциала электрода (φ). Достаточную малость амплитуды Δq подтверждают сохранением формы осциллограммы при увеличении амплитуды в два раза. Сохранение формы осциллограммы при изменении амплитуды эквивалентно достижению предела Δγ/Δq→∂γ/∂q, что позволяет использовать приближенное равенство ∂γ/∂q≈Δγ/Δq.
В процессе предварительного электролиза потенциал медного электрода изменяют со скоростью 0.1 В/с от -1.74 В до -0.06 В относительно насыщенного каломельного электрода. Проходят указанный интервал в анодном и затем в катодном направлениях (фиг.12). Признаком анодного окисления поверхности электрода является гистерезис в левой части осциллограммы. Признаком катодного восстановления поверхности служит совпадение прямого и обратного хода кривой в правой части осциллограммы. Заметно развитие ступени при обратном ходе осциллограммы. Место появления изгиба показано символом φSM
Повторяют чередование анодной и катодной разверток потенциала до полного выявления ступенчатого участка осциллограммы. Затем расширяют интервал изменения потенциала и получают осциллограмму фиг.13. Ее анодный ход воспроизводит осциллограмму, показанную на фиг.1.
Аналогично получают осциллограмму зависимости |∂γ/∂q| от φ на серебряном электроде в растворе фтористого натрия (фиг.2).
Техника регистрации производной поверхностного натяжения твердых тел по поверхностной плотности заряда подробно описана в цитированной выше книге автора. Ниже кратко дано пояснение, касающееся определения масштаба осциллограмм.
На экране осциллографа регистрируемый сигнал отображается в виде амплитуды напряжения на обкладках пьезоэлемента, с которым соединен исследуемый электрод. Для перевода регистрируемого сигнала в производную поверхностного натяжения по поверхностной плотности заряда используют эталонный сигнал, создаваемый известным тепловым натяжением.
После основного опыта водный раствор электролита (например, фтористого натрия) заменяют на водный раствор окислительно-восстановительной системы
0.2 M K3Fe(CN)6 + 0.2 M K4Fe(CN)6,
в которой переменный ток расходуется не на заряжение поверхности электрода, а на электрохимическую реакцию, в которой поочередно выделяется и поглощается известное тепло Пельтье. Основной и эталонный опыт проводят на одном и том же электроде, что избавляет от необходимости учитывать его форму.
Перед указанным тепловым моделированием медный и серебряный электроды покрывают тонким (5 мкм) слоем более химически стойкого металла, например никеля. Эталонный тепловой нагрев поверхности электрода может быть достигнут также другими средствами, в частности периодическим облучением.
На приведенных осциллограммах абсолютной величины |∂γ/∂q| знаками «плюс» (+) и «минус» (-) выделены участки положительных и отрицательных значений ∂γ/∂q. Ступени квантовых осцилляций показаны вертикальными стрелками. Величина ∂γ/∂q проходит через нуль при потенциале φ=φEO (где фаза Δγ меняется на противоположную). Абсолютная величина |γqφ| безразмерного наклона γqφ при φ=φEO показана пунктирной линией.
В случае меди (фиг.1) четыре ступени расположены на интервале потенциалов длиной 1.2 В (от φSN до φS0). При прохождении производной ∂γ/∂q через нуль соответствующий минимум величины |∂γ/∂q| незначительно поднят над нулевой линией, что обусловлено относительно слабым побочным эффектом.
В данных условиях |γqφ| =5,1 и
γqφ=∂(∂γ/∂q)/∂φ=-5,1.
Подстановка этого значения в уравнение
(∂С/∂ϑ)/С=-1-∂(∂γ/∂q)/∂φ
дает
(∂С/∂ϑ)/С=4.1
- значение, аномально большое по сравнению с коэффициентом Пуассона, который не может превзойти 0.5.
Полученная из опыта величина (∂С/∂ϑ)/С показывает, что основная часть избыточного заряда металлической обкладки двойного электрического слоя расположена под поверхностью металла - в противоположность электронному облаку, определяющему работу выхода и образующемуся над поверхностью. Поверхностные атомы металла оказываются внутри двойного электрического слоя. Именно по этой причине толщина и емкость двойного электрического слоя существенно меняются при упругом растяжении металла вдоль поверхности.
Левая часть неравенства
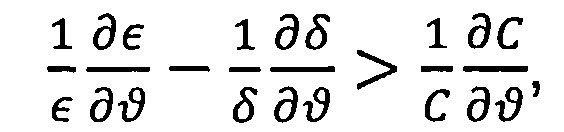
включает относительные изменения толщины и диэлектрической проницаемости металлической секции двойного электрического слоя при упругом растяжении вдоль поверхности металла, тогда как справа стоит относительное изменение емкости двойного электрического слоя в целом. Отсюда следует выполнение по крайней мере одного из неравенств
-(∂С/∂ϑ)/δ≥2, (∂С/∂ϑ)/∈≥2
Обычно, например, для льда, диэлектрическая проницаемость уменьшается при растяжении, ∂∈/∂ϑ<0. Это делает вероятным выполнение неравенства -(∂δ/∂ϑ)/δ≥2, которое означает аномальное поперечное сжатие слоя поверхностных атомов металла при упругом растяжении в условиях квантового перехода.
На фиг.3, 4 знаки величины ∂γ/∂q восстановлены путем отражения осциллограммы сверху вниз относительно нулевой линии, обозначенной равенством ∂γ/∂q=0. На фиг 3-5 ступени функции ∂γ/∂q(φ) выделены точкой минимума S0 и точками перегиба S1, S2, S3, S4. Показаны также точки максимального наклона γqφ функции ∂γ/∂q(φ), обозначенные как М1, М2, М3. Точка прохождения функции ∂γ/∂q(φ) через нуль обозначена как Е0. Указанным точкам соответствуют потенциалы
φS0, φS1, …, φM1, φM2, …, φEO.
Протяженности ступеней составляют для меди (фиг.1, 3)
|φS1-φS0|=0.20 B,
|φS2-φS1|=0.23 В,
|φS3-φS2|=0.27 В,
|φS4-φS3|=0.66 В,
для серебра (фиг.2, 4, 5)
|φS1-φS0|=0.30 B,
|φS2-φS1|=0.41 В,
|φS3-φS2|=0.89 В.
Найденные интервалы, умноженные на заряд электрона, приближенно равны расстояниям между дискретными уровнями энергии электронов в квантовой яме двойного электрического слоя.
Квантовые осцилляции поверхностного натяжения свойственны многим металлам. Осцилляции могут происходить не только на восстановленной поверхности, но также и на поверхности, покрытой слоем окисла. Дополнительные примеры осцилляции на восстановленной поверхности металла показаны на фиг.6, 7, 8. В случаях платины (фиг.6) и никеля (фиг.7) область квантовых осцилляций ограничена с катодной стороны областью адсорбции водорода. Это уменьшает доступное наблюдению число ступеней функции ∂γ/∂q (φ). В случае свинца (фиг.8) область квантовых осцилляции ограничена с анодной стороны электрохимической реакцией образования сульфата свинца.
Платина и никель относятся к числу переходных металлов, свойства которых во многом определяются d-электронами. Благородные металлы - медь и серебро - имеют в атомарном состоянии заполненные d-оболочки с одним s-электроном над ними, однако в твердом теле эти оболочки перекрываются и участвуют в образовании металлической связи. У свинца d-оболочки экранированы четырьмя s- и р-электронами. Общим является то, что поверхностные свойства этих металлов существенно зависят от квантовых эффектов, приводящих к наблюдаемым осцилляциям поверхностного натяжения.
Свидетельством такой зависимости служат снятые одновременно осциллограммы тока и производной поверхностного натяжения (фиг.14). На осциллограмме тока выделяются анодная волна WA, образованная током окисления поверхности меди, а также катодные волны WC1 и WC2, соответствующие двум стадиям восстановления окисленной поверхности. На осциллограмме производной поверхностного натяжения экстремум D0 при потенциале φSO является анодной границей ступенчатого участка функции ∂γ/∂q (φ).
Замечательно то, что экстремум D0 достигается одновременно с началом JO анодной волны WA окисления поверхности металла. Совпадение этих элементов не случайно. Оно характерно для ряда других металлов, в том числе для платины.
Отсюда следует, что наблюдаемые ступени сопровождаются дискретным уменьшением прочности связи поверхностных атомов металла. Последняя в анодном направлении ступень с экстремумом D0 является критической. Она способствует соединению металла с кислородом.
Прочность связи поверхностных атомов металла определяется числом электронов в их окрестности. Отсюда следует вывод, что число электронов в поверхностном слое металла ступенчато уменьшается при изменении потенциала в анодном направлении. Ряд признаков наблюдаемого явления - в том числе ступенчатый характер и связь с числом электронов - позволяют увидеть за этим явлением двухмерную квантовую яму в слое поверхностных атомов металла.
Уровни энергии электронов в квантовой яме дискретны. Поэтому электронная плотность состояний является ступенчатой функцией потенциала. Протяженность ступеней плотности состояний возрастает по мере заполнения квантовой ямы электронами, то есть при сдвиге потенциала металлического электрода в катодном направлении. Такая же закономерность наблюдается у ступеней производной поверхностного натяжения.
Возникновение квантовой ямы в поверхностном слое металла может быть объяснено деформацией в поле двойного электрического слоя с образованием узких поверхностных зон проводимости, электроны которых свободны только в двух измерениях. При благоприятных условиях поверхностные зоны проводимости частично заполнены d-электронами.
Блокировкой третьего измерения для определенной категории электронов может быть объяснен еще один экспериментальный факт, представленный на фиг.14. При изменении потенциала от φEO до φSO (развертка в анодном направлении, справа налево) производная поверхностного натяжения имеет четко выраженные ступени, тогда как осциллограмма тока представляет собой ровную наклонную линию, лишенную ступеней.
Ток создается движением электронов по нормали к поверхности металла, тогда как осцилляции поверхностного натяжения связаны с состоянием электронов, движущихся вдоль поверхности металла, но не способных к ее пересечению по нормали. В этом опыте поверхностное натяжение твердого тела проявляет избирательную чувствительность к явлениям, замкнутым в пределах поверхностного слоя металла.
Сходство ступенчатого изменения производной поверхностного натяжения со ступенчатым изменением электронной плотности состояний схематически показано на диаграмме фиг.15. Прямоугольные ступени плотности состояний соответствуют упрощенной ситуации, когда барьеры квантовой ямы бесконечны и абсолютная температура равна нулю. В реальности ступени размыты вдоль оси потенциала на величину, превышающую kT/e. При T=293 К крутизна фронта ступени ограничена значением расположенного под ним интервала kT/e=25,4 мВ. Уменьшение высоты барьеров квантовой ямы также снижает крутизну фронта ступеней.
В условиях описываемых опытов ступени производной поверхностного натяжения доступны наблюдению благодаря их значительной протяженности, превосходящей 0.1 B. Размер наиболее короткой ступени дает возможность оценить эффективную массу электронов в квантовой яме двойного электрического слоя. В случае меди Фmin=|φS1-φS0|=0.20 B, δ≈0.36 нм (постоянная решетки). Подстановка этих значений в формулу
m=(ħπ/δ)2/(2eФmin)
дает m=13.2·10-30 кг, m/me=14.5, где me=0.911·10-30 кг - масса покоя электрона. Превосходство эффективной массы над массой покоя электрона характерно для узких зон.













Изобретение относится к способам изучения поверхностных явлений. Из меди и серебра изготавливают электроды, приводят их в контакт с раствором электролита, осуществляют предварительный электролиз с чередованием анодного окисления и катодного восстановления поверхности металла, регистрируют зависимость производной поверхностного натяжения по поверхностной плотности заряда от потенциала электрода, сопоставляют указанные зависимости, полученные на меди и серебре, отмечают в качестве их общих признаков участок ступенчатого спада в анодном направлении, убывание протяженности ступеней вдоль оси потенциала. Происхождение ступеней объясняют локализацией электронов поверхностной проводимости в двухмерной квантовой яме, что приводит к ступенчатой зависимости плотности состояний этих электронов от потенциала. Указывают на соответствие между протяженностью ступеней и расстоянием между дискретными уровнями энергии электронов в двойном электрическом слое. На диаграмме в одном и том же диапазоне изменения потенциала сопоставлены график производной поверхностного натяжения по поверхностной плотности заряда и график плотности состояний электронов, имеющий вид ступенчатой функции потенциала, которая убывает при изменении потенциала в сторону более положительных значений и достигает нуля при потенциале минимума производной поверхностного натяжения. Технический результат заключается в повышении наглядности и достоверности демонстрации квантовых осцилляций поверхностного натяжения. 14 з.п. ф-лы, 15 ил.
1. Способ демонстрации квантовых осцилляций поверхностного натяжения твердого тела, отличающийся тем, что в качестве твердых тел используют металлы - медь и серебро, изготавливают из них электроды, приводят каждый из электродов в контакт с жидким раствором электролита, осуществляют предварительный электролиз с чередованием анодного окисления и катодного восстановления поверхности металла, после чего на восстановленной поверхности металла регистрируют зависимость производной поверхностного натяжения по поверхностной плотности заряда от потенциала электрода, сопоставляют указанные зависимости, полученные на меди и серебре, отмечают в качестве их общих признаков участок ступенчатого спада указанной производной в анодном направлении, убывание протяженности ступеней регистрируемой зависимости вдоль оси потенциала в анодном направлении, а также аномальную величину безразмерного наклона регистрируемой зависимости, который на указанном участке ступенчатого спада превосходит по абсолютной величине число 2, происхождение наблюдаемых ступеней объясняют локализацией электронов в квантовой яме двойного электрического слоя, что приводит к ступенчатой зависимости плотности состояний этих электронов от потенциала, при этом протяженность наблюдаемых ступеней рассматривают как источник информации о расстоянии между дискретными уровнями энергии электронов в двойном электрическом слое и об эффективной массе электронов.
2. Способ по п.1, отличающийся тем, что возможность наблюдения осцилляции поверхностного натяжения твердых тел обосновывают выполнением условия
kT<еФmin,
где k - постоянная Больцмана,
Т - абсолютная температура,
е - заряд электрона,
Фmin - протяженность наиболее короткой ступени производной поверхностного натяжения вдоль оси потенциала.
3. Способ по п.2, отличающийся тем, что измеренную экспериментально протяженность наиболее короткой ступени производной поверхностного натяжения вдоль оси потенциала используют для оценки эффективной массы электрона в двойном электрическом слое по формуле
m=(ħπ/δ)2/(2eФmin),
где m - эффективная масса электрона,
ħ - постоянная Планка,
δ - толщина металлической секции двойного электрического слоя, равная глубине проникания в металл электрического поля, создаваемого свободными зарядами, поступающими из внешней цепи, и приближенно совпадающая с постоянной кристаллической решетки в объеме металла.
4. Способ по п.1, отличающийся тем, что в качестве раствора электролита приготавливают водный раствор фтористого натрия с концентрацией в пределах от 0.001 до 0.5 моля на литр в диапазоне температур от 10 до 30°C, используют поликристаллические образцы металлов, их поверхность после предварительного электролиза рассматривают как изотропную,
5. Способ по п.1, отличающийся тем, что регистрируют зависимость производной поверхностного натяжения по поверхностной плотности заряда от потенциала на платине в водном растворе серной кислоты с концентрацией в пределах от 0.001 до 0.1 моля на литр, сравнивают ее с зависимостями, полученными на меди и серебре, и находят общий признак в виде ступенчатого спада указанной производной в анодном направлении.
6. Способ по п.1, отличающийся тем, что из безразмерного наклона регистрируемой зависимости рассчитывают относительную производную дифференциальной емкости двойного электрического слоя на границе металла с раствором по упругой деформации поверхности металла, используют для этого уравнение
 ,
,
где С - дифференциальная емкость двойного электрического слоя на границе металла с раствором электролита, отнесенная к единице площади поверхности металла,
ϑ - упругая деформация поверхности металла, равная относительному увеличению площади поверхности металла при его упругом растяжении,
φ - потенциал металла относительно электрода сравнения,
γ - поверхностное натяжение твердого металла,
q - поверхностная плотность заряда металла,
∂γ/∂q - производная поверхностного натяжения по поверхностной плотности заряда,
∂(∂γ/∂q)/∂φ - безразмерный наклон регистрируемой зависимости,
(∂С/∂ϑ)/С - относительная производная дифференциальной емкости двойного электрического слоя по упругой деформации поверхности металла,
(∂С/∂φ)/С - относительная производная дифференциальной емкости двойного электрического слоя по потенциалу.
7. Способ по п.6, отличающийся тем, что при нулевом значении производной поверхностного натяжения твердого металла по поверхностной плотности заряда используют упрощенное уравнение  ,
,
выражающее относительную производную дифференциальной емкости двойного электрического слоя по упругой деформации поверхности металла непосредственно через безразмерный наклон регистрируемой зависимости,
8. Способ по п.7, отличающийся тем, что область ступенчатого спада регистрируемой зависимости характеризуют неравенством
max(∂С/∂ϑ)/С>1,
объясняют это неравенство аномальным поперечным сжатием поверхностного слоя металла при упругом растяжении в условиях квантовых переходов, показывают более чем двукратное превосходство величины (∂С/∂ϑ)/С над коэффициентом Пуассона для того же металла.
9. Способ по п.1, отличающийся тем, что через границу металла с раствором электролита пропускают переменный ток с заданной частотой, на той же частоте избирательно детектируют колебания поверхностного натяжения металла, производную поверхностного натяжения по поверхностной плотности заряда определяют как предел отношения комплексных амплитуд поверхностного натяжения и поверхностной плотности заряда:
∂γ/∂q=lim(Δγ/Δq) при Δq→0,
где Δ - обозначение амплитуды, характеризуемой модулем
|Δ| и фазой arg Δ,
Δγ - амплитуда колебаний поверхностного натяжения, зависящая от потенциала φ,
Δq=ΔJ/(Sω) - амплитуда колебаний поверхностной плотности заряда,
ΔJ - амплитуда колебаний заданного переменного тока, поддерживаемая постоянной при изменении потенциала φ,
S - площадь границы металла с раствором электролита,
ω - угловая частота переменного тока.
10. Способ по п.9, отличающийся тем, что выделяют абсолютную величину производной поверхностного натяжения по поверхностной плотности заряда, которую определяют как предел отношения модулей амплитуд колебаний поверхностного натяжения и поверхностной плотности заряда,
|∂γ/∂q|=lim(|Δγ|/|q|) при Δq→0,
изменение знака указанной производной при прохождении ее через нуль определяют по изменению фазы колебаний поверхностного натяжения, численное значение указанной производной определяют путем сравнения с эталонным значением, полученным путем теплового моделирования переменного поверхностного натяжения твердого тела.
11. Способ по п.10, отличающийся тем, что при частоте переменного тока ниже 10 кГц знак производной поверхностного натяжения как функции потенциала восстанавливают путем зеркального отражения графика ее абсолютной величины относительно нулевой линии.
12. Способ по п.6, отличающийся тем, что по величине относительной производной дифференциальной емкости двойного электрического слоя по упругой деформации поверхности металла оценивают относительное поперечное сжатие слоя поверхностных атомов металла при упругом растяжении металла вдоль его поверхности, используют неравенство
 ,
,
где δ - толщина металлической секции двойного электрического слоя,
(∂δ/∂ϑ)/δ - относительное поперечное сжатие указанной секции при упругом растяжении металла вдоль его поверхности
∈ - эффективная диэлектрическая проницаемость указанной секции.
13. Способ по п.1, отличающийся тем, что зависимость производной поверхностного натяжения твердого металла по поверхностной плотности заряда от потенциала сравнивают с зависимостью электрического тока от потенциала на той же границе металла с раствором, изменяют потенциал в пределах, достигающих анодной волны тока окисления поверхности металла и катодной волны тока восстановления поверхности металла, указанные волны тока используют для определения интервала значений потенциала, в котором поверхность металла восстановлена.
14. Способ по п.13, отличающийся тем, что при изменении потенциала в анодном направлении отмечают отсутствие ступеней тока в диапазоне потенциала, содержащем ступени производной поверхностного натяжения, объясняют этот экспериментальный факт избирательной чувствительностью поверхностного натяжения твердого тела к образованию двухмерной квантовой ямы в металлической секции двойного электрического слоя.
15. Способ по п.13, отличающийся тем, что показывают совпадение экстремума наиболее анодной ступени производной поверхностного натяжения с началом анодной волны тока окисления поверхности металла в процессе сдвига потенциала в анодном направлении, объясняют такое соответствие достижением нулевой плотности состояний электронов, участвующих в образовании связи поверхностных атомов металла с его объемом, что приводит к ослаблению этой связи и облегчает соединение поверхностных атомов металла с кислородом, причем в случае благородных и переходных металлов в качестве указанной плотности состояний рассматривают плотность состояний d-электронов в двойном электрическом слое.
| Гохштейн А.Я | |||
| Поверхностное натяжение твердых тел и адсорбция, Наука | |||
| Планшайба для точной расточки лекал и выработок | 1922 |
|
SU1976A1 |
| Способ фотографической записи звуковых колебаний | 1922 |
|
SU400A1 |
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ ЗАВИСИЛ\ОСТИ ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ ТВЕРДЫХ ЭЛЕКТРОДОВ | 0 |
|
SU277399A1 |
| УСТРОЙСТВО для ИЗМЕРЕНИЯ ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ ТВЕРДЫХ ЭЛЕКТРОДОВ | 0 |
|
SU178161A1 |
Авторы
Даты
2015-06-10—Публикация
2013-12-31—Подача