Изобретение относится к радиотеплолокации, а именно к радиотеплолокационным системам наблюдения за объектами с помощью сканирующего радиометра [1, 2], а также может быть использовано в радиолокации, радиоастрономии и в оптико-электронных системах.
Известны способы восстановления изображений [3, 4] по результатам наблюдений с помощью сканирующей по угловым координатам (азимуту и углу места) антенны или фоточувствительного приемника. Моделью наблюдений в таких системах является свертка вида:
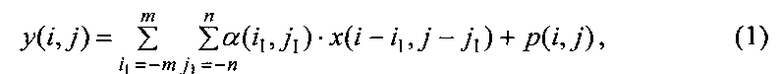
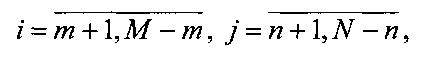
где y(ij) - результат измерения сигнала, принятого с i,j-го дискретного углового направления в координатах θ - угла места, φj - азимута и прошедшего тракт первичной обработки; 2m+1 и 2n+1 - ширина диаграммы направленности антенны (ДНА) соответственно по углу места и азимуту (на уровне 0,5 мощности); α(i,j) - коэффициенты аппаратной функции, отражающие действие ДНА и преобразований в тракте первичной обработки; x(i,j) - искомые величины, имеющие смысл интенсивности излучения в i,j-м направлении объекта наблюдения; p(i,j) - шумы аппаратуры.
Совокупность X={x(i,j)}, 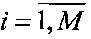 ,
, 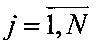 представляет матрицу искомого изображения объекта наблюдения, Y={y(i,j)} - матрицу наблюдений, P={p(i,j)} - матрицу помех,
представляет матрицу искомого изображения объекта наблюдения, Y={y(i,j)} - матрицу наблюдений, P={p(i,j)} - матрицу помех, 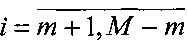 ,
, 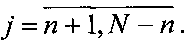 Восстановление X осуществляется в пространственной или частотной областях [5] на основе наблюдений Y и аппаратной функции α(i, j),
Восстановление X осуществляется в пространственной или частотной областях [5] на основе наблюдений Y и аппаратной функции α(i, j), 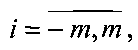
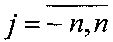 .
.
Проблема заключается в том, что аппаратная функция α(i,j) точно неизвестна, и для ее нахождения требуется проведение эксперимента. Известен метод нахождения аппаратной функции [5, с. 23], основанный на фильтрующем свойстве дельта функции δ(θ,φ) или функции Кронекера k(ij) для дискретной модели (1). Если в качестве x(i,j) взять точечный источник излучения с амплитудой U: x(i,j)=U·k(i-i0, j-j0), то измерения, полученные при сканировании относительно точки (i0,j0), повторяют форму аппаратной функции с точностью до помех: y(i,j)=Uα(i,j)+p(i,j). Однако значения аппаратной функции при таком подходе будут искажены действием помех, и требуется поиск оптимальных решений подавления помех.
Рассмотрим в качестве прототипа способ восстановления изображения [3] в пространственной области, который заключается в следующих матричных преобразованиях:
1. Матрица наблюдений Y построчно переписывается в (M-2m)(N-2n)-вектор 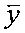 , матрица искомого изображения X - построчно в MN-вектор
, матрица искомого изображения X - построчно в MN-вектор 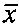 , матрица помех P представляется (М-2m)(N-2n)-вектором
, матрица помех P представляется (М-2m)(N-2n)-вектором 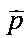 , значения аппаратной функции α(i,j) располагаются в составе (М-2m)(N-2n)xMN-матрицы A по определенному правилу, изложенному, например, на языке MATLAB:
, значения аппаратной функции α(i,j) располагаются в составе (М-2m)(N-2n)xMN-матрицы A по определенному правилу, изложенному, например, на языке MATLAB:

2. В принятых обозначениях выражение (1) принимает вид векторно-матричного уравнения:

Решением уравнения (2) по критерию минимума квадрата нормы ошибок восстановления:
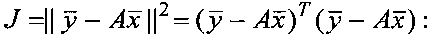
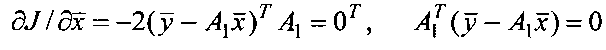
то есть метода наименьших квадратов (МНК), является вектор оценок:
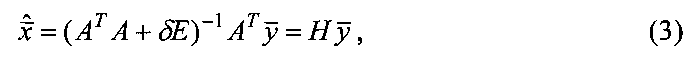
где T - символ транспонирования, Е - единичная матрица, δ - параметр регуляризации, необходимый для устойчивого обращения матрицы АT A, причем матрица весовых коэффициентов Н=(АTА+δE)-1 АT вычисляется на основе известной матрицы А.
3. Вектор 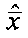 построчно переписывается в матрицу
построчно переписывается в матрицу 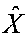 , которая представляет восстановленное изображение объекта.
, которая представляет восстановленное изображение объекта.
Рассмотренный способ, как и другие способы восстановления изображений как в пространственной, так и в частотной областях, обладает следующим недостатком. Ошибки восстановления сильно зависят от ошибок задания аппаратной функции, и способ оказывается неустойчивым к ошибкам аппаратной функции. Поэтому перед операциями восстановления требуется нахождение оптимальных оценок 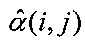 аппаратной функции α(i,j) с наименьшими ошибками оценивания, например, в смысле МНК.
аппаратной функции α(i,j) с наименьшими ошибками оценивания, например, в смысле МНК.
Технический результат направлен на нахождение аппаратной функции α(i,j) по методу МНК при восстановлении изображений объектов.
Технический результат предлагаемого технического решения достигается тем, что способ восстановления изображений при неизвестной аппаратной функции заключается в умножении вектора наблюдений 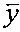 справа на матрицу весовых коэффициентов Н, рассчитанную по МНК ошибок восстановления, что дает в результате оптимальный вектор искомого изображения
справа на матрицу весовых коэффициентов Н, рассчитанную по МНК ошибок восстановления, что дает в результате оптимальный вектор искомого изображения 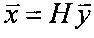 , отличающийся тем, что перед операциями восстановления формируется вектор наблюдений
, отличающийся тем, что перед операциями восстановления формируется вектор наблюдений 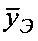 эталонного изображения
эталонного изображения 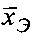 , который умножается справа на матрицу весовых коэффициентов W, рассчитанную для эталонного изображения
, который умножается справа на матрицу весовых коэффициентов W, рассчитанную для эталонного изображения 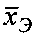 по критерию МНК ошибок оценивания аппаратной функции, в результате получается оптимальный вектор
по критерию МНК ошибок оценивания аппаратной функции, в результате получается оптимальный вектор 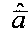 оценок аппаратной функции
оценок аппаратной функции 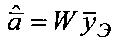 , элементы которого используются при вычислении матрицы весовых коэффициентов Н.
, элементы которого используются при вычислении матрицы весовых коэффициентов Н.
Расчетная часть.
Модель измерения (1) записывается в виде:
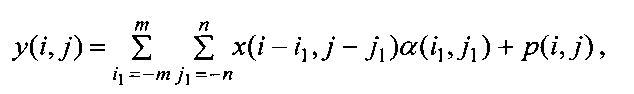
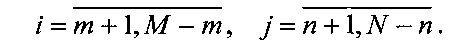
или в векторно-матричной форме:

где 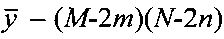 - вектор-столбец измерений y(i,j), считанных построчно из матрицы Y={y(i,j)};
- вектор-столбец измерений y(i,j), считанных построчно из матрицы Y={y(i,j)}; 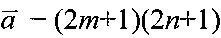 - вектор-столбец искомых значений аппаратной функции α(i,j), записанных построчно из матрицы {α{i,j)};
- вектор-столбец искомых значений аппаратной функции α(i,j), записанных построчно из матрицы {α{i,j)}; 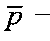
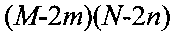 - вектор-столбец помех p(i,j); Х1-(M-2m)(N-2n)×(2m+1)(2n+1) - матрица элементов x(i,j), переписанных из матрицы X по определенному правилу, изложенному, например, на языке MATLAB:
- вектор-столбец помех p(i,j); Х1-(M-2m)(N-2n)×(2m+1)(2n+1) - матрица элементов x(i,j), переписанных из матрицы X по определенному правилу, изложенному, например, на языке MATLAB:

Из (4) по критерию минимума квадрата нормы
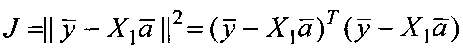
то есть МНК, находится оценка 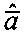 вектора
вектора 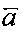 относительно
относительно 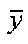 и Х1:
и Х1:
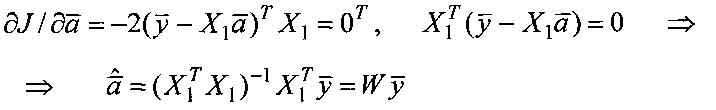
умножением справа вектора 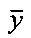 на матрицу весовых коэффициентов:
на матрицу весовых коэффициентов:

При необходимости для обращения матрицы в (5) используется регуляризация: 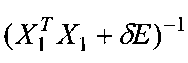 . Однако число наблюдений в у больше числа оцениваемых параметров в векторе
. Однако число наблюдений в у больше числа оцениваемых параметров в векторе 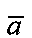 и матрица
и матрица 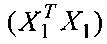 хорошо обусловлена.
хорошо обусловлена.
Способ осуществляют следующим образом.
1. Предварительно выполняют следующие операции:
1.1. Известная матрица ХЭ={xЭ(i,j)}, 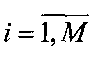 ,
, 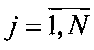 эталонного изображения представляется в форме матрицы Х1.
эталонного изображения представляется в форме матрицы Х1.
1.2. При сканировании поля эталонного изображения ХЭ по пространству 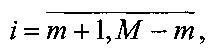
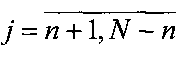 получается матрица YЭ, которая переписывается в вектор
получается матрица YЭ, которая переписывается в вектор 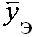 .
.
1.3. По формуле (5) вычисляется матрица весовых коэффициентов W и вектор 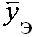 умножается справа на эту матрицу. В результате получается вектор оптимальных оценок
умножается справа на эту матрицу. В результате получается вектор оптимальных оценок 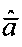 , элементы которого записываются в матрицу оценок значений аппаратной функции
, элементы которого записываются в матрицу оценок значений аппаратной функции 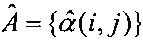 .
.
1.4. Для найденной матрицы 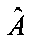 вычисляется матрица весовых коэффициентов
вычисляется матрица весовых коэффициентов 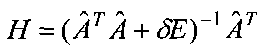 .
.
2. В рабочем режиме при восстановлении изображения X выполняют следующие операции:
2.1. При сканировании поля искомого изображения X по пространству 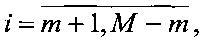
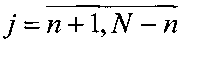 получается матрица наблюдений Y, которая переписывается в вектор
получается матрица наблюдений Y, которая переписывается в вектор 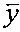 .
.
2.2. Вектор 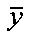 умножается справа на матрицу Н, в результате получается вектор оптимальных оценок
умножается справа на матрицу Н, в результате получается вектор оптимальных оценок 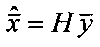 .
.
2.3. Элементы вектора 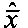 построчно переписываются в матрицу
построчно переписываются в матрицу 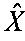 , которая представляет восстановленное изображение объекта.
, которая представляет восстановленное изображение объекта.
Замечание. Взятые из состава вектора 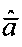 оценки аппаратной функции
оценки аппаратной функции 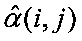 можно использовать и при других способах восстановления изображений, например с помощью восстанавливающего фильтра Винера в частотной области [5].
можно использовать и при других способах восстановления изображений, например с помощью восстанавливающего фильтра Винера в частотной области [5].
Литература
1. Николаев А.Г., Перцов С.В. Радиотеплолокация (пассивная радиолокация). М.: Сов. радио, 1964. 335 с.
2. Шарков Е.А. Радиотепловое дистанционное зондирование Земли: физические основы: в 2 т. / Т. 1. М.: ИКИ РАН, 2014. 544 с.
3. Патент RU 2292060.
4. Патент RU 2379706.
5. Василенко Г.И., Тараторин A.M. Восстановление изображений. М.: Радио и связь, 1986. 304 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЙ В МНОГОКАНАЛЬНЫХ РТЛС И РЛС | 2007 |
|
RU2368917C1 |
| СПОСОБ ФОРМИРОВАНИЯ ТРЕХМЕРНОГО ИЗОБРАЖЕНИЯ ПОВЕРХНОСТИ НА БАЗЕ БОРТОВОГО РАДИОТЕПЛОЛОКАТОРА | 2008 |
|
RU2368918C1 |
| СПОСОБ ПОВЫШЕНИЯ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ РАДИОТЕПЛОВЫХ ИЗОБРАЖЕНИЙ | 2008 |
|
RU2379706C2 |
| СПОСОБ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЙ ОБЪЕКТОВ В ДВУХКАНАЛЬНОЙ РАДИОМЕТРИЧЕСКОЙ СИСТЕМЕ | 2016 |
|
RU2612193C1 |
| СПОСОБ ФОРМИРОВАНИЯ РАДИОЛОКАЦИОННОГО ИЗОБРАЖЕНИЯ В БОРТОВЫХ СИСТЕМАХ РАДИОВИДЕНИЯ | 2008 |
|
RU2373552C1 |
| СПОСОБ ПОВЫШЕНИЯ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ ИЗОБРАЖЕНИЙ В МНОГОКАНАЛЬНЫХ РТЛС | 2017 |
|
RU2656355C1 |
| СПОСОБ ДВУХЭТАПНОГО ВОССТАНОВЛЕНИЯ ИЗОБРАЖЕНИЙ В МНОГОКАНАЛЬНЫХ РАДИОЛОКАЦИОННЫХ И РАДИОТЕПЛОЛОКАЦИОННЫХ СТАНЦИЯХ | 2008 |
|
RU2379705C2 |
| СПОСОБ ВОССТАНОВЛЕНИЯ ИЗОБРАЖЕНИЙ ОБЪЕКТОВ ПО РАЗРЕЖЕННОЙ МАТРИЦЕ РАДИОМЕТРИЧЕСКИХ НАБЛЮДЕНИЙ | 2015 |
|
RU2600573C1 |
| Способ формирования радиотеплового изображения | 2017 |
|
RU2661491C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ АППАРАТНОЙ ФУНКЦИИ РАДИОМЕТРА | 2016 |
|
RU2622899C1 |
Изобретение относится к радиотеплолокации, а именно к радиотеплолокационным системам наблюдения за объектами с помощью сканирующего радиометра, а также может быть использовано в радиолокации, радиоастрономии и в оптико-электронных системах. Достигаемый технический результат - нахождение аппаратной функции по методу наименьших квадратов (МНК) при восстановлении изображений объектов. Способ восстановления изображений при неизвестной аппаратной функции заключается в умножении вектора наблюдений на матрицу весовых коэффициентов, вычисляемую предварительно на основе МНК-оценок аппаратной функции, найденных для эталонного изображения.
Способ восстановления изображений при неизвестной аппаратной функции, заключающийся в умножении вектора наблюдений 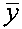 справа на матрицу весовых коэффициентов H, рассчитанную по методу наименьших квадратов (МНК) ошибок восстановления, что дает в результате оптимальный вектор искомого изображения
справа на матрицу весовых коэффициентов H, рассчитанную по методу наименьших квадратов (МНК) ошибок восстановления, что дает в результате оптимальный вектор искомого изображения 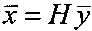 , отличающийся тем, что перед операциями восстановления формируется вектор наблюдений
, отличающийся тем, что перед операциями восстановления формируется вектор наблюдений 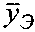 эталонного изображения
эталонного изображения 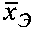 , который умножается справа на матрицу весовых коэффициентов W, рассчитанную для эталонного изображения
, который умножается справа на матрицу весовых коэффициентов W, рассчитанную для эталонного изображения 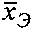 по критерию МНК ошибок оценивания аппаратной функции, в результате получается оптимальный вектор
по критерию МНК ошибок оценивания аппаратной функции, в результате получается оптимальный вектор 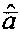 оценок аппаратной функции
оценок аппаратной функции 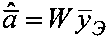 , элементы которого используются при вычислении матрицы весовых коэффициентов H.
, элементы которого используются при вычислении матрицы весовых коэффициентов H.
| СПОСОБ НАБЛЮДЕНИЯ ЗА ВОЗДУШНЫМИ ОБЪЕКТАМИ И ПОВЕРХНОСТЬЮ НА БАЗЕ БОРТОВОЙ РЛС | 2005 |
|
RU2292060C1 |
| СПОСОБ ДВУХЭТАПНОГО ВОССТАНОВЛЕНИЯ РАДИОЛОКАЦИОННОГО ИЗОБРАЖЕНИЯ | 2009 |
|
RU2411536C1 |
| СПОСОБ ИЗМЕРЕНИЯ РАДИОМЕТРИЧЕСКИХ КОНТРАСТОВ ЦЕЛЕЙ И РАДИОМЕТР ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2005 |
|
RU2285940C2 |
| СПОСОБ ФОРМИРОВАНИЯ РАДИОЛОКАЦИОННОГО ИЗОБРАЖЕНИЯ В БОРТОВЫХ СИСТЕМАХ РАДИОВИДЕНИЯ | 2008 |
|
RU2373552C1 |
| US 20130106642 A1, 02.05.2013 | |||
| JP 4977806 B2, 18.07.2012 | |||
| US 20140168007 A1, 19.06.2014. | |||
Авторы
Даты
2016-12-10—Публикация
2015-12-28—Подача