Область техники, к которой относится изобретение
Изобретение относится к способу и устройству для оценки дыхательного импеданса по вынужденным колебаниям давления.
Уровень техники
Дыхательный или акустический импеданс дыхательной системы человека может быть измерен, чтобы получать информацию, касающуюся сопротивления, растяжимости и инерции дыхательных путей, легких и стенки грудной клетки. Эта информация является полезной в диагностировании природы и серьезности многообразия респираторных заболеваний, таких как хроническая обструктивная болезнь легких (COPD), астма и бронхит.
В способе вынужденных колебаний (FOT), таком который описан в "Expiratory Flow Limitation Detected by Forced Oscillation and Negative Expiratory Pressure" автора Dellac и др., страницы 363-374, European Respiratory Journal, том 29, номер 2 (ссылка 1), акустические волны направляются в дыхательную систему, в то время как человек дышит нормально, и измеряется отклик, чтобы определять дыхательный импеданс.
Дыхательный импеданс описывает зависящее от частоты соотношение в колебаниях, происходящих от акустических волн, в терминах потока и давления. Там где дыхательный импеданс изменяется от вдоха к выдоху (как при некоторых заболеваниях и других медицинских состояниях), дыхательный импеданс должен оцениваться с точным временным разрешением. Однако в предшествующем уровне техники мало внимания уделяется надежности способов для оценки дыхательного импеданса во временных интервалах, которые являются достаточно короткими для физиологических целей (т.е. более короткими, чем продолжительность вдоха или выдоха).
Поэтому имеется необходимость в способе и устройстве для надежной оценки дыхательного импеданса в коротких временных интервалах.
Сущность изобретения
Согласно первому аспекту изобретения, обеспечивается способ оценки дыхательного импеданса, при этом способ содержит генерирование волн давления в устройстве взаимодействия с пациентом в сообщении с дыхательным путем субъекта; определение потока и давления газа в пневматической системе, которая включает в себя устройство взаимодействия с пациентом и дыхательный путь такого субъекта, чтобы вырабатывать соответствующие временные ряды, представляющие поток и давление; преобразование соответствующих временных рядов в частотно-временную область, чтобы создавать преобразованные временные ряды; оценку мощности потока и давления из соответствующих преобразованных временных рядов; оценку соответствующих взаимных спектров потока и давления на основе преобразованных временных рядов; и оценку дыхательного импеданса субъекта по оцененной мощности и взаимным спектрам.
Согласно второму аспекту изобретения, обеспечивается устройство для оценки дыхательного импеданса, при этом устройство содержит устройство взаимодействия с - пациентом;
источник возбуждения для генерирования колеблющегося давления, потока, или объема газа в таком дыхательном пути такого субъекта; средство для определения потока и давления газа в пневматической схеме, заданной посредством устройства взаимодействия с пациентом и дыхательного пути такого субъекта, и для вывода соответствующих временных рядов значений, представляющих поток и давление; процессор, сконфигурированный с возможностью преобразовывать соответствующие временные ряды в частотно-временную область; оценивать мощность потока и давления по соответствующим преобразованным временным рядам; оценивать соответствующие взаимные спектры потока и давления на основе соответствующих преобразованных временных рядов; и оценивать дыхательный импеданс субъекта по оцененной мощности и взаимным спектрам.
Согласно третьему аспекту изобретения, обеспечивается компьютерный программный продукт, содержащий считываемый компьютером носитель со считываемым компьютером кодом, воплощенным на нем, при этом считываемый компьютером код сконфигурирован так, что, при исполнении посредством подходящего процессора или компьютера, процессор или компьютер выполняет способ, описанный выше.
Оценка дыхательного импеданса может быть выполнена посредством диагностического инструмента, который использует оценку, чтобы давать оценку непроходимости дыхательных путей или чтобы оценивать серьезность заболевания. Диагностический инструмент поэтому может также использоваться, чтобы давать оценку эффективности лечения (фармакологического или иного), которое должно оказывать влияние на дыхательный импеданс.
Таким образом, согласно четвертому аспекту изобретения, обеспечивается способ диагностирования физиологического состояния, при этом способ содержит измерение дыхательного импеданса, как описано выше, и диагностирование физиологического состояния на основе измеренного дыхательного импеданса.
Оценки дыхательного импеданса могут также или в качестве альтернативы быть использованы, чтобы адаптировать настройки машины, используемой в лечении медицинского состояния, например неинвазивный вентилятор, который используется для противодействия непроходимости дыхательного пути, или в определении схемы лечения (например, какое конкретное лекарство или устройство использовать, дозировку лекарства и т.д.) для физиологического состояния.
Таким образом, согласно пятому аспекту изобретения, обеспечивается способ лечения физиологического состояния, при этом способ содержит измерение дыхательного импеданса, как описано выше, и определение и/или назначение лечения для физиологического состояния на основе измеренного дыхательного импеданса.
Краткое описание чертежей
Предпочтительные варианты осуществления изобретения теперь будут подробно описываться, только в качестве примера, со ссылкой на последующие чертежи, на которых:
фиг. 1 является блок-схемой устройства для оценки дыхательного импеданса по вынужденным колебаниям давления в соответствии с изобретением;
фиг. 2 является схематической диаграммой линейной модели, используемой, чтобы оценивать дыхательный импеданс в соответствии с изобретением;
фиг. 3A и 3B иллюстрируют предположение цикличности и неопределенность в дискретной временной области соответственно;
фиг. 4A и 4B иллюстрируют временной ряд, для которого 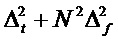
фиг. 5 иллюстрирует двумерные наименьшие квадраты в частотно-временной области;
фиг. 6 иллюстрирует доверительную область в комплексной плоскости;
фиг. 7 иллюстрирует дыхательный импеданс в здоровом пациенте в зависимости от времени и частоты с доверительными пределами для вынужденных колебаний давления при пяти разных частотах;
фиг. 8 иллюстрирует дыхательный импеданс в пациенте с COPD в зависимости от времени и частоты с доверительными пределами для вынужденных колебаний давления при пяти разных частотах;
фиг. 9 является блок-схемой последовательности операций, иллюстрирующей этапы в способе оценки дыхательного импеданса в соответствии с изобретением;
фиг. 10 является блок-схемой последовательности операций, более подробно иллюстрирующей этапы обработки, выполняемые посредством устройства согласно изобретению;
фиг. 11 показывает минимальные и максимальные сингулярные значения матрицы С в зависимости от числа событий N во временном ряде;
фиг. 12 иллюстрирует соотношение между неопределенностью во времени Δt и центрами тяжести собственных векторов CHC для N=16;
фиг. 13 иллюстрирует соотношение между неопределенностью во времени Δt и неопределенностью в частоте Δƒ для N=16;
фиг. 14 является графиком, изображающим νmin,n по отношению к ƒn;
фиг. 15 иллюстрирует неопределенность в графике NΔƒ в сравнении с Δt для N=16;
фиг. 16 иллюстрирует оценку 100(1-α)% доверительных пределов для 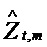
фиг. 17 иллюстрирует квадрат коэффициента связи в зависимости от времени и частоты для здорового субъекта; и
фиг. 18 иллюстрирует квадрат коэффициента связи в зависимости от времени и частоты для субъекта с COPD.
Подробное описание предпочтительных вариантов осуществления
Как описано выше, акустический импеданс дыхательной системы может быть выведен из вынужденных колебаний давления в наконечнике (респираторе) или маске для лица (способ вынужденных колебаний, FOT). Так как этот «дыхательный импеданс» зависит от сопротивления, растяжимости и инерции дыхательных путей, легких и стенки грудной клетки, он обеспечивает понимание природы и серьезности многообразия респираторных заболеваний. Зависящий от частоты импеданс является часто переменным во времени. В хронической обструктивной болезни легких сопротивление дыхательного пути обычно увеличивается в течение выдоха. При остановке дыхания во время сна или храпении сопротивление может увеличиваться в течение вдоха. Это требует надежной оценки импеданса в коротких временных интервалах, более коротких, чем продолжительность дыхания.
Дыхательный импеданс определяется как комплекснозначная передаточная функция, которая описывает линейное отношение между потоком q и давлением p в зависимости от частоты f,

где импеданс обозначается посредством z(ƒ). Это уравнение удовлетворяется, только если z(ƒ) является постоянной и время является бесконечным. Если система является временно устойчивой, z(ƒ) может все еще оцениваться в коротком временном интервале. Это ограничивается, однако, принципом неопределенности, который говорит, что для сигнала не может точно определяться положение в обеих временной и частотной областях. В дополнение, использование коротких временных интервалов делает оценку все более зависящей от случайных событий. Вопрос состоит в том, как это влияет на оценку передаточной функции, такой как z(ƒ), которая может быть устойчивой только в части дыхательного цикла.
В последующем передаточная функция временно стационарного процесса оценивается посредством линейной регрессии в дискретной частотно-временной области. Отношение неопределенности выводится для дискретного времени и частоты, которое используется, чтобы получать оптимальное частотно-временное разрешение. Анализ статистических свойств используемой оценки импеданса дает зависящий от частоты параметр дыхательной механики, за которым и оцененные значения, и доверительные пределы могут следовать во времени.
В конце подробного описания содержится Таблица (Таблица 1), которая предоставляет глоссарий символов и аббревиатур, используемых в последующем описании изобретения.
Способы
Этот раздел подробного описания устанавливает математическую основу для способа и устройства согласно изобретению. Меньшее математическое описание изобретения предоставляется в разделе "Обсуждение" ниже.
Схематическая диаграмма устройства 2 согласно изобретению показана на фиг. 1. Кратко используемое устройство 2 FOT состоит из устройства 4 взаимодействия с пациентом, соединенного с дыхательным путем субъекта, чтобы создавать пневматическую систему, которая включает в себя дыхательный путь такого субъекта. Устройство 4 взаимодействия с пациентом является любым устройством, подходящим, чтобы обеспечивать пневматическое соединение с дыхательным путем субъекта, таким как маска или наконечник. Устройство 4 взаимодействия с пациентом является функционально соединенным с источником 6 возбуждения, который генерирует волны давления, изменения потока или изменения объема с относительно низкими частотами, например частотами от 8 до 24 Гц. В примерном варианте осуществления настоящего изобретения устройство 4 взаимодействия с пациентом является громкоговорителем.
В проиллюстрированном варианте осуществления пациент дышит воздухом через сопротивление 9 проволочной сетки, которое находится рядом с головкой 8 пневмотахометра, который располагается между устройством 4 взаимодействия с пациентом и источником 6 возбуждения. Вынужденные волны частично отражаются в дыхательных путях и легких пациента и ведут к колебаниям в потоке воздуха и давлении, которые измеряются в устройстве 2 FOT. Поток воздуха через головку 8 пневмотахометра измеряется с использованием дифференциального преобразователя 10 давления, и давление измеряется с использованием второго преобразователя 12 давления рядом с наконечником 4. Аналого-цифровой преобразователь 14 дает соответствующие временные ряды потока и давления, {qt} и {pt}, где целое число t является дискретным временным индексом, которые обеспечиваются в процессор или компьютер 16 для анализа. Компьютер или процессор 16 также может обеспечивать сигналы для управления частотой акустических волн, генерируемых громкоговорителем 6, через аналого-цифровой преобразователь 14 и усилитель 18. Дополнительные детали конкретного варианта осуществления устройства 2 предоставляются в разделе ниже, озаглавленном "Устройство измерения".
Настоящее изобретение также предусматривает, что другие устройства доставки потока газа могут соединяться с дыхательным путем субъекта в дополнение к источнику 6 возбуждения. Например, система поддержки давления или вентилятор может соединяться с устройством 4 взаимодействия с пациентом, чтобы обеспечивать поток газа, например, в то время как источник 6 возбуждения генерирует колебания дыхательного пути субъекта. Следует также отметить, что измерения потока и давления могут осуществляться в любом местоположении вдоль пневматической системы, включая сюда измерение давления и потока внутри системы поддержки давления или вентилятора. Измеренное давление и поток могут затем использоваться, чтобы определять поток и давление газа в пневматической системе, как, например, в дыхательном пути пациента, с использованием любого стандартного способа.
Настоящее изобретение также предусматривает, что источник 6 возбуждения может представлять собой составляющие системы поддержки давления или вентилятора, а не автономное устройство. Например, система поддержки давления или вентилятор могут включать в себя клапан, чтобы управлять потоком/давлением газа, доставляемого в пациента. Настоящее изобретение предусматривает колебание такого клапана, чтобы вырабатывать низкочастотные волны давления, изменения потока или изменения объема. Конечно, любое другое устройство или система, которое способно генерировать низкочастотные волны давления, изменения потока или изменения объема, как, например, поршень, может использоваться как источник 6 возбуждения.
Вместо того чтобы измерять давление и/или поток с использованием датчиков давления и/или потока, настоящее изобретение также предусматривает, что поток или давление могут устанавливаться или управляться, как, например, посредством системы поддержки давления или вентилятора. В этом случае установленное давление или установленный поток используется как поток давления для настоящих целей, нежели вывод дифференциального преобразователя 10 давления или второго преобразователя 12 давления.
Интервал между двумя выборками (в секундах) является обратным частоте выборки (в Гц). В этом разделе зависящий от времени и частоты импеданс выводится из этих временных рядов с использованием относительно простой линейной алгебры. Читатель, который хорошо не знаком с линейной алгеброй, отсылается к разделу «Обсуждение ниже», где главные результаты подытоживаются словами.
Простая линейная модель. Чтобы учитывать случайные события, будем предполагать, что двумерный временной ряд {qt,pt} является реализацией двумерного стохастического процесса {Qt,Pt}. Детерминированные переменные записываются строчными буквами и случайные переменные (RV) - прописными буквами. Дополнительно предполагается, что время является бесконечно длинным (t = …, -1, 0, 1, …). Ссылаясь теперь на фиг. 2, ввод xt источника возбуждения фильтруется через линейные временно-инвариантные фильтры (2 и 3) с последовательностями импульсной характеристики {hqx,l} и {hpx,l). Это дает поток и давление, как предсказывается линейной моделью,
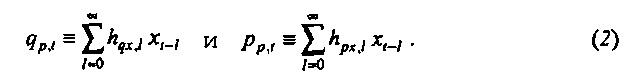
Предположим, что эти «истинные» значения возмущаются посредством двух независимых источников белого шума нулевого среднего с соответствующими дисперсиями 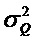
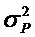

где средние значения μQ и μP являются константами. Так как результирующие Qt и Pt являются нормально распределенными, предполагаемый двумерный процесс {Qt,Pt} является полностью стационарным.
Предположение цикличности. В то время как описанный стационарный процесс является бесконечно долгим, является целью изобретения описать преходящие явления, где стационарность может предполагаться только для конечной последовательности N событий. Это может решаться посредством предположения, что время является циклическим, в смысле, что последнее событие предшествует первому. Результирующий временной ряд может тогда представляться посредством помещения N событий на регулярных интервалах вдоль круга, как часы. Можно бесконечно следовать по кругу в одном и том же направлении без покидания его. Результирующий бесконечный временной ряд является периодическим по N. То есть для любого целого числа j,

Подставляя u=t-l+jN, первая свертка в Уравнении 2 может быть перезаписана как
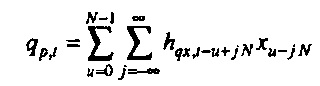 .
.
Вследствие предполагаемого периодического характера xt (Уравнение 4) xu-jN=xu. Бесконечная сумма в вышеуказанном уравнении может определяться как hqx,t-u «с периодизацией по длине N», обозначаемое посредством

Как результат,

Так как 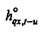 также является периодической по N, индекс t-u может увеличиваться с помощью N, если t-u является отрицательным (так что индекс всегда попадает в диапазон от нуля до N-1, что является удобным). Когда последовательности представляются посредством столбцовых векторов, Уравнение 6 также может быть записано как (если N=4)
также является периодической по N, индекс t-u может увеличиваться с помощью N, если t-u является отрицательным (так что индекс всегда попадает в диапазон от нуля до N-1, что является удобным). Когда последовательности представляются посредством столбцовых векторов, Уравнение 6 также может быть записано как (если N=4)
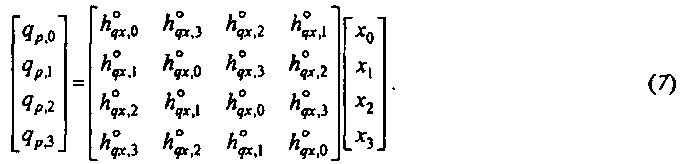
N×N матрица в этом уравнении является циркулянтом (квадратной матрицей, чьи строки являются сдвинутыми вправо версиями предыдущей строки, с циклическим переходом на краях). Когда первая строка обозначается посредством 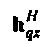 , где верхний индекс Н обозначает эрмитово транспонирование, циркулянт также может быть записан как
, где верхний индекс Н обозначает эрмитово транспонирование, циркулянт также может быть записан как 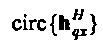 . Пусть x≡{x0, …, xN-1},
. Пусть x≡{x0, …, xN-1}, 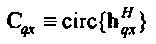 и qp≡{qp, 0, …, qp, N-1}. Тогда qp=Cqxx. Аналогично pp=Cpxx, так что Уравнение 3 становится
и qp≡{qp, 0, …, qp, N-1}. Тогда qp=Cqxx. Аналогично pp=Cpxx, так что Уравнение 3 становится
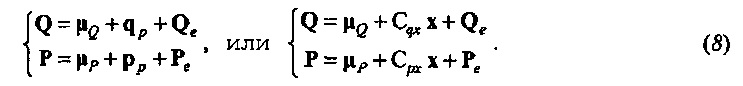
Дискретная частотная область. Чтобы вывести зависящий от частоты импеданс, модель из Уравнения 8 должна быть преобразована в дискретную частотную область. Как шаг к частотно-временному анализу, это кратко резюмируется в данном документе. Преобразование заданного временного ряда х≡{x0, …, xN-1} в дискретную частотную область разбивает ряд в набор гармонических колебаний с дискретными частотами ƒn≡n/N, для n=0, …, N-1. Такое колебание описывается посредством N-вектора
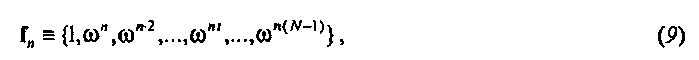
где ω≡exp(2πi/N) и i2=-1. Вследствие теоремы Эйлера
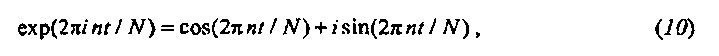
так что вектор fn фактически описывает комбинированное колебание вдоль действительной и мнимой оси с частотой ƒn. Непосредственно показывается, что

Как результат, квадрат нормы 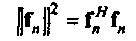 равняется N, в то время как два колебания при разных гармонических частотах являются ортогональными.
равняется N, в то время как два колебания при разных гармонических частотах являются ортогональными.
Преобразование x в дискретную частотную область выполняется посредством матрицы «ортонормального дискретного преобразования Фурье» (ODFT) F, определенной как

где n,t = 0, …, N-1. Это преобразование дает N-вектор Fx, составляющие которого являются внутренними произведениями 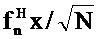

где I является N×N единичной матрицей. Это разрешает синтез x из N колебаний,
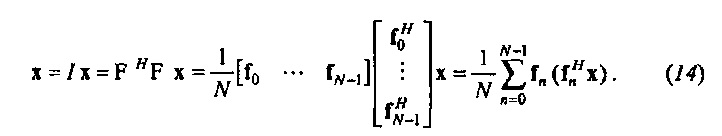
Соответственно x записывается как взвешенная сумма N гармонических колебаний с частотами ƒn
Векторы fn являются собственными векторами циркулянтных матриц, так что мы можем записать

Комплексное число Hqx,n является передаточной функцией от x к q для частоты ƒn, определенной как

Когда Нрх,n определяется аналогичным образом, импеданс для частоты ƒn - это

Когда собственные значения помещаются в диагональную матрицу 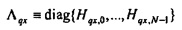 , и соответствующие собственные векторы как столбцы в N×N матрицу FH, Уравнение 15 становится
, и соответствующие собственные векторы как столбцы в N×N матрицу FH, Уравнение 15 становится 
Циркулянты являются нормальными матрицами (они коммутируют с их эрмитовым транспонированием). Уравнение 18 поэтому согласуется со спектральной теоремой, которая говорит, что N×N нормальная матрица имеет N ортогональных собственных векторов (в этом случае N ортогональных столбцовых векторов fn).
Принцип неопределенности для дискретного времени и частоты. Составляющие х≡{xt} имеют точное положение во временной области, но неопределенное в частотной области.
Обратно составляющие преобразования Фурье F х имеют точное положение в частотной области, но неопределенное во временной области. Чтобы получить сигнал с маленькой неопределенностью в обеих областях, должна быть определена мера неопределенности.
Предполагая, что время является циклическим, подход Форбса (Forbes) и Алонсо (Alonso) кажется наиболее соответствующим (см. ссылку 3). Ссылаясь теперь на фиг. 3A, во временной области квадраты составляющих |xt|2 помещаются как точечные массы на регулярных интервалах, на круге с радиусом rt в комплексной плоскости, с центром в начале, с размером каждой точечной массы на фиг. 3A, соответствующим весу каждого события. Время представляется посредством длины дуги между двумя событиями. Окружность круга является полным периодом N (где N=12 на этой иллюстрации), так что радиус равняется rt=N/(2π). Заданное событие в момент времени t располагается в точке rtωt в комплексной плоскости. Форбс и Алонсо (ссылка 3) предложили несколько мер неопределенности. Здесь используется незначительно отличающаяся мера, определенная как взвешенное среднее квадратов расстояний между каждым событием в момент времени t и событием в опорное время tR,
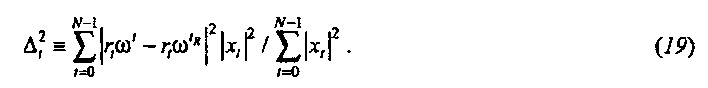
Это мера неопределенности имеет преимущество, что она может легко быть выражена как отношение квадратичных форм. Без потери общности можно предполагать, что tR=0 (как показано на фиг. 3A). Тогда квадрат неопределенности 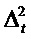
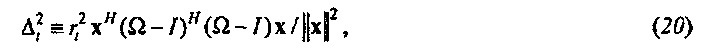
где диагональная матрица 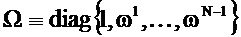

где A≡Ω-I. Физически 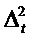
В частотной области составляющие F x являются ассоциированными с частотами ƒn≡n/N. Одни и те же составляющие будут получаться для частот n/N+j, где j является любым целым числом (см. Уравнения 9, 10). Составляющие F x являются поэтому периодическими в частотной области, с единичным периодом. Соизмеримая мера неопределенности, таким образом, может быть определена в частотной области, относительно опорной частоты ƒR. Квадраты модулей составляющих F x снова помещаются как точечные массы на круг в комплексной плоскости. Радиус теперь равняется rƒ≡1/(2π), так что окружность равняется единице. Если ƒR=0, то

Диагональная матрица Ω относится к «оператору сдвига по времени» Т≡circ{0,…,0,1}. Умножение слева x на Т круговым образом сдвигает составляющие x на одно место вниз. Из Уравнения 18 непосредственно следует, что FT-1=ΩF («теорема сдвига»), так что
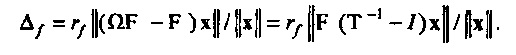
Так как F является унитарной, 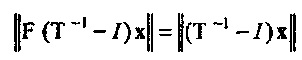 . Пусть В≡Т-1-I, тогда
. Пусть В≡Т-1-I, тогда

Теперь рассмотрим матрицу
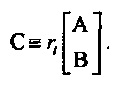
Полная неопределенность во времени и частоте может быть выражена посредством отношения
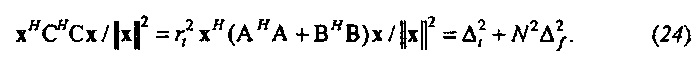
Это отношение (коэффициент Релея) может принимать значения в диапазоне от минимального к максимальному квадрату сингулярного значения С. Это дает соответствующий принцип неопределенности для дискретного времени и частоты,

Соответственно является невозможным, чтобы Δt и Δƒ обе были очень маленькими, так как полная неопределенность 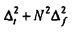 должна быть, по меньшей мере, равной
должна быть, по меньшей мере, равной 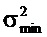
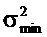
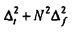 является минимальной. На фиг. 4A собственный вектор выводится для опорного времени tR=0 и частоты fR=0 (верхний график). Он также является собственным вектором матрицы Фурье F (с единичным собственным значением), так что временной ряд остается неизменным после преобразования в дискретную частотную область (нижний график). На этих графиках обе из осей времени и частоты являются круговым образом сдвинутыми по визуальным причинам. Фиг. 4B соответствует фиг. 4A, но с опорной частотой
является минимальной. На фиг. 4A собственный вектор выводится для опорного времени tR=0 и частоты fR=0 (верхний график). Он также является собственным вектором матрицы Фурье F (с единичным собственным значением), так что временной ряд остается неизменным после преобразования в дискретную частотную область (нижний график). На этих графиках обе из осей времени и частоты являются круговым образом сдвинутыми по визуальным причинам. Фиг. 4B соответствует фиг. 4A, но с опорной частотой 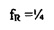 . На фиг. 4B закрытые круги представляют действительные значения, открытые круги представляют мнимые значения, и кресты показывают абсолютные значения.
. На фиг. 4B закрытые круги представляют действительные значения, открытые круги представляют мнимые значения, и кресты показывают абсолютные значения.
См. раздел, озаглавленный "Вывод принципа неопределенности" ниже для более детального анализа принципа неопределенности.
Дискретная частотно-временная область. ODFT разбивает временной ряд из N событий в набор колебаний с N разными частотами. Простой способ выполнить частотно-временной анализ - это вычислять ODFT повторно для короткодлящихся последовательностей М последовательных событий (с M<N). Соответственно ряд разбивается на М колебаний с частотами ƒm≡m/M (с m=0, …, М-1), что сводится к дискретному «коротко-временному преобразованию Фурье». Результирующая неопределенность во времени и частоте является минимальной, если каждое коротко длящееся колебание является «оконным» с составляющими vmin.
Для последовательности М событий такое оконное колебание описывается посредством М-вектора

Пример показан на фиг. 4B. Отметим, что 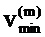
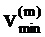
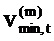
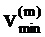
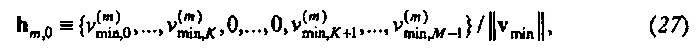
где K является наименьшим целым числом, меньшим чем или равным М/2. Это колебание является центрированным относительно момента времени t=0 и частоты ƒm=m/M. В общем, колебание в

является центрированным относительно момента времени t и частоты ƒm.
Наилучшим образом подходящее линейное соотношение между x и hm,t в смысле наименьших квадратов следует из ортогональной проекции x на (комплексное) одномерное подпространство, порожденное hm,t. Принимая во внимание, что hm,t определяется как единичный вектор (см. Уравнение 27), эта проекция является

Для заданной частоты ƒm пусть N×N матрица Mm определяется как

Она является циркулянтом, который действует полосовым фильтром с резонансной частотой ƒm. Умножение слева x на Mm дает N-вектор, который может быть обозначен посредством тильды или «знака волны»,

Составляющие 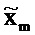
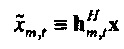 .
.
Полное частотно-временное преобразование (TFT) охватывает все частоты ƒm для m=0, …, М-1. Пусть MN×N матрица М определяется как

Преобразование в дискретную частотно-временную область (частотно-временную область) выполняется посредством умножения слева x на М (специально для заданного М). Это дает MN-вектор 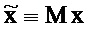
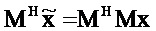

Обратное преобразование, таким образом, восстанавливает исходный временной ряд, так как MHMx=Ix=x. Это делает частотно-временной синтез x возможным согласно

Временной ряд, таким образом, записывается как взвешенная сумма MN коротко длящихся колебаний, каждое центрировано относительно времени t и частоты ƒm (ср. Уравнение 14). Для заданного М эти колебания дают оптимальное частотно-временное разрешение согласно принципу неопределенности из Уравнения 25. Как показано в разделе "Вывод принципа неопределенности" ниже, колебания могут аппроксимироваться посредством усеченного гауссиана с M'=10⋅Δ, ненулевыми элементами.
Ввод в источник возбуждения. Является удобным использовать набор гармонических колебаний в качестве ввода х источника возбуждения. Чтобы анализировать данные, масштаб М TFT тогда может выбираться так, что частоты этих колебаний совпадают с резонансными частотами TFT ƒm. Во-первых рассмотрим одиночный синусоидальный ввод с частотой ƒn и амплитудой am. Вследствие теоремы Эйлера (Уравнение 10) действительнозначное гармоническое колебание является суммой комплекснозначного колебания и его комплексного сопряжения. Ввод источника возбуждения может, таким образом, быть записан

где звездочка обозначает комплексное сопряжение. Из Уравнений 9 и 10 следует, что 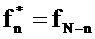
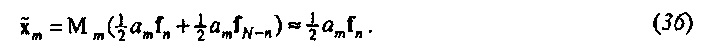
Последняя аппроксимация является действительной, если М является достаточно большим и соответствующее Δƒ достаточно маленьким, чтобы подавлять колебание на частоте ƒN-n посредством фильтра TFT с резонансной частотой ƒn=ƒm. Полное представление ввода источника возбуждения в частотно-временной области получается, если составляющая на «комплементарной частоте» ƒN-n (здесь равняется ƒM-m) также включается посредством добавления MM-m к Mm в Уравнении 36.
Модель из Уравнения 8 преобразуется в частотно-временную область посредством умножения слева обоих уравнений на М. Концентрируясь на интересующих частотах (например, частоте вынужденного колебания, описанного посредством Уравнения 35), умножение верхней части Уравнения 8 на Mm дает
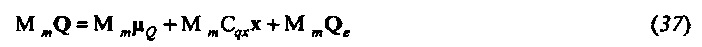
Непосредственно показывается, что MmμQ является нулем, если m≠0. Таким образом,

Так как циркулянты все коммутируют, следует, что 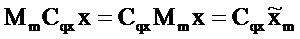
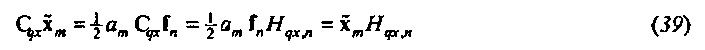
Когда Hqx,n для ƒn=ƒm обозначается посредством bQ,m (и соответствующее Hpx,n посредством bP,m), модель из Уравнения 8 редуцируется к

Импеданс для ƒn=ƒm - это

Набор других колебаний может добавляться к вводу источника возбуждения Уравнения 35, при условии что Δƒ использованного TFT является достаточно маленьким, так что эти колебания являются хорошо разделенными в частотно-временной области.
Анализ дисперсии в частотно-временной области. TFT позволяет выполнять анализ дисперсии в частотно-временной области (см. раздел ниже, озаглавленный "Анализ дисперсии в частотно-временной области"). Например, квадрат нормы шума в потоке (см. Уравнение 8) может быть разбит на

Случайная переменная 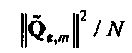 может называться «спектр мощности выборки TFT» шума Qe. Предположим, что передаточная функция фильтра от шума I к Qe,t (фиг. 2) является относительно плоской в полосе пропускания фильтра TFT около ƒm. Тогда
может называться «спектр мощности выборки TFT» шума Qe. Предположим, что передаточная функция фильтра от шума I к Qe,t (фиг. 2) является относительно плоской в полосе пропускания фильтра TFT около ƒm. Тогда 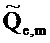
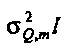 . Как результат,
. Как результат, 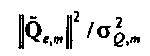 следует приблизительному распределению хи-квадрат с эквивалентными степенями свободы η. См. раздел "Анализ дисперсии в частотно-временной области" ниже для вывода η, где включаются только те составляющие
следует приблизительному распределению хи-квадрат с эквивалентными степенями свободы η. См. раздел "Анализ дисперсии в частотно-временной области" ниже для вывода η, где включаются только те составляющие 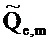
Двумерные наименьшие квадраты в частотно-временной области. Теперь предполагается, что в каждый момент времени t начинается новый временно стационарный процесс, что описывается с помощью модели из фиг. 2. Процесс охватывает N событий и предполагается циклическим (то есть периодическим по N). В частотно-временной области, модель становится (из Уравнения 40)

где векторы - это «коротко длящиеся» N-векторы теперь, с началом в момент времени t. Отметим, что константы bQ,m и bP,m также получили индекс t, так как они предполагаются специальными для момента времени, в котором процесс начинается. Константы, также как вводы в модель, могут поэтому быть разными в разные моменты времени t (даже если два процесса перекрываются во времени). Наилучшим образом подходящие оценки для bQ,t,m и bP,t,m могут выводиться из 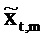
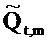
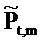
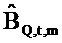
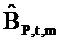

где оцененный «прогнозируемый» вектор 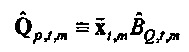 является ортогональным к оцененной «ошибке»
является ортогональным к оцененной «ошибке» 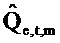
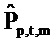
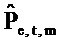
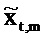
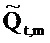
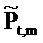
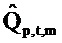
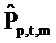
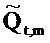
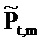
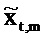
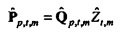 . Векторы ошибки
. Векторы ошибки 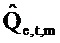
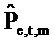
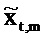
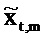
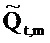
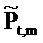
Степень линейного отношения между 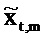
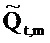

Случайная переменная 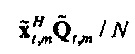 может называться «взаимный спектр выборки TFT» от x к Q. Геометрически
может называться «взаимный спектр выборки TFT» от x к Q. Геометрически 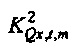 равняется cos2ϕ , где ϕ является углом от
равняется cos2ϕ , где ϕ является углом от 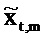
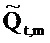
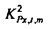 равняется cos2θ. Оценки наименьших квадратов выводятся стандартным способом. Это дает
равняется cos2θ. Оценки наименьших квадратов выводятся стандартным способом. Это дает

Соответственно 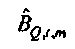 является отношением взаимного спектра выборки от x к Q к спектру мощности выборки х. Когда
является отношением взаимного спектра выборки от x к Q к спектру мощности выборки х. Когда 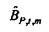 выводится аналогичным образом, импеданс оценивается посредством
выводится аналогичным образом, импеданс оценивается посредством

«Истинный» импеданс zt,m имеет действительную часть rt,m («сопротивление») и мнимую часть xt,m («реактивность»). Соответствующие оценки являются действительной и мнимой частями 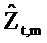

Как изображено на фиг. 6A, 100(1-α)% доверительная область для bQ,t,m ограничивается посредством круга в комплексной плоскости, центрированного относительно 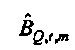 . Доверительная область дается посредством
. Доверительная область дается посредством

где 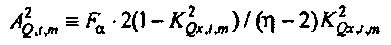 и Fα является верхней 100(1-α)% точкой F-распределения (см. раздел, озаглавленный "Вывод доверительных пределов", ниже). Ввод источника возбуждения xt является безразмерной переменной, так что
и Fα является верхней 100(1-α)% точкой F-распределения (см. раздел, озаглавленный "Вывод доверительных пределов", ниже). Ввод источника возбуждения xt является безразмерной переменной, так что 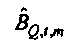 имеет единицы потока (так как
имеет единицы потока (так как 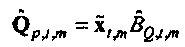 из фиг. 5). Значения, которые зависят от предположения цикличности, здесь отброшены (эффективное число выборок - это NS=N-M+1). Отношение будет отклонено, если источник находится внутри круга (тогда
из фиг. 5). Значения, которые зависят от предположения цикличности, здесь отброшены (эффективное число выборок - это NS=N-M+1). Отношение будет отклонено, если источник находится внутри круга (тогда 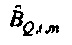 не является значимо отличным от нуля при 100⋅α% уровне достоверности). Следовательно, из Уравнения 49 следует, что значимость получается, если AQ,t,m<1 Доверительная область для
не является значимо отличным от нуля при 100⋅α% уровне достоверности). Следовательно, из Уравнения 49 следует, что значимость получается, если AQ,t,m<1 Доверительная область для 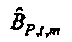 ограничивается посредством соизмеримого круга, и отношение между
ограничивается посредством соизмеримого круга, и отношение между 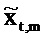
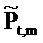
Консервативная оценка доверительной области для 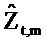
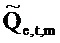
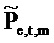
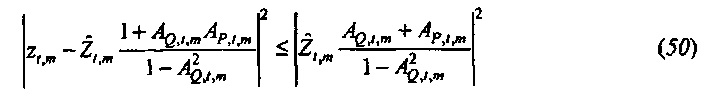
Ссылаясь на фиг. 6B, ограничивающий круг не является концентрическим относительно оценки 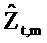
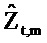
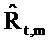
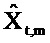
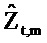
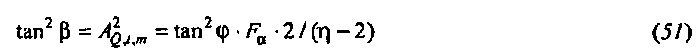
Если шум в потоке равен нулю, то 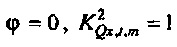 и
и 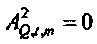 , так что β=0 и доверительная область является симметричной относительно
, так что β=0 и доверительная область является симметричной относительно 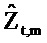
Раздел, озаглавленный "Вывод доверительных пределов", ниже дает дополнительный анализ того, что происходит, если предполагается, что либо шум в потоке, либо шум в давлении равен нулю. Соответствующие оценки тогда будут равны
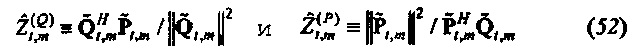
Это сводится к линейной регрессии от потока к давлению (или обратно) в частотно-временной области. Переменные 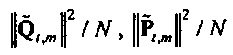 и
и 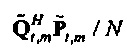 являются соответствующими спектрами мощности выборки и взаимным спектром выборки. Главное различие между оценками из Уравнения 52 и
являются соответствующими спектрами мощности выборки и взаимным спектром выборки. Главное различие между оценками из Уравнения 52 и 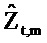
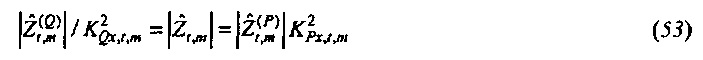
Следует, что, если шум присутствует как в потоке, так и давлении, величина импеданса является недооцененной, если 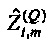 используется вместо
используется вместо 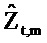
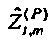 ).
).
Установки. При использовании устройства 2 поток и давление записывались на частоте выборки 800 Гц. TFT выполнялось с Δt=50 (что сводится к 50/800=0,0625 с). Это требует ширины фильтра TFT 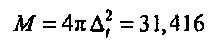 . Однако коэффициенты фильтра TFT аппроксимировались посредством гауссиана, усеченного при M'=10⋅Δt=500 (см. раздел "Вывод принципа неопределенности" ниже). Ассоциированная неопределенность в частоте - это Δƒ=1/(4πΔt)=0,0016 (или 0,0016 800=1,27 Гц). TFT было выведено для ƒm=0,01, 0,015, 0,02, 0,025, 0,03, соответствуя наложенным частотам FOT 8, 12, 16, 20, 24 Гц. Спектр мощности выборки и взаимный спектр выборки были вычислены для NS=500 (то есть по временному интервалу 500/800=0,625 с). Были использованы только данные, которые являются независимыми от предположения цикличности. Это ведет к приблизительному распределению хи-квадрат спектров выборки с η=6,72. Доверительные пределы для импеданса выводились для 90% уровня достоверности (Fα=4.05). Частотно-временные спектры были выровнены во времени с исходным временным рядом.
. Однако коэффициенты фильтра TFT аппроксимировались посредством гауссиана, усеченного при M'=10⋅Δt=500 (см. раздел "Вывод принципа неопределенности" ниже). Ассоциированная неопределенность в частоте - это Δƒ=1/(4πΔt)=0,0016 (или 0,0016 800=1,27 Гц). TFT было выведено для ƒm=0,01, 0,015, 0,02, 0,025, 0,03, соответствуя наложенным частотам FOT 8, 12, 16, 20, 24 Гц. Спектр мощности выборки и взаимный спектр выборки были вычислены для NS=500 (то есть по временному интервалу 500/800=0,625 с). Были использованы только данные, которые являются независимыми от предположения цикличности. Это ведет к приблизительному распределению хи-квадрат спектров выборки с η=6,72. Доверительные пределы для импеданса выводились для 90% уровня достоверности (Fα=4.05). Частотно-временные спектры были выровнены во времени с исходным временным рядом.
Примеры
Фиг. 7 показывает действительную и мнимую части оцененного импеданса 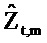
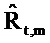
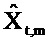
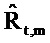
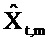
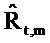
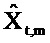
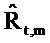
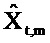
Фиг. 8 показывает импеданс для пациента с COPD с большими отрицательными качаниями в 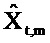
Обсуждение
Фиг. 9 - это блок-схема последовательности операций, которая подытоживает этапы в способе согласно изобретению. В этом примерном варианте осуществления волны давления генерируются с использованием громкоговорителя, соединенного с наконечником как устройством 4 взаимодействия с пациентом, которое находится в сообщении с дыхательным путем субъекта (этап 101). Колебания в потоке и давлении газа, проходящего через наконечник 4, измеряются, чтобы давать соответствующий временной ряд измерений (этап 103). В устойчивом состоянии дыхательный импеданс может выводиться из вынужденных колебаний давления в наконечнике 4 спокойно дышащего субъекта. Так как механические свойства дыхательной системы часто изменяются от вдоха к выдоху, способ оценивает импеданс при обстоятельствах временной «устойчивости». Главная проблема состоит в том, что импеданс является зависящей от частоты величиной, и что высокое временное разрешение неизбежно ведет к низкочастотному разрешению, тем самым искажая оценку. Так как данные состоят из дискретных временных рядов (последовательные измерения потока и давления в наконечнике 4), это требует оптимального частотно-временного анализа коротко-временных рядов.
Как описано в разделе "Способы" выше, настоящее изобретение основывается на понятии, что коротко-временной ряд может быть стационарным, если время предполагается циклическим (см. ниже). Как описано, для такого временного ряда была выведена новая версия принципа неопределенности, что ставит нижний предел на полную неопределенность во временной и частотной области. На этапе 105 этот принцип используется, чтобы разбивать дисперсию каждого временного ряда на составляющие, которые ассоциированы с конкретным временем и частотой (через преобразование к «дискретной частотно-временной области» или «частотно-временной области»). Анализ наименьших квадратов в частотно-временной области тогда дает несмещенную оценку импеданса с оптимальным частотно-временным разрешением (этап 107). В конце концов, доверительные пределы для импеданса построены в зависимости от времени и частоты. Главные этапы подытоживаются и обсуждаются ниже.
Линейная модель. Оценка дыхательного импеданса основывается на простой линейной модели (Уравнение 3, фиг. 2). Колебания в наконечнике 4 устройства 2 вызываются громкоговорителем 6. Результирующие изменения в потоке и давлении зависят от механических свойств дыхательной системы пациента (акустики этой системы). В модели это выражается посредством двух линейных временно-инвариантных фильтров (2 и 3 на фиг. 2), которые модифицируют ввод громкоговорителя. Результирующие флуктуации в потоке и давлении возмущаются посредством двух независимых источников шума как в потоке, так и давлении. Дыхательный импеданс определяется посредством двух линейных фильтров (2 и 3).
Возможные источники шума - это: 1) составляющие дыхания пациента в частотном диапазоне вынужденных колебаний, что является, вероятно, наиболее важной проблемой (см. ссылку 2), 2) глотание, кашель или другие движения пациента, 3) кардиогенные колебания, в частности, когда сопротивление дыхательного пути является низким, 4) зависящие от времени изменения в самом дыхательном импедансе и 5) случайные ошибки измерения.
Линейная модель использовалась ранее, чтобы объяснять зависящее от частоты соотношение между потоком и давлением в течение аналогичных экспериментов (см. ссылку 2), хотя имелись указания, что нелинейные взаимодействия в дыхательной системе не являются незначительными. Линейное описание соотношения между потоком и давлением в устройстве 2 FOT, однако, поддерживается фактом, что различия давления являются маленькими по сравнению со средним абсолютным давлением. Использование импеданса, чтобы описывать соотношение, является упрощением взаимодействия стоящих волн, которые могут ожидаться при этих обстоятельствах. Главное ограничение, однако, кажется, лежит во времени, в течение которого дыхательная система может рассматриваться как устойчивая.
Предположение цикличности. Чтобы учитывать случайные события, предполагалось, что поток и давление являются случайными переменными (RV) с заданным распределением вероятностей. Короткая последовательность N спаренных измерений потока и давления, таким образом, рассматривается как выборка из конечного двумерного стохастического процесса (набора N хронологически упорядоченных спаренных случайных переменных RV). Зависящее от частоты соотношение между потоком и давлением в таком процессе может описываться только посредством устойчивого импеданса, если двумерный стохастический процесс предполагается (второго порядка) стационарным. Это означает, что ожидаемые значения потока и давления являются постоянными, также как ковариации между одновременными и последовательными значениями. Ковариации между последовательными значениями не могут быть постоянными для конечной последовательности, однако вследствие эффектов начала и конца (если эти ковариации не равны нулю).
Однако эта проблема решается посредством предположения, что время является циклическим, в смысле что последнее событие предшествует первому. Этим способом ковариации между последовательными значениями могут быть постоянными, в то время как последовательность все еще состоит из конечного числа случайных переменных RV. Это является прямым последствием дискретной и конечной природы последовательности. Рассмотрим часы, для которых является возможным отслеживать только полные часы (хронологическая последовательность N=12 событий). Если вы смотрите на один час (момент времени t1) и на два часа (момент времени t2), является возможным, что один час прошел от t1 до t2, но является также возможным, что 13 часов прошли, или что событие в t2 случилось 11 часами прежде t1. Без дополнительного знания не является возможным распознать между временной разницей одного часа и одного часа плюс или минус целое кратное 12. Эта неопределенность напрямую относится к «неоднозначности» (которая происходит, если кто-то пытается реконструировать непрерывный сигнал из такого временного ряда). Еще случайные изменения в последней части измеренной последовательности могут вызывать флуктуации в обеих переменных, которые не продолжаются в первой части. Это будет вызывать смещение в оценке импеданса, которое, однако, исключается в примененном частотно-временном анализе (см. ниже).
Принцип неопределенности. «Неопределенность во времени» является свойством временного ряда, который выражает то, сколько составляющих ряда разбросаны во времени. Для дискретного, конечного и циклического временного ряда это дает фигуру, как показано на фиг. 3A. Составляющие временного ряда представляются посредством точечных масс, помещенных на регулярных интервалах вокруг временного круга (каждая масса равняется квадрату абсолютного значения составляющей). Неопределенность Δt определяется по отношению к опорной точке (здесь точке, где t=0, Уравнение 19) и близко связана с центром тяжести (Уравнение В3). Если временной ряд имеет только одну ненулевую составляющую (в момент времени t=0), то центр тяжести располагается в t=0 и Δt является нулевым. Если все составляющие имеют равный вес, то центр тяжести располагается в центре, и Δt является высоким (ассоциированным с максимальным разбросом во временной области).
Аналогично «неопределенность в частоте» Δƒ выражает разброс в частотной области (Уравнение 22). Посредством дискретного преобразования Фурье каждый временной ряд с N составляющими может быть записан как сумма N гармонических колебаний с заданной амплитудой и частотой (представление в дискретной частотной области). Для дискретного временного ряда эти частоты также являются циклическими. Разброс в частотной области может визуализироваться посредством помещения квадратов амплитуд как N точечных масс вокруг круга, соизмеримого с циклом на фиг. 3A (каждая точка соответствует конкретной частоте).
Для непрерывного времени и частоты было показано, что имеется компромисс между неопределенностью во времени и частоте, выраженный посредством отношения неопределенности

Это имеет место для непрерывного и бесконечного временного ряда (при некоторых условиях). Если Δt является маленьким, Δƒ должно быть большим, так как произведение должно, по меньшей мере, быть равным 1/(4π), и наоборот. Это неравенство напрямую относится к знаменитому принципу неопределенности Гейзенберга для положения и импульса частицы. Для дискретного временного ряда, однако, нижний предел произведения ΔtΔƒ является нулем (см. также "Вывод принципа неопределенности" ниже). Еще имеется ограничение на объединенные значения Δt и Δƒ. В разделе "Способы" выше (Уравнение 25) показано, что для дискретного, конечного и циклического временного ряда

где σmin является функцией N. Таким образом, Δt и Δƒ не могут быть оба очень маленькими. Сумма  является минимальной для временного ряда, чье дискретное преобразование Фурье точно равняется исходному временному ряду (фиг. 4A). По мере того как N становится большим, этот временной ряд с минимальной объединенной неопределенностью во времени и частоте приближается к гауссовской функции времени. Этот временной ряд является аналогичным состоянию минимальной неопределенности двух притягивающихся частиц в квантовой механике (так называемый «квантовый гармонический осциллятор»). Форбс и др. (см. ссылку 4) вывели аналогичный временной ряд из волнового уравнения для такого осциллятора. В настоящем случае, однако, это состояние минимальной неопределенности просто выводится из определений Δt и Δƒ для дискретного и конечного временного ряда. В "Вывод принципа неопределенности" ниже показано, как принцип неопределенности из Уравнения 55 относится к принципу неопределенности Габора для большого N (см. фиг. 14).
является минимальной для временного ряда, чье дискретное преобразование Фурье точно равняется исходному временному ряду (фиг. 4A). По мере того как N становится большим, этот временной ряд с минимальной объединенной неопределенностью во времени и частоте приближается к гауссовской функции времени. Этот временной ряд является аналогичным состоянию минимальной неопределенности двух притягивающихся частиц в квантовой механике (так называемый «квантовый гармонический осциллятор»). Форбс и др. (см. ссылку 4) вывели аналогичный временной ряд из волнового уравнения для такого осциллятора. В настоящем случае, однако, это состояние минимальной неопределенности просто выводится из определений Δt и Δƒ для дискретного и конечного временного ряда. В "Вывод принципа неопределенности" ниже показано, как принцип неопределенности из Уравнения 55 относится к принципу неопределенности Габора для большого N (см. фиг. 14).
Дискретная частотно-временная область. Представленное частотно-временное преобразование (TFT) разбивает дискретный и конечный временной ряд на набор коротко длящихся колебаний М составляющих с M<N (преобразование в частотно-временную область). Каждое колебание центрировано относительно конкретного времени и частоты, с минимальной неопределенностью в обоих областях согласно принципу из Уравнения 55. TFT сводится к оконному «краткосрочному преобразованию Фурье» или «скользящему преобразованию Фурье». Коротко длящиеся колебания максимально перекрывают друг друга во времени, так что результат является независимым от момента времени, в который первое колебание начинается. Только колебания, которые начинаются до начала и оканчиваются после конца временного ряда, являются зависимыми от предположения цикличности (они исключаются в анализе, чтобы избежать смещения). В разделе "Вывод частотно-временного преобразования" ниже показано, что преобразование является «ортонормальным» (Уравнение 33), что влечет, что вся информация во временном ряде сохраняется после преобразования в дискретную частотно-временную область. Ничто не приобретается, ничто не теряется. Обратное преобразование восстанавливает исходный временной ряд.
Чтобы быть точными, не является возможным ссылаться на дискретную частотно-временную область, но только относительно частотно-временной области для выбранного значения М. Это целое число определяет продолжительность каждого краткосрочного колебания, но это также равняется числу разных частот, относительно которых эти колебания центрируются (резонансные частоты TFT). Как показано в "Вывод принципа неопределенности" ниже, оптимальное Δt и Δƒ согласно принципу неопределенности из Уравнения 55 зависит от М (заменить N на М в Уравнении В8, см. также фиг. 11). Не является неожиданным то, что чем более большим является М, тем более большим является соответствующее оптимальное Δt и меньшим соответствующее Δƒ. В настоящем анализе М выбирается так, что Δƒ является достаточно маленьким, чтобы иметь способность распознавать разные колебания, вызванные громкоговорителем.
Ввод в громкоговоритель. В примерном варианте осуществления набор пяти гармонических колебаний мы использовали в качестве ввода в громкоговоритель 6 (на частотах 8, 12, 16, 20 и 24 Гц соответственно). Для анализа значение М (в действительности эффективное значение, см. Уравнение В6) было выбрано так, чтобы неопределенности были, выраженные во временных единицах, Δt=0,0625 с и Δƒ=1,27 Гц. Коэффициенты TFT вычислялись только для этих пяти частот, что сводится к полосно-пропускающей фильтрации с пятью резонансными частотами. Один подход предшествующего уровня техники использует одиночную частоту для ввода громкоговорителя. Это налагает меньшие требования на частотно-временной анализ (они использовали полосовой фильтр с прямоугольным окном, с более большим Δƒ для заданного Δt, чем в настоящем изобретении). Для одиночной частоты частотное разрешение является менее критичным, хотя может все же быть полезным отфильтровывать более высокие гармоники дыхания пациента. С другой стороны, частотная зависимость импеданса может обеспечивать дополнительную информацию о дыхательной механике. Альтернативно, может накладываться широкополосный шум, что имеет недостаток, что мощность входного сигнала постепенно распределяется по всем частотам, с относительно меньшей мощностью на исследованных частотах (более низкое отношение сигнала к шуму при одной и той же полной мощности громкоговорителя). В еще другом подходе была применена волновая форма вентилятора, которая была построена из негармонических синусоид, к вентилированным пациентам, чтобы предотвращать взаимодействие между колебаниями на гармонических частотах. Такой подход, однако, не является применимым в свободнодышащих субъектах. Некоторое вмешательство дыхательной системы на гармонических частотах может, в самом деле, происходить в настоящем изобретении, хотя это не было наблюдаемо в частотном отклике системы после широкополосной стимуляции.
Анализ дисперсии в частотно-временной области. Ортонормальное свойство TFT делает возможным разбивать дисперсию стохастического процесса на частотно-временные зависящие составляющие, что дает частотно-временной спектр мощности (см. "Анализ дисперсии в частотно-временной области" ниже). Мощность выборки TFT выражает вклад коротко длящегося колебания около заданного времени и частоты в полную дисперсию выборки. Анализ TFT спектра мощности, таким образом, сводится к анализу дисперсии в частотно-временной области (Уравнение 42). В модели (Уравнение 43) предполагается, что имеются независимые источники шума в потоке и давлении, вместе формирующие двумерный циклический стационарный стохастический процесс. Когда значения, которые зависят от предположения цикличности, отбрасываются, некоторое число NS=500 последовательных значений в частотно-временной области рассматривается как выборка из этого процесса (эпизод 0,625 с на частоте выборки 800 Гц). Предполагалось, что в каждый момент (800 раз в секунду) новый стохастический процесс этого типа начинается с дисперсией, которая не необходимо равна предыдущей дисперсии. Таким образом, измерения были подразделены в максимально перекрывающиеся эпизоды 500 значений, каждый из которых рассматривался как выборка из разного стационарного стохастического процесса. Источники шума не предполагались «белыми», но предполагалось, что мощность была постоянной в каждом частотном диапазоне фильтра TFT. Средняя мощность в течение каждого эпизода 500 значений тогда следует приблизительному распределению хи-квадрат, для которого были выведены эквивалентные степени свободы.
Двумерные наименьшие квадраты в частотно-временной области. Для каждого эпизода NS=500 последовательных значений коэффициенты линейного отношения между вводом громкоговорителя и потоком (bQ,t,m) и отношения между вводом и давлением (bP,t,m) оценивались посредством простой линейной регрессии в частотно-временной области (Уравнение 44, фиг. 5). Это дает результатом несмещенные оценки, ассоциированные с моментом времени t и частотой ƒm (соответственно 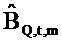
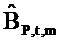
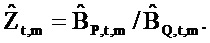
Выбор N зависит от момента времени, в течение которого система может рассматриваться как стационарная. Для дыхания эпизод ~ 0.5 с кажется приемлемым, предполагая, что импеданс является приблизительно устойчивым в середине каждого вдоха и выдоха. В показанных примерах это работало хорошо (фиг. 7 и 8). В большинстве способов предшествующего уровня техники, однако, спектры усредняются по более долгому эпизоду, обычно более чем 10 с. Некоторые усредненные спектральные значения выводились из неперекрывающихся сегментов ~0.65 с по полному эпизоду 16 с.
Использование неперекрывающихся сегментов, однако, дает значительно меньшие степени свободы для эпизода одной и той же длины по сравнению с максимально перекрывающимися сегментами, используемыми здесь (т.е. сегментами М значений, используемых в TFT). Главная проблема состоит в том, что использование эпизода 16 с взаимно сводит на нет возможные физиологические различия между вдохом и выдохом, которые являются обычно более резко выраженными в заболеваниях, таких как COPD. В этом случае низкий коэффициент связи между потоком и давлением по 16 с не является только отражением шума, но также изменчивости в дыхании импеданса (что является частью заболевания). Продолжительность предполагаемой стационарности также не должна выбираться слишком короткой. В примере из фиг. 8 доверительные интервалы являются относительно широкими в точках поворота от вдоха к выдоху и наоборот. Это может быть вследствие высокочастотных составляющих собственного дыхания пациента. Эти изменения являются, очевидно, более короткими, чем 0,5 с, так что они появляются как шум в оценке. Продолжительность предполагаемой стационарности должна быть поэтому достаточно длительной, чтобы «интерпретировать» эти изменения как шум.
Так как оценка импеданса 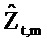
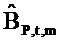
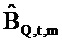
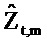
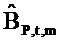
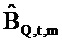
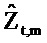
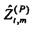 в Уравнении 52.
в Уравнении 52.
С другой стороны, другие документы использовали оценку, аналогичную 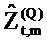
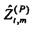 и
и 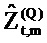
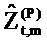
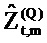
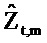
До сих пор доверительные пределы на оцененном импедансе выводились только для относительно длинных по времени интервалов. Частотно-временные зависимые доверительные пределы в вариантах осуществления настоящего изобретения обеспечивают непрерывное ощущение действенности гипотезы, что коротко длящиеся последовательности являются выборками из стационарного стохастического процесса. Они делают возможным тестировать значимость изменений в импедансе в ходе времени и обеспечивают основу, чтобы автоматически отклонять ненадежные оценки (как в течение глотка на фиг. 7), что имеет практический интерес в мониторинге реального времени.
Фиг. 10 - это блок-схема последовательности операций, иллюстрирующая способ, выполняемый посредством устройства 2 согласно изобретению (и конкретно этапы обработки, выполняемые посредством компьютера 16) более подробно. Как на фиг. 9, на этапе 121 волны давления генерируются с использованием громкоговорителя 6, соединенного с наконечником 4, который используется субъектом, и колебания в потоке и давлении воздуха, проходящего через наконечник 4, измеряются и оцифровываются, чтобы давать соответствующий временной ряд измерений (этап 123). Таким образом, поток и давление задаются в зависимости от дискретного времени t, qt и pt.
Затем на этапе 125 временные ряды, каждый, преобразуются в дискретную частотно-временную область, чтобы давать поток 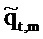
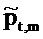
Этап 125 содержит вычисление:

для временного ряда потока qt, где i2=-1 и весовой коэффициент 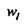 аппроксимируется посредством гауссовской функции времени,
аппроксимируется посредством гауссовской функции времени, 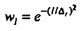 и Δt, является выбранной неопределенностью во времени. Фильтр усекается на K1=5⋅Δt В то время как весовой коэффициент wl описывается здесь как аппроксимируемый посредством гауссовской функции, следует понимать, что настоящим изобретением предполагаются другие окна или весовые коэффициенты, такие как треугольное окно, кусочно-линейная аппроксимация или полиномиальная функция.
и Δt, является выбранной неопределенностью во времени. Фильтр усекается на K1=5⋅Δt В то время как весовой коэффициент wl описывается здесь как аппроксимируемый посредством гауссовской функции, следует понимать, что настоящим изобретением предполагаются другие окна или весовые коэффициенты, такие как треугольное окно, кусочно-линейная аппроксимация или полиномиальная функция.
Давление 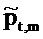

Затем на этапе 127 мощность и взаимные спектры выводятся в зависимости от времени и частоты. Мощность потока задается посредством:

где NS является числом выборок в частотно-временной области, 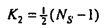 , если NS является нечетным, и |⋅| обозначает абсолютное значение.
, если NS является нечетным, и |⋅| обозначает абсолютное значение.
Мощность давления, представленная посредством Pp,t,m, выводится аналогично из

Взаимный спектр от ввода 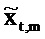
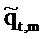

где звездочка обозначает комплексное сопряжение.
Взаимный спектр от ввода громкоговорителя к давлению, Cxp,t,m, выводится из 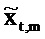
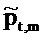

На этапе 129 мощность и взаимные спектры используются, чтобы определять передаточные функции от ввода громкоговорителя к потоку и давлению соответственно.
В частности, передаточная функция от ввода громкоговорителя к потоку задается посредством отношения взаимных спектров к мощности:

и передаточная функция от ввода громкоговорителя к давлению, Bxp,t,m, выводится аналогично:

Таким образом, на этапе 131 импеданс дыхательной системы может определяться из отношения передаточных функций:

с действительной составляющей Rrst,m и мнимой составляющей Xrst,m.
Дополнительно, доверительные пределы на дыхательном импедансе могут выводиться (этап 133) следующим образом.
Эквивалентное число степеней свободы η мощности и взаимных спектров задается посредством:

где Р является N×N матрицей, Н обозначает эрмитово транспонирование и tr{⋅} обозначает след матрицы. Матрица Р определяется как

где S - это диагональная матрица S, которая имеет NS единиц на главной диагонали (и остальные нули), т.е.

(Сдвинутая) матрица частотно-временного преобразования Mm является циркулянтом, чьи вхождения на первой строке - это 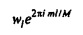 , для l=-K3, …, K3 и
, для l=-K3, …, K3 и 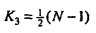 , где N является нечетным. Fα помечается как верхняя 100(1-α)% точка F-распределения на 2,η-2 степенях свободы.
, где N является нечетным. Fα помечается как верхняя 100(1-α)% точка F-распределения на 2,η-2 степенях свободы.
Квадрат коэффициента связи между 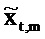
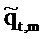

и квадрат коэффициента связи между 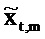
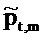
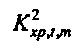 , выводится аналогично из
, выводится аналогично из

Связанная с потоком переменная 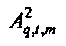 определяется как
определяется как

и аналогичная связанная с давлением переменная, обозначенная 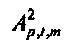 , выводится аналогичным образом из
, выводится аналогичным образом из

Поэтому 100(1-α)% доверительные пределы для действительной и мнимой частей дыхательного импеданса задаются посредством, соответственно,
Rrs⋅c1±c2 и Xrs⋅c1±c2,
с 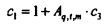 ,
, 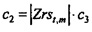 , и
, и 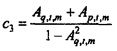 .
.
Оценки дыхательного импеданса для заданного времени и частоты отклоняются как незначительные, если либо Aq,t,m≥ первого порога, либо Ap,t,m≥ второго порога. В примерном варианте осуществления первый порог и второй порог устанавливаются на 1 (единицу), так что оценки дыхательного импеданса для заданного времени и частоты отклоняются как не значимые, если либо Aq,t,m≥1, либо Ap,t,m≥1.
Чтобы иметь дело с эффектами начала и конца, алгоритм содержит несколько циклических буферов данных.
Устройство измерения
Измерения. Поток воздуха может измеряться с помощью головки 8 пневмотахометра и встроенного преобразователя 10 давления (например, Jaeger Masterscreen pneumotach type BF/IEC 601-1, Hoechberg, Germany). Давление на наконечнике 4 может измеряться со ссылкой на окружающий воздух с помощью дифференциального преобразователя 12 давления (например, Hans Rudolph Pneumotach amplifier 1 series 1110, Shawnee, KS). Колебания давления могут генерироваться в устройстве 2 FOT посредством громкоговорителя 6 (например, Jaeger Masterscreen IOS, Hoechberg, Germany), который управляется посредством аналогового выходного сигнала из персонального компьютера 16 (например, Hewlett Packard Compac dc 7600, Palo Alto, CA) с помощью платы 14 аналогово-цифрового преобразования (например, National Instruments PCI-6221, Dallas, TX), который усиливается посредством усилителя 18 (например, Harman Kardon HK 970 amplifier, Washington DC)). Субъекты могут вдыхать и выдыхать через сопротивление 9 проволочной сетки, соединенное с головкой 8 пневмотахометра. Аналоговые входные сигналы могут преобразоваться в цифровые последовательности посредством той же платы 14 аналогово-цифрового преобразования на частоте выборки 800 Гц и сохраниться в персональном компьютере 16. Генерирование выходного сигнала и анализ данных могут выполняться посредством компьютера или процессора 16, исполняющего соответствующее компьютерное программное обеспечение.
Измерения могут делаться с использованием устройства 2 в течение периода, покрывающего некоторое число циклов дыхания, например, 90 секунд спокойного дыхания.
Вывод принципа неопределенности
Геометрическая интерпретация неопределенности во времени и частоте. Согласно определению из Уравнения 20, неопределенность Δt напрямую относится к «центру тяжести» временного ряда х≡{xt}. События во временном ряде представляются как точечные массы со значением |xt|2, помещенные на регулярных интервалах вокруг периметра круга с радиусом rt в комплексной плоскости, центрированном относительно начала. Каждое событие происходит в точке rtωt в комплексной плоскости, с rt=N/(2π) и ω≡exp(2πi/N). Взвешенное среднее 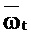

Центр тяжести располагается в 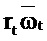

где 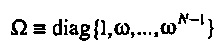 . С использованием факта, что Ω является унитарной матрицей, квадрат неопределенности
. С использованием факта, что Ω является унитарной матрицей, квадрат неопределенности 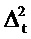
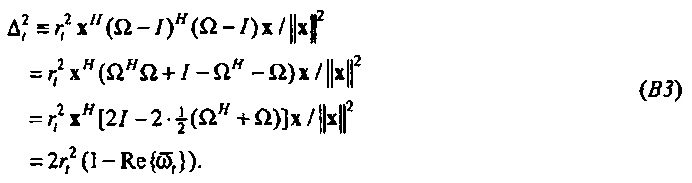
Это находится в соответствии с «теоремой параллельных осей» для второго момента инерции относительно оси (перпендикулярной к плоскости круга) через опорную точку R на фиг. 12. Фиг. 12 иллюстрирует соотношение между неопределенностью во времени Δt и центрами тяжести собственных векторов CHC для N=16. Собственные векторы отображаются вдоль временного круга в комплексной плоскости с радиусом rt, центрированным относительно начала. Центры тяжести каждого собственного вектора изображаются посредством черных точек. Соответствующее сингулярное значение С является минимальным для центра тяжести справа (рядом с опорной точкой R) и постепенно увеличивается влево на фигуре. Неопределенность Δt для каждого собственного вектора является косым расстоянием от R до одной из точек пересечения вертикальной линии через центр тяжести и круга. В представлении фиг. 13 из Уравнения 11 следует, что 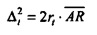 , где
, где 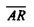 является расстоянием от А до R на фиг. 12. С использованием теоремы Пифагора следует, что
является расстоянием от А до R на фиг. 12. С использованием теоремы Пифагора следует, что 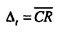 , так как
, так как
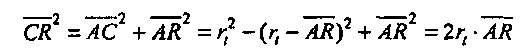
В частотной области неопределенность Δƒ может геометрически интерпретироваться аналогичным образом.
Сингулярные значения матрицы С. Принцип неопределенности из Уравнения 25 определяется посредством 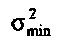 и
и 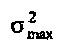 квадратами минимальных и максимальных сингулярных значений С. Сингулярные значения σ могут выводиться из
квадратами минимальных и максимальных сингулярных значений С. Сингулярные значения σ могут выводиться из

где det(⋅) обозначает определитель матрицы. Для N=2
непосредственно следует, что 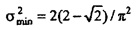 и
и 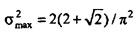 . Для более высокого N различные стратегии были разработаны, чтобы выводить сингулярные значения С (собственные значения CHC). Фиг. 11 показывает σmin и σmax в зависимости от N. Выходит, что для более большого N (скажем, N>15), σmin приближается к
. Для более высокого N различные стратегии были разработаны, чтобы выводить сингулярные значения С (собственные значения CHC). Фиг. 11 показывает σmin и σmax в зависимости от N. Выходит, что для более большого N (скажем, N>15), σmin приближается к 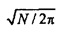 и σmax приближается к
и σmax приближается к 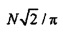 . В терминах радиуса временного круга это означает, что
. В терминах радиуса временного круга это означает, что 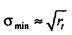 и
и 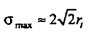 .
.
Пусть v будет единичным собственным вектором CHC, который соответствует сингулярному значению σ. Нормальные уравнения (CHC-σ2I)v=0 могут быть переписаны как
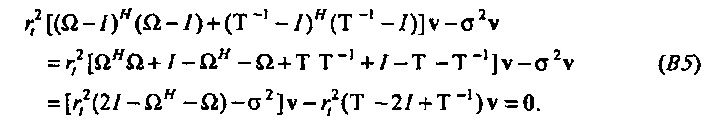
Первый член зависит от отхода составляющих v от опорной точки R вдоль действительной оси (ср. Уравнение В3). Второй член может рассматриваться как вторая производная составляющих v (для дискретного и циклического времени). Уравнение В5 является сравнимым с уравнением Шредингера для квантового гармонического осциллятора. Решения могут рассматриваться как дискретные ортогональные функции Матье. Собственный вектор vmin, который соответствует σmin, является унимодальной функцией времени (как на фиг. 4A). Для большого N vmin может аппроксимироваться посредством вектора 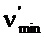
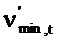

где N должно вычитаться из t, если 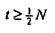 . Так как составляющие
. Так как составляющие 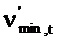
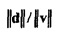 меньше чем 0,005, если N>75.
меньше чем 0,005, если N>75.
Так как CHC коммутирует с F, эти матрицы имеют одни и те же собственные векторы.
Так как F4=I, собственные значения F - это 1, -1, i и -i. Как результат, для каждого единичного собственного вектора v неопределенность во времени напрямую относится к неопределенности в частоте,
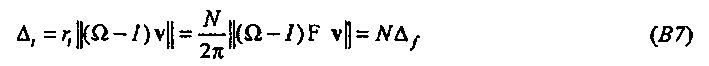
Это означает, что для каждого собственного вектора v полная неопределенность является равномерно распределенной по времени и частоте,
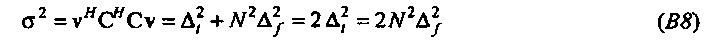
Таким образом, для каждого собственного вектора v 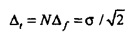 . Отметим, что гауссовская аппроксимация vmin согласно Уравнению В6 может быть перезаписана как
. Отметим, что гауссовская аппроксимация vmin согласно Уравнению В6 может быть перезаписана как 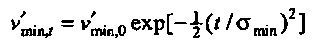 . Полная неопределенность
. Полная неопределенность 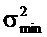
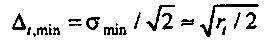 и
и 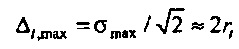 . Последнее является интуитивно разумным, так как 2rt является наибольшим возможным Δt внутри временного круга (см. фиг. 13). Фиг. 13 иллюстрирует соотношение между неопределенностью во времени Δt и неопределенностью в частоте Δƒ для N=16. Доступная область для всех возможных N-векторов х ограничена посредством двух кругов с радиусом σmin и σmax (минимальное и максимальное сингулярное значение С). На фиг. 13 rt является радиусом временного круга, черные точки принадлежат собственным векторам CHC, vmin и vmax являются собственными векторами, соответствующими σmin и σmax, е0 и е8 являются каноническими векторами, соответствующими t=0 и t=8, f0 и f8 являются гармоническими колебаниями с частотами ƒn=0 и ƒn=8/16=1/2.
. Последнее является интуитивно разумным, так как 2rt является наибольшим возможным Δt внутри временного круга (см. фиг. 13). Фиг. 13 иллюстрирует соотношение между неопределенностью во времени Δt и неопределенностью в частоте Δƒ для N=16. Доступная область для всех возможных N-векторов х ограничена посредством двух кругов с радиусом σmin и σmax (минимальное и максимальное сингулярное значение С). На фиг. 13 rt является радиусом временного круга, черные точки принадлежат собственным векторам CHC, vmin и vmax являются собственными векторами, соответствующими σmin и σmax, е0 и е8 являются каноническими векторами, соответствующими t=0 и t=8, f0 и f8 являются гармоническими колебаниями с частотами ƒn=0 и ƒn=8/16=1/2.
Как описано выше, фиг. 12 показывает центры тяжести для всех собственных векторов v во временном круге для N=16. Так как CHC является нормальной матрицей, она имеет N ортогональных собственных векторов согласно спектральной теореме. Как следует из Уравнения В3, соответствующее Δt зависит от горизонтального расстояния от R до центра тяжести в комплексной плоскости. Оно может быть считано из фиг. 12 как длина хорды от R до пересечения круга с вертикальной линией через центр тяжести. Центр тяжести, самый близкий к R, соответствует σmin. Центры тяжести, которые лежат дальше, соответствуют возрастающим значениям σ (и 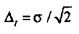 ). Для относительно большого N расстояние между центром тяжести vmin и R приближается к
). Для относительно большого N расстояние между центром тяжести vmin и R приближается к 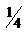
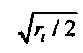 . Имеется множественность собственных значений CHC в смысле, что имеются два ортогональных собственных вектора с одним и тем же собственным значением σ2=N2/π2. Такая множественность собственных значений, вероятно, происходит, только если N является делящимся на четыре. Центры тяжести этих двух ортогональных собственных векторов оба располагаются на мнимой оси. Они имеют одно и то же Δt, равное
. Имеется множественность собственных значений CHC в смысле, что имеются два ортогональных собственных вектора с одним и тем же собственным значением σ2=N2/π2. Такая множественность собственных значений, вероятно, происходит, только если N является делящимся на четыре. Центры тяжести этих двух ортогональных собственных векторов оба располагаются на мнимой оси. Они имеют одно и то же Δt, равное 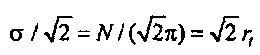 . Соответствующее Δƒ равняется
. Соответствующее Δƒ равняется 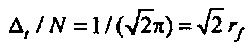 . Эти два собственных вектора имеют наибольший возможный разброс как во временной, так и частотной области (идентично значениям, которые получаются, если центр тяжести располагается в центре как временного, так и частотного круга). Собственные векторы, соответствующие более высоким значениям σ, являются ассоциированными с более большой «неопределенностью» Δt (относительно R), но с более маленьким разбросом во времени. Вес векторов фактически становится более и более сконцентрированным на противоположной стороне как временного, так и частотного круга до тех пор, когда максимальная полная неопределенность
. Эти два собственных вектора имеют наибольший возможный разброс как во временной, так и частотной области (идентично значениям, которые получаются, если центр тяжести располагается в центре как временного, так и частотного круга). Собственные векторы, соответствующие более высоким значениям σ, являются ассоциированными с более большой «неопределенностью» Δt (относительно R), но с более маленьким разбросом во времени. Вес векторов фактически становится более и более сконцентрированным на противоположной стороне как временного, так и частотного круга до тех пор, когда максимальная полная неопределенность 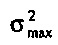 достигается для собственного вектора vmax и Δt почти равняется 2rt. Отметим очевидную симметрию на фиг. 12 (центры тяжести отражаются в мнимой оси).
достигается для собственного вектора vmax и Δt почти равняется 2rt. Отметим очевидную симметрию на фиг. 12 (центры тяжести отражаются в мнимой оси).
Фиг. 13 показывает NΔƒ в зависимости от Δt. Вследствие принципа неопределенности из Уравнения 25 доступная область ограничена посредством двух кругов, центрированных относительно начала, с радиусом σmin и σmax. Это не означает, что все значения между этими кругами являются возможными, но что все значения вне кругов являются невозможными. Координаты, которые принадлежат собственным векторам CHC, все располагаются на линии тождества (вследствие Уравнения В7). Некоторые экстремальные случаи также показаны. Один является каноническим вектором е0≡{1, 0, … ,0}. Его «вес» 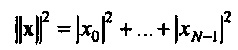 полностью сконцентрирован в t=0, таким образом, Δt является нулем. Преобразование в частотную область дает
полностью сконцентрирован в t=0, таким образом, Δt является нулем. Преобразование в частотную область дает
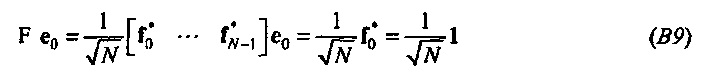
где fn определяется как в Уравнении 9, знак «*» обозначает комплексное сопряжение, и 1 является N-вектором, который содержит только единицы. Таким образом, вес е0 является равномерно распределенным по всем частотам в частотной области и 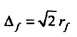 или
или 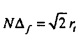 . Другим экстремальным случаем является е8. (Пусть канонический вектор et будет определен как {0, …, 0, 1, 0, …, 0}, где единица стоит на t-ом месте, начиная с нуля.) Вес е8 является полностью сконцентрированным в точке (-rt,0) в комплексной плоскости, и, таким образом, Δt является максимальным, равным 2rt. В частотной области
. Другим экстремальным случаем является е8. (Пусть канонический вектор et будет определен как {0, …, 0, 1, 0, …, 0}, где единица стоит на t-ом месте, начиная с нуля.) Вес е8 является полностью сконцентрированным в точке (-rt,0) в комплексной плоскости, и, таким образом, Δt является максимальным, равным 2rt. В частотной области
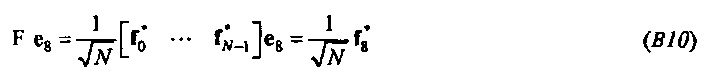
Столбцовый вектор 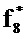
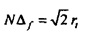 . Начиная от временной области, другими экстремумами являются колебания f0, чей вес является равномерно распределенным во временной области и точно сконцентрированным в частотной области при
. Начиная от временной области, другими экстремумами являются колебания f0, чей вес является равномерно распределенным во временной области и точно сконцентрированным в частотной области при 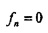 (
(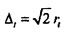 и
и 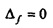 ), и f8, чей вес является также равномерно распределенным во временной области, но точно сконцентрированным в частотной области при ƒn=1/2 (так что
), и f8, чей вес является также равномерно распределенным во временной области, но точно сконцентрированным в частотной области при ƒn=1/2 (так что 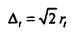 и NΔƒ=2rt). Так как возможные значения для Δt и NΔƒ являются ограниченными диапазоном [0,2rt], можно ожидать, что все возможные комбинации (Δt,NΔƒ) являются ограниченными областью на фиг. 13, которая является ограниченной координатами для vmin, е0, f8, vmax, e8 и f0. Эти экстремальные векторы также являются иллюстрациями общего правила: взятие преобразования Фурье вектора временного ряда х (посредством умножения слева на F) производит обмен (Δt,NΔƒ) координат на графике из фиг. 13. Иным образом положим: координаты для х и F х являются отраженными в линии тождества. Это непосредственно проверяется с использованием определений из Уравнений 21 и 23.
и NΔƒ=2rt). Так как возможные значения для Δt и NΔƒ являются ограниченными диапазоном [0,2rt], можно ожидать, что все возможные комбинации (Δt,NΔƒ) являются ограниченными областью на фиг. 13, которая является ограниченной координатами для vmin, е0, f8, vmax, e8 и f0. Эти экстремальные векторы также являются иллюстрациями общего правила: взятие преобразования Фурье вектора временного ряда х (посредством умножения слева на F) производит обмен (Δt,NΔƒ) координат на графике из фиг. 13. Иным образом положим: координаты для х и F х являются отраженными в линии тождества. Это непосредственно проверяется с использованием определений из Уравнений 21 и 23.
Сравнение с принципом неопределенности Габора. Принцип неопределенности, который был описан Габором в 1946 г.(см. ссылку 5 ниже), определяет нижний предел для произведения ΔtΔƒ для непрерывного времени и частоты

Как это неравенство связано с принципом неопределенности для дискретного времени и частоты согласно Уравнению 25? В уравнении В11 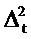
Главное различие между неравенствами Уравнения В11 и Уравнения 25 лежит в факте, что, согласно принципу неопределенности Габора, нижний предел ΔtΔƒ достигается для гауссовских функций t (такой же формы, как в Уравнении В6) с любым ненулевым значением Δt, (см. ссылку 5). Это является набором линейно независимых (бесконечных) векторов. Нижний предел полной неопределенности 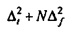 согласно Уравнению 25, однако, достигается только для одного собственного пространства CHC (комплексного одномерного подпространства, порожденного посредством vmin), которое соответствует одному одиночному значению Δt (равному
согласно Уравнению 25, однако, достигается только для одного собственного пространства CHC (комплексного одномерного подпространства, порожденного посредством vmin), которое соответствует одному одиночному значению Δt (равному 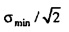 ). С другой стороны, векторы в этом собственном пространстве действительно достигают нижний предел принципа неопределенности Габора (в предельной ситуации при
). С другой стороны, векторы в этом собственном пространстве действительно достигают нижний предел принципа неопределенности Габора (в предельной ситуации при 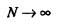 ). Для каждого собственного вектора CHC из Уравнения В8 следует, что
). Для каждого собственного вектора CHC из Уравнения В8 следует, что

Для vmin (или любого другого вектора в соответствующем собственном пространстве), σ приближается к 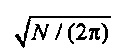 по мере того, как N становится большим (фиг. 11). Числовая аппроксимация тогда показывает, что при
по мере того, как N становится большим (фиг. 11). Числовая аппроксимация тогда показывает, что при 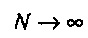 ,
,

Для конечного N, однако, 1/(4π) не является абсолютным нижним пределом для ΔtΔƒ. Произведение является нулевым для е0 и f0, и добавление маленьких случайных чисел показывает, что оно является близким к нулю для незначительно разных векторов.
Соотношение между двумя принципами неопределенности становится более очевидным, если мы рассмотрим N-векторы, которые выводятся из vmin векторов, которые были получены для более короткого временного ряда (состоящего из М событий, с 1<M≤N). См. пример из фиг. 14, где vmin был выведен из 8×8 матрицы CHC. Составляющие F vmin показаны в зависимости от частоты ƒn (черные точки). Эти частоты являются кратными 1/8. Вставим блок 8 нулей между двумя наименьшими составляющими 8-вектора vmin, (так что унимодальная структура вектора остается нетронутой на основе циклического времени), что дает результатом 16-вектор
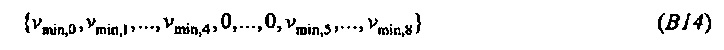
Это дает незначительное увеличение в Δt (от 0,7583 к 0,7900) и почти незначительное увеличение в Δƒ (от 0,0948 к 0,0949). Открытые круги на фиг. 14 представляют интерполированные значения в частотной области, когда блок восьми нулей вставляется между двумя наименьшими значениями собственного вектора во временной области, непрерывная линия представляет интерполированные значения по мере того, как число добавленных нулей во временной области стремится к бесконечности. Результирующий 16-вектор ведет к интерполяции в частотной области на частотах, которые являются кратными 1/16 (открытые круги). Это является хорошо известной формой интерполяции в частотной области (посредством «заполнения нулями» во временной области).
Этим способом для заданного N число N-1 векторов может выводиться посредством добавления нулей к меньшим М-мерным vmin векторам, которые получаются из М×М матриц CHC. Тривиальный пример - это е0, который выводится посредством добавления нулей к 1-вектору» vmin=1 для М=1. Фиг. 15 показывает соответствующие неопределенности на графике NΔƒ в сравнении с Δt для N=16. Эти значения появляются в зоне I, ограниченной посредством линий Δt=0, 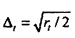 ,
, 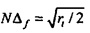 и
и 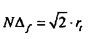 . Значение для М=1 совпадает с е0, значение для М=2 показывается посредством стрелки и значения для более высоких М постепенно приближаются к значению для M=N=16, расположенному на линии тождества (которая соответствует vmin для N=16). Для относительно больших М, Δt и Δƒ едва изменяются посредством добавления нулей, в то время как ассоциированное σ приближается к
. Значение для М=1 совпадает с е0, значение для М=2 показывается посредством стрелки и значения для более высоких М постепенно приближаются к значению для M=N=16, расположенному на линии тождества (которая соответствует vmin для N=16). Для относительно больших М, Δt и Δƒ едва изменяются посредством добавления нулей, в то время как ассоциированное σ приближается к 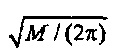 , так что
, так что
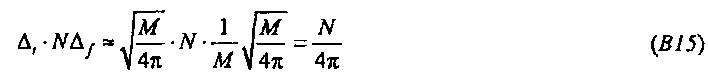
Как результат, значения для относительно больших М вычерчиваются незначительно ниже гиперболы x⋅y=N/(4π) на фиг. 15. По мере того как время идет и N становится более большим, след значений растет вдоль этой гиперболы, с новыми значениями, появляющимися на линии тождества. Если Δƒ вычерчивается в соответствии с Δt, соответствующая гипербола задается посредством x⋅y=1/(4π) и содержит все возможные значения, соответствующие разным гауссианам в нижнем пределе принципа неопределенности Габора. Без формального математического доказательства можно предполагать, что N-векторы, выведенные из vmin для M<N, ставят дополнительный предел на доступную область в (Δt,NΔƒ) - плоскости из фиг. 15. Так как эти векторы имеют минимально возможную полную неопределенность для последовательности M ненулевых событий, может ожидаться, что значения вне области, отмеченной посредством черных точек на фиг. 15, не будут встречаться. Это также имеет место для значений в зоне II, которая была выведена посредством умножения слева векторов в зоне I на Ω8, что кругообразно сдвигает векторы в частотной области (к противоположной части частотного круга), без изменения весов во временной области. Таким образом, Δƒ этих векторов максимизируется без изменения в Δt. Обратно точки в зоне VI получаются из векторов в зоне I, умноженных слева посредством T8 что кругообразно сдвигает векторы во временной области (тем самым максимизируя Δt без изменения в Δƒ). Векторы в зоне V следуют из векторов в зоне II посредством умножения слева на Т8. Векторы в зоне VIII следуют из векторов в зоне I посредством взятия преобразования Фурье (умножения слева на F означает отражение в линии тождества). Умножение слева этих векторов на Ω8 дает векторы в зоне III, умножение слева на Т8 дает векторы в зоне VII, и умножение слева последнего снова на Ω8 дает векторы в зоне IV. (Будет ясно, что имеется больше способов, чтобы переходить от одной частотно-временной зоны к другой, например взятие преобразования Фурье векторов в зоне VI перемещает их в зону III). В заключение можно ожидать, что возможные комбинации Δt,NΔƒ ограничены лепестковой областью, очерченной посредством черных точек (и открытых кругов) на фиг. 15.
Принцип неопределенности для ненулевого среднего времени и частоты. Если опорному времени tR в Уравнении 19 разрешается быть ненулевым, то
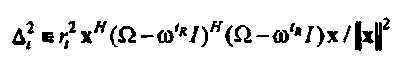 , или
, или

Аналогично для ненулевой опорной частоты fR≡nR/N,
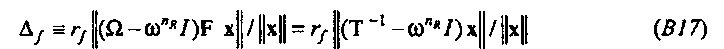
Пусть 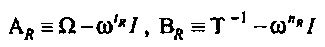 и
и
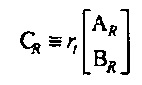
Когда С все еще определяется по отношению к tR=0 и fR=0, то выходит, что 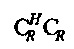 и CHC являются подобными,
и CHC являются подобными,

Это непосредственно показывается с использованием соотношения TkΩn=ω-nkΩnTk, которое является действительным для любого целого числа k, n. Таким образом, если (σ2,v) является парой собственное значение - собственный вектор CHC, то

означая, что 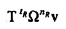 является собственным вектором
является собственным вектором 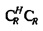 с собственным значением σ2. Следует, что неопределенность
с собственным значением σ2. Следует, что неопределенность 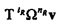 относительно tR во временной области и ƒR в частотной области является равной неопределенности v относительно нуля в обеих областях. Это не является неожиданностью. Квадраты абсолютных значений («веса»), составляющих
относительно tR во временной области и ƒR в частотной области является равной неопределенности v относительно нуля в обеих областях. Это не является неожиданностью. Квадраты абсолютных значений («веса»), составляющих 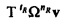 , являются идентичными весам v, даже после цикличного сдвига в частотной области (посредством
, являются идентичными весам v, даже после цикличного сдвига в частотной области (посредством 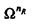 ) и во временной области (посредством
) и во временной области (посредством 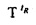 ).
).
Вывод частотно-временного преобразования
Столбцы матрицы М частотно-временного преобразования являются ортонормальными,

Это может доказываться следующим образом. Произведение может быть записано как сумма циркулянтных матриц,
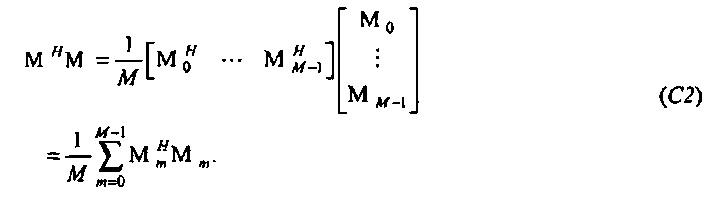
Так как умножение в обычном порядке 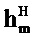

Так как циркулянты являются нормальными матрицами, они коммутируют их с эрмитовым транспонированием,
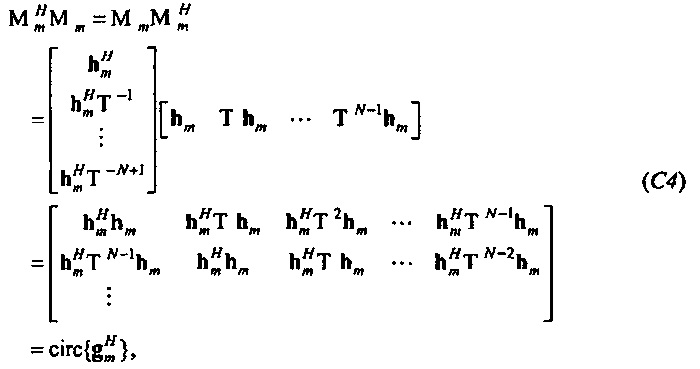
где 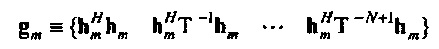 является «комплексной автокорреляцией» hm.
является «комплексной автокорреляцией» hm.
Его составляющие являются
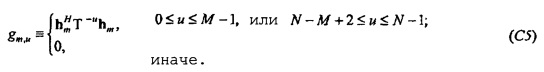
Согласно определению N-вектора hm (Уравнения 26 и 27), он может также быть записан как ΩmN/Mh0. С использованием TkΩn=ω-nkΩnTk следует, что ненулевые составляющие равны
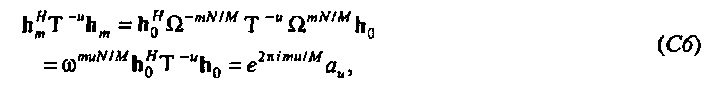
где 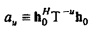 . Когда эти составляющие суммируются по m, мы имеем
. Когда эти составляющие суммируются по m, мы имеем
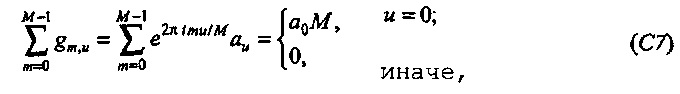
что следует из факта, что {e2πimu/M} является геометрической прогрессией для m=0, …, М-1. Отметим, что 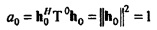 , так как hm берется единичным вектором. Как результат, сумма в Уравнении С2 может быть перезаписана как
, так как hm берется единичным вектором. Как результат, сумма в Уравнении С2 может быть перезаписана как
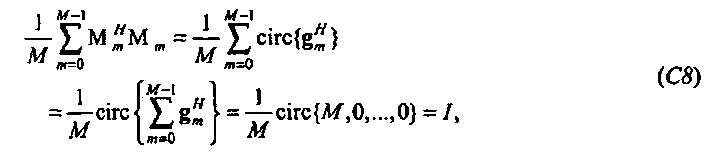
что завершает доказательство Уравнения С1.
Свойство ортонормированности (Уравнение С1) все еще удовлетворяется, если h0 аппроксимируется посредством усеченного нормализованного гауссиана с неопределенностью Δt, и M'=10⋅Δt ненулевыми составляющими (с использованием Уравнения В4), так как оно не зависит от выбора h0 (при условии что 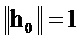
Частотно-временной синтез. Прямое следствие свойства ортонормированности состоит в том, что заданный вектор х временного ряда может быть записан как взвешенная сумма коротко длящихся колебаний (Уравнение 34). С использованием определения из Уравнения 28
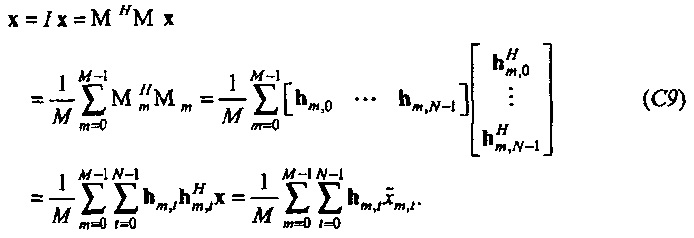
Анализ дисперсии в частотно-временной области
Другое прямое следствие свойства ортонормированности TFT состоит в том, что «энергия» (квадрат нормы) N-вектора х сохраняется после преобразования
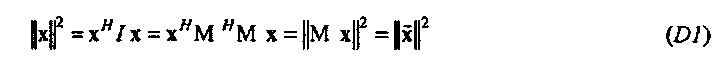
Это разрешает «анализ дисперсии» (ANOVA) в частотно-временной области. Вышеуказанное также обозначит, что энергия х может разделяться на М зависящих от частоты составляющих
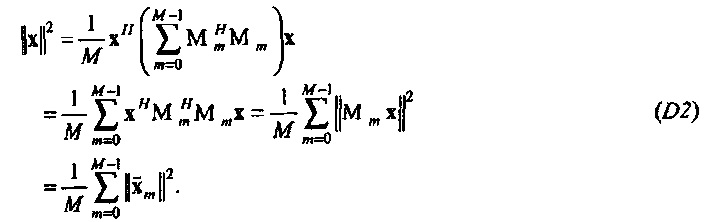
Предположим, что случайный N-вектор X имеет многовариантное
нормальное распределение с ожиданием E{Х}=0 и дисперсией var{X}=σ2I. Тогда квадратичная форма 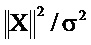
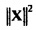 может быть разбито на М зависящих от частоты составляющих
может быть разбито на М зависящих от частоты составляющих 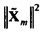 . Квадратичная форма
. Квадратичная форма 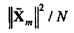 может называться «спектр мощности выборки TFT X для частоты ƒm. Для белого шума ожидание этой RV является
может называться «спектр мощности выборки TFT X для частоты ƒm. Для белого шума ожидание этой RV является
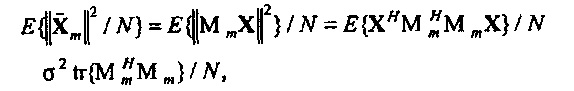
где tr{⋅} обозначает след матрицы. С использованием Уравнения С4 следует, что 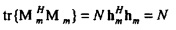 , так что
, так что

Спектр мощности выборки согласно определению выше является, однако, чувствительным к смещению вследствие предположения цикличности. Отметим, что составляющие 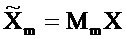
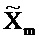

Умножение слева 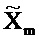
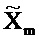
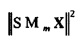 . Когда комплементарная частота ƒM-m также включается, «полная» несмещенная мощность выборки может определяться как
. Когда комплементарная частота ƒM-m также включается, «полная» несмещенная мощность выборки может определяться как
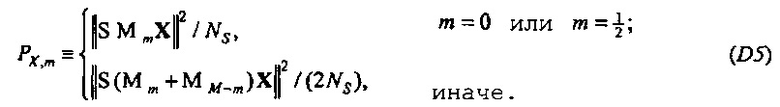
Число «выборок» в t-f области - это NS=N-M+1.
Мощность выборки (разделенная на σ2) следует приблизительному распределению хи-квадрат с эквивалентными степенями свободы (EDOFs)

Пусть Р≡S(Mm+MM-m)/(2NS) для m≠0 и 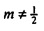 , тогда следует, что для белого шума нулевого среднего X
, тогда следует, что для белого шума нулевого среднего X

что дает

В настоящем документе η численно вычислялось согласно Уравнению D8 с использованием математического компьютерного программного обеспечения.
Вывод доверительных пределов
Среднее и дисперсия 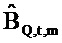
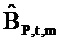
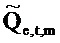
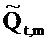
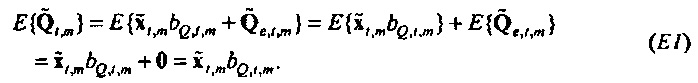
Дисперсия 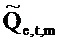
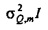 . Так как произведение
. Так как произведение 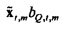 является детерминированным,
является детерминированным,
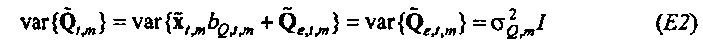
Среднее и дисперсия 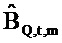
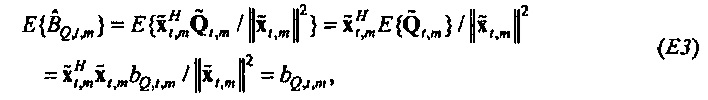
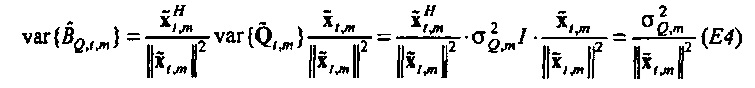
Как результат, 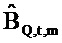
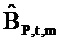
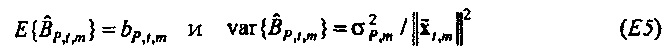
Доверительные пределы. Доверительные пределы для 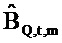
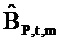
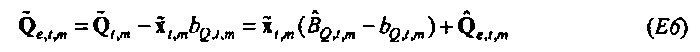
Вследствие ортогональности между 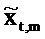
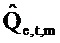
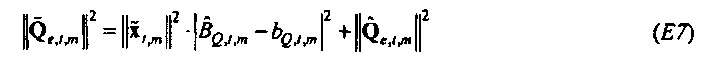
Случайная переменная 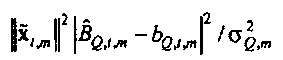 имеет форму
имеет форму
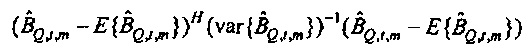
и является, таким образом, (точно) распределенной как хи-квадрат переменная (на одной степени свободы). Когда 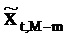
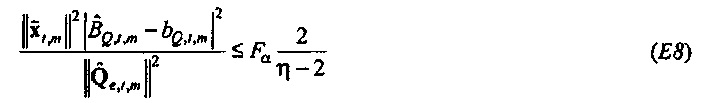
С использованием определения коэффициента связи выборки TFT (Уравнение 45) и предполагая, что 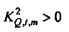 , это может быть перезаписано как
, это может быть перезаписано как
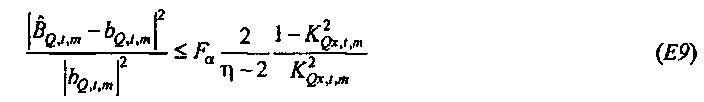
Обозначая правую сторону этого неравенства посредством 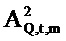

100(1-α)% доверительная область для 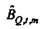 , таким образом, описывается посредством круга в комплексной плоскости с центром
, таким образом, описывается посредством круга в комплексной плоскости с центром 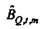 и радиусом
и радиусом 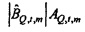 . Доверительная область для
. Доверительная область для 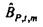 выводится аналогичным образом
выводится аналогичным образом

Чтобы прийти к доверительной области для 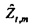 , умножим обе стороны Уравнения 10 на
, умножим обе стороны Уравнения 10 на 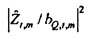 и подставим
и подставим 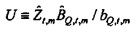 , что дает
, что дает

С использованием действительной и мнимой частей комплексных переменных, это может быть преобразовано в
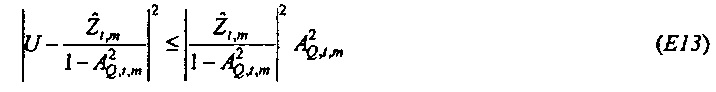
Далее разделим обе стороны Уравнения E11 на 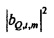 . Заменяя
. Заменяя 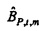 на
на 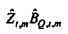
(Уравнение 47), и 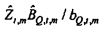 посредством U
посредством U

Доверительная область для 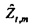 теперь может быть выведена в двухэтапном подходе. Согласно Уравнению Е13, U лежит внутри круга с центром
теперь может быть выведена в двухэтапном подходе. Согласно Уравнению Е13, U лежит внутри круга с центром 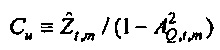 и радиусом
и радиусом 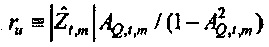 , при 100(1-α)% случаев (фиг. 16A). Предположим, что
, при 100(1-α)% случаев (фиг. 16A). Предположим, что 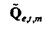 и
и 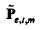 являются некоррелированными. Тогда для заданного значения U, zt,m лежит внутри второго круга, с центром U и радиусом
являются некоррелированными. Тогда для заданного значения U, zt,m лежит внутри второго круга, с центром U и радиусом 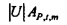 , при 100(1-α)% случаев (Уравнение Е14). Рассмотрим два экстремальных значения для
, при 100(1-α)% случаев (Уравнение Е14). Рассмотрим два экстремальных значения для 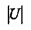 , которые являются величинами
, которые являются величинами 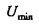 и
и 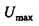 на фиг. 16A. Соответствующие экстремальные значения для |zt,m| являются величинами zmin и zmax на фиг. 16B. Из Уравнений Е13 и Е14
на фиг. 16A. Соответствующие экстремальные значения для |zt,m| являются величинами zmin и zmax на фиг. 16B. Из Уравнений Е13 и Е14
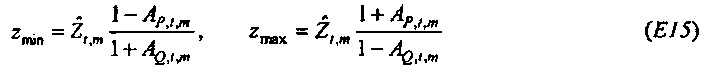
Консервативный предел 100(1-α)% доверительной области для 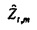 теперь задается посредством круга, который содержит Zmin и zmax и чей центр лежит на линии через
теперь задается посредством круга, который содержит Zmin и zmax и чей центр лежит на линии через 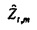 и начало. Как результат, соответствующая доверительная область описывается посредством
и начало. Как результат, соответствующая доверительная область описывается посредством
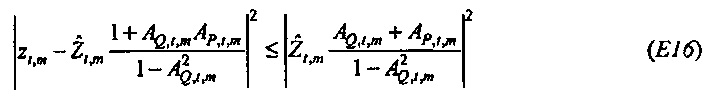
Эта область ограничивается посредством круга на фиг. 16B и 16C с центром 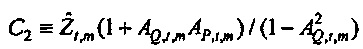 и радиусом
и радиусом 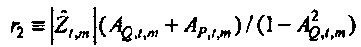 . Этот круг не является концентрическим относительно
. Этот круг не является концентрическим относительно 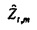 . Распределение возможных значений для zt,m для заданного
. Распределение возможных значений для zt,m для заданного 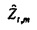 является антисимметричным относительно
является антисимметричным относительно 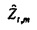 (фиг. 16D). Асимметрия выражается посредством tanβ на фиг. 16C. Из Уравнения E16 следует, что
(фиг. 16D). Асимметрия выражается посредством tanβ на фиг. 16C. Из Уравнения E16 следует, что

Специальный случай 1: нет шума в потоке. Если шум в потоке является нулевым, 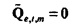 , то
, то 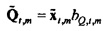 и
и 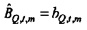 (Уравнения 43 и 46). Пусть соответствующая оценка zt,m обозначается посредством
(Уравнения 43 и 46). Пусть соответствующая оценка zt,m обозначается посредством 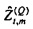 Предполагая, что bQ,t,m≠0,
Предполагая, что bQ,t,m≠0,
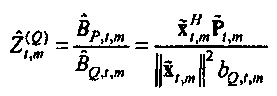
Так как в этом случае 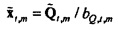 ,
,

Это является «обычной оценкой наименьших квадратов». Тогда 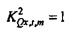 и AQ,t,m=0. Доверительные пределы все еще описываются посредством Уравнения Е16, хотя с AQ,t,m=0. Доверительный круг теперь является центрированным относительно
и AQ,t,m=0. Доверительные пределы все еще описываются посредством Уравнения Е16, хотя с AQ,t,m=0. Доверительный круг теперь является центрированным относительно 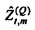 , с радиусом
, с радиусом 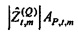 . Параметр асимметрии tanβ равняется нулю.
. Параметр асимметрии tanβ равняется нулю.
Специальный случай 2: нет шума в давлении. Если шум в давлении является нулевым, 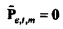 , то
, то 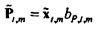 и
и 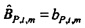 . Когда соответствующая оценка zt,m обозначается посредством
. Когда соответствующая оценка zt,m обозначается посредством 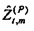
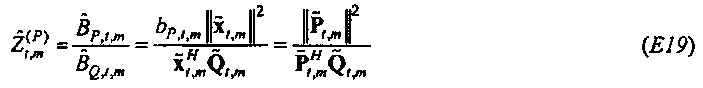
Это является «оценкой наименьших квадратов данных». Теперь 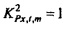 и AP,t,m=0. Из Уравнения Е16 доверительный круг имеет центр
и AP,t,m=0. Из Уравнения Е16 доверительный круг имеет центр 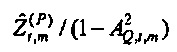 и радиус
и радиус 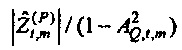 . Параметр асимметрии tanβ равняется AQ,t,m. Две оценки
. Параметр асимметрии tanβ равняется AQ,t,m. Две оценки 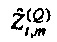 и
и 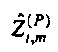 связаны посредством квадрата коэффициента связи между потоком и давлением
связаны посредством квадрата коэффициента связи между потоком и давлением
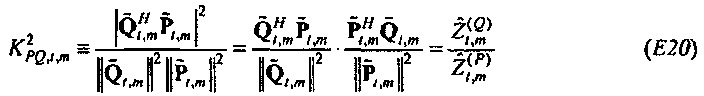
Примеры: квадраты коэффициента связи в зависимости от времени и частоты. Фиг. 17 показывает квадраты коэффициента связи для той же записи, как на фиг. 7. В этом примере коэффициент связи между вводом громкоговорителя и потоком был, в общем, более низким, чем коэффициент связи между вводом и давлением. Как является очевидным из фигуры, коэффициенты связи изменяются в зависимости от обоих - времени и частоты. Наименьшие коэффициенты связи получаются в точках поворота от вдоха к выдоху и наоборот и на наименьших частотах. Глоток имеет сильное воздействие на коэффициент связи, особенно между вводом и потоком. Фиг. 18 показывает квадраты коэффициента связи в зависимости от времени и частоты для оцененного импеданса, показанного на фиг. 8, для пациента с COPD. Падения в коэффициенте связи в точках поворота между дыхательными фазами являются намного более выраженными, чем в нормальном примере из фиг. 17. На обеих фиг. 17 и 18 полужирные линии представляют квадрат коэффициента связи 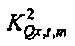 между вводом громкоговорителя и потоком в зависимости от времени для разных резонансных частот (8 по 24 Гц), и тонкие линии представляют квадрат коэффициента связи
между вводом громкоговорителя и потоком в зависимости от времени для разных резонансных частот (8 по 24 Гц), и тонкие линии представляют квадрат коэффициента связи 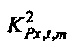 между вводом громкоговорителя и давлением. "Поток" представляет низкочастотную составляющую потока воздуха, "insp" представляет вдох и "ехр" представляет выдох.
между вводом громкоговорителя и давлением. "Поток" представляет низкочастотную составляющую потока воздуха, "insp" представляет вдох и "ехр" представляет выдох.
В заключение, представляется способ, чтобы оценивать передаточную функцию дыхательной системы субъекта с оптимальным частотно-временным разрешением.
Как описано выше, оценка дыхательного импеданса может делаться посредством диагностического инструмента, который использует оценку, чтобы оценивать непроходимость дыхательных путей, или чтобы оценивать серьезность заболевания. Диагностический инструмент может поэтому также использоваться, чтобы оценивать эффективность лечений (фармакологических или иных), которые должны влиять на дыхательный импеданс.
Например, оценки дыхательного импеданса могут использоваться, чтобы обнаруживать (i) ограничение выдыхаемого потока в хроническом обструкционном заболевании легких (COPD); (ii) серьезность непроходимости дыхательного пути в COPD или астме, что само используется, чтобы оценивать эффект расширителей дыхательного пути после ингаляции (например, симпатомиметические или парасимпатиколитические медикаменты) с течением времени (это может быть применимым к окружению исследования и также к клиническому окружению, где пациент является неспособным выполнять стандартные вынужденные дыхательные процедуры; (iii) непроходимость дыхательного пути в астме или COPD в течение сна; или (iv) верхнюю непроходимость дыхательного пути в течение сна в пациентах с предполагаемым синдромом обструктивного апноэ-гипапноэ сна.
Оценки дыхательного импеданса могут также или альтернативно использоваться, чтобы адаптировать настройки машины, используемой в лечении медицинского состояния. Например, оценки дыхательного импеданса могут использоваться в регулировке настроек неинвазивной вентиляции в COPD. Дыхательный импеданс может использоваться в качестве ввода в вентилятор, чтобы обеспечивать информацию о серьезности импеданса дыхательного пути на непрерывной основе (при этом ненадежные значения, как показывается посредством доверительных значений, отбрасываются). Эта информация может также использоваться, чтобы регулировать уровень двухуровневого положительного давления дыхательного пути, с которым ограничение выдыхательного потока только преодолевается. Как альтернативный пример, оценка дыхательного импеданса может использоваться как помощь, чтобы направлять уровень непрерывного положительного давления дыхательного пути в пациентах с обструкционным синдромом апноэ сна.
В то время как изобретение было проиллюстрировано и описано подробно на чертежах и в предшествующем описании, такая иллюстрация и описание должны рассматриваться иллюстративными или примерными и не ограничительными; изобретение не ограничено раскрытыми вариантами осуществления.
Изменения в раскрытых вариантах осуществления могут пониматься и осуществляться специалистами в данной области техники в использовании на практике заявленного изобретения, из изучения чертежей, раскрытия и прилагаемой формулы изобретения. В формуле изобретения слово "содержит" не исключает другие элементы или этапы, и единственное число не исключает множественность. Одиночный процессор или другой блок могут исполнять функции нескольких элементов, перечисленных в пунктах формулы изобретения. Простой факт, что некоторые меры перечисляются во взаимно разных зависимых пунктах формулы изобретения, не указывает, что комбинация этих мер не может использоваться для получения преимущества. Компьютерная программа может храниться/распространяться на подходящем носителе, таком как оптический запоминающий носитель или твердотельный носитель, предоставленный вместе с или как часть другого аппаратного обеспечения, но может также распространяться в других формах, таких как посредством сети Интернет или других проводных или беспроводных телекоммуникационных систем. Любые ссылочные знаки в пунктах не должны толковаться как ограничивающие объем.
Ссылки
1. Dellac et al. Expiratory flow limitation detected by forced oscillation and negative expiratory pressure, European Respiratory Journal Vol. 29 No. 2, pages 363-374.
2. Dar czy B, Hantos Z. An improved forced oscillation estimation of respiratory impedance. Int J Biomed Comput 13: 221-235, 1982.
3. Forbes GW, Alonso MA. Consistent analogs of the Fourier uncertainty relation. Am J Physics 69: 340-347, 2001.
4. Forbes GW, Alonso MA, Siegman AE. Uncertainty relations and minimal uncertainty states for the discrete Fourier transform and the Fourier series. J Phys A: Math Gen 36: 7027-7047, 2003.
5. Gabor D. Theory of communications. J Inst Electr Eng 93: 429-457, 1946.
| название | год | авторы | номер документа |
|---|---|---|---|
| ОДНОВРЕМЕННАЯ ОЦЕНКА ПАРАМЕТРОВ ДЫХАНИЯ ПУТЕМ ОБЛАСТНОЙ АППРОКСИМАЦИИ ПАРАМЕТРОВ ДЫХАНИЯ | 2016 |
|
RU2712040C2 |
| СПОСОБ ДОПЛЕРОВСКОЙ ФИЛЬТРАЦИИ ИОНОСФЕРНЫХ СИГНАЛОВ | 2012 |
|
RU2516589C1 |
| СПОСОБ РАСЧЕТА ДОПУСТИМОЙ МОЩНОСТИ БАТАРЕЙ С ИСПОЛЬЗОВАНИЕМ УСОВЕРШЕНСТВОВАННЫХ МЕТОДИК ПРЕДСКАЗАНИЯ НА ОСНОВЕ МОДЕЛИ ЭЛЕМЕНТА | 2004 |
|
RU2336618C2 |
| СПОСОБЫ И СИСТЕМЫ ДЛЯ ОБРАБОТКИ МИКРОСЕЙСМИЧЕСКИХ ДАННЫХ | 2008 |
|
RU2457513C2 |
| НЕИНВАЗИВНАЯ ОЦЕНКА ВНУТРИПЛЕВРАЛЬНОГО ДАВЛЕНИЯ И/ИЛИ ВЫЧИСЛЕНИЕ РАБОТЫ ДЫХАНИЯ НА ОСНОВАНИИ НЕИНВАЗИВНОЙ ОЦЕНКИ ВНУТРИПЛЕВРАЛЬНОГО ДАВЛЕНИЯ | 2014 |
|
RU2700981C2 |
| СХЕМА МОДУЛЯЦИИ НА НЕСКОЛЬКИХ НЕСУЩИХ, А ТАКЖЕ ПЕРЕДАЮЩЕЕ УСТРОЙСТВО И ПРИЕМНОЕ УСТРОЙСТВО, ИСПОЛЬЗУЮЩИЕ УКАЗАННУЮ СХЕМУ | 2006 |
|
RU2454808C2 |
| Способ автоматизированного контроля источников радиоизлучений | 2017 |
|
RU2659813C1 |
| СПОСОБ ПЕЛЕНГАЦИИ ИОНОСФЕРНЫХ СИГНАЛОВ В УСЛОВИЯХ ИНТЕРФЕРЕНЦИИ ЛУЧЕЙ | 2012 |
|
RU2516688C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОРТОГОНАЛЬНЫХ СОСТАВЛЯЮЩИХ ВЕКТОРА СКОРОСТИ КОСМИЧЕСКОГО АППАРАТА С ИСПОЛЬЗОВАНИЕМ ЗЕМНЫХ СТАНЦИЙ И ИЗЛУЧАЮЩЕЙ ОПОРНОЙ РЕПЕРНОЙ СТАНЦИИ | 2021 |
|
RU2788518C1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЯ В КОРИОЛИСОВОМ МАССОВОМ РАСХОДОМЕРЕ | 1997 |
|
RU2182696C2 |
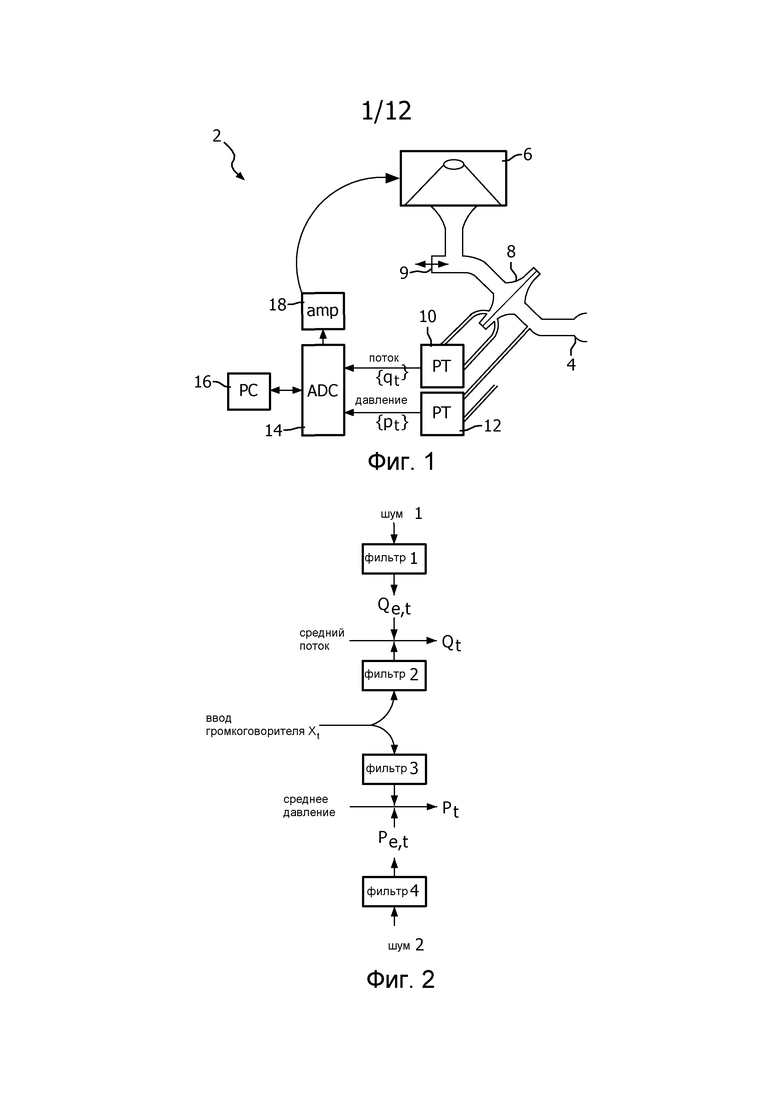
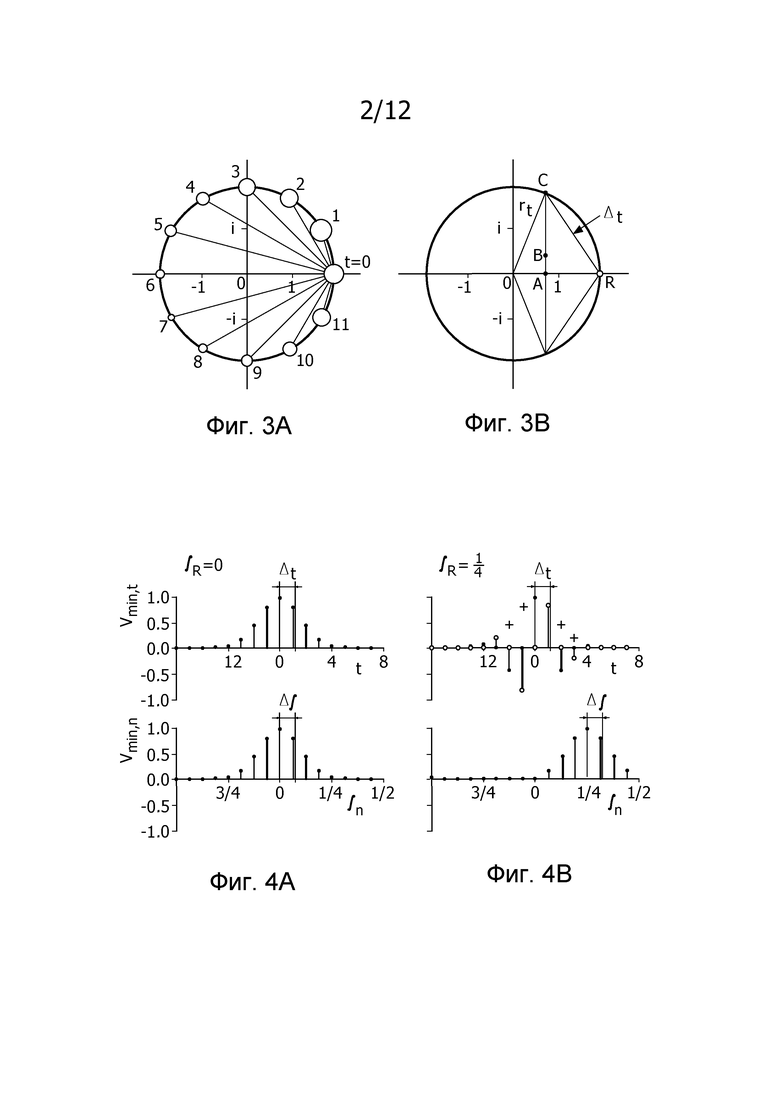
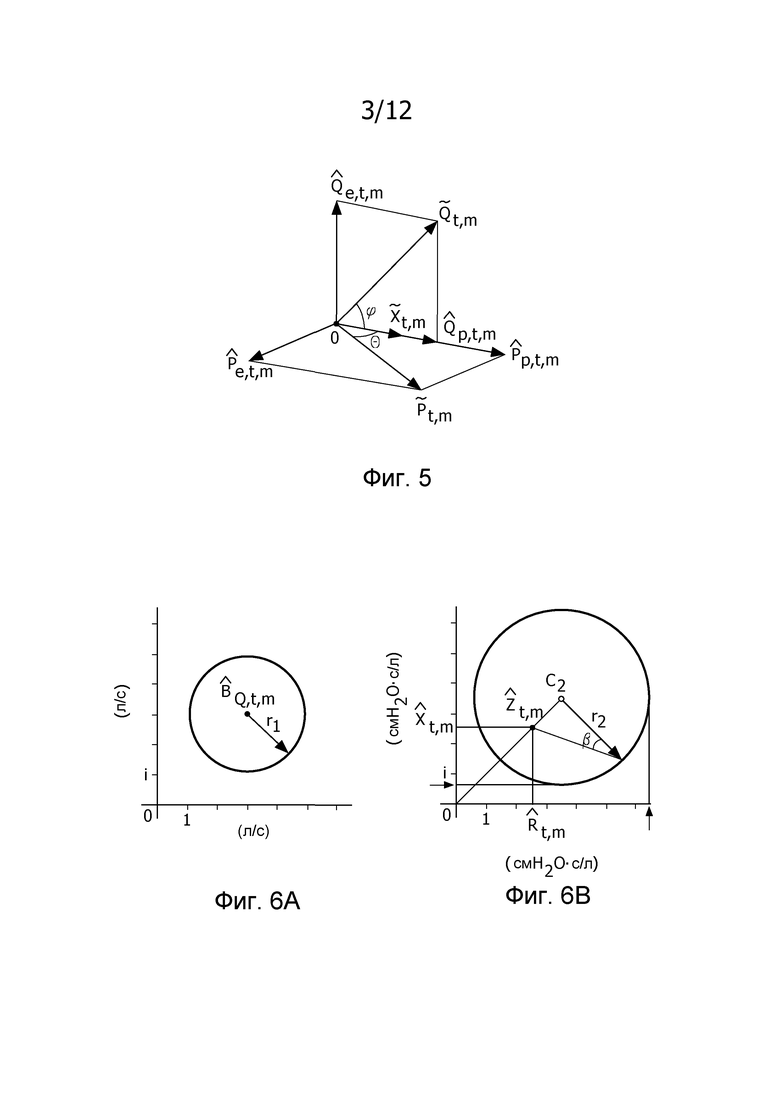
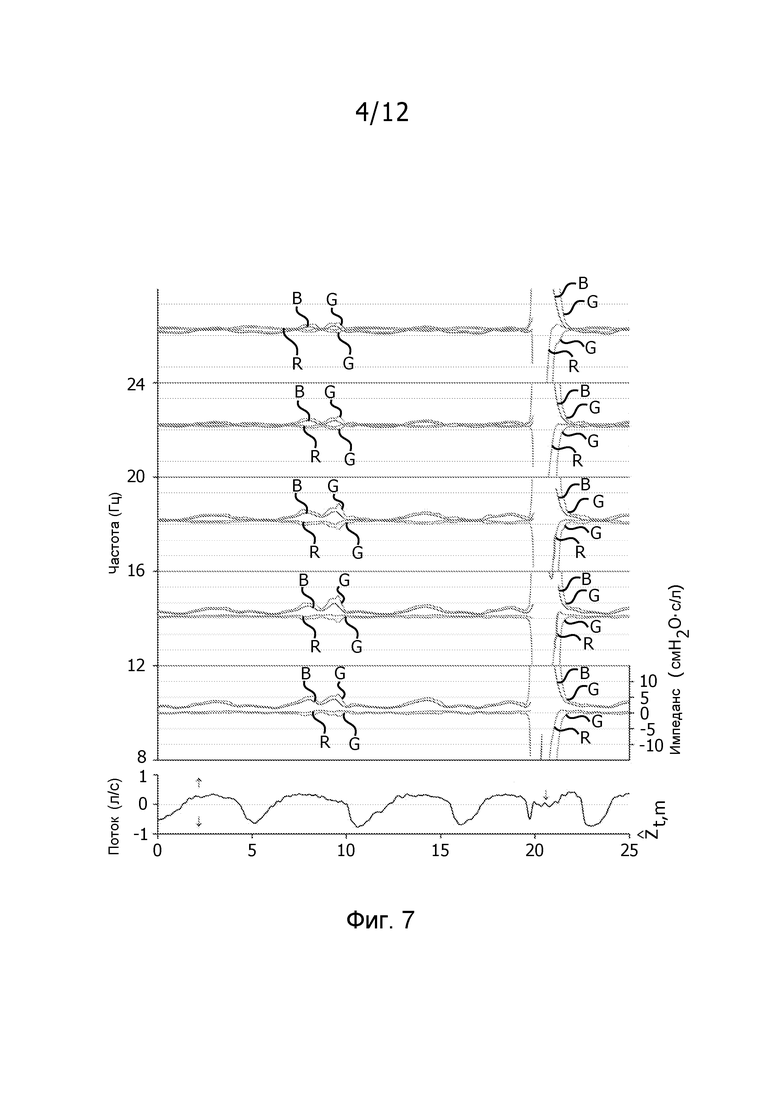
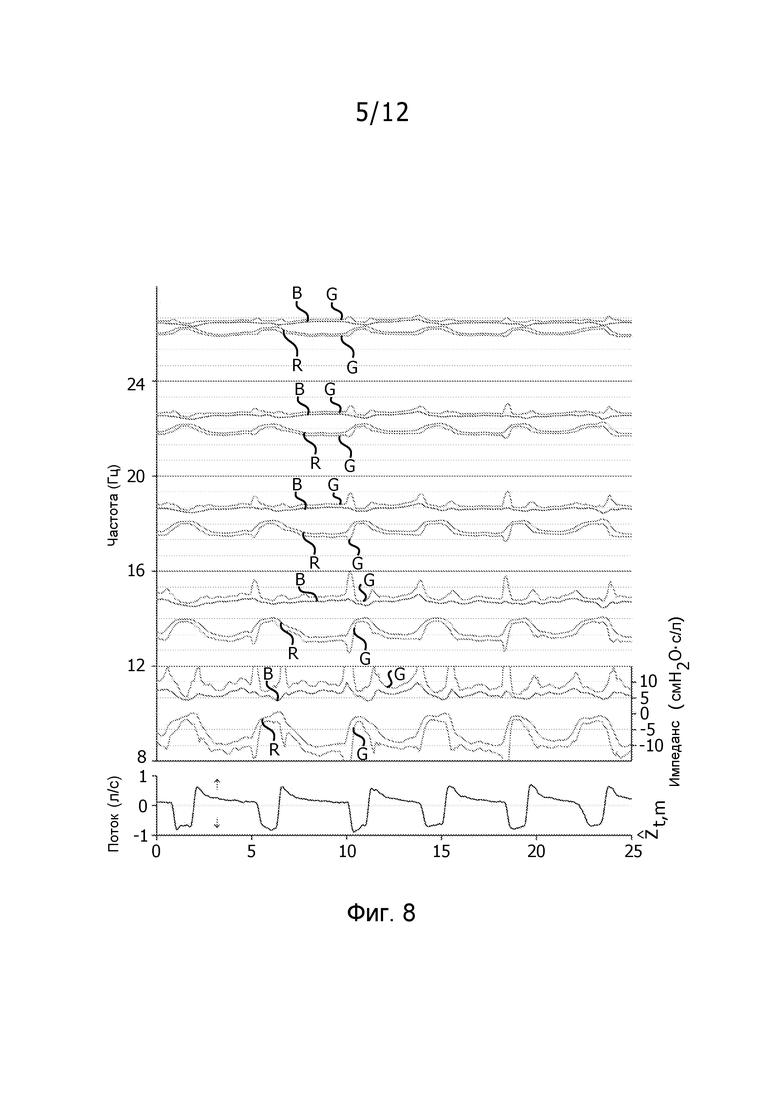
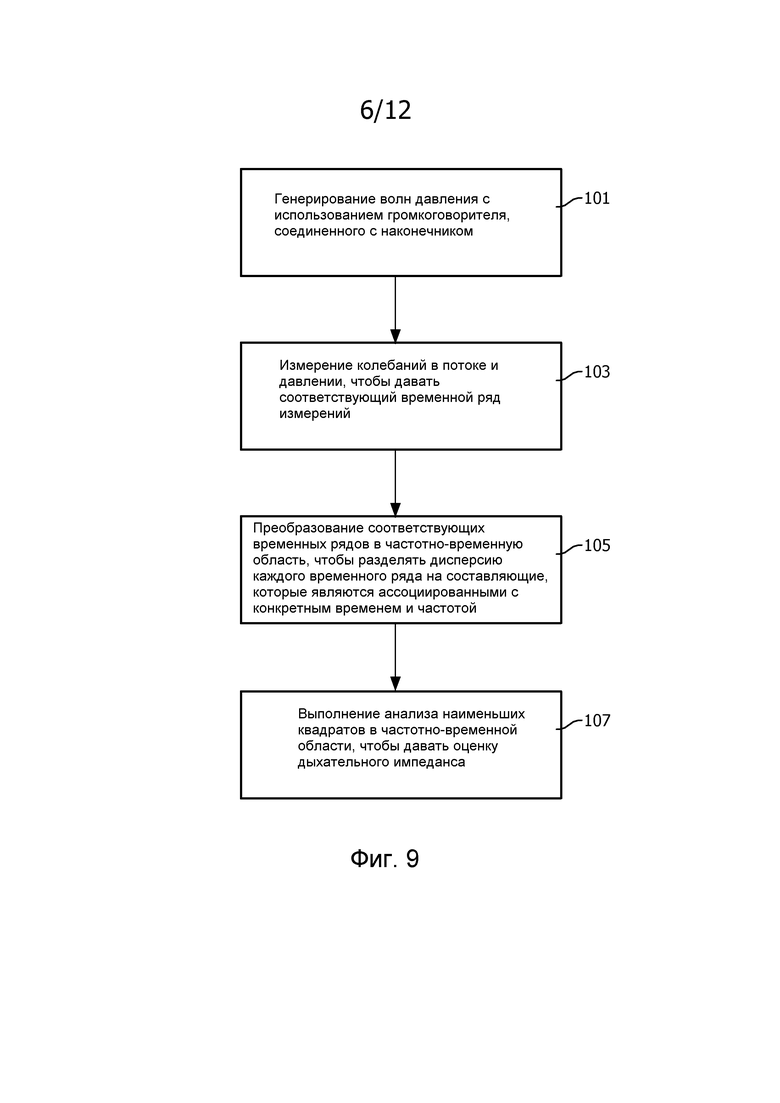
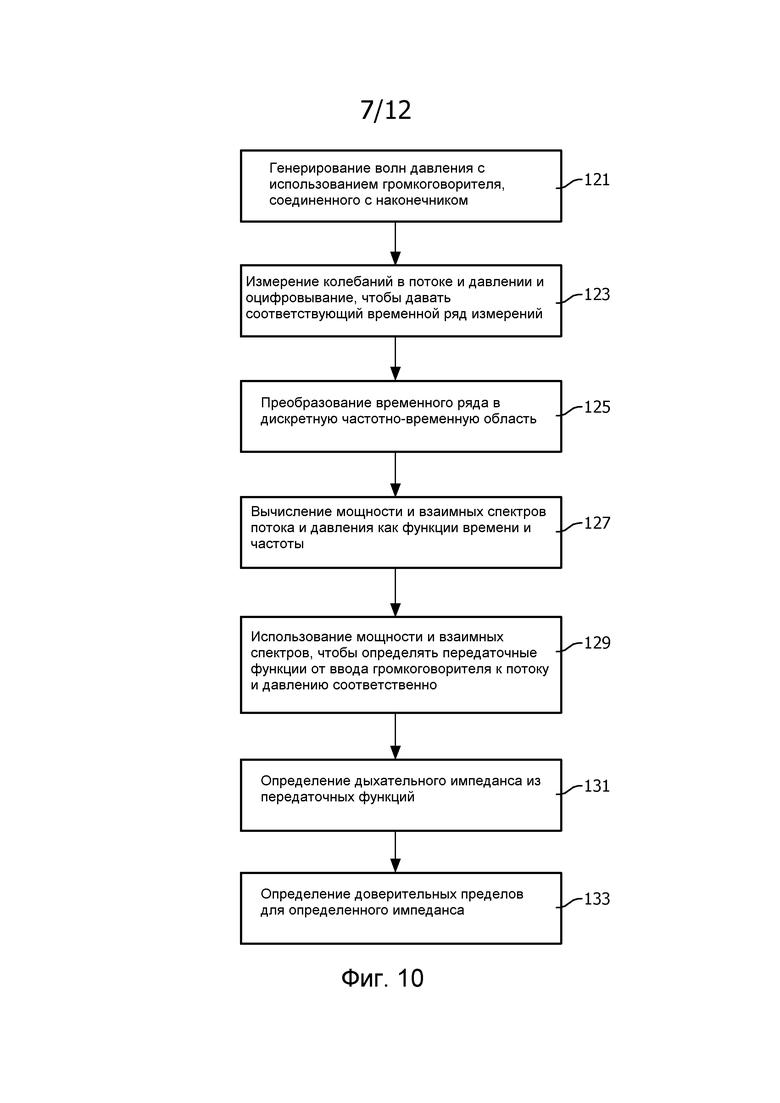
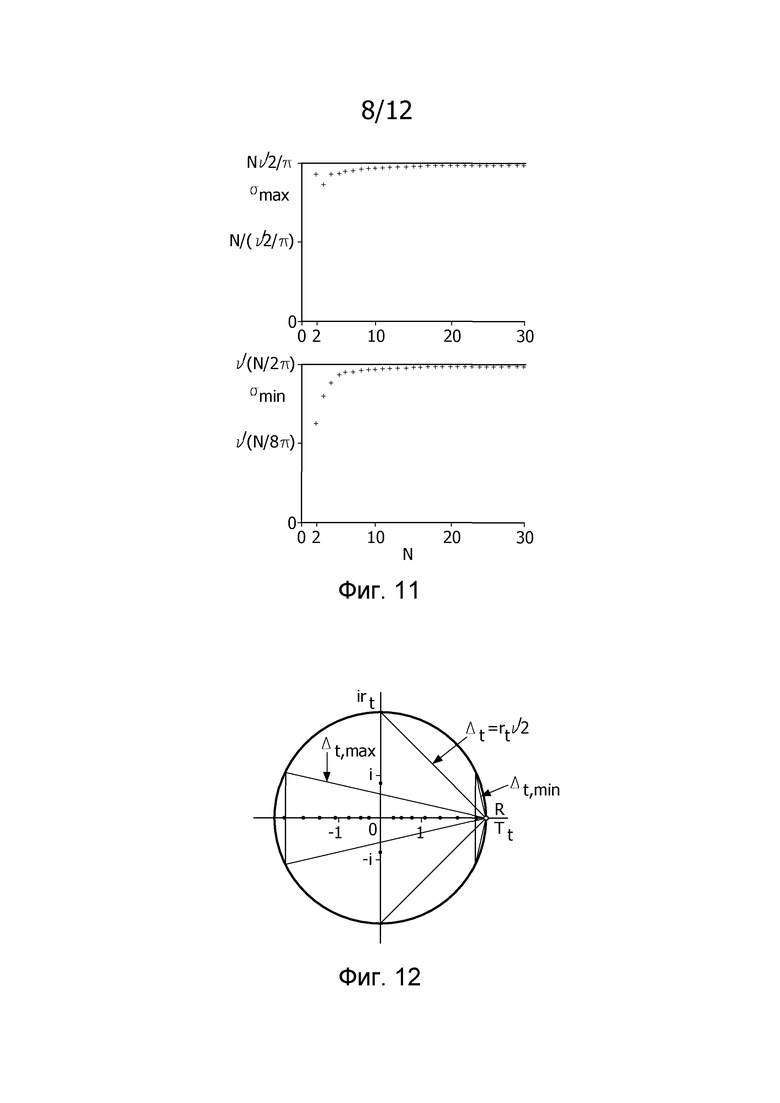
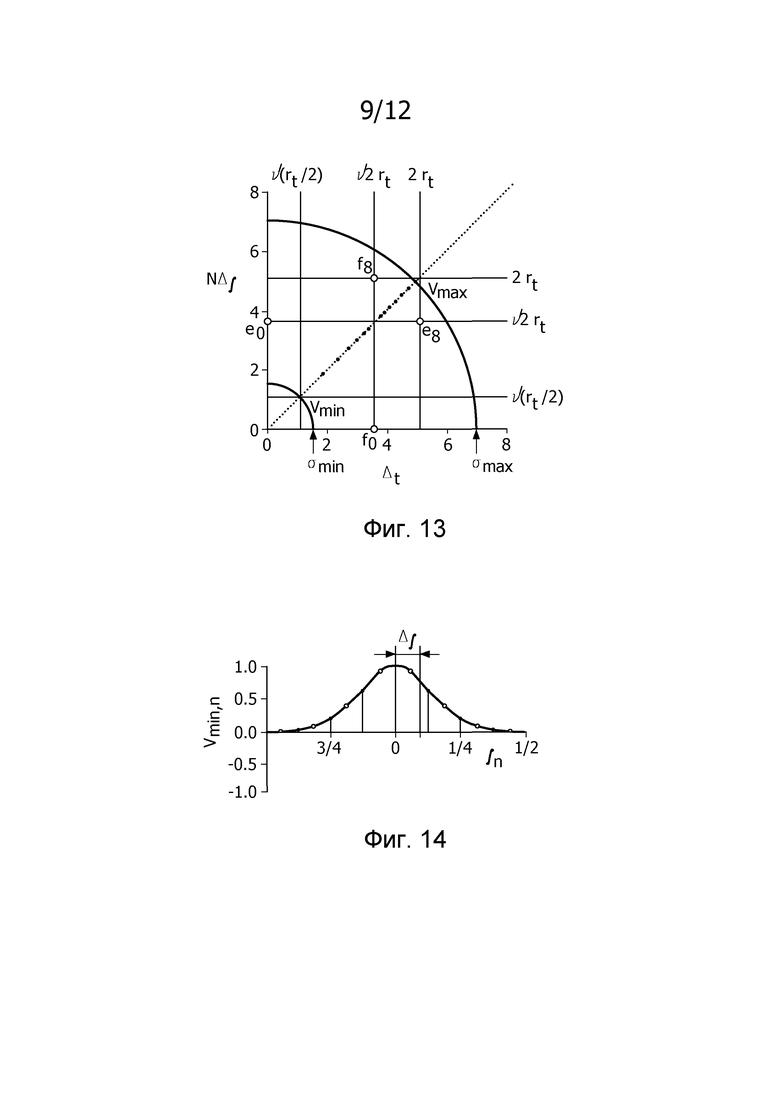
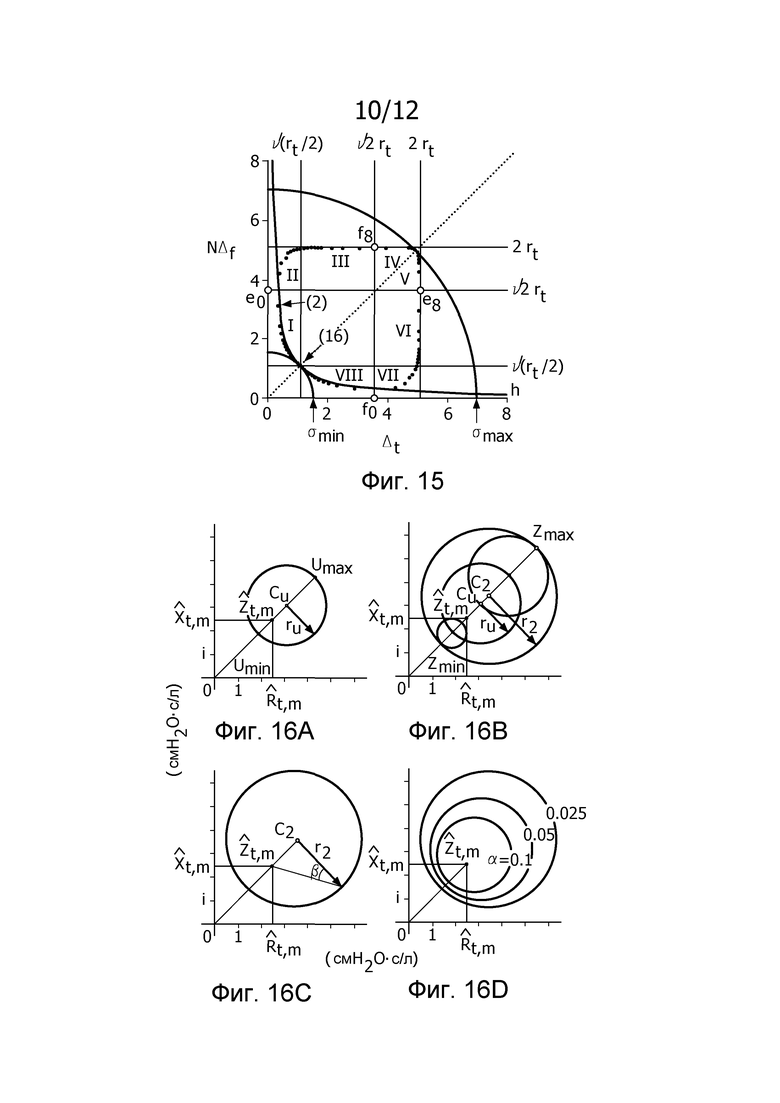
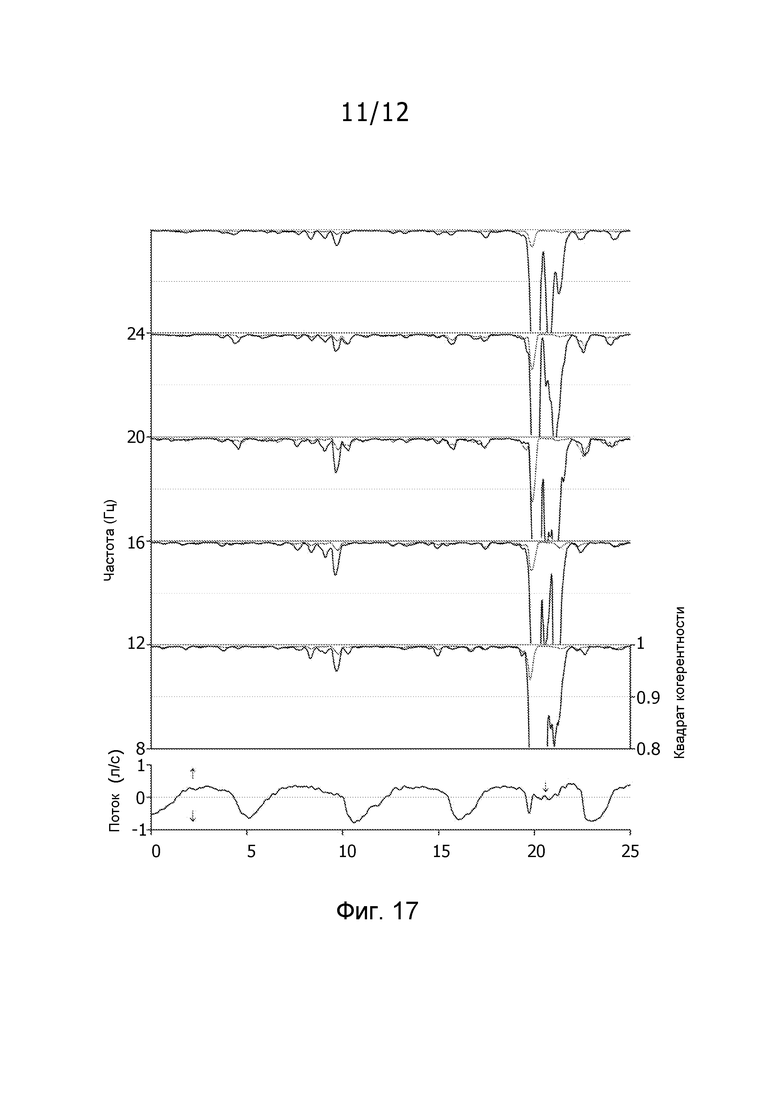
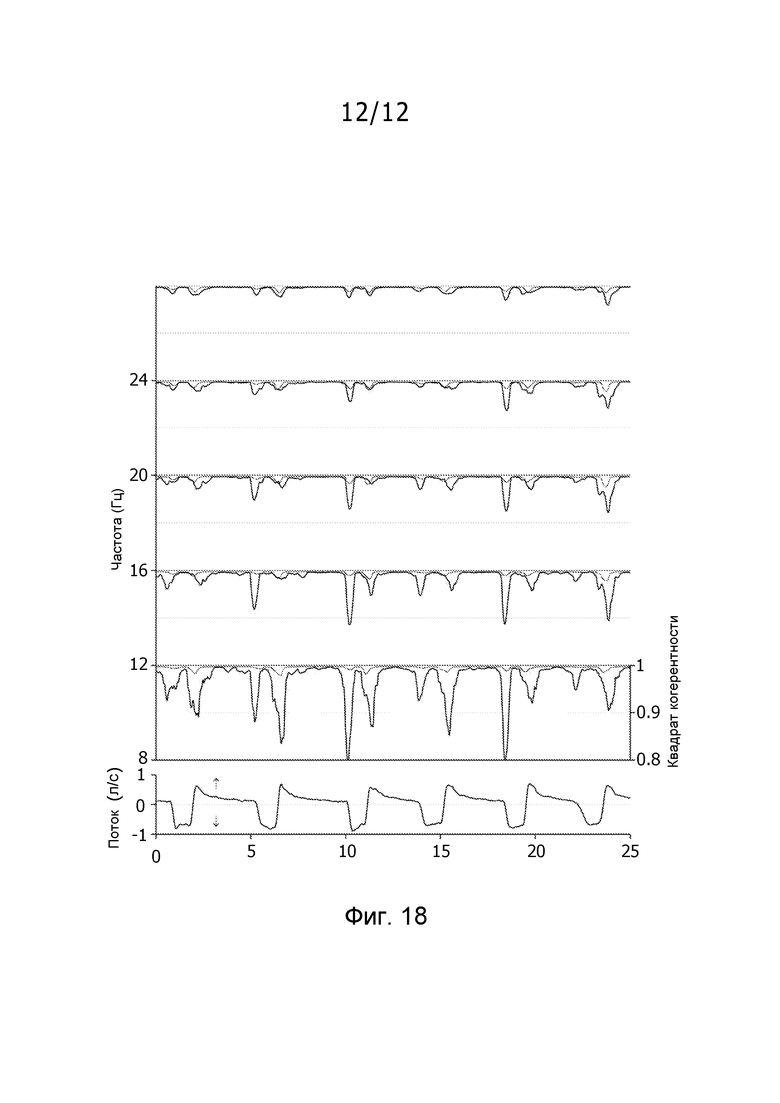
Группа изобретений относится к медицинской технике. Способ диагностики физиологического состояния включает генерирование колебаний давления, расхода или объема газа в дыхательных путях посредством источника возбуждения, определение расхода и давления газа для выработки соответствующих временных рядов, представляющих расход и давление, преобразование временных рядов в частотно-временную область для создания преобразованных временных рядов, оценку мощности расхода и давления, оценку соответствующих взаимных спектров расхода и давления в зависимости от времени и частоты, оценку дыхательного импеданса, определение связанных с давлением и расходом переменных производится с использованием выбранного уровня достоверности, числа степеней свободы оцененных мощности и взаимных спектров давления и квадрата коэффициента связи между источником возбуждения и давлением. Оценка импеданса отклоняется, если либо определенная связанная с расходом переменная равна или больше первого порога, либо определенная связанная с давлением переменная равна или больше второго порога. Диагностика физиологического состояния проводится на основании надежной оценки дыхательного импеданса. Раскрыты устройство диагностики, считываемый компьютером носитель, способ адаптации настроек вентилятора, устройство адаптации настроек вентилятора, способ определения схемы лечения и устройство определения схемы лечения. Изобретения направлены на повышение эффективности лечения. 7 н. и 14 з.п. ф-лы, 18 ил.
1. Способ диагностики физиологического состояния на основании оценки дыхательного импеданса, содержащий:
соединение устройства (4) взаимодействия с пациентом с дыхательными путями для создания пневматической системы, которая включает устройство взаимодействия с пациентом и дыхательные пути такого пациента;
генерирование колебаний давления, расхода или объема газа в дыхательных путях посредством источника (6) возбуждения, функционально соединенного с устройством взаимодействия с пациентом;
определение расхода и давления газа в пневматической системе для выработки соответствующих временных рядов, представляющих расход и давление (123);
преобразование соответствующих временных рядов в частотно-временную область (125) для создания преобразованных временных рядов;
оценку мощности расхода и давления в зависимости от времени и частоты из преобразованных временных рядов (127);
оценку соответствующих взаимных спектров расхода и давления в зависимости от времени и частоты на основе преобразованных временных рядов (127);
оценку дыхательного импеданса из оцененной мощности и оцененных взаимных спектров (129, 131);
определение связанной с расходом переменной в частотно-временной области для оцененного импеданса с использованием
выбранного уровня достоверности, числа степеней свободы оцененных мощности и взаимных спектров расхода и квадрата коэффициента связи между источником возбуждения и расходом;
определение связанной с давлением переменной в частотно-временной области для оцененного импеданса с использованием выбранного уровня достоверности, числа степеней свободы оцененных мощности и взаимных спектров давления и квадрата коэффициента связи между источником возбуждения и давлением;
отклонение оценки импеданса, если либо определенная связанная с расходом переменная равна или больше первого порога, либо определенная связанная с давлением переменная равна или больше второго порога; и
диагностику физиологического состояния на основании надежной оценки дыхательного импеданса.
2. Способ по п. 1, в котором этап оценки дыхательного импеданса пациента из оцененных мощности и взаимных спектров (129, 131) содержит:
определение передаточной функции от волн давления к расходу и давлению соответственно из соответствующих мощности и взаимных спектров (129); и
оценку дыхательного импеданса из передаточных функций расхода и давления (131).
3. Способ по п. 1 или 2, в котором временные ряды измерений для расхода и давления обозначаются qt и pt соответственно, и этап преобразования соответствующих временных рядов в частотно-временную область (125) содержит оценку 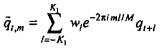 для временного ряда расхода и
для временного ряда расхода и 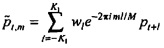 для временного ряда давления для обеспечения расхода
для временного ряда давления для обеспечения расхода 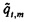 и давления
и давления 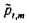 в зависимости от дискретного времени t и разных частот ƒm=m/М, где m является индексом частоты и М является эффективной шириной частотно-временного фильтра, i2=-1, весовой коэффициент w1 аппроксимируется посредством оконной функции времени,
в зависимости от дискретного времени t и разных частот ƒm=m/М, где m является индексом частоты и М является эффективной шириной частотно-временного фильтра, i2=-1, весовой коэффициент w1 аппроксимируется посредством оконной функции времени, 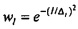 , и Δt является неопределенностью во времени.
, и Δt является неопределенностью во времени.
4. Способ по п. 3, в котором оконная функция является Гауссовой функцией, треугольной функцией, функцией кусочно-линейной аппроксимации или полиномиальной функцией.
5. Способ по п. 3, в котором этап оценки мощности расхода и давления (127) содержит оценку 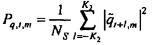 для расхода и
для расхода и 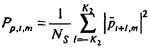 для давления, где NS является числом отсчетов в частотно-временной области ,
для давления, где NS является числом отсчетов в частотно-временной области ,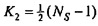 , где NS является нечетным и
, где NS является нечетным и 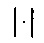 обозначает абсолютное значение.
обозначает абсолютное значение.
6. Способ по п. 5, в котором этап оценки взаимных спектров расхода и давления со сгенерированными волнами (127) давления содержит оценку 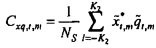 для расхода и
для расхода и 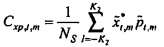 для давления, где звездочка обозначает комплексное сопряжение и
для давления, где звездочка обозначает комплексное сопряжение и 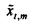 представляет волны давления.
представляет волны давления.
7. Способ по п. 6, в котором этап оценки дыхательного импеданса пациента из оцененных мощности и взаимных спектров (129, 131) содержит определение передаточной функции от волн давления к расходу (129) посредством оценки 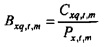 и передаточной функции от волн давления к давлению (129) посредством оценки
и передаточной функции от волн давления к давлению (129) посредством оценки 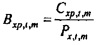 , и в котором дыхательный импеданс оценивается (131) посредством оценки
, и в котором дыхательный импеданс оценивается (131) посредством оценки 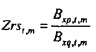 с действительной составляющей Rrst,m и мнимой составляющей Xrst,m.
с действительной составляющей Rrst,m и мнимой составляющей Xrst,m.
8. Способ по п. 7, дополнительно содержащий этап определения доверительных пределов оцененного импеданса (133), который включает в себя:
определение квадрата коэффициента связи между волнами давления и расходом с использованием 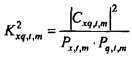 ;
;
определение квадрата коэффициента связи между волнами давления и давлением с использованием 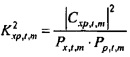 ;
;
определение числа степеней свободы, η, мощности и взаимных спектров;
определение связанной с расходом переменной 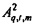 из
из
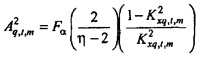 ;
;
определение связанной с давлением переменной 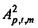 из
из
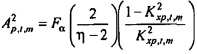 ;
;
определение 100(1-α)% доверительных пределов для действительной и мнимой частей оцененного импеданса из, соответственно, Rrs⋅c1±c2 и Xrs⋅c1±c2, где
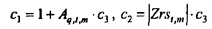 и
и 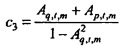
9. Способ по п. 8, в котором этап отклонения оценки импеданса содержит отклонение оценок дыхательного импеданса для заданного времени и частоты, если либо Aq,t,m≥ упомянутого первого порога, либо Ap,t,m≥ упомянутого второго порога.
10. Способ по п. 1 или 9, в котором упомянутый первый порог равен 1, и в котором упомянутый второй порог равен 1.
11. Способ по п. 1, в котором оценка соответствующих взаимных спектров расхода и давления на основе преобразованных временных рядов осуществляется на основе критерия наименьших квадратов с использованием модели с колеблющимся давлением, расходом или объемом газа в качестве входных данных и расходом и давлением в качестве выходных данных.
12. Способ по п. 1, в котором определение расхода газа в пневматической системе выполняется посредством измерения расхода с использованием датчика расхода, функционально соединенного с пневматической системой, и в котором определение давления газа в пневматической системе выполняется с использованием датчика давления, функционально соединенного с пневматической системой.
13. Устройство (2) для диагностики физиологического состояния на основании оценки дыхательного импеданса, содержащее:
устройство (4) взаимодействия с пациентом;
источник (6) возбуждения для генерирования колебаний давления, расхода или объема газа в дыхательных путях пациента;
средство (8, 10, 12) для определения расхода и давления газа в пневматической схеме, определенной посредством устройства взаимодействия с пациентом и дыхательных путей пациента, и для вывода соответствующих временных рядов значений, представляющих расход или давление;
процессор (16), сконфигурированный с возможностью:
преобразовывать соответствующие временные ряды в частотно-временную область (125);
оценивать мощность расхода и давления в зависимости от времени и частоты на основе соответствующих преобразованных временных рядов (127);
оценивать соответствующие взаимные спектры расхода и давления в зависимости от времени и частоты на основе соответствующих преобразованных временных рядов;
оценивать дыхательный импеданс из оцененных мощности и взаимных спектров (129, 131);
определять связанную с расходом переменную в частотно-временной области для оцененного импеданса с использованием выбранного уровня достоверности, числа степеней свободы оцененных мощности и взаимных спектров расхода и квадрата коэффициента связи между источником возбуждения и расходом;
определять связанную с давлением переменную в частотно-временной области для оцененного импеданса с использованием выбранного уровня достоверности, числа степеней свободы оцененных мощности и взаимных спектров давления и квадрата коэффициента связи между источником возбуждения и давлением;
отклонять оценку импеданса, если либо определенная связанная с расходом переменная равна или больше первого порога, либо определенная связанная с давлением переменная равна или больше второго порога; и
диагностировать физиологическое состояние на основании надежной оценки дыхательного импеданса.
14. Устройство (2) по п. 13, в котором средство для определения расхода и давления газа в пневматической схеме содержит:
датчик расхода, функционально соединенный с пневматической системой; и
датчик давления, функционально соединенный с пневматической системой.
15. Устройство (2) по п. 13, в котором оценка соответствующих взаимных спектров расхода и давления на основе преобразованных временных рядов осуществляется на основе критерия наименьших квадратов с использованием модели с колеблющимся давлением, расходом или объемом газа в качестве входных данных и расходом и давлением в качестве выходных данных.
16. Устройство (2) по п. 13, в котором процессор (16) сконфигурирован с возможностью оценивать дыхательный импеданс пациента из оцененных мощности и взаимных спектров (129, 131) посредством
определения передаточной функции от волн давления к расходу и давлению соответственно из соответствующих мощности и взаимных спектров (129); и
оценки дыхательного импеданса из передаточных функций расхода и давления (131).
17. Считываемый компьютером носитель со считываемым компьютером кодом, воплощенным на нем, при этом считываемый компьютером код сконфигурирован так, что при исполнении посредством подходящего процессора или компьютера, процессор или компьютер выполняет способ по любому из пп. 1-12.
18. Способ адаптации настроек вентилятора, используемого для противодействия непроходимости дыхательных путей на основании оценки дыхательного импеданса, содержащий:
соединение устройства (4) взаимодействия с пациентом с дыхательными путями пациента для создания пневматической системы, которая включает в себя устройство взаимодействия с пациентом и дыхательные пути пациента;
генерирование колебаний давления, расхода или объема газа в дыхательных путях пациента посредством источника (6) возбуждения, функционально соединенного с устройством взаимодействия с пациентом;
определение расхода и давления газа в пневматической системе для выработки соответствующих временных рядов, представляющих расход и давление (123);
преобразование соответствующих временных рядов в частотно-временную область (125) для создания преобразованных временных рядов;
оценку мощности расхода и давления в зависимости от времени и частоты из преобразованных временных рядов (127);
оценку соответствующих взаимных спектров расхода и давления в зависимости от времени и частоты на основе преобразованных временных рядов (127);
оценку дыхательного импеданса из оцененной мощности и оцененных взаимных спектров (129, 131);
определение связанной с расходом переменной в частотно-временной области для оцененного импеданса с использованием выбранного уровня достоверности, числа степеней свободы оцененных мощности и взаимных спектров расхода и квадрата коэффициента связи между источником возбуждения и расходом;
определение связанной с давлением переменной в частотно-временной области для оцененного импеданса с использованием выбранного уровня достоверности, числа степеней свободы оцененных мощности и взаимных спектров давления и квадрата коэффициента связи между источником возбуждения и давлением;
отклонение оценки импеданса, если либо определенная связанная с расходом переменная равна или больше первого порога, либо определенная связанная с давлением переменная равна или больше второго порога; и
адаптацию настроек вентилятора на основании надежной оценки дыхательного импеданса.
19. Устройство для адаптации настроек вентилятора, используемого в лечении медицинских состояний, на основании оценки дыхательного импеданса, содержащее:
устройство (4) взаимодействия с пациентом;
источник (6) возбуждения для генерирования колебаний давления, расхода или объема газа в дыхательных путях пациента;
средство (8, 10, 12) для определения расхода и давления газа в пневматической схеме, определенной посредством устройства взаимодействия с пациентом и дыхательных путей пациента, и для вывода соответствующих временных рядов значений, представляющих расход или давление;
процессор (16), сконфигурированный с возможностью:
преобразовывать соответствующие временные ряды в частотно-временную область (125);
оценивать мощность расхода и давления в зависимости от времени и частоты на основе соответствующих преобразованных временных рядов (127);
оценивать соответствующие взаимные спектры расхода и давления в зависимости от времени и частоты на основе соответствующих преобразованных временных рядов;
оценивать дыхательный импеданс пациента из оцененных мощности и взаимных спектров (129, 131);
определять связанную с расходом переменную в частотно-временной области для оцененного импеданса с использованием выбранного уровня достоверности, числа степеней свободы оцененных мощности и взаимных спектров расхода и квадрата коэффициента связи между источником возбуждения и расходом;
определять связанную с давлением переменную в частотно-временной области для оцененного импеданса с использованием выбранного уровня достоверности, числа степеней свободы оцененных мощности и взаимных спектров давления и квадрата коэффициента связи между источником возбуждения и давлением;
отклонять оценку импеданса, если либо определенная связанная с расходом переменная равна или больше первого порога, либо определенная связанная с давлением переменная равна или больше второго порога; и
адаптировать настройки вентилятора на основании надежной оценки дыхательного импеданса.
20. Способ определения схемы лечения для физиологического состояния на основании оценки дыхательного импеданса, содержащий:
соединение устройства (4) взаимодействия с пациентом с дыхательными путями пациента для создания пневматической системы, которая включает устройство взаимодействия с пациентом и дыхательные пути пациента;
генерирование колебаний давления, расхода или объема газа в дыхательных путях пациента посредством источника (6) возбуждения, функционально соединенного с устройством взаимодействия с пациентом;
определение расхода и давления газа в пневматической системе для выработки соответствующих временных рядов, представляющих расход и давление (123);
преобразование соответствующих временных рядов в частотно-временную область (125) для создания преобразованных временных рядов;
оценку мощности расхода и давления в зависимости от времени и частоты из преобразованных временных рядов (127);
оценку соответствующих взаимных спектров расхода и давления в зависимости от времени и частоты на основе преобразованных временных рядов (127);
оценку дыхательного импеданса пациента из оцененной мощности и оцененных взаимных спектров (129, 131);
определение связанной с расходом переменной в частотно-временной области для оцененного импеданса с использованием выбранного уровня достоверности, числа степеней свободы оцененных мощности и взаимных спектров расхода и квадрата коэффициента связи между источником возбуждения и расходом;
определение связанной с давлением переменной в частотно-временной области для оцененного импеданса с использованием выбранного уровня достоверности, числа степеней свободы оцененных мощности и взаимных спектров давления и квадрата коэффициента связи между источником возбуждения и давлением;
отклонение оценки импеданса, если либо определенная связанная с расходом переменная равна или больше первого порога, либо определенная связанная с давлением переменная равна или больше второго порога; и
определение схемы лечения для физиологического состояния на основании надежной оценки дыхательного импеданса.
21. Устройство для определения схемы лечения для физиологического состояния на основании оценки дыхательного импеданса, содержащее:
устройство (4) взаимодействия с пациентом;
источник (6) возбуждения для генерирования колебаний давления, расхода или объема газа в дыхательных путях пациента;
средство (8, 10, 12) для определения расхода и давления газа в пневматической схеме, определенной посредством устройства взаимодействия с пациентом и дыхательными путями пациента, и для вывода соответствующих временных рядов значений, представляющих расход или давление;
процессор (16), сконфигурированный с возможностью:
преобразовывать соответствующие временные ряды в частотно-временную область (125);
оценивать мощность расхода и давления в зависимости от времени и частоты на основе соответствующих преобразованных временных рядов (127);
оценивать соответствующие взаимные спектры расхода и давления в зависимости от времени и частоты на основе соответствующих преобразованных временных рядов;
оценивать дыхательный импеданс пациента из оцененных мощности и взаимных спектров (129, 131);
определять связанную с расходом переменную в частотно-временной области для оцененного импеданса с использованием выбранного уровня достоверности, числа степеней свободы оцененных мощности и взаимных спектров расхода и квадрата коэффициента связи между источником возбуждения и расходом;
определять связанную с давлением переменную в частотно-временной области для оцененного импеданса с использованием выбранного уровня достоверности, числа степеней свободы оцененных мощности и взаимных спектров давления и квадрата коэффициента связи между источником возбуждения и давлением;
отклонять оценку импеданса, если либо определенная связанная с расходом переменная равна или больше первого порога, либо определенная связанная с давлением переменная равна или больше второго порога; и
определять схему лечения для физиологического состояния на основании надежной оценки дыхательного импеданса.
| US 2008114261 A1, 15.05.2008 | |||
| Колосоуборка | 1923 |
|
SU2009A1 |
| Способ определения нарушений бронхиальной проходимости | 1987 |
|
SU1635959A1 |
| DAVIS K.A | |||
| et al, Time serias versus Fourier transform methods for estimation of respiratory impedance spectra, International journal of bio-medical computing | |||
| Elsevier science publishers | |||
| Shannon | |||
| Прибор с двумя призмами | 1917 |
|
SU27A1 |
| Одновальный, снабженный дробителем, торфяной пресс | 1919 |
|
SU261A1 |
Авторы
Даты
2017-01-10—Публикация
2010-11-24—Подача