Изобретение относится к физике материального контактного взаимодействия и служит для однозначного определения твердости материальной среды, полученной по методам (НВ) Бринелля Ю.А., (HV) «Виккерса», (HRc) Роквелла С.П. через ее прочностные параметры - угол ϕ° внутреннего трения и удельное сцепление - С (МПа).
Известен способ определения твердости материальной среды по методу (НВ) Бринелля Ю.А., заключающийся в том, что в испытываемую поверхность твердого материального тела вдавливают стальной закаленный шарик диаметром D=2,5 мм, D=5 мм или D=10 мм при заданной нагрузке Nо=625 Н…3000 Н и определяют число твердости по Бринеллю как HB=Nо/F (Н/мм2), где Nо (Н) - нагрузка на штамп, F=π⋅D⋅So (мм2) - площадь поверхности (сферического) отпечатка глубиной So (мм), при этом при НВ>130 испытывают твердые материалы при No/D2=30, материалы средней твердости НВ≈30…130 - при No/D2=10 и мягкие материалы НВ<30 - при No/D2=2,5, причем при плавном вдавливании шарика постоянство выдержки нагрузки Nо к шарику обеспечивают в течение 30 сек [1].
Метод Бринелля характеризуется тремя шкалами твердости НВ материальных сред и подбором диаметра шарика, при котором при нагрузке N упругий контакт по Герцу завершается, и далее может происходить только упругопластическое деформирование среды. При этом до нагрузки N эпюра контактных напряжений имеет седлообразную форму, а свыше нагрузки N - вытянутую эллипсоидную форму, то есть она носит неравномерный характер.
В работе [2] установлено соотношение между твердостью по Бринеллю (НВ) и нижним пределом текучести σнт в виде НВ=2,77⋅σнт.
Известен способ определения твердости материальной среды по методу (HV) «Виккерса», заключающийся в том, что в поверхность образца твердой материальной среды вдавливают алмазный индентор (наконечник) по форме правильной четырехгранной пирамиды с двухгранным углом 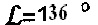 при вершине, нагрузку N на индентор задают и выдерживают постоянной по шкале Nо=50, 100, 200, 300, 500, 1000 (Н) в зависимости от твердости и толщины образца среды, а твердость по «Виккерсу» определяют как HV=No/F, где
при вершине, нагрузку N на индентор задают и выдерживают постоянной по шкале Nо=50, 100, 200, 300, 500, 1000 (Н) в зависимости от твердости и толщины образца среды, а твердость по «Виккерсу» определяют как HV=No/F, где 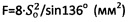 - площадь пирамидальной поверхности отпечатка глубиной h (мм) при замере двух диагоналей отпечатка с погрешностью 1 мкм [3].
- площадь пирамидальной поверхности отпечатка глубиной h (мм) при замере двух диагоналей отпечатка с погрешностью 1 мкм [3].
Постоянную нагрузку No на индентор задают для испытываемого материала несколько раз, пока она не попадет в необходимый диапазон шкалы No нагрузок. Твердость по «Виккерсу» (HV) не совпадает с твердостью по Бринеллю (НВ).
Известен способ определения твердости материальной среды по методу (HRc) Роквелла С.П., заключающийся в том, что в поверхность образца твердой материальной среды вдавливают алмазный индентор с углом при вершине 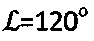 (шкала А и С) или стальной закаленный шарик диаметром D=1/16'', или D=1,588 мм (шкала В), а за единицу твердости принимают условную величину усилия при осевом перемещении индентора на глубину 0,002 мкм [4].
(шкала А и С) или стальной закаленный шарик диаметром D=1/16'', или D=1,588 мм (шкала В), а за единицу твердости принимают условную величину усилия при осевом перемещении индентора на глубину 0,002 мкм [4].
Твердость по Роквеллу (HRc) - условная эмпирическая величина, не совпадающая с твердость по Бринеллю (НВ) и твердостью по методу «Виккерса» (HV).
Способы определения твердости материалов по Бринеллю (НВ), «Виккерсу» (HV) и Роквеллу (HRc) преимущественно предназначены для металлов.
Известен способ определения несущей способности дисперсной пористой материальной среды (грунт, торф и др.) методом пенетрации коническим индентором, заключающийся в том, что конический индентор с углом при вершине 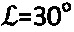 (конус Васильева) погружают в грунтовую поверхность полупространства на глубину 10 мм, в процессе погружения индентора замеряют усилие Ni (Н) его погружения в грунт с фиксацией значения N10 на глубине 10 мм, а удельное сопротивление пенетрации определяют по зависимости
(конус Васильева) погружают в грунтовую поверхность полупространства на глубину 10 мм, в процессе погружения индентора замеряют усилие Ni (Н) его погружения в грунт с фиксацией значения N10 на глубине 10 мм, а удельное сопротивление пенетрации определяют по зависимости 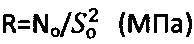 , где No (Н) - осевое усилие на конический индентор,
, где No (Н) - осевое усилие на конический индентор, 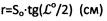 - радиус отпечатка конического индентора на поверхности полупространства глубиной So (см) [5].
- радиус отпечатка конического индентора на поверхности полупространства глубиной So (см) [5].
Физико-механические характеристики пористых грунтов, полученные по результатам пенетрации конусными инденторами при различных углах  при вершине имеют большой разброс данных, а угол
при вершине имеют большой разброс данных, а угол  необходимо для исследуемого вида грунта принимать индивидуально методом подбора. При этом глубина So=10 мм пенетрации среды строго ограничена, так как с дальнейшим ее увеличением нарушается линейная связь усилия пенетрации Ni от глубины
необходимо для исследуемого вида грунта принимать индивидуально методом подбора. При этом глубина So=10 мм пенетрации среды строго ограничена, так как с дальнейшим ее увеличением нарушается линейная связь усилия пенетрации Ni от глубины 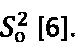
Известен способ определения прочности пористых глинистых грунтов методом вдавливания шарового индентора, заключающийся в том, что для данного вида глинистого грунта опытным путем подбирают предельную нагрузку N, прикладываемую к шаровому индентору, исходя из условия 0,005⋅D≤S15≤0,05⋅D, где S15 - осадка штампа через 15 мин после приложения нагрузки N, к поверхности грунта через шаровой индентор прикладывают подобранную нагрузку N, замеряют установившуюся длительную осадку грунта Sдл и определяют прочность или длительное сопротивление грунта по зависимости σдл=N/(π⋅D⋅Sдл) (МПа), а для пластичных глинистых грунтов - величину длительного сцепления 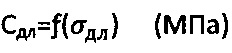 при выдержке длительного сопротивления σдл во времени t до стабилизации его значения [7].
при выдержке длительного сопротивления σдл во времени t до стабилизации его значения [7].
Известен способ определения параметров прочности материальной мерзлой грунтовой и торфяной среды, включающий ее нагружение усилием Nо жесткого сферического штампа диаметром D до стабилизации осадки St, нагрузку штампа с замером мессурой его осадки 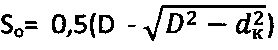 по остаточному диаметру dк лунки сжатия, определение длительного сопротивления σдл и длительного сцепления мерзлой среды как Сдл=0,18⋅N/(π⋅D⋅So)=σдл (МПа) [8].
по остаточному диаметру dк лунки сжатия, определение длительного сопротивления σдл и длительного сцепления мерзлой среды как Сдл=0,18⋅N/(π⋅D⋅So)=σдл (МПа) [8].
Недостатком известного способа является низкая расчетная точность параметров прочности мерзлой среды при несоответствии остаточной осадки лунки сжатия контактной осадке So сферы, взаимодействующей с мерзлой средой. Диаметр остаточной лунки сжатия соответствует только остаточной пластической деформации, так как упругие остаточные деформации после разгрузки сферы в лунке сжатия восстанавливаются.
Цель изобретения - однозначное определение твердости любой материальной среды через общефизические параметры - угол ϕ° внутреннего трения и удельное сцепление - С (МПа).
Технический результат по способу определения твердости и параметров прочности материальной среды, заключающемуся в том, что в исследуемую твердую беспористую материальную среду с поверхности полупространства вертикально погружают жесткий индентор конической или сферической формы соответственно с углом  при вершине или диаметром D (см) усилием Ni (Н), возрастающим по мере погружения на глубину Si (см) до момента стабилизации усилия No=const (Н) на соответствующей глубине 50 (см), которые фиксируют динамометром и индикатором деформации, определяют твердость материальной среды: по Ю.А. Бринеллю - HB=No/(π⋅D⋅So)=2,77σнт (МПа), где σнт - нижний предел текучести материальной среды; по «Виккерсу» -
при вершине или диаметром D (см) усилием Ni (Н), возрастающим по мере погружения на глубину Si (см) до момента стабилизации усилия No=const (Н) на соответствующей глубине 50 (см), которые фиксируют динамометром и индикатором деформации, определяют твердость материальной среды: по Ю.А. Бринеллю - HB=No/(π⋅D⋅So)=2,77σнт (МПа), где σнт - нижний предел текучести материальной среды; по «Виккерсу» - 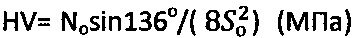 , где 136° - угол при вершине четырехгранной пирамиды индентора; по С.П. Роквеллу -
, где 136° - угол при вершине четырехгранной пирамиды индентора; по С.П. Роквеллу - 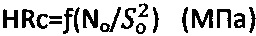 , где So - заданная глубина погружения конусного индентора с углом при вершине 120° (шкалы А, С) или шарикового индентора диаметром D (см) (шкала В), методами пенетрации твердой пористой материальной среды с поверхности полупространства шариковым индентором по зависимости σдл=No/(π⋅D⋅Sдл) (МПа), где σдл - длительное сопротивление среды пенетрации, и конусным индентором с углом 30° при вершине по зависимости
, где So - заданная глубина погружения конусного индентора с углом при вершине 120° (шкалы А, С) или шарикового индентора диаметром D (см) (шкала В), методами пенетрации твердой пористой материальной среды с поверхности полупространства шариковым индентором по зависимости σдл=No/(π⋅D⋅Sдл) (МПа), где σдл - длительное сопротивление среды пенетрации, и конусным индентором с углом 30° при вершине по зависимости 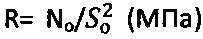 , где R - удельное сопротивление среды пенетрации, достигается тем, что для твердой материальной среды определяют ее прочностные параметры - угол ϕ° внутреннего трения и С (МПа) - удельное сцепление в ненарушенном структурированном состоянии по зависимостям ϕ°=arccos[(D/2-Sо)/(D/2)], C=(σт/2)⋅(1+sinϕ°)/cosϕ° (МПа), где σт (МПа) - предел текучести материальной среды, а твердость любой материальной среды определяют по зависимости
, где R - удельное сопротивление среды пенетрации, достигается тем, что для твердой материальной среды определяют ее прочностные параметры - угол ϕ° внутреннего трения и С (МПа) - удельное сцепление в ненарушенном структурированном состоянии по зависимостям ϕ°=arccos[(D/2-Sо)/(D/2)], C=(σт/2)⋅(1+sinϕ°)/cosϕ° (МПа), где σт (МПа) - предел текучести материальной среды, а твердость любой материальной среды определяют по зависимости 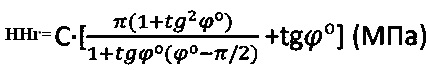 .
.
Максимальная твердость материальной среды проявляется перед нарушением ее структурной прочности, когда среда еще в структурированном состоянии и обладает углом ϕ° внутреннего трения и удельным сцеплением - С (МПа), а давление ее разрушения достигает предельного значения 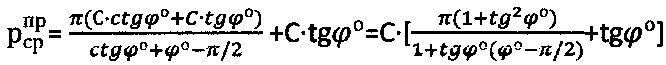 , где действующее бытовое давление р6=(γh-C)tgϕ°=(C/cos2ϕ°-C)tgϕ°=G⋅tgϕ° (МПа), а начальное (первое) критическое разрушающее давление
, где действующее бытовое давление р6=(γh-C)tgϕ°=(C/cos2ϕ°-C)tgϕ°=G⋅tgϕ° (МПа), а начальное (первое) критическое разрушающее давление 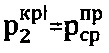 под краями штампа [9].
под краями штампа [9].
Для твердой материальной среды методы испытания дисперсных материалов на сжимаемость и сдвиг в массиве или в образце не пригодны и параметры прочности твердой среды получают через аналитические зависимости ϕ°=arccos[(D/2-Sо)/(D/2)], C=(σт/2)⋅(1+sinϕ°)/cosϕ° (МПа), где σт (МПа) - предел текучести материала, легко определяемый из предельного состояния материальной среды Ш. Кулона-Мора.
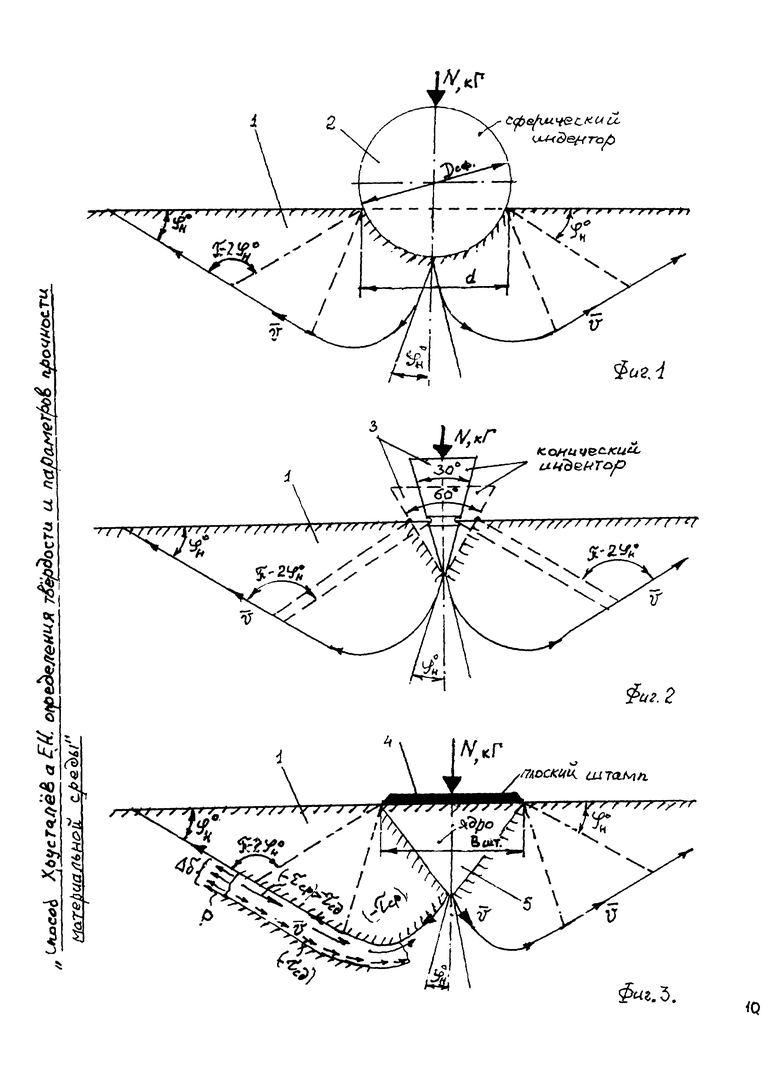
Предлагаемое изобретение поясняется графическими материалами, где на фиг. 1 - схема испытания структурированной (упругой) материальной среды перед разрушением шариковым индентором Ю.А. Бринелля; на фиг. 2 - схема испытания структурированной (упругой) материальной среды перед разрушением методом С.П. Роквелла; на фиг. 3 - схема испытания структурированной (упругой) материальной среды перед разрушением под плоским жестким штампом.
Способ определения твердости и параметров прочности материальной среды реализуется следующим образом.
1. В твердую структурированную (упругую) материальную среду 1 с поверхности полупространства (фиг. 1) вертикально погружают подобранный по диаметру D шариковый индентор 2 фиксируемым по мере погружения на регистрируемую глубину Si (см) усилием вдавливания Ni(H). В момент стабилизации усилия No=const регистрируют глубину So погружения шарикового индентора 2 диаметром D (см). Твердость по Бринеллю определяют как HB=No/(π⋅D⋅So) (МПа), а длительное сопротивление пенетрации шариковым индентором 2 дисперсных пористых твердых материалов или их прочность определяют как σдл=N/(π⋅D⋅Sдл) (МПа), где Sдл (см) - длительная осадка шарикового индентора 2.
2. В твердую структурированную (упругую) материальную среду 1 с поверхности полупространства (фиг. 2) вертикально погружают подобранный по углу  конический индентор 3 фиксируемым усилием Ni(H). Для дисперсной грунтовой среды 1 для конусного индентора 3 при Sо=1 см угол при вершине принимают равным
конический индентор 3 фиксируемым усилием Ni(H). Для дисперсной грунтовой среды 1 для конусного индентора 3 при Sо=1 см угол при вершине принимают равным  . Твердость по Роквеллу определяют как
. Твердость по Роквеллу определяют как 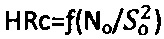 для металла при
для металла при 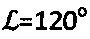 (шкала А и С) и So=0,002 (мкм), а удельное сопротивление пенетрации для дисперсных грунтов -
(шкала А и С) и So=0,002 (мкм), а удельное сопротивление пенетрации для дисперсных грунтов - 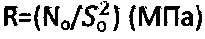 , где No (Н) - замеренное осевое усилие конусного индентора;
, где No (Н) - замеренное осевое усилие конусного индентора; 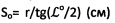 - осадка конусного индентора при радиусе r отпечатка индентора на поверхности дисперсной среды.
- осадка конусного индентора при радиусе r отпечатка индентора на поверхности дисперсной среды.
3. По результатам лабораторных испытаний образца твердой материальной среды определяют ее предел текучести σт (кГ/см2), а дисперсной твердой материальной среды - ее параметры прочности - угол ϕ° внутреннего трения и C (МПа) - удельное сцепление на приборах одноплоскостного среза образцов, обжатых давлением рi по зависимости Ш. Кулона-Мора τi=pitgϕ°+C (МПа).
Для сплошной твердой материальной среды устанавливают угол внутреннего трения ϕ°=arccos[(D/2-So)/(D/2)], где D - диаметр сферического индентора 2 (фиг. 1), So - осадка индентора 2 перед разрушением среды при постоянстве вдавливающего усилия No=const, а также удельное сцепление среды как С=(σт/2)(1+sinϕ°)/cosϕ° (МПа).
Твердость материальной среды рассчитывают как 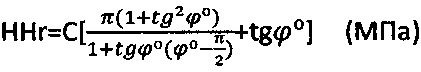 . Твердость HHr материальной среды соответствует предельному давлению
. Твердость HHr материальной среды соответствует предельному давлению 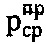 , предшествующему ее разрушению после трещинообразования среды 1 под жестким плоским штампом 4 и образования под ним лидирующего ядра 5 уплотнения (фиг. 3), под которым, как под жестким конусом 3 (фиг. 2) после нарушения структурной прочности среды, развиваются линии
, предшествующему ее разрушению после трещинообразования среды 1 под жестким плоским штампом 4 и образования под ним лидирующего ядра 5 уплотнения (фиг. 3), под которым, как под жестким конусом 3 (фиг. 2) после нарушения структурной прочности среды, развиваются линии  сдвигов, выходящие на дневную поверхность под углом
сдвигов, выходящие на дневную поверхность под углом 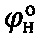 внутреннего трения среды с нарушенной структурой.
внутреннего трения среды с нарушенной структурой.
Пример 1. Металлический образец испытывают на твердость по Бринеллю шариком диаметром D=10 мм под нагрузкой No=30000 Н с выдержкой t=10 сек. При деформации образца шариком So=0,0239 мм рассчитывают твердость образца по Бринеллю как НВ=No/(π⋅D⋅So)=30000/(π⋅1⋅0,0239)=399550 (МПа)=4000 (Н/мм2) или получают НВ400.
Лабораторные испытания образца металла предоставили данные о пределе текучести σт=950 (Н/мм2).
По предлагаемому способу угол внутреннего трения образцов металла равен ϕ°=arccos[(D/2-So)/(D/2)]=arccos[(1/2-,0239)/(1/2)]=arccos0,9522=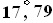 . Удельное сцепление определяют как C=(σт/2)(1+sinϕ°)/cosϕ°=(9500/2)(1+sin
. Удельное сцепление определяют как C=(σт/2)(1+sinϕ°)/cosϕ°=(9500/2)(1+sin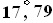 )/cos
)/cos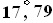 =651,3 (МПа).
=651,3 (МПа).
Предельное давление для образца среды составляет величину
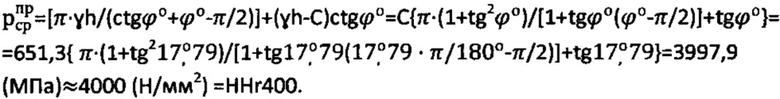
Пример 2. Образец мерзлого торфа испытывают на твердость по Бринеллю шариком диаметром D=20 мм под нагрузкой No=2140 Н с выдержкой t=10 сек. При деформации образца шариком So=0,212 мм рассчитывают твердость образца по Бринеллю как НВ=Nо/(π⋅D⋅Sо)=2140/(π⋅2⋅0,0212)=160,66 (МПа)=160 (Н/мм2).
При испытании образца торфа на твердость по Роквеллу конусным индентором с углом при вершине 30° стабилизированное усилие вдавливания при его заглублении на глубину 0,5 см составило No=405 (Н), а твердость по Роквеллу 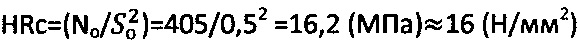 .
.
Лабораторные испытания образца мерзлого торфа предоставили данные о пределе текучести σт=1,06 (МПа).
По предлагаемому способу угол внутреннего трения образца мерзлого торфа равен ϕ°=arccos[(D/2-Sо)/(D/2)]=arccos[(2/2-,0202)/1]=11°,54. Удельное сцепление определяют как C=(σт/2)(1+sinϕ°)/cosϕ°=(1/06/2)(1+sin11°,54)/cos11°,54=0,65 (МПа).
Предельное давление для образца мерзлого торфа составляет величину 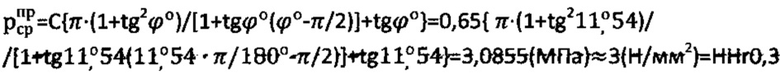
Пример 3. Образец грунта испытывают на твердость пенетрацией конусным индентором с углом 30° при вершине. При погружении индентора на глубину So=1 см - const усилие вдавливания в момент стабилизации составило величину No=8,3 (H). Твердость по Роквеллу составила величину 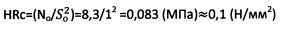 .
.
При испытании грунта на твердость сферическим индентором диаметром D=2,7 см получили отпечаток на поверхности образца диаметром d=1,08 см при глубине So=0,0462 мм твердость по Бринеллю составила величину НВ=No/(π⋅D⋅So)=8,3/(π⋅2,7⋅0,0462)=0,211 (МПа)=0,2 (Н/мм2).
Лабораторные испытания образцов грунта на сжимаемость и одноплоскостной срез в сдвиговом приборе дали данные об угле внутреннего трения грунта ϕ=30° и его удельном сцеплении C=0,02 (МПа). Твердость грунта составила величину 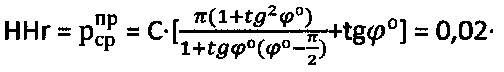
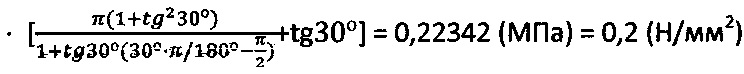
Впервые через общефизическую величину угла ϕ° внутреннего трения и удельного сцепления С (МПа) получена однозначная величина твердости любой материальной среды.
Источники информации
1. Артоболевский И.И. Политехнический словарь. - М.: «Советская Энциклопедия», 1977. - С. 60.
2. Ишлинский А.Ю. Осесимметричная задача пластичности и проба Бринелля. // ППИ, 1944. - Т. 8, ВЫТТ. 8 - С. 201-202.
3. Артоболевский И.И. Политехнический словарь. - М.: «Советская Энциклопедия», 1977. - С. 78.
4. Артоболевский И.И. Политехнический словарь. - М.: «Советская Энциклопедия», 1977. - С. 428.
5. Черкасов И.И. Механические свойства грунтов в дорожном строительстве. - М.: Транспорт, 1976. - С. 141-144, 154-167.
6. Разоренов В.Ф. Пенетрационные испытания грунтов. - М.: Издательство литературы по строительству, 1968. - С. 42.
7. Зиангиров Р.С., Роот П.Э., Филимонов С.Д. Практикум по механике грунтов. - М.: Изд-во МГУ, 1984. - С. 130-132.
8. Роман Л.Т., Веретехина Э.Г. Определение деформационных характеристик мерзлых грунтов вдавливанием шарового штампа. / Основания, фундаменты и механика грунтов. - 2004. - №2. - С. 21-24.
9. Кузьмин П.Г., Ферронский В.И. Проектирование фундаментов по предельным состояниям. - Росвузиздат, 1963. - С. 17.
10. Анурьев В.И. Справочник конструктора-машиностроителя. Книга 1. - М.: «Машиностроение», 1974. - С. 8-12, 14-19, 24-30.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ХРУСТАЛЕВА Е.Н. ОПРЕДЕЛЕНИЯ ФИЗИЧЕСКИХ ПАРАМЕТРОВ ПРОЧНОСТИ МАТЕРИАЛЬНОЙ СРЕДЫ | 2015 |
|
RU2615598C1 |
| СПОСОБ ХРУСТАЛЕВА Е.Н. ОПРЕДЕЛЕНИЯ НЕСУЩЕЙ СПОСОБНОСТИ И КОЭФФИЦИЕНТА АНИЗОТРОПИИ ТОРФЯНОЙ ЗАЛЕЖИ | 2016 |
|
RU2657590C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НЕСУЩЕЙ СПОСОБНОСТИ ГРУНТОВОГО ОСНОВАНИЯ И ТОРФЯНОЙ ЗАЛЕЖИ | 2004 |
|
RU2270990C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОНТАКТНЫХ НАПРЯЖЕНИЙ В ГРУНТЕ | 2004 |
|
RU2265823C1 |
| СПОСОБ ХРУСТАЛЁВА Е.Н. ОПРЕДЕЛЕНИЯ ДЕФОРМАЦИИ МАТЕРИАЛЬНОЙ СРЕДЫ ПОД ДАВЛЕНИЕМ | 2014 |
|
RU2569404C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕХАНИЧЕСКИХ ХАРАКТЕРИСТИК ГРУНТОВОГО, ТОРФЯНОГО И МЕРЗЛОГО ОСНОВАНИЙ | 2007 |
|
RU2345360C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРЕДЕЛЬНО МАКСИМАЛЬНОЙ КОНТАКТНОЙ ПРОЧНОСТИ ГРУНТОВОГО ОСНОВАНИЯ В УСЛОВИЯХ ПЛОСКОЙ ДЕФОРМАЦИИ | 2004 |
|
RU2265824C1 |
| СПОСОБ ХРУСТАЛЕВА Е.Н. ОПРЕДЕЛЕНИЯ СРЕДНЕГО ПРЕДЕЛЬНОГО ДАВЛЕНИЯ ДЛЯ СЖИМАЕМОЙ ШТАМПОМ МАТЕРИАЛЬНОЙ СРЕДЫ | 2015 |
|
RU2624592C2 |
| СПОСОБ ХРУСТАЛЁВА Е.Н. ОПРЕДЕЛЕНИЯ ДАВЛЕНИЯ ПОВЕРХНОСТНОГО И ВНУТРЕННЕГО ТРЕЩИНООБРАЗОВАНИЯ | 2015 |
|
RU2620127C2 |
| Способ определения средней твердости для неоднородных материалов | 2024 |
|
RU2836614C1 |
Изобретение относится к области физики материального контактного взаимодействия, конкретно к способу определения твердости и параметров прочности любой материальной среды через общефизические параметры: угол ϕ° внутреннего трения и удельное сцепление C (МПа).
По предлагаемому способу определяют для твердой беспористой среды угол ϕ°=arccos[(D/2-So)/(D/2)] и удельное сцепление C=(σт/2)(1+sinϕ°)/cosϕ° (МПа), а для пористой дисперсной материальной среды угол ϕ° и удельное сцепление C (МПа) определяют по закону Ш. Кулона-Мора τi=pitgϕ°+C, а твердость любой материальной среды определяют как 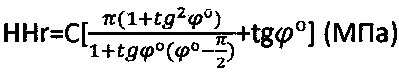 .
.
Технический результат – повышение точности определения твердости. 3 ил.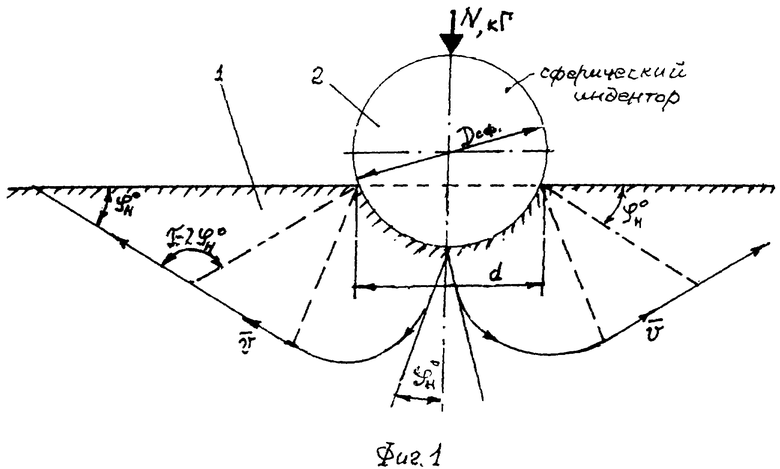
Способ определения твердости и параметров прочности материальной среды, заключающийся в том, что в твердую беспористую материальную среду с поверхности полупространства вертикально погружают жесткий индентор конической или сферической формы соответственно с углом  при вершине или диаметром D (см) усилием Ni(Н), возрастающим по мере погружения на глубину Si (см) до момента стабилизации усилия No=const(Н) на соответствующей глубине So (см), которые фиксируют динамометром и индикатором деформации, определяют твердость материальной среды: по Ю.И. Бринеллю - HB=No/(π⋅D⋅So)=2,77 σнт (МПа), где σнт - нижний предел текучести материальной среды; по «Виккерсу» -
при вершине или диаметром D (см) усилием Ni(Н), возрастающим по мере погружения на глубину Si (см) до момента стабилизации усилия No=const(Н) на соответствующей глубине So (см), которые фиксируют динамометром и индикатором деформации, определяют твердость материальной среды: по Ю.И. Бринеллю - HB=No/(π⋅D⋅So)=2,77 σнт (МПа), где σнт - нижний предел текучести материальной среды; по «Виккерсу» - 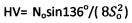 (МПа), где 136° - угол при вершине четырехгранной пирамиды индентора; по С.П. Роквеллу -
(МПа), где 136° - угол при вершине четырехгранной пирамиды индентора; по С.П. Роквеллу - 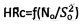 (МПа), где So - заданная глубина погружения конусного индентора с углом при вершине 120° (шкалы А, С) или шарикового индентора диаметром D (см) (шкала В), методами пенетрации твердой пористой материальной среды с поверхности полупространства шариковым индентором по зависимости σдл=No/(π⋅D⋅Sдл) (МПа), где σдл - длительное сопротивление среды пенетрации, и конусным наконечником с углом 30° при вершине по зависимости
(МПа), где So - заданная глубина погружения конусного индентора с углом при вершине 120° (шкалы А, С) или шарикового индентора диаметром D (см) (шкала В), методами пенетрации твердой пористой материальной среды с поверхности полупространства шариковым индентором по зависимости σдл=No/(π⋅D⋅Sдл) (МПа), где σдл - длительное сопротивление среды пенетрации, и конусным наконечником с углом 30° при вершине по зависимости 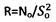 (МПа), где R - удельное сопротивление среды пенетрации, отличающийся тем, что для твердой материальной среды определяют ее прочностные параметры - угол ϕ° внутреннего трения и С (МПа) - удельное сцепление в ненарушенном структурированном состоянии по зависимостям ϕ°=arccos[(D/2-So)/(D/2)], C=(σт/2)⋅(1+sinϕ°)/cosϕ° (МПа), где σт (МПа) - предел текучести материальной среды, а твердость любой материальной среды определяют по зависимости
(МПа), где R - удельное сопротивление среды пенетрации, отличающийся тем, что для твердой материальной среды определяют ее прочностные параметры - угол ϕ° внутреннего трения и С (МПа) - удельное сцепление в ненарушенном структурированном состоянии по зависимостям ϕ°=arccos[(D/2-So)/(D/2)], C=(σт/2)⋅(1+sinϕ°)/cosϕ° (МПа), где σт (МПа) - предел текучести материальной среды, а твердость любой материальной среды определяют по зависимости  (МПа).
(МПа).
| ЭЛЕКТРИЧЕСКАЯ ДУГОВАЯ ЛАМПА ДЛЯ ПРОЖЕКТОРА | 1927 |
|
SU12248A1 |
| - М., 1997 | |||
| СПОСОБ ОПРЕДЕЛЕНИЯ ФИЗИКО-МЕХАНИЧЕСКИХ ХАРАКТЕРИСТИК СЛОЯ ПОЧВОГРУНТА, ПРЕИМУЩЕСТВЕННО ИМЕЮЩЕГО НИЗКУЮ И СРЕДНЮЮ ПЛОТНОСТЬ, И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1999 |
|
RU2192006C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НЕСУЩЕЙ СПОСОБНОСТИ ГРУНТОВОГО ОСНОВАНИЯ И ТОРФЯНОЙ ЗАЛЕЖИ | 2004 |
|
RU2270990C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СЦЕПЛЕНИЯ ГРУНТОВ ПРИ ОЦЕНКЕ ИХ ДЛИТЕЛЬНОЙ ПРОЧНОСТИ | 1991 |
|
RU2021598C1 |
Авторы
Даты
2017-04-05—Публикация
2016-01-26—Подача