Область техники, к которой относится изобретение
Настоящее изобретение относится к способу анализа набора полетных данных, зарегистрированных в течение по меньшей мере одного полета по меньшей мере одного воздушного судна.
Уровень техники
Нормативные требования к обслуживанию техники и движению воздушных судов определяют стандарты, обеспечение соответствия которым авиакомпаниями необходимо для обеспечения максимального уровня безопасности пользователей.
Для оптимизации процедур обслуживания техники авиакомпании устанавливают системы анализа полетных данных.
Известны системы анализа полетных данных, такие как FDM (Flight Data Monitoring, контроль полетных данных) или же FOQA (Flight Operational Quality Assurance, операционный контроль качества полета). При использовании таких систем воздушное судно оборудуют регистратором полетных данных. Такой регистратор может представлять собой «черный ящик» или специализированный регистратор, например, типа ACMS (Aircraft Condition Monitoring System, система контроля состояния воздушного судна).
Такие системы позволяют авиакомпании восстанавливать подробную картину полета по регулярно регистрируемым значениям полетных данных, получаемым в ходе каждого полета каждого из ее воздушных судов.
Для этого такие системы выявляют заранее определенные события, происходящие в течение полета, после чего специалист анализирует такие события, указывающие на возникновение в ходе полета технических неисправностей или на несоблюдение правил или условий, определенных правилами полета, тем самым обеспечивая раннее предупреждение о возможных происшествиях или авариях.
Применение таких технологий требует заблаговременного определения правил выявления событий, которые обычно определяют как превышение пороговых значений одного или более параметров, что может вызвать срабатывание предупреждения, наличие которого позволяет специалисту выделить данный полет для более подробного анализа.
Недостаток таких технологий состоит в отсутствии возможности выявления единичных событий, не подпадающих под заранее определенные правила, что может привести к пропуску детектирования полета с отклонениями от нормы.
Раскрытие изобретения
Задача, на решение которой направлено настоящее изобретение, состоит в обеспечении возможности выявления полетов с отклонениями от нормы без необходимости задания правил выявления.
Для решения поставленной задачи в соответствии с изобретением предлагается способ анализа полетных данных, зарегистрированных в течение N полетов по меньшей мере одного воздушного судна, причем данные группируют по полету i в сигнатурный вектор Xi полета размерности d, компоненты которого соответствуют данным, зарегистрированным в течение указанного полета i воздушного судна, так что полет i задан указанным сигнатурным вектором Xi, причем способ включает этапы, на которых:
- производят Гауссовский покомпонентный анализ энтропии ядра полетных сигнатур Xi для получения области нормальных полетов и классифицируют полетные сигнатуры Xi по их расстоянию до указанной области;
- определяют для каждого полета i уровень zi, отклонения от нормы, определенный расстоянием полетной сигнатуры Xi относительно области нормальных полетов;
- выявляют по меньшей мере один полет с отклонением от нормы в зависимости от уровня zi отклонения от нормы.
В оптимальном варианте осуществления изобретения предусмотрены следующие дополнительные признаки, которые могут быть использованы по отдельности или в любом возможном техническом сочетании:
- для каждого выявленного полета с отклонением от нормы определяют модельный полет, ближайший к выявленному полету с отклонением от нормы и расположенный в пределах области нормальных полетов;
- параметры выявленного полета с отклонением от нормы сравнивают с параметрами определенного таким образом модельного полета с целью выявления по меньшей мере одного параметра полета с отклонением от нормы, который вызвал отклонение от нормы указанного выявленного полета с отклонением от нормы;
- Гауссовский покомпонентный анализ энтропии включает этапы, на которых:
- определяют матрицу К сходства размерности N×N, компоненты которой выражают в численном виде близость между двумя полетными сигнатурами Xi;
- производят разложение матрицы К сходства на собственные векторы, получая N собственных векторов а1,…,aN и N собственных значений λ1,…,λN, таких, что ∀i=1,…,N K⋅ai=λi⋅ai;
- определяют для каждого собственного вектора соответствующий ему коэффициент энтропии Yi;
- отбирают такое подмножество собственных векторов 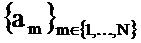
- коэффициент энтропии определяют по формуле
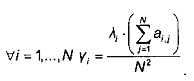
- уровень отклонения от нормы полета i определяют по формуле
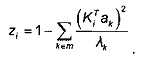
- компоненты матрицы К сходства определяют по формуле
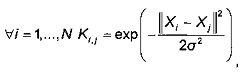
где σ2 - заранее определенный параметр сглаживания;
- параметр σ2 сглаживания определяют следующим образом:
- определяют матрицу D размерности N×N, соответствующую расстоянию между двумя полетами и заданную следующим образом: 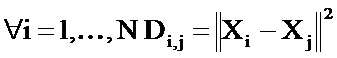
- все компоненты каждого столбца располагают в порядке возрастания, получая матрицу D’;
- отбирают первые k строк полученной таким образом матрицы D’, а оставшиеся строки удаляют, в результате чего получают матрицу D’ размерности k×N;
- определяют среднее каждого из столбцов матрицы D’, получая таким образом N значений y1,…,yN;
- определяют абсолютное медианное отклонение значений y1,...,yN, определенное как 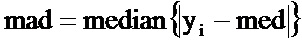
- определяют параметр σ2 сглаживания по абсолютному медианному отклонению значений y1,…,yN в соответствии с формулой 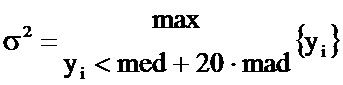
- данные полета i группируют в матрицу Fi размерности Т×Р, где Т - количество элементов данных, зарегистрированных в течение полета i, а Р - количество зарегистрированных параметров, причем компоненты вектора Xi представляют собой столбцы матрицы Fi один за другим, так что вектор Xi имеет размерность d=T×P и определен формулой
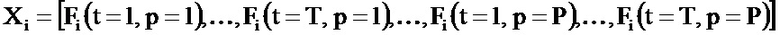
- данные полета i группируют в матрицу Fi размерности Т×Р, где T - количество элементов данных, зарегистрированных в течение полета i, а Р - количество зарегистрированных параметров, причем компоненты вектора Xi представляют собой столбцы матрицы Fi, из которых отобраны n<T записей 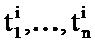
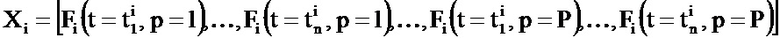
- данные полета i группируют в матрицу Fi размерности Т×Р, где T - количество элементов данных, зарегистрированных в течение полета i, а Р - количество зарегистрированных параметров, причем компоненты вектора Xi представляют собой среднее значение, дисперсию, минимальное значение и максимальное значение параметра по всем записям данного параметра, так что вектор Xi определен формулой
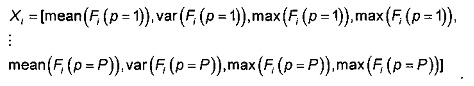
Решение по изобретению обладает многочисленными преимуществами.
Выявление полетов с отклонением от нормы в соответствии с изобретением может быть осуществлено автоматически, не требуя вмешательства специалиста для такого выявления.
В соответствии с изобретением осуществлено статистическое выявление с учетом параметров. Таким образом, происходит автоматическое обучение системы.
Изобретение обеспечивает возможность выявления неожиданных проблем.
Изобретение обеспечивает возможность выявления проблем, порожденных вкладами нескольких параметров.
Способ по изобретению может быть использован неспециалистом в области статистики или углубленного анализа данных.
Кроме того, настоящее изобретение позволяет упростить диагностику полетов с отклонением от нормы, так как обеспечивает возможность создания эталонного полета, модельного полета для каждого из выявленных полетов с отклонением от нормы.
Краткое описание чертежей
Другие особенности, задачи и преимущества настоящего изобретения станут ясны из нижеследующего описания, приведенного исключительно в иллюстративных целях и не накладывающего каких-либо ограничений, содержащего ссылки на прилагаемые чертежи. На чертежах:
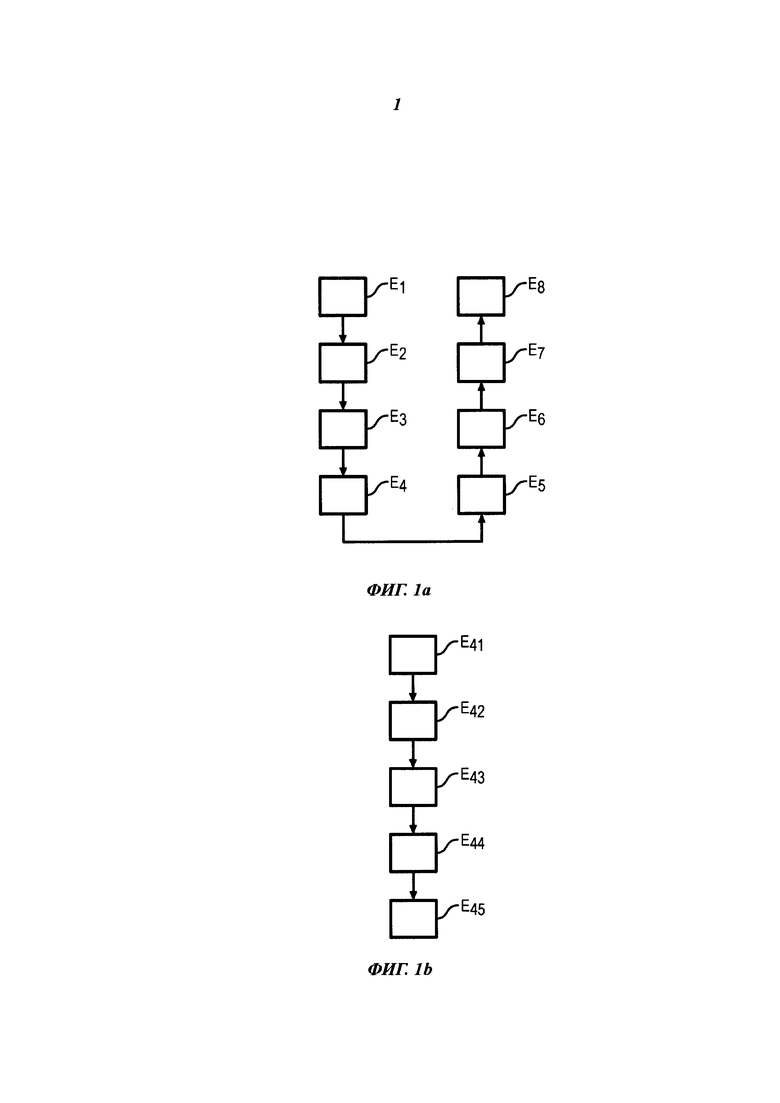
- фиг. 1а и 1b схематически иллюстрируют этапы способа по одному из вариантов осуществления изобретения;
- фиг. 2 иллюстрирует представление полетных данных по одному из вариантов осуществления изобретения.
Аналогичные элементы обозначены на всех чертежах одинаковыми ссылочными номерами.
Осуществление изобретения
На предварительном этапе (подробно не описан) способа анализа полетных данных получают полетные данные, зарегистрированные в течение нескольких полетов по меньшей мере одного воздушного судна.
Такие полетные данные соответствуют параметрам полета, например, таким как скорость, высота, температура и т.д.
Затем, на первом этапе Е1 для каждого полета i следует извлечь из всех данных, зарегистрированных в течение полета i, данные, характеризующие полет i, или сигнатуру каждого полета i.
Для N≥1 полетов существует некоторое количество Р0 параметров, зарегистрированных в течение времени Т0 полета. Например, в некоторых регистраторах это количество может составлять Р0=2000 параметров.
Подразумевается, что регистрация/выборка параметров производятся с одной и той же частотой; при необходимости к данным могут быть применены хорошо известные технологии передискретизации и линейной аппроксимации.
Для извлечения на этапе Е1 данных, характеризующих полет i, в соответствии с одним из вариантов осуществления выполняется ограничение до одной из стадий полета (например, стадии посадки) с ограничением по времени Т<Т0 и оставляется лишь ограниченное количество Р<Р0 релевантных параметров для анализа данных данного полета i. Например, могут быть установлены ограничения Т=1000 секунд и Р=30 параметров.
В нижеследующем описании значение каждого из элементов данных полета i обозначено следующим образом: Fi, (t=5, p=1), т.е. значение первого параметра, зарегистрированное на пятой секунде (если периодичность выборки измеряется в секундах) для полета i.
После извлечения на этапе Е1 данные группируются на этапе Е2 в сигнатурный вектор Xi полета i, имеющий размерность d.
Таким образом, каждый сигнатурный вектор Xi содержит набор релевантной информации, относящейся к полету i.
Группирование, производимое на этапе Е2, может быть осуществлено в соответствии с одним из трех вариантов.
В соответствии с первым вариантом группирование данных в вектор на этапе Е2 происходит с сохранением всех данных. Такой подход называют исчерпывающим.
В соответствии с данным вариантом осуществления для получения вектора Xi следует взять матрицу Fi и поставить ее столбцы один за другим.
Получаемый при этом вектор Xi имеет размерность d=Т×Р и определен следующим образом:
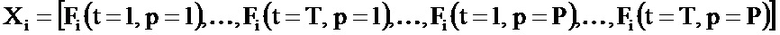
Например, при T=1000 и Р=30 получают вектор Xi размерности 30000 (а не матрицу размерности 1000×30).
Группирование в соответствии с описываемым первым вариантом осуществления может быть полезно, например, при отсутствии значительного количества подробной информации и позволяет легко выявить любые отклонения от маршрута полета.
В соответствии со вторым вариантом осуществления при группировании в вектор Xi на этапе Е2 происходит фокусирование на значениях параметров в конкретные моменты, так называемых моментальных снимков. Такие конкретные моменты соответствуют определенным рабочим операциям; например, на стадии посадки моментальные снимки могут быть произведены, начиная с высоты в 10000 футов через каждые 1000 футов снижения или же в моменты определенных событий - выпуска посадочного шасси и т.п.
Если определены n моментов моментальных снимков, то для полета i отбирают данные моментальных снимков 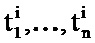
В таком случае вектор Xi имеет размерность d=n×Р и определен следующим образом:
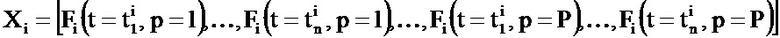
Второй вариант осуществления позволяет получить лучшие результаты, чем первый. Действительно, в описываемом втором варианте осуществления, поскольку T>>n, объем обрабатываемых данных значительно меньше, чем в первом варианте осуществления.
В соответствии с третьим вариантом осуществления группирование в вектор Xi на этапе Е2 состоит в «обобщении» каждой «кривой» каждого из параметров с использованием малого набора из k значений, где k ≈5 или 10: такие k значений могут, например, соответствовать среднему, дисперсии, максимальному значению, минимальному значению каждого из зарегистрированных параметров.
Такие k значений затем комбинируются для всех параметров с получением сигнатурного вектора Xi размерности d=k×Р при k≈4, определяемого по формуле
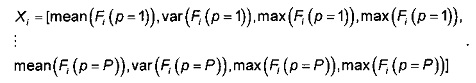
Например, если Р=30 параметров, сигнатурный вектор Xi имеет размерность d=120.
В конце этапа Е2 группирования как результат имеются N≥1 сигнатурных векторов Xi размерности d, компоненты которых соответствуют релевантным данным, зарегистрированным во время указанного полета/воздушного судна.
Дополнительно может быть предусмотрен необязательный этап Е3 нормализации каждого из компонентов каждого сигнатурного вектора Xi.
Такая нормализация может быть полезна, если компоненты каждого сигнатурного вектора Xi имеют величины разных порядков.
В результате нормализации на этапе Е3 в наборах данных для всех полетов предпочтительно получают компоненты с нулевым средним значением и стандартным отклонением, равным 1.
В нижеследующем описании символ Xi обозначает сигнатурный вектор полета i, компоненты которого могут быть или не быть нормализованы.
Для определения того, отклоняется ли полет от нормы, сигнатурные векторы Xi проходят несколько этапов обработки.
Для этого на этапе Е4 производят Гауссовский покомпонентный анализ энтропии ядра сигнатурных векторов Xi для определения области Е нормальных полетов и классифицируют сигнатурные векторы Xi по их расстоянию до указанной области.
Другими словами, все полетные сигнатуры Xi группируют так, чтобы демаркировать область Е нормальных полетов.
Анализ, производимый на этапе Е4, описан, например, в публикации R. Jenssen: "Kernel entropy component analysis", IEEE transactions on pattern analysis and machine intelligence, vol. 32, n°5, pages 847-860, May 2010.
Для осуществления такого анализа на этапе Е41 определяют матрицу К сходства размерности N×N, компоненты которой выражают в численном виде близость между двумя сигнатурными векторами Xi (т.е. между двумя полетами).
Матрица К известна под названием матрицы Грама.
Матрицу К получают из матрицы D расстояний, к которой применяют функцию Гаусса с заранее определенным параметром σ2 сглаживания (определение этого параметра описано ниже).
Матрица К определена следующим выражением:
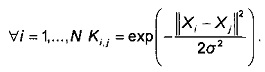
Параметр сглаживания получают путем вычисления расстояний между каждым из сигнатурных векторов Xi и его k ближайшими соседями, где k - целое число в диапазоне от 4 до 10. Значение k зависит от числа N полетов и размерности d. Для определения параметра σ2 сглаживания на этапе Е42 определяют матрицу D размерности N×N, соответствующую расстоянию между двумя полетами и определенную следующим образом: 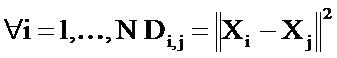
Затем элементы каждого из столбцов матрицы D располагают в порядке возрастания, получая матрицу D’, такую, что 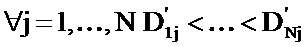
Затем отбирают первые k строк полученной таким образом матрицы D’, а оставшиеся строки удаляют, в результате чего получают матрицу D’ размерности k×N.
После этого определяют среднее каждого из столбцов матрицы D’, получая таким образом N значений y1,…,yN, которые по существу выражают среднее расстояние между каждым из векторов и его к ближайшими соседями.
Затем удаляют аберрантные значения y1,…,yN. Для этого сначала определяют медианное значение med набора y1,…,yN, которое выражают в виде med=median{y1,…,yN}. Затем определяют абсолютное медианное отклонение mad значений y1,…,yN, определенное как медианное значение набора 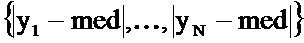
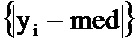
Тогда параметр σ2 сглаживания можно определить по абсолютному медианному отклонению значений y1,…,yN в соответствии с формулой 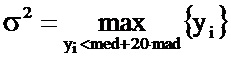
После получения матрицы К на этапе Е43 осуществляют разложение матрицы К сходства на собственные векторы, получая при этом N собственных векторов a1,…,aN и N собственных значений λ1,…,λN, таких, что ∀i=1,…,N K⋅aj=λi⋅ai.
Следует отметить, что каждый из собственных векторов ai имеет размерность N:ai∈ℜN, а символ ai,j обозначает j-й компонент вектора ai. Величины λi также называют коэффициентами энергии.
По полученным векторам и собственным значениям на этапе Е44 для каждого собственного вектора определяют его коэффициент энтропии Yi по следующей формуле
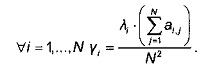
Коэффициенты энтропии представляют собой критерий релевантности, позволяющий отобрать из набора сигнатурных векторов всех полетов лишь наиболее релевантные данные.
А именно на этапе Е45 отбирают такое подмножество собственных векторов 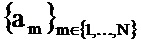
Такая доля предпочтительно составляет от 75 до 95% и предпочтительно равна 90%.
Отбор такого подмножества позволяет, возвращаясь к параметрам каждого из векторов Xi, соответствующих отобранным собственным векторам, определить область Е нормальных полетов.
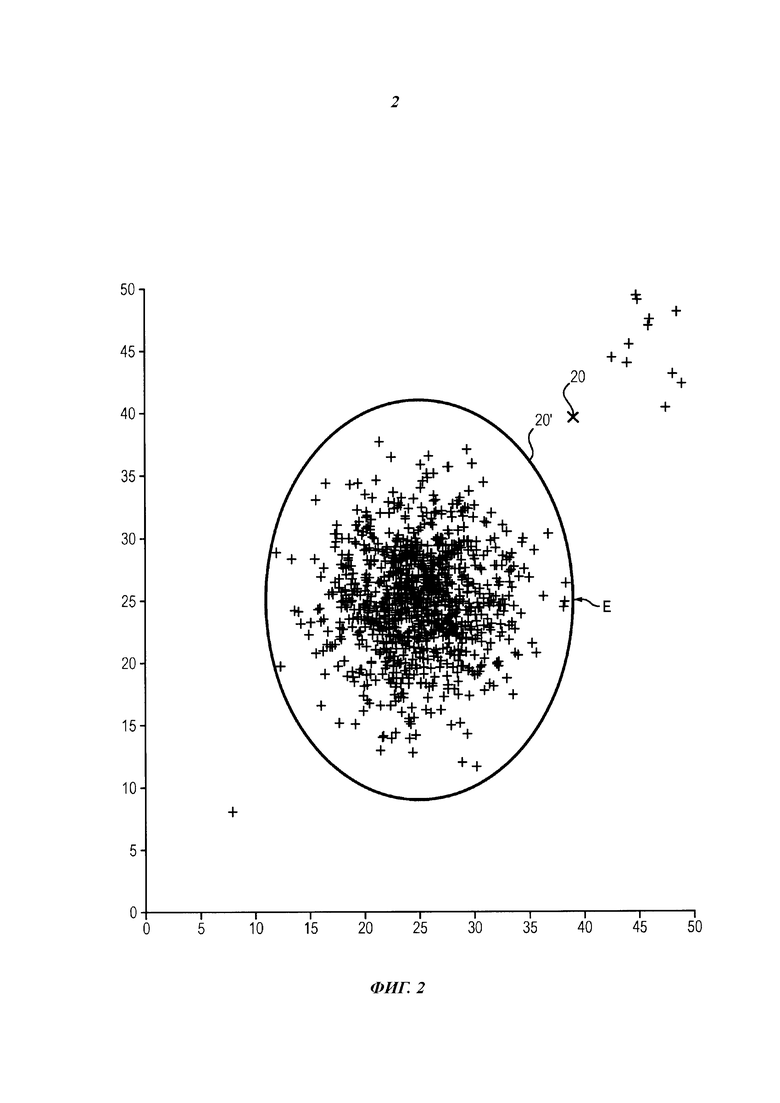
На фиг. 2 представлен простой пример, в котором использованы два параметра, что позволяет представить все полеты на двумерном графике и определить область Е нормальных полетов в виде окружности, окружающей кластер данных.
Затем на этапе Е5 для каждого полета i определяют уровень z, отклонения от нормы, определяемый расстоянием полета Xi относительно области Е нормальных полетов.
Уровень отклонения от нормы определяют по формуле 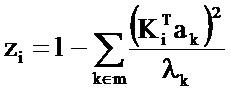
где ak - отобранные собственные векторы, а λk - соответствующие им собственные значения.
Уровень отклонения от нормы имеет значения в диапазоне от 0 до 1. Чем ближе его значение к 1, тем более отклоняющимся от нормы считают данный полет.
Представленные на фиг. 2 полеты, расположенные вдали от области Е нормальных полетов, имеют высокий уровень отклонения от нормы.
В соответствии с предпочтительным вариантом осуществления изобретения полеты i, уровень отклонения от нормы которых превышает 0,99, являются отклоняющимися от нормы с высокой вероятностью, а полеты i, уровень аномальности которых превышает 0,999, считают отклоняющимися от нормы практически наверняка.
Затем на этапе Е6 в зависимости от уровня zi отклонения от нормы определяют, является ли по меньшей мере один полет отклоняющимся от нормы.
Уровень отклонения от нормы может быть отображен для рассмотрения аналитиком.
Следует отметить, что для определения того, отклоняется ли полет от нормы, в соответствии с данным способом критерии, соответствие которым определяет нормальный полет, а несоответствие которым, соответственно, свидетельствует об отклонении от нормы, определяют с использованием имеющихся данных. Таким образом, необходимость в предварительном определении правил выявления отсутствует.
В случае выявления полета с отклонением от нормы для него на этапе Е7 определяют условный эталонный полет, называемый «модельным полетом», ближайший к данному полету с отклонением от нормы, но находящийся при этом в области нормальных полетов, причем модельный полет может быть отличным от сигнатурного полета.
Другими словами, модельный полет определяют как теоретический полет, расположенный в области нормальных полетов, ближайший к выявленному полету с отклонением от нормы.
В частности, определяют сигнатуру Z0 модельного полета.
Уровень z отклонения от нормы для модельного полета составляет менее 0,99 (или менее 0,95, если необходимо гарантированно обеспечить нормальность такого полета).
Таким образом, модельный полет представляет собой проекцию выявленного полета с отклонением от нормы на область нормальных полетов. В частности, он представляет собой ближайшую такую проекцию.
Модельный полет, сформированный в соответствии со способом по изобретению, потенциально не зависит от проанализированных полетов.
Модельный полет с сигнатурой Z0, соответствующий выявленному полету с отклонением от нормы с сигнатурой Xi, формируют при помощи процедуры нелинейной условной оптимизации. Такая процедура оптимизации для заданного постоянного порогового значения seuil может быть выражена следующей формулой:
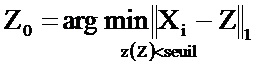
Следует отметить, что вышеописанная нормализация на единицу позволяет обеспечить минимизацию числа компонентов, различных в данном полете с отклонением от нормы и соответствующем ему модельном полете.
Процедура оптимизации требует вычисления величины уровня z(Z) для получения сигнатуры Z0 модельного полета.
Для этого для всех Z∈ℜd определяют следующий вектор kz:
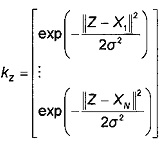
Тогда функция z, определяющая уровень любого вектора, принадлежащего ℜd, определена следующим образом:
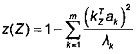
где a1,…,am - m ранее определенных собственных векторов (которые охватывают 90% суммарной энтропии), а λ1,…,λm - их соответствующие собственные значения.
Если полет, соответствующий параметрам, обозначенным на фиг. 2 как 20, отклоняется от нормы, то ему соответствует модельный полет, параметры которого обозначены как 20’.
Это позволяет сравнить на этапе Е8 параметры выявленного полета с отклонением от нормы с параметрами определенного таким образом модельного полета с целью выявления по меньшей мере одного параметра полета с отклонением от нормы, который вызвал отклонение от нормы указанного выявленного полета с отклонением от нормы.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ МНОГОПОЗИЦИОННОГО ОПРЕДЕЛЕНИЯ ПОЛОЖЕНИЯ УТЕЧЕК В ТРУБОПРОВОДЕ НА ОСНОВЕ УЛУЧШЕННОЙ ВМД | 2020 |
|
RU2750516C1 |
| СПОСОБ РАСПОЗНАВАНИЯ РАДИОСИГНАЛОВ | 2015 |
|
RU2613733C1 |
| СПОСОБ И СИСТЕМА МОНИТОРИНГА СОСТОЯНИЯ ВЕРТОЛЕТОВ | 2017 |
|
RU2741453C2 |
| СПОСОБ ФОРМИРОВАНИЯ КЛЮЧА ШИФРОВАНИЯ/ДЕШИФРОВАНИЯ | 2018 |
|
RU2695050C1 |
| СПОСОБ ФОРМИРОВАНИЯ КЛЮЧА ШИФРОВАНИЯ/ДЕШИФРОВАНИЯ | 2018 |
|
RU2684492C1 |
| Способ кластеризации электронных писем, являющихся спамом | 2021 |
|
RU2769633C1 |
| СПОСОБ АВТОНОМНОГО ОЦЕНИВАНИЯ ИЗМЕНЕНИЙ ОРБИТЫ ВИЗИРУЕМОГО КОСМИЧЕСКОГО АППАРАТА | 2015 |
|
RU2624408C2 |
| Малогабаритная адаптивная курсовертикаль | 2016 |
|
RU2714144C2 |
| АНАЛИЗ ЯМР-ДАННЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ НА ОСНОВЕ МАКСИМАЛЬНОЙ ЭНТРОПИИ | 2004 |
|
RU2334975C2 |
| СПОСОБ И СИСТЕМА КАЛИБРОВКИ КАМЕРЫ | 2012 |
|
RU2601421C2 |
Изобретение относится к способу анализа полетных данных. Для анализа полетных данных, зарегистрированных при помощи регистратора полетных данных воздушного судна, группируют данные определенным образом, производят Гауссовский покомпонентный анализ энтропии ядра полетных сигнатур для получения области нормальных полетов, классифицируют сигнатуры по расстоянию до указанной области, определяют уровень отклонения от нормы для каждого полета, выявляют полеты с отклонением от нормы в зависимости от уровня отклонения. Обеспечивается выявление полетов с отклонением от нормы без необходимости задания правил выявления. 10 з.п. ф-лы, 3 ил.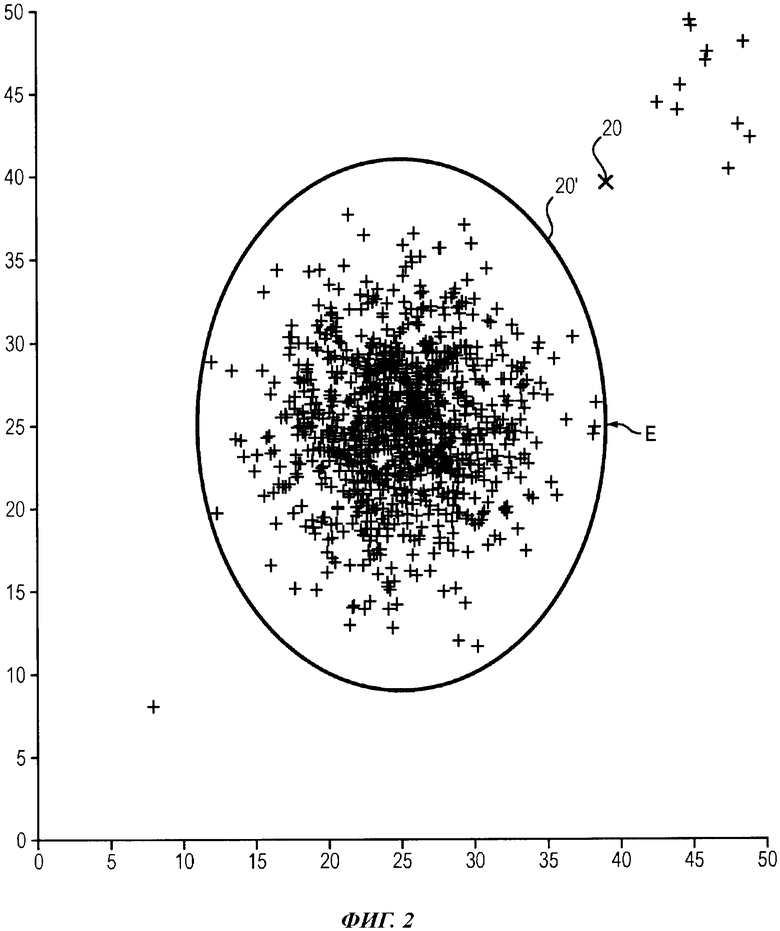
1. Способ анализа полетных данных, зарегистрированных в течение N полетов по меньшей мере одного воздушного судна при помощи регистратора полетных данных воздушного судна, в котором данные группируют (Е2) по полету i в сигнатурный вектор Xi полета размерности d, компоненты которого соответствуют данным, зарегистрированным в течение указанного полета i воздушного судна, так что полет i задан указанным сигнатурным вектором Хi, причем способ включает этапы, на которых:
- производят (Е4) Гауссовский покомпонентный анализ энтропии ядра полетных сигнатур Xi для получения области (Е) нормальных полетов и классифицируют полетные сигнатуры Xi по их расстоянию до указанной области;
- определяют (Е5) для каждого полета i уровень zi отклонения от нормы, определенный расстоянием полетной сигнатуры Xi относительно области (Е) нормальных полетов;
- выявляют (Е6) по меньшей мере один полет с отклонением от нормы в зависимости от уровня zi отклонения от нормы.
2. Способ по п. 1, отличающийся тем, что для каждого выявленного полета с отклонением от нормы определяют модельный полет, ближайший к выявленному полету с отклонением от нормы и расположенный в пределах области нормальных полетов.
3. Способ по п. 2, отличающийся тем, что параметры выявленного полета с отклонением от нормы сравнивают с параметрами определенного таким образом модельного полета с целью выявления по меньшей мере одного параметра полета с отклонением от нормы, который вызвал отклонение от нормы указанного выявленного полета с отклонением от нормы.
4. Способ по п. 1, отличающийся тем, что Гауссовский покомпонентный анализ энтропии включает в себя этапы, на которых:
- определяют матрицу K сходства размерности N×N, компоненты которой выражают в численном виде близость между двумя полетными сигнатурами Xi;
- производят разложение матрицы K сходства на собственные векторы, получая N собственных векторов a1,…,aN и N собственных значений λ1,…,λN, таких, что ∀i=1,…,N K⋅аi=λi⋅аi;
- определяют для каждого собственного вектора соответствующий ему коэффициент энтропии yi;
- отбирают такое подмножество собственных векторов 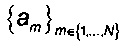 , в котором сумма значений энтропии ym больше, чем доля суммы N значений энтропии yi.
, в котором сумма значений энтропии ym больше, чем доля суммы N значений энтропии yi.
5. Способ по п. 4, отличающийся тем, что коэффициент энтропии определяют по формуле
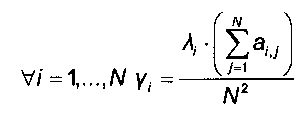 .
.
6. Способ по п. 4, отличающийся тем, что уровень отклонения от нормы полета i определяют по формуле
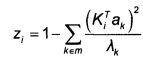 .
.
7. Способ по п. 4, отличающийся тем, что компоненты матрицы K сходства определяют по формуле
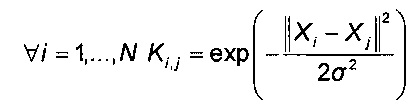 ,
,
где σ2 - заранее определенный параметр сглаживания.
8. Способ по п. 7, отличающийся тем, что параметр σ2 сглаживания определяют следующим образом:
- определяют матрицу D размерности N×N, соответствующую расстоянию между двумя полетами и заданную следующим образом: 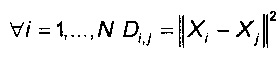 ;
;
- все компоненты каждого столбца располагают в порядке возрастания, получая матрицу D';
- отбирают первые k строк полученной таким образом матрицы D', а оставшиеся строки удаляют, в результате чего получают матрицу D' размерности k×N;
- определяют среднее каждого из столбцов матрицы D', получая таким образом N значений y1,…,yN;
- определяют абсолютное медианное отклонение значений y1,…,yN, определенное как mad = median{|yi-med|}, где med = median{y1,…,yN};
- определяют параметр σ2 сглаживания по абсолютному медианному отклонению значений y1,…,yN в соответствии с формулой 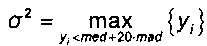 .
.
9. Способ по п. 4, отличающийся тем, что данные полета i группируют в матрицу Fi размерности T×P, где Т - количество элементов данных, зарегистрированных в течение полета i, а P - количество зарегистрированных параметров, причем компоненты вектора Xi представляют собой столбцы матрицы Fi один за другим, так что вектор Xi имеет размерность d=T×P и определен формулой
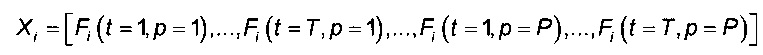 .
.
10. Способ по п. 1, отличающийся тем, что данные полета i группируют в матрицу Fi размерности T×P, где Т - количество элементов данных, зарегистрированных в течение полета i, а P - количество зарегистрированных параметров, причем компоненты вектора Xi представляют собой столбцы матрицы Fi, из которых отобраны n<Т записей 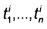 параметров, так что вектор Xi имеет размерность d=n×P и определен формулой
параметров, так что вектор Xi имеет размерность d=n×P и определен формулой
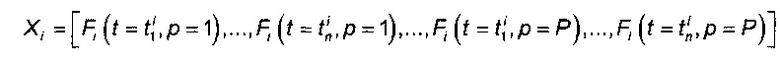 .
.
11. Способ по п. 1, отличающийся тем, что данные полета i группируют в матрицу Fi размерности T×P, где T - количество элементов данных, зарегистрированных в течение полета i, а P - количество зарегистрированных параметров, причем компоненты вектора Xi представляют собой среднее значение, дисперсию, минимальное значение и максимальное значение параметра по всем записям данного параметра, так что вектор Xi определен формулой
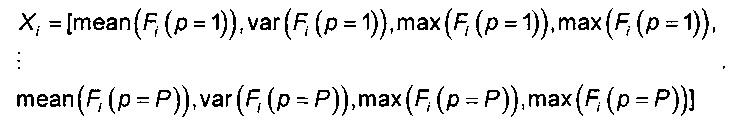
| US 20080091630 A1, 17.04.2008 | |||
| КЛАПАН ЗАПОРНО-РЕГУЛИРУЮЩИЙ | 2007 |
|
RU2354876C1 |
| US 6937924 B1, 30.08.2005 | |||
| US 20030225492 A1, 04.12.2003 | |||
| Реостатный микрофон | 1929 |
|
SU21238A1 |
Авторы
Даты
2017-05-03—Публикация
2013-02-26—Подача