Изобретение относится к области радиолокационной техники, а именно к способам определения угловых координат измерений произвольного количества точечных близко расположенных целей, в частности определения угловых координат:
- низколетящей цели (НЛЦ) над подстилающей морской (земной) поверхностью,
- групповой (множественной) цели, такой как самолет-носитель и авиабомба, возможно на фоне ложных целей,
- цели в условиях применения противником активных помех.
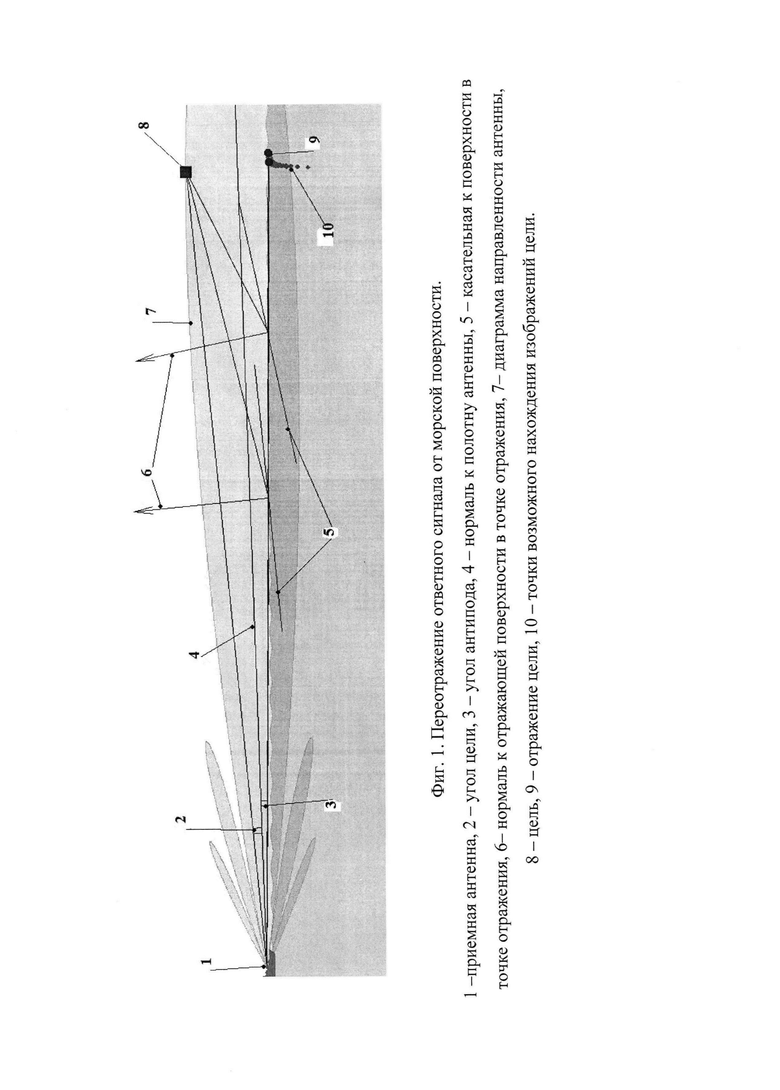
Принято считать, что существуют четыре пути, по которым отраженная от цели и от подстилающей поверхности электромагнитная волна (ЭМВ) возвращается к приемнику (фиг. 1):
- непосредственно отраженный от цели истинный сигнал «излучатель - цель - приемник»;
- истинный сигнал «излучатель - поверхность - цель - приемник»;
- ложный сигнал «излучатель - цель - поверхность - приемник», типа одиночного зеркального отражения;
- ложный сигнал «излучатель - цель - поверхность - приемник», описывающий диффузное рассеяние отраженного от цели сигнала.
Аналогом алгоритмического способа определения углового измерения двух близко расположенных целей является метод Уайта. Этот метод предполагает формирование трех суммарных диаграмм направленности, одна из которых центрируется строго на среднюю точку между целями, а две оставшиеся разносятся относительно первой на некоторые равные углы в положительном и отрицательном направлениях.
При таком формировании диаграмм сигнал первой (центральной) диаграммы оказывается синфазным с суммарным сигналом двух других диаграмм, а их отношение зависит исключительно от разности углов целей, что позволяет определить углы целей путем решения некоторого нелинейного уравнения. На практике направление на среднюю точку никогда не бывает известно точно, что приводит к систематической ошибке, зависящей от взаимного расположения оси центральной диаграммы и направления на среднюю точку.
В ряде работ рассматриваются различные специальные случаи, подобно методу Уайта, позволяющие решить задачу в том или ином частном случае, при выполнении тех или иных предположений, делающихся относительно принимаемых сигналов и их функциональной и/или статистической взаимосвязи.
Наиболее близким аналогом является способ определения угломестной координаты низколетящей цели (НЛЦ), содержащий прием суммарного сигнала, отраженного от цели и подстилающей поверхности, на выходах четырех идентичных антенн, формирование дискриминационных характеристик (ДХ) измерителя координат Sx и Sy, представляющих собой разности сигналов на выходах пар антенн, располагающихся в горизонтальной и вертикальной плоскостях, соответственно отнесенные к суммарному сигналу, и позиционирование максимума главного лепестка суммарной диаграммы направленности (ДН) антенной системы измерителя координат в направлении точки проекции цели на подстилающую поверхность (RU 2444750 C2, 10.03.2012). Известный способ не позволяет точно определить угловые координаты даже двух близко расположенных целей. Алгоритм, основанный на известном способе, достаточно чувствителен к расхождениям с реальной ситуацией и может давать значительные статистические ошибки даже в двухлучевой модели распространения электромагнитных волн.
Задача состоит в разработке способа, позволяющего разрешать произвольное количество близко расположенных целей, а по сложности сопоставимого с обычным фазовым разностно-суммарным методом. Традиционным способом - формированием моноимпульсного отношения (то есть отношения измерений разностной и суммарной диаграмм) - этого добиться невозможно.
Технический результат состоит в повышении точности определения (измерения) угловых координат произвольного числа N близко расположенных целей, возможно в условиях воздействия активных помех.
Предлагаемый способ измерений угловых координат группы N близко расположенных целей, возможно в условиях воздействия активных помех, заключается в том, что отраженные от целей истинные и ложные сигналы принимаются посредством цифровой линейной эквидистантной фазированной антенной решетки, представляющей собой матрицу, состоящую из 2N×2N лучей, всего 4N2 лучей, и представляющую собой эквидистантную линейку диаграмм направленности, с одинаковыми суммарными диаграммами направленности и фазовыми центрами, расположенными на одинаковом расстоянии друг от друга, из полученных суммарных сигналов формируют вектор 2N сигналов строковых диаграмм 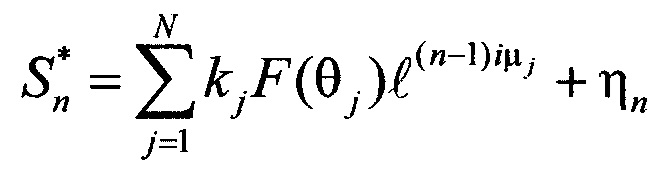 и вектор 2N сигналов столбцевых диаграмм, n=1, …, 2N,
и вектор 2N сигналов столбцевых диаграмм, n=1, …, 2N, 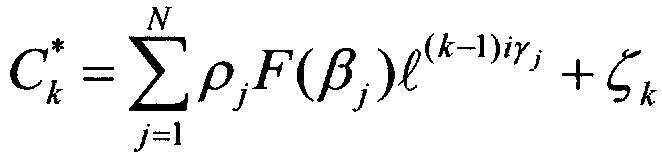 , k=1, …, 2N, где
, k=1, …, 2N, где 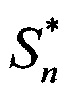 и
и 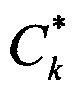 - векторы сигналов строковой диаграммы с номером n и столбцевой диаграммы с номером k, θj - угол места цели и βj - азимут цели с номером j относительно нормали к антенне,ηn и ζk - помехи - внутренние шумы строковой диаграммы с номером n и столбцевой диаграммы с номером k, описывающиеся комплексным «белым» шумом с нулевым средним и известной дисперсией:
- векторы сигналов строковой диаграммы с номером n и столбцевой диаграммы с номером k, θj - угол места цели и βj - азимут цели с номером j относительно нормали к антенне,ηn и ζk - помехи - внутренние шумы строковой диаграммы с номером n и столбцевой диаграммы с номером k, описывающиеся комплексным «белым» шумом с нулевым средним и известной дисперсией:
Mηn=0, 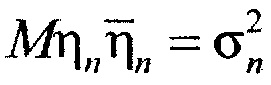 ,
, 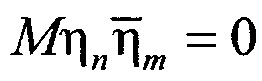 , m≠n,
, m≠n,
Мζn=0, 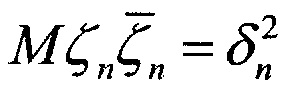 ,
, 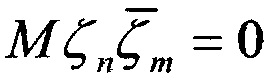 , m≠n,
, m≠n,
a F(θ) - функция амплитудно-фазового распределения суммарной диаграммы направленности, общая для всех строковых и столбцевых диаграмм, kj и ρj - комплексные коэффициенты отражения целей в вертикальной и горизонтальной плоскостях, μj и γj - обобщенные углы цели с номером j в горизонтальной и вертикальной плоскостях: 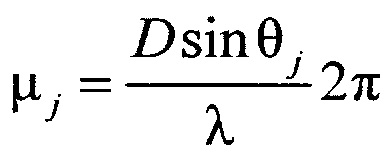 ,
, 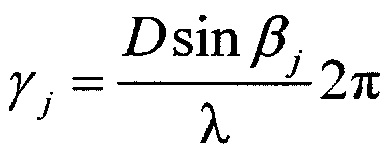 , D - расстояние между фазовыми центрами приемных диаграмм, λ - длина волны, через
, D - расстояние между фазовыми центрами приемных диаграмм, λ - длина волны, через 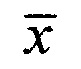 обозначено комплексно сопряженное число с числом x; далее осуществляют цифровую обработку вектора сигналов
обозначено комплексно сопряженное число с числом x; далее осуществляют цифровую обработку вектора сигналов 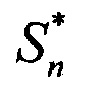 и
и 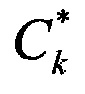 для формирования вектора измерений целей по углу места и курсовому углу, по которым определяют обобщенные углы целей, корреляционную матрицу ошибок измерений и корреляционную матрицу векторного шума и, используя матрицу Вандермонда, определяют угловые координаты близкорасположенных целей.
для формирования вектора измерений целей по углу места и курсовому углу, по которым определяют обобщенные углы целей, корреляционную матрицу ошибок измерений и корреляционную матрицу векторного шума и, используя матрицу Вандермонда, определяют угловые координаты близкорасположенных целей.
На фиг. 1 показаны ответные переотраженные от морской поверхности сигналы. Здесь 1 - приемная антенна, 2 - угол цели, 3 - угол антипода, 4 - нормаль к полотну антенны, 5 - касательная к поверхности в точке отражения, 6 - нормаль к отражающей поверхности в точке отражения, 7 - диаграмма направленности антенны, 8 - цель, 9 - отражение цели, 10 - точки возможного нахождения изображений цели.
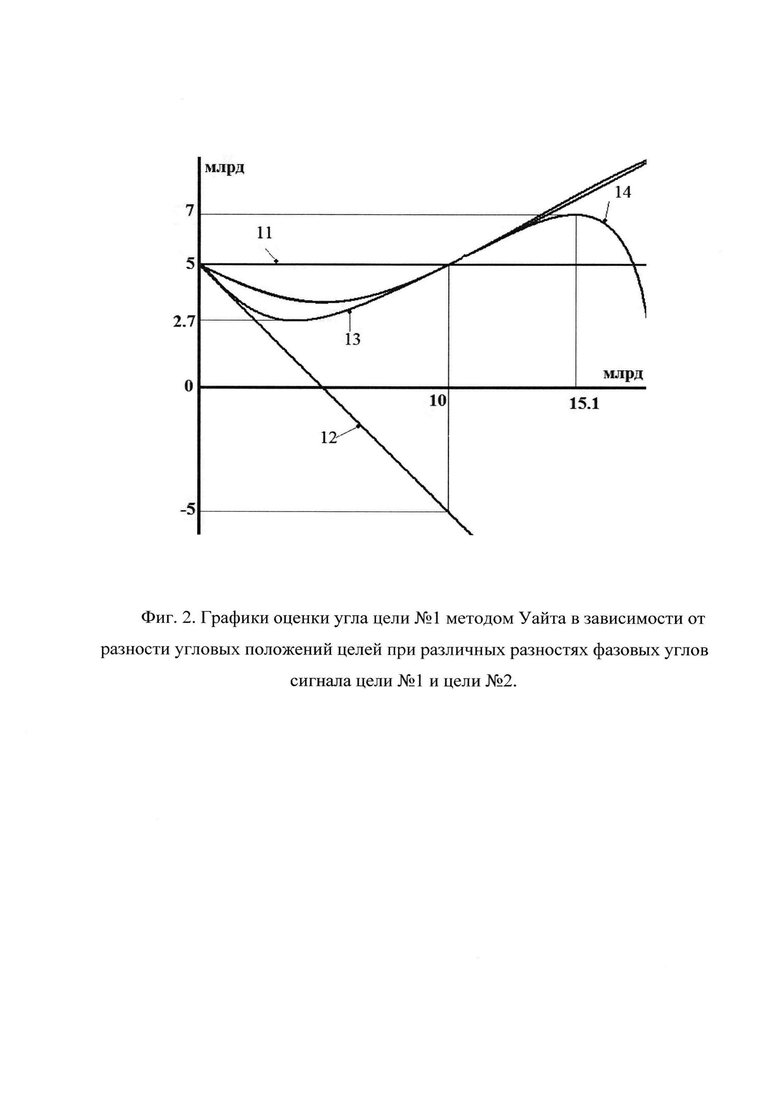
На фиг. 2 изображены графики измерений углов двух близко расположенных целей методом Уайта в идеальных условиях, когда внутренние шумы антенны равны нулю: 11 - истинный угол цели №1; 12 - истинный угол цели №2; 13, 14 - оценка угла цели №1 при разности углов сигналов 0° и 90°.
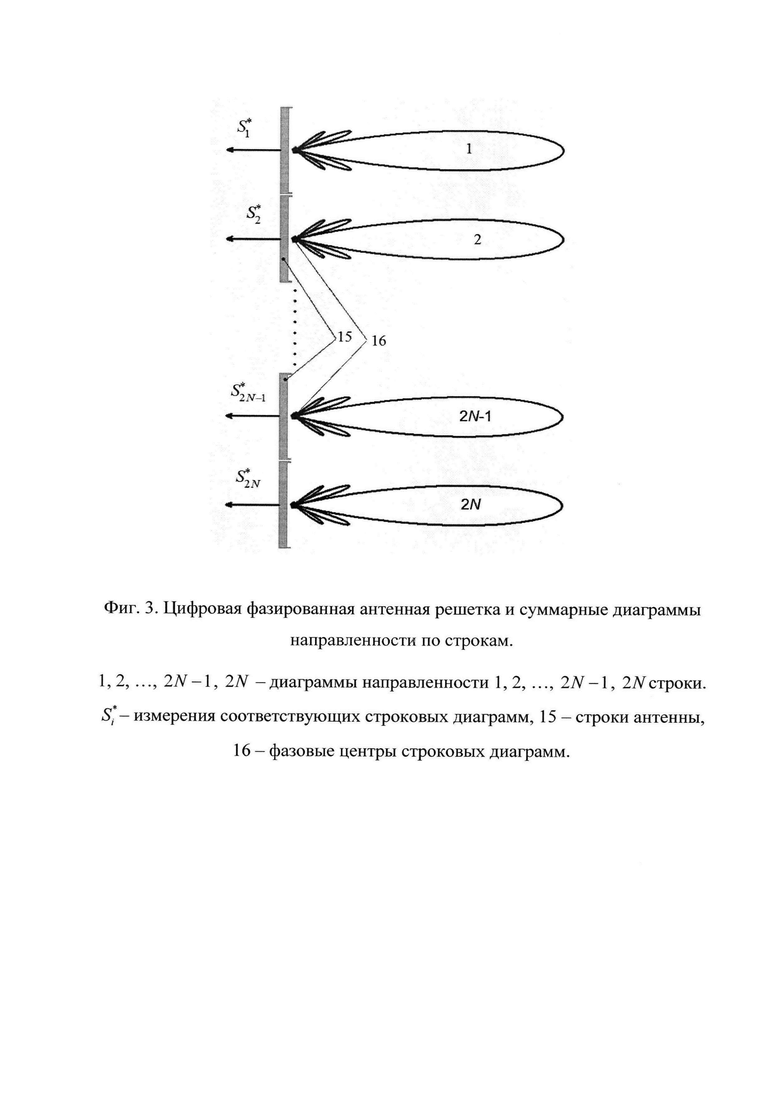
На фиг. 3 показана заявленная цифровая фазированная антенная решетка (ЦФАР) и суммарные диаграммы направленности по строкам. 0, 1, 2, …, 2N-1, 2N - диаграммы направленности 1, 2, …, 2N-1, 2N строки. 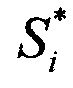 - измерения соответствующих строковых диаграмм, 15 - строки антенны, 16 - фазовые центры строковых диаграмм.
- измерения соответствующих строковых диаграмм, 15 - строки антенны, 16 - фазовые центры строковых диаграмм.
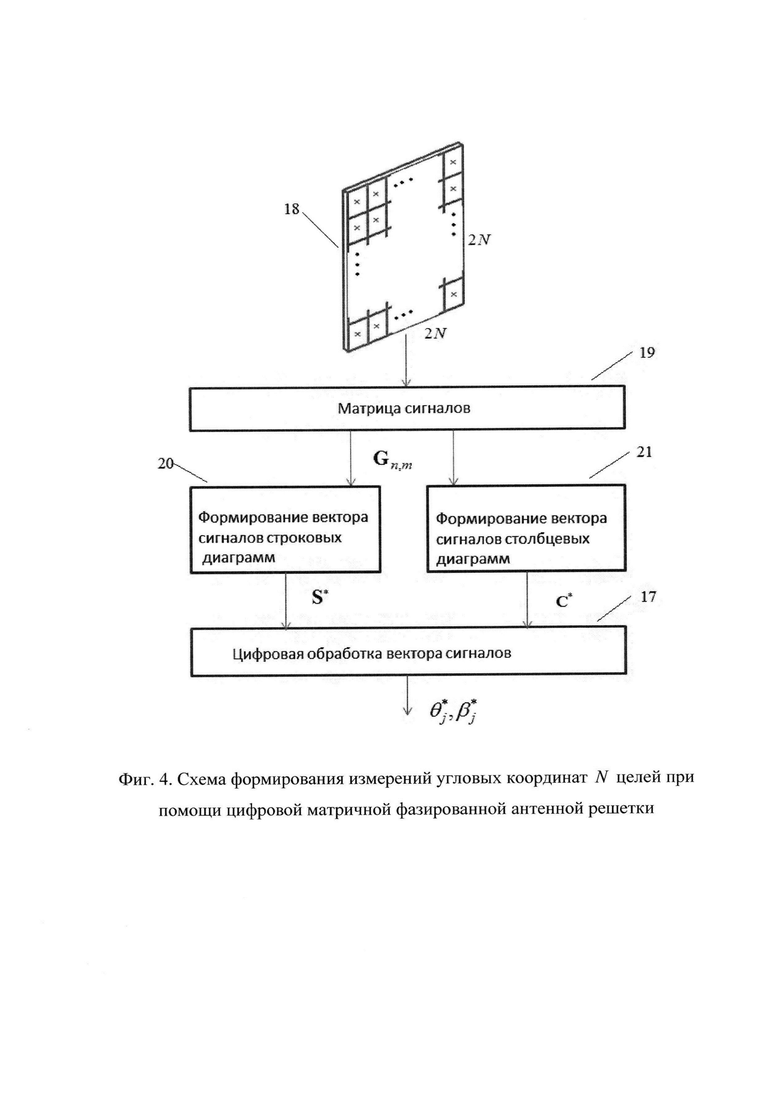
На фиг. 4 показана схема формирования измерений угловых координат N целей при помощи заявленной цифровой матричной фазированной антенной решетки, на которой показаны блок 17 цифровой обработки сигналов, антенна 18 с N строковыми диаграммами, матрица 19 сигналов, формирователь 20 вектора сигналов строковых диаграмм, формирователь 21 вектора сигналов столбцевых диаграмм.
Учитывая сложную природу переотражений, предполагается, что принимаемый сигнал будет распределен в области своего возможного нахождения, изображенной на фиг. 1 точками, отмеченными символом 10, имея при этом какие-то, заранее неизвестные точки концентрации. В частности, при идеально гладкой морской поверхности ложный сигнал, сформированный переотражениями, будет сконцентрирован в единственной точке-антиподе - зеркальном отражении цели относительно поверхности воды. Заранее определить с какой фазой и амплитудой ложные сигналы вернутся к приемной антенне 18, не представляется возможным. Кроме того, заранее не известно количество точек концентрации отраженного от подстилающей поверхности сигнала (количество антиподов). Поэтому способ определения угловой координаты НЛЦ должен предполагать наличие нескольких антиподов и обеспечивать при этом эффективную работу.
В настоящем изобретении предлагается способ определения угловых координат произвольного, но заранее известного числа неразрешенных точечных целей (фиг. 1) для произвольных величин принимаемых от них комплексных сигналов (то есть без каких бы то ни было дополнительных предположений о функциональной зависимости принимаемых от целей сигналов). Для решения задачи разрешения N целей предлагается способ измерений и алгоритмический метод обработки этих измерений.
Для определенности считается, что разрешение производится по вертикальному углу (углу места). Тогда для реализации предлагаемого способа необходимо сформировать 2N одинаковых суммарных строковых «поддиаграмм», находящихся в вертикальной плоскости на одинаковом расстоянии друг от друга, как это проиллюстрировано на фиг. 3. Тогда углы целей найдутся посредством решения уравнения степени N.
Для разрешения 2-х целей необходимо сформировать 4 строковые диаграммы, 3-х целей - 6 диаграмм, и, соответственно, решать квадратное и кубическое уравнения. Для этого при измерении угловых координат группы близко расположенных целей, в условиях воздействия активных помех, отраженные от целей истинные и ложные сигналы принимаются посредством антенны 18 в виде цифровой линейной эквидистантной фазированной антенной решетки, включающей матрицу 19, состоящую из 2N×2N лучей, всего 4N2 лучей, и представляющую собой эквидистантную линейку диаграмм направленности 15, с одинаковыми суммарными диаграммами направленности и фазовыми центрами 16, расположенными на одинаковом расстоянии друг от друга. Из полученных суммарных сигналов формируют вектор 2N сигналов строковых диаграмм 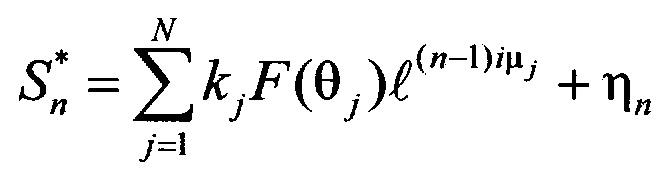 и вектор 2N сигналов столбцевых диаграмм, n=1, …, 2N,
и вектор 2N сигналов столбцевых диаграмм, n=1, …, 2N, 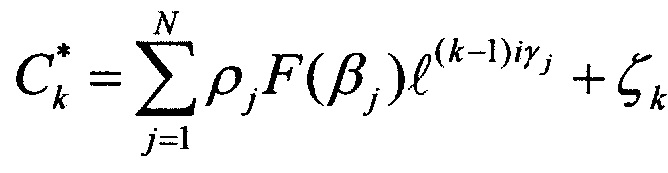 , k=1, …, 2N, где
, k=1, …, 2N, где 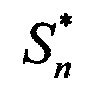 и
и 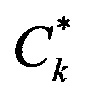 - векторы сигналов строковой диаграммы с номером n и столбцевой диаграммы с номером k, θj - угол места цели и βj - азимут цели с номером j относительно нормали к антенне, ηn и ζk - помехи - внутренние шумы строковой диаграммы с номером n и столбцевой диаграммы с номером k, описывающиеся комплексным «белым» шумом с нулевым средним и известной дисперсией:
- векторы сигналов строковой диаграммы с номером n и столбцевой диаграммы с номером k, θj - угол места цели и βj - азимут цели с номером j относительно нормали к антенне, ηn и ζk - помехи - внутренние шумы строковой диаграммы с номером n и столбцевой диаграммы с номером k, описывающиеся комплексным «белым» шумом с нулевым средним и известной дисперсией:
Mηn=0, 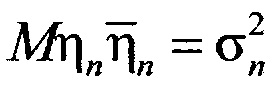 ,
, 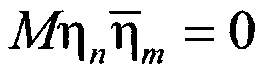 , m≠n,
, m≠n,
Мζn=0, 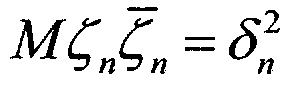 ,
, 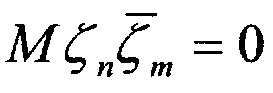 , m≠n,
, m≠n,
а F(θ) - функция амплитудно-фазового распределения суммарной диаграммы направленности, общая для всех строковых и столбцевых диаграмм, kj и ρj - комплексные коэффициенты отражения целей в вертикальной и горизонтальной плоскостях, μj и γj - обобщенные углы цели с номером j в горизонтальной и вертикальной плоскостях: 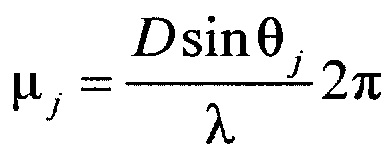 ,
, 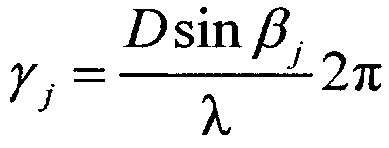 , D - расстояние между фазовыми центрами приемных диаграмм, λ - длина волны, через
, D - расстояние между фазовыми центрами приемных диаграмм, λ - длина волны, через 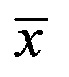 обозначено комплексно сопряженное число с числом х.
обозначено комплексно сопряженное число с числом х.
Для цифровой фазированной антенной решетки формирование таких строковых диаграмм не является принципиальной проблемой. Единственное требование заключается в том, чтобы количество общих строк элементарных излучателей в антенне 18 было бы кратно 2N.
Для формирования угловых измерений N целей используется цифровая матричная фазированная антенная решетка 18, состоящая из матрицы эквидистантных антенных подрешеток, состоящей из 2N строк и 2N столбцов. Фазовые центры 16 подрешеток отстоят друг от друга на расстоянии D по горизонтали и вертикали и имеют одинаковые суммарные диаграммы направленности. Выходной информацией, поступающей с ЦФАР, является матрица 19 комплексных сигналов измерений (квадратур) подрешеток Gn.m, n,m=1, …, 2N.
На основании выходной информации в формирователе 20 формируется вектор 2N сигналов строковых диаграмм путем суммирования комплексных величин сигналов по каждой строке:
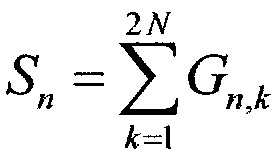 ,
,
а в формирователе 21 - вектор 2N сигналов столбцовых диаграмм, путем суммирования комплексных сигналов по каждому столбцу:
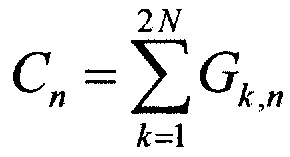 .
.
Далее каждый из этих векторов подается в виде входной информации на блок 17 цифровой обработки вектора сигнала для формирования вектора измерений углов целей.
Опишем работу этого блока 17 для формирования вектора измерений по углу места. По курсовому углу обработка производится аналогичным способом.
1. Вычисляется вектор коэффициентов 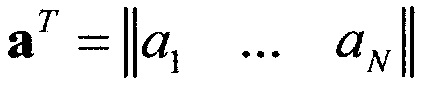 :
:
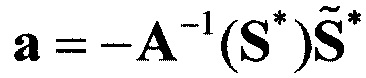 ,
,
где 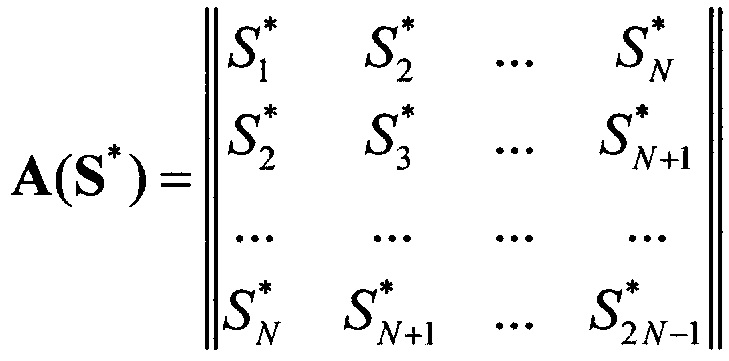 , а
, а 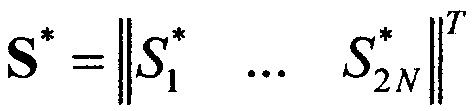 - вектор измерений строковых диаграмм.
- вектор измерений строковых диаграмм.
2. Находятся корни полинома z1, …, zN, которые являются комплексными углами целей:
P(z)=zN+aNzN- 1 +…+a 2 z+a 1 =0.
3. Находятся обобщенные углы целей 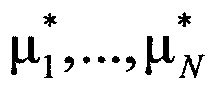 :
:
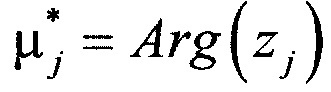 .
.
4. Находятся измерения углов целей 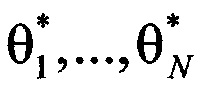 :
:
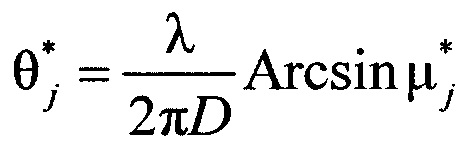 , j=1, …, N.
, j=1, …, N.
5. Находится корреляционная матрица 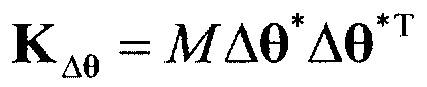 ошибок измерения вектора углов целей:
ошибок измерения вектора углов целей:
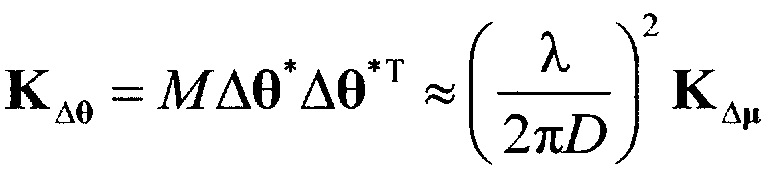 .
.
K Δμ - корреляционная матрица ошибок измерения обобщенных углов:
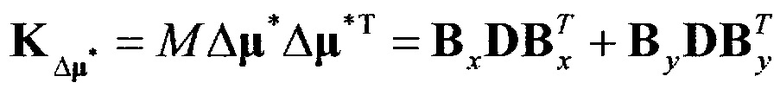 ,
,
где Вх и By, - действительная и мнимая части матрицы В
В=Вх+iBy, a D - корреляционная матрица векторного шума η:
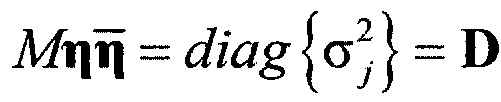 .
.
Элементы матрицы В выражаются через элементы матрицы Q следующим образом:
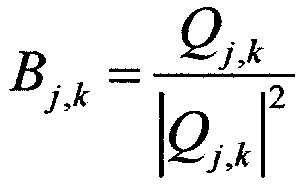 , где
, где 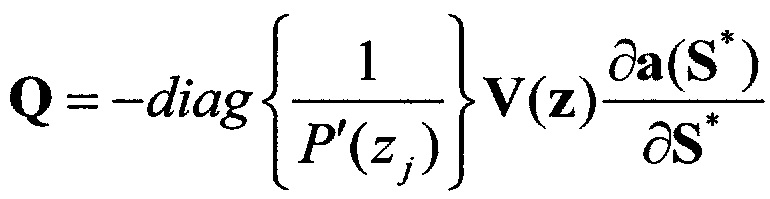 ,
,
V(z) - матрица Вандермонда: 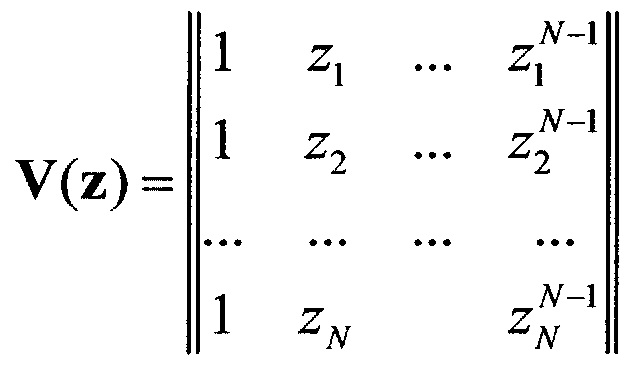 .
.
Таким образом осуществляют цифровую обработку вектора сигналов 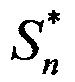 и
и 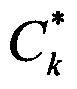 для формирования вектора измерений целей по углу места и курсовому углу, по которым определяют обобщенные углы целей, корреляционную матрицу ошибок измерений и корреляционную матрицу векторного шума и, используя матрицу Вандермонда, с высокой точностью определяют угловые координаты близко расположенных целей.
для формирования вектора измерений целей по углу места и курсовому углу, по которым определяют обобщенные углы целей, корреляционную матрицу ошибок измерений и корреляционную матрицу векторного шума и, используя матрицу Вандермонда, с высокой точностью определяют угловые координаты близко расположенных целей.
Изобретение относится к области радиолокационной техники, а именно к способам определения угловых координат измерений произвольного количества точечных близко расположенных целей. Достигаемый технический результат - повышение точности определения (измерения) угловых координат произвольного числа N близкорасположенных целей, возможно в условиях активных помех. Указанный результат достигается за счет того, что в способе измерений угловых координат группы N близкорасположенных целей в условиях воздействия активных помех, отраженные от целей истинные и ложные сигналы принимаются посредством цифровой линейной эквидистантной фазированной антенной решетки, представляющей собой матрицу, состоящую из 2N×2N лучей, всего 4N2 лучей, и представляющую собой эквидистантную линейку диаграмм направленности, с одинаковыми суммарными диаграммами направленности и фазовыми центрами, расположенными на одинаковом расстоянии друг от друга, из полученных суммарных сигналов формируют вектор 2N сигналов строковых диаграмм и вектор 2N сигналов столбцевых диаграмм, далее осуществляют цифровую обработку вектора сигналов 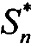 и
и 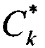 для формирования вектора измерений целей по углу места и курсовому углу, по которым определяют обобщенные углы целей, корреляционную матрицу ошибок измерений и корреляционную матрицу векторного шума и, используя матрицу Вандермонда, определяют угловые координаты близкорасположенных целей. 4 ил.
для формирования вектора измерений целей по углу места и курсовому углу, по которым определяют обобщенные углы целей, корреляционную матрицу ошибок измерений и корреляционную матрицу векторного шума и, используя матрицу Вандермонда, определяют угловые координаты близкорасположенных целей. 4 ил.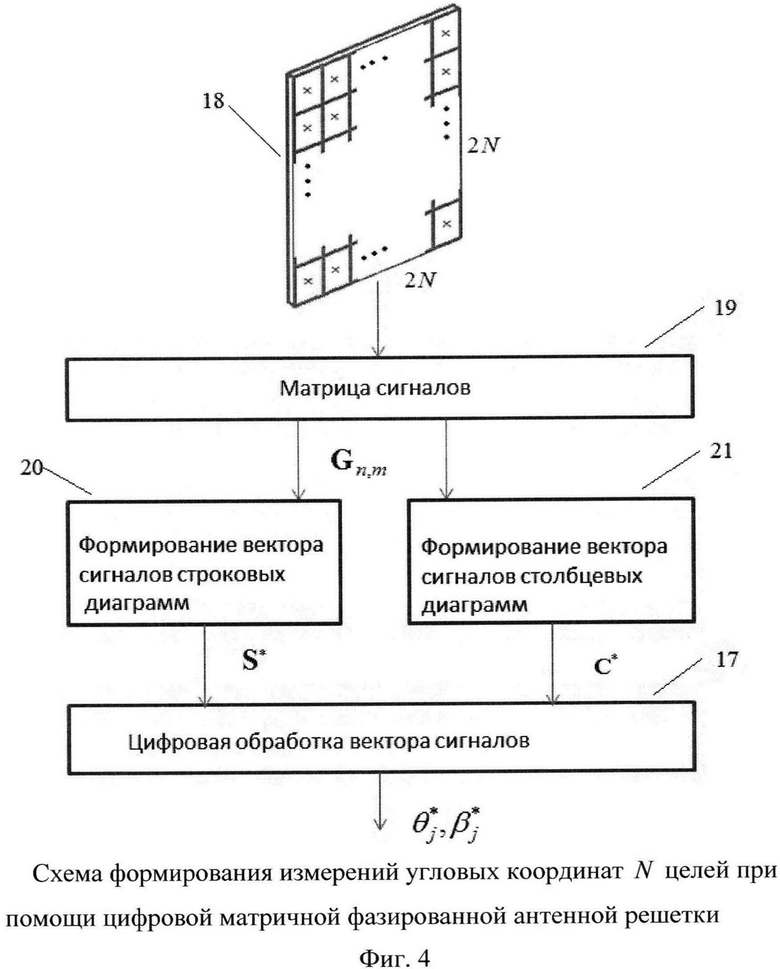
Способ измерений угловых координат группы N близко расположенных целей, в условиях воздействия активных помех, заключающийся в том, что отраженные от целей истинные и ложные сигналы принимаются посредством цифровой линейной эквидистантной фазированной антенной решетки, представляющей собой матрицу, состоящую из 2N×2N лучей, всего 4N2 лучей, и представляющую собой эквидистантную линейку диаграмм направленности, с одинаковыми суммарными диаграммами направленности и фазовыми центрами, расположенными на одинаковом расстоянии друг от друга, из полученных суммарных сигналов формируют вектор 2N сигналов строковых диаграмм 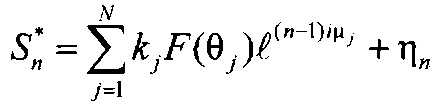 и вектор 2N сигналов столбцевых диаграмм, n=1, …, 2N,
и вектор 2N сигналов столбцевых диаграмм, n=1, …, 2N, 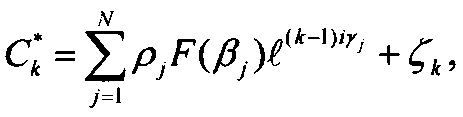 k=1, …, 2N, где
k=1, …, 2N, где 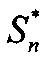 и
и 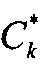 - векторы сигналов строковой диаграммы с номером n и столбцевой диаграммы с номером k, θj - угол места цели и βj - азимут цели с номером j относительно нормали к антенне, ηn и ζk - помехи - внутренние шумы строковой диаграммы с номером n и столбцевой диаграммы с номером k, описывающиеся комплексным «белым» шумом с нулевым средним и известной дисперсией:
- векторы сигналов строковой диаграммы с номером n и столбцевой диаграммы с номером k, θj - угол места цели и βj - азимут цели с номером j относительно нормали к антенне, ηn и ζk - помехи - внутренние шумы строковой диаграммы с номером n и столбцевой диаграммы с номером k, описывающиеся комплексным «белым» шумом с нулевым средним и известной дисперсией:
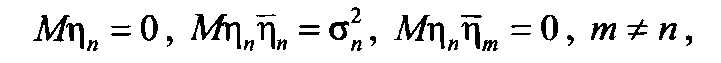
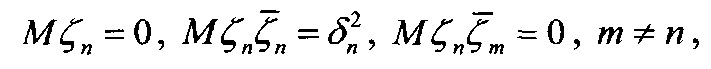
a F(θ) - функция амплитудно-фазового распределения суммарной диаграммы направленности, общая для всех строковых и столбцевых диаграмм, kj и ρj - комплексные коэффициенты отражения целей в вертикальной и горизонтальной плоскостях, μj и γj - обобщенные углы цели с номером j в горизонтальной и вертикальной плоскостях: 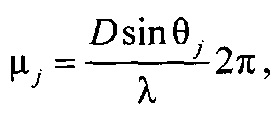
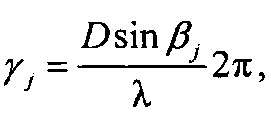 D - расстояние между фазовыми центрами приемных диаграмм, λ - длина волны, через
D - расстояние между фазовыми центрами приемных диаграмм, λ - длина волны, через 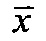 обозначено комплексно сопряженное число с числом x; далее осуществляют цифровую обработку вектора сигналов
обозначено комплексно сопряженное число с числом x; далее осуществляют цифровую обработку вектора сигналов 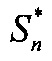 и
и 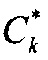 для формирования вектора измерений целей по углу места и курсовому углу, по которым определяют обобщенные углы целей, корреляционную матрицу ошибок измерений и корреляционную матрицу векторного шума и, используя матрицу Вандермонда, определяют угловые координаты близко расположенных целей.
для формирования вектора измерений целей по углу места и курсовому углу, по которым определяют обобщенные углы целей, корреляционную матрицу ошибок измерений и корреляционную матрицу векторного шума и, используя матрицу Вандермонда, определяют угловые координаты близко расположенных целей.
| СПОСОБ ОПРЕДЕЛЕНИЯ УГЛОМЕСТНОЙ КООРДИНАТЫ НИЗКОЛЕТЯЩЕЙ ЦЕЛИ | 2010 |
|
RU2444750C2 |
| СПОСОБ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ ЦЕЛЕЙ | 2008 |
|
RU2366971C1 |
| УСТРОЙСТВО ИЗМЕРЕНИЯ УГЛОВЫХ И ЛИНЕЙНЫХ КООРДИНАТ ОБЪЕКТА | 2013 |
|
RU2519512C1 |
| СПОСОБ РАДИОЛОКАЦИОННОГО ОБНАРУЖЕНИЯ И ИЗМЕРЕНИЯ КООРДИНАТ ОБЪЕКТОВ | 2000 |
|
RU2211458C2 |
| US 7071868 B2, 04.07.2006 | |||
| US 4806936 A, 21.02.1989 | |||
| Устройство для измерения геометрии зеркального отражателя | 1987 |
|
SU1500952A1 |
Авторы
Даты
2018-04-05—Публикация
2016-11-16—Подача