Область техники
Изобретение относится к области антенной техники, а именно к способам определения координат низколетящей цели (НЛЦ).
Уровень техники
Определение угломестной координаты или высоты НЛЦ представляет собой определенную трудность для радиолокационного измерителя координат целей. Физическая причина возникающего затруднения связана с тем, что облучение цели, располагающейся под малым углом места над подстилающей поверхностью, сопровождается облучением этой поверхности и, как следствие, формированием не только сигнала, отраженного от цели, но и сигнала, отраженного от подстилающей поверхности. Этот эффект приводит к искажению дискриминационных (пеленгационных) характеристик (ДХ) измерителя и к ошибке определения угломестной координаты НЛЦ (см., например, Бартон Д., Вард Г. «Справочник по радиолокационным измерениям». - М.: Советское радио, 1976).
Известны способы определения высоты или угломестной координаты НЛЦ (см. Бартон Д. «Радиолокационное сопровождение цели при малых углах места», ТИИЭР, 1974, т.62, №6, с.37-61). Однако в известных способах угломестная координата (или высота) НЛЦ определяется, как правило, с использованием ДХ в угломестной плоскости, которая формируется как отношение сигнала на выходе угломестного разностного канала к сигналу на выходе суммарного канала. При работе по НЛЦ эта характеристика претерпевает искажения, вид и степень которых зависят от взаимного расположения НЛЦ и антенной системы измерителя, а также от отражательных и поглощающих свойств подстилающей поверхности. Эти искажения приводят, в частности, к изменению крутизны и смещению нуля ДХ в угломестной плоскости, традиционно используемой для определения угломестной координаты и, при известной дальности, высоты НЛЦ.
Чтобы минимизировать эти искажения, в ближайшем аналоге заявляемого способа (см. P.R.Dax. «Accurate tracking of low elevation targets with a monopulse radar», in:Radar - Present and Future, IEE Conf. Publ. No.105, oct. 23-25, 1973, pp.160-165; Бартон Д. «Радиолокационное сопровождение цели при малых углах места», ТИИЭР, 1974, т.62, №6, с.37-61) максимум диаграммы направленности (ДН) антенной системы измерителя координат перемещается в угломестной плоскости до совпадения с направлением, соответствующим середине отрезка между целью и антиподом. В предположении, что фаза сигнала в главных суммарном и разностном лепестках постоянна, предлагается оценивать угол места цели и отмечается, что в этом случае результат измерения не зависит от фазы и амплитуды сигнала от зеркального источника. Однако условия создания таких ДН в ближайшем аналоге не указаны, за исключением следующего: первый нуль разностной ДН должен лежать в нуле суммарной ДН. Кроме того, подход, основанный на использовании ДХ в угломестной плоскости, может оказаться неэффективным при маневре цели. Он в общем случае не устраняет эффект изменения крутизны ДХ в угломестной плоскости при определении угломестной координаты НЛЦ. Ниже предлагается способ определения координаты НЛЦ, свободный от перечисленных выше недостатков.
В предлагаемом способе определения угломестной координаты НЛЦ формируется и используется ДХ измерителя, которая не зависит от характеристик подстилающей поверхности.
Сущность изобретения
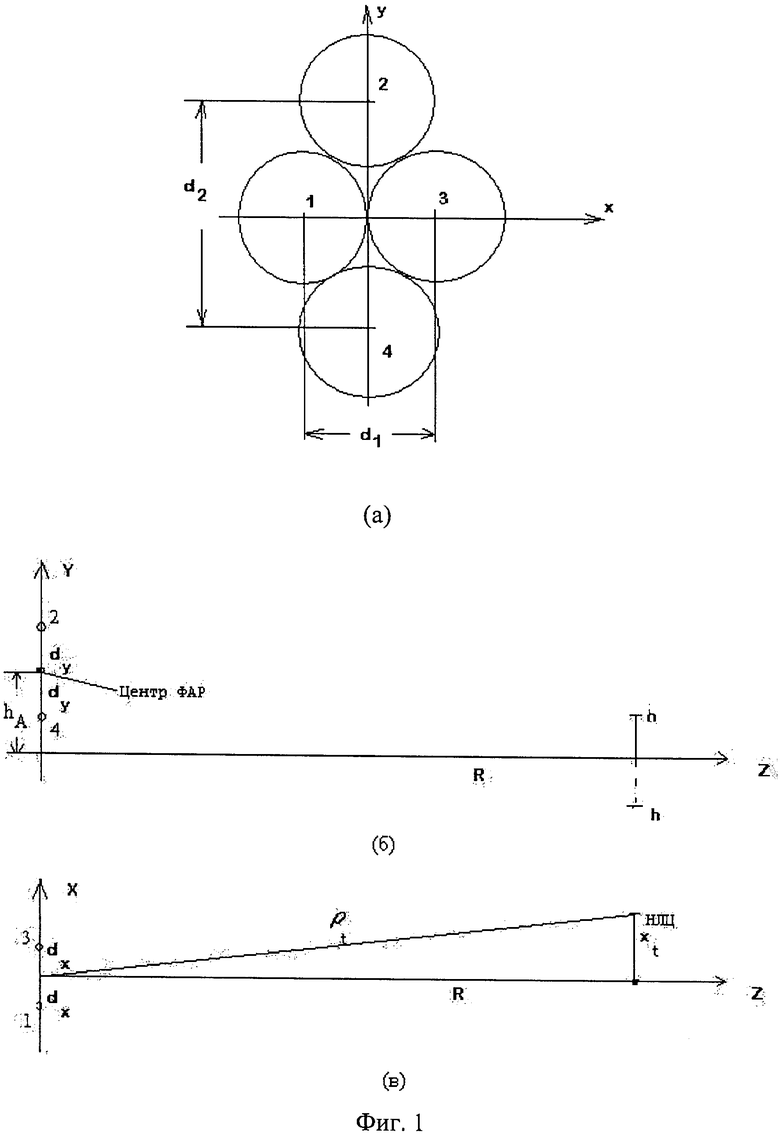
В предлагаемом способе определения угломестной координаты НЛЦ плоскость полотна антенной системы измерителя координат разбивается на 4 идентичные субапертуры (парциальные каналы измерителя) таким образом, что их фазовые центры располагаются в угломестной и азимутальной плоскостях в вершинах ромба (фиг.1а).
Плоскость антенной системы измерителя совпадает с плоскостью (x, y) в декартовой пространственной системе координат, изображенной на фиг.1б и 1в, центр антенной системы располагается на высоте hA на оси y, а НЛЦ располагается на высоте h по оси y над подстилающей поверхностью на расстоянии R от начала координат вдоль оси z и смещена от этой оси на расстояние xt.
Предполагается, что цель располагается в дальней зоне антенной системы измерителя, подстилающая поверхность считается плоской и гладкой, а отражение от нее - зеркальным и исходящим из точки зеркального изображения цели (антипода), располагающейся на глубине h под подстилающей поверхностью. Эти предположения справедливы при выполнении следующих условий:
1) условия дальней зоны 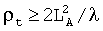 ,
,
где ρt - наклонная дальность цели, LA - максимальное расстояние между центрами излучения элементов ФАР, λ - рабочая длина волны;
2) условия прямой видимости 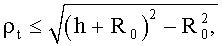
где R0=6370 км - радиус Земли;
3) условия преимущественно зеркального отражения от подстилающей поверхности (см. ссылку на стр.2), согласно которому угломестная координата НЛЦ должна удовлетворять соотношению: θt<0.7Δϑ0.5,
где Δϑ0.5 - ширина ДН антенной системы измерителя в угломестной плоскости.
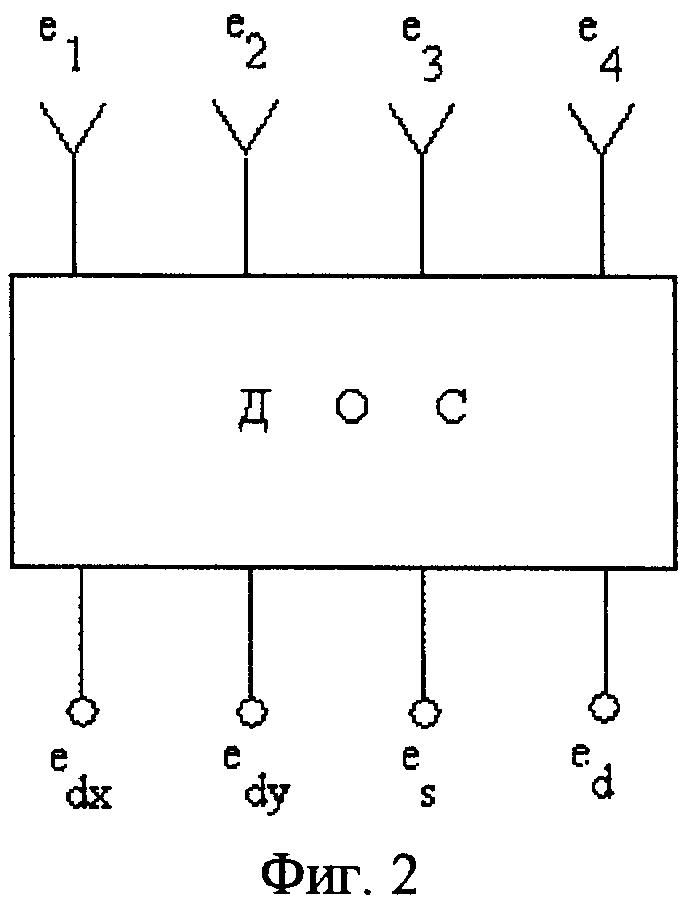
На выходах парциальных каналов измерителя формируются сигналы ei, i=1, …, 4, являющиеся суммой сигналов от локально плоских волн, приходящих с направления цели (θ1, φ1) и антипода (θ2, φ2). К этим каналам подключена диаграммообразующая схема (ДОС) (см. фиг.2), аналогичная по структуре известным ДОС измерителей координат, описанных в литературе (см., например, Амиантов И.Н. Избранные вопросы статистической теории связи», М.: Советское радио, 1971, с.225-230). Пусть сигналы на выходах ДОС определяются соотношениями:
edx=a(e3-e1); edy=a(e2-e4);
es=b(e1+e2+e3+e4); ed=b(e1+e2-e3-e4),
где a и b - заданные константы.
Сигналы es, edx, edy традиционно используются для формирования ДХ измерителя в азимутальной и угломестной плоскостях Sx и Sy:
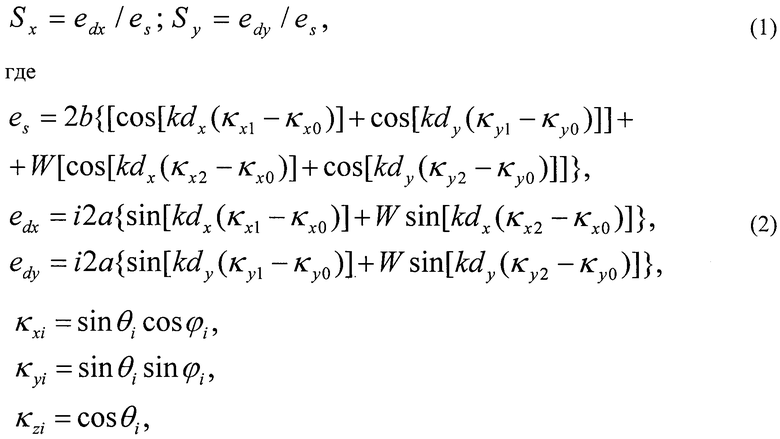
где i=0, 1, 2 - направляющие косинусы, соответствующие направлению сканирования (θ0, φ0), направлению на цель (θ1, φ1) и направлению на антипод (θ2, φ2), множитель W определяется коэффициентом отражения от подстилающей поверхности и разностью хода прямого и отраженного лучей.
Если предположить, что


то выражения для дискриминационных характеристик Sx и Sy приобретают вид:
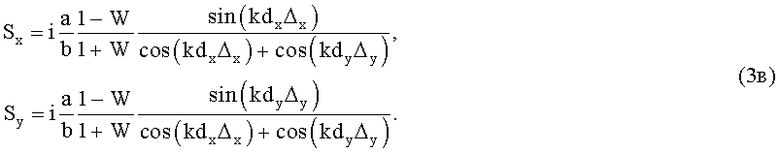
Из формул (3) видно, что формулы для вычисления Sx и Sy содержат множитель W, величина которого зависит от свойств подстилающей поверхности, угла отражения от нее и разности хода прямого и отраженного лучей. Это обстоятельство практически не влияет на точность измерения координаты НЛЦ в азимутальной плоскости, поскольку на практике φ1≈φ2. Однако угломестные координаты цели и антипода принципиально различны. Это обстоятельство не позволяет использовать ДХ Sy для определения угломестной координаты НЛЦ.
Поэтому для измерения угла места НЛЦ используется ДХ следующего вида:

Как видно из формулы (4), при сделанных выше предположениях выражение для Sd не зависит от свойств подстилающей поверхности и, таким образом, может быть использовано для определения координат НЛЦ.
При выполнении условий (3а) и (3б) формулы для координат НЛЦ могут быть получены из следующих соотношений:
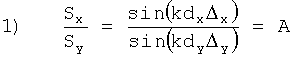
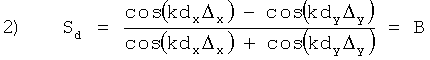
Значения A и B считаются известными из измерений.
Таким образом, получаем:
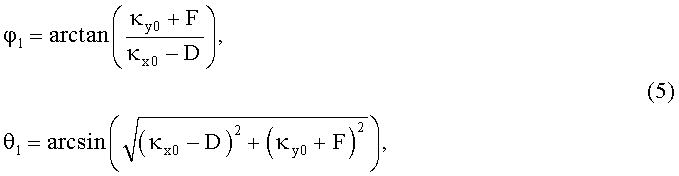
где
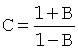 ,
,
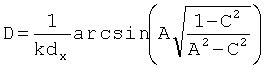 ,
,
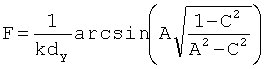 .
.
Формулы для расчета высоты цели:

Таким образом, в случае выполнения соотношений (3а) и (3б), измеряя сигналы на выходах ДОС и формируя ДХ по формулам (3) и (4), можно определить сферические угловые координаты цели по формулам (5) и найти из них угломестную и курсовую координаты НЛЦ, исходя из определений соответствующих координат. Зная наклонную дальность цели, можно определить высоту цели по формулам (6). Как видно из приведенных соотношений, оценка угломестной координаты НЛЦ может, в принципе, быть получена по результатам единичного замера сигналов на выходах ДОС и, таким образом, пригодна для использования в моноимпульсных измерителях координат целей.
Анализ условий (3б) показывает, что эти соотношения примерно эквивалентны следующим соотношениям:

Как видно из формул (7), условия (3а) и (3б) выполняются с высокой точностью в случае, когда максимум главного лепестка суммарной ДН антенной системы измерителя направлен в точку на подстилающей поверхности, располагающуюся между целью и антиподом.
Перечень фигур чертежей
Фиг.1. Схема измерителя координат НЛЦ: dx=d1/2; dy=d2/2.
Фиг.2. Схема ДОС.
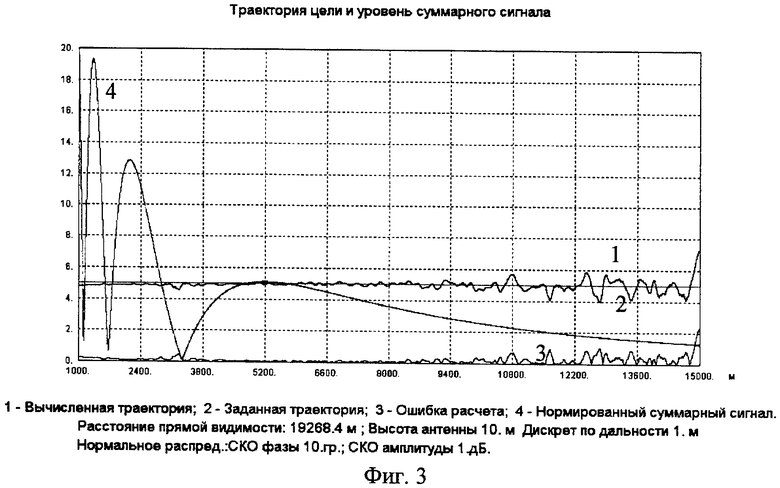
Фиг.3. Результаты моделирования работы измерителя координат для случая, когда цель движется горизонтально на высоте 5 м.
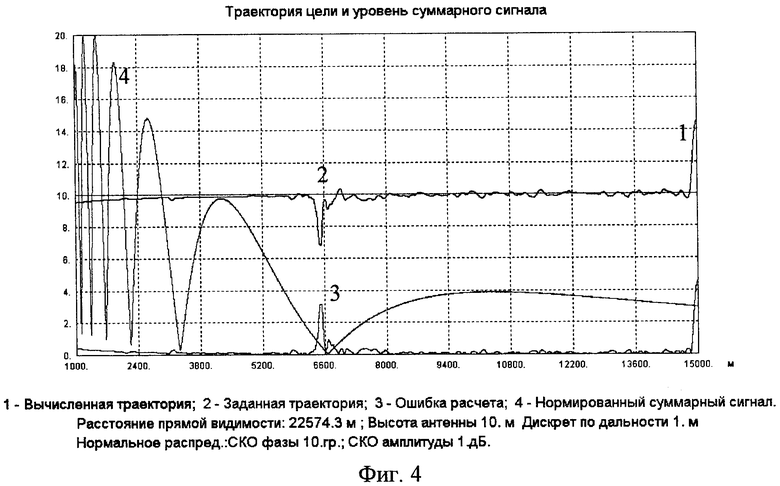
Фиг.4. Результаты моделирования работы измерителя координат для случая, когда цель движется горизонтально на высоте 10 м.
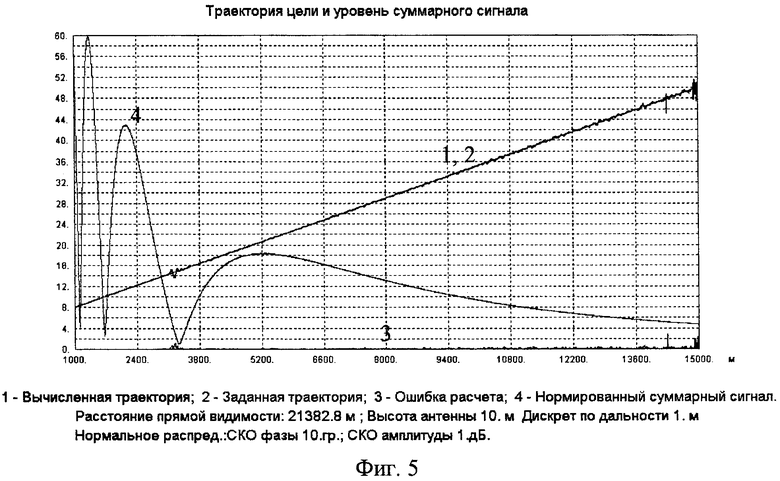
Фиг.5. Результаты моделирования работы измерителя координат для случая, когда цель снижается с высоты 50 м до высоты 5 м.
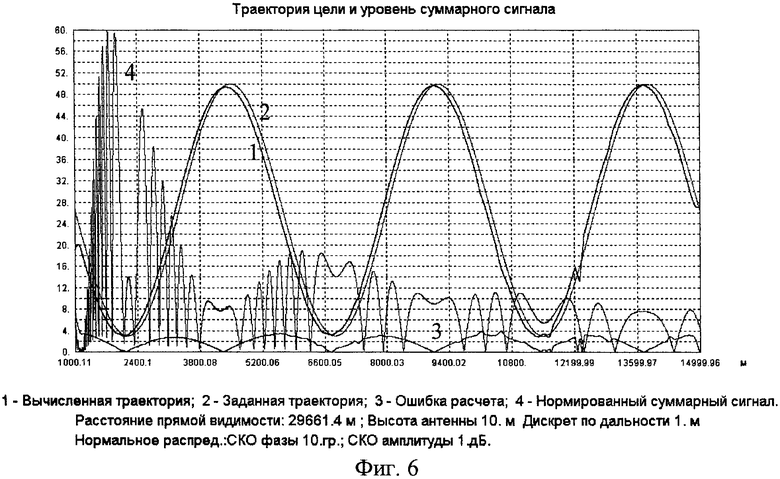
Фиг.6. Результаты моделирования работы измерителя координат для случая, когда цель движется по синусоидальной траектории с максимальной высотой 50 м и минимальной высотой 3 м.
Сведения, подтверждающие возможность осуществления изобретения
Приводится описание предпочтительной реализации, но при этом необходимо иметь в виду, что возможно внесение незначительных изменений без отклонения от рамок и духа настоящего изобретения.
Рассматриваемая реализация описанного выше способа построена на основе антенной системы моноимпульсной РЛС, содержащей четыре идентичных антенных модуля, расположенных согласно конфигурации, изображенной на фиг.1а таким образом, что антенные модули (1, 3) и (2, 4) расположены симметрично относительно центра антенной системы, а пары модулей (1, 3) и (2, 4) ортогональны друг другу. Расстояния между центрами модулей в вертикальной и горизонтальной плоскостях равны 24.8 и 14.3 длин волн, соответственно.
Выведенные выше соотношения были использованы для разработки математической модели и реализующей ее компьютерной программы, моделирующей процедуру определения угломестной координаты и высоты НЛЦ, приближающейся к антенной системе измерителя по заданной траектории. При этом предполагалось, что наклонная дальность до НЛЦ известна из результатов независимых измерений. В процессе моделирования были сделаны следующие предположения.
1. Параметры подстилающей поверхности совпадают с параметрами морской воды. Коэффициент отражения от подстилающей поверхности равен среднему арифметическому коэффициентов отражения Френеля для вертикальной и горизонтальной поляризаций, определенных для заданного угла падения плоской волны на подстилающую поверхность.
2. Луч антенной системы измерителя координат направлен на подстилающую поверхность в точку, дальность и курсовой угол которой совпадают со значениями соответствующих параметров цели.
3. Амплитудно-фазовое распределение на элементах ФАР подвержено случайным искажениям, распределение которых аппроксимируется нормальным законом со следующими параметрами: среднеквадратическое отклонение (СКО) амплитуды тока на элементе равно 1 дБ, а СКО фазы равно 10°.
Результаты моделирования приведены на рисунках фиг.3-6. На всех рисунках кривая 1 (синяя) представляет собой значение высоты цели, определенное по результатам обработки измеренных значений ДХ с использованием формул (5) и (6) для текущего значения наклонной дальности, а кривая 2 (розовая) - истинную (заданную) траекторию НЛЦ. Кривая 3 (зеленая) представляет собой ошибку определения высоты цели (отклонение полученного результата от истинной траектории цели). Кривая 4 есть нормированная к единице амплитуда суммарного сигнала на выходе измерителя. По горизонтальной оси откладываются значения наклонной дальности цели, а по вертикальной оси - значения истинной высоты цели (кривая 2), найденной высоты (кривая 1) и ошибки определения высоты (кривая 3). Высота центра антенной системы измерителя координат hA полагалась равной 10 м.
Результаты моделирования позволяют сделать следующие выводы.
1. Применение описанного выше способа определения угломестной координаты НЛЦ при отсутствии случайных искажений АФР обеспечивает практически точное определение высоты цели.
2. Точность определения высоты НЛЦ существенно зависит от величины искажений АФР и электрических размеров антенной системы измерителя координат.
3. Простое усреднение ряда последовательно полученных результатов моделирования позволяет заметно улучшить точность определения высоты цели. Поэтому на фиг.3-6 приведены данные, полученные путем усреднения результатов моделирования по 100 последовательно полученным значениям для шага по дальности, равного 1 м.
4. При горизонтальном движении цели точность определения координат растет с высотой цели.
5. Точность определения высоты цели заметно снижается в минимумах суммарного сигнала. Однако участки увеличения погрешности измерения имеют относительно малую протяженность, а увеличение числа усредняемых результатов моделирования может заметно снизить амплитуду погрешности измерения в этой области.
Приведенные данные позволяют сделать вывод о работоспособности описанного выше способа определения угломестной координаты НЛЦ.
Предложен способ определения угломестной координаты низколетящей цели (НЛЦ), содержащий прием суммарного сигнала, отраженного от цели и подстилающей поверхности, на выходах четырех антенн, формирование дискриминационных характеристик (ДХ) измерителя координат в двух ортогональных плоскостях Sx и Sy и позиционирование максимума главного лепестка суммарной диаграммы направленности (ДН) антенной системы измерителя координат в направлении точки проекции цели на подстилающую поверхность, отличающийся тем, что центры четырех антенн измерителя координат располагаются попарно симметрично в горизонтальной и вертикальной плоскостях, на одном их выходов измерителя координат формируется дополнительный сигнал, представляющий собой разность суммарных сигналов пар элементов антенной системы, расположенных в горизонтальной и вертикальной плоскостях, который используется для формирования дополнительной ДХ, а угломестная координата и (при известной наклонной дальности) высота НЛЦ определяются из соотношений, использующих найденные таким образом ДХ. Достигаемый технический результат - повышение точности определения координат цели. 6 ил.
Способ определения угломестной координаты низколетящей цели (НЛЦ), содержащий прием суммарного сигнала, отраженного от цели и подстилающей поверхности, на выходах четырех идентичных антенн, формирование дискриминационных характеристик (ДХ) измерителя координат Sx и Sy, представляющих собой разности сигналов на выходах пар антенн, располагающихся в горизонтальной и вертикальной плоскостях, соответственно, отнесенные к суммарному сигналу, и позиционирование максимума главного лепестка суммарной диаграммы направленности (ДН) антенной системы измерителя координат в направлении точки проекции цели на подстилающую поверхность, отличающийся тем, что центры четырех идентичных антенн измерителя координат располагаются попарно симметрично в горизонтальной и вертикальной плоскостях, на одном из выходов измерителя координат формируется сигнал, который используется для формирования ДХ Sd, представляющей собой разность суммарных сигналов на выходах пар антенн, располагающихся в горизонтальной и вертикальной плоскостях соответственно, отнесенную к суммарному сигналу, с использованием соотношения
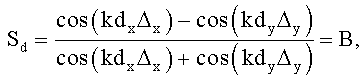
а сферические координаты НЛЦ определяются из соотношений
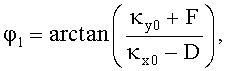
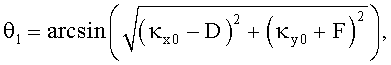
где φ1, θ1 - направление на цель,
κxi=sinθicosφi,
κyi=sinθisinφi, (i=0, 1, 2) - направляющие косинусы, соответствующие направлению сканирования (θ0, φ0), направлению на цель (θ1, φ1) и направлению на антипод (θ2, φ2),
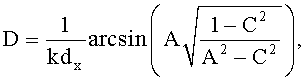
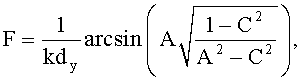
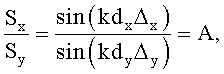
sin(kdxΔx)=Asin(kdyΔy),
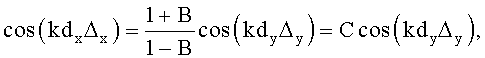
Δx=(κx2-κx0)=-(κx1-κx0),
Δy=(κy1-κy0)=-(κy1-κy0),
dx и dy - расстояния между центрами антенн измерителя координат в горизонтальной и вертикальной плоскостях, соответственно, k=2π/λ - волновое число, λ - рабочая длина волны, и при известном значении наклонной дальности НЛЦ высота НЛЦ определяется из соотношений
γt=ρt·κy1,
h=yt+hA,
где ρt - наклонная дальность цели, hA - высота центра антенной системы измерителя координат над подстилающей поверхностью.
| БАРТОН Д | |||
| Радиолокационное сопровождение цели при малых углах места | |||
| ТИИЭР, 1974, т.62, №6, с.37-61 | |||
| СПОСОБ ИЗМЕРЕНИЯ УГЛА МЕСТА НИЗКОЛЕТЯЩЕЙ ЦЕЛИ И РАДИОЛОКАЦИОННАЯ СТАНЦИЯ ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2006 |
|
RU2307375C1 |
| РАДИОЛОКАЦИОННАЯ СТАНЦИЯ ОБНАРУЖЕНИЯ МАЛОВЫСОТНЫХ МАЛОСКОРОСТНЫХ ЦЕЛЕЙ НА ФОНЕ ПОМЕХОВЫХ ОТРАЖЕНИЙ ОТ ЗЕМЛИ | 1992 |
|
RU2040008C1 |
| ДАЛЬНОМЕРНО-РАЗНОСТНО-ДАЛЬНОМЕРНЫЙ СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЯ И РЕАЛИЗУЮЩЕЕ ЕГО УСТРОЙСТВО | 2007 |
|
RU2363010C2 |
| US 4459592 А, 10.07.1984 | |||
| US 4606514 А, 19.08.1986 | |||
| WO 9829756 A1, 09.07.1998 | |||
| WO 2006114426 A1, 02.11.2006. | |||
Авторы
Даты
2012-03-10—Публикация
2010-06-11—Подача