Изобретение относится к технике измерений токов или напряжений и может быть использовано для восстановления сигнала, прошедшего через фильтр с известной характеристикой.
Во многих случаях электрические сигналы, несущие информацию, не могут быть измерены непосредственно. Они проходят различного рода электрические цепи, в том числе обладающие фильтрующими свойствами. Таким образом, имеем дело с определенными вносимыми устройствами искажениями, которые желательно устранить и восстановить исходный входной сигнал.
Известен способ (прототип) восстановления входного сигнала, прошедшего через фильтр с известной характеристикой [1], который называется инверсной фильтрацией. Способ-прототип заключается в том, что по измеренному временному выходному сигналу фильтра определяют его частотное представление Y(ω), вместо импульсной характеристики фильтра также используют ее частотное представление - передаточную функцию H(ω), находят спектр входного сигнала расчетным путем по формуле 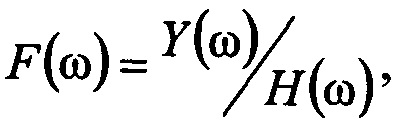 после чего по спектру входного сигнала находят его оригинал - временной сигнал
после чего по спектру входного сигнала находят его оригинал - временной сигнал 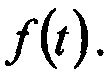
Недостатки прототипа следующие.
1) В общем случае найти спектральное представление выходного сигнала Y(ω) весьма сложно. Обусловлено это следующим. Для нахождения спектра необходимо измерить весь сигнал, иначе спектр окажется искаженным. В случае непрерывного сигнала сделать это практически невозможно, в результате чего выходной сигнал при формировании его спектра воспринимается как ограниченный интервалом измерения и в спектре его появляются несуществующие частоты. Наоборот, при конечном во времени выходном сигнале ширина его спектра будет в пределе бесконечно большой, в этом случае будем иметь дело с обрезанием высоких частот спектра сигнала. В обоих случаях это приводит к неизбежным искажениям. В результате искаженным получится и спектр входного сигнала.
2) Как определение спектра выходного сигнала, так и восстановление временного входного сигнала по его спектру сопряжено с существенными вычислительными затратами. Фактически, речь идет о цифровой реализации прямого и обратного преобразований Фурье.
3) Способ-прототип не приспособлен в принципе для восстановления одиночных коротких импульсов, поскольку ширина их спектров стремится к бесконечности, получить ее приведенной выше вычислительной процедурой невозможно.
Технической задачей данного изобретения является повышение точности и уменьшение вычислительных затрат при восстановлении входного сигнала, прошедшего через фильтр с известной характеристикой, а также расширение области применения способа на одиночные короткие импульсы.
Поставленная задача достигается тем, что в способе восстановления входного сигнала, прошедшего через фильтр с известной характеристикой, заключающемся в измерении выходного сигнала фильтра и восстановлении расчетным путем входного сигнала по этим измерениям и информации о характеристике фильтра, согласно изобретению задают шаг дискретизации по времени T, с которым необходимо восстановить входной сигнал, определяют число дискрет N такое, что N⋅Т=Θ, где Θ - временной интервал, на котором требуется восстановить входной сигнал, с заданным шагом дискретизации измеряют N значений выходного сигнала и объединяют полученные значения в вектор измерений 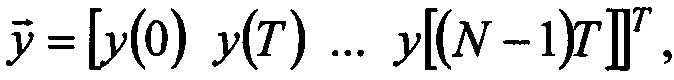 где верхний индекс T обозначает транспонирование, t=0 - начало отсчета, t - время, y(t) - выходной сигнал фильтра, с этим же шагом дискретизируют импульсную характеристику фильтра h(t) и из полученных дискретных значений формируют матрицу
где верхний индекс T обозначает транспонирование, t=0 - начало отсчета, t - время, y(t) - выходной сигнал фильтра, с этим же шагом дискретизируют импульсную характеристику фильтра h(t) и из полученных дискретных значений формируют матрицу
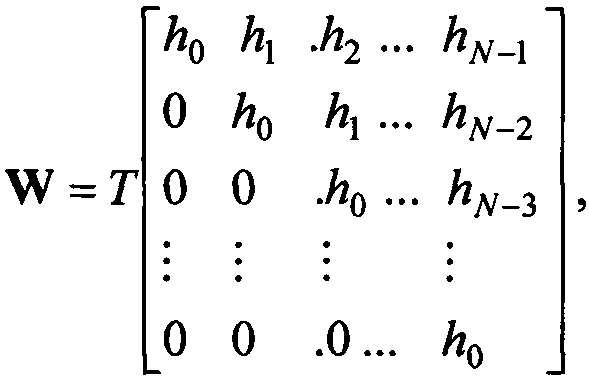
где hi=h(iT), восстанавливают входной сигнал в форме вектора 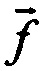 расчетным путем, решая относительно
расчетным путем, решая относительно 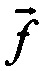 уравнение
уравнение 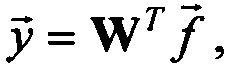 например, методом псевдообращения по формуле
например, методом псевдообращения по формуле 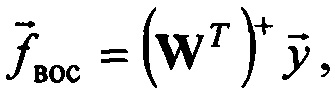 где индекс + обозначает операцию псевдообращения матрицы,
где индекс + обозначает операцию псевдообращения матрицы, 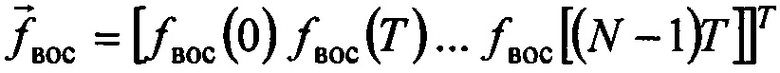 - вектор, компонентами которого являются значения восстановленного входного сигнала с шагом дискретизации T.
- вектор, компонентами которого являются значения восстановленного входного сигнала с шагом дискретизации T.
Принципиальным отличием предлагаемого способа является то, что вся обработка проводится во временной области без перехода к спектральному представлению сигналов и характеристики фильтра. При этом теоретически искажающие факторы вообще отсутствуют, если не считать дискретного представления сигналов, которое неизбежно и в прототипе.
Обоснование способа.
Обозначим искомый входной сигнал как 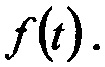 Он поступает на вход фильтра с известной импульсной характеристикой h(t). Выходной сигнал обозначим как y(t) и представим его известным соотношением - сверткой входного сигнала с импульсной характеристикой фильтра
Он поступает на вход фильтра с известной импульсной характеристикой h(t). Выходной сигнал обозначим как y(t) и представим его известным соотношением - сверткой входного сигнала с импульсной характеристикой фильтра

Задача состоит в восстановлении входного сигнала 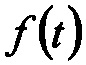 на заданном временном интервале Θ. Восстанавливать сигнал будем в дискретизированной форме в виде вектора
на заданном временном интервале Θ. Восстанавливать сигнал будем в дискретизированной форме в виде вектора 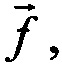 состоящего из дискретных значений сигнала.
состоящего из дискретных значений сигнала.
Зададим шаг дискретизации T, с которым необходимо восстановить входной сигнал. Определим число дискрет N такое, что N⋅T=Θ, где Θ - временной интервал, на котором требуется восстановить входной сигнал. Теперь известен размер искомого вектора 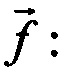 он включает N компонент:
он включает N компонент: 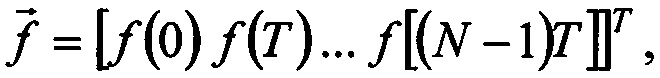 где верхний индекс T обозначает транспонирование, t=0 - начало отсчета.
где верхний индекс T обозначает транспонирование, t=0 - начало отсчета.
Перейдем от интеграла (1) к интегральной сумме с выбранным шагом дискретизации по времени T: 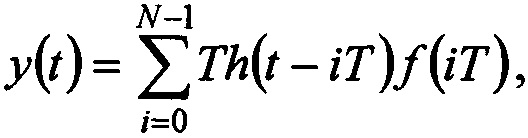 где i - номер отсчета, N - число отсчетов.
где i - номер отсчета, N - число отсчетов.
Обозначим wi(t)=Th(t-iT), 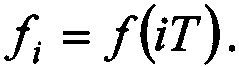 С учетом этих обозначений получим
С учетом этих обозначений получим

где 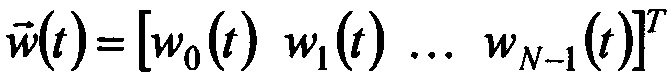 - вектор характеристики фильтра, выполняющий роль весового вектора,
- вектор характеристики фильтра, выполняющий роль весового вектора, 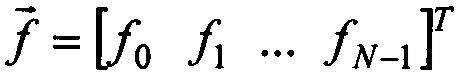 - искомый вектор входного сигнала.
- искомый вектор входного сигнала.
Заметим, что вектор 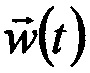 известен для любого заданного t, поскольку определяется он априори известной импульсной характеристикой цепи.
известен для любого заданного t, поскольку определяется он априори известной импульсной характеристикой цепи.
С заданным ранее шагом дискретизации измерим N значений выходного сигнала и объединим полученные значения в вектор измерений  Необхоимо выбрать именно N отсчетов выходного сигнала: если отсчетов будет K<N, то N-K дискрет не отобразятся в выходной выборке, а если взять число отсчетов выходного сигнала K>N, то это будет эквивалентно тому, что входной сигнал закончился на N-й дискрете, а остальные (K-N) дискрет на входе - нулевые. При входном сигнале, длительность которого превышает N⋅Т это внесет искажение при последующем восстановлении.
Необхоимо выбрать именно N отсчетов выходного сигнала: если отсчетов будет K<N, то N-K дискрет не отобразятся в выходной выборке, а если взять число отсчетов выходного сигнала K>N, то это будет эквивалентно тому, что входной сигнал закончился на N-й дискрете, а остальные (K-N) дискрет на входе - нулевые. При входном сигнале, длительность которого превышает N⋅Т это внесет искажение при последующем восстановлении.
Полученные выборочные значения выходного сигнала представим интегральными суммами аналогично (2):
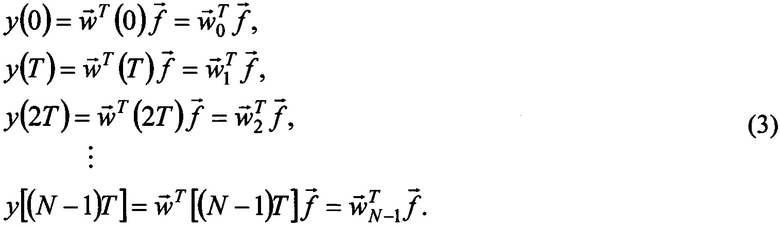
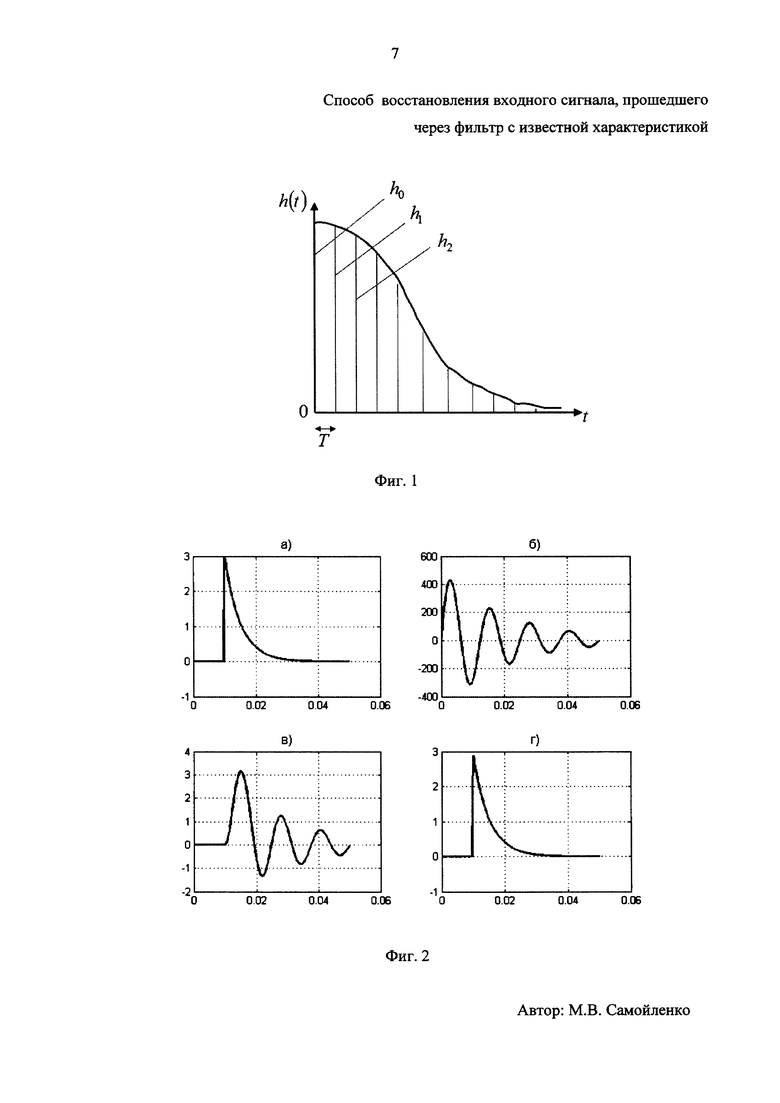
С тем же шагом T дискретизируем импульсную характеристику фильтра h(t), как показано на фиг. 1, где hi=h(iT). С учетом приведенных на фиг. 1 обозначений, запишем структуру весовых векторов, входящих в (3):
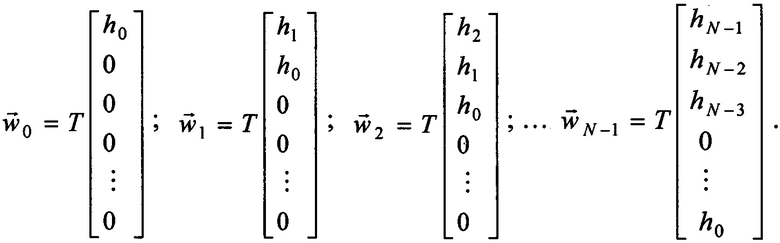
Представим теперь систему равенств (3) в виде векторно-матричного уравнения

где 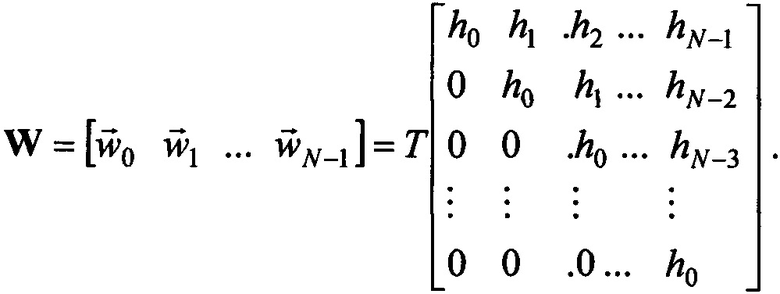
Восстанавливаем входной сигнал расчетным путем, решая уравнение (4), например, методом псевдообращения по формуле

где индекс + обозначает операцию псевдообращения матрицы.
Получаем вектор 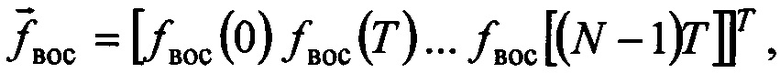 компонентами которого являются значения восстановленного входного сигнала с шагом дискретизации T. Сигнал восстанавливается на интервале Θ=N⋅Т.
компонентами которого являются значения восстановленного входного сигнала с шагом дискретизации T. Сигнал восстанавливается на интервале Θ=N⋅Т.
Метод псевдообращения наиболее универсальный, он позволяет решить задачу даже при вырожденной матрице W. Однако структура этой матрицы, если h0≠0, позволяет рассчитывать на ее несингулярность. В этом случае (WT)+=(WT)-1 и решение находится с помощью обращения матрицы:

Как явствует из выражений (5) и (6), задача восстановления сигнала, прошедшего через фильтр с известной характеристикой, решается посредством вычислительной обработки измеренных значений выходного сигнала. При этом матрица W может быть сформирована заранее при заданных значениях N и T. Соответственно, заранее можно вычислить матрицу восстановления (WT)+ или (WT)-1. После этого в оперативном режиме останется провести нужное число замеров и умножить их слева на вычисленную заранее матрицу.
На фиг. 2 представлено моделирование работы предложенного способа - восстановление экспоненциального импульса, прошедшего через колебательный контур. Моделирование проводилось в среде MATLAB. На фиг. 2 а) - входной сигнал 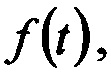 б) - импульсная характеристика фильтра h(t), в) - выходной сигнал y(t), г) - восстановленный сигнал
б) - импульсная характеристика фильтра h(t), в) - выходной сигнал y(t), г) - восстановленный сигнал 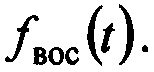
Шаг дискретизации при моделировании составлял T=200 мкс. Имитация выходного сигнала осуществлялась посредством вычисления свертки входного сигнала и импульсной характеристики фильтра с шагом, составляющим 0.2T. Временной интервал Θ, на котором определяется восстанавливаемый сигнал 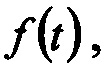 взят от 0 до 50 мс.
взят от 0 до 50 мс.
Импульсная характеристика колебательного контура задана формулой h(t)≈ω0 exp(-αt)sin(ω0t), где α - коэффициент затухания, ω0 - собственная частота контура. Моделирование проведено с параметрами колебательного контура ω0=500 рад/с, α=50 Гц.
Как видно из фиг. 2, предлагаемый способ позволил качественно восстановить входной сигнал.
Преимущества предлагаемого способа по сравнению с прототипом следующие.
1) Предлагаемый способ позволяет восстанавливать входной сигнал без использования частотных представлений сигналов - входного и выходного. Отсутствие переходов в частотную область и обратно позволяет избежать искажений результата, характерных для соответствующих преобразований.
2) Предлагаемый способ реализуется с существенно меньшими вычислительными затратами, чем прототип, поскольку в нем отсутствуют две вычислительно емкие процедуры - вычисления прямого и обратного преобразований при нахождении спектрального представления выходного сигнала и обратного преобразования изображения входного сигнала.
3) Полезным свойством предлагаемого способа является возможность априори, еще до проведения измерений сигнала на выходе цепи, рассчитать матрицу восстановления (WT)+ или (WT)-1. Это позволяет свести весь оперативный режим реализации способа к измерению выходного сигнала, формированию из этих измерений вектора и умножению этого вектора на заранее вычисленную матрицу восстановления. Это еще более сокращает вычислительные процедуры, а также и время восстановления сигнала.
4) Предлагаемый способ позволяет восстанавливать одиночные короткие импульсы,, поскольку эти сигналы могут быть полностью, от начала и до конца, представлены во временной области вектором 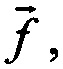 чего невозможно достичь, например, в отношении их бесконечных спектров, которые используются при восстановлении с использованием способа-прототипа - инверсной фильтрации.
чего невозможно достичь, например, в отношении их бесконечных спектров, которые используются при восстановлении с использованием способа-прототипа - инверсной фильтрации.
Источники информации
1. Зражевский А.Ю., Коротков В.А. Исследование восстановления сигнала, прошедшего через неидеальный фильтр низких частот. // «Журнал радиоэлектроники», №4, 2013 (прототип).
Способ восстановления входного сигнала, прошедшего через фильтр с известной характеристикой позволяет решать задачу во временной области, без использования преобразований из временной области в частотную и обратно. Способ заключается в измерении с заданным шагом дискретизации N значений выходного сигнала, объединении полученных значений в вектор измерений 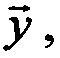 дискретизации с тем же шагом импульсной характеристики фильтра h(t) и формировании матрицы
дискретизации с тем же шагом импульсной характеристики фильтра h(t) и формировании матрицы 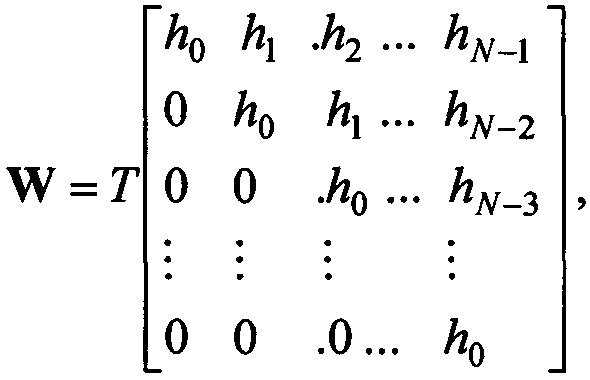 где hi=h(iT), восстановлении входного сигнала в форме вектора
где hi=h(iT), восстановлении входного сигнала в форме вектора 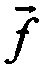 расчетным путем, решая относительно
расчетным путем, решая относительно 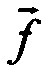 уравнение
уравнение 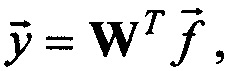 например, методом псевдообращения по формуле
например, методом псевдообращения по формуле 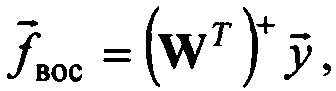 где индекс + обозначает операцию псевдообращения матрицы,
где индекс + обозначает операцию псевдообращения матрицы, 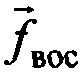 - вектор, компонентами которого являются значения восстановленного входного сигнала с шагом дискретизации T. Достигаемый технический результат заключается в уменьшении вычислительных затрат, повышении точности восстановления сигнала и расширении области применения способа на одиночные короткие импульсы. 2 ил.
- вектор, компонентами которого являются значения восстановленного входного сигнала с шагом дискретизации T. Достигаемый технический результат заключается в уменьшении вычислительных затрат, повышении точности восстановления сигнала и расширении области применения способа на одиночные короткие импульсы. 2 ил.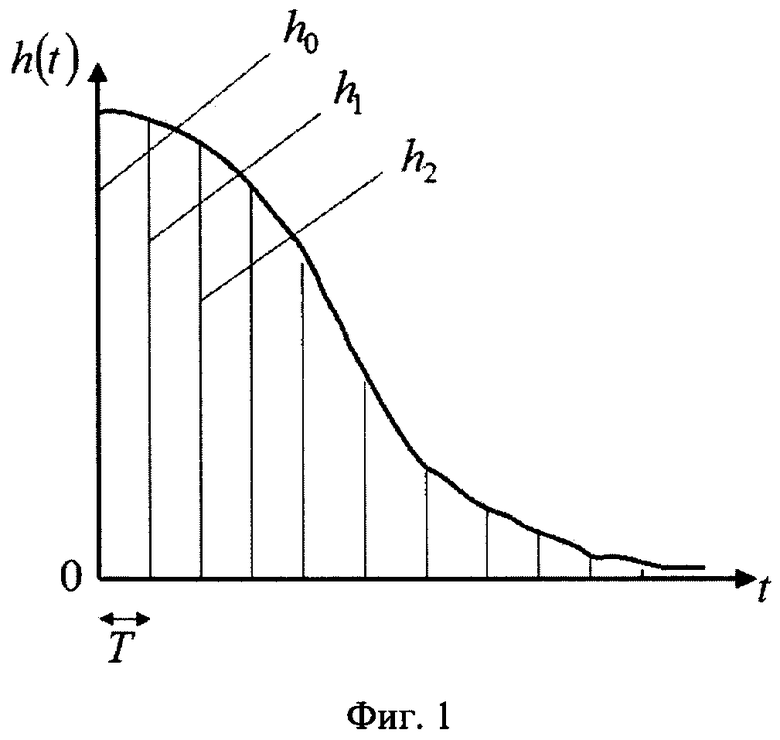
Способ восстановления входного сигнала, прошедшего через фильтр с известной характеристикой, заключающийся в измерении выходного сигнала фильтра и восстановлении расчетным путем входного сигнала по этим измерениям и информации о характеристике фильтра, отличающийся тем, что задают шаг дискретизации по времени T, с которым необходимо восстановить входной сигнал, определяют число дискрет N такое, что N⋅T=Θ, где Θ - временной интервал, на котором требуется восстановить входной сигнал, с заданным шагом дискретизации измеряют N значений выходного сигнала и объединяют полученные значения в вектор измерений 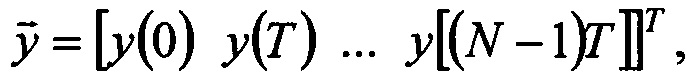 где верхний индекс T обозначает транспонирование, t=0 - начало отсчета, t - время, y(t) - выходной сигнал фильтра, с этим же шагом дискретизируют импульсную характеристику фильтра h(t) и из полученных дискретных значений формируют матрицу
где верхний индекс T обозначает транспонирование, t=0 - начало отсчета, t - время, y(t) - выходной сигнал фильтра, с этим же шагом дискретизируют импульсную характеристику фильтра h(t) и из полученных дискретных значений формируют матрицу
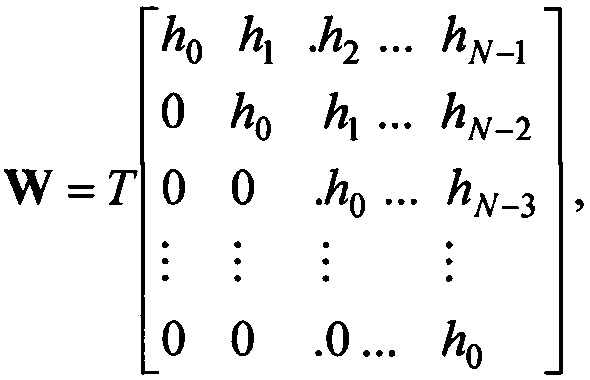
где hi=h(iT), восстанавливают входной сигнал в форме вектора 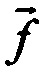 расчетным путем, решая относительно
расчетным путем, решая относительно 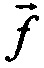 уравнение
уравнение 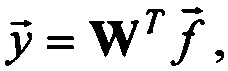 например, методом псевдообращения по формуле
например, методом псевдообращения по формуле 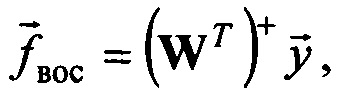 где индекс + обозначает операцию псевдообращения матрицы,
где индекс + обозначает операцию псевдообращения матрицы, 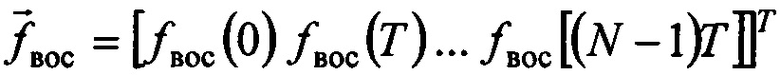 - вектор, компонентами которого являются значения восстановленного входного сигнала с шагом дискретизации T.
- вектор, компонентами которого являются значения восстановленного входного сигнала с шагом дискретизации T.
| Статья: "Математические аспекты применения томографического подхода в обработке многоканальных сигналов", т.17, номер 3, 2010 | |||
| СПОСОБ СПЕКТРАЛЬНОГО АНАЛИЗА ЭЛЕКТРИЧЕСКОГО СИГНАЛА | 2011 |
|
RU2455653C1 |
| ЦИФРОВОЙ МАЛОГАБАРИТНЫЙ USB ОСЦИЛЛОГРАФ | 2009 |
|
RU2402024C1 |
| US 20090076737 A1, 19.03.2009. | |||
Авторы
Даты
2018-04-11—Публикация
2017-02-20—Подача