Изобретение относится к области радиоэлектроники, а именно к способам определения автокорреляционной функции электрического сигнала.
В ряде случаев обработки электрических сигналов требуется знать автокорреляционную функцию сигнала: эта функция является вероятностной характеристикой сигнала, которая используется в задачах построения оптимальных и трансверсальных фильтров, по ней определяются длительность и мощность сигнала. Это говорит об актуальности решения задачи определения автокорреляционной функции электрического сигнала.
Часто информацией о сигнале, которую можно измерить, является его спектральная плотность мощности. Настоящее изобретение относится к способам определения автокорреляционной функции электрического сигнала по его спектральной плотности мощности.
Для стационарных сигналов автокорреляционная функция определяется как 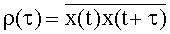
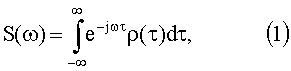
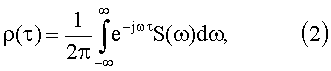
где ω - круговая частота, τ - временная переменная автокорреляционной функции, представляющая собой временной сдвиг сигналов.
Соотношения (1) и (2) справедливы как для случайных стационарных, так и для детерминированных сигналов.
Согласно прототипу [1] автокорреляционную функцию стационарного сигнала определяют как обратное преобразование Фурье спектральной плотности мощности этого сигнала (2). В [1] приведены примеры нахождения автокорреляционной функции по аналитически записанной спектральной плотности.
На практике, однако, чаще всего спектральная плотность определяется не аналитически, а посредством измерений на дискретных частотах, входящих в полосу анализируемых частот измерителя спектра. В этом случае вместо интегрального преобразования Фурье используют [2] дискретное преобразование Фурье (ДПФ), в рассматриваемой задаче - обратное дискретное преобразование Фурье (ОДПФ).
Способ-прототип объединяет способ определения автокорреляционной функции как обратного преобразования Фурье спектральной плотности мощности и способ реализации этого преобразования по измеренным значениям спектральной плотности - ОДПФ.
Способ-прототип заключается в том, что измеряют дискретные значения спектральной плотности мощности анализируемого сигнала и по ним определяют автокорреляционную функцию этого сигнала с помощью ОДПФ.
Согласно прототипу автокорреляционная функция определяется интегральной суммой дискретных значений спектральной плотности мощности, которая получается при переходе от интегрального обратного преобразования Фурье (2) к ОДПФ:

где S(mΩ) - дискретное значение спектральной плотности мощности, Ω - шаг дискретизации по оси частот, m - номер шага дискретизации спектральной плотности мощности, М - число отсчетов влево и вправо от нулевого значения частоты.
Недостатки прототипа следующие.
1. При переходе от интеграла (2) к интегральной сумме (3) необходимо, в соответствии с теоремой Котельникова, обеспечить достаточно малый шаг дискретизации спектральной плотности мощности Ω для однозначного представления подынтегральной функции ejωτS(ω) ее выборочными значениями. Шаг этот определяется характером изменения спектральной плотности в зависимости от частоты. Ввиду ограниченной разрешающей способности измерителей спектров, при анализе высокочастотных и сложных сигналов, например ЛЧМ импульсов, определение автокорреляционной функции методом ОДПФ становится проблематичным. Это ограничивает класс сигналов, для которых возможно определить автокорреляционную функцию по ее спектральной плотности мощности.
2. При анализе широкополосных сигналов спектральная плотность имеет большую протяженность по оси частот. Однако измерители спектров обладают ограниченным интервалом анализируемых частот. Часть спектра, в действительности существующая, но не попавшая в этот интервал, воспринимается при выполнении ОДПФ как равная нулю. Это приводит к искажению определяемой методом ОДПФ автокорреляционной функции, поскольку каждое значение автокорреляционной функции, согласно (2) и (3), определяется всей совокупностью значений спектральной плотности. В результате того, что совокупность эта искажена из-за учета в правой части (3) лишь части значений спектральной плотности, автокорреляционная функция тоже искажается, в ней появляются ложные составляющие за пределами ее действительной протяженности. Это явление аналогично известному явлению просачивания мощности в соседние частотные области, проявляющемуся при оценивании спектральной плотности мощности по периодограмме [3].
Технической задачей данного изобретения является создание способа определения автокорреляционной функции электрического сигнала по его спектральной плотности мощности, который расширяет класс анализируемых сигналов на сложные и высокочастотные сигналы и устраняет искажение автокорреляционной функции вследствие ограниченности полосы анализируемых частот измерителя спектра.
Поставленная задача достигается тем, что в способе определения автокорреляционной функции электрического сигнала по его спектральной плотности мощности, который заключается в измерении дискретных значений спектральной плотности мощности анализируемого сигнала и определении по ним автокорреляционной функции этого сигнала, согласно изобретению контролируемый интервал - τmax÷τmax временной переменной автокорреляционной функции, включающий автокорреляционную функцию, разбивают на малые элементы разрешения, величина которых θ определяется требуемой точностью определения автокорреляционной функции, присваивают элементам разрешения номера -К, -(К-1), …, -1, 0, 1, …, (К-1), К, где К - число элементов разрешения на положительном и отрицательном участках оси временной переменной, для каждого элемента разрешения формируют весовую функцию wk(ω)=θe-jωkθ, где k - номер элемента разрешения, ω - круговая частота, j - комплексная единица, задают фиксированный набор частот ω1, ω2, …, ωN, удобных для измерения на них спектральной плотности мощности, формируют весовую матрицу
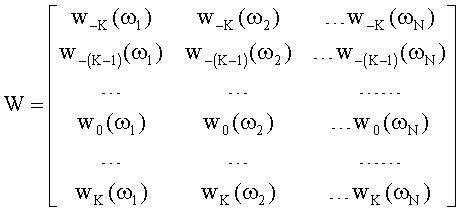
измеряют значения спектральной плотности мощности на заданных частотах S(ω1), S(ω2), …, S(ωN), где N - число измерений и объединяют в вектор измерений 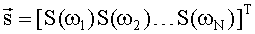 , где индекс Т обозначает транспонирование, составляют уравнение измерений
, где индекс Т обозначает транспонирование, составляют уравнение измерений 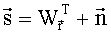
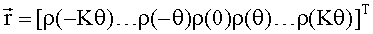
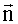
Поставленная задача решается за счет того, что автокорреляционная функция определяется не из обратного преобразования Фурье (2), а из прямого преобразования Фурье (1), в котором она входит в подынтегральное выражение. При переходе от интеграла в правой части (1) к интегральной сумме требуется, в соответствии с теоремой Котельникова, малый шаг дискретизации по временной переменной τ, а не по оси частот. При этом значения спектральной плотности могут определяться в произвольных точках оси частот, на промежуток между которыми не накладывается ограничение теоремы Котельникова, аналогично тому, как выражение (3) позволяет определить автокорреляционную функцию в любой точке временной оси.
Заявляемый способ позволяет определить автокорреляционную функцию на основе таких интегральных сумм.
Обоснование способа.
Будем решать задачу определения автокорреляционной функции ρ(τ) по измеренным значениям спектральной плотности мощности, основываясь на преобразовании Фурье (1):
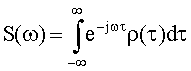
Будем полагать, что автокорреляционная функция анализируемого сигнала лежит в контролируемом интервале - τmax÷τmax временной переменной автокорреляционной функции. Разобьем контролируемый интервал на малые элементы разрешения, величина которых θ определяется требуемой точностью определения автокорреляционной функции, и присвоим элементам разрешения номера - К, -(К-1), …, -1, 0, 1, …, (К-1), К, где К - число элементов разрешения на положительном и отрицательном участках оси временной переменной. С учетом изложенного перейдем от интеграла (1) к интегральной сумме
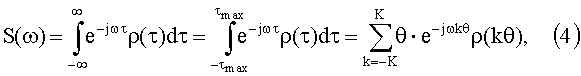
где k - номер элемента разрешения.
Для каждого элемента разрешения сформируем весовую функцию
wk(ω)=θe-jωkθ
и с учетом этих функций перепишем (4) в виде
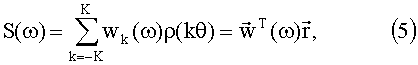
где 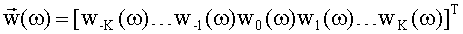 - весовой вектор,
- весовой вектор, 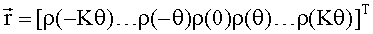
Зададим фиксированный набор частот ω1, ω2, …, ωN, удобных для измерения на них спектральной плотности мощности, и измерим на этих частотах спектральные плотности мощности S(ω1), S(ω2), …, S(ωN), например, с помощью высокодобротных резонаторов. Для всех N измеренных значений составим уравнения вида (5):
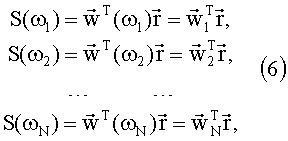
где введены обозначения 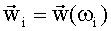 для весовых векторов, соответствующих всем частотам, на которых проводятся измерения.
для весовых векторов, соответствующих всем частотам, на которых проводятся измерения.
Из системы линейных уравнений (6) будем искать автокорреляционную функцию в форме дискретизированных по элементам разрешения значений, т.е. в виде вектора корреляций 
Объединим измеренные значения спектральной плотности в вектор измерений
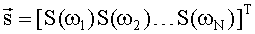 ,
,
а из весовых векторов на всех частотах измерений сформируем весовую матрицу
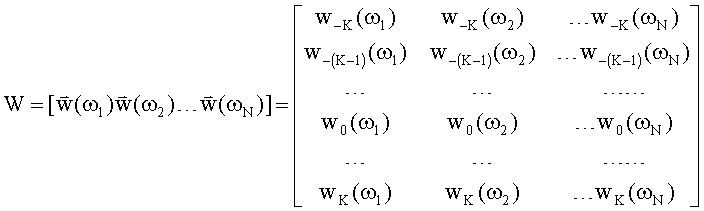
и запишем систему уравнений (6) в векторно-матричной форме

С учетом ошибок измерений спектральной плотности составим уравнение измерений, которое основано на векторно-матричном уравнении (7), в правую часть которого добавлен вектор ошибок измерений спектральной плотности 

Из уравнения измерений (8) определим автокорреляционную функцию в форме оценки вектора корреляций 

где Н - матрица размером K×N, 
Приняв за критерий оценивания минимум среднего квадратического отклонения
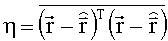
найдем матрицу Hopt:
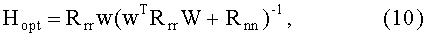
где Rrr и Rnn - ковариационные матрицы соответственно искомой автокорреляционной функции и ошибок измерений.
Подставив (10) в (9), найдем искомую оценку вектора корреляций
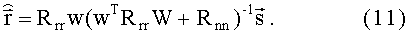
При пренебрежимых ошибках измерений или в отсутствие вероятностных характеристик автокорреляционной функции и ошибок измерений оценить вектор корреляций можно методом псевдообращения [5]:

где индекс + обозначает псевдообращение.
Оценка вектора корреляций, полученная согласно (11) или (12), представляет собой вектор
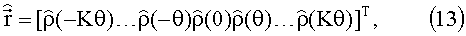
где 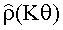
Таким образом, получена оценка вектора корреляций, компоненты которой представляют собой оценки автокорреляционной функции во всех элементах разрешения. Автокорреляционная функция определена с точностью элемента разрешения, размер которого θ задается априори.
Заметим, что, поскольку автокорреляционная функция лежит в контролируемом интервале временной переменной, все ее дискретизированные по элементам разрешения значения входят в правую часть векторно-матричного уравнения измерений (8), из которого и определяются. Определив таким образом вектор корреляций, мы находим значения автокорреляционной функции, приходящиеся на все элементы разрешения (в частности, полученные значения могут быть равными нулю в каких-то элементах разрешения). Принцип определения автокорреляционной функции из уравнения измерений (8), в основе которого лежит система уравнений (6), устраняет появление ложных составляющих за пределами действительной протяженности автокорреляционной функции из-за ограниченной полосы анализируемых частот измерителя спектральной плотности, свойственное прототипу, в котором автокорреляционная функция определяется всей совокупностью выборочных значений спектральной плотности, входящих в правую часть выражения ОДПФ (3).
Заметим также, что измеренные значения спектральной плотности, составляющие вектор измерений в уравнении измерений (8), могут выбираться произвольно в пределах области существования ненулевых значений, исходя из удобства измерений и без таких ограничений, как условие теоремы Котельникова. Это дает возможность анализировать высокочастотные сигналы и сигналы со сложными спектрами за счет использования «разреженной» выборки значений спектральной плотности.
Преимущества предлагаемого способа по сравнению с прототипом следующие.
1. Расширение класса анализируемых сигналов на высокочастотные и сложные сигналы с быстро меняющейся спектральной плотностью. Преимущество это обусловлено тем, что используемые в заявляемом способе выборочные значения спектральной плотности мощности сигнала могут измеряться с произвольным шагом дискретизации по оси частот или даже вообще произвольно. На них не накладывается условие теоремы Котельникова, как в прототипе, что позволяет использовать «разреженные» значения спектральной плотности. Это снимает ограничение на характер изменения спектральной плотности и позволяет определять автокорреляционную функцию, в том числе, по быстро меняющимся и высокочастотным спектральным плотностям.
2. Отсутствие искажения автокорреляционной функции из-за ограниченной полосы анализируемых частот измерителя спектральной плотности мощности, свойственное прототипу. Это преимущество обусловлено новым принципом определения автокорреляционной функции - из уравнения измерений (8) вместо ОДПФ и проявляется тем ощутимее, чем шире спектр анализируемого сигнала.
Источники информации
1. Гоноровский И.С. Радиотехнические цепи и сигналы. Издание четвертое. - М.: Радио и связь, с.120-121 (прототип).
2. Голд Б., Рэйдер Ч. Цифровая обработка сигналов. Пер. с англ. - М: Сов. радио, 1973, с.191.
3. Кей С.М., Март С.Л. Современные методы спектрального анализа: Обзор. // ТИИЭР, Том 69, №11, 1981 г., с.11.
4. Самойленко В.И., Пузырев В.А., Грубрин И.В. Техническая кибернетика. - М.: Изд-во МАИ, 1994, с.130-132.
5. Гантмахер Ф.Р. Теория матриц. 4-е изд. - М.: Наука, Гл. ред. физ.-мат. лит., 1988, с.35.
Изобретение относится к способам определения автокорреляционной функции электрического сигнала. Контролируемый интервал временной переменной автокорреляционной функции, включающий автокорреляционную функцию, разбивают на малые элементы разрешения, присваивают элементам разрешения номера от -К до K, где K - число элементов разрешения на положительном и отрицательном участках оси временной переменной, для каждого элемента разрешения формируют весовую функцию wk(ω)=θe-jωkθ, где k - номер элемента разрешения, ω - круговая частота, j - комплексная единица, задают фиксированный набор частот, удобных для измерения на них спектральной плотности мощности, формируют весовую матрицу W из весовых функций на заданном наборе частот, измеряют значения спектральной плотности мощности на этих частотах и объединяют их в вектор измерений 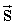

Способ определения автокорреляционной функции электрического сигнала по его спектральной плотности мощности, заключающийся в том, что измеряют дискретные значения спектральной плотности мощности анализируемого сигнала и по ним определяют автокорреляционную функцию этого сигнала, отличающийся тем, что контролируемый интервал -τmax÷τmax временной переменной автокорреляционной функции, включающий автокорреляционную функцию, разбивают на малые элементы разрешения, величина которых θ определяется требуемой точностью определения автокорреляционной функции, присваивают элементам разрешения номера -К, -(К-1), …, -1, 0, 1, …, (К-1), К, где К - число элементов разрешения на положительном и отрицательном участках оси временной переменной, для каждого элемента разрешения формируют весовую функцию wk(ω)=θe-jωkθ, где k - номер элемента разрешения, ω - круговая частота, j - комплексная единица, задают фиксированный набор частот ω1, ω2, …, ωN, удобных для измерения на них спектральной плотности мощности, формируют весовую матрицу
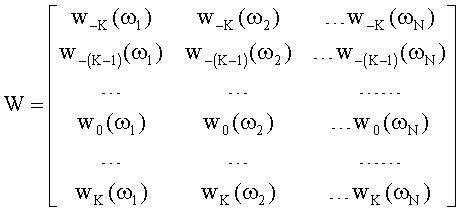
измеряют значения спектральной плотности мощности на заданных частотах S(ω1), S(ω2), …, S(ωN), где N - число измерений, и объединяют в вектор измерений 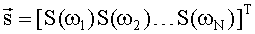 , где индекс Т обозначает транспонирование, составляют уравнение измерений
, где индекс Т обозначает транспонирование, составляют уравнение измерений 
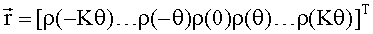
| Кей СМ., Марпл С.Л | |||
| Современные методы спектрального анализа: Обзор | |||
| // ТИИЭР, Том 69, N11, 1981 г., с.9-10 | |||
| 0 |
|
SU293215A1 | |
| US 4982150 A, 01.01.1991 | |||
| Устройство для определения спектральной плотности колебаний параметров режима электроэнергетических систем | 1989 |
|
SU1647761A1 |
| ТРАНСФОРМАТОРНАЯ ПОДСТАНЦИЯ | 0 |
|
SU243054A1 |
| WO 2009135633 A1, 12.11.2009 | |||
Авторы
Даты
2015-01-10—Публикация
2013-08-12—Подача