Изобретение относится к области радиоэлектроники, а именно - к способам определения спектральной плотности мощности электрических сигналов.
Часто задача спектрального анализа заключается в определении спектральной плотности мощности электрического сигнала. Одним из подходов к решению этой задачи является определение спектральной плотности мощности анализируемого сигнала по его автокорреляционной функции. Согласно теореме Винера - Хинчина, автокорреляционная функция стационарного случайного сигнала связана с его спектральной плотностью мощности преобразованием Фурье

где φ(ω) - спектральная плотность мощности, ω - круговая частота, 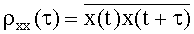
Проведя дискретизацию по переменной интегрирования τ, получим оценку Блэкмана и Тьюки [1 - прототип], которая позволяет определить спектральную плотность мощности по дискретным значениям автокорреляционной функции, взятым с шагом дискретизации T, согласно выражению

Способ-прототип заключается в определении М дискретных значений автокорреляционной функции ρxx(mT), m=1, 2, …, М и определении по ним согласно (2) дискретных значений спектральной плотности мощности для заданных значений ω, которые обычно выбираются с фиксированным шагом дискретизации Ω, обеспечивающим реализацию дискретного преобразования Фурье.
Недостатки прототипа следующие.
1. При переходе от интеграла (1) к дискретному преобразованию Фурье (2) должно выполняться условие теоремы Котельникова 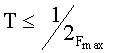
2. Точность спектрального анализа ограничена характерной для дискретного преобразования Фурье величиной, которая, согласно [2], определяется выражением 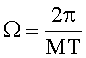
3. Для неискаженного восстановления спектра анализируемого сигнала необходимо получить выборочные значения на всем протяжении автокорреляционной функции. В противном случае спектральная плотность будет искажаться в сторону увеличения ее протяженности по оси частот. Этот эффект [3] называется просачиванием мощности в соседние частотные области. Как известно, чем меньшую полосу частот занимает спектр сигнала, тем протяженнее во времени его автокорреляционная функция, поэтому, если истинный спектр сигнала сосредоточен в узкой полосе частот, то для неискаженного определения спектральной плотности требуется оцифровывать автокорреляционную функцию на достаточно большой ее длительности. Это само по себе является сложным в реализации, хотя бы уже потому, что априори приходится делать анализ протяженности автокорреляционной функции во времени, а кроме того, требуется достаточно большое время спектрального анализа в связи с необходимостью оцифровывать всю эту функцию с шагом дискретизации, отвечающим условию теоремы Котельникова.
Технической задачей данного изобретения является создание способа определения спектральной плотности мощности электрического сигнала по автокорреляционной функции этого сигнала, который позволяет снизить стоимости спектрального анализа, расширить класс анализируемых сигналов на сигналы с высокочастотной автокорреляционной функцией, повысить точность спектрального анализа, устранить искажения спектра в связи с эффектом просачивания мощности в соседние частотные области, сократить время спектрального анализа.
Поставленная задача достигается тем, что в способе определения спектральной плотности мощности электрического сигнала по автокорреляционной функции этого сигнала, который заключается в определении дискретных значений автокорреляционной функции анализируемого сигнала и определении по ним дискретных значений спектральной плотности мощности, согласно изобретению, диапазон контролируемых частот, включающий спектр анализируемого сигнала, разбивают на малые элементы разрешения, размер которых Ω определяется требуемой точностью спектрального анализа, нумеруют эти элементы разрешения, формируют для каждого элемента разрешения весовую функцию 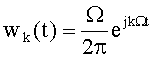
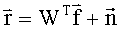

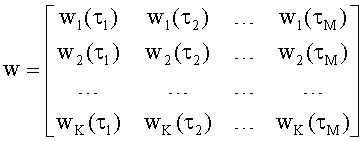
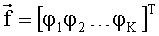
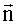
Поставленная задача решается за счет того, что вместо определения спектральной плотности мощности из прямого преобразования Фурье (1), согласно заявляемому способу, эта спектральная плотность определяется из обратного преобразования Фурье 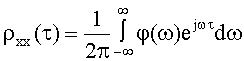
Обоснование способа.
Запишем автокорреляционную функцию сигнала как обратное преобразование Фурье спектральной плотности мощности

где ω - круговая частота, τ - временной сдвиг.
Будем полагать, что спектр анализируемого сигнала лежит в диапазоне контролируемых частот (-ω∂, ω∂). Это позволяет переписать (3) в виде
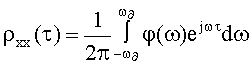
Разобьем диапазон контролируемых частот, включающий спектр анализируемого сигнала, на малые элементы разрешения, размер которых Ω определяется требуемой точностью спектрального анализа, пронумеруем эти элементы разрешения и перепишем полученный интеграл в виде интегральной суммы

где k - номер элемента разрешения, К - число элементов разрешения в диапазоне контролируемых частот.
Для каждого элемента разрешения сформируем весовую функцию

где t - время, k - номер элемента разрешения.
C учетом весовых функций (5) запишем (4) в форме

где τ - временной сдвиг, 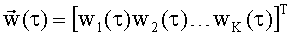
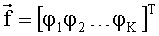
Для заданного значения τ автокорреляционную функцию полагаем известной: она может быть определена, например, усреднением произведения измеренных значений анализируемого сигнала х(t) и x(t+τ) при постоянном заданном временном сдвиге τ. Весовой вектор 
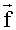
Чтобы оценить спектральный вектор 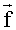

Для автоматизированной цифровой обработки значения τi удобно выбирать с постоянным шагом дискретизации, на который, в отличие от прототипа, не накладывается условие теоремы Котельникова, т.е. шаг дискретизации автокорреляционной функции может быть выбран достаточно большим. В общем случае, постоянный шаг дискретизации не обязателен.
Перепишем (7) в векторно-матричной форме

где 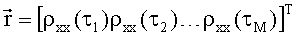
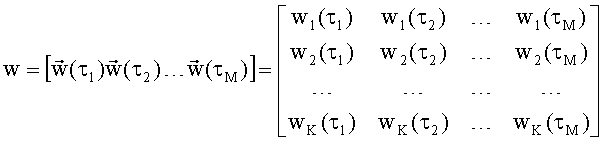
С учетом ошибок определения значений компонент вектора корреляций перепишем (8) в виде уравнения измерений


где 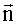
По уравнению измерений (9) найдем оценку спектрального вектора 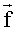

и найдем матрицу Н из условия минимума среднеквадратической ошибки оценивания
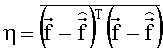
Полагая статистически независимыми ошибки 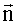
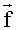

где 
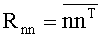
Подставив полученную матрицу (11) в (10), найдем оценку спектрального вектора

Если ошибками определения автокорреляционной функции можно пренебречь, то определить оценку спектрального вектора можно методом псевдообращения [5]:

где индекс + обозначает псевдообратную матрицу.
Компоненты оценки спектрального вектора 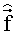
Преимущества предлагаемого способа по сравнению с прототипом следующие.
1. Снижение стоимости спектрального анализа. Это обусловлено снижением стоимости АЦП, применяемых для оцифровки выборочных значений автокорреляционной функции в результате того, что в заявляемом способе выборка автокорреляционной функции формируется при дискретных значениях временной переменной τ, удобных для определения выборки, а не с шагом дискретизации, обусловленным теоремой Котельникова, как в прототипе. Выбрав шаг дискретизации по временной переменной автокорреляционной функции достаточно большим, можно использовать менее быстродействующие и, соответственно, более дешевые АЦП.
2. Расширение класса анализируемых сигналов на сигналы с высокочастотным характером автокорреляционной функции. Это преимущество также обусловлено тем, что оцифровка автокорреляционной функции в заявляемом способе производится с произвольным шагом дискретизации по временной переменной τ, который может быть выбран достаточно большим даже при высокочастотной автокорреляционной функции, так, чтобы имеющийся АЦП "успевал" оцифровывать ее дискретные значения.
3. Повышение точности спектрального анализа. Это преимущество обусловлено тем, что точность в заявляемом способе обусловлена априори выбранным размером элемента разрешения Ω, который, теоретически, может быть выбран сколь угодно малым.
В отличие от прототипа, в заявляемом способе отсутствует ограничение по точности 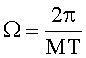
4. Устранение искажения спектра в связи с эффектом просачивания мощности в соседние частотные области. Это обусловлено тем, что каждое измеренное значение автокорреляционной функции, согласно системе уравнений (7), включает полный набор компонент искомого спектрального вектора, поэтому неискаженная оценка этого вектора возможна из указанной системы уравнений при достаточном числе замеров автокорреляционной функции независимо от интервала временной переменной, на котором эти замеры получены.
5. Сокращение времени спектрального анализа. Это преимущество обусловлено возможностью использовать дискретные значения автокорреляционной функции, полученные с произвольным шагом дискретизации на произвольном участке функции. Нужно лишь получить их необходимое количесство. В прототипе же требуется с достаточно малым шагом дискретизации (в соответствии с теоремой Котельникова) оцифровать автокорреляционную функцию на всем ее протяжении или, по крайней мере, на достаточно большом ее участке. В противном случае возникает искажение спектра. Кроме того, выражение (13), полученное в заявляемом способе, позволяет определять спектральную плотность при длине выборки автокорреляционной функции М, меньшем числа элементов разрешения по оси частот К, что также ведет к сокращению времени спектрального анализа.
Источники информации
1. Кей С.М., Марпл С.Л. Современные методы спектрального анализа: Обзор. // ТИИЭР, Том 69, №11, 1981 г., с.9-10 (прототип).
2. Голд Б., Рэйдер Ч. Цифровая обработка сигналов. Пер. с англ. - М.: «Сов. радио», 1973, с.191.
3. Кей С.М., Марпл С.Л. Современные методы спектрального анализа: Обзор. // ТИИЭР, Том 69, №11, 1981 г., с.11.
4. Самойленко В.И., Пузырев В.А., Грубрин И.В. Техническая кибернетика. - М.: Изд-во МАИ, 1994, с.130-132.
5. Гантмахер Ф.Р. Теория матриц. 4-е изд. - М.: Наука. Гл. ред. физ.-мат. лит., 1988, с.35.
Изобретение относится к области радиоэлектроники, а именно - к способам определения спектральной плотности мощности электрических сигналов. Определяют дискретные значения автокорреляционной функции анализируемого сигнала и по ним определяют дискретные значения спектральной плотности мощности. Причем диапазон контролируемых частот, включающий спектр анализируемого сигнала, разбивают на малые элементы разрешения, размер которых определяется требуемой точностью спектрального анализа. Нумеруют их и для каждого элемента разрешения формируют весовую функцию, зависящую от времени, номера и размера элемента разрешения. Определяют дискретные значения автокорреляционной функции анализируемого сигнала при временных сдвигах, удобных для их определения. Составляют векторно-матричное уравнение измерений 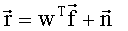
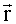
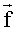
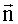
Способ определения спектральной плотности мощности электрического сигнала по автокорреляционной функции этого сигнала, заключающийся в том, что определяют дискретные значения автокорреляционной функции анализируемого сигнала и по ним определяют дискретные значения спектральной плотности мощности, отличающийся тем, что диапазон контролируемых частот, включающий спектр анализируемого сигнала, разбивают на малые элементы разрешения, размер которых Ω определяется требуемой точностью спектрального анализа, нумеруют эти элементы разрешения, формируют для каждого элемента разрешения весовую функцию 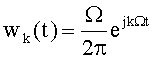
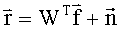
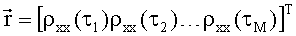
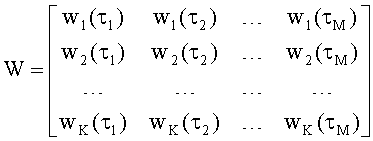
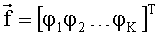
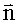
| Кей СМ., Марпл С.Л | |||
| Современные методы спектрального анализа: Обзор | |||
| // ТИИЭР, Том 69, N11, 1981 г., с.9-10 | |||
| 0 |
|
SU293215A1 | |
| US 4982150 A, 01.01.1991 | |||
| Устройство для определения спектральной плотности колебаний параметров режима электроэнергетических систем | 1989 |
|
SU1647761A1 |
| ТРАНСФОРМАТОРНАЯ ПОДСТАНЦИЯ | 0 |
|
SU243054A1 |
| WO 2009135633 A1, 12.11.2009 | |||
Авторы
Даты
2015-01-10—Публикация
2013-06-20—Подача