ОБЛАСТЬ ТЕХНИКИ
Настоящее изобретение относится к устройству имитационного моделирования и способу имитационного моделирования для прогнозирования динамического поведения моделируемой системы точечных масс с использованием компьютера. Изобретение также относится к программе и носителю записи для реализации способа.
УРОВЕНЬ ТЕХНИКИ
С развитием компьютерной технологии были проведены интенсивные исследования с целью логического пояснения поведения биологических макромолекул при большой динамической деформации, например, белков, нуклеиновых кислот, липидов и полисахаридов на атомном уровне посредством имитационных моделирований с использованием теоретических вычислений. В частности, такие исследования могут включать в себя лекарственный скрининг, в котором теоретически прогнозируется сродство между целевым белком и молекулой-кандидатом на связывание (целевой молекулой для анализа наличия сродства связывания с целевым белком) и анализ механизма укладки белка, в котором выявляется механизм построения трехмерной структуры из первичной последовательности белка для теоретического построения структуры более высокой размерности из первичной структуры.
Способы имитационного моделирования для прогнозирования динамического поведения биологических макромолекул могут включать в себя, например, метод молекулярной динамики, способный к осуществлению имитационного моделирования даже для макромолекулы на атомном уровне, и способы имитационного моделирования на основе метода Монте-Карло, как описано, например, в следующих непатентных документах: T.J.A. Ewing and I.D. Kuntz, “Critical evaluation of search algorithms for automated molecular docking and database screening”, Journal of Computational Chemistry, Vol. 18, Issue 9, pp. 1175-1189, 1997, G.M. Morris et al., “Automated docking using a Lamarckian genetic algorithm and an empirical binding free energy function”, Journal of Computational Chemistry, Vol. 19, Issue 14, pp. 1639-1662, 1998, M. Rarey et al., “A Fast Flexible Docking Method using an Incremental Construction”, Journal of Molecular Biology, Vol. 261, Issue 3, pp. 470-489, 1996, R. Abagyan et al., “ICM - A new method for protein modeling and design: Applications to docking and structure prediction from the distorted native conformation”, Journal of Computational Chemistry, Vol. 15, Issue 5, pp. 488-506, 1994, G. Jones et al., “Development and validation of a genetic algorithm for flexible docking”, Journal of Molecular Biology, Vol. 267, Issue 3, pp. 727-748, 1997, R.A. Friesner et al., “Glide: A New Approach for Rapid, Accurate Docking and Scoring. 1. Method and Assessment of Docking Accuracy”, Journal of Medicinal Chemistry, Vol. 47, Issue 7, pp. 1739-1749, 2004, T.A. Halgren et al., “Glide: A New Approach for Rapid, Accurate Docking and Scoring. 2. Enrichment Factors in Database Screening”, Journal of Medicinal Chemistry, Vol. 47, Issue 7, pp. 1750-1759, 2004. Согласно методу молекулярной динамики, временная эволюция многоатомной системы можно последовательно прослеживать с малым интервалом времени согласно уравнению движения. Поскольку на потенциальной поверхности многоатомной системы, которая включает в себя биологическую макромолекулу присутствует много локальных минимумов или много энергетических барьеров, вышеупомянутый способ сталкивается с проблемой в том, что состояние многоатомной системы захватывается локальным минимумом вблизи начальной структуры, в связи с чем, для вычисления требуется большое количество времени. Эта проблема также свойственна способам на основе метода Монте-Карло.
РАСКРЫТИЕ ИЗОБРЕТЕНИЯ
Следовательно, в качестве способа решения проблемы захватывания локальным минимумом, известен способ вычисления, в котором “движущая сила” применяется к вычислению на основе метода молекулярной динамики, чтобы вырваться из ловушки локального минимума. Например, в опубликованной японской патентной заявке, не прошедшей экспертизы, № 2005-267592 и опубликованной японской патентной заявке PCT № 2005-524129, повторно опубликованной японской патентной заявке PCT № 2006/068271, и непатентных документах, Y. Fukunishi et al., “The Filling Potential Method: A Method for Estimating the Free Energy Surface for Protein-Ligand Docking”, THE JOURNAL OF PHYSICAL CHEMISTRY B, Vol. 107, Issue 47, pp. 13201-13210, 2003,and Y. Sugita and Y. Okamoto, “Replica-exchange molecular dynamics method for protein folding”, Chemical Physics Letters, Vol. 314, Issues 1-2, pp. 141-151, 1999, раскрыто, что виртуальные взаимодействия вступают последовательно, поэтому многоатомная система никогда не возвращается к прежней структуре, или структуры, найденные в ускоренном движении многоатомной системы в высокотемпературной фазе, последовательно отражаются в движении многоатомной системы в низкотемпературной фазе. Такое вступление взаимных взаимодействий и пр. может ускорять поиск маршрута на потенциальной поверхности, через которую проходит многоатомная система, что позволяет вычислять динамическое поведение биологической макромолекулы.
Однако вычисление на основании уравнения движения, описывающего систему точечных масс, представляющую моделируемую биологическую макромолекулу и т.п., и с использованием молекулярной динамики для прогнозирования поведения системы точечных масс путем интегрирования по времени, сталкивается с необходимостью поиска компромиссного соотношения между временем вычисления имитационного моделирования и точностью вычисления. В частности, в способах имитационного моделирования, описанных в опубликованной японской патентной заявке, не прошедшей экспертизы, № 2005-267592 и опубликованной японской патентной заявке PCT № 2005-524129, повторно опубликованной японской патентной заявке PCT № 2006/068271, и непатентных документах, Y. Fukunishi et al., “The Filling Potential Method: A Method for Estimating the Free Energy Surface for Protein-Ligand Docking”, THE JOURNAL OF PHYSICAL CHEMISTRY B, Vol. 107, Issue 47, pp. 13201-13210, 2003 and Y. Sugita and Y. Okamoto, “Replica-exchange molecular dynamics method for protein folding”, Chemical Physics Letters, Vol. 314, Issues 1-2, pp. 141-151, 1999, порядок движения, присущий системе точечных масс, нарушается за счет применения “движущей силы”, благодаря чему в результате вычисления вычисляется поведение нереалистично большой деформации, хотя время вычисления сокращается. Эта тенденция усиливается с увеличением “движущей силы”, прилагаемой, чтобы более эффективно вырваться из ловушки локального минимума.
Настоящее изобретение было сделано ввиду вышеописанных обстоятельств, и задачей настоящего изобретения является обеспечение устройства имитационного моделирования и способа имитационного моделирования, позволяющих повысить точность вычисления и одновременно сократить время вычисления в имитационного моделирования для прогнозирования динамического поведения системы точечных масс. Еще одной задачей настоящего изобретения является обеспечение программы и носителя записи для реализации способа.
Для решения вышеупомянутых проблем, устройством имитационного моделирования согласно настоящему изобретению является устройство для прогнозирования поведения системы точечных масс, образованной моделируемыми N точечными массами, причем устройство включает в себя:
средство задания координат для задания медленных координат, которые представляют собой M координат, в основном предполагающих структурное изменение в системе точечных масс на основании 3N координат точечных масс, описывающих структуру системы точечных масс, и быстрых координат, которые являются координатами, описывающими структуру системы точечных масс, и не зависят от медленных координат;
средство извлечения координат для получения структуры быстрых координат как функции медленных координат путем подчинения быстрых координат медленным координатам и получения, с учетом влияния изменения быстрых координат на медленные координаты вследствие изменения медленных координат, структуры медленных координат как функции K коллективных координат общей координаты, которая связана с медленными координатами каноническим преобразованием, причем общая координата образована переменной составляющей, которая изменяется со временем, и постоянной составляющей, которая служит константой относительно времени, и K коллективных координат являются переменной составляющей общей координаты; и
средство обратного преобразования для прогнозирования временной эволюции системы точечных масс на основании коллективной(ых) координаты() как функции времени, которую(ые) можно получить, решая уравнение движения относительно коллективной(ых) координаты(), структуры медленных координат и структуры быстрых координат.
K, M, и N здесь удовлетворяют соотношению K<M<3N, и каждое из них представляет целое число, не меньшее 1.
Используемый здесь термин “структура системы точечных масс” означает трехмерную структуру, образованную N точечными массами, составляющими систему точечных масс.
Используемый здесь термин “медленные координаты, в основном, предполагающие структурное изменение в системе точечных масс” означает координаты, которые оказывают большое влияние на формирование трехмерной структуры системы точечных масс.
Используемый здесь термин “задание медленных координат” означает задание, в качестве медленных координат, некоторых из координат самих точечных масс, координат, которые можно задавать путем объединения координат точечных масс, или их комбинации. То же самое справедливо для быстрых координат.
Предпочтительно, средство извлечения координат устройства имитационного моделирования согласно настоящему изобретению является средством, которое получает структуру медленных координат путем:
осуществления первого этапа для получения потенциальной энергии V, представленной как функция медленных координат и быстрых координат;
осуществления второго этапа для подчинения быстрых координат медленным координатам согласно условию адиабатического приближения с использованием потенциальной энергии;
осуществления, в текущем состоянии медленных координат и быстрых координат, третьего этапа для получения производной потенциальной энергии по медленным координатам с учетом влияния вышеописанный;
осуществления, на основании производной потенциальной энергии, четвертого этапа для получения производной медленных координат по коллективной(ым) координате(ам) согласно основному уравнению метода самосогласованных коллективных координат с использованием производной потенциальной энергии;
осуществления, на основании производной медленных координат, пятого этапа для обновления коллективной(ых) координаты() на малую величину и получения обновленных медленных координат;
осуществления, на основании обновленных медленных координат, шестого этапа для осуществления структурной релаксации на быстрых координатах, подчиненных медленным координатам; и
после этого повторения этапов с третьего по шестой на основании медленных координат и быстрых координат в состоянии после структурной релаксации быстрых координат.
Используемый здесь термин “на основании медленных координат и быстрых координат в текущем состоянии” означает, что третий этап осуществляется, когда медленные координаты и быстрые координаты находятся в состоянии, заданном средством задания координат в первый момент времени, и когда медленные координаты и быстрые координаты находятся в состоянии после структурной релаксации, осуществляемой на быстрых координатах во второй момент времени непосредственно до осуществления шестого этапа.
Предпочтительно, в устройстве имитационного моделирования настоящего изобретения, вышеописанное влияние учитывается способом, который использует, по меньшей мере, одну из нижеприведенных формул 1-3.

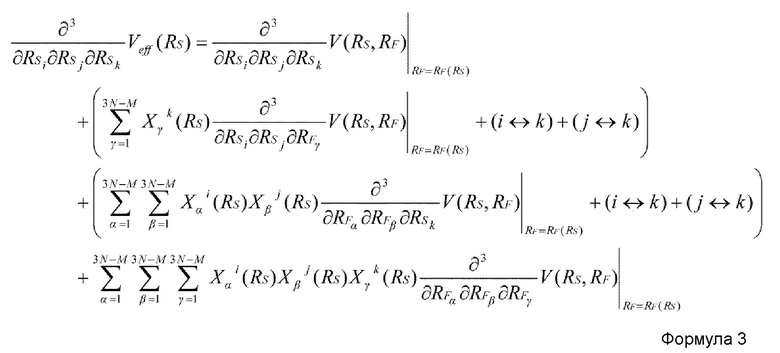
Используемое здесь далее означает следующее:
каждое из i, j и k представляет целое число в диапазоне от 1 до M;
каждое из α, β и γ представляет целое число в диапазоне от 1 до 3N-M;
RSi представляет i-ю медленную координату в системе точечных масс;
RFα представляет α-ю быструю координату в системе точечных масс;
RS представляет (RS1, RS2, ------, RSM);
RF представляет (RF1, RF2, ------, RF(3N-M));
RF(RS) представляет быстрые координаты, подчиненные медленным координатам;
V(RS,RF) представляет потенциальную энергию системы точечных масс, представленной медленными координатами и быстрыми координатами; и
Veff(RS) представляет эффективную потенциальную энергию, получаемую подстановкой RF(RS) в V(RS,RF).
В формуле 2, (i↔j) в третьем члене представляет член, выведенный взаимной заменой индексов i и j во втором члене (то есть члене, выведенном путем замены i на j и j на i во втором члене, то же самое справедливо ниже).
В формуле 3, (i↔k) в третьем члене представляет член, выведенный взаимной заменой индексов i и k во втором члене, (j↔k) в четвертом члене представляет член, выведенный взаимной заменой индексов j и k во втором члене, (i↔k) в шестом члене представляет член, выведенный взаимной заменой индексов i и k в пятом члене, и (j↔k) в седьмом члене представляет член, выведенный взаимной заменой индексов j и k в пятом члене.
Кроме того, в формулах 1-3, используется нижеприведенная формула 4.

где: Kαβ-1(RS) представляет матрицу, обратную Kαβ(RS), и
Kαβ(RS) и Jαi(RS) задаются нижеприведенными формулами 5 и 6, соответственно.
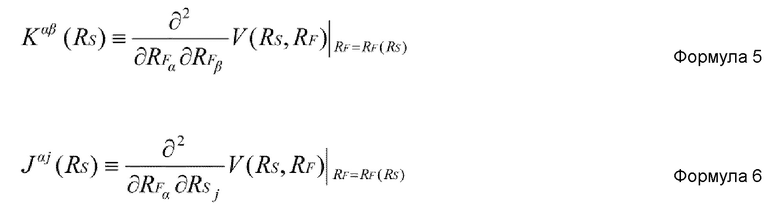
Предпочтительно, в устройстве имитационного моделирования настоящего изобретения, условие адиабатического приближения выражается нижеприведенной формулой 7.

Предпочтительно, в устройстве имитационного моделирования настоящего изобретения, количество K коллективных координат удовлетворяет условию K=1, и основное уравнение метода самосогласованных коллективных координат представлено нижеприведенными формулами 8 и 9.
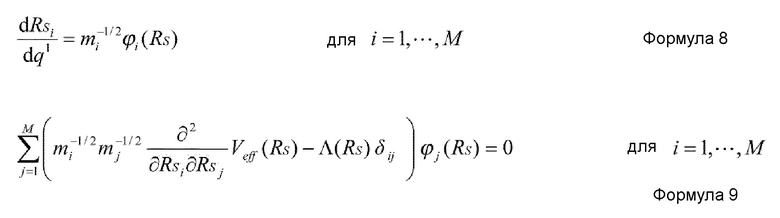
Используемое здесь далее означает следующее:
q1 представляет коллективную координату;
mi представляет массу i-й медленной координаты в системе точечных масс;
ϕi(RS) представляет i-ю составляющую функции (собственный вектор), которая удовлетворяет формуле 9; и
Λ(RS) представляет функцию (собственное значение), которая удовлетворяет формуле 9.
Альтернативно, предпочтительно, чтобы в устройстве имитационного моделирования настоящего изобретения количество K коллективных координат удовлетворяло условию K=1, и основное уравнение метода самосогласованных коллективных координат было представлено нижеприведенными формулами 10-12.

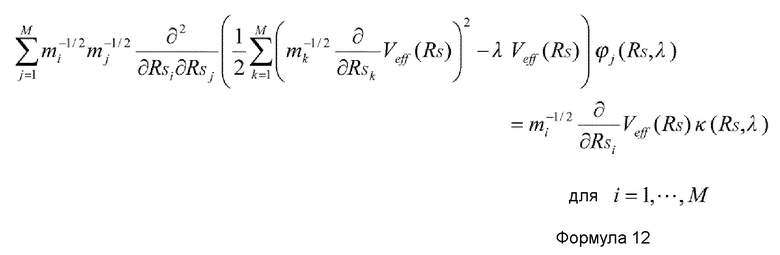
где ϕi(RS, λ) и κ(RS, λ) - функции, которые подчиняются формуле 12, и ϕi(RS, λ) представляет i-ю составляющую, и λ представляет вспомогательную координату (переменную, рассматриваемую как независимую от медленных координат и как функцию коллективной(ых) координаты()).
Предпочтительно, в устройстве имитационного моделирования настоящего изобретения, средство извлечения координат является средством, которое осуществляет вычисление на четвертом этапе путем увеличения количества переменных, рассматриваемых как независимые от медленных координат и как функции коллективной(ых) координаты() (т.е. вспомогательных координат) при решении основного уравнения для исключения произвольности знака производной медленных координат или вспомогательных координат относительно коллективной(ых) координаты() в основном уравнении.
Кроме того, в случае, когда количество вспомогательных координат увеличивается, предпочтительно, чтобы средство извлечения координат являлось средством, которое осуществляет вычисление согласно основному уравнению, представленному нижеприведенной формулой 13, полученной в результате этого. Кроме того, в этом случае, количество K коллективных координат удовлетворяет условию K=1.
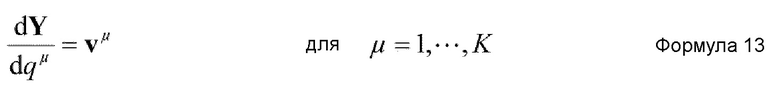
где Y - MK+M+K-мерный вектор, заданный нижеприведенной формулой 14, и vμ - вектор решения неоднородного линейного уравнения нижеприведенной формулы 15.

C и sμ в формуле 15 задаются нижеприведенными формулами 16 и 17, соответственно.
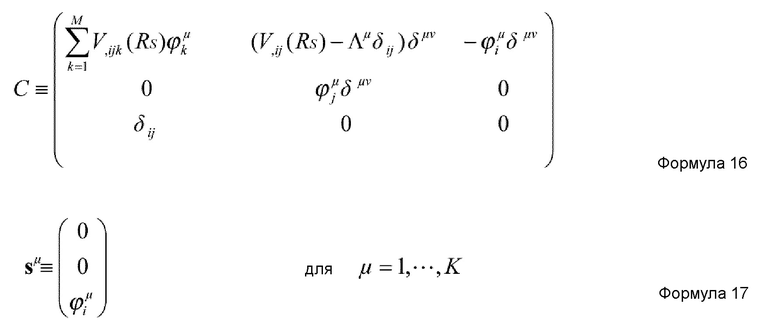
где Vij(RS) и Vijk(RS) задаются нижеприведенными формулами 18 и 19, соответственно.
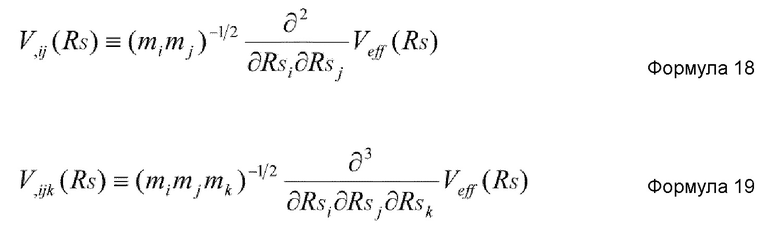
где каждое из μ и ν представляет целое число в диапазоне от 1 до K, qμ представляет μ-ю коллективную координату, и каждое из ϕiμ и Λμ представляет вспомогательную координату.
Альтернативно, в случае, когда количество вспомогательных координат увеличивается, предпочтительно, чтобы средство извлечения координат являлось средством, которое осуществляет вычисление согласно основному уравнению, представленному нижеприведенной формулой 20, полученной в результате этого. Кроме того, в этом случае, количество K коллективных координат удовлетворяет условию K=1.
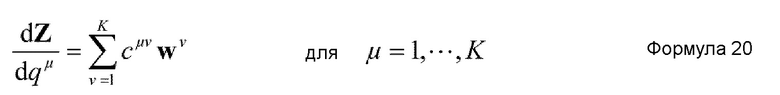
где Z - MK+M+2K-мерный вектор, заданный нижеприведенной формулой 21, cμν - константа, уникально определенная так, чтобы минимизировать значение, представленное нижеприведенной формулой 22, задаваемое относительно каждого μ, и wμ представляет один из K MK+M+2K-мерных единичных векторов, образующих базис K-мерного пространства сингулярных значений матрицы D, заданной нижеприведенной формулой 23. Заметим, что каждое из λμ и ρμ представляет вспомогательную координату, независимую от RS, наподобие ϕiμ.
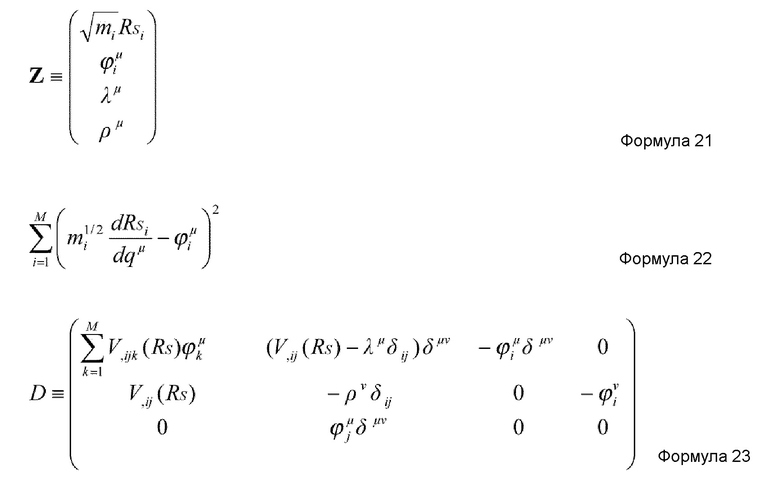
Предпочтительно, в устройстве имитационного моделирования настоящего изобретения, средство извлечения координат является средством, которое вычисляет член третьей производной потенциальной энергии на основании нижеприведенной формулы 24. ϕi представляет i-ю составляющую произвольного вектора, и n задается нижеприведенной формулой 25.
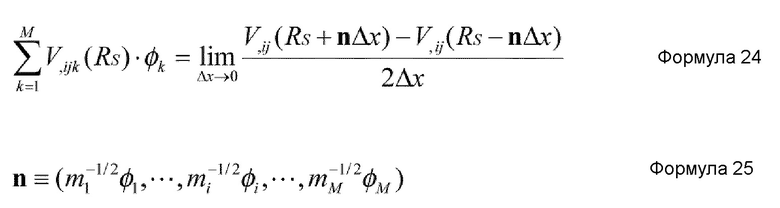
Предпочтительно, в устройстве имитационного моделирования настоящего изобретения, средство задания координат является средством, которое задает репрезентативные координаты, извлеченные из и представляющие каждую характеристическую частичную структуру структуры системы точечных масс в качестве медленных координат.
Используемый здесь термин “характеристическая частичная структура” означает частичную структуру структуры системы точечных масс, имеющую морфологические и/или функциональные характеристики.
В устройстве имитационного моделирования настоящего изобретения, система точечных масс может представлять собой многоатомную систему, который включает в себя биологическую макромолекулу, частичная структура может представлять собой вторичную структуру, строительный блок или основную цепь биологической макромолекулы, и репрезентативная координата каждой частичной структуры является координатой каждого из атомов, составляющих частичную структуру, координатой, заданной путем объединения координат атомов, или шагом частичных структур.
В устройстве имитационного моделирования настоящего изобретения, если система точечных масс является многоатомной системой, которая включает в себя биологическую макромолекулу, предпочтительно, чтобы биологическая макромолекула была белком, частичная структура была вторичной структурой белка, и репрезентативная координата вторичной структуры была координатой центра тяжести группы атомов, составляющей вторичную структуру, или углом сгиба вторичной структуры. В этом случае, предпочтительно, чтобы вторичная структура была, по меньшей мере, одной из спиральной структуры, β-листа, витка, петли и случайной спирали.
Кроме того, в устройстве имитационного моделирования настоящего изобретения, если система точечных масс является многоатомной системой, которая включает в себя биологическую макромолекулу, предпочтительно, чтобы биологическая макромолекула была белком, частичная структура была остатком белка, и репрезентативная координата остатка была координатой центра тяжести группы атомов, составляющих остаток.
Кроме того, в устройстве имитационного моделирования настоящего изобретения, если система точечных масс является многоатомной системой, которая включает в себя биологическую макромолекулу, предпочтительно, чтобы биологическая макромолекула была белком, частичная структура была основной цепью белка, и репрезентативная координата основной цепи была координатой каждого атома составляющего основную цепь.
Кроме того, в устройстве имитационного моделирования настоящего изобретения, если система точечных масс является многоатомной системой, которая включает в себя биологическую макромолекулу, предпочтительно, чтобы биологическая макромолекула была нуклеиновой кислотой, частичная структура была вторичной структурой нуклеиновой кислоты, и репрезентативная координата вторичной структуры была координатой центра тяжести группы атомов, составляющей вторичную структуру, или углом сгиба вторичной структуры. В этом случае, предпочтительно, чтобы вторичная структура была спиральной структурой.
Кроме того, в устройстве имитационного моделирования настоящего изобретения, если система точечных масс является многоатомной системой, которая включает в себя биологическую макромолекулу, предпочтительно, чтобы биологическая макромолекула была нуклеиновой кислотой, частичная структура была остатком нуклеиновой кислоты, и репрезентативная координата остатка была координатой центра тяжести группы атомов, составляющих остаток.
Кроме того, в устройстве имитационного моделирования настоящего изобретения, если система точечных масс является многоатомной системой, которая включает в себя биологическую макромолекулу, предпочтительно, чтобы биологическая макромолекула была нуклеиновой кислотой, частичная структура была основной цепью нуклеиновой кислоты, и репрезентативная координата основной цепи была координатой каждого атома составляющего основную цепь.
Кроме того, в устройстве имитационного моделирования настоящего изобретения, если система точечных масс является многоатомной системой, которая включает в себя биологическую макромолекулу, предпочтительно, чтобы биологическая макромолекула была нуклеиновой кислотой, частичная структура была спиральной структурой нуклеиновой кислоты, и репрезентативная координата спиральной структуры была шагом спиральной структуры.
Кроме того, в устройстве имитационного моделирования настоящего изобретения, многоатомная система может включать в себя молекулу-кандидат на связывание для биологической макромолекулы.
Способ имитационного моделирования настоящего изобретения представляет собой способ, используемый с вышеописанным устройством имитационного моделирования для прогнозирования поведения системы точечных масс, образованной моделируемыми N точечными массами, причем способ включает в себя этапы, на которых:
задают медленные координаты, которые представляют собой M координат, в основном, предполагающих структурное изменение в системе точечных масс на основании 3N координат точечных масс, описывающих структуру системы точечных масс;
задают быстрые координаты, которые являются координатами, описывающими структуру системы точечных масс, и не зависят от медленных координат;
получают структуру быстрых координат как функции медленных координат путем подчинения быстрых координат медленным координатам;
получают, с учетом влияния изменения быстрых координат на медленные координаты вследствие изменения медленных координат, структуру медленных координат как функции K коллективных координат общей координаты, которая связана с медленными координатами каноническим преобразованием, причем общая координата образована переменной составляющей, которая изменяется со временем, и постоянной составляющей, которая служит константой относительно времени, и K коллективных координат являются переменной составляющей общей координаты; и
прогнозируют временную эволюцию системы точечных масс на основании коллективной(ых) координаты() как функции времени, которую(ые) можно получить, решая уравнение движения относительно коллективной(ых) координаты(), структуры медленных координат и структуры быстрых координат.
Программа имитационного моделирования настоящего изобретения представляет собой программу, которая предписывает компьютеру осуществлять вышеописанный способ имитационного моделирования.
Компьютерно-считываемый носитель записи настоящего изобретения представляет собой носитель, на котором записана вышеописанная программа имитационного моделирования.
Устройство имитационного моделирования настоящего изобретения включает в себя вышеописанные средство задания координат, средство извлечения координат и средство обратного преобразования, и прогнозирует временную эволюцию координат точечных масс, вводя иерархически упорядоченные медленные координаты, извлекая, с учетом влияния изменения быстрых координат на медленные координаты вследствие изменения медленных координат, коллективную координату в теории коллективного движения, которая описывает коллективное и собственное поведение системы точечных масс, и решая уравнение движения относительно коллективной координаты. Таким образом, извлечение коллективной координаты позволяет осуществлять имитационное моделирование на атомном уровне, и введение медленных координат позволяет сокращать количество координат, обрабатываемых для извлечения коллективной координаты. В результате, можно добиться, как повышения точности вычисления, так и сокращения времени вычисления при имитационного моделирования для прогнозирования динамического поведения системы точечных масс.
Способ имитационного моделирования настоящего изобретения представляет собой способ, используемый с вышеописанным устройством имитационного моделирования, и предусматривает прогнозирование временной эволюции координат точечных масс посредством ввода иерархически упорядоченных медленных координат, извлечения, с учетом влияния изменения быстрых координат на медленные координаты вследствие изменения медленных координат, коллективной координаты в теории коллективного движения, которая описывает коллективное и собственное поведение системы точечных масс, и решения уравнения движения относительно коллективной координаты. Таким образом, извлечение коллективной координаты позволяет осуществлять имитационное моделирование на атомном уровне, и введение медленных координат позволяет сокращать количество координат, обрабатываемых для извлечения коллективной координаты. В результате, можно добиться, как повышения точности вычисления, так и сокращения времени вычисления при имитационного моделирования для прогнозирования динамического поведения системы точечных масс.
Программа и носитель записи настоящего изобретения могут предписывать осуществление вышеупомянутого способа имитационного моделирования, что позволяет достигать повышенной точности вычисления и сокращенного времени вычисления в имитационного моделирования для прогнозирования динамического поведения системы точечных масс.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Фиг. 1 - схема, демонстрирующая процесс связывания белка и молекулы-кандидата на связывание в случае, когда индуцированное соответствие учитывается в способе имитационного моделирования настоящего изобретения.
Фиг. 2 - схема, демонстрирующая путь реакции на принципиальной потенциальной поверхности многоатомной системы, которая включает в себя белок и молекулу-кандидат на связывание, где учитывается индуцированное соответствие.
Фиг. 3 - вид, принципиально демонстрирующий процесс для получения пути реакции многоатомной системы с использованием извлечения коллективной координаты.
Фиг. 4 иллюстрирует принцип преобразования переменных и обратного преобразования.
Фиг. 5 - блок-схема устройства имитационного моделирования согласно варианту осуществления, схематически демонстрирующая его конфигурацию.
Фиг. 6A - блок-схема операций, схематически демонстрирующая этапы вычисления способа имитационного моделирования согласно варианту осуществления.
Фиг. 6B - блок-схема операций, схематически демонстрирующая этапы вычисления способа имитационного моделирования согласно варианту осуществления.
Фиг. 7 схематически иллюстрирует соотношение между медленными координатами RS, быстрыми координатами RF и атомными координатами x.
Фиг. 8 - график, демонстрирующий путь реакции заранее определенного составного тела, полученного способом имитационного моделирования согласно варианту осуществления.
Фиг. 9 - схема, демонстрирующая процесс связывания составного тела, показанного на графике на Фиг. 8, в котором A и B иллюстрируют начальное состояние и конечное состояние процесса связывания составного тела соответственно.
Фиг. 10 - график, демонстрирующий результат сравнения между вычислением, в котором произвольность знака исключается, и вычислением, в котором произвольность знака не исключается.
ПРЕДПОЧТИТЕЛЬНЫЕ ВАРИАНТЫ ОСУЩЕСТВЛЕНИЯ ИЗОБРЕТЕНИЯ
Вариант осуществления настоящего изобретения будет описан ниже со ссылкой на прилагаемые чертежи, но следует понимать, что настоящее изобретение не ограничивается вариантом осуществления. Заметим, что каждая деталь в чертежах не обязательно изображена в масштабе для простоты визуального распознавания.
Прежде чем перейти к подробному описанию, сначала опишем техническую идею, лежащую в основе настоящего изобретения, и предпосылки настоящего изобретения для пояснения технических преимуществ настоящего изобретения над уровнем техники. Для наглядности объяснения, конкретное описание будет приведено для случая прогнозирования динамического поведения многоатомной системы, которая включает в себя составное тело биологической макромолекулы и молекулы-кандидаты на связывание.
Прогнозирование динамического поведения многоатомной системы наподобие вышеописанной играет важную роль, например, при разработке нового лекарственного препарата с точки зрения сокращения периода и стоимости разработки. Физиологически активное вещество, например лекарственный препарат, может демонстрировать химическое свойство за счет связывания с конкретным белком. Поэтому при разработке нового лекарственного препарата необходимо сужать круг кандидатов, которые с большой вероятностью связываются с целевым белком, из большого количества соединений в пределах от нескольких сотен тысяч до нескольких миллионов (лекарственный скрининг). Кроме того, в конце концов, требуется сужать круг кандидатов в лекарственные препараты до нескольких кандидатов. Чтобы эффективно сужать круг кандидатов в лекарственные препараты от большого количества соединений, необходимо рассматривать поведение многоатомной системы на атомном уровне и точно оценивать взаимодействия между молекулами и, далее, между атомами.
На Фиг. 1 показана схема, демонстрирующая процесс связывания белка и молекулы-кандидата на связывание в случае, при рассмотрении динамического поведения белка. Белок 2 имеет карман 4 для связывания молекулы-кандидата 6 на связывание. То есть можно сказать, что молекула-кандидат 6 на связывание является физиологически активным веществом белка 2. Заметим однако, что карман 4 не обязательно имеет форму, которая позволяет молекуле-кандидату 6 на связывание непосредственно усаживаться в нем (Фиг. 1a). Например, Фиг. 1 иллюстрирует, что размер отверстия кармана 4 меньше, чем размер молекулы-кандидата 6 на связывание. Следовательно, в таком случае, белок 2 изменяет свою структуру, чтобы адаптировать форму и размер отверстия к форме и размеру молекулы-кандидата 6 на связывание согласно взаимодействию с приближающейся молекулой-кандидатом 6 на связывание (Фиг. 1b и c).
Явление, состоящее в том, что биологическая макромолекула, например, белок, нуклеиновая кислота, и т.п., изменяет свою структуру в результате взаимодействия с физиологически активным веществом вышеописанным образом, именуется “индуцированным соответствием”. Для точного вычисления взаимодействия между молекулами, естественно, следует учитывать “индуцированное соответствие”. Это можно реализовать, рассматривая многоатомную систему на атомном уровне.
На Фиг. 2 показана схема, демонстрирующая путь реакции на принципиальной потенциальной поверхности многоатомной системы, в которой учитывается индуцированное соответствие. Горизонтальная ось X1 на Фиг. 2 принципиально иллюстрирует структурное изменение в белке, и вертикальная ось X2 иллюстрирует расстояние между белком и молекулой-кандидатом на связывание. Таким образом, Фиг. 2 представляет потенциальную поверхность многоатомной системы согласно структурному изменению в белке и расстоянию между молекулами. Как показано на Фиг. 2, система, в которой возникает индуцированное соответствие, имеет энергетический барьер B (седловую точку) на пути RP реакции, соединяющем две стабильные точки (точку A, в которой составное тело находится в диссоциированных телах, и точку B, в которой связывание составного тела завершено).
Таким образом, анализ процесса связывания белка 2 и молекулы-кандидата 6 на связывание с учетом индуцированного соответствия сводится, в сущности, к поиску пути реакции, соединяющего две стабильные точки A и C, через энергетический барьер B на потенциальной поверхности по отношению к белку 2 и молекуле-кандидату 6 на связывание.
Ввиду вышеизложенного, для достижения повышенной точности вычисления и сокращенного времени вычисления в имитационного моделирования для прогнозирования динамического поведения многоатомной системы, необходимо иметь возможность рассматривать многоатомную систему на атомном уровне и облегчать поиск неэмпирического пути реакции.
Однако поведение многоатомной системы, содержащей от нескольких тысяч до нескольких миллионов атомов, является медленным, и большая деформация, которая возникает в масштабе времени порядка от получаса до часа. В связи с этим, традиционные способы имитационного моделирования сталкиваются с проблемой, состоящей в том, что теоретическое вычисление требует большого количества времени, нескольких декад, хотя они могут рассматривать многоатомную систему на атомном уровне. Следовательно, чтобы иметь возможность осуществлять теоретическое вычисление поведения многоатомной системы в течение практически приемлемого периода времени, были изучены или разработаны различные способы имитационного моделирования. Метод молекулярной динамики, в котором прилагается “движущая сила”, является одним из таких способов имитационного моделирования, но он сталкивается с вышеупомянутой проблемой. Также исследуется другой способ, который сокращает объем вычислений за счет аппроксимации целевого белка твердым телом и уменьшения количества используемых переменных. Однако такое грубое приближение, естественно, не может учитывать влияние динамического поведения белка, что не позволяет точно вычислять взаимодействия, действующие между молекулами. В таком случае, например, один миллион соединений-кандидатов можно сузить лишь до около десяти тысяч соединений в качестве кандидатов в лекарственные препараты. Проблема компромиссного соотношения между временем вычисления и точностью вычисления сохраняется и в других способах имитационного моделирования.
Автор настоящего изобретения предложил идею моделировать многоатомную систему, которая включает в себя биологическую макромолекулу, системой точечных масс, имеющей N точечных масс, и рассматривать поведение системы точечных масс как коллективное движение, и извлекать коллективную координату, имеющую меньшую степень свободы, чем у координат точечных масс (координат точечных масс, которые одномерно описывают структуру системы точечных масс) из коллективного движения на основании координат точечных масс.
Коллективная координата
Ниже будет описана коллективная координата. В общем случае, термин “коллективная координата” означает элемент координаты коллективной переменной. Термин “коллективная переменная” означает одну из общих переменных (q, p), связанных с каноническими переменными системы точечных масс (координатами точечных масс и импульсом точечных масс в системе точечных масс) каноническим преобразованием, имеющим меньшую степень свободы, чем каноническая переменная. В общей переменной (q, p), связанной каноническим преобразованием, q представляет элемент координаты, и p представляет элемент импульса. Элемент q координаты и элемент p импульса задаются нижеприведенными формулами 26 и 27, соответственно.
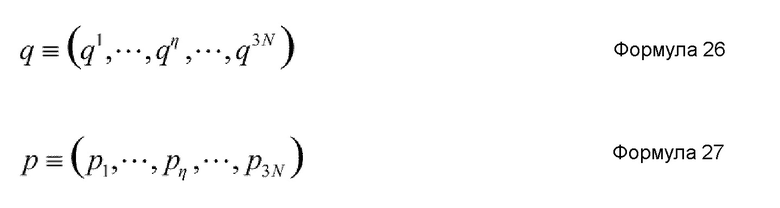
В формулах 26 и 27, η представляет целое число в диапазоне от 1 до 3N.
Таким образом, с использованием q† и p†, заданных, соответственно, нижеприведенными формулами 28 и 29, коллективную переменную можно представить как (q†,p†).
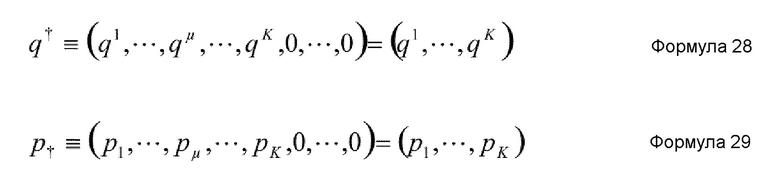
Формулы 28 и 29 указывают, что коллективная переменная (q†,p†) включает в себя 2K переменных, указанных индексом μ=1~K в каждой из формул 28 и 29. Другими словами, можно сказать, что коллективная переменная (q†,p†) является общей координатой, образованной переменной составляющей, которая изменяется со временем (q1, q2, -----, qK, p1, p2, -----, pK), и постоянной составляющей, которая служит константой относительно времени (qK+1=0, qK+2=0, -----, q3N=0, pK+1=0, pK+2=0, -----, p3N=0), переменной составляющей. Хотя формулы 28 и 29 указывают, что постоянная составляющая принимает значение нуль как константа, но константа не ограничивается нулем.
Тогда, поскольку коллективная координата является элементом координаты коллективной переменной (q†,p†), ее можно представить как q†. В частности, коллективная координата является набор переменных, образованным (q1, q2, -----, qK). Заметим, что коллективную координату можно получить только из координат точечных масс каноническим преобразованием.
Преобразование переменных из координат, подлежащих рассмотрению как коллективное движение, в коллективные координаты, имеющие меньшую степень свободы, вышеописанным образом, также именуется “разделением переменных”.
Не существует никаких ограничений на степень свободы коллективной координаты при условии, что она меньше, чем у целевых координат разделения переменных. Однако, поскольку уменьшение степени свободы облегчает последующие вычислительные операции, степень свободы коллективной координаты, предпочтительно равна 1 (то есть K=1).
Рассмотрение в качестве коллективного движения
Осуществление разделения переменных на координатах точечных масс позволяет описывать собственное движение, то есть коллективное движение более низкой размерности в поведении системы точечных масс коллективной координатой q†. В результате, описание движения 3N-мерными координатами точечных масс заменяется описанием движения K-мерной коллективной координатой q†, что упрощает описание движения системы точечных масс. В частности, уравнение движения, описанное координатами точечных масс, упрощается до комбинации структуры x=x(q†) координаты x точечной массы, имеющей коллективную координату q† в качестве аргумента, и уравнения движения относительно q†. Заметим, что x представляет (x1, x2, -----, x3N). Конкретная структура координат точечных масс представляет режим поведения как коллективное движение системы точечных масс, и уравнение движения относительно коллективной координаты q† представляет основной закон поведения. Таким образом, по мере уменьшения степени свободы рассматриваемых переменных для решения уравнения движения, теоретические вычисления упрощаются.
Затем разделение переменных осуществляется на координате x точечной массы для нахождения пути реакции на потенциальной поверхности относительно коллективной координаты q†, и коллективная координата q† обратно преобразуется в координату x точечной массы для представления пути реакции на потенциальной поверхности относительно координаты x точечной массы. Таким образом, можно получить путь реакции системы точечных масс. Согласно вышеупомянутому способу, преобразование переменных из коллективной координаты q† в координату x точечной массы осуществляется только после решения уравнения движения более низкой размерности. Таким образом, системе точечных масс не будет присущ захват локальным минимумом.
В порядке примера на Фиг. 2 показан принципиальный процесс для получения пути реакции многоатомной системы, которая включает в себя составное тело. Фиг. 3 - это чертеж, принципиально демонстрирующий процесс для получения пути реакции многоатомной системы с использованием извлечения коллективной координаты. Сначала потенциальная поверхность относительно координат точечных масс X1, X2 (Фиг. 3a) преобразуется в потенциальную поверхность извлеченных коллективных координат q1, q2 (Фиг. 3b). Здесь, в качестве коллективных координат важно использовать коллективные координаты, в которых две стабильные точки A, C и энергетический барьер B выровнены на прямой. Путь RP реакции, соединяющий две стабильные точки A, C можно сразу же вычертить (Фиг. 3b) на потенциальной поверхности относительно таких коллективных координат q1, q2. После этого координаты подвергаются обратному преобразованию, и получается путь RP реакции на потенциальной поверхности относительно переменных X1, X2 (Фиг. 3c). Полученная здесь одномерная траектория может представлять собой переменные, идентифицированные как “реакционная координата”, которая давно используется в теоретической химии.
Проблема с рассмотрением поведения многоатомной системы, которая включает в себя биологическую макромолекулу, как коллективного движения
Разделение переменных осуществляется на основании теории коллективного движения. В качестве одной из теорий коллективного движения можно упомянуть, например, метод самосогласованной коллективной координаты (SCC). Метод SCC является одной из теорий коллективного движения в физике, которая изучается в области атомного ядра. В частности, метод SCC является теорией движения, которая получает внутренние коллективные переменные, описывающие коллективное движение системы, затем находит дискретное многообразие из 6N-мерного фазового пространства, построенного на канонических переменных, входящих в гамильтониан системы, и описывает коллективное движение гамильтонианом, заданным на дискретном многообразии или его окрестности. Используемый здесь термин “дискретное многообразие” означает частичное пространство 6N-мерного фазового пространства, построенного на канонических переменных, входящих в гамильтониан системы, в котором заключена траектория, представляющая поведение системы. Таким образом, в случае, когда любая произвольная точка в дискретном многообразии берется как начальное значение, траектория всегда заключена в дискретном многообразии. Дополнительную информацию о методе SCC можно найти в S. Tomonaga, “Elementary Theory of Quantum-Mechanical Collective Motion of Particles, II”, Progress of Theoretical Physics, Vol. 13, No. 5, pp. 482-496, 1955, T. Marumori et al., “Self-Consistent Collective-Coordinate Method for the Large-Amplitude Nuclear Collective Motion”, Progress of Theoretical Physics, Vol. 64, No. 4, pp. 1294-1314, 1980, and G.D. Dang et al., “Self-consistent theory of large-amplitude collective motion: applications to approximate quantization of nonseparable systems and to nuclear physics”, Physics Reports, Vol. 335, Issues 3-5, pp. 93-274, 2000, и пр.
Таким образом, можно предположить, что замещая нуклон (протон и нейтрон), рассматриваемый в ядерной реакции, атомом, рассматриваемом в химической реакции, и применяя метод SCC, можно рассматривать динамическое поведение многоатомной системы как коллективное движение и можно получить путь реакции многоатомной системы.
Автор настоящего изобретения недавно обнаружил, что прямое применение традиционной теории коллективного движения, например метода SCC, к крупномасштабной системе наподобие системы, которая включает в себя биологическую макромолекулу, которая является предметом настоящего изобретения, не позволяет в достаточной степени повысить точность вычисления и сократить время вычисления. Это обусловлено тем, что, в отличие от ядерной реакции, которая требует рассмотрения, самое большее, нескольких сотен нуклонов, химическая реакция многоатомной системы, которая включает в себя биологическую макромолекулу в воде, требует рассмотрения от нескольких тысяч до нескольких миллионов атомов. Таким образом, в существующем подходе, хотя и основанном на теории коллективного движения, контроль переменных, т.е. разделение переменных, усложняется.
Вышеупомянутая проблема не ограничивается случаем получения пути реакции многоатомной системы, которая включает в себя составное тело. Таким образом, в более общем смысле, легко представить, что такая же проблема возникает в случае получения пути реакции системы, которая включает в себя биологическую макромолекулу.
ОПИСАНИЕ ИЗОБРЕТЕНИЯ
В ходе вышеописанного исследования автор настоящего изобретения изобрел устройство имитационного моделирования и способ имитационного моделирования для прогнозирования динамического поведения системы точечных масс на основе новой теории коллективного движения, которая описывает коллективное движение коллективными координатами, имеющими меньшую степень свободы, чем у координат точечных масс, и применима к структурному вычислению многоатомной системы, которая включает в себя биологическую макромолекулу, которая является большой группой атомов, и программу и носитель записи для реализации способа.
В частности, устройством имитационного моделирования согласно настоящему изобретению является устройство для прогнозирования поведения системы точечных масс, образованной моделируемыми N точечными массами, причем устройство включает в себя:
средство задания координат для задания медленных координат, которые представляют собой M координат, в основном, предполагающих структурное изменение в системе точечных масс на основании 3N координат точечных масс, описывающих структуру системы точечных масс, и быстрых координат, которые являются координатами, описывающими структуру системы точечных масс, и не зависят от медленных координат;
средство извлечения координат для получения структуры быстрых координат как функции медленных координат путем подчинения быстрых координат медленным координатам и получения, с учетом влияния изменения быстрой координаты на медленные координаты вследствие изменения медленных координат, структуры медленных координат как функции K коллективных координат общей координаты, которая связана с медленными координатами каноническим преобразованием, причем общая координата образована переменной составляющей, которая изменяется со временем, и постоянной составляющей, которая служит константой относительно времени, и K коллективных координат являются переменной составляющей общей координаты; и
средство обратного преобразования для прогнозирования временной эволюции системы точечных масс на основании коллективной(ых) координаты() как функции времени, которую(ые) можно получить, решая уравнение движения относительно коллективной(ых) координаты(), структуры медленных координат и структуры быстрых координат.
Способ имитационного моделирования настоящего изобретения представляет собой способ, используемый с вышеупомянутым устройством имитационного моделирования для прогнозирования поведения системы точечных масс, образованной моделируемыми N точечными массами, причем способ включает в себя этапы, на которых:
задают медленные координаты, которые представляют собой M координат, в основном, предполагающих структурное изменение в системе точечных масс на основании 3N координат точечных масс, описывающих структуру системы точечных масс;
задают быстрые координаты, которые являются координатами, описывающими структуру системы точечных масс, и не зависят от медленных координат;
получают структуру быстрых координат как функции медленных координат путем подчинения быстрых координат медленным координатам;
получают, с учетом влияния изменения быстрых координат на медленные координаты вследствие изменения медленных координат, структуру медленных координат как функции K коллективных координат общей координаты, которая связана с медленными координатами каноническим преобразованием, причем общая координата образована переменной составляющей, которая изменяется со временем, и постоянной составляющей, которая служит константой относительно времени, и K коллективных координат являются переменной составляющей общей координаты; и
прогнозируют временную эволюцию системы точечных масс на основании коллективной(ых) координаты() как функции времени, которую(ые) можно получить, решая уравнение движения относительно коллективной(ых) координаты(), структуры медленных координат и структуры быстрых координат.
Программа имитационного моделирования согласно настоящему изобретению представляет собой программу, которая предписывает компьютеру осуществлять вышеописанный способ имитационного моделирования.
Компьютерно-считываемый носитель записи согласно настоящему изобретению представляет собой носитель, на котором записана вышеописанная программа имитационного моделирования.
Используемый здесь термин “система точечных масс, имеющая N точечных масс” означает, что суммарное количество точечных масс, которые являются составными элементами системы точечных масс, равно N.
Средство задания координат
Средство задания координат является средством для задания медленных координат, которые представляют собой M координат, в основном, предполагающих структурное изменение в системе точечных масс на основании 3N координат точечных масс, описывающих структуру системы точечных масс, и быстрых координат, которые являются координатами, описывающими структуру системы точечных масс, и не зависят от медленных координат. Используемый здесь термин “3N координат точечных масс”, в частности, означает координаты N точечных масс в трехмерном пространстве.
Сначала средство задания координат задает M медленных координат, которые, в основном, предполагают структурное изменение в системе точечных масс при описании макроскопического коллективного движения (коллективного движения большой амплитуды) системы точечных масс на основании структуры координат точечных масс. Затем средство извлечения координат осуществляет разделение переменных на медленных координатах. Другими словами, в настоящем изобретении, независимые координаты из тех, которые описывают систему точечных масс, оказывающие незначительное влияние на структурное изменение в системе точечных масс, обусловленное коллективным движением большой амплитуды координат точечных масс, исключаются, поскольку они заранее известны из цели разделения переменных в теории коллективного движения. Таким образом, вычисление для разделения переменных упрощается путем извлечения коллективных координат из M-мерных медленных координат вместо извлечения из 3N-мерных координат точечных масс. Здесь, M - целое число, которое удовлетворяет условию K<M<3N. K представляет количество элементов коллективной координаты q†, как в формулах 28 и 29.
Заметим, что дальнейшее иерархическое упорядочение может осуществляться из медленных координат. Таким образом, на основании структуры медленных координат, заданной вышеописанным образом, можно задавать вторичные медленные координаты, имеющие более низкую размерность, и из вторичных медленных координат можно извлекать коллективную координату.
Медленные координаты задаются на основании степени влияния коллективного движения большой амплитуды на структурное изменение в системе точечных масс. Координаты, оказывающие большое влияние, более пригодны в качестве медленных координат. Другими словами, способ задания медленных координат и их конкретное содержание зависят от типа целевого коллективного движения большой амплитуды системы точечных масс.
В частности, медленные координаты задаются с использованием некоторых из координат точечных масс, координат, которые можно задавать путем объединения координат точечных масс, или их комбинации. Предпочтительно, медленные координаты задаются, например, в отношении характеристической частичной структуры для структуры системы точечных масс. В этом случае, более предпочтительно, чтобы каждая из медленных координат была репрезентативной координатой, извлеченной из каждой характеристической частичной структуры и представляла частичную структуру. Множество репрезентативных координат можно задавать одной характеристической частичной структуре.
Используемый здесь термин “характеристическая частичная структура” означает часть структуры системы точечных масс, имеющую морфологические и/или функциональные характеристики. В случае, когда система точечных масс является многоатомной системой, которая включает в себя биологическую макромолекулу, характеристической частичной структурой является, например, вторичная структура (частичная структура укладки) биологической макромолекулы, строительный блок биологической макромолекулы и основная цепь биологической макромолекулы. Используемый здесь термин “репрезентативная координата” характеристической частичной структуры означает координату, репрезентативно указывающую характеристическую частичную структуру. Репрезентативной координатой является, например, сама координата точечной массы (атома), составляющей характеристическую частичную структуру, координата, которую можно задавать путем объединения координат точечных масс (атомов), циклический интервал частичных структур и т.п.
В частности, в случае, когда биологическая макромолекула является белком, вторичную структуру белка можно называть характеристической частичной структурой. Конкретные вторичные структуры включают в себя спиральные структуры (310 спираль, α спираль, п спираль, β спираль, и пр.), β лист, виток, петлю, случайную спираль, и пр. Что касается репрезентативной координаты вторичной структуры, можно назвать координату центра тяжести группы атомов, составляющей вторичную структуру, или угол сгиба вторичной структуры. Например, количество характеристических частичных структур (структур более высокой размерности), включенных в общий белок, составляет от нескольких единиц до, самое большее, нескольких дюжин. Это может значительно сокращать количество целевых переменных для разделения переменных. В случае прогнозирования хода реакции связывания между биологической макромолекулой и молекулой-кандидатом на связывание, саму структуру кандидата на связывание можно рассматривать как одну из характеристических частичных структур многоатомной системы.
Иначе, в случае, когда биологическая макромолекула является белком, характеристической частичной структурой может быть остаток белка (аминокислотный участок, который является строительным блоком белка, включающий в себя n-концевой остаток и c-концевой остаток). Затем, что касается репрезентативной координаты в отношении остатка белка, можно назвать координату центра тяжести группы атомов, составляющей остаток.
Кроме того, в случае, когда биологическая макромолекула является белком, характеристической частичной структурой может быть основная цепь белка. Затем, что касается репрезентативной координаты в отношении основная цепь белка, можно назвать координаты соответствующих атомов, составляющих основную цепь.
Иначе, в случае, когда биологическая макромолекула является нуклеиновой кислотой, характеристической частичной структурой может быть вторичная структура нуклеиновой кислоты. Конкретной вторичной структурой может быть спиральная структура и т.п. В случае спиральной структуры, каждый заранее определенный шаг рассматривается как характеристическая частичная структура. Затем, что касается репрезентативной координаты в отношении вторичной структуры нуклеиновой кислоты, можно назвать координату центра тяжести группы атомов, составляющей вторичную структуру, или можно назвать угол сгиба вторичной структуры.
Иначе, в случае, когда биологическая макромолекула является нуклеиновой кислотой, характеристической частичной структурой может быть остаток нуклеиновой кислоты (нуклеотидный участок, который является строительным блоком нуклеиновой кислоты). Затем, что касается репрезентативной координаты в отношении остатка нуклеиновой кислоты, можно назвать координату центра тяжести группы атомов, составляющей остаток.
Кроме того, в случае, когда биологическая макромолекула является нуклеиновой кислотой, характеристической частичной структурой может быть основная цепь нуклеиновой кислоты. Затем, что касается репрезентативной координаты в отношении основной цепи нуклеиновой кислоты, можно назвать координаты соответствующих атомов, составляющих основную цепь.
Иначе, в случае, когда биологическая макромолекула является нуклеиновой кислотой и спиральной структурой нуклеиновой кислоты, в качестве репрезентативной координаты можно использовать интервал шага спиральной структуры.
Определение, как фактически задавать характеристическую частичную структуру, производится надлежащим образом согласно структуре и/или явлению имитационного моделирования целевой системы точечных масс. Например, в случае, когда целью анализа является процесс формирования структуры укладки белка или процесс формирования спиральной структуры нуклеиновой кислоты, предпочтительно использовать основную цепь, которую можно назвать строительным блоком биологической макромолекулы или фундаментальным скелетом биологической макромолекулы, в качестве характеристической частичной структуры. В отношении основной цепи биологической макромолекулы, одну основную цепь, связанную ковалентными связями, можно целиком использовать в качестве одной характеристической частичной структуры, или каждую частичную структуру, полученную делением одной основной цепи, можно использовать в качестве характеристической частичной структуры. В случае, когда целью анализа является ход реакции связывания между белком и молекулой-кандидатом на связывание, каждый(ую) из спиральной структуры, β листа, витка, петли, случайной спирали, и пр. или их комбинацию можно использовать в качестве характеристической частичной структуры, отличной от вышеописанной основной цепи. Характеристическая частичная структура может включать в себя множество вторичных структур. Таким образом, каждую из вторичных структур можно рассматривать как одну характеристическую частичную структуру, или множество соседних вторичных структур вдоль основной цепи можно группировать в качестве одной характеристической частичной структуры. Кроме того, в случае, когда целью анализа является реакция, в которой ингибитор захватывается и связывается со спиральной структурой нуклеиновой кислоты, также можно использовать вышеописанную основную цепь, периодическую структуру спиральной структуры, или их комбинацию. В отношении спиральной структуры, полный объем можно использовать в качестве одной характеристической частичной структуры или каждой частичной структуры, полученный делением спиральной структуры с заранее определенным шагом можно использовать в качестве характеристической частичной структуры.
“Быстрые координаты” это координаты, описывающие структуру системы точечных масс, и не зависящие от медленных координат. Как и в медленных координатах, быстрые координаты задаются с использованием некоторых из координат самих точечных масс, включенных в систему точечных масс, координат, которые можно задавать путем объединения координат точечных масс, или их комбинации. В зависимости от комбинации координат точечных масс, участок формирования быстрых координат можно представить некоторым медленным координатам. Однако поскольку быстрые координаты не зависят от медленных координат, формирование быстрых координат никогда не представляются лишь некоторыми медленными координатами. В случае, когда координаты некоторых из точечных масс задаются как медленные координаты, быстрые координаты являются координатами N точечных масс за минусом точечных масс, заданных в качестве медленных координат. В случае, когда только координаты, которые можно задавать путем объединения координат точечных масс задаются в качестве медленных координат, быстрые координаты являются координатами, которые можно задавать путем объединения всех или некоторых из координат точечных масс, и не зависящими от медленных координат.
Опишем два примера конкретных способов задания медленных координат.
Один примерный способ представляет собой способ, в котором N атомов, входящих в многоатомную систему, группируются по отношению к каждой характеристической частичной структуре для извлечения центра тяжести для каждой группы и только координаты этих центров тяжести задаются как медленные координаты. В этом случае, предпочтительно, чтобы каждая быстрая координата была относительной и независимой координатой относительно координаты центра тяжести частичной структуры, которой принадлежат атомы. Таким образом, количество быстрых координат равно 3N-M. Это обусловлено тем, что, когда 3N координат точечных масс разделены на M координат центров тяжести и 3N относительных координат, M реляционных выражений возникает между относительными координатами по определению, т.е. M относительных координат всех относительных координат не являются независимыми координатами. Этот способ предусматривает, что позиционное соотношение между характеристическими частичными структурами оказывает значительное влияние на структурное изменение в многоатомной системе вследствие коллективного движения большой амплитуды. Масштаб деформации самой характеристической частичной структуры мал, и масштаб времени деформации короче, чем у химической реакции, поэтому влияние деформации на структурное изменение в многоатомной системе мало.
Другой примерный способ представляет собой способ, в котором координата каждого из атомов, составляющих основную цепь биологической макромолекулы, задается как медленная координата. В этом случае, предпочтительно, чтобы координаты других атомов, например, боковая цепь и сольватация, задаются как быстрые координаты. Таким образом, количество быстрых координат равно 3N-M. Этот способ предусматривает, что форма многоатомной системы оказывает значительное влияние на структурное изменение в многоатомной системе вследствие коллективного движения большой амплитуды. Поскольку боковая цепь движется зависимо от основной цепи, влияние деформации боковой цепи на структурное изменение в многоатомной системе мало. В этом случае, если молекула, отличная от биологической макромолекулы, например, молекула-кандидат на связывание и т.п., включена в многоатомную систему, центр тяжести молекулы можно задавать как медленную координату. В этом случае, например, координаты атомов, составляющих молекулу, задаются как быстрые координаты.
Заметим, что первый вариант осуществления, описанный далее, использует первый способ задания.
Предпочтительно, медленные координаты задаются после осуществления полной структурной релаксации в состоянии, в котором все точечные массы освобождены (состоянии, не привязанном к системе точечных масс) по мере необходимости. Используемый здесь термин “полная структурная релаксация” означает, что координаты точечных масс перемещаются так, что потенциальная энергия системы точечных масс постоянно снижается от надлежащего начального состояния пока градиент потенциальной энергии не обратится в нуль. В общем случае, термин “полная структурная релаксация” является синонимом так называемой структурной релаксации, и этот термин используется для указания отличия от частичной структурной релаксации, которая будет описана ниже. Состояние системы точечных масс, найденное по полной структурной релаксации, является одним из локальных минимумов вблизи вышеописанного начального состояния. Таким образом, полная структурная релаксация не является операцией для нахождения пути реакции, соединяющего стабильные точки и точку минимума, повторяя подъемы и спуски на потенциальной поверхности. В частности, полная структурная релаксация отличается от “частичной структурной релаксации” тем, что перемещает все атомы, составляющие цель структурной релаксации. Полная структурная релаксация осуществляется с использованием известного метода, например, метода сопряженных градиентов, метода наискорейшего спуска, метода обратного гессиана, и пр.
Средство извлечения координат
Средство извлечения координат является средством для получения структуры быстрых координат как функции медленных координат и структуры медленных координат как функции коллективных координат. Используемый здесь термин “структура быстрых координат как функция медленных координат” означает конкретное содержание функции RF(RS) относительно быстрых координат RF, представленных медленными координатами RS, и используемый здесь термин “структура медленных координат как функции коллективных координат” означает конкретное содержание функции RS(q†) относительно медленных координат RS, представленных коллективной координатой q†.
Структура быстрых координат как функции медленных координат
Структуру RF(RS) быстрых координат можно получить путем подчинения быстрых координат RF медленным координатам RS, т.е. путем задания условного выражения, которое определяет соотношение между быстрыми координатами RF и медленными координатами RS. Не существует никакого конкретного ограничения на условное выражение, и можно использовать, например, нижеприведенное условное выражение формулы 30, полученное из условия адиабатического приближения. Используемый здесь термин “адиабатическое приближение” означает приближение, в котором предполагается, что быстрые координаты RF способны мгновенно следовать за изменением медленных координат RS (см. M. Born, and J.R. Oppenheimer, “On the Quantum Theory of Molecules”, Ann. Physik, Vol. 84, pp. 457-484, 1927 and H. Haken, “Nonequilibrium Phase Transitions and Self-Organization in Physics, Chemistry, and Biology”, Synergetics 2nd Edition, Springer-Verlag, 1978). Формула 30 представляет условие, что, для данного RS, RF находится в локальной стабильной точке потенциальной энергии V, т.е. в точке, где градиент потенциальной энергии V относительно RF равен нулю.

В формуле 30, V(RS,RF) представляет потенциальную энергию системы точечных масс, представленной медленными координатами RS и быстрыми координатами RF. V(RS,RF) можно получить путем подстановки структуры x(RS,RF) координаты x точечной массы определенной, когда медленные координаты RS задаются в потенциальной энергии V(x), представленной координатой x точечной массы. Например, структуру x(RS,RF) координаты x точечной массы можно получить путем получения, на основании структуры RS(x) медленных координат RS и структуры RF(x) быстрых координат RF, определенных, когда заданы медленные координаты RS, их обратных функций.
Заметим, что необходимо осуществлять частое дифференцирование V(RS,RF) по всем быстрым координатам от RF1 до RF(3N-M) для подчинения всех быстрых координат от RF1 до RF(3N-M) медленным координатам RS.
В системе точечных масс, где быстрые координаты RF подчинены медленным координатам RS, быстрые координаты RF представлены через медленные координаты RS согласно нижеприведенной формуле 31, и потенциальная энергия V системы точечных масс представлена нижеприведенной формулой 32. В дальнейшем, потенциальная энергия Veff системы точечных масс, представленная как функция только медленных координат RS при условии, что быстрые координаты RF подчиненны медленным координатам RS, также именуется эффективной потенциальной энергией.
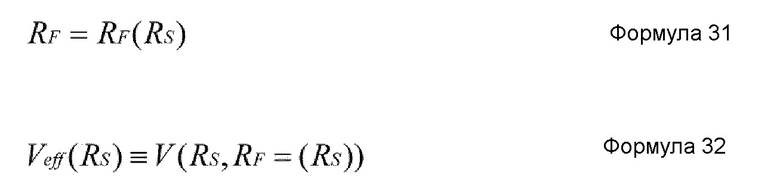
В случае, когда быстрые координаты RF подчинены медленным координатам RS согласно формуле 31, координату x точечной массы можно представить как функцию медленных координат согласно нижеприведенной формуле 33.

Структура медленных координат как функция коллективной координаты
Структуру RS(q†) медленных координат можно получить путем решения основного уравнения теории коллективного движения относительно медленных координат RS при условии, что быстрые координаты RF подчинены медленным координатам RS с учетом влияния изменения быстрых координат RF на медленные координаты RS вследствие изменения медленных координат RS. Важными моментами при получении структуры RS(q†) являются “решение основного уравнения теории коллективного движения относительно медленных координат RS” и “учет влияния (обратной связи) изменения быстрых координат RF на медленные координаты RS вследствие изменения медленных координат RS” при решении основного уравнения.
Далее будут описаны два вышеупомянутых важных момента.
Причина, по которой основное уравнение теории коллективного движения решается относительно медленных координат RS, состоит в упрощении вычисления разделения переменных путем извлечения коллективной координаты q† из M-мерных медленных координат RS вместо извлечения коллективной координаты q† из 3N-мерной координаты x точечной массы, как описано выше.
Наиболее фундаментальное основное уравнение метода SCC представлено нижеприведенными формулами 34-36 (G.D. Dang et al., “Self-consistent theory of large-amplitude collective motion: applications to approximate quantization of nonseparable systems and to nuclear physics”, Physics Reports, Vol. 335, Issues 3-5, pp. 93-274, 2000).
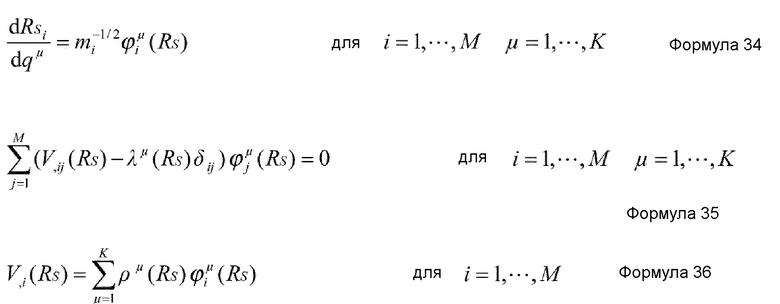
где mi представляет массу i-й медленной координаты в системе точечных масс. Заметим, что, если i-я медленная координата является координатой центра тяжести множества точечных масс, mi является полной массой этих точечных масс. В случае, когда медленная координата является координатой из объединенных координат точечных масс, но координатой центра тяжести, mi не является их простой полной массой. В таком случае, общий импульс, соответствующий медленной координате, получается по формуле общей аналитической динамики, затем записывается гамильтониан, и масса медленной координаты получается как коэффициент члена, выражающего общий импульс гамильтониана. ϕiμ(RS), λμ(RS) и ρμ(RS) это функции, которые подчиняются формулам 35 и 36, из которых ϕiμ(RS) является (i,μ)-я составляющая, а λμ(RS) и ρμ(RS) являются μ-ми составляющими. V,i(RS) и V,ij(RS) задаются, соответственно, нижеприведенными формулами 37 и 38.
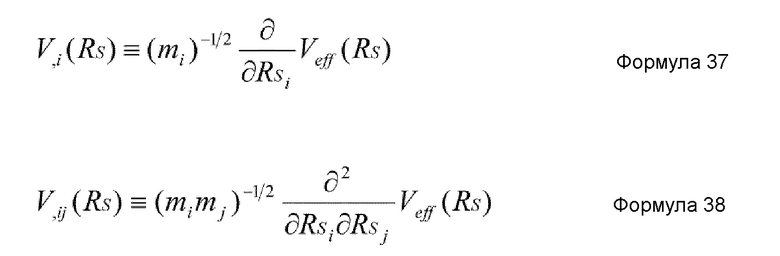
В общем случае, таким образом, функцию RSi(qμ) можно получить путем формирования K-мерной гиперплоскости (в дальнейшем именуемой просто “плоскостью”), параметризованной K коллективными координатами (q1, q2, -----, qK) в M-мерном подпространстве, образованном M координатами (RS1, RS2, -----, RSM) согласно формулам 34-36.
Что касается основного уравнения, также можно использовать основное уравнение для приближенного вычисления в G.D. Dang et al., “Self-consistent theory of large-amplitude collective motion: applications to approximate quantization of nonseparable systems and to nuclear physics”, Physics Reports, Vol. 335, Issues 3-5, pp. 93-274, 2000. При этом, например, в случае, когда структура RS(q1) медленных координат получается как функция коллективной координаты q† со степенью свободы 1 (K=1), основное уравнение в теории коллективного движения с использованием медленных координат RS можно представить нижеприведенными формулами 39-40.
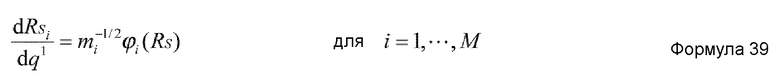
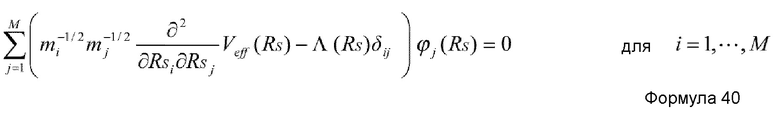
где ϕi(RS) представляет i-ю составляющую функции (собственный вектор) которая удовлетворяет формуле 40, и Λ(RS) представляет функцию (собственное значение), которая удовлетворяет формуле 40.
Между тем, приближенное вычисление осуществляется традиционным методом SCC, в G.D. Dang et al., “Self-consistent theory of large-amplitude collective motion: applications to approximate quantization of nonseparable systems and to nuclear physics”, Physics Reports, Vol. 335, Issues 3-5, pp. 93-274, 2000, который может не позволять разделять переменные с высокой точностью. Поэтому автор настоящего изобретения вывел новое основное уравнение на основании нового метода аппроксимации, который позволяет более точно вычислять разделения переменных относительно медленных координат RS, и развил теорию нового метода SCC (метода SCC 2) на основании нового основного уравнения.
Например, в случае, когда структура RS(q1) медленных координат получается как функция коллективной координаты q† со степенью свободы 1 (K=1) на основе метода SCC 2, основное уравнение в теории коллективного движения с использованием медленных координат RS можно представить нижеприведенными формулами 41-43.

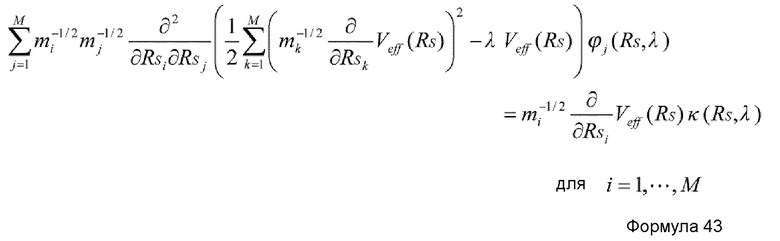
где ϕi(RS,λ) и κ(RS,λ) - функции, которые подчиняются формуле 43, причем ϕi(RS,λ) представляет i-ю составляющую и λ представляет вспомогательную координату.
В качестве решения формулы 39 или 41, в конце концов, получается структура медленных координат RS, представленная формулой 44.

Здесь основное уравнение описано для случая, когда K=1, но настоящее изобретение не ограничивается случаем K=1. В частности, когда K≥2, формулы 39 и 40 можно распространить на основное уравнение метода SCC с использованием теоремы Фробениуса, как описано, например, в G.D. Dang et al., “Self-consistent theory of large-amplitude collective motion: applications to approximate quantization of nonseparable systems and to nuclear physics”, Physics Reports, Vol. 335, Issues 3-5, pp. 93-274, 2000. Также, формулы 41-43 очевидно можно таким же образом распространить на основное уравнение метода SCC 2, где K≥2.
Как описано выше, введение иерархически упорядоченных переменных, именуемых медленными координатами (переменных более низкой размерности, вторично описывающих структуру системы точечных масс) может сводить задачу сжатия от 3N измерений к K измерениям к задаче сжатия от M измерений к K измерениям, что облегчает вычисление для разделения переменных.
В настоящем изобретении, однако, необходимо осуществлять разделение переменных с учетом обратной связи для точного вычисления структуры системы точечных масс. Отсутствие учета обратной связи эквивалентно осуществлению вычисления, исходя из того, что существующие точечные массы (или быстрые координаты) не существуют, и если разделение переменных осуществляется без учета их влияния, может возникать расхождение в вычислении, что может отрицательно сказываться на результате вычисления. Поэтому существующая теория коллективного движения модифицируется на основании новой теории для учета обратной связи. Новая теория это теория, в которой производная потенциальной энергии по координатам в основном уравнении теории коллективного движения вычисляется точно при условии, что быстрые координаты RF подчинены медленным координатам RS, и частичная структурная релаксация осуществляется на быстрых координатах RF при каждом малом обновлении медленной координаты RS(q†), (RS(q†)→RS(q†+Δq†).
В традиционной теории коллективного движения, малое обновление (x(q†)→x(q†+Δq†)) координаты x точечной массы повторяется только в направлении заранее определенного собственного вектора ϕ производной потенциальной энергии V(x) по координате x точечной массы.
В настоящем изобретении, уравнения обратной связи, выраженные формулами 45-47, можно применять при вычислении производной потенциальной энергии V по координатам.
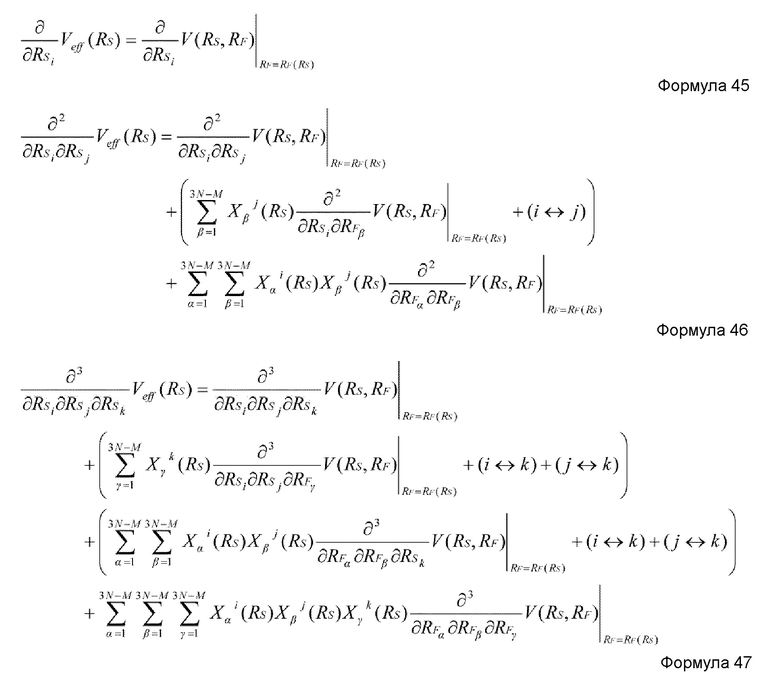
В формуле 46, (i↔j) в третьем члене представляет член, выведенный взаимной заменой индексов i и j во втором члене.
В формуле 47, (i↔k) в третьем члене представляет член, выведенный взаимной заменой индексов i и k во втором члене, (j↔k) в четвертом члене представляет член, выведенный взаимной заменой индексов j и k во втором члене, (i↔k) в шестом члене представляет член, выведенный взаимной заменой индексов i и k в пятом члене, и (j↔k) в седьмом члене представляет член, выведенный взаимной заменой индексов j и k в пятом члене.
В формулах 45-47, используется нижеприведенная формула 48.
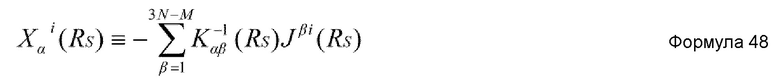
где Kαβ-1(RS) представляет матрицу, обратную Kαβ(RS), и Kαβ(RS) и Jαi(RS) задаются нижеприведенными формулами 49 и 50, соответственно.
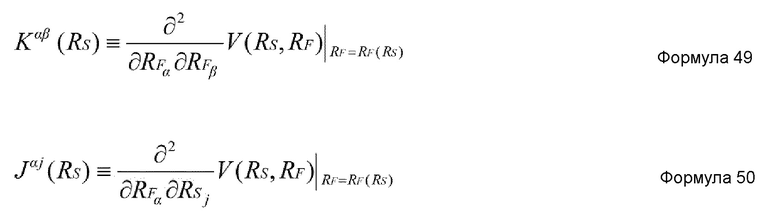
В каждой из формул 45-47, члены, отличные от первого члена в правой стороне, представляют влияние изменения быстрых координат RF на медленные координаты RS вследствие изменения медленных координат RS. Такая конфигурация уравнения обратной связи до сих пор не была известна и впервые найдена автором настоящего изобретения. Уравнение обратной связи включает в себя три формулы дифференциальных уравнений первого порядка, второго порядка и третьего порядка и только необходимое уравнение можно использовать согласно содержанию основного уравнения в теории коллективного движения. Например, в случае, когда формулы 39 и 40 используются в качестве основного уравнения в теории коллективного движения, только дифференциального уравнения второго порядка формулы 46 достаточно в качестве уравнения обратной связи.
Затем частичная структурная релаксация для быстрых координат RF осуществляется путем осуществления малого обновления (RS(q†)→RS(q†+Δq†)) на медленных координатах RS(q†) в направлении собственного вектора производной, заданной уравнением обратной связи, и осуществления структурной релаксации согласно условию, что быстрые координаты RF подчинены медленным координатам RS на основании обновленных медленных координат (q†+Δq†). Используемый здесь термин “на основании обновленных медленных координат (q†+Δq†)” означает “в состоянии, в котором обновленные медленные координаты (q†+Δq†) установлены в системе точечных масс”. Кроме того, используемый здесь термин “осуществление структурной релаксации согласно условию, что быстрые координаты RF подчинены медленным координатам RS” означает такое перемещение быстрых координат RF, при котором потенциальная энергия системы точечных масс постоянно снижается, пока градиент потенциальной энергии не обратится в нуль, при поддержании состояния, в котором быстрые координаты RF подчинены медленным координатам RS. Структурная релаксация, осуществляемая, когда медленные координаты RS привязаны к системе точечных масс, именуется “частичной структурной релаксацией”. Как описано выше, частичная структурная релаксация отличается от полной структурной релаксации тем, что осуществляется, когда медленные координаты RS привязаны к системе точечных масс. Но, что касается способа осуществления частичной структурной релаксации, можно использовать известный метод, например, метод сопряженных градиентов, метод наискорейшего спуска или метод обратного гессиана, как в полной структурной релаксации. Предпочтительно, собственный вектор ϕ, который определяет направление обновления, соответствует собственному вектору с минимальным собственным значением. Причина в том, что предметом настоящего изобретения является коллективное движение большой амплитуды.
В случае, когда K=1, начальное состояние быстрых координат RF в частичной структурной релаксации может быть RFα(RS(q1)), но, предпочтительно, является состоянием, в котором быстрые координаты RF изменяются на малую величину, заданную нижеприведенной формулой 51, т.е. состоянием RFα†, представленным нижеприведенной формулой 52.
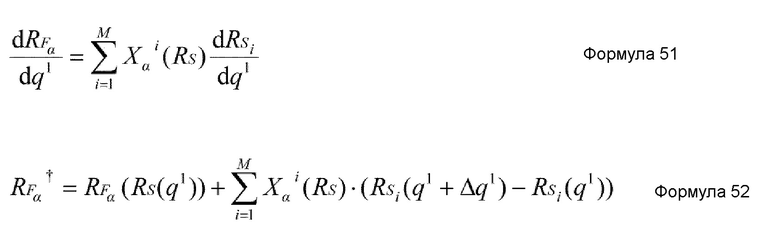
Координата RFα†, представленная формулой 52, соответствует быстрой координате RF(RS(q1+Δq1)), если малое обновление бесконечно мало. Однако при фактическом вычислении малое обновление является конечным. Задавая начальное состояние быстрых координат RF в частичной структурной релаксации как RFα†, можно повысить безопасность частичной структурной релаксации.
Процесс, осуществляемый средством извлечения координат
Ниже будет описано несколько конкретных этапов, осуществляемых средством извлечения координат.
Сначала средство извлечения координат осуществляет первый этап для получения потенциальной энергии V (RS,RF), представленной функцией медленных координат RS и быстрых координат RF.
Затем средство извлечения координат осуществляет второй этап для подчинения быстрых координат RF медленным координатам RS. Структура быстрых координат RF получается как функция медленных координат RS. Здесь, в порядке примера, предполагается, что быстрые координаты RF подчинены медленным координатам RS согласно условию адиабатического приближения формулы 30.
Затем, в состоянии медленных координат RS и быстрых координат RF, заданных средством задания координат, средство извлечения координат осуществляет третий этап для получения производной потенциальной энергии V по медленным координатам RS согласно, например, уравнению обратной связи формулы 46.
Затем, на основании производной потенциальной энергии V, средство извлечения координат осуществляет четвертый этап для получения производной медленной координаты RS(q) по коллективной координате q согласно, например, основному уравнению метода SCC формул 39 и 40 при K=1.
Затем средство извлечения координат осуществляет пятый этап для обновления коллективной координаты q на малую величину Δq согласно производной медленной координаты RS(q) и получения обновленной медленной координаты RS(q+Δq).
Затем, согласно обновленной медленной координате RS(q+Δq), средство извлечения координат осуществляет шестой этап для осуществления частичной структурной релаксации на быстрых координатах RF, подчиненных медленным координатам RS, согласно условию адиабатического приближения. В этом случае, если состояние RFα†, представленное формулой 52, используется как начальное состояние частичной структурной релаксации, производная быстрой координаты RF(q) по коллективной координате q получается из производной медленной координаты RS(q), полученной на четвертом этапе согласно формуле 51, и быстрые координаты обновляются на малую величину Δq согласно полученной производной.
Затем средство извлечения координат получает структуру медленных координат RS как функцию коллективной координаты q, повторяя этапы с третьего по шестой, например, пока не будет достигнут следующий локальный минимум, при этом попеременно обновляя медленные координаты RS и быстрые координаты RF. Таким образом, на третьем этапе после второго момента времени, производная потенциальной энергии V по медленным координатам RS будет получена, как на вышеописанном третьем этапе, когда медленные координаты RS и быстрые координаты RF находятся в состоянии после осуществления частичной структурной релаксации быстрых координат RF непосредственно до осуществления шестого этапа. Не существует никакого конкретного ограничения на способ определения локального минимума, и, например, в качестве примера можно привести способ, который производит определение, достигает ли нуля производная потенциальной энергии V.
Средство обратного преобразования
Средство обратного преобразования прогнозирует временную эволюцию координаты x точечной массы на основании коллективной координаты q†(t) как функции времени t, которую можно получить, решая уравнение движения относительно коллективной координаты q†, структуры RS(q), представленной формулой 44, и структуры RF(RS) быстрых координат RF, представленной формулой 31.
Далее следует более детальное описание. Фиг. 4 иллюстрирует принцип преобразования переменных и обратного преобразования. Фиг. 4 иллюстрирует, в порядке примера, случай, когда некоторые из координат x точечной массы используются в качестве медленных координат RS, и коллективная координата q†=q1 со степенью свободы 1 извлекается из медленных координат RS.
Фиг. 4a иллюстрирует задание медленных координат RS и быстрых координат RF на основании координаты x точечной массы. Согласно Фиг. 4a, M координат точечных масс задаются в качестве медленных координат RS, и остальные 3N-M координат точечных масс задаются в качестве быстрых координат RF. Как описано выше, медленные координаты RS и быстрые координаты RF задаются средством задания координат. Фиг. 4b указывает, что быстрые координаты RF заданы как функция медленных координат RS. Фиг. 4c иллюстрирует, что медленные координаты RS заданы как функция коллективной координаты q1. Как описано выше, структуры быстрых координат RF и медленных координат RS получаются средством извлечения координат.
Фиг. 4d указывает, что коллективная координата q1 задается как функция времени t, которую можно получить, решая уравнение движения относительно коллективной координаты q1. Уравнение движения относительно коллективной координаты q1 можно получить путем получения уравнения движения относительно медленных координат RS и быстрых координаты RF путем подстановки структуры x(RS, RF), определенной при задании медленных координат RS, в уравнение движения относительно координаты x точечной массы и подстановки формул 31 и 44 в полученное уравнение движения.
Использование соотношений, представленных на Фиг. 4a-d, позволяет получать все координаты x точечной массы как функцию времени t (Фиг. 4e). Таким образом, средство обратного преобразования является средством, которое получает структуру координаты x точечной массы как функцию времени t, x(t), путем получения коллективной координаты q1 как функции времени t и обратного преобразования для преобразования переменных из координаты x точечной массы в коллективную координату q1 через медленные координаты RS. Поскольку функция x(t) представляет поведение координаты x точечной массы по отношению к изменению во времени, функция x(t) это именно то, что нужно получить в соответствии с путем реакции. Таким образом, наблюдая изменение функции x(t) с течением времени, можно прогнозировать временную эволюцию.
Первый вариант осуществления настоящего изобретения
На Фиг. 5 показана блок-схема устройства 10 имитационного моделирования согласно настоящему варианту осуществления, схематически демонстрирующая его конфигурацию. На Фиг. 6A, 6B показаны блок-схемы операций, схематически демонстрирующие этапы вычисления в способе имитационного моделирования согласно настоящему варианту осуществления. Согласно варианту осуществления, будет описан случай, когда координаты центров тяжести, извлеченные из каждой характеристической частичной структуры для структуры многоатомной системы, образованной N атомами, включающей в себя биологическую макромолекулу и молекулу-кандидат на связывание для биологической макромолекулы, задаются как M медленных координат, и степень свободы коллективной координаты равна 1 (K=1).
Устройство 10 имитационного моделирования настоящего варианта осуществления представляет собой устройство для прогнозирования поведения составного тела, образованного биологической макромолекулой и молекулой-кандидатом на связывание. Как показано на Фиг. 5, устройство 10 имитационного моделирования включает в себя средство 12 ввода для ввода данных, необходимых для указания целевой многоатомной системы анализа (входных данных), средство 14 управления для управления каждой секцией устройства, средство 16 задания координат, средство 18 извлечения координат, средство 20 обратного преобразования и средство 22 отображения для отображения результатов анализа.
Способ имитационного моделирования настоящего варианта осуществления представляет собой способ, осуществляемый устройством 10 имитационного моделирования, включающий в себя этапы ввода входных данных средством 12 ввода, задания M медленных координат RS и 3N-M быстрых координат RF средством 16 задания координат, получения структуры медленных координат RS как функции коллективной координаты q1 и структуры быстрых координат RF как функции медленных координат RS средством 18 извлечения координат, получения координат атомов как функции времени x(t) средством 20 обратного преобразования, и отображения результатов анализа на средстве 22 отображения.
Программа имитационного моделирования настоящего варианта осуществления представляет собой программу, которая предписывает компьютеру осуществлять вышеописанный способ имитационного моделирования.
Компьютерно-считываемый носитель записи настоящего варианта осуществления представляет собой носитель, на котором записана вышеописанная программа имитационного моделирования.
Средство ввода
Средство 12 ввода это секция, с помощью которой пользователь вводит входные данные. Введенные входные данные выводятся на средство 14 управления. Не существует никакого конкретного ограничения на способ ввода входных данных, и в качестве примера можно привести, например, ручной способ посредством операции, осуществляемой пользователем над устройством 10 имитационного моделирования, способ считывания с заранее определенного носителя записи и т.п.
Средство управления
Средство 14 управления это секция, которая управляет обработкой, включающей в себя обмен данными с каждой секцией и пр. Входные данные, введенные в средство 14 управления из средства 12 ввода, выводятся на средство 16 задания координат. Когда входные данные выводятся на средство 16 задания координат, начинается вычисление поведения многоатомной системы. Средство управления включает в себя носитель данных, например память, для записи промежуточных и окончательных результатов вычислений, генерируемых посредством обмена данными с каждой секцией.
Кроме того, средство 14 управления управляет средством 22 отображения для отображения результата с использованием диаграммы или графика на основании данных координат атомов x(t), полученных средством 20 обратного преобразования.
Средство задания координат
Средство 16 задания координат является средством, которое оптимизирует составное тело на основании входных данных, принятых от средства 14 управления и задает M медленных координат RS и 3N-M быстрых координат RF. Данные в отношении полученных медленных координат RS и быстрых координат RF выводятся на средство 18 извлечения координат через средство 14 управления.
Средство извлечения координат
Средство 18 извлечения координат является средством, которое получает потенциальную энергию V(RS,RF) всей многоатомной системы на основании данных по отношению к медленной координате RS и быстрым координатам RF, полученным средством 16 задания координат, и, на основании полученной V(RS,RF), получает структуру медленных координат RS как функцию коллективной координаты q1 и структуры быстрых координат RF как функции медленных координат RS. Данные в отношении полученных структур медленных координат RS и быстрых координат RF выводятся на средство 20 обратного преобразования через средство 14 управления.
Средство обратного преобразования
Средство 20 обратного преобразования является средством, которое получает координаты атомов как функцию времени x(t) на основании данных в отношении структур медленных координат RS и быстрых координат RF, полученных средством 18 извлечения координат. Данные в отношении полученных координат атомов x(t) выводятся на средство 14 управления.
Средство отображения
Средство отображения является средством, которое отображает, например, потенциальную энергию V многоатомной системы в виде графика, структуру в процессе связывания составного тела и/или структуру конечного состояния в виде изображения, процесс связывания составного тела в виде движущегося изображения, и пр. согласно инструкции от средства 14 управления. Не существует никакого конкретного ограничения на способ отображения, и можно использовать любой известный способ, например 2D дисплей, 3D дисплей, и т.п.
Далее, процесс способа имитационного моделирования с использованием устройства настоящего варианта осуществления будет описан со ссылкой на Фиг. 6A и 6B.
Этап 1
Сначала входные данные вводятся из средства 12 ввода в устройство 10 имитационного моделирования (ST1 на Фиг. 6A). Конкретное содержание входных данных включают в себя тип, количество и координаты x, представляющие начальное расположение N атомов, составляющих многоатомную систему, которая включает в себя биологическую макромолекулу и молекула-кандидат на связывание, правило формирования потенциальной энергии V(x) из координат x, и пр.
Этап 2
Затем многоатомная система, которая включает в себя составное тело, оптимизируется, и получается структура начального состояния (ST2 на Фиг. 6A).
Далее следует более детальное описание. Сначала средство 16 задания координат независимо осуществляет полную структурную релаксацию на биологической макромолекуле и молекуле-кандидате на связывание для оптимизации структур биологической макромолекулы и молекулы-кандидата на связывание, соответственно. Затем биологическая макромолекула и молекула-кандидат на связывание, оптимизированные в структурах, располагаются на расстоянии, которое позволяет инициировать взаимодействие между ними (например, молекула-кандидат на связывание слегка касается биологической макромолекулы). Это состояние является начальным состоянием составного тела, образованного биологической макромолекулой и молекулой-кандидатом на связывание.
Этап 3
Затем медленные координаты RS и быстрые координаты RF задаются на основании структуры начального состояния, полученной на этапе 2(ST3 на Фиг. 6A).
Средство 16 задания координат делит структуру биологической макромолекулы на (M-3)/3 характеристических частичных структур, рассматривая всю молекулу-кандидат на связывание как одну частичную структуру, и извлекает центр тяжести из каждой из M/3 частичных структур. Затем, координаты M/3 центров тяжести задаются в качестве медленных координат RS, и координаты относительный каждого центра тяжести атомов, входящих в каждую из M/3 частичных структур, задаются как 3N-M быстрых координат RF. В настоящем варианте осуществления, в качестве быстрой координаты RF, задается координата относительно координат центра тяжести частичной структуры, в которую включены атомы.
Этап 4
Затем получается потенциальная энергия V(RS,RF) многоатомной системы, представленной медленными координатами RS и быстрыми координатами RF (ST4 на Фиг. 6A).
Фиг. 7 схематически иллюстрирует соотношение между медленными координатами RS, быстрыми координатами RF и атомными координатами x настоящего варианта осуществления. Согласно Фиг. 7, количество атомов, входящих в m-ую (M - целое число, которое удовлетворяет 1≤m≤M/3) характеристическую частичную структуру, представлено как Nm. Таким образом, N1+N2+----- +Nm+-----NM/3=N. В настоящем изобретении, M представляет количество атомных координат (точечных масс) в трехмерном пространстве, поэтому M/3 обычно является целым числом. Кроме того, в настоящем варианте осуществления, из Фиг. 7 известно, что медленные координаты RS, быстрые координаты RF и атомные координаты x имеют соотношения, представленные нижеприведенными формулами 53 и 54.
Формула 53 это формула, представляющая соотношение между m-ой медленной координатой RS, т.е. координатой центра тяжести m-ой характеристической частичной структуры, и атомными координатами x. Формула 54 это формула, представляющая соотношение между координатой x n-го атома, принадлежащего m-ой характеристической частичной структуре, медленными координатами RS и быстрыми координатами RF. В формулах 53 и 54, n представляет порядковый номер атомов, входящих в каждую характеристическую частичную структуру. Таким образом, n по отношению к m-ой характеристической частичной структуре принимает целочисленное значение в диапазоне от 1 до Nm. Кроме того, 3N1+3N2+-----3Nm-1 равно нулю при m=1.
Таким образом, потенциальную энергию V(RS,RF) можно получить, применяя формулу 54 к потенциальной энергии V(x).
Этап 5
Затем быстрые координаты RF подчиняются медленным координатам RS согласно условию адиабатического приближения формулы 30 с использованием потенциальной энергии V(RS,RF) (ST5 на Фиг. 6A). В настоящем варианте осуществления, берутся частные производные V(RS,RF) по всем быстрым координатам от RF1 до RF3N.
Этап 6
Затем, согласно текущим медленным координатам RS и быстрым координатам RF, вторая производная потенциальной энергии V по медленным координатам RS получается согласно уравнению обратной связи формулы 46 (ST6 на Фиг. 6A).
Этап 7
Затем, после получения второй производной на этапе 6, производная dRS/dq1 по коллективной координате q1 получается согласно основному уравнению метода SCC в формулах 39 и 40 (ST7 на Фиг. 6A).
Этап 8
Затем, после получения производной dRS/dq1 на этапе 7, производная dRF/dq1 быстрых координат RF по коллективной координате q1 получается согласно формуле 51 (ST8 на Фиг. 6B).
Этап 9
Затем, после получения производной dRS/dq1 на этапе 7 и получения производной dRF/dq1 на этапе 8, коллективная координата q1 обновляется на малую величину Δq1 (ST9 на Фиг. 6B).
Этап 10
Затем получаются медленная координата RS(q1+Δq1), обновленная на Δq1 и обновленная быстрая координата RF(q1+Δq1) (ST10 на Фиг. 6B).
Например, в случае, когда начальное состояние на этапе 2 задается как начальное условие коллективной координаты q1 (то есть многоатомная система находится в начальном состоянии, когда q1=0), медленную координату RS(q1+Δq1) и быструю координату RF(q1+Δq1) можно представить нижеприведенной формулой 55.
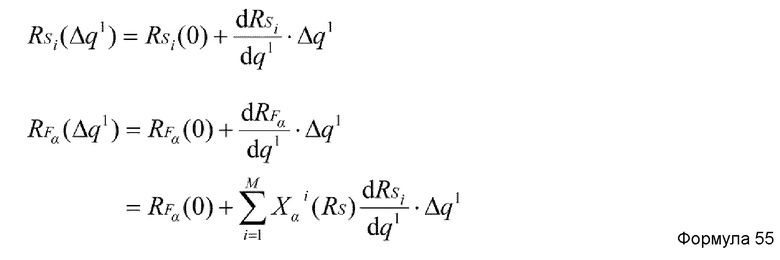
В случае, когда этапы с 6 по 12 повторяются согласно результату определения на этапе 13, RSi(2Δq1), RSi(3Δq1)-----, которые можно представить формулой 56, получаются по одному на этапе 10 после второго момента времени при условии, однако, что производная dRS/dq1 не каждый раз принимает одно и то же значение. Повторяя вышеописанную операцию, в конце концов, получаем структуру RS(q1) медленных координат RS как функцию коллективной координаты q1.
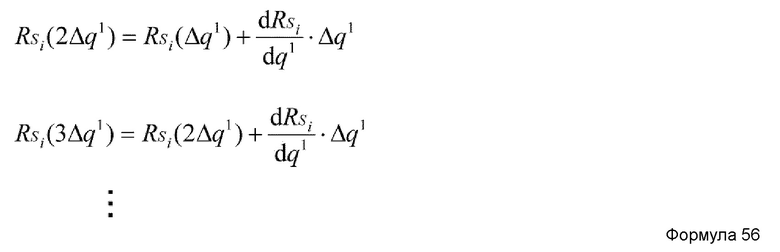
Этап 11
На этапе 11, после обновления медленной координаты RS(q1+Δq1) на этапе 10, частичная структурная релаксация осуществляется на быстрой координате RF, при том, что быстрая координата RF(q1+Δq1) обновляется на этапе 10 как начальное состояние (ST11 на Фиг. 6B).
Этап 12
Затем, на этапе 12, вычисляется потенциальная энергия V многоатомной системы в состоянии после частичной структурной релаксации (ST12 на Фиг. 6B). Заметим, что, согласно результату определения на этапе 13, потенциальная энергия V вычисляется при каждом повторе. Численное вычисление потенциальной энергии может представлять собой вычисление на основании эффективной потенциальной энергии Veff.
Этап 13
Затем, на этапе 13, производится определение, достигла ли потенциальная энергия V, вычисленная на этапе 12, локального минимума (ST13 на Фиг. 6B). Ввиду химической реакции между биологической макромолекулой и молекулой-кандидатом на связывание, конечной точкой химической реакции является точка, в которой потенциальная энергия V достигнет очередного локального минимума, т.е. следующая стабильная точка на потенциальной поверхности. Следовательно, конечная точка химической реакции определяется на основании значения потенциальной энергии. Если определено, что потенциальная энергия V достигла следующего локального минимума, процесс переходит к этапу 14, в противном случае повторяются этапы с 6 по 12. Кроме того, даже в случае, когда определено, что потенциальная энергия достигла локального минимума, при необходимости, можно также продолжать анализ, пока потенциальная энергия V не достигнет следующего локального минимума.
Этап 14
Если на этапе 13 определено, что потенциальная энергия V достигла локального минимума, структура многоатомной системы при потенциальной энергии V на этапе 14 является структурой конечного состояния, подлежащей получению (ST14 на Фиг. 6B).
Затем, помимо структуры конечного состояния, получаются структура RS(q1) медленных координат RS, представленная формулой 44, и структура RF(RS) быстрых координат RF, представленная формулой 31. После этого, получаются координаты x(t) как функция времени.
Положительные результаты
На Фиг. 8 показан график, демонстрирующий путь реакции составного тела из заранее определенного белка 2 и физиологически активного вещества 6 (лекарственного препарата), полученного способом имитационного моделирования настоящего варианта осуществления. Фиг. 9 схематически иллюстрирует процесс связывания составного тела, показанного на Фиг. 8. Фиг. 9A и b иллюстрируют, соответственно, начальное состояние и конечное состояние процесса связывания составного тела.
На Фиг. 8, горизонтальная ось представляет расстояние между остатками 2a, 2b заранее определенного белка 2, а вертикальная ось представляет расстояние между лекарственным препаратом 6 и остатком 2c. Остатки 2a, 2b это остатки, расположенные у отверстия кармана 4 белка 2, тогда как остаток 2c это остаток, расположенный в позиции, противоположной лекарственному препарату 6, когда белок и лекарственный препарат связаны (Фиг. 9). Точки A и C на графике соответствуют, например, стабильным точкам A и C на Фиг. 2, и точка B на графике соответствует, например, энергетическому барьеру B на Фиг. 2. Линия на графике указывает равноудаленные точки на временной оси. График демонстрирует, что реакция протекает медленно до достижения энергетического барьера B, и реакция протекает быстро после преодоления энергетического барьера B. Время, необходимое для получения пути реакции в многоатомной системе, которая включает в себя около 2000 атомов, способом имитационного моделирования настоящего варианта осуществления составляет около 30 минут.
Позиция “рентгеновского анализа” на графике, показанном на Фиг. 8, указывает измеренное значение, фактически полученное в результате структурного анализа кристалла посредством измерения дифракции рентгеновских лучей. Это показывает, что способ имитационного моделирования позволяет вычислять состояние связывания составного тела с очень высокой точностью, хотя настоящее изобретение осуществляет имитационное моделирование неэмпирически.
Как описано выше, устройство имитационного моделирования настоящего варианта осуществления включает в себя средство задания координат, средство извлечения координат и средство обратного преобразования и прогнозирует временную эволюцию координат точечных масс, вводя иерархически упорядоченные медленные координаты, извлекая, с учетом влияния изменения быстрых координат на медленные координаты вследствие изменения медленных координат, коллективную координату в теории коллективного движения, которая описывает коллективное и собственное поведение системы точечных масс, и решая уравнение движения относительно коллективной координаты. Таким образом, извлечение коллективной координаты позволяет осуществлять имитационное моделирование на атомном уровне, и введение медленных координат позволяет сокращать количество координат, обрабатываемых для извлечения коллективной координаты. В результате, можно добиться, как повышения точности вычисления, так и сокращения времени вычисления при имитационного моделирования для прогнозирования динамического поведения системы точечных масс.
Способ имитационного моделирования настоящего варианта осуществления представляет собой способ, используемый с вышеописанным устройством имитационного моделирования, и прогнозирует временную эволюцию координат точечных масс, вводя иерархически упорядоченные медленные координаты, извлекая, с учетом влияния изменения быстрых координат на медленные координаты вследствие изменения медленных координат, коллективную координату в теории коллективного движения, которая описывает коллективное и собственное поведение системы точечных масс, и решая уравнения движения относительно коллективной координаты. Таким образом, извлечение коллективной координаты позволяет осуществлять имитационное моделирование на атомном уровне, и введение медленных координат позволяет сокращать количество координат, обрабатываемых для извлечения коллективной координаты. В результате, можно добиться, как повышения точности вычисления, так и сокращения времени вычисления при имитационного моделирования для прогнозирования динамического поведения системы точечных масс.
Программа и носитель записи настоящего варианта осуществления могут предписывать осуществление вышеупомянутого способа имитационного моделирования, поэтому повышенная точность вычисления и сокращенное время вычисления может достигаться в имитационного моделирования для прогнозирования динамического поведения системы точечных масс.
Второй вариант осуществления настоящего изобретения
Далее будет описан второй вариант осуществления. Настоящий вариант осуществления отличается от первого варианта осуществления тем, что для получения решения основных уравнений (формулы 39 и 40) с применением метода SCC, описанного в G.D. Dang et al., “Self-consistent theory of large-amplitude collective motion: applications to approximate quantization of nonseparable systems and to nuclear physics”, Physics Reports, Vol. 335, Issues 3-5, pp. 93-274, 2000, или решения метода SCC 2 (формулы 41-43), предусмотрено решение уравнения, эквивалентного этим основным уравнениям. Таким образом, компоненты, идентичные компонентам первого варианта осуществления, подробно здесь не рассмотрены, если иное конкретно не требуется.
Устройство 10 имитационного моделирования настоящего варианта осуществления включает в себя средство 12 ввода, средство 14 управления, средство 16 задания координат, средство 18 извлечения координат, средство 20 обратного преобразования и средство 22 отображения для отображения результатов анализа, как в первом варианте осуществления.
В настоящем варианте осуществления, средство 18 извлечения координат использует формулу 57 в качестве основного уравнения метода SCC для получения того же решения, которое дают формулы 39 и 40.
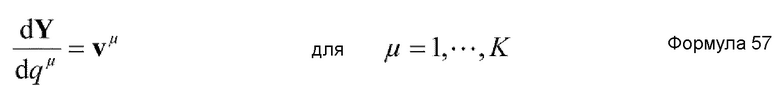
где Y - MK+M+K-мерный вектор, заданный нижеприведенной формулой 58. Таким образом, Y включает в себя каждую составляющую, полученную перебором каждого из i и μ: m11/2RS1, -----, mM1/2RSM; ϕ11, -----,ϕM1, -----,ϕ1K, -----,ϕMK; и λ1, -----,λK. Заметим, что ϕiμ и λμ представляют вспомогательные координаты.

где vμ - вектор решения неоднородного линейного уравнения нижеприведенной формулы 59. Заметим, что vμ это MK+M+K-мерный вектор.
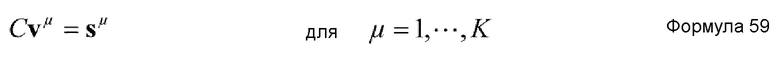
C и sμ в формуле 59 задаются нижеприведенными формулами 60 и 61 соответственно. C это квадратная матрица (MK+M+K)×(MK+M+K). Хотя C выглядит, как матрица 3×3, каждая составляющая также имеет матрицу. Таким образом, в C, представленной в виде матрицы 3×3, составляющая в первой строке и первом столбце является матрицей MK×M (то есть с MK строками и M столбцами), составляющая в первой строке и втором столбце является матрицей MK×MK, составляющая в первой строке и третьем столбце является матрицей MK×K, составляющая во второй строке и втором столбце является матрицей K×MK, составляющая в третьей строке и первом столбце является матрицей M×M, и другие составляющие являются нулевыми матрицами. Элементы каждой составляющей получены перебором i или μ, i=1~M или μ=1~K, в качестве переменной в строках и j или ν, j=1~M или ν=1~K, в качестве переменной в столбцах. sμ это MK+M+K-мерный вектор. Как и C, sμ также выглядит, как трехмерный вектор, но каждая составляющая сама имеет вектор. Таким образом, третья составляющая в качестве трехмерного вектора sμ является M-мерным вектором, и другие составляющие являются нулевыми векторами. Элементы третьей составляющей получены перебором i от 1 до M.
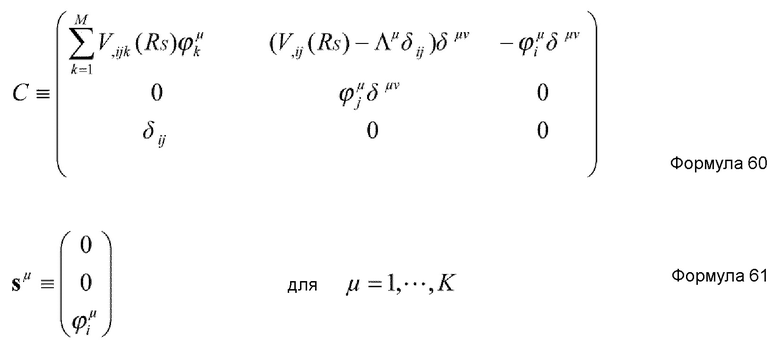
V,ijk(RS) задается нижеприведенной формулой 62.
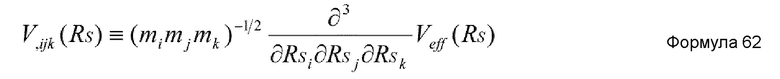
Формула 57 является основным уравнением, когда K генерализовано, и если K=1, формула 57 эквивалентна нижеприведенной формуле 63. Кроме того, как описано в G.D. Dang et al., “Self-consistent theory of large-amplitude collective motion: applications to approximate quantization of nonseparable systems and to nuclear physics”, Physics Reports, Vol. 335, Issues 3-5, pp. 93-274, 2000, формулу 57 относительно генерализованного K можно вывести из формулы 63, где K=1, с использованием теоремы Фробениуса.
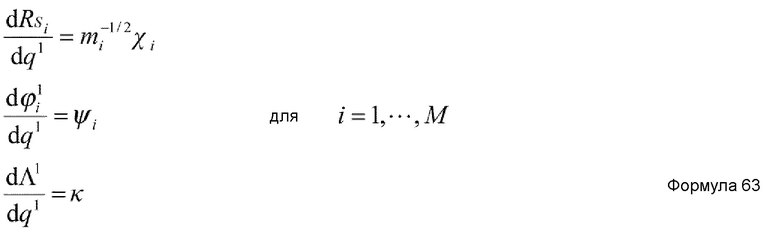
В формуле 63, (χ1, -----,χM, ψ1, -----, ψM, κ) является 2M+1-мерным вектором решения неоднородного линейного уравнения, представленного нижеприведенный формулой 64.
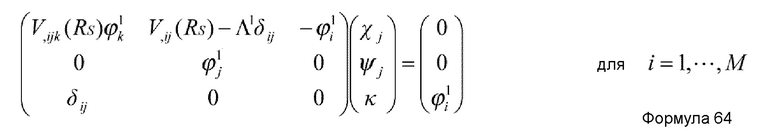
В формуле 64, берется произведение матрицы и собственного вектора, и когда формула 60 представлена тремя уравнениями, сумма от 1 до M берется по j и k.
Эквивалентность формул 63 и 64 формулам 39 и 40 можно доказать следующим образом. Если проинтегрировать формулу 64 по q1 относительно (ϕi1, λ1) обращая внимание на формулы 38, 62 и 63, можно получить нижеприведенную формулу 65.
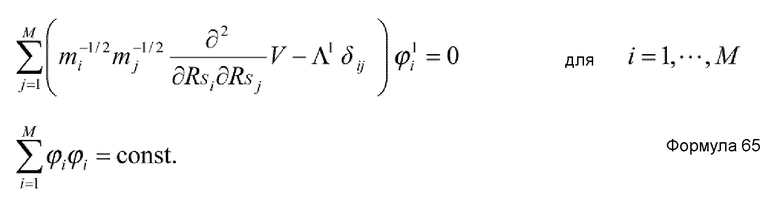
Кроме того, если тождество χi=ϕi1 включенное в формулу 64, подставить в первое уравнение формулы 63, то можно получить нижеприведенную формулу 66.
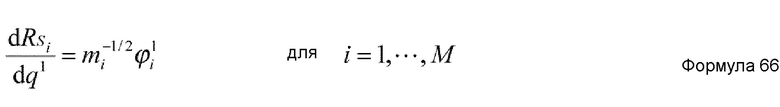
Здесь, путем замены ϕi1 и λ1 в первом уравнении формулы 65 и в формуле 66 с ϕi(RS) и λ(RS)(т.е. когда ϕi1 и λ1 рассматриваются как функции RS), формулы 39 и 40 воспроизводятся.
В случае, когда получаются такие же решения, как для формул 41-43, средство 18 извлечения координат использует формулу 67 в качестве основного уравнения метода SCC 2.
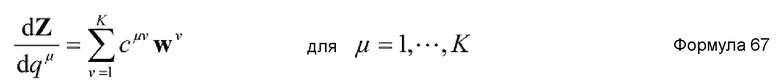
где Z - MK+M+2K-мерный вектор, заданный нижеприведенной формулой 68. Таким образом, Z включает в себя каждую составляющую, полученную перебором каждого из i и μ: m11/2RS1, -----, mM1/2RSM; ϕ11, -----,ϕM1, -----,ϕ1K, -----,ϕMK; λ1, -----, λK; и ρ1, -----,ρK. Заметим, что λμ и ρμ представляют вспомогательные координаты наподобие ϕiμ. cμν это константа, уникально определенная так, чтобы минимизировать значение, представленное нижеприведенной формулой 65, заданное относительно каждого m, и wμ представляет один из K MK+M+2K-мерных единичных векторов, образующих базис K-мерного пространства сингулярных значений (MK+M+K)×(MK+M+2K)-мерной вырожденной матрицы D, заданной нижеприведенной формулой 70. Хотя D выглядит, как матрица 3×4, каждая составляющая также имеет матрицу. Таким образом, в D, представленной в виде матрицы 3×4, составляющая в первой строке и первом столбце является матрицей MK×M, составляющая в первой строке и втором столбце является матрицей MK×MK, составляющая в первой строке и третьем столбце является матрицей MK×K, составляющая во второй строке и первом столбце является матрицей M×M, составляющая во второй строке и втором столбце является матрицей M×MK, составляющая во второй строке и четвертом столбце является матрицей M×K, составляющая в третьей строке и втором столбце является матрицей K×MK, и другие составляющие являются нулевыми матрицами. Элементы каждой составляющей получены перебором i или μ, i=1~M или μ=1~K, в качестве переменной в строках и j или ν, j=1~M или ν=1~K, в качестве переменной в столбцах.

Формула 67 является основным уравнением, когда K генерализовано, и если K=1, формула 67 эквивалентна нижеприведенный формуле 71. Кроме того, как описано в G.D. Dang et al., “Self-consistent theory of large-amplitude collective motion: applications to approximate quantization of nonseparable systems and to nuclear physics”, Physics Reports, Vol. 335, Issues 3-5, pp. 93-274, 2000, формулу 67 относительно генерализованного K можно вывести из формулы 71, где K=1, с использованием теоремы Фробениуса.
В формуле 71, (χ1, -----,χM, ψ1, -----, ψM, κ, σ) является 2M+2-мерным вектором решения (неопределенным решением) однородного линейного уравнения на основе вырожденной матрицы (2M+1)×(2M+2), представленного нижеприведенной формулой 72.
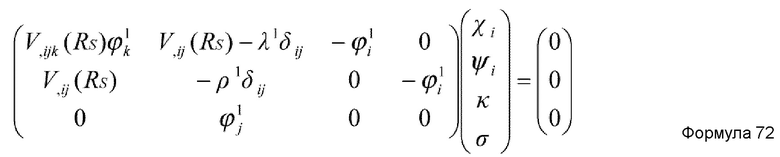
В формуле 72, берется произведение матрицы и собственного вектора, и когда формула 68 представлена тремя уравнениями, берется сумма от 1 до M по j и k. Таким образом, (χ1, -----,χM, ψ1, -----, ψM, κ, σ) можно представить формулой 73 с использованием единичного вектора μ, принадлежащего одномерному пространству сингулярных значений вырожденной матрицы формулы 72. Здесь, c - константа, уникально определенная так, чтобы минимизировать значение, представленное нижеприведенной формулой 74.

Эквивалентность формул 71 и 72 формулам 41-43 можно доказать следующим образом. Если проинтегрировать формулу 72 по q1 относительно (ϕi1, λ1, ρ1), обращая внимание на формулы 38, 62, 71, и 73, можно получить нижеприведенной формулу 75.
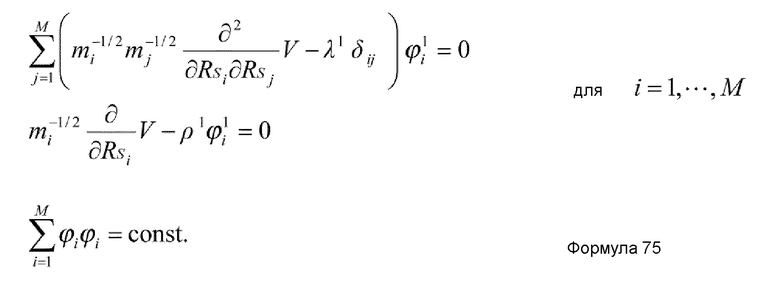
Если исключить ϕi1 и ρ1 из первого и второго уравнений формулы 75, то можно получить нижеприведенную формулу 76. Затем, если продифференцировать формулу 76 с учетом того, что RSi и λ1 являются функциями q1, и использовать первое и третье уравнения формулы 71, то можно получить нижеприведенную формулу 77.
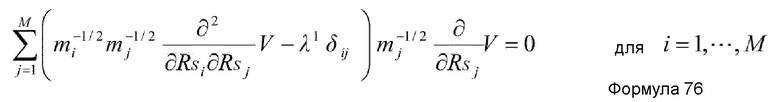
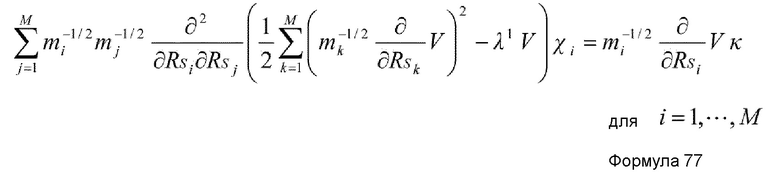
Здесь, путем замены λ1, χi, κ и V в первом и третьем уравнениях формулы 71 и в формуле 77 на λ, ϕi(RS, λ), κ(RS, λ), и Veff(RS), воспроизводятся формулы 41-43.
В настоящем варианте осуществления, как известно, например, из формулы 63 или 71, количество переменных как функций q1, рассматриваемых как независимые координаты при решении основного уравнения (все медленные координаты RS и вспомогательные координаты, в дальнейшем именуемые “независимыми переменными”), увеличивается. В частности, в формулах 39 и 40, независимыми переменными являются только M RSi(i=1~M), тогда как в формуле 63, которая эквивалентна формулам 39 и 40, независимыми переменными являются M RSi(i=1~M), M ϕi1 (i=1~M) и Λ1, что в сумме дает 2M+1. Между тем, в формулах 41-43, независимыми переменными являются только M RSi(i=1~M) и λ, тогда как в формуле 71, которая эквивалентна формулам 41-43, независимыми переменными являются M RSi(i=1~M), M ϕi1 (i=1~M), λ1 и ρ1, что в сумме дает 2M+2.
Ниже будут описаны преимущества увеличения количества независимых переменных (в частности, вспомогательных координат) для эквивалентного преобразования уравнения вышеописанным образом.
Например, в случае, когда ϕi(RS) получается из формулы 40, остается произвольность знака ϕi(RS), отражающая тот факт, что формула 40 инвариантна к инверсии знака ϕi(RS). Кроме того, то же самое справедливо для случая, когда ϕi(RS, λ) и κ(RS, λ) получаются из формулы 43. Произвольность знака говорит о том, что путь, обратный по направлению пути реакции, также включен. Исходя из того, что, если путь, который однажды был пройден в обратном направлении может возвращаться к прямому направлению путем повторного прохождения в обратном порядке, то путь реакции, в конце концов, можно найти, можно утверждать, что произвольность знака является достаточно естественным явлением. Однако произвольность знака может создавать проблему в том, что обратное прохождение затрудняет эффективное формирование пути реакции. Кроме того, формулы 40 и 43 на практике решаются дифференцированием, и степень дифференцирования Δq1 имеет конечное значение, поэтому, когда происходит обратное прохождение, состояние системы может не возвратиться к первоначальному пути реакции, то есть такое обратное прохождение может стать триггером, формирующим ошибочный путь реакции.
Таким образом, в настоящем варианте осуществления, произвольность знака исключается путем увеличения количества независимых переменных ϕiμ(RS). В результате, решается проблема обратного прохождения, и путь реакции можно формировать более эффективно и точно. Заметим, что даже если удвоить количество независимых переменных, последствиями увеличения вычислительной нагрузки можно пренебречь.
На Фиг. 10 показан график, демонстрирующий результат сравнения между вычислением, в котором произвольность знака исключается, и вычислением, в котором произвольность знака не исключается. В частности, график, указанный ссылочной позицией 24, иллюстрирует результат вычисления потенциальной энергии белка под названием мелиттин в отношении каждого его структурного изменения с использованием формул 71-74, а график, указанный ссылочной позицией 26, иллюстрирует результат вычисления потенциальной энергии того же белка в отношении каждого его структурного изменения с использованием формул 41-43. Горизонтальная ось представляет угол θ сгиба мелиттина для облегчения визуализации структурного изменения, и вертикальная ось представляет потенциальную энергию системы. Состояние, в котором θ=140 градусов, соответствует начальному состоянию.
При вычислении, где оставлена произвольность знака, энергия резко возрастает при около θ=95 градусов, когда имеет место обратное прохождение. Напротив, при вычислении, где произвольность знака устранена, такое явление не наблюдается, и энергия достигает точки локального максимума при около θ=80 градусов. Отдельная точка при θ=60 градусов на графике 24 является еще одной локальной стабильной точкой системы, полученной из состояния в точке локального максимума путем к системе применения общей структурной релаксации.
Как описано выше, устройство имитационного моделирования и способ имитационного моделирования согласно настоящему варианту осуществления также прогнозируют временную эволюцию координат точечных масс, вводя иерархически упорядоченные медленные координаты, извлекая, с учетом влияния изменения быстрых координат на медленные координаты вследствие изменения медленных координат, коллективную координату в теории коллективного движения, которая описывает коллективное и собственное поведение системы точечных масс, и решая уравнение движения относительно коллективной координаты. Таким образом, настоящий вариант осуществления может обеспечивать такие же положительные результаты, как в первом варианте осуществления.
Изменение конструкции
В каждом вышеописанном варианте осуществления, член третьей производной потенциальной энергии V(RS) возникает в основных уравнениях (например, формулах 43, 60, 64, 70 и 72). Порядок величины времени, необходимого для вычисления третьей производной, пропорционален M3 (M представляет количество медленных координат) и ввиду того, что прядок величины времени, необходимого для вычисления второй производной пропорционален M2, вычисление третьей производной является очень тяжелой нагрузкой для имитационного моделирования. Таким образом, например, в отношении V,ijk(RS)·ϕk1 в формуле 64, потребуется много времени, если сначала вычислять V,ijk(RS), а затем брать произведение вычисленного значения и ϕk1. Поэтому автор настоящего изобретения вывел нижеприведенную формулу 78, которая позволяет вычислять V,ijk(RS)·ϕk1, беря непосредственно разность между двумя вторыми производными. Применение формулы 78 позволяет снизить порядок величины времени вычисления от около M3 до около M2. Кроме того, уравнение обратной связи формулы 41 предпочтительно применять ко вторым производным в правой стороне формулы 78.

где ϕi представляет i-ю составляющую произвольного вектора, и n задается нижеприведенной формулой 79.
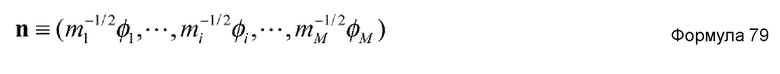
Основное уравнение метода SCC
Наконец, кратко опишем соотношение между наиболее фундаментальным основным уравнением (формулы 34-36) и четырьмя системами основных уравнений (системой формул 39 и 40, системой формул 41-43, формулой 57 и формулой 67).
Как описано выше, функция RSi(qμ), в общем случае, можно получить путем формирования плоскости согласно наиболее фундаментальным основным уравнениям. Однако при формировании плоскости фактически возникают две проблемы. Одна из них является фундаментальной проблемой, состоящей в том, что плоскость, которая строго удовлетворяет формулам 34-36, не всегда существует для общей потенциальной энергии. Другая является практической проблемой, состоящей в том, что может происходить обратное прохождение при попытке сформировать плоскость согласно формулам 34-36 (вышеописанная проблема обратного прохождения). В частности, причина последней проблемы ясна. Таким образом, формулы 35 и 36 не позволяют определить знак ϕiμ(RS) и ρμ(RS), другими словами, они инвариантны к инверсии знака.
Следовательно, для фундаментальной проблемы, эффективен способ, в котором плоскость, которая удовлетворяет формулам 34-36 определяется путем аппроксимации. Фактически, в описании G.D. Dang et al., “Self-consistent theory of large-amplitude collective motion: applications to approximate quantization of nonseparable systems and to nuclear physics”, Physics Reports, Vol. 335, Issues 3-5, pp. 93-274, 2000, формула 36 игнорируется, и предпринимается попытка сформировать плоскость только согласно формулам 34 и 35. Эта мера дает формулы 39 и 40 при K=1. Кроме того, автор настоящего изобретения разработал способ, в котором плоскость формируется согласно формулам 35 и 36, в то время, как формула 34 удовлетворяется в максимальной степени. Эта мера дает формулу 43 из формулы 41 при K=1. В частности, если продифференцировать формулу 80, полученную исключением ϕi1(RS) и ρ1(RS) из формул 35 и 36, по q1 с учетом того, что λ1 является функцией q1, а также RS,, формулу 43 можно получить из формулы 41.
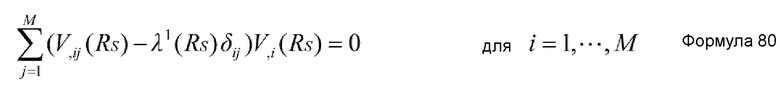
В отношении практической проблемы, эффективен способ, в котором ϕiμ, λμ и ρμ в формулах 34-36 предполагаются независимыми от RS и переменными как функции q† (т.е. вспомогательных координат). Причина в том, что, если ϕiμ, λμ и ρμ предполагаются независимыми от RS, каждая из них становится величиной, которая непрерывно претерпевает небольшие изменения, как RS, при формировании плоскости, поэтому внезапного изменения знака не происходит. Чтобы обрабатывать ϕiμ, λμ и ρμ как вспомогательные координаты, требуется формула, которая включает в себя дифференцирование по qν, наподобие формулы 34. Следовательно, каждая из формул 35 и 36 полностью дифференцируется по qν, и результат делится на dqν для получения нижеприведенных формул 81 и 82. Таким образом, наиболее фундаментальное основное уравнение преобразуется в основное уравнение, образованное формулами 34, 81 и 82, при этом практическая проблема устраняется.
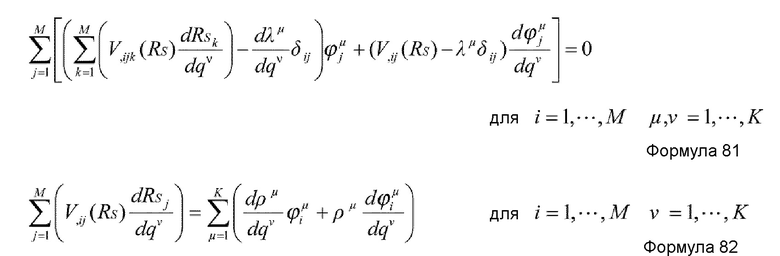
Теперь рассмотрим подходы к решению фундаментальной проблемы в основном уравнении, образованном формулами 34, 81 и 82. Способом решения проблемы является, например, способ, в котором плоскость, которая удовлетворяет формулам 34, 81 и 82, находится путем аппроксимации, как описано выше. В частности, мера, в которой плоскость формируется только формулами 34 и 81, задается формулой 57, тогда как мера, в которой плоскость формируется формулами 81 и 82, в то время, как формула 34 удовлетворяется в максимальной степени, дает формулу 67.
ПРОМЫШЛЕННОЕ ПРИМЕНЕНИЕ
В каждом варианте осуществления было приведено описание случая, когда настоящее изобретение применяется к процессу связывания составного тела, образованного белком и лекарственным препаратом, но изобретение этим не ограничивается. Таким образом, настоящее изобретение можно применять более полно к процессам формирования составных тел, образованных биологической макромолекулой и молекулой-кандидатом на связывание. Изобретение также применимо к анализу поведения многоатомных систем, которые включает в себя биологическую макромолекулу, например, процесса диссоциации составного тела, структуры apo тело белка, механизма укладки биологической макромолекулы, и пр., отличного от процесса связывания составного тела.
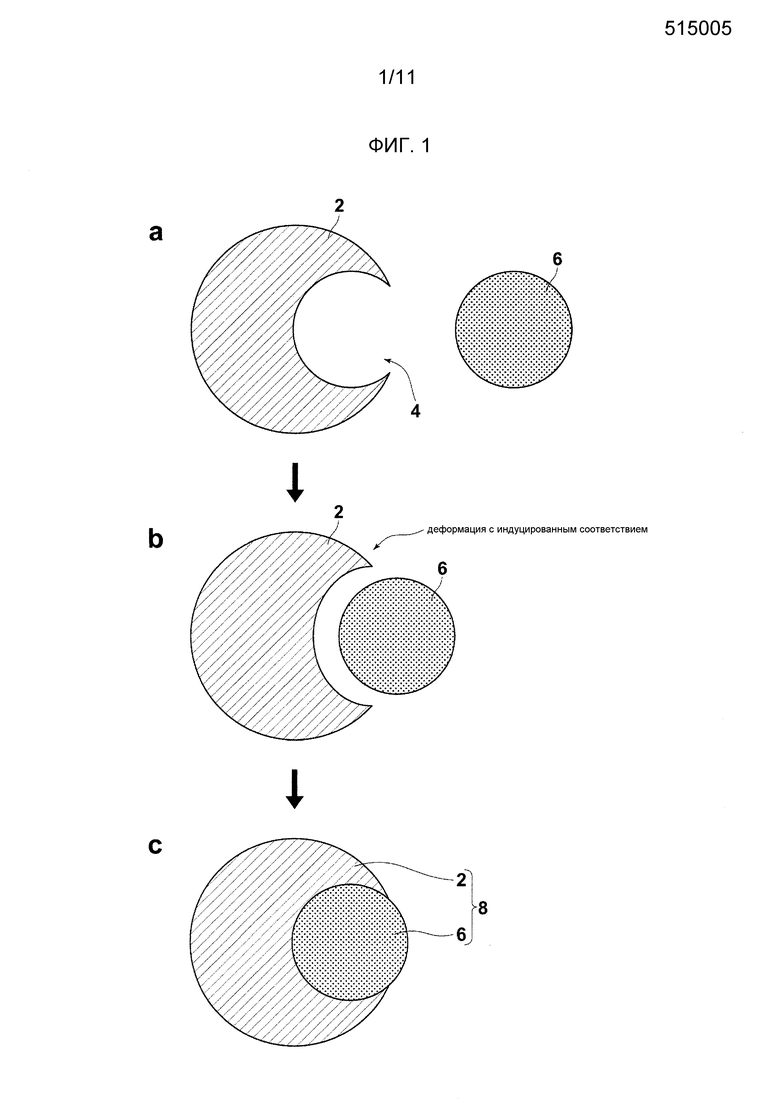
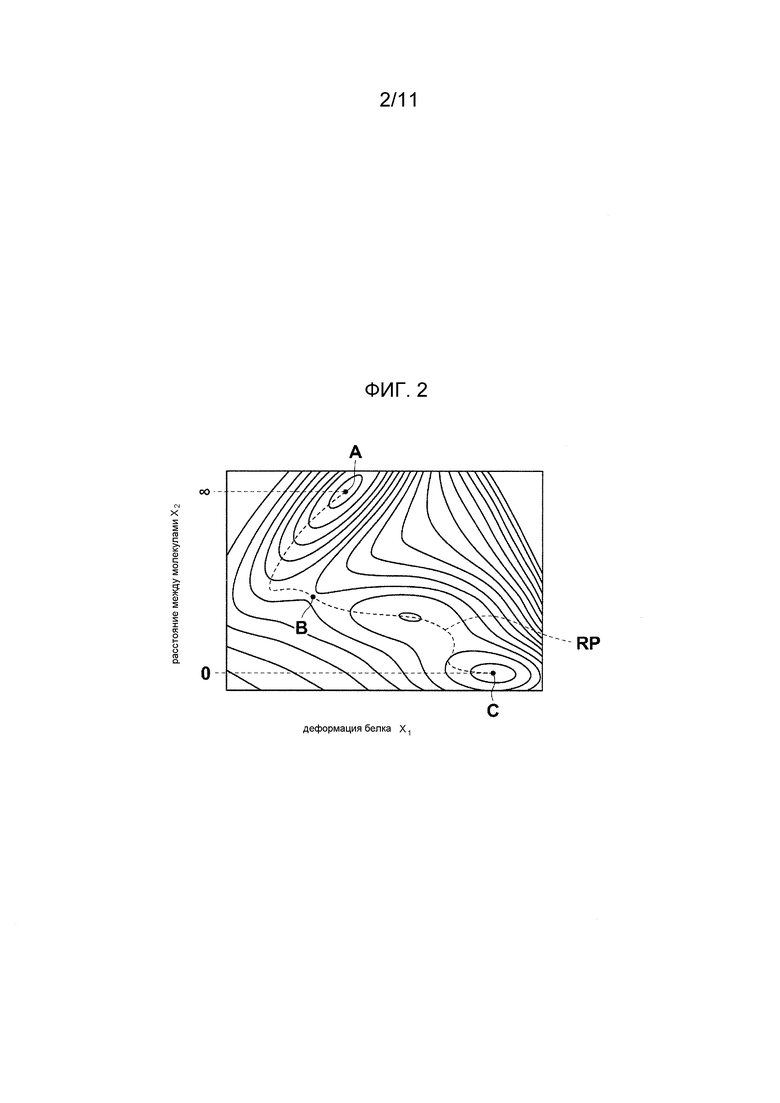
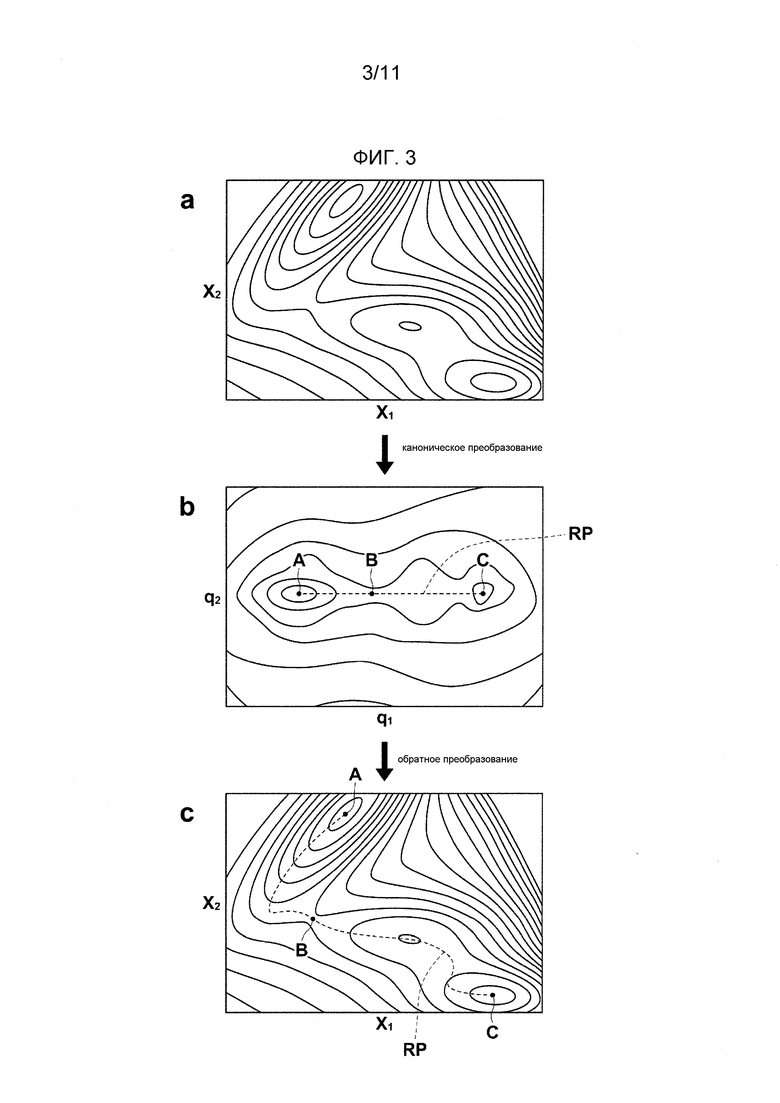
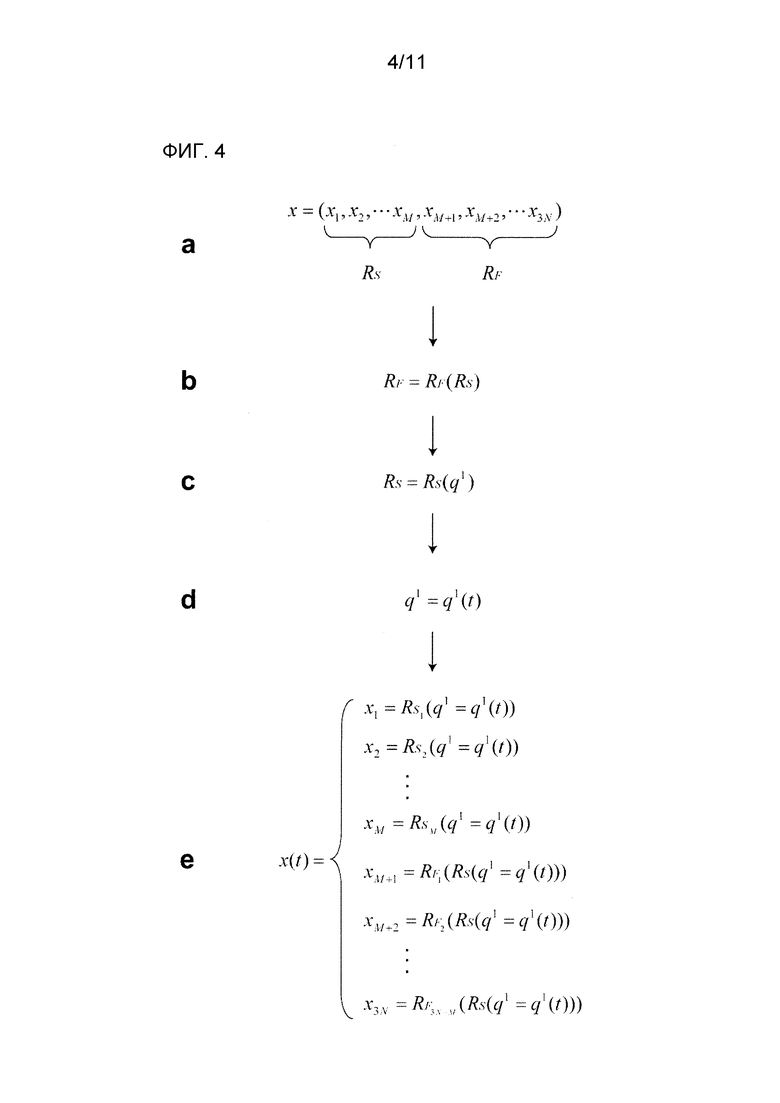
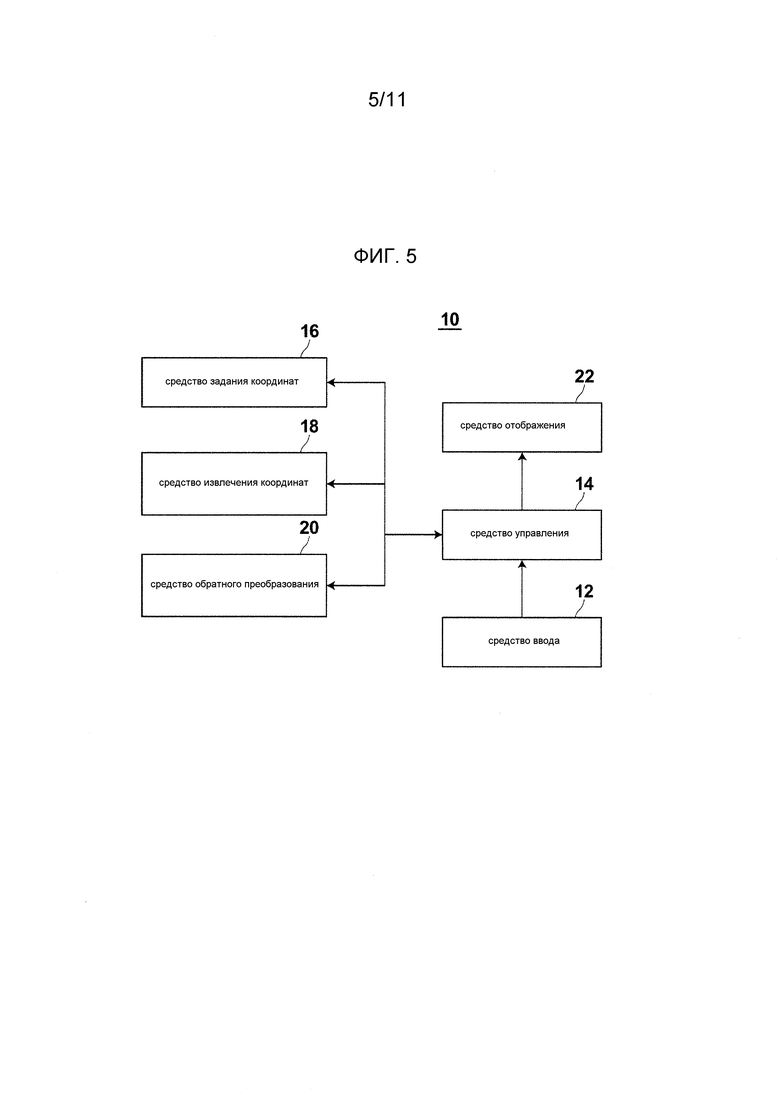
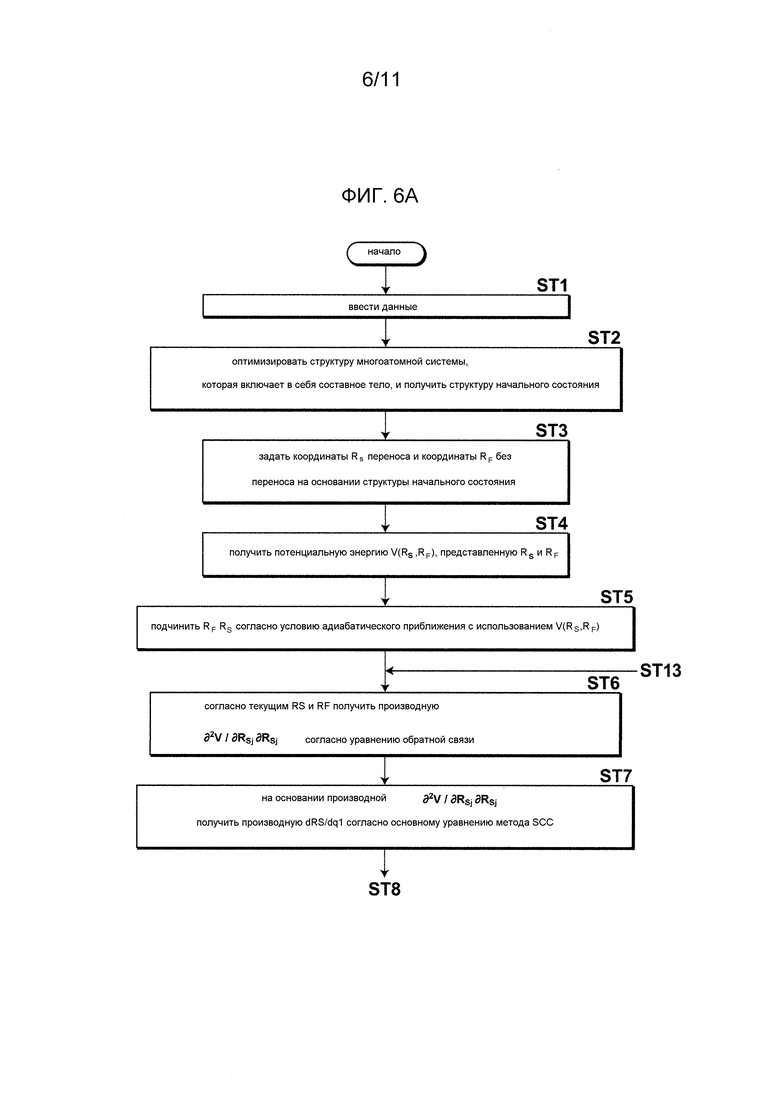
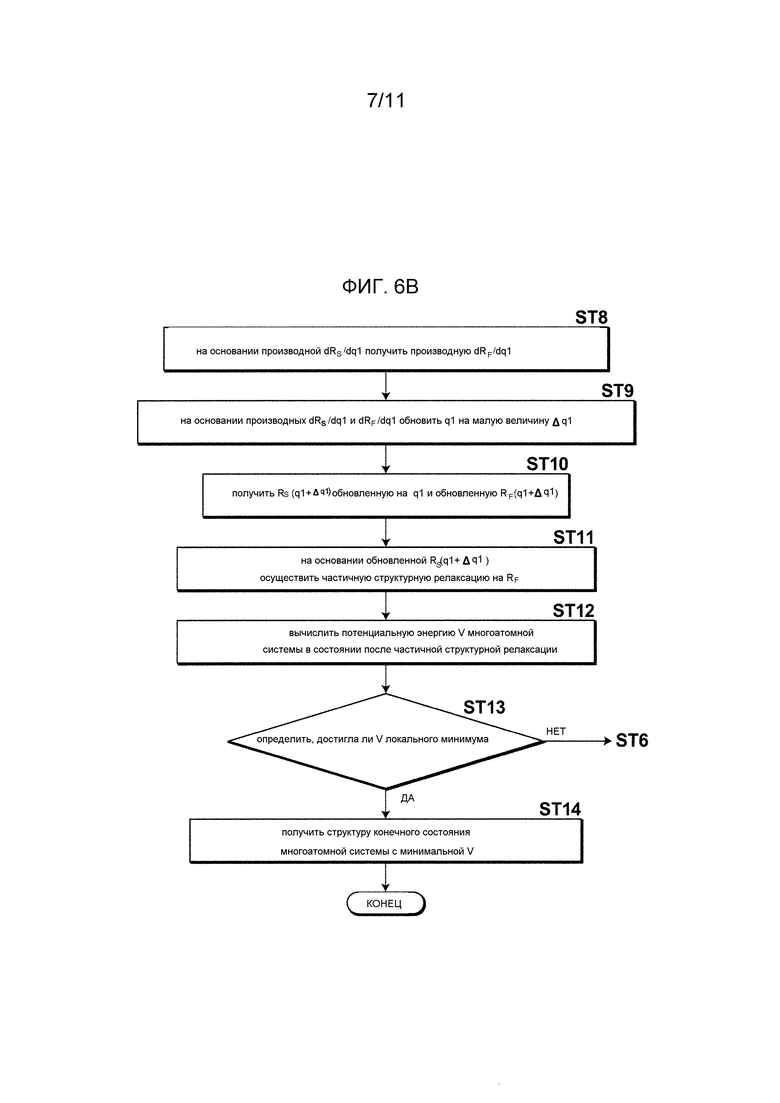
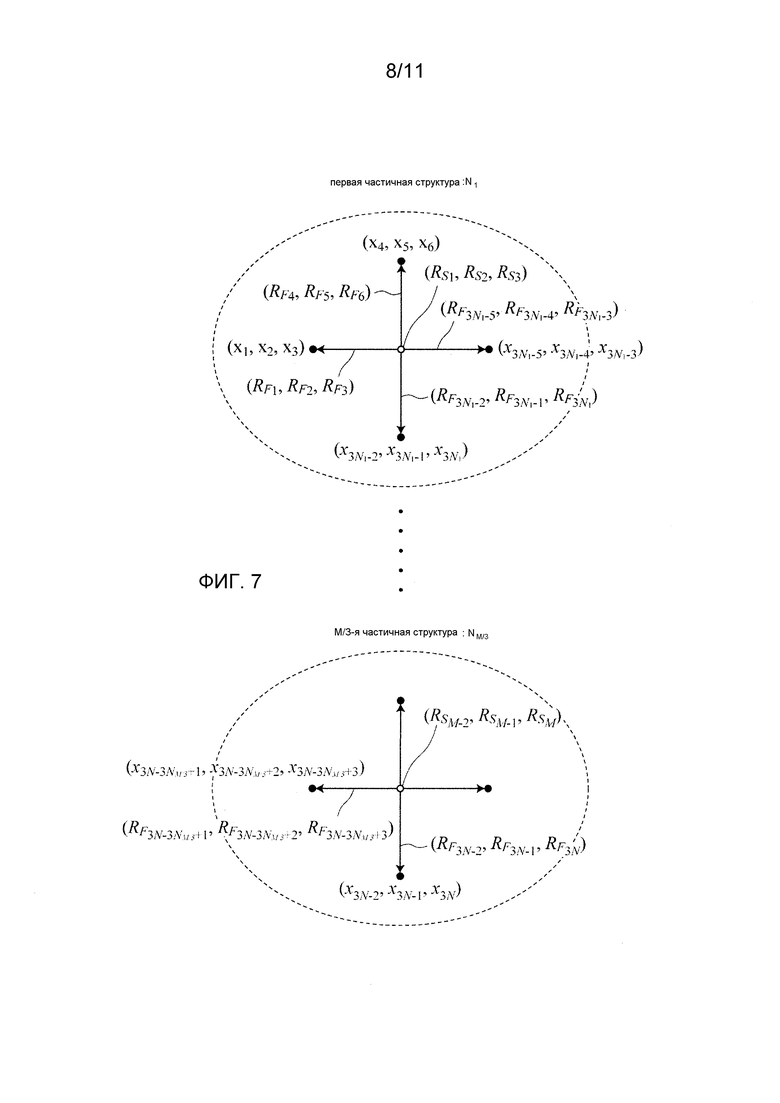
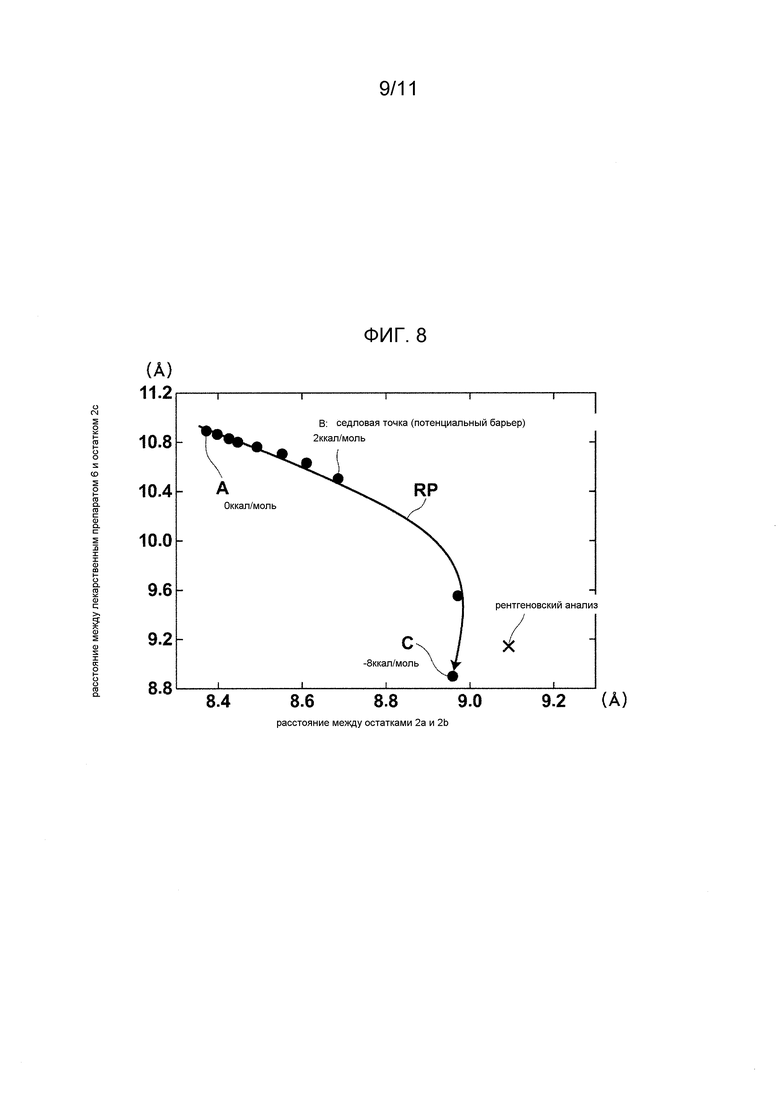
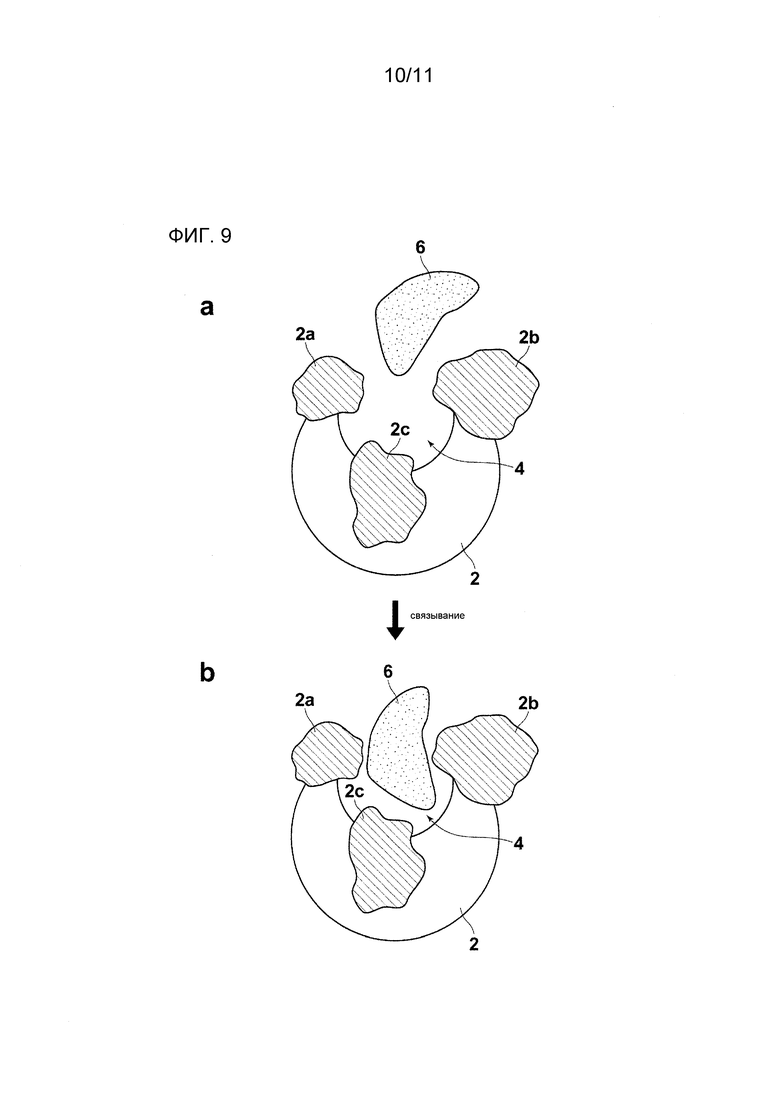
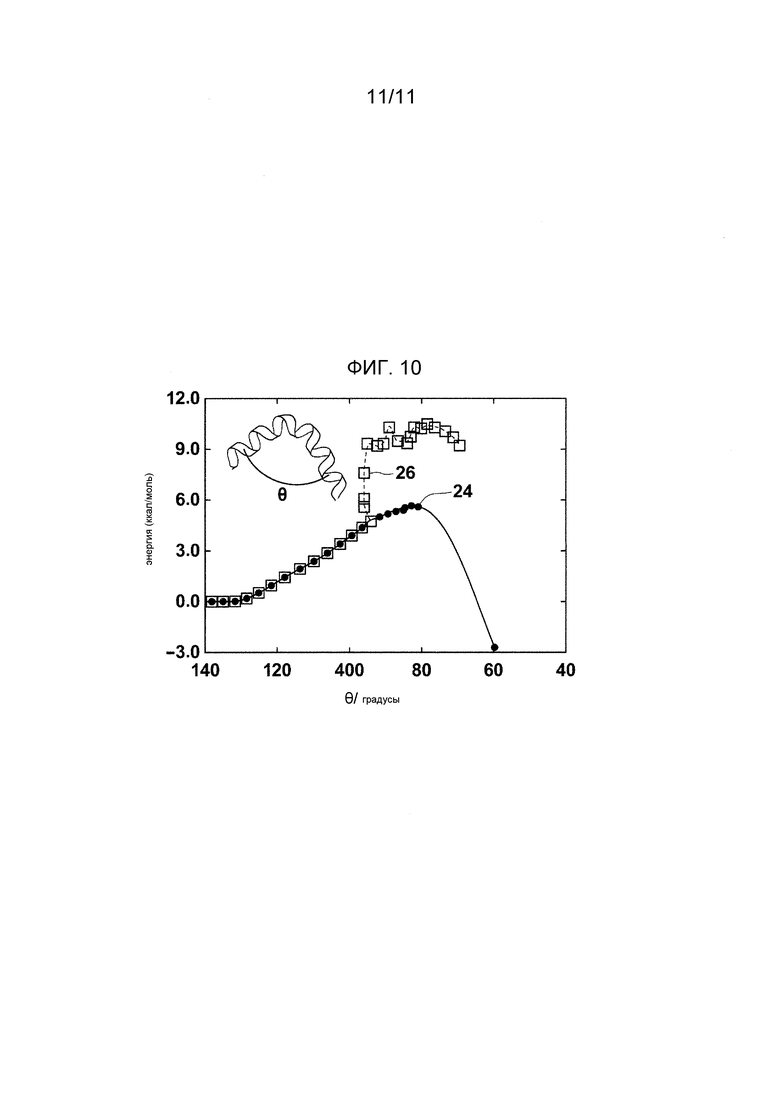
Данное изобретение относится к биоинформатике. Предложены устройство и способ имитационного моделирования для прогнозирования поведения многоатомной системы, включающей биологическую макромолекулу, а также компьютерно-считываемый носитель. Настоящее изобретение основано на использовании быстрых и медленных координат, реализуется с использованием компьютера и обеспечивает повышенную точность и сокращение времени имитационного моделирования. 3 н. и 17 з.п. ф-лы, 10 ил.
1. Устройство имитационного моделирования для прогнозирования поведения моделируемой многоатомной системы, образованной N атомами и включающей в себя биологическую макромолекулу, причем упомянутое устройство содержит компьютер, запрограммированный для реализации:
средства задания координат для задания медленных координат, которые представляют собой M координат, заданных координатами центров тяжести частичных структур многоатомной системы, на основании 3N координат точечных масс, описывающих структуру многоатомной системы, и быстрых координат, которые являются координатами атомов и координатами, описывающими структуру многоатомной системы, и не зависят от центров тяжести частичных структур;
средства извлечения координат для получения быстрых координат как функции медленных координат и получения, с учетом влияния изменения атомов на частичные структуры вследствие изменения частичных структур, медленных координат как функции K коллективной координаты (коллективных координат) обобщенной координаты, которая связана с медленными координатами каноническим преобразованием, причем обобщенная координата образована переменной составляющей, для которой относительные взаимные расположения между частичными структурами изменяются со временем, и постоянной составляющей, которая служит константой относительно времени, и K коллективная координата (коллективных координат) является переменной составляющей обобщенной координаты; и
средства обратного преобразования для прогнозирования временной эволюции многоатомной системы на основании коллективной координаты (коллективных координат) как функции времени, которую можно получить в качестве решения уравнения движения относительно коллективной координаты (коллективных координат), медленных координат и быстрых координат,
причем K, M и N удовлетворяют соотношению K<M<3N, и каждое из них представляет целое число, не меньшее 1,
при этом средство извлечения координат получает структуру медленных координат путем:
осуществления первого этапа для получения потенциальной энергии V, представленной как функция медленных координат и быстрых координат;
осуществления второго этапа для представления медленными координатами быстрых координат согласно условию адиабатического приближения с использованием потенциальной энергии;
осуществления, в текущем состоянии медленных координат и быстрых координат, третьего этапа для получения производной потенциальной энергии по медленным координатам с учетом упомянутого влияния;
осуществления, на основании производной потенциальной энергии, четвертого этапа для получения производной медленных координат по коллективной (ым) координате (ам) согласно основному уравнению метода самосогласованных коллективных координат с использованием производной потенциальной энергии;
осуществления, на основании производной медленных координат, пятого этапа для обновления коллективной координаты (коллективных координат) на малую величину и получения обновленных медленных координат;
осуществления, на основании обновленных медленных координат, шестого этапа для осуществления структурной релаксации на быстрых координатах, подчиненных медленным координатам; и
после этого, повторения этапов с третьего по шестой на основании медленных координат и быстрых координат в состоянии после структурной релаксации быстрых координат,
при этом упомянутое влияние учитывается способом, который использует по меньшей мере одну из нижеприведенных формул 1-3
 ,
,
где каждое из i, j и k представляет целое число в диапазоне от 1 до M;
каждое из α, β и γ представляет целое число в диапазоне от 1 до 3N-M;
RSi представляет i-ю медленную координату в многоатомной системе;
RFα представляет α-ю быструю координату в многоатомной системе;
RS представляет (RS1, RS2, ------, RSM);
RF представляет (RF1, RF2, ------, RF(3N- M));
RF(RS) представляет быстрые координаты как функцию медленных координат;
V(RS,RF) представляет потенциальную энергию, представленную медленными координатами и быстрыми координатами;
Veff(RS) представляет эффективную потенциальную энергию, получаемую подстановкой RF(RS) в V(RS,RF);
в формуле 2, (i↔j) в третьем члене представляет член, выведенный взаимной заменой индексов i и j во втором члене;
в формуле 3, (i↔k) в третьем члене представляет член, выведенный взаимной заменой индексов i и k во втором члене, (j↔k) в четвертом члене представляет член, выведенный взаимной заменой индексов j и k во втором члене, (i↔k) в шестом члене представляет член, выведенный взаимной заменой индексов i и k в пятом члене, и (j↔k) в седьмом члене представляет член, выведенный взаимной заменой индексов j и k в пятом члене; и далее
в формулах 1-3, используется нижеприведенная формула 4
 ,
,
где: Kαβ-1(RS) представляет матрицу, обратную Kαβ(RS), и
Kαβ(RS) и Jαi(RS) задаются нижеприведенными формулами 5 и 6 соответственно
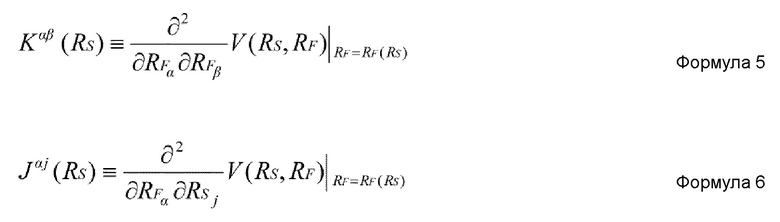 ,
,
при этом количество K коллективной координаты (коллективных координат) удовлетворяет условию K=1, и основное уравнение представлено нижеприведенными формулами 8 и 9
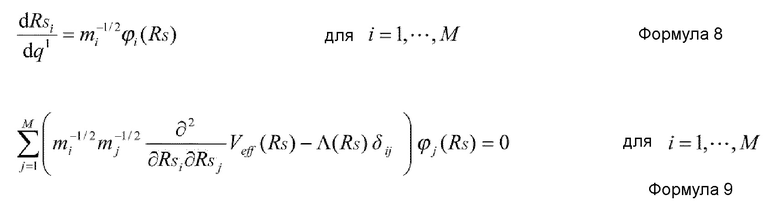 ,
,
где каждое из i и j представляет целое число в диапазоне от 1 до M;
RSi представляет i-ю медленную координату в многоатомной системе;
RS представляет (RS1, RS2, ------, RSM);
q1 представляет коллективную координату;
mi представляет массу i-й медленной координаты в многоатомной системе;
ϕ i(RS) представляет i-ю составляющую функции (собственный вектор), которая удовлетворяет формуле 9;
Λ(RS) представляет функцию (собственное значение), которая удовлетворяет формуле 9; и
Veff(RS) представляет эффективную потенциальную энергию.
2. Устройство имитационного моделирования по п.1, в котором условие адиабатического приближения выражается нижеприведенной формулой 7
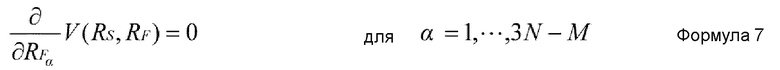 ,
,
где RFα представляет α-ю быструю координату в многоатомной системе;
RS представляет (RS1, RS2, ------, RSM);
RF представляет (RF1, RF2, ------, RF(3N-M)); и
V(RS,RF) представляет потенциальную энергию, представленную медленными координатами и быстрыми координатами.
3. Устройство имитационного моделирования по п.1, в котором количество K коллективной координаты (коллективных координат) удовлетворяет условию K=1, и основное уравнение представлено нижеприведенными формулами 10-12

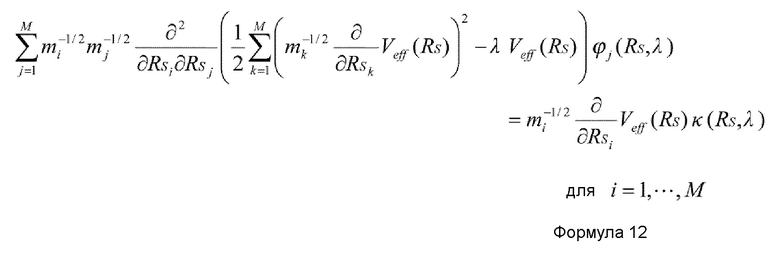 ,
,
где каждое из i, j и k представляет целое число в диапазоне от 1 до M;
RSi представляет i-ю медленную координату в многоатомной системе;
RS представляет (RS1, RS2, ------, RSM);
q1 представляет коллективную координату;
mi представляет массу i-й медленной координаты в многоатомной системе;
ϕ i(RS, λ) и κ(RS, λ) представляют i-ю составляющую функции, которая удовлетворяет формуле 12 и λ представляет вспомогательную координату; и
Veff(RS) представляет эффективную потенциальную энергию.
4. Устройство имитационного моделирования по любому из пп.1-3, в котором средство извлечения координат является средством, которое осуществляет вычисление на четвертом этапе путем увеличения количества переменных, рассматриваемых как независимые от медленных координат и как функции коллективной координаты(коллективных координат) при решении основного уравнения для исключения произвольности знака производной медленных координат или вспомогательных координат относительно коллективной координаты(коллективных координат) в основном уравнении.
5. Устройство имитационного моделирования по п.4, в котором средство извлечения координат является средством, которое осуществляет вычисление согласно основному уравнению, представленному нижеприведенной формулой 13, полученной в результате увеличения количества переменных, рассматриваемых как независимые от медленных координат и как функции коллективной координаты(коллективных координат)
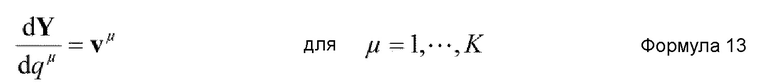 ,
,
где Y - MK+M+K-мерный вектор, заданный нижеприведенной формулой 14, и vμ - вектор решения неоднородного линейного уравнения нижеприведенной формулы 15
 ,
,
C и sμ в формуле 15 задаются нижеприведенными формулами 16 и 17 соответственно
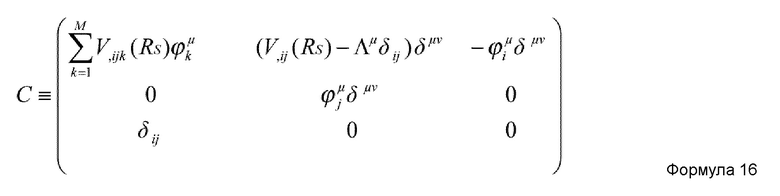
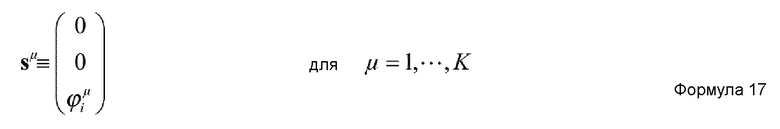 ,
,
где V,ij(RS) и V,ijk(RS) задаются нижеприведенными формулами 18 и 19 соответственно
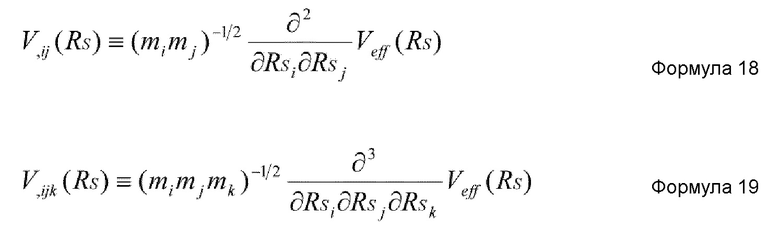
где каждое из i, j и k представляет целое число в диапазоне от 1 до M;
каждое из μ и ν представляет целое число в диапазоне от 1 до K;
qμ представляет μ-ю коллективную координату;
RSi представляет i-ю медленную координату в многоатомной системе;
RS представляет (RS1, RS2, ------, RSM);
mi представляет массу i-й медленной координаты в многоатомной системе;
каждое из ϕiμ и Λu представляет вспомогательную координату, независимую от RS; и
Veff(RS) представляет эффективную потенциальную энергию.
6. Устройство имитационного моделирования по п.5, в котором количество K коллективной координаты (коллективных координат) удовлетворяет условию K=1.
7. Устройство имитационного моделирования по п.4, в котором средство извлечения координат является средством, которое осуществляет вычисление согласно основному уравнению, представленному нижеприведенной формулой 20, полученной в результате увеличения количества переменных, рассматриваемых как независимые от медленных координат и как функции коллективной координаты(коллективных координат)
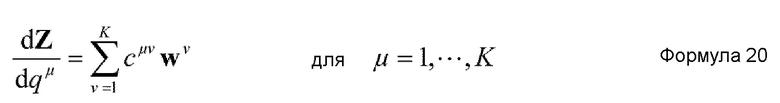
где Z - MK+M+2K-мерный вектор, заданный нижеприведенной формулой 21;
cμν - константа, уникально определенная так, чтобы минимизировать значение, представленное нижеприведенной формулой 22, задаваемое относительно каждого μ; и
wμ представляет один из K MK+M+2K-мерный (ых) единичный вектор (единичных векторов), образующий базис K-мерного пространства сингулярных значений матрицы D, заданной нижеприведенной формулой 23

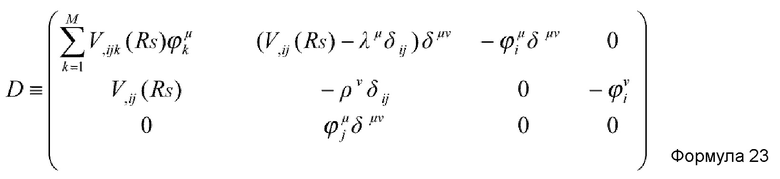 ,
,
где V,ij(RS) и V,ijk(RS) задаются нижеприведенными формулами 24 и 25 соответственно
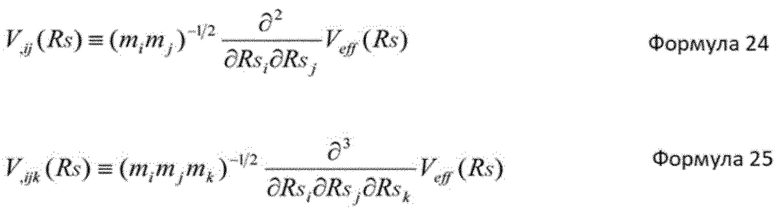 ,
,
где каждое из i, j и k представляет целое число в диапазоне от 1 до M;
каждое из μ и ν представляет целое число в диапазоне от 1 до K;
qμ представляет μ-ю коллективную координату;
RSi представляет i-ю медленную координату в многоатомной системе;
RS представляет (RS1, RS2, ------, RSM);
mi представляет массу i-й медленной координаты в многоатомной системе;
каждое из ϕiμ, λu и ρu представляет вспомогательную координату, независимую от RS; и
Veff(RS) представляет эффективную потенциальную энергию.
8. Устройство имитационного моделирования по п.7, в котором количество K коллективной координаты (коллективных координат) удовлетворяет условию K=1.
9. Устройство имитационного моделирования по п.3, в котором средство извлечения координат является средством, которое вычисляет член третьей производной потенциальной энергии на основании нижеприведенной формулы 26
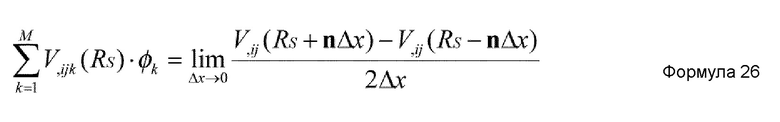
где ϕi представляет i-ю составляющую произвольного вектора, и
V,ij(RS), V,ijk(RS) и n задаются соответственно нижеприведенными формулами 27-29
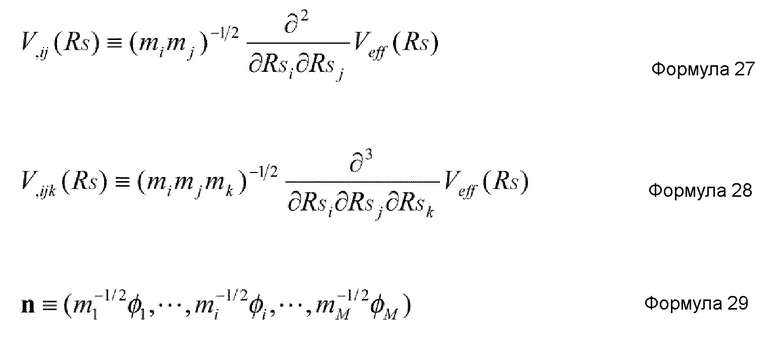 .
.
10. Устройство имитационного моделирования по п.9, в котором биологическая макромолекула является белком, частичная структура является вторичной структурой белка и медленная координата вторичной структуры является координатой центра тяжести группы атомов, составляющей вторичную структуру.
11. Устройство имитационного моделирования по п.10, в котором вторичная структура является по меньшей мере одной из спиральной структуры, β-листа, витка, петли и случайной спирали.
12. Устройство имитационного моделирования по п.9, в котором биологическая макромолекула является белком, частичная структура является остатком белка и медленная координата остатка является координатой центра тяжести группы атомов, составляющих остаток.
13. Устройство имитационного моделирования по п.9, в котором биологическая макромолекула является белком, частичная структура является основной цепью белка и медленная координата основной цепи является координатой каждого атома составляющего основную цепь.
14. Устройство имитационного моделирования по п.9, в котором биологическая макромолекула является нуклеиновой кислотой, частичная структура является вторичной структурой нуклеиновой кислоты и медленная координата вторичной структуры является координатой центра тяжести группы атомов, составляющей вторичную структуру.
15. Устройство имитационного моделирования по п.14, в котором вторичная структура является спиральной структурой.
16. Устройство имитационного моделирования по п.9, в котором биологическая макромолекула является нуклеиновой кислотой, частичная структура является остатком нуклеиновой кислоты и медленная координата остатка является координатой центра тяжести группы атомов, составляющих остаток.
17. Устройство имитационного моделирования по п.9, в котором биологическая макромолекула является нуклеиновой кислотой, частичная структура является основной цепью нуклеиновой кислоты и медленная координата основной цепи является координатой каждого атома составляющего основную цепь.
18. Устройство имитационного моделирования по любому из пп.9-17, в котором многоатомная система включает в себя молекулу-кандидат на связывание для биологической макромолекулы.
19. Способ имитационного моделирования для использования устройством имитационного моделирования по любому из пп.1-18 для прогнозирования поведения моделируемой многоатомной системы, образованной N атомами и включающей в себя биологическую макромолекулу, причем упомянутый способ содержит этапы, на которых:
задают медленные координаты, которые представляют собой M координат, заданных координатами центров тяжести частичных структур многоатомной системы, на основании 3N координат точечных масс, описывающих структуру многоатомной системы;
задают быстрые координаты, которые являются координатами атомов и координатами, описывающими структуру многоатомной системы, и не зависят от центров тяжести частичных структур;
получают быстрые координаты как функцию медленных координат;
получают, с учетом влияния изменения атомов на частичные структуры вследствие изменения частичных структур, медленные координаты как функцию K коллективной координаты (коллективных координат) обобщенной координаты, которая связана с медленными координатами каноническим преобразованием, причем обобщенная координата образована переменной составляющей, для которой относительные взаимные расположения между частичными структурами изменяются со временем, и постоянной составляющей, которая служит константой относительно времени, и K коллективная координата (коллективных координат) является переменной составляющей обобщенной координаты; и
прогнозируют временную эволюцию многоатомной системы на основании коллективной координаты (коллективных координат) как функции времени, которую можно получить, решая уравнение движения относительно коллективной координаты (коллективной координаты), медленных координат и быстрых координат,
причем K, M и N удовлетворяют соотношению K<M<3N, и каждое из них представляет целое число, не меньшее 1,
при этом структуру медленных координат получают путем:
осуществления первого этапа для получения потенциальной энергии V, представленной как функция медленных координат и быстрых координат;
осуществления второго этапа для представления медленными координатами быстрых координат согласно условию адиабатического приближения с использованием потенциальной энергии;
осуществления, в текущем состоянии медленных координат и быстрых координат, третьего этапа для получения производной потенциальной энергии по медленным координатам с учетом упомянутого влияния;
осуществления, на основании производной потенциальной энергии, четвертого этапа для получения производной медленных координат по коллективной (ым) координате (ам) согласно основному уравнению метода самосогласованных коллективных координат с использованием производной потенциальной энергии;
осуществления, на основании производной медленных координат, пятого этапа для обновления коллективной координаты (коллективных координат) на малую величину и получения обновленных медленных координат;
осуществления, на основании обновленных медленных координат, шестого этапа для осуществления структурной релаксации на быстрых координатах, подчиненных медленным координатам; и
после этого, повторения этапов с третьего по шестой на основании медленных координат и быстрых координат в состоянии после структурной релаксации быстрых координат,
при этом упомянутое влияние учитывается способом, который использует по меньшей мере одну из нижеприведенных формул 1-3
 ,
,
где каждое из i, j и k представляет целое число в диапазоне от 1 до M;
каждое из α, β и γ представляет целое число в диапазоне от 1 до 3N-M;
RSi представляет i-ю медленную координату в многоатомной системе;
RFα представляет α-ю быструю координату в многоатомной системе;
RS представляет (RS1, RS2, ------, RSM);
RF представляет (RF1, RF2, ------, RF(3N- M));
RF(RS) представляет быстрые координаты как функцию медленных координат;
V(RS,RF) представляет потенциальную энергию, представленную медленными координатами и быстрыми координатами;
Veff(RS) представляет эффективную потенциальную энергию, получаемую подстановкой RF(RS) в V(RS,RF);
в формуле 2, (i↔j) в третьем члене представляет член, выведенный взаимной заменой индексов i и j во втором члене;
в формуле 3, (i↔k) в третьем члене представляет член, выведенный взаимной заменой индексов i и k во втором члене, (j↔k) в четвертом члене представляет член, выведенный взаимной заменой индексов j и k во втором члене, (i↔k) в шестом члене представляет член, выведенный взаимной заменой индексов i и k в пятом члене, и (j↔k) в седьмом члене представляет член, выведенный взаимной заменой индексов j и k в пятом члене; и далее
в формулах 1-3, используется нижеприведенная формула 4

где: Kαβ-1(RS) представляет матрицу, обратную Kαβ(RS), и
Kαβ(RS) и Jαi(RS) задаются нижеприведенными формулами 5 и 6 соответственно
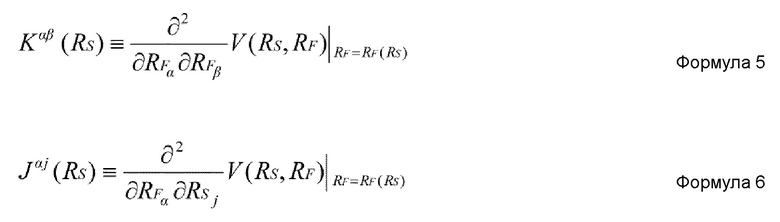 ,
,
при этом количество K коллективной координаты (коллективных координат) удовлетворяет условию K=1 и основное уравнение представлено нижеприведенными формулами 8 и 9
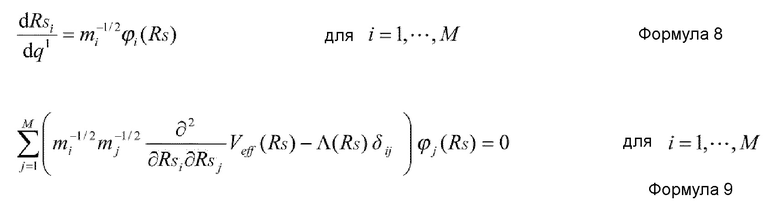 ,
,
где каждое из i и j представляет целое число в диапазоне от 1 до M;
RSi представляет i-ю медленную координату в многоатомной системе;
RS представляет (RS1, RS2, ------, RSM);
q1 представляет коллективную координату;
mi представляет массу i-й медленной координаты в многоатомной системе;
ϕ i(RS) представляет i-ю составляющую функции (собственный вектор), которая удовлетворяет формуле 9;
Λ(RS) представляет функцию (собственное значение), которая удовлетворяет формуле 9; и
Veff(RS) представляет эффективную потенциальную энергию.
20. Компьютерно-считываемый носитель записи, на котором записана программа имитационного моделирования, содержащая код, который при исполнении его на компьютере заставляет компьютер осуществлять все этапы способа имитационного моделирования для прогнозирования поведения моделируемой многоатомной системы по п.19.
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| MARUMORI TOSHIO et al | |||
| "Self-consistent collective-coordinate method for the large-amplitude nuclear collective motion." Progress of Theoretical Physics, 1980, 64(4): 1294-1314 | |||
| TUCKERMAN MARK E., BERNE BRUCE J | |||
| "Molecular dynamics in systems with multiple time scales: Systems with stiff and soft degrees of freedom and with short and long range forces." The Journal of chemical physics, 1991, 95(11): 8362-8364 | |||
| BARBATTI MARIO | |||
| "Nonadiabatic dynamics with trajectory surface hopping method." Wiley Interdisciplinary Reviews: Computational Molecular Science, июль-август 2011, 1(4): 620-633 | |||
| OKUNBOR DANIEL I., SKEEL ROBERT D | |||
| "Canonical numerical methods for molecular dynamics simulations." Journal of Computational Chemistry, 1994, 15(1): 72-79. | |||
Авторы
Даты
2018-07-11—Публикация
2012-09-26—Подача