Изобретение относится к разработке новых соединений для медицины, биотехнологии, физики конденсированных сред и различных областей материаловедения, в которых существенны межмолекулярные взаимодействия, и может быть использовано при разработке новых лекарственных препаратов методами in silico - то есть путем численного моделирования комплекса лекарственного вещества с рецептором или целевым белком. В ходе такого моделирования могут быть получены значения энергетических величин, характеризующих интенсивность взаимодействия белка и лекарственного вещества. На основании этих значений можно сделать вывод об устойчивости комплекса лекарственного вещества с рецептором или целевым белком. Устойчивость комплекса прямо связана с возможной эффективностью лекарственного соединения.
Для этой цели в настоящее время широко используются модели силового поля (например, такие, как AMBER2002, OPLS-AA, CHARMM, ab-initio силовое поле MMFF), в которых атомы в молекулах рассматриваются как классические частицы, взаимодействующие друг с другом с помощью потенциалов взаимодействия.
Несмотря на широкое использование моделей силового поля для численного моделирования взаимодействия молекул друг с другом, эта методология часто неадекватно описывает поведение молекулярных систем. Это обусловлено тем, что поведение атомов в молекулах и электронов в атомах подчиняется законам квантовой, а не классической механики. В настоящее время квантовая механика широко применяется для вычисления характеристик молекул сравнительно небольшого размера (десятки атомов) и их взаимодействия между собой. В последнее время в связи с быстрым увеличением мощности компьютеров стали возможны квантовые расчеты молекулярных систем, содержащих сотни и даже тысячи атомов. Точность и время таких расчетов зависят от применяемых методов вычислений и используемых вычислительных мощностей. Учитывая интенсивное развитие первых и быстрый рост вторых, ясно, что применение квантовой механики для численного моделирования молекулярных систем будет возрастать. В частности, для вычисления интенсивности связывания молекулы-лиганда с молекулой-мишенью методы классических силовых полей будут вытесняться методами, основанными на уравнениях квантовой механики.
Однако методы квантовой механики ранее крайне редко использовались для описания биологических молекул, которые, как правило, являются макромолекулами, содержащими сотни и тысячи атомов. Так, неэмпирический метод Хартри-Фока и метод функционала плотности (DFT) использованы в работах [1-3] для описания квантовой части системы, которая погружена в молекулярное окружение, описываемое классически с помощью некоторого силового поля. Это так называемое QM/MM приближение, в котором описание части системы происходит по законам квантовой механики (QM), а другой части системы - по законам классической молекулярной механики (MM). В частности, вычисление энергии взаимодействия (а точнее энтальпии взаимодействия) между двумя биологическими молекулами проведено в работе [2], в которой моделировалась фермент-субстратная реакция.
Более простой и соответственно более быстрый квантово-химический полуэмпирический метод PM3 использован в работе [4] для моделирования активного центра в ферменте цитидин деаминаза. Рассмотренная при моделировании молекулярная система содержала активный центр из 1330 атомов. Для расчета столь большой молекулярной системы использовался так называемый метод Divide-and-Conquer (разделяй и побеждай) или сокращенно D&C или DAC.
Полуэмпирический квантово-механический метод AM1 применялся для исследования электронной структуры биологических макромолекул в растворе [5], при этом использовалась континуальная модель растворителя. Энтальпии связывания белок - белок и белок - ДНК получены как разность между энтальпиями образования соответствующих комплексов и энтальпиями образования отдельных их компонентов, однако полученные данные оказались достаточно нереалистическими (около 5-20 эВ).
Несколько органических макромолекул, содержащих от 256 до 9378 атомов, были рассчитаны в рамках полуэмпирического метода PM3 с использованием метода D&C в рамках пакета квантово-химических программ MOPAC [6]. При этом расчеты проводились как в вакууме, так и в водном растворе с использованием приближения COSMO, в котором растворитель моделировался континуально. При этом также не определялись энергетические характеристики исследуемых химических систем, и основное внимание уделялось получению оптимизированных структур макромолекул и времени, требуемому на оптимизацию.
Большинство известных квантово-механических исследований биологических макромолекул посвящено расчету энергетических характеристик различных ферментативных реакций. При этом исследовались механизмы различных реакций с участием молекул воды, их переходные комплексы и соответствующие энергетические барьеры. Однако во всех этих работах нет оценок интенсивности связывания белков и лигандов в их межмолекулярных комплексах, и не учитывается влияние растворителя на рассматриваемые процессы в макромолекулах.
Таким образом, из известной литературы видно, что при применении методов квантовой механики в способах моделирования биологических макромолекул отсутствует единый подход в определении интенсивности связывания молекул-лигандов с молекулами-мишенями. В известных способах с помощью методов квантовой механики определяются, в основном, структурные и электронные характеристики индивидуальных макромолекул с использованием механизмов и энергетических барьеров ферментативных реакций разрыва пептидной связи в белках. Сравнение таких вычисленных данных с экспериментально полученными данными свидетельствует о неудовлетворительной точности полученных величин. Из уровня техники не известны способы моделирования на основе квантово-механических расчетов энергетических характеристик межмолекулярного взаимодействия молекул-лигандов и молекул-мишеней. Кроме того, в существующих способах квантово-механического исследования макромолекул не обеспечивается корректным образом учет влияния растворителя, что очень важно при моделировании связывания биологических молекул-мишеней с молекулами-лигандами, где существенную роль играют водородные связи.
В связи с этим задачей настоящего изобретения является создание способа моделирования межмолекулярного взаимодействия в водном растворе на основе методов квантовых расчетов с учетом влияния растворителя, как на молекулярном уровне, так и в виде экранирующего континуума, с учетом пространственной релаксации атомов и перераспределения электронной плотности при образовании межмолекулярного комплекса. Такой способ моделирования должен быть применим к определению интенсивности связывания молекул-лигандов с молекулами-мишенями независимо от состава и размера этих молекул, а также независимо от типа применяемого метода квантового расчета. Этот способ должен использовать минимальное количество подгоночных параметров и опираться по возможности только на основные принципы квантовой механики. Техническим результатом является создание способа моделирования и прогнозирования связывания молекул-лигандов с молекулами-мишенями методами квантовой механики с учетом влияния растворителя.
Указанный результат достигается тем, что предложен способ моделирования и прогнозирования связывания молекул-мишеней и молекул-лигандов, при котором, исходя из структуры и состава межмолекулярного комплекса мишень-лиганд, молекулы-мишени и молекулы-лиганды, формируют модели межмолекулярного комплекса и его компонентов с явным и неявным учетом растворителя, которые используются далее при моделировании связывания молекулы-лиганда и молекулы-мишени с учетом влияния растворителя методами квантовой механики с выбранными параметрами моделирования. Используя результаты этого моделирования, вычисляют энтальпию, энтропию и свободную энергию связывания выбранной молекулы-лиганда и молекулы-мишени, характеризующие интенсивность связывания молекулы-лиганда с молекулой-мишенью, которые для известных лигандов сравнивают с известными экспериментальными данными. Для новых лигандов вычисленные величины при подобранных параметрах моделирования являются критерием интенсивности связывания молекулы-лиганда с молекулой-мишенью и, следовательно, являются критерием при прогнозировании лигандов как потенциальных лекарственных веществ.
В заявленном способе моделирования структуру и состав молекулы-мишени и молекулы-лиганда получают с помощью экспериментальных измерений, из базы данных PDB (Protein Data Bank) [7], кроме того, структуру, состав и координаты атомов новой молекулы-лиганда могут получать с помощью специальных программ - построителей новых лигандов. Если в исходных структурах молекул-мишеней и молекул-лигандов отсутствуют данные о декартовых координатах водородных атомов, координаты недостающих атомов добавляют к координатам атомов молекулы-мишени и молекулы-лиганда, используя различные компьютерные программы построения молекулярных структур. Положения в пространстве добавленных атомов водорода определяют при молекулярно-механической или квантово-механической оптимизации из условия, при котором полная энергия молекулы-мишени и молекулы-лиганда достигает минимума при варьировании координат добавленных водородных атомов.
Структуру межмолекулярного комплекса молекулы-мишени и молекулы-лиганда получают с помощью стыковки молекулы-лиганда и молекулы-мишени или, как чаще принято называть, докинга, для чего выполняют преобразование координат атомов этих молекул таким образом, чтобы наименьшее расстояние между каждым из атомов лиганда и заданными атомами молекулы-мишени находилось в заданном диапазоне.
Для того чтобы учесть при моделировании влияние растворителя на связывание молекулы-мишени и молекулы-лиганда в рамках явного учета растворителя, множество координат молекул растворителя добавляют к множеству координат межмолекулярного комплекса мишень-лиганд и к множествам координат молекулы-лиганда и молекулы-мишени по отдельности. Это делают так, чтобы молекулы растворителя заполняли собой без взаимопересечений и пересечений с атомами межмолекулярного комплекса, молекулы-мишени и молекулы-лиганда все пространство вокруг этих молекулярных систем. Положение молекул растворителя оптимизируют, как правило, в рамках пакетов молекулярной механики или молекулярной динамики вблизи межмолекулярного комплекса и его компонентов, взятых индивидуально.
Квантово-механические модели молекулы-мишени, молекулы-лиганда и их межмолекулярного комплекса строят на основе полученных структур этого межмолекулярного комплекса и его компонентов с явно учитываемым растворителем. Для этого проводят сортировку атомов межмолекулярного комплекса, молекулы-мишени и молекулы-лиганда вместе с атомами растворителя на две группы. Для межмолекулярного комплекса в первую группу должны войти все атомы молекулы-лиганда, а также атомы молекулы-мишени и молекулы растворителя, расстояния от которых до каждого из атомов молекулы-лиганда не превышают заданное значение, а во вторую группу входят все остальные атомы молекулы-мишени и все остальные молекулы растворителя. Для модели молекулы-мишени в первую группу атомов должны войти те же атомы молекулы-мишени, которые входят в первую группу атомов межмолекулярного комплекса. Кроме этого, в первую группу должны войти молекулы растворителя, которые находятся от атомов молекулы-мишени, включенных в первую группу, на расстоянии, не превышающем заданную величину, а во вторую группу входят все остальные атомы молекулы-мишени и все остальные молекулы растворителя. Для модели молекулы-лиганда в первую группу атомов должны войти все атомы молекулы-лиганда, а также молекулы растворителя, которые находятся от атомов молекулы-лиганда на расстоянии, не превышающем заданную величину, а во вторую группу входят все остальные молекулы растворителя.
Как правило, атомы первой группы всех рассматриваемых молекулярных систем моделируются методами квантовой механики, а атомы второй группы моделируются методами классической механики, или же атомы второй группы исключаются из моделирования. Для моделирования стыковки двух групп атомов, рассчитываемых в рамках квантового и классического методов, вводятся дополнительные атомы вблизи области пространства, где атомы первой и второй групп находятся на расстоянии друг от друга, не превышающем заданную величину. При этом дополнительные пограничные атомы рассчитывают одновременно в классическом и квантовом приближениях. Если только атомы первой группы рассчитываются в рамках квантового метода, а атомы второй группы исключаются из моделирования, добавленные атомы также рассчитываются в рамках квантового подхода. При этом дополнительные атомы добавляют таким образом, чтобы они образовывали новые ковалентные связи взамен оборванных ковалентных связей между атомами первой и второй групп.
Для полученных моделей определяют зарядовые состояния различных молекулярных групп и согласно этому добавляют или убирают дополнительные атомы в соответствующих местах этих молекулярных групп. По этим зарядовым состояниям определяют полный заряд построенных моделей межмолекулярного комплекса мишень-лиганд, молекулы-мишени и молекулы-лиганда.
Когда растворителем является вода, для того, чтобы лучше воспроизвести образование и разрыв водородных связей, при переходе от комплекса к его компонентам, в модели вводят дополнительные молекулы воды. К межмолекулярному комплексу добавляют молекулы воды так, чтобы они находились между молекулой-мишенью и молекулой-лигандом и образовывали с ними водородные связи. К молекуле-мишени и к молекуле-лиганду добавляют молекулы воды так, чтобы с их участием восстановить оборванные водородные связи, которые присутствовали в межмолекулярном комплексе между молекулой-мишенью и молекулой-лигандом и которые были оборваны при удалении молекулы-лиганда из молекулы-мишени.
Однако для правильного учета влияния растворителя, как правило, недостаточно учесть явно некоторое количество молекул растворителя, и в этом случае требуется учесть растворитель в неявной модели, когда его экранирующее влияние учитывается путем введения в модель непрерывной среды с нужным значением диэлектрической проницаемости. В предложенном методе моделирования связывания мишени и лиганда использованы три типа модели неявного учета растворителя, а именно модель, реализующая решение уравнения Пуассона, модель непрерывного проводника и модель, реализующая решение уравнения Пуассона-Больцмана.
Все данные, полученные на этапе построения моделей молекулы-мишени, молекулы-лиганда и межмолекулярного комплекса, используются для формирования входных файлов для квантово-механического моделирования. В этих входных файлах содержится информация о координатах и типах всех атомов рассматриваемых молекулярных систем, их полный заряд и мультиплетность, координаты и тип атомов молекул растворителя, добавленных в явной модели к межмолекулярному комплексу и его компонентам, параметры растворителя в неявной модели. Кроме того, во входных файлах содержится информация о параметрах оптимизационного процесса, а именно метод и параметры метода моделирования, тип оптимизационной процедуры, пределы самосогласования и минимизации.
Входные файлы используют для того, чтобы с помощью соответствующей программы моделирования полной энергии молекулярной системы, основанной или на комбинации квантово-механического и классического приближения или только на квантово-механическом приближении, найти минимум полной энергии трех рассматриваемых молекулярных систем при варьировании положений всех или некоторых дополнительно определенных атомов. Полученные значения полных энергий молекулы-мишени, молекулы-лиганда и их межмолекулярного комплекса используют для вычисления энтальпии связывания компонентов в комплексе. Энтальпия связывания вычисляется как разность между полной энергией межмолекулярного комплекса мишень-лиганд в растворителе, с одной стороны, и суммой полных энергий молекулы-мишени в растворителе и молекулы-лиганда в растворителе, с другой стороны, при соблюдении и при не соблюдении баланса молекул растворителя.
В соответствии с настоящим изобретением вычисление энтальпии связывания молекулы-мишени и молекулы-лиганда можно проводить, используя другой метод, при котором полные энергии молекулы-мишени, молекулы-лиганда и их межмолекулярного комплекса рассчитывают не в точке минимума, а как средние значения полных энергий, полученных для ряда конфигураций межмолекулярного комплекса мишень-лиганд. При этом координаты атомов молекулы-мишени, молекулы-лиганда и их межмолекулярного комплекса, соответствующие каждой из таких конфигураций, могут быть получены в рамках молекулярно-динамического моделирования. В качестве исходных данных при таком виде моделирования также используется структура молекулы-мишени и молекулы-лиганда и их межмолекулярного комплекса, полученного стыковкой координат его компонентов. При молекулярно-динамическом моделировании может использоваться как явная, так и неявная модели растворителя, которые вводятся способами, описанными ранее.
Для межмолекулярного комплекса, вне зависимости от модели растворителя, моделирование осуществляется путем решения уравнений Ньютона или Лагранжа при учете теплового движения всех взаимодействующих друг с другом атомов молекулы-мишени и молекулы-лиганда с учетом наличия молекул растворителя, при этом определяют состояние молекулярной системы, при котором она достигает теплового равновесия. Затем определяют траектории движения всех атомов системы после достижения их теплового равновесия и определяют координаты всех атомов взаимодействующих молекулы-мишени, молекулы-лиганда и молекул растворителя через определенные промежутки времени заданное количество раз для заданного набора конфигураций межмолекулярного комплекса мишень-лиганд. Аналогично получают набор конфигураций молекулы-мишени и молекулы-лиганда.
Для каждого набора координат межмолекулярного комплекса мишень-лиганд, молекулы-мишени, молекулы-лиганда в явной или неявной модели растворителя проводят сортировку всех атомов на группы аналогично тому, как это осуществлялось ранее. Для каждой конфигурации межмолекулярного комплекса мишень-лиганд, молекулы-мишени, молекулы-лиганда формируют входной файл для квантово-механического моделирования межмолекулярного комплекса мишень-лиганд в растворителе, как описано выше. Для каждого входного файла, то есть для каждой конфигурации межмолекулярного комплекса мишень-лиганд, молекулы-мишени, молекулы-лиганда, с помощью выбранного метода моделирования проводят расчет полной энергии этих молекулярных систем в растворителе без оптимизации пространственного строения комплекса. Затем вычисляют средние значения полной энергии межмолекулярного комплекса мишень-лиганд, молекулы-мишени, молекулы-лиганда в растворителе по всему выбранному набору конфигураций этой молекулярной системы. Используя полученные средние значения полных энергий межмолекулярного комплекса мишень-лиганд в растворителе, молекулы-мишени в растворителе и молекулы-лиганда в растворителе, вычисляют энтальпию связывания молекулы-лиганда с молекулой-мишенью в растворителе как разность между полной энергией межмолекулярного комплекса мишень-лиганд в растворителе, с одной стороны, и суммой полных энергий молекулы-мишени в растворителе и молекулы-лиганда в растворителе, с другой стороны.
Расчет энтропии связывания молекулы-лиганда с молекулой-мишенью в растворителе связывания можно разделить на расчет трех ее компонентов, а именно колебательной, поступательной и вращательной составляющих.
Энтропия, связанная с потерей колебательных степеней свободы при переходе от свободных состояний молекулы-мишени и молекулы-лиганда в растворителе к их межмолекулярному комплексу, определяется колебательными частотами молекул, участвующих в рассматриваемом процессе. Для получения колебательных частот рассматриваемых молекулярных систем, в рамках используемого способа квантово-механического моделирования рассчитываются силовые постоянные или вторые производные полных энергий, относящиеся к межмолекулярному комплексу, молекуле-мишени и молекуле-лиганду, по всем координатам атомов в точках соответствующих минимумов.
В изменение энтропии при связывании молекулы-лиганда с молекулой-мишенью вносит вклад и то, что эти молекулы при связывании теряют и поступательные и вращательные степени свободы, которыми они обладали в свободном состоянии. Для вычисления этой части энтропии используются только координаты и атомные веса атомов молекулы-мишени, молекулы-лиганда и их межмолекулярного комплекса, и этот расчет, как правило, вынесен за рамки квантово-механического моделирования. Полное изменение энтропии при связывании молекулы-лиганда с молекулой-мишенью рассчитывают как сумму изменений различных ее компонент.
Процесс связывания молекулы-лиганда с молекулой-мишенью происходит в растворителе. Каждая из этих молекул создает в растворителе полость, расталкивая молекулы растворителя. Этот процесс требует затраты определенной свободной энергии, которая называется энергией кавитации, и она зависит только от свойств растворителя и формы молекулы, помещаемой в растворитель. Изменение кавитационной энергии при связывании молекулы-мишени и молекулы-лиганда вычисляется дополнительно и учитывается при расчете свободной энергии связывания в комплексе. Последняя рассчитывается как сумма энтальпийного, энтропийного членов и члена, характеризующего изменение кавитационной энергии.
Рассчитанные энтальпия, энтропия и свободная энергия связывания являются энергетическими характеристиками интенсивности связывания молекулы-мишени и молекулы-лиганда и используются для прогнозирования связывания новых лигандов с молекулами-мишенями.
Изобретение поясняется на примерах осуществления, иллюстрируемых чертежами, на которых представлено следующее:
Фиг.1 - блок-схема способа квантово-механического моделирования и прогнозирования связывания молекулы-лиганда с молекулой-мишенью;
Фиг.2 - блок-схема способа выбора молекулы-мишени и молекулы-лиганда и построения межмолекулярного комплекса, состоящего из лиганда и мишени;
Фиг.3 - блок-схема способа построения квантово-механических моделей межмолекулярного комплекса лиганд-мишень и его компонентов с явным и неявным учетом растворителя;
Фиг.4 - блок-схема способа квантово-механического моделирования межмолекулярного взаимодействия между молекулой-лигандом и молекулой-мишенью с учетом растворителя, включающего вычисления энтальпии, энтропии, свободной энергии связывания лиганда и мишени.
Фиг.5 - блок-схема молекулярно-динамического способа квантово-механического моделирования связывания молекул-лигандов с молекулами-мишенями в растворителе.
Фиг.6 - структурные формулы (левая колонка) и квантово-механически оптимизированные структуры (правая колонка) лигандов, соответствующих комплексам белок-лиганд, которые были выбраны как тестовые системы для моделирования связывания в системе белок-лиганд методами квантовой механики.
Фиг.7 - модель активного центра комплекса 1AJ6 (система 5 по таблице 1). Белок представлен тонкими палочками, молекулы воды представлены толстыми палочками, молекула лиганда представлена шариками и палочками. Пунктирные линии обозначают водородные связи в комплексе белок-лиганд.
Фиг.8 - схема способа W1 добавления молекул воды к компонентам комплекса белок-лиганд.
Фиг.9 - схема способа W2 добавления молекул воды к компонентам комплекса белок-лиганд.
На фиг.1 изображена общая схема заявленного способа моделирования и прогнозирования связывания молекулы-лиганда с молекулой-мишенью. На этапе 1 выбирают молекулу-мишень и молекулу-лиганд и получают их структуру. Из выбранных молекулы-мишени и молекулы-лиганда на этапе 2 формируют их межмолекулярный комплекс. Исходя из структуры и состава этого межмолекулярного комплекса, на этапе 3 формируют модели межмолекулярного комплекса мишень-лиганд и его компонентов с явным и неявным учетом растворителя, которые используются далее на этапе 4 при моделировании связывания молекулы-лиганда и молекулы-мишени с учетом влияния растворителя методами квантовой механики с выбранными параметрами моделирования. Используя результаты этого моделирования, на этапе 5 вычисляют числовые данные, характеризующие интенсивность связывания молекулы-лиганда с молекулой-мишенью, а именно энтальпию, энтропию и свободную энергию связывания выбранной молекулы-лиганда и молекулы-мишени, и записывают эти величины в виде числовых данных на носитель информации. На этапе 6 экспериментально измеряются аналогичные величины, характеризующие интенсивность связывания заданной молекулы-лиганда с заданной молекулой-мишенью. Затем рассчитанные при моделировании величины, характеризующие интенсивность связывания молекулы-лиганда с молекулой-мишенью, сравниваются на этапе 7 с измеренными на этапе 6 соответствующими величинами. В случае расхождения выше заданного предела рассчитанных и измеренных величин на этапе 8 корректируются модель построения межмолекулярного комплекса и параметры квантово-механического моделирования взаимодействия молекулы-мишени и молекулы-лиганда, в частности корректируется модель учета влияния растворителя на связывание. Затем снова проводят моделирование на этапе 4 и рассчитывают на этапе 5 величины, характеризующие интенсивность связывания молекулы-лиганда с молекулой-мишенью. Этот процесс выработки оптимальной модели и параметров моделирования продолжается до тех пор, пока расхождение между рассчитанными и измеренными величинами, характеризующими связывание молекул между собой, не станет меньше заданной величины. После этого процесс подгонки параметров моделирования для заданной пары молекулы-мишени и молекулы-лиганда считается законченным.
Далее, выбирается другая пара молекулы-лиганда и молекулы-мишени, и для нее повторяются описанные выше этапы формирования модели межмолекулярного комплекса (3), квантово-механического моделирования (4), вычисления величин, характеризующих связывание молекулы-лиганда с молекулой-мишенью (5), измерения этих величин (6), сравнения вычисленных и измеренных величин (7) и корректировки параметров (8). В качестве начальных параметров используются значения параметров моделирования, полученные для предыдущей пары молекулы-мишени и молекулы-лиганда. Затем выбирается следующая пара молекулы-мишени и молекулы-лиганда и т.д.
В результате такой самосогласованной процедуры определяются параметры моделирования, которые позволяют получать с заданной точностью значения величин, характеризующих интенсивность связывания молекулы-лиганда с молекулой-мишенью, а именно энтальпию, энтропию и свободную энергию связывания, для определенного множества пар молекул-мишеней и молекул-лигандов. Этот процесс расширения множества пар молекул-мишеней и молекул-лигандов и самосогласованной подгонки параметров моделирования продолжается до тех пор, пока для очередной взятой вновь пары молекулы-мишени и молекулы-лиганда характеризующие интенсивность связывания величины, вычисленные с использованием параметров моделирования, полученных для других пар молекул, не будут совпадать с заданной точностью с измеренными для данной пары молекул величинами, характеризующими интенсивность связывания. После этого окончательные значения параметров моделирования записываются на этапе 7 (фиг.1) на носитель информации, и в дальнейшем они используются для прогнозирования.
На этапе 9 проводится подтверждение правильности выбранных методов формирования квантово-механических моделей и методов моделирования межмолекулярного взаимодействия в комплексе путем демонстрации совпадения с заданной точностью (которая должна быть порядка точности самих квантовых расчетов 0,1-2,0 ккал/моль) экспериментальных и вычисленных в рамках выработанной модели величин, характеризующих интенсивность связывания для очередных пар молекул-мишеней и молекул-лигандов, которые не использовались в итерационной процедуре разработки способа моделирования. В дальнейшем процедура построения квантово-механической модели и моделирования межмолекулярного взаимодействия в комплексе, состоящем из молекулы-лиганда и молекулы-мишени, используются для определения на этапе 10 группы новых лигандов, имеющих лучшее связывание с заданной молекулой-мишенью.
Прогнозирование на этапе 11 молекул-лигандов, которые достаточно сильно связываются с заданной молекулой-мишенью и могут быть новыми потенциальными лекарственными веществами, заключается в следующем. Для заданной молекулы-мишени формируется множество молекул-лигандов, кандидатов для прогнозирования, исходя из различных баз данных и библиотек фрагментов с помощью программ, использующих определенные правила построения лигандов в активном центре молекулы-мишени. Исходные базы данных содержат информацию о структуре молекул или структуре фрагментов молекул, полученную в различных экспериментах, или содержат координаты атомов молекул или фрагментов молекул, построенных с помощью различных компьютерных программ. Количество молекул в таком множестве молекул-лигандов, являющихся кандидатами для прогнозирования, может быть огромно, до нескольких миллионов, и каждая из этих молекул существует в реальности или может быть синтезирована. Важно, чтобы для молекул этого множества имелась информация об их химическом составе, трехмерной структуре и координатах всех атомов. Для каждой молекулы-лиганда из выбранного множества проводится моделирование на этапе 5 (фиг.1) процесса связывания и вычисление на этапе 6 величин, характеризующих связывание, с учетом влияния растворителя, молекулы-лиганда с заданной молекулой-мишенью, а именно энтальпии, энтропии и свободной энергии связывания с использованием окончательных значений параметров моделирования, полученных на предыдущем этапе. В результате такого моделирования получают величины, характеризующие интенсивность связывания всех молекул-лигандов из выбранного множества с заданной молекулой-мишенью. По результатам моделирования выбирают ряд наиболее перспективных молекул-лигандов, имеющих лучшие значения величин, характеризующих интенсивность связывания. Те молекулы-лиганды, для которых прогнозируется хорошее связывание, могут быть использованы в реальных химических экспериментах по связыванию с заданной молекулой-мишенью. Очевидно, что при таком подходе существенно сокращается число молекул-лигандов, для которых необходимо проводить экспериментальные тестирования. Таким образом, предлагаемый способ компьютерного прогнозирования молекул-лигандов, которые могут быть новыми потенциальными лекарственными веществами, позволяет избежать значительных временных и материальных затрат на синтез новых веществ и проведение экспериментов по измерению величин, характеризующих интенсивность связывания молекул-лигандов с молекулами-мишенями.
Далее подробно описаны основные этапы, представленные на фиг.1, заявленного квантово-механического способа моделирования связывания молекулы-лиганда с молекулой-мишенью с учетом влияния растворителя.
На фиг.2 представлена блок-схема, иллюстрирующая способ формирования межмолекулярного комплекса молекулы-мишени и молекулы-лиганда (этап 2 на фиг.1) в соответствии с изобретением.
Исходя из множества 12 известных молекул-лигандов на этапе 13 выбирают молекулу-мишень, для которой необходимо произвести моделирование и прогнозирование связывания с ней различных молекул-лигандов. Структуру и состав этой молекулы-мишени получают на этапе 14 с помощью экспериментальных измерений, например с помощью рентгеноструктурного анализа, методами рассеяния нейтронов или ядерного магнитного резонанса. Структуру и состав молекулы-мишени можно также получить в виде набора декартовых координат соответствующих атомов, полученных в ходе молекулярно-механического или молекулярно-динамического моделирования, проводимого после считывания с соответствующих носителей информации предварительно сохраненных данных, извлеченных из различных баз данных о строении молекулы-мишени. В том случае, когда молекула-мишень является белком, ее структуру и состав получают из базы данных PDB (Protein Data Bank) [7], доступной через Интернет.
Как правило, в исходных структурах молекул-мишеней отсутствуют данные о декартовых координатах водородных атомов. Координаты недостающих атомов водорода добавляют на этапе 15 там, где это необходимо, к координатам тяжелых атомов молекулы-мишени, используя различные компьютерные программы построения молекулярных структур. Оптимизированные значения декартовых координат добавленных атомов водорода определяют на этапе 16 из условия, при котором полная энергия молекулы-мишени достигает минимума (при молекулярно-механической или квантово-механической оптимизации) при варьировании координат добавленных водородных атомов.
Информацию о структуре и составе, а также о координатах всех атомов, включая координаты добавленных атомов водорода молекулы-мишени, записывают на этапе 17 на носитель информации в соответствующем формате.
Исходя из множества 18 известных молекул-лигандов на этапе 19 выбирают молекулу-лиганд, для которой далее будет проводиться моделирование связывания ее с выбранной молекулой-мишенью. Помимо этого можно построить множество 20 новых лигандов, исходя из различного рода баз данных или библиотек фрагментов лигандов, и выбрать на этапе 19 из этого множества молекулу-лиганд, для которой далее будет проводиться прогнозирование связывания ее с выбранной молекулой-мишенью. Структуру, состав и координаты атомов известной молекулы-лиганда получают на этапе 21 аналогично тому, как это делалось для молекулы-мишени, а именно или с помощью экспериментальных измерений, в рамках молекулярно-механического или молекулярно-динамического моделирования или исходя из базы данных PDB. Структуру, состав и координаты атомов новой молекулы-лиганда могут получать с помощью специальных программ - построителей новых лигандов.
Если экспериментально известная или вновь сформированная структура молекулы-лиганда не содержит атомов водорода, то на этапе 22 к координатам тяжелых атомов лиганда добавляют там, где это необходимо, координаты недостающих атомов водорода, используя различные компьютерные программы формирования молекулярных структур. Координаты этих атомов водорода определяют на этапе 23 путем минимизации (или в рамках молекулярной механики, или в рамках квантовой механики) полной энергии молекулы-лиганда при варьировании координат добавленных атомов водорода. Координаты всех атомов молекулы-лиганда, включая координаты добавленных атомов водорода, записывают на этапе 24 на носитель информации в соответствующем формате.
Затем на этапе 25 с помощью стыковки молекулы-лиганда и молекулы-мишени получают структуру межмолекулярного комплекса молекулы-мишени и молекулы-лиганда (2 на фиг.1), который впоследствии используется в квантово-механическом моделировании. Для этого считывают координаты всех атомов молекулы-мишени и молекулы-лиганда, включая координаты добавленных атомов водорода, с носителя информации в память компьютера. После этого выполняют преобразование координат атомов этих молекул таким образом, чтобы наименьшее расстояние между каждым из атомов лиганда и заданными атомами молекулы-мишени находилось в заданном диапазоне. Такая процедура стыковки или, как чаще принято называть, докинга, необходима для совмещения в пространстве двух молекул, так как обычно координаты их атомов получаются из различных источников информации. Полученные таким образом координаты атомов межмолекулярного комплекса молекулы-мишени и молекулы-лиганда записывают на этапе 26 в память компьютера и используют для построения квантово-механической модели соответствующего межмолекулярного комплекса.
Далее межмолекулярный комплекс и его компоненты преобразуют таким образом, чтобы учесть при моделировании влияние растворителя на связывание молекулы-мишени и молекулы-лиганда на основе модели явного учета растворителя. Для этого на этапе 27 множество координат молекул растворителя добавляют к множеству координат межмолекулярного комплекса мишень-лиганд. На этапах 28 и 29 множество координат молекул растворителя добавляют к множеству координат компонентов этого комплекса, взятых индивидуально, а именно к множеству координат молекулы-мишени (на этапе 28) и к множеству координат молекулы-лиганда (на этапе 29). Для межмолекулярного комплекса это делают на этапе 27 путем компьютерного вычисления координат, соответствующих положениям в пространстве множества молекул растворителя, так чтобы их средняя плотность соответствовала экспериментально наблюдаемой плотности растворителя. Молекулы растворителя должны заполнять собой без взаимопересечений и пересечений с атомами межмолекулярного комплекса молекулы-мишени и молекулы-лиганда пространство как между молекулой-мишенью и молекулой-лигандом, так и вокруг них. Аналогично координаты множества молекул растворителя добавляют только к множеству координат молекулы-мишени на этапе 28, так чтобы их средняя плотность соответствовала экспериментально наблюдаемой плотности растворителя, и они заполняли собой без взаимопересечений и пересечений с атомами молекулы-мишени пространство вокруг нее. Также координаты множества молекул растворителя добавляют только к множеству координат молекулы-лиганда на этапе 29, так чтобы их средняя плотность соответствовала экспериментально наблюдаемой плотности растворителя, и они заполняли собой без взаимопересечений и пересечений с атомами молекулы-лиганда пространство вокруг нее. Положение молекул растворителя оптимизируют, как правило, в рамках пакетов молекулярной механики или молекулярной динамики вблизи межмолекулярного комплекса на этапе 30, а также вблизи его компонентов, взятых индивидуально, а именно вблизи молекулы-мишени на этапе 31 и молекулы-лиганда на этапе 32. На этапе 33 записывают на носитель информации в соответствующем формате координаты атомов межмолекулярного комплекса мишень-лиганд вместе с координатами атомов молекул растворителя, находящимися вблизи поверхности комплекса. Кроме того, на этапе 33 отдельно на носитель записывают в соответствующем формате координаты атомов молекулы-мишени вместе с координатами атомов молекул растворителя, находящимися вблизи ее поверхности, и координаты атомов молекулы-лиганда вместе с координатами атомов молекул растворителя, находящимися вблизи ее поверхности.
Исходя из структуры полученного межмолекулярного комплекса, состоящего из молекулы-мишени и молекулы-лиганда, а также молекул растворителя затем формируют (этап 3 на фиг.1) квантово-механические модели этого межмолекулярного комплекса и его компонентов с явным и неявным учетом растворителя, используемые в квантово-механическом моделировании. На фиг.3 представлена блок-схема, иллюстрирующая соответствующий изобретению способ формирования таких квантово-механических моделей и, соответственно, формирования входных файлов, используемых далее для моделирования связывания в межмолекулярном комплексе мишень-лиганд.
С помощью компьютерной программы на этапе 34 считывают из памяти компьютера координаты атомов межмолекулярного комплекса мишень-лиганд вместе с добавленными молекулами растворителя, а также считывают координаты атомов молекулы-мишени, вместе с добавленными к ней молекулами и координаты атомов молекулы-лиганда, вместе с добавленными к ней молекулами растворителя. Затем вычисляют расстояния от атомов молекулы-лиганда в межмолекулярном комплексе до каждого атома молекулы-мишени и растворителя. Для формирования модели межмолекулярного комплекса мишень-лиганд на этапе 35 проводят сортировку атомов этого комплекса на две группы. Это делают таким образом, чтобы в первую группу вошли все атомы молекулы-лиганда, а также атомы молекулы-мишени и молекулы растворителя, расстояния от которых до каждого из атомов молекулы-лиганда не превышают заданное значение, а во вторую группу включают все остальные атомы молекулы-мишени и все остальные молекулы растворителя. При этом, если хотя бы один атом какой-либо молекулы растворителя находится в пределах заданного расстояния от атомов молекулы-лиганда, то в первую группу атомов включаются все атомы этой молекулы растворителя. После этого на этом же этапе 35 начинают формировать с использованием координат атомов первой и второй групп входной файл для расчета межмолекулярного комплекса мишень-лиганд в растворителе с помощью соответствующей программы моделирования таким образом, что атомы первой группы моделируются методами квантовой механики, а атомы второй группы моделируются методами классической механики. При этом оператор полной энергии строится в виде суммы следующих операторов: оператора полной энергии для квантовой части, состоящей из атомов первой группы, оператора полной энергии для классической части, состоящей из атомов второй группы, и оператора взаимодействия между классической и квантовой частями.
Для формирования модели молекулы-мишени на этапе 36 проводят сортировку атомов молекулы-мишени и относящихся к ней молекул растворителя таким образом, что в первую группу атомов включают те же атомы молекулы-мишени, которые входят в первую группу атомов, сформированную на этапе 35. Кроме того, в первую группу включают также молекулы растворителя, которые находятся от атомов молекулы-мишени, включенных в первую группу, на расстоянии, не превышающем заданную величину, а во вторую группу включают все остальные атомы молекулы-мишени и все остальные молекулы растворителя. После этого на этом же этапе 36 начинают формировать с использованием координат атомов первой и второй групп входной файл для расчета молекулы-мишени в растворителе с помощью соответствующей программы моделирования таким образом, что атомы первой группы моделируются методами квантовой механики, а атомы второй группы моделируются методами классической механики.
Для формирования модели молекулы-лиганда на этапе 37 проводят сортировку атомов молекулы-лиганда и молекул растворителя таким образом, что в первую группу атомов включаются все атомы молекулы-лиганда, а также молекулы растворителя, которые находятся от атомов молекулы-лиганда на расстоянии, не превышающем заданную величину, а во вторую группу включают все остальные молекулы растворителя. После этого на этом же этапе 37 начинают формировать с использованием координат атомов первой и второй групп входной файл для расчета молекулы-лиганда в растворителе с помощью соответствующей программы моделирования таким образом, что атомы первой группы моделируются методами квантовой механики, а атомы второй группы моделируются методами классической механики.
В случае, когда молекула-мишень является белком, сортировку атомов на две группы (на этапе 35) в межмолекулярном комплексе проводят следующим образом. В первую группу атомов включают атомы молекулы-лиганда, атомы молекул растворителя, находящиеся на расстоянии, не превышающем заданное значение от атомов молекулы-лиганда, и атомы молекулы-мишени, которые составляют целые аминокислотные остатки, хотя бы один атом которых находится на расстоянии, не превышающем заданное значение от каждого атома молекулы-лиганда. Во вторую группу включают все остальные атомы молекулы-мишени и молекул растворителя. При построении модели молекулы-мишени, которая является белком, в первую группу атомов включают (на этапе 36) атомы молекулы-мишени, которые составляют целые аминокислотные остатки, отнесенные в первую группу атомов для межмолекулярного комплекса.
Для более корректного моделирования стыковки двух групп атомов, для которых обработка данных осуществляется в рамках квантового и классического методов, на этапах 38, 39 и 40 добавляют координаты дополнительных атомов во входные файлы для соответствующей программы моделирования межмолекулярного комплекса мишень-лиганд, молекулы-мишени и молекулы-лиганда соответственно. Эти дополнительные атомы расположены вблизи области пространства, где атомы первой и второй групп находятся на расстоянии друг от друга, не превышающем заданную величину.
Моделирование связывания компонентов в межмолекулярном комплексе мишень-лиганд можно выполнять также и другим образом так, что координаты атомов второй группы не включаются во входные файлы соответствующей программы моделирования межмолекулярного комплекса мишень-лиганд, молекулы-мишени и молекулы-лиганда, а атомы первой группы моделируются методами квантовой механики. При этом координаты добавленных дополнительно атомов включаются во входные файлы соответствующей программы моделирования так, что они вместе с атомами первой группы моделируются методами квантовой механики. При таком способе моделирования, когда у атомов первой группы, которые имели ковалентные связи с атомами второй группы, остаются ненасыщенные оборванные связи, необходимо восстановить или скомпенсировать потерю этих ковалентных связей. В этом случае при формировании модели межмолекулярного комплекса мишень-лиганд на этапе 41 и модели молекулы-мишени на этапе 42 добавляют дополнительные атомы к атомам первой группы таким образом, чтобы они образовывали новые ковалентные связи взамен оборванных ковалентных связей между атомами первой и второй групп.
В случае, когда молекула-мишень является белком, оборванные ковалентные связи N-концов основной цепи белка замыкаются группами -C(O)-(CH3), а оборванные ковалентные связи С-концов основной цепи белка замыкаются группами -N(H)-(CH3).
В ходе формирования входных файлов для моделирования связывания в комплексе белок-лиганд на этапах 43, 44 и 45 определяют зарядовые состояния различных молекулярных групп межмолекулярного комплекса мишень-лиганд, молекулы-мишени и молекулы-лиганда в растворителе (как правило, это определяется физико-химическими свойствами этих молекулярных групп в растворителе или непосредственно в экспериментах). Согласно этому добавляют или убирают дополнительные атомы в соответствующих местах межмолекулярного комплекса мишень-лиганд на этапе 46, молекулы-мишени на этапе 47 и молекулы-лиганда на этапе 48. Когда растворителем является вода, требуемые зарядовые состояния различных молекулярных групп компонентов межмолекулярного комплекса мишень-лиганд, молекулы-мишени и молекулы-лиганда в растворителе получаются добавлением или убиранием дополнительных атомов водорода в соответствующих местах молекулы-мишени и молекулы-лиганда.
Далее на этапе 49 проводят определение полного заряда межмолекулярного комплекса мишень-лиганд, молекулы-мишени и молекулы-лиганда. Полный заряд межмолекулярного комплекса и его компонентов по отдельности, т.е. молекулы-мишени и молекулы-лиганда, получают простым сложением всех зарядов, которые были определены для отдельных молекулярных групп, входящих в состав рассматриваемых молекулярных систем. Полученные данные по полным зарядам моделей межмолекулярного комплекса мишень-лиганд, молекулы-мишени и молекулы-лиганда используются далее при формировании трех входных файлов для соответствующей программы моделирования связывания в комплексе наряду с данными по мультиплетности рассматриваемых молекулярных систем, координатами и типами их атомов.
В случае, когда растворителем является вода, для того чтобы более точно учесть в явном виде влияние растворителя на процесс связывания молекулы-мишени и молекулы-лиганда в каждый из трех входных файлов молекулы-мишени, молекулы-лиганда и их межмолекулярного комплекса необходимо добавить координаты атомов дополнительных молекул воды. Эти дополнительные молекулы воды вводятся в процесс моделирования для того, чтобы лучше воспроизвести образование и разрыв водородных связей, которые играют существенную роль в межмолекулярном комплексе мишень-лиганд, молекулы-мишени и молекулы-лиганда.
На этапе 50 добавляются дополнительные молекулы воды к межмолекулярному комплексу так, чтобы они находились между молекулой-мишенью и молекулой-лигандом и образовывали с ними водородные связи.
Добавление молекул воды к молекуле-мишени на этапе 51 и к молекуле-лиганду на этапе 52 осуществляют так, чтобы с их участием восстановить оборванные водородные связи, которые присутствовали в межмолекулярном комплексе между молекулой-мишенью и молекулой-лигандом и которые были оборваны при удалении молекулы-лиганда из молекулы-мишени. Кроме того, если молекулы воды располагались между молекулой-мишенью и молекулой-лигандом и были связаны с ними обеими водородными связями, эти молекулы воды добавляются дважды каждая и во входной файл для расчета молекулы-мишени на этапе 51, и во входной файл для расчета молекулы-лиганда на этапе 52 при моделировании компонент межмолекулярного комплекса по отдельности.
Как правило, растворитель имеет значение диэлектрической проницаемости, отличное от значения диэлектрической проницаемости вакуума и значения диэлектрической проницаемости макромолекулы-мишени. Например, диэлектрическая проницаемость воды равна приблизительно 80 при комнатной температуре и нормальном давлении, в то время как диэлектрическая проницаемость растворенного в ней белка не превышает нескольких единиц, и при этом диэлектрическая проницаемость вакуума равна 1. В этом случае наличие растворителя вокруг рассматриваемых молекул существенно изменяет электрический потенциал и поле, которые создаются зарядами атомов вокруг молекул. Для того чтобы учесть это экранирующее влияние растворителя, как правило, недостаточно учесть явно некоторое количество молекул растворителя, и в этом случае требуется учесть растворитель в неявной модели, когда его экранирующее влияние учитывается путем введения в модель непрерывной среды с нужным значением диэлектрической проницаемости.
В рамках неявной модели растворителя на этапе 53 во входные файлы для расчетов межмолекулярного комплекса, молекулы-мишени и молекулы-лиганда с помощью соответствующей программы моделирования молекулярных систем в растворителе включаются параметры растворителя в неявной модели. Для этого с использованием координат атомов молекулы-мишени, молекулы-лиганда и молекул растворителя, координаты которых включены в соответствующие входные файлы, формируют координаты точек, находящихся на поверхности, доступной растворителю. Эта поверхность охватывает молекулу-мишень, молекулу-лиганд и молекулы растворителя, в случае расчета межмолекулярного комплекса в растворителе, или охватывает только молекулу-мишень и молекулы растворителя, в случае расчета молекулы-мишени в растворителе, или охватывает только молекулу-лиганд и молекулы растворителя, в случае расчета молекулы-лиганда в растворителе. С помощью точек, находящихся на этих поверхностях, формируется математическая модель неявного учета растворителя.
В предлагаемом изобретении рассматриваются три типа модели неявного учета растворителя.
В первой из них в качестве математической модели неявного учета растворителя используют совокупность программных средств, реализующих решение уравнения Пуассона и описывающих взаимодействие молекулы-мишени и молекулы-лиганда с непрерывной средой, заполняющей все пространство вне поверхности, доступной растворителю и имеющей диэлектрическую проницаемость, равную диэлектрической проницаемости растворителя.
При использовании растворителя с большим значением диэлектрической проницаемости растворителя (например, вода имеет диэлектрическую проницаемость около 80 при комнатной температуре) в качестве математической модели неявного учета растворителя используют совокупность программных средств, реализующих решение уравнений, описывающих взаимодействие молекулы-мишени и молекулы-лиганда с непрерывным проводником, заполняющим все пространство вне поверхности, доступной растворителю.
При использовании растворителя, характеризуемого отличными от нуля диэлектрической проницаемостью и проводимостью, в качестве математической модели неявного учета растворителя используют совокупность программных средств, реализующих решение уравнения Пуассона-Больцмана. Это уравнение описывает взаимодействие молекулы-мишени и молекулы-лиганда с непрерывной средой, имеющей отличную от нуля диэлектрическую проницаемость и отличную от нуля проводимость и заполняющей все пространство вне поверхности, доступной растворителю.
Формирование файлов, описывающих модели для квантово-механического расчета межмолекулярного комплекса мишень-лиганд, молекулы-мишени и молекулы-лиганда в растворителе, заканчивается на этапе 54, и соответствующие входные файлы для квантово-механического расчета записываются на носитель информации.
Эти файлы используются, как правило, в зависимости от выбранного метода расчета в двух вариантах квантово-механического моделирования. В первом варианте моделирования расчет межмолекулярного комплекса, молекулы-мишени, молекулы-лиганда в растворителе проводят так, что первая группа атомов комплекса, молекулы-мишени и молекулы-лиганда (описанная выше) рассчитывается методами квантовой механики, а вторая - классической механики. Во втором варианте моделирования расчет межмолекулярного комплекса, молекулы-мишени, молекулы-лиганда в растворителе проводят так, что первая группа атомов рассчитывается методами квантовой механики, а вторая не включается в моделирование.
Далее описывается процесс квантово-механического моделирования взаимодействия молекулы-лиганда и молекулы-мишени с учетом растворителя (этап 4 на фиг.1) и вычисления энергетических величин, характеризующих связывание молекулы-мишени и молекулы-лиганда (этап 5 на фиг.1). На фиг.4 представлена блок-схема, иллюстрирующая соответствующий изобретению способ квантово-механического моделирования межмолекулярного взаимодействия между молекулой-лигандом и молекулой-мишенью с учетом растворителя, включающего вычисление энтальпии, энтропии и свободной энергии связывания лиганда и мишени.
Входные файлы, в которых записана информация о структуре и свойствах межмолекулярного комплекса, молекулы-мишени и молекулы-лиганда, считываются с носителя информации на этапе 55. В этих входных файлах содержится информация о координатах и типах всех атомов рассматриваемых молекулярных систем, их полный заряд и мультиплетность, координаты и тип атомов молекул растворителя, добавленных в явной модели к межмолекулярному комплексу и его компонентам, параметры растворителя в неявной модели. Кроме того, во входных файлах содержится информация о параметрах оптимизационного процесса, а именно метод и параметры квантово-механического моделирования, тип оптимизационной процедуры, пределы самосогласования и минимизации.
На этапе 56 могут быть выбраны различные методы квантово-механического моделирования полной энергии молекулярных систем. При подходе, когда часть атомов межмолекулярного комплекса, молекулы-мишени и молекулы-лиганда рассчитывается в рамках квантово-механического приближения, а другая часть атомов рассчитывается в рамках классического приближения, используют различные комбинации классических молекулярно-механических и молекулярно-динамических методов, с одной стороны, и квантово-механических методов, с другой стороны. Последние могут варьироваться от строгих неэмпирических методов и методов функционала плотности [1-3] до более быстрых, однако, менее точных полуэмпирических методов [4-7]. Такой подход, получивший широкую известность под названием QM/MM, реализован в настоящее время в виде ряда прикладных пакетов программ [8].
Кроме того, возможен и другой подход, в котором часть атомов межмолекулярного комплекса, молекулы-мишени и молекулы-лиганда рассчитывается в рамках квантово-механического приближения, а другая часть атомов полностью исключается из процесса моделирования. Для того чтобы более точно воспроизвести энергетические характеристики связывания в межмолекулярном комплексе, при таком подходе приходится брать для квантово-механического моделирования как можно большие участки молекулы-мишени, описывающие место связывания с молекулой-лигандом при минимальном влиянии краевых эффектов. При этом наиболее перспективными методами квантово-механического моделирования являются относительно быстрые в расчетах полуэмпирические методы, которые в последнее время реализованы в ряде прикладных пакетов программ с ускоренным счетом [9]. Однако применение для такого вида моделирования более точных, но более медленных неэмпирических методов и методов функционала плотности также возможно.
В начале оптимизационной процедуры на этапах 57, 58 и 59 проводят определение варьируемых параметров межмолекулярного комплекса мишень-лиганд, молекулы-мишени, молекулы-лиганда и относящихся к этим системам молекул растворителя, а именно проводят определение варьируемых координат атомов, при изменении которых будет находиться минимум полной энергии каждой из молекулярных систем.
Затем на этапе 60 с помощью соответствующей программы моделирования полной энергии молекулярной системы, основанной или на комбинации квантово-механического и классического приближения или основанной только на квантово-механическом приближении, находят минимум полной энергии межмолекулярного комплекса мишень-лиганд и растворителя при варьировании положений всех или некоторых определенных атомов комплекса и растворителя. После этого записывают на носитель информации найденные новые координаты атомов и полную энергию системы, состоящей из межмолекулярного комплекса мишень-лиганд и растворителя, и соответствующих координат атомов.
Аналогично на этапе 61 находят минимум полной энергии молекулы-мишени и растворителя при варьировании положений всех или части атомов молекулы-мишени и растворителя, и проводят запись на носитель информации найденные новые координаты атомов и полную энергию системы, состоящей из молекулы-мишени и растворителя, и соответствующих координат атомов.
Наконец на этапе 62 находят минимум полной энергии молекулы-лиганда и растворителя при варьировании положений всех или части атомов молекулы-мишени и растворителя, и проводят запись на носитель информации найденные новые координаты атомов и полную энергию системы, состоящей из молекулы-лиганда и растворителя, и соответствующих координат атомов.
Используя полученные полные энергии межмолекулярного комплекса мишень-лиганд и растворителя, молекулы-мишени и растворителя, а также молекулы-лиганда и растворителя, на этапе 63 вычисляют энтальпию связывания молекулы-лиганда с молекулой-мишенью в растворителе. При этом возможны два случая расчета энтальпии.
Первый случай реализуется, когда в процессе связывания молекулы-лиганда с молекулой-мишенью соблюдается баланс молекул растворителя, то есть если сумма молекул растворителя, включенных в расчет молекулы-мишени, и молекул растворителя, включенных в расчет молекулы-лиганда, равна числу молекул растворителя, включенных в расчет межмолекулярного комплекса мишень-лиганд. В этом случае на этапе 63 энтальпия связывания ΔHсвяз. молекулы-мишени и молекулы-лиганда вычисляется как разность между полной энергией межмолекулярного комплекса мишень-лиганд в растворителе, с одной стороны, и суммой полных энергий молекулы-мишени в растворителе и молекулы-лиганда в растворителе, с другой стороны, согласно формуле:
ΔHсвяз.=Екомплекса_Nмол.раств.-(Емишени_Lмол.раств.+Елиганда_Mмол.раств.),
где Екомплекса_Nмол.раств. - полная энергия комплекса мишень-лиганд, связанного с N молекулами растворителя, Емишени_Lмол.раств. - полная энергия комплекса мишень-лиганд, связанного с L молекулами растворителя, Елиганда_Mмол.раств - полная энергия комплекса мишень-лиганд, связанного с M молекулами растворителя. В случае соблюдения баланса молекул растворителя N=L+M.
Второй случай реализуется, когда в процессе связывания молекулы-лиганда с молекулой мишенью не соблюдается баланс молекул растворителя, то есть если сумма молекул растворителя, включенных в расчет молекулы-мишени, и молекул растворителя, включенных в расчет молекулы-лиганда, не равна числу молекул растворителя, включенных в расчет межмолекулярного комплекса мишень-лиганд. В этом случае на этапе 63 энтальпия связывания ΔHсвяз. молекулы-мишени и молекулы-лиганда также вычисляется как разность между полной энергией межмолекулярного комплекса мишень-лиганд в растворителе, с одной стороны, и суммой полных энергий молекулы-мишени в растворителе и молекулы-лиганда в растворителе, с другой стороны. Однако при расчете энтальпии связывания ΔHсвяз. на этом этапе следует учесть энергию, которую необходимо затратить, чтобы удалить из растворителя то количество молекул растворителя, которое необходимо добавить в рассматриваемую систему для соблюдения баланса по числу молекул растворителя в процессе связывания молекулы-лиганда с молекулой-мишенью, согласно формуле
ΔHсвяз.=Екомплекса_Nмол.раств.+K*Eмол.раств.-(Емишени_Lмол.раств.+Елиганда_Mмол.раств.),
где Екомплекса_Nмол.раств. - полная энергия комплекса мишень-лиганд, связанного с N молекулами растворителя, Емишени_Lмол.раств. - полная энергия комплекса мишень-лиганд, связанного с L молекулами растворителя, Елиганда_Mмол.раств - полная энергия комплекса мишень-лиганд, связанного с M молекулами растворителя, Eмол.раств -энергия удаления одной молекулы воды из растворителя, рассчитанная в том же квантово-механическом приближении, что и полные энергии межмолекулярного комплекса, молекулы-мишени и молекулы-лиганда. В случае несоблюдения баланса молекул растворителя, то есть когда N=L+M-K, для соблюдения энергетического баланса в формуле, по которой рассчитывается энтальпия связывания молекулы-мишени и молекулы-лиганда, необходимо учесть также энергию К*Eмол.раств.
Расчет энтропии связывания молекулы-лиганда с молекулой-мишенью в растворителе проводят в рамках используемого квантово-механического приближения для тех же моделей межмолекулярного комплекса, молекулы-мишени и молекулы-лиганда, используя те же входные файлы, которые были использованы в расчетах полных энергий этих молекулярных систем. Эта энтропия связывания определяется колебательными частотами молекул, участвующих в рассматриваемом процессе. Для вычисления колебательных частот на этапах 64, 65 и 66 для межмолекулярного комплекса, молекулы-мишени и молекулы-лиганда рассчитываются силовые постоянные или вторые производные полных энергий этих молекулярных систем по всем координатам атомов в точках соответствующих минимумов (глобальных или локальных). Из этих величин составляется матрица (матрица Гессе), и колебательные частоты находятся затем путем решения задачи на собственные значения матрицы Гессе. По значениям этих частот на этапе 67 рассчитывают составляющую энтропии (по формулам, например, в [10]), связанную с потерей колебательных степеней свободы при переходе от свободных состояний молекулы-мишени и молекулы-лиганда в растворителе к их межмолекулярному комплексу. Энтропия связывания, обусловленная потерей колебательных степеней свободы ΔSсвяз._колебат., вычисляется по формуле
ΔSсвяз._колебат=Sкомплекса_Nмол.раств.-(Sмишени_Lмол.раств.+Sлиганда_Mмол.раств.),
при соблюдении баланса молекул растворителя, и по формуле
ΔSсвяз._колебат=Sкомплекса_Nмол.раств.+K*Sмол.раств.-(Sмишени_Lмол.раств.+Sлиганда_Mмол.раств.), при не соблюдении баланса молекул растворителя.
В изменение энтропии при связывании молекулы-лиганда с молекулой-мишенью дает вклад и то, что эти молекулы при связывании теряют каждая три поступательных и три вращательных степени свободы, которыми они обладают в свободном состоянии. Эта часть энтропии вычисляется на этапе 68 по формуле Сакура-Титрода, и для этого используются только координаты и атомные веса атомов молекулы-мишени, молекулы-лиганда и их межмолекулярного комплекса (см., например, [11]). При этом атомные веса атомов однозначно определяются их типом (т.е. положением в Таблице Д.И. Менделеева), который записан в исходных файлах, считанных с носителя информации на этапе 55 (фиг.4). При связывании сравнительно небольших молекул-лигандов (обычно это молекулы с атомным весом, не превышающим 500 дальтон) с макромолекулами-мишенями, такими как протеины, молекулу-мишень можно считать неподвижной, и изменение энтропии, рассчитываемое на этапе 68, будет определяться только характеристиками молекулы-лиганда.
На этапе 69, используя величины, рассчитанные на этапах 67 и 68, вычисляют полное изменение энтропии при связывании молекулы-лиганда с молекулой-мишенью как сумму изменений энтропии, полученных на этапах 67 и 68.
Процесс связывания молекулы-лиганда с молекулой-мишенью происходит в растворителе. Каждая из этих молекул, будучи помещенной в растворитель, создает в нем полость, расталкивая молекулы растворителя. Этот процесс требует затраты определенной свободной энергии, которая зависит от свойств растворителя. Эта свободная энергия называется энергией кавитации, и она зависит только от свойств растворителя и формы молекулы, помещаемой в растворитель. В настоящее время известны некоторые способы расчета кавитационной энергии растворения (см., например, работу [12] и приведенные в ней ссылки). Поскольку при связывании молекулы-лиганда с молекулой-мишенью и образовании межмолекулярного комплекса изменяется форма полостей, в которых находятся рассматриваемые молекулы, то при этом будет изменяться и кавитационная свободная энергия. Ее изменение ΔGкав вычисляется на этапе 70, и результат, будучи сложенным на этапе 71 с результатами расчетов энтальпии связывания ΔHсвяз, полученной на этапе 63 и энтропийного вклада -TΔSсвяз, вычисленного на этапе 69, дает значение полной свободной энергии связывания молекулы-лиганда с молекулой-мишенью в растворителе согласно формуле
ΔGсвяз.=ΔHсвяз.-TΔSсвяз+ΔGкав
В соответствии с настоящим изобретением вычисление энтальпии связывания молекулы-мишени и молекулы-лиганда (этап 63 на фиг.4) можно проводить, используя другой метод, при котором полные энергии молекулы-мишени, молекулы-лиганда и их межмолекулярного комплекса рассчитывают не в точке минимума, а как средние значения полных энергий, полученных для ряда конфигураций межмолекулярного комплекса мишень-лиганд. При этом координаты атомов молекулы-мишени, молекулы-лиганда и их межмолекулярного комплекса, соответствующие каждой из таких конфигураций, могут быть получены в рамках молекулярно-динамического моделирования. На фиг.5 представлена блок-схема, иллюстрирующая способ молекулярно-динамического формирования координат атомов молекулы-мишени, молекулы-лиганда и межмолекулярного комплекса мишень-лиганд для набора конфигураций межмолекулярного комплекса, а также способ расчета энтальпии связывания молекулы-мишени с молекулой-лигандом, на основе средних значений полных энергий, полученных для набора этих конфигураций.
Исходными данными для формирования входных файлов для набора конфигураций межмолекулярного комплекса, молекулы-мишени и молекулы-лиганда являются считываемые на этапе 72 с носителя информации координаты атомов молекулы-мишени, молекулы-лиганда и их межмолекулярного комплекса, которые можно получить из базы данных PDB или с помощью различных программ-построителей молекулярных структур. Кроме того, если используется явная модель растворителя, исходными данными являются координаты атомов молекул растворителя, которые вводятся на этапе 73, аналогично тому, как это осуществлялось ранее на этапах 27, 28 и 29. Если используется неявная модель растворителя, которая вводится на этапе 74, аналогично вышеописанному этапу 53, координаты атомов молекул растворителя явным образом не включаются в моделирование.
Процедура молекулярно-динамического формирования входных файлов с координатами атомов молекулы-мишени, молекулы-лиганда и межмолекулярного комплекса мишень-лиганд для ряда конфигураций с явной моделью растворителя включает следующие этапы.
Используя координаты атомов межмолекулярного комплекса, молекулы-мишени и молекулы-лиганда, а также молекул растворителя (этапы 26, 27 и 30 на фиг.2) и, если это необходимо, вводя дополнительные атомы для установления нужного заряда межмолекулярного комплекса мишень-лиганд (этапы 46, 49 на фиг.3), проводят молекулярно-динамическое моделирование комплекса мишень-лиганд на этапе 75 в рамках явной модели растворителя. При этом путем решения уравнений Ньютона или Лагранжа при учете теплового движения всех взаимодействующих друг с другом атомов молекулы-мишени и молекулы-лиганда с учетом наличия молекул растворителя определяют состояние молекулярной системы, при котором она достигает теплового равновесия. Затем определяют траектории движения всех атомов системы после достижения ими теплового равновесия, когда средние значения наблюдаемых величин (например, энергия взаимодействия молекулы-лиганда с молекулой-мишенью) перестают меняться со временем (обычно это длины траекторий по времени около одной наносекунды), и записывают на этапе 76 на носитель информации координаты всех атомов взаимодействующих молекулы-мишени, молекулы-лиганда и молекул растворителя через определенные промежутки времени заданное количество раз для заданного набора конфигураций межмолекулярного комплекса мишень-лиганд.
Используя координаты атомов молекулы-мишени, а также молекул растворителя (этапы 17, 28 и 31 на фиг.2) и, если это необходимо, вводя дополнительные атомы для установления нужного заряда молекулы-мишени (этапы 47, 49 на фиг.3), проводят на этапе 77 молекулярно-динамическое моделирование молекулы-мишени в рамках явной модели растворителя. При этом путем решения уравнений Ньютона или Лагранжа при учете теплового движения всех взаимодействующих друг с другом атомов молекулы-мишени с учетом наличия молекул растворителя определяют состояние молекулярной системы, при котором она достигает теплового равновесия. Затем определяют траектории движения всех атомов системы после достижения их теплового равновесия и записывают на этапе 78 на носитель информации координаты всех атомов взаимодействующих молекулы-мишени и молекул растворителя через определенные промежутки времени заданное количество раз для заданного набора конфигураций молекулы-мишени.
Используя координаты атомов молекулы-лиганда, а также молекул растворителя (этапы 24, 29 и 32 на фиг.2) и, если это необходимо, вводя дополнительные атомы для установления нужного заряда молекулы-лиганда (этапы 48, 49 на фиг.3), проводят на этапе 79 молекулярно-динамическое моделирование в рамках явной модели растворителя. При этом путем решения уравнений Ньютона или Лагранжа при учете теплового движения всех взаимодействующих друг с другом атомов молекулы-лиганда с учетом наличия молекул растворителя на этапе 79 определяют состояние молекулярной системы, при котором она достигает теплового равновесия. Затем определяют траектории движения всех атомов системы после достижения их теплового равновесия и записывают на этапе 80 на носитель информации координаты всех атомов взаимодействующих молекулы-лиганда и молекул растворителя через определенные промежутки времени заданное количество раз для заданного набора конфигураций молекулы-лиганда.
Процедура молекулярно-динамического формирования входных файлов с координатами атомов молекулы-мишени, молекулы-лиганда и межмолекулярного комплекса мишень-лиганд для ряда конфигураций с неявной моделью растворителя включает следующие этапы.
Используя координаты атомов межмолекулярного комплекса молекулы-мишени и молекулы-лиганда (этап 26 на фиг.2) и, если это необходимо, вводя дополнительные атомы для установления нужного заряда межмолекулярного комплекса мишень-лиганд (этапы 46, 49 на фиг.3), проводят молекулярно-динамическое моделирование в рамках неявной модели растворителя. Растворитель в этом случае учитывается с помощью неявной модели, как описано выше (этап 53 на фиг.3) в рамках решения уравнений Пуассона, Пуассона-Больцмана, уравнения для непрерывного проводника или иным способом, учитывающим влияние растворителя без использования координат молекул растворителя. Затем аналогично тому, как это было сделано в рамках явной модели растворителя, путем решения уравнений Ньютона или Лагранжа при учете теплового движения всех взаимодействующих друг с другом атомов молекулы-мишени и молекулы-лиганда на этапе 75 определяют состояние молекулярной системы, при котором она достигает теплового равновесия. Затем определяют траектории движения всех атомов системы после достижения их теплового равновесия и записывают на этапе 76 на носитель информации координаты всех атомов взаимодействующих молекулы-мишени, молекулы-лиганда и молекул растворителя через определенные промежутки времени заданное количество раз для заданного набора конфигураций межмолекулярного комплекса мишень-лиганд.
Используя координаты атомов молекулы-мишени и, если это необходимо, вводя дополнительные атомы для установления нужного заряда молекулы-мишени (этапы 47, 49 на фиг.2), проводят молекулярно-динамическое моделирование в рамках неявной модели растворителя. Растворитель в этом случае учитывается с помощью неявной модели (этап 53 на фиг.3) в рамках решения уравнений Пуассона, Пуассона-Больцмана, уравнения для непрерывного проводника или иным способом, учитывающим влияние растворителя без использования координат молекул растворителя. Затем аналогично тому, как это было сделано в рамках явной модели растворителя, путем решения уравнений Ньютона или Лагранжа при учете теплового движения всех взаимодействующих друг с другом атомов молекулы-мишени с учетом наличия молекул растворителя на этапе 77 определяют состояние молекулярной системы, при котором она достигает теплового равновесия. Затем определяют траектории движения всех атомов системы после достижения их теплового равновесия и записывают на этапе 78 на носитель информации координаты всех атомов взаимодействующих молекулы-мишени и молекул растворителя через определенные промежутки времени заданное количество раз для заданного набора конфигураций молекулы-мишени.
Используя координаты атомов молекулы-лиганда и, если это необходимо, вводя дополнительные атомы для установления нужного заряда молекулы-лиганда (этапы 47, 49 на фиг.3), проводят молекулярно-динамическое моделирование в рамках неявной модели растворителя. Растворитель в этом случае учитывается с помощью неявной модели (этап 53 на фиг.3) в рамках решения уравнений Пуассона, Пуассона-Больцмана, уравнения для непрерывного проводника или иным способом, учитывающим влияние растворителя без использования координат молекул растворителя. Затем аналогично тому, как это было сделано в рамках явной модели растворителя, путем решения уравнений Ньютона или Лагранжа при учете теплового движения всех взаимодействующих друг с другом атомов молекулы-лиганда с учетом наличия молекул растворителя на этапе 79 определяют состояние молекулярной системы, при котором она достигает теплового равновесия. Затем определяют траектории движения всех атомов системы после достижения их теплового равновесия и записывают на этапе 80 на носитель информации координаты всех атомов взаимодействующих молекулы-лиганда и молекул растворителя через определенные промежутки времени заданное количество раз для заданного набора конфигураций молекулы-лиганда.
Далее для каждого набора координат межмолекулярного комплекса мишень-лиганд в явной или неявной модели растворителя, полученного на этапе 76, проводят на этапе 81 разбиение всех атомов на группы аналогично тому, как это осуществлялось ранее (этап 35 на фиг.3).
Для каждого набора координат молекулы-мишени в растворителе, полученного на этапе 78, проводят разбиение всех атомов на группы по способу 82, аналогичному способу 36.
Для каждого набора координат молекулы-лиганда в растворителе, полученного по способу 80, проводят на этапе 83 разбиение всех атомов на группы аналогично тому, как это осуществлялось ранее (этап 37 на фиг.3).
Для каждой конфигурации межмолекулярного комплекса мишень-лиганд, то есть для каждого полученного в молекулярно-динамическом моделировании набора его координат, формируют на этапе 84 входной файл для квантово-механического моделирования межмолекулярного комплекса мишень-лиганд в растворителе, как описано выше (этап 4 на фиг.1 и этап 56 на фиг.4).
Аналогично для каждой конфигурации молекулы-мишени, то есть для каждого полученного в молекулярно-динамическом моделировании набора ее координат, формируют на этапе 85 входной файл для квантово-механического моделирования молекулы-мишени в растворителе, как описано выше (этап 4 на фиг.1 и этап 56 на фиг.4).
Для каждой конфигурации молекулы-лиганда, то есть для каждого полученного в молекулярно-динамическом моделировании набора ее координат, формируют на этапе 86 входной файл для квантово-механического моделирования молекулы-лиганда в растворителе, как описано выше (этап 4 на фиг.1 и этап 56 на фиг.4).
Для каждого входного файла, сформированного на этапе 84, то есть для каждой конфигурации межмолекулярного комплекса мишень-лиганд, с помощью выбранного на этапе 87 метода моделирования на этапе 88 проводят расчет полной энергии межмолекулярного комплекса мишень-лиганд в растворителе без оптимизации пространственного строения комплекса. Затем на этапе 89 вычисляют среднее значение полной энергии межмолекулярного комплекса мишень-лиганд в растворителе по всему выбранному набору конфигураций этой молекулярной системы.
Для каждого входного файла, сформированного на этапе 85, то есть для каждой конфигурации молекулы-мишени, с помощью выбранного на этапе 87 метода моделирования на этапе 90 проводят расчет полной энергии молекулы-мишени в растворителе без оптимизации ее пространственного строения. Затем на этапе 91 вычисляют среднее значение полной энергии молекулы-мишени в растворителе по всему выбранному набору конфигураций этой молекулярной системы.
Для каждого входного файла, сформированного на этапе 86, то есть для каждой конфигурации молекулы-лиганда, с помощью выбранного на этапе 87 метода моделирования на этапе 92 проводят расчет полной энергии молекулы-лиганда в растворителе без оптимизации ее пространственного строения. Затем на этапе 93 вычисляют среднее значение полной энергии молекулы-лиганда в растворителе по всему выбранному набору конфигураций этой молекулярной системы.
Используя полученные средние значения полных энергий межмолекулярного комплекса мишень-лиганд в растворителе, молекулы-мишени в растворителе и молекулы-лиганда в растворителе, полученные на этапах 89, 91 и 93 соответственно, на этапе 94 вычисляется энтальпия связывания молекулы-лиганда с молекулой-мишенью в растворителе как разность между средним значением полной энергии межмолекулярного комплекса мишень-лиганд в растворителе, с одной стороны, и суммой средних значений полных энергий молекулы-мишени в растворителе и молекулы-лиганда в растворителе, с другой стороны. Далее вычисляется энтропия связывания молекулы-лиганда с молекулой-мишенью в растворителе и свободная энергия связывания молекулы-лиганда с молекулой-мишенью в растворителе (этапы 69 и 71 на фиг.4).
Приведенный выше способ моделирования связывания молекул-лигандов с молекулами-мишенями методами квантовой механики с учетом влияния растворителя был осуществлен авторами настоящего изобретения для ряда межмолекулярных комплексов белков и лигандов, для которых экспериментально были известны энергетические характеристики связывания, а именно энтальпия связывания. В соответствии с заявленным способом для этих тестовых комплексов было проведено вычисление энтальпии связывания белок-лиганд. Путем сравнения полученных результатов с соответствующими экспериментальными величинами была дана первоначальная оценка точности заявленного способа моделирования.
Для проведения тестового моделирования были выбраны восемь комплексов белков с лигандами, для которых были известны не только экспериментальные значения энтальпии связывания, но и структуры, полученные с помощью рентгеноструктурного анализа и занесенные в базу данных PDB (Protein Data Bank) [7]. В таблице 1 представлен список исследованных комплексов. В этой таблице приведены названия этих комплексов согласно базе данных PDB, латинские названия соответствующих белков и лигандов, экспериментальные значения энтальпий связывания для каждого комплекса, а также ссылки на работы, из которых эти данные были получены. На фиг.6 приведены структурные формулы и оптимизированные в рамках квантовой механики структуры лигандов соответствующих комплексов.
Комплексы белок-лиганд с экспериментально известными значениями энтальпии связывания, которые были выбраны как тестовые системы для моделирования связывания в системе белок-лиганд методами квантовой механики
Как видно из приведенной таблицы 1 и из фиг.6, выбранные комплексы содержат лиганды, которые представляют собой различные по химическому составу и свойствам органические соединения. Среди них есть углеводы (системы 1, 2, 6 и 7 по нумерации таблицы 1), гетероциклические соединения (системы 3 и 4 по нумерации таблицы 1), ароматическое соединение (система 5 по нумерации таблицы 1) и олигопептид (система 8 по нумерации таблицы 1). Некоторые из этих лигандов отрицательно заряжены, некоторые нейтральны, число атомов в них колеблется от 20 атомов до 94. Экспериментальные значения энтальпий связывания изменяются в выбранном ряду комплексов от -2,7 до -28,6 ккал/моль. Два выбранных комплекса (системы 3 и 4 по нумерации таблицы 1) содержат одинаковые лиганды и разные белки, другие два комплекса (системы 6 и 7 по нумерации таблицы 1) содержат разные лиганды и одинаковые белки. Таким образом, выбранный ряд межмолекулярных комплексов белок-лиганд представлял собой достаточно широкий ряд систем, представляющий собой интерес при тестировании заявленного метода моделирования.
Исходные структуры комплексов, а именно декартовы координаты их атомов, были взяты из базы данных PDB. Практически все исходные структуры белков и лигандов содержали только координаты тяжелых (C, N, O, S) атомов. Водородные атомы были добавлены к структурам белков всех комплексов с помощью программы REDUCE [19] на первом этапе построения моделей комплексов. Водородные атомы были добавлены к структурам лигандов всех комплексов с помощью пакета Materials Studio Visualizer, предоставляемого компанией Accelrys [20].
В данном случае учет влияния растворителя проводился в рамках явной модели воды, однако в настоящем моделировании не проводилось добавление молекул воды в молекулярной механике или в молекулярной динамике. Положения молекул воды, связанных с комплексом и его компонентами, были взяты из экспериментальных данных (PDB данные рентгеноструктурного анализа) о структурированных в комплексе молекулах воды.
Для каждого комплекса была проведена сортировка атомов на две группы согласно способу, предложенному в заявленном изобретении. Эта процедура была выполнена с помощью программы LigEnv [21], разработанной в компании Алгодайн. Для каждого комплекса в первую группу атомов включили атомы лиганда и атомы белка, которые составляли целые аминокислотные остатки, хотя бы один атом которых находился на расстоянии, не превышающем заданное значение от каждого атома лиганда. Кроме того, в первую группу включили атомы молекул воды, которые присутствовали во входных данных, полученных из базы данных PDB, каждый из которых находился на расстоянии, не превышающем заданное значение от атомов лиганда. Во вторую группу включили все остальные атомы белка и молекул воды. При построении модели белка в первую группу атомов включили атомы белка, отнесенные в первую группу атомов для межмолекулярного комплекса. Для моделирования энтальпии связывания во всех выбранных комплексах был выбран подход, при котором атомы белка, лиганда и их комплекса вместе с молекулами воды, относящиеся к первым группам, моделировались методами квантовой механики, а атомы вторых групп исключались из моделирования. При таком способе моделирования, как уже говорилось, во-первых, необходимо было выбирать достаточно большие модели белка, адекватно описывающие место связывания лиганда, а следовательно, для ускорения счета был выбран полуэмпирический квантово-механический метод расчета PM3 [22]. Этот метод наряду с достаточно высокой скоростью счета дает удовлетворительную точность при расчете полной энергии молекулярных систем, имеющих водородные связи. Во вторых, при таком подходе необходимо было вводить ряд дополнительных атомов, которые восстанавливали оборванные ковалентные связи атомов белков при разбиении их на группы. Оборванные ковалентные связи N-концов основных цепей белков замыкались группами -C(O)-(CH3), а оборванные ковалентные связи С-концов основных цепей белков замыкались группами -N(H)-(CH3). Дополнительно добавленные атомы при этом включались наряду с атомами первой группы в моделирование методами квантовой механики. В качестве оптимизируемых параметров выбирались координаты атомов лигандов, молекул воды и боковых цепей белков. Для поддержания трехмерной структуры белка, взятой из эксперимента, координаты тяжелых атомов (C, N, O) основных цепей белков и координаты добавленных атомов полагались как не оптимизируемые параметры.
В ходе формирования входных данных для моделирования определялись зарядовые состояния различных молекулярных групп белков и лигандов в воде при известных значениях pH. Согласно этому были добавлены или убраны дополнительные протоны в соответствующих кислотных или основных аминогруппах белка. Путем суммирования зарядовых состояний кислотных и основных аминогрупп определялся полный заряд моделей белков, лигандов и их межмолекулярных комплексов.
На фиг.7 представлена оптимизированная структура построенной таким образом модели одного из исследованных комплексов. Структуры всех остальных моделей, в общем случае, выглядят аналогично и для облегчения восприятия материала опускаются.
В ходе моделирования было показано, что особое внимание необходимо уделять моделированию воды как растворителю, учитываемому явным образом. Были предложены два способа учета разрыва и образования водородных связей при переходе от комплекса к его компонентам и участия в этом процессе молекул воды. Соответственно, были рассмотрены два способа добавления молекул воды при переходе от комплекса к его компонентам. Условно эти способы были названы как подходы W1 и W2.
Согласно подходу W1, молекулы воды, положение которых было взято из эксперимента из базы данных PDB, связанные в комплексе с белком, рассчитывались при моделировании индивидуальных компонентов комплекса вместе с белком. Молекулы воды, положение которых было взято из эксперимента из базы данных PDB, связанные в комплексе с лигандом, рассчитывались при моделировании индивидуальных компонентов комплекса вместе с лигандом. Молекулы воды, связанные в комплексе одновременно и с белком, и с лигандом и образующие с ними мостики с водородными связями, учитывались при расчете по отдельности белка и лиганда два раза.
Согласно подходу W2, молекулы воды, положение которых было взято из эксперимента, учитывались также способом, аналогичным способу W1. Кроме этого, в этом случае дополнительные молекулы воды добавлялись и к белку, и к лиганду в тех местах, где в комплексе были водородные связи между белком и лигандом, так, чтобы заменить порванные водородные связи при переходе от межмолекулярного комплекса к его компонентам.
Схематичное представление этих двух способов W1 и W2 учета молекул воды явным образом представлено на фиг.8 и 9 соответственно.
Согласно приведенным схемам, вычисление энтальпии связывания белка и лиганда в комплексе согласно способу W1 производился согласно формуле
ΔHсвяз (W1)=ΔHLP-(ΔHP[nW(P), kW(LP)]+ΔHL[mW(L), kW(LP)])+k·ΔHW,
Здесь ΔHLP - рассчитанная энергия комплекса белок-лиганд (LP), взятого вместе со всеми молекулами воды, взаимодействующими с комплексом. ΔHP[nW(P),kW(LP)] - рассчитанная энергия белка (P), взятого вместе со всеми (n+k) молекулами воды, взаимодействующими с ним (см. фиг.8), ΔHL[mW(L),kW(LP)] - рассчитанная энергия лиганда (L), взятого вместе со всеми (m+k) молекулами воды, взаимодействующими с ним (см. фиг.8). k·ΔHW - рассчитанная энергия k молекул воды W(LP) (см. фиг.8), которая должна быть добавлена к сумме для поддержания энергетического баланса. ΔHW - это энергия молекулы воды, которая рассчитывается с учетом удаления ее из капли воды. В данном случае рассчитанная энергия ΔHW=-53,43 ккал/моль.
Вычисление энтальпии связывания белка и лиганда в комплексе согласно способу W2 выполнялось согласно формуле
ΔHbind (W2)=ΔHLP - (ΔHP[nW(P), kW(LP), qW(PHB)]+ΔHL[mW(L), kW(LP), tW(LHB)])+(k+q+t)ΔHW.
Здесь ΔHLP - рассчитанная энергия комплекса белок-лиганд (LP), взятого вместе со всеми молекулами воды, взаимодействующими с комплексом. ΔHP[nW(P), kW(LP), qW(PHB)] - рассчитанная энергия белка (P), взятого вместе со всеми молекулами (n+k+q) воды, взаимодействующими с ним (см. фиг.9), ΔHL[mW(L), kW(LP), tW(LHB)] - рассчитанная энергия лиганда (L), взятого вместе со всеми (m+k+t) молекулами воды, взаимодействующими с ним (см. фиг.9). (k+q+t)ΔHW - рассчитанная энергия (k+q+t) молекул воды W(LP), W(PHB) и W(LHB) (см. фиг.9), которая должна быть добавлена к сумме для поддержания энергетического баланса.
Полученные в приближениях W1 и W2 согласно заявленному изобретению энтальпии связывания белков и лигандов для комплексов, взятых как тестовые системы (см. таблицу 1, системы 1-8), приведены в таблице 2 вместе с соответствующими экспериментальными данными и отклонениями вычисленных от экспериментальных величин.
Как видно из этой таблицы, при обоих способах учета воды явным образом было получено достаточно разумное согласие вычисленных и экспериментальных данных по энтальпии связывания в комплексах белок-лиганд. Среднеквадратичное отклонение (RMS) вычисленных для всех комплексов энтальпий связывания в подходе W1 составило 7,0 ккал/моль, аналогичное среднеквадратичное отклонение, полученное для метода W2, составило 1,85 ккал/моль. Последняя точность вычисления энтальпии связывания является достаточно высокой и сравнима с точностью существующих экспериментальных методов измерения энтальпии связывания в комплексах белок-лиганд.
Рассчитанные энтальпии связывания белков и лигандов для комплексов 1-8 согласно таблице 1
Список используемой литературы
1. Mulholland A.J.; Lyne P.D.; Richards W.G. Proteins: Struct Funct Genet 1997, 27, 9-25.
2. Mulholland A.J.; Lyne P.D.; Karplus M., Ab initio QM/MM study of the citrate synthase mechanism. A low-barrier hydrogen bond is not involved, J. Am. Chem. Soc. 2000, 122, 534-535.
3. Lyne P.D.; Hodoscek M.; Karplus M., A hybrid QM-MM potential employing Hartree-Fock of Density functional methods in the quantum region, J. Phys. Chem. A, 1999, 103, 3462-3471.
4. Lewis J.P., Carter C.W., Jr, Hermans J., Pan W., Lee T.-S., Yand W., Active species for the ground-state complex of cytidine deaminase: a linear-scaling quantum mechanical investigation, J. Am. Chem. Soc. 1998, 120, 5407-5410.
5. York D.M., Lee T.-S., Yang W., Quantum mechanical treatment of biological macromolecules in solution using linear-scaling electronic structure methods, Phys. Rev. Lett. 1998, 80, 5011-5014.
6. Lee T.-S., York D.M., Yang W., Linear-scaling semiempirical quantum calculations for macromolecules, J. Chem. Phys. 1996, 105, 2744-2750.
7. H.M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T.N. Bhat, H. Weissig, I.N. Shindyalov, P.E. Bourne, Nucleic Acids Research 28 (2000) 235-242, http://www.rcsb.org/pdb.
8. Murphy R.B.; Philipp D.M.; Friesner R.A. J. Comp. Chem. 2000, 21, 1442-1457.
9. Stewart J. J. P. J Mol Struct (Theochem) 1997, 401, 195-205.
10. B. Tidor, M. Karplus, The contribution of vibrational entropy to molecular association, J.Mol.Biol. 238 (1994) 405-414.
11. Sonja Schwartzl et al. J. Comput. Chem. 23 (2002) 1143-1149.
12. R.M. Levy, E. Gallicchio, Ann. Rev. Phys. Chem. 49 (1998) 531.
13. Fukada H.; Sturtevant J.M.; Quiocho F.A. J. Biol. Chem. 1983, 258, 13193-13198.
14. Schwarz F.P.; Ahmed H.; Bianchet M.A., Amzel L.M.; Vasta G.R. Biochem 1998, 37, 5867-5877.
15. Hyre D.E.; Trong I.L.; Freitag S.; Stenkamp R.E.; Stayton P.S. Prot. Sci. 2000, 9, 878-885.
16. Holdgate G.A.; Tunnicliffe A.; Ward W.H.; Weston S.A.; Rosenbrock G.; Barth P.T.; Taylor I.W.; Paupti,t R.A.; Timms D. Biochem 1997, 36, 9663-9673.
17. Klotz I.M. Ligand-Receptor Energetics/ a guide for the perplexed, John Wiley & Sons, New York, Chichester, Weinheim, Brisbane, Singapore, Toronto, 1997, p.77.
18. Henriques D.A.; Ladbury J.E.; Jackson R.M. Prot. Sci. 2000, 9, 1975-1985.
19. Word J.M.; J. Mol. Biol. 1999, 285, 1733-1745.
20. Materials Studio Visualizer, Materials Studio Release 2.2, San Diego: Accelrys Inc. 2002, http://www.accelrys.com/mstudio/visualizer.html.
21. Vlasov P. LigEnv: program for construction of a model represented an active site of protein-ligand complex from PDB molecular structure, Algodign, LLC, Moscow, 2002.
22. Stewart J.J.P. J. Comput. Chem. 1989, 10, 2, 209-264.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБЫ МОДЕЛИРОВАНИЯ МЕЖМОЛЕКУЛЯРНОГО ВЗАИМОДЕЙСТВИЯ И ОСНОВАННЫЙ НА НИХ СПОСОБ ПРОГНОЗИРОВАНИЯ СВЯЗЫВАНИЯ МОЛЕКУЛЫ-ЛИГАНДА С МОЛЕКУЛОЙ-МИШЕНЬЮ | 2003 |
|
RU2265243C2 |
| СПОСОБЫ И ПРИБОРЫ ДЛЯ ОБНАРУЖЕНИЯ И ИДЕНТИФИКАЦИИ ЗАКОДИРОВАННЫХ ГРАНУЛ И БИОЛОГИЧЕСКИХ МОЛЕКУЛ | 2007 |
|
RU2487169C2 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЭПИТОПОВ Т-КЛЕТОК И ЕГО ПРИМЕНЕНИЕ ДЛЯ ПОЛУЧЕНИЯ МОЛЕКУЛ СО СНИЖЕННОЙ ИММУНОГЕННОСТЬЮ | 2002 |
|
RU2303264C2 |
| СПОСОБ ИДЕНТИФИКАЦИИ УЧАСТКОВ СВЯЗЫВАНИЯ БЕЛКОВЫХ КОМПЛЕКСОВ | 2020 |
|
RU2743316C1 |
| СПОСОБ ОПТИМИЗАЦИИ УСЛОВИЙ КРИСТАЛЛИЗАЦИИ БЕЛКОВ С ПРИМЕНЕНИЕМ МЕТОДА МОЛЕКУЛЯРНОЙ ДИНАМИКИ | 2021 |
|
RU2781051C1 |
| БИОМОЛЕКУЛЯРНЫЕ КОМПЛЕКСЫ ДЛЯ СВЯЗЫВАНИЯ С МОЛЕКУЛАМИ ДНК НА ОСНОВЕ CAS-БЕЛКОВ И ХИМЕРНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ РНК, СОДЕРЖАЩИХ ДИМЕРИЗУЮЩИЕСЯ РНК-ПОСЛЕДОВАТЕЛЬНОСТИ | 2023 |
|
RU2835928C1 |
| ДОМЕН СВЯЗЫВАНИЯ БАКТЕРИАЛЬНОЙ АТР-СИНТАЗЫ | 2005 |
|
RU2418001C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ИНГИБИТОРА, КОВАЛЕНТНО СВЯЗЫВАЮЩЕГО ЦЕЛЕВОЙ ПОЛИПЕПТИД | 2009 |
|
RU2542963C2 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ СПЕКТРОСКОПИИ ЖИВОЙ ТКАНИ | 2019 |
|
RU2752711C2 |
| СИСТЕМЫ И СПОСОБЫ ПРОГНОЗИРОВАНИЯ СТРУКТУРЫ И СВОЙСТВ АТОМАРНЫХ ВЕЩЕСТВ И ИХ СПЛАВОВ | 2019 |
|
RU2727631C1 |
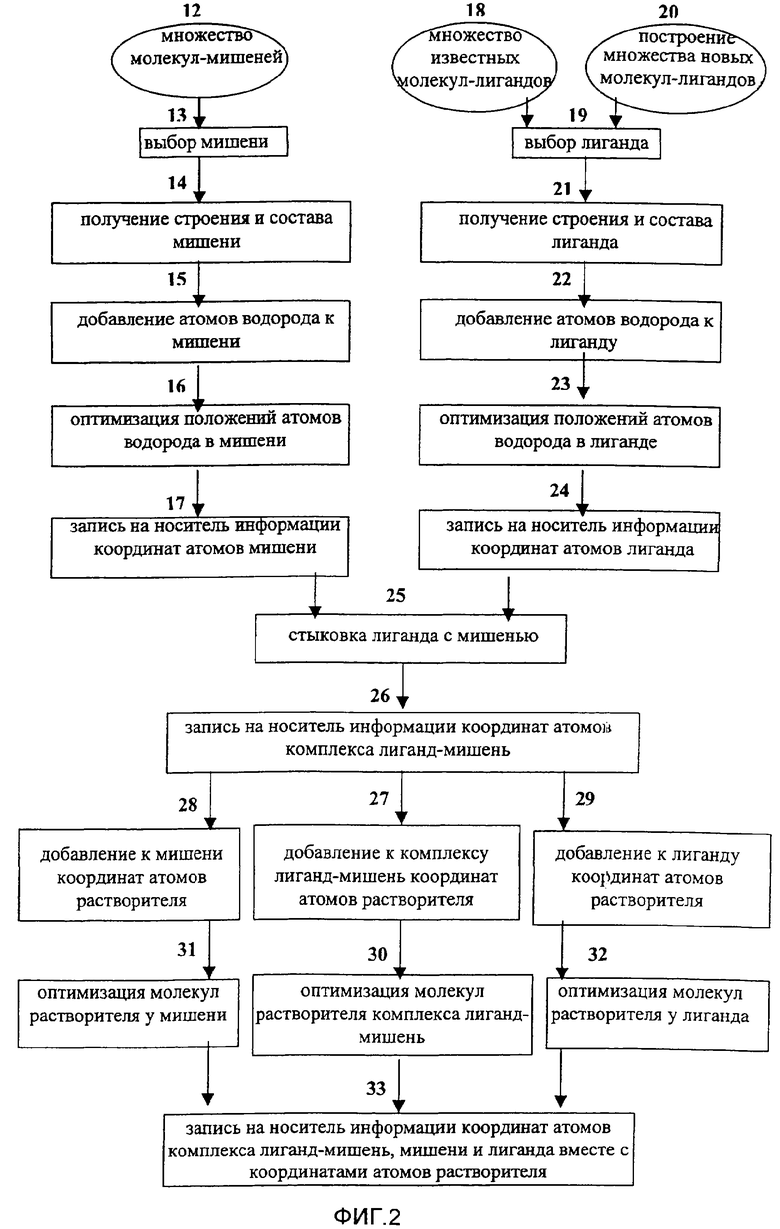
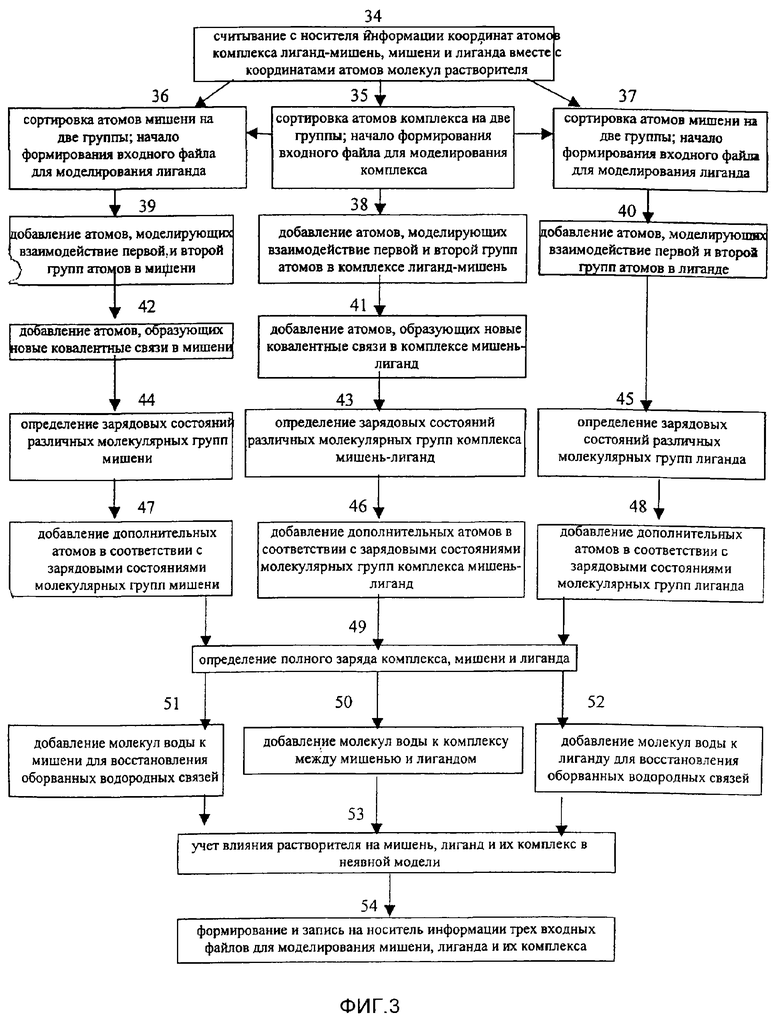

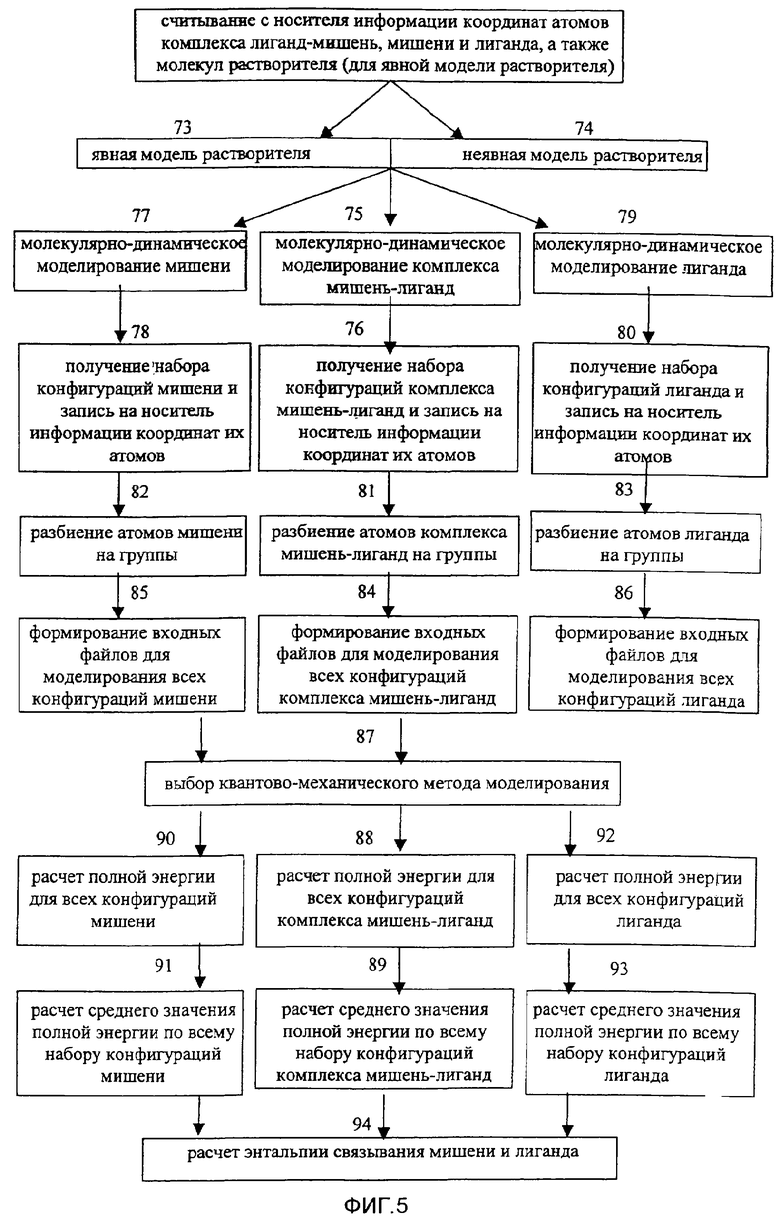
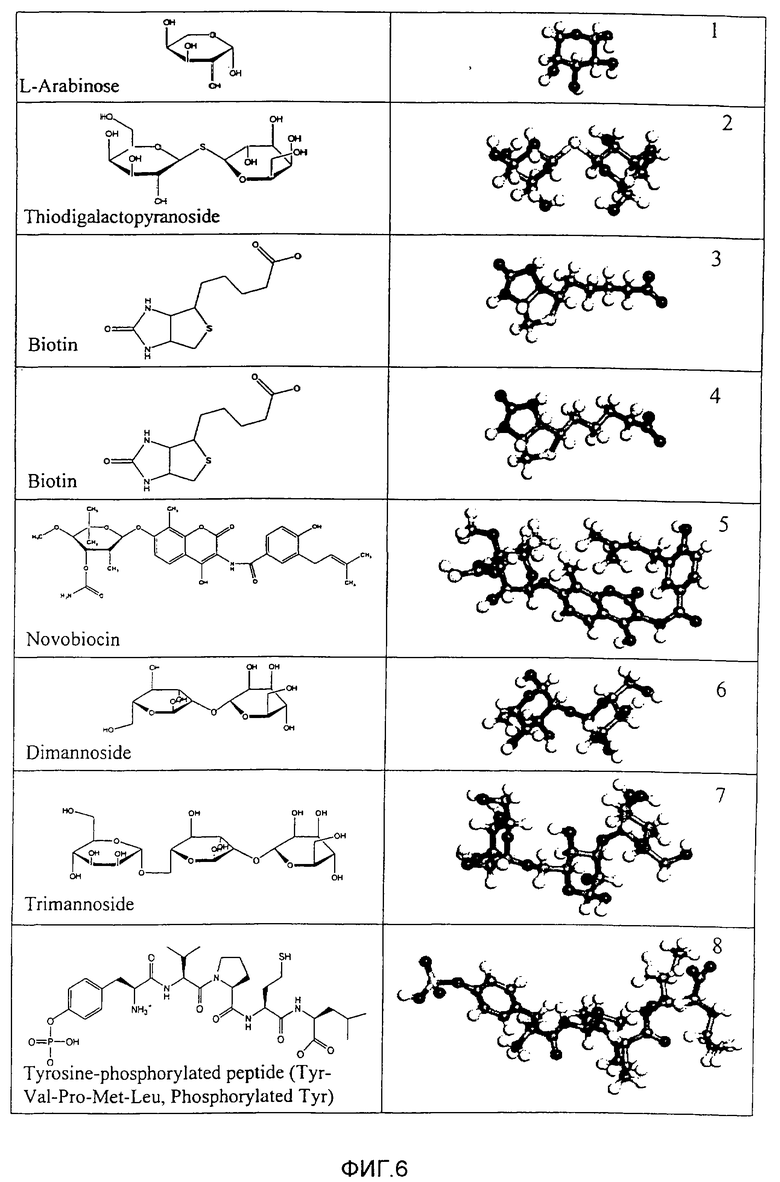
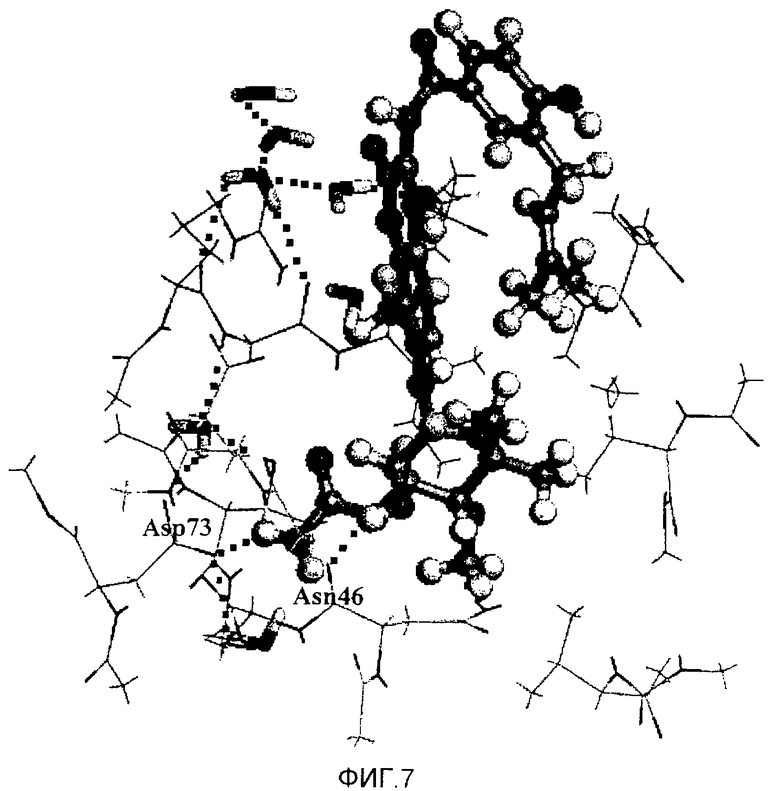
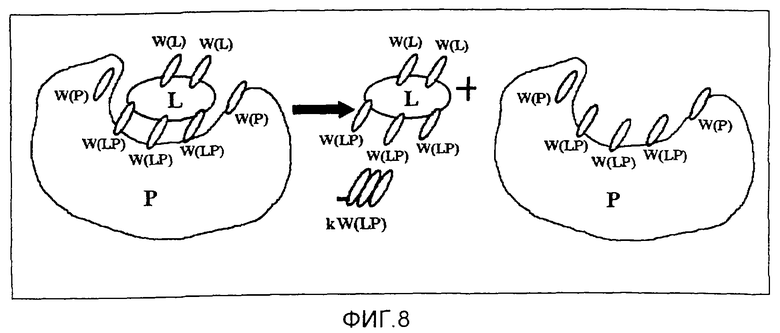
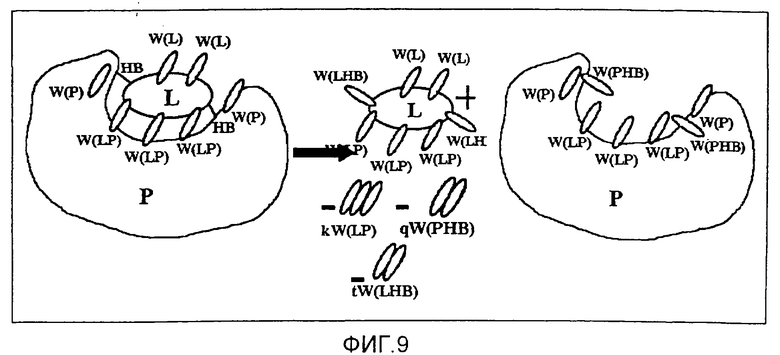
Изобретение относится к разработке новых лекарственных соединений путем численного моделирования комплекса нового лекарственного вещества или лиганда с рецептором или мишенью. Техническим результатом является получение с заданным уровнем точности энергетических величин, которые характеризуют интенсивность связывания рецептора и лекарственного вещества и, следовательно, являются критерием при прогнозировании лигандов как потенциальных лекарственных веществ. В рамках предложенного способа моделирования и прогнозирования связывания молекулы-мишени с молекулой-лигандом, используя данные по структуре и составу молекулы-мишени и молекулы-лиганда, строятся модели межмолекулярного комплекса и его компонентов. Вводятся модели явного и неявного учета растворителя. Моделирование связывания молекулы-лиганда и молекулы-мишени с учетом влияния растворителя производят или в рамках квантово-механического, или в рамках смешанного квантово-механического и классического подходов. Расчет энтальпии связывания молекулы-мишени и молекулы-лиганда проводят, используя полные энергии молекулярных систем, рассчитанные в точке минимума, или используя средние значения полных энергий, полученных для ряда конфигураций межмолекулярного комплекса мишень-лиганд. В последнем случае координаты атомов молекулы-мишени, молекулы-лиганда и их межмолекулярного комплекса, соответствующие каждой из таких конфигураций, получают в рамках молекулярно-динамического моделирования. Расчет энтропии связывания молекулы-лиганда и молекулы-мишени производится на основе расчета ее колебательной, вращательной и поступательной составляющих. Свободная энергия связывания молекулы-лиганда и молекулы-мишени выполняется на основе энтальпийного, энтропийного члена и кавитационной энергии. 3 н. и 27 з.п. ф-лы, 9 ил., 2 табл.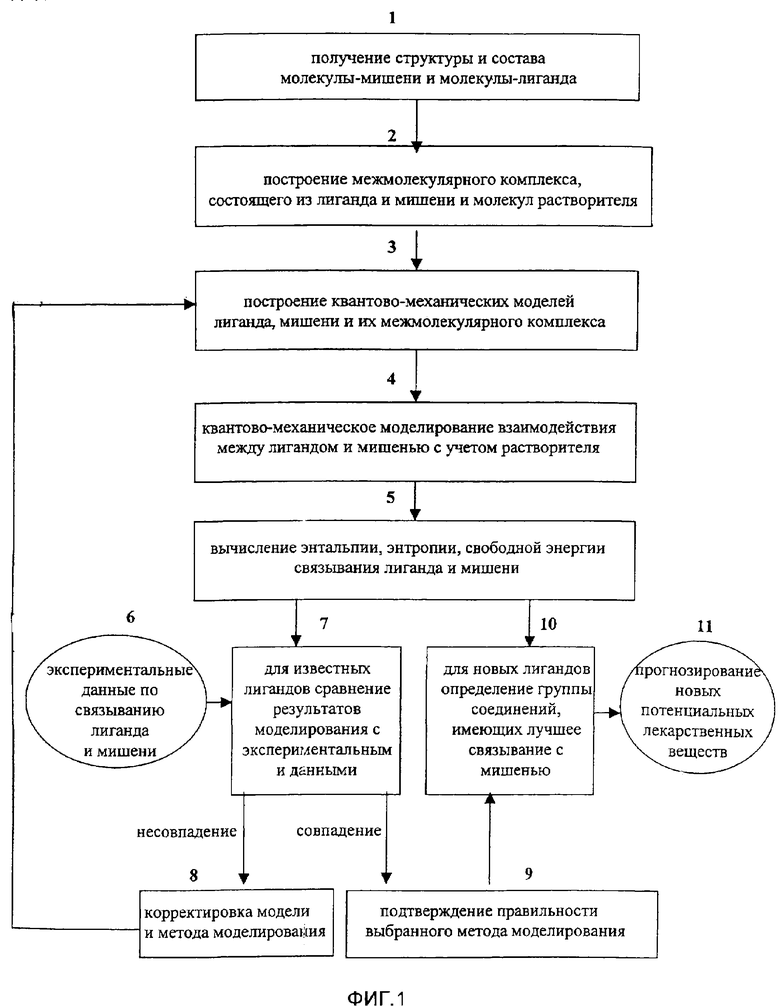
a) получают структуру и состав молекулы-мишени в виде набора координат и типов атомов и записывают эти данные на носитель информации;
б) получают структуру и состав молекулы-лиганда в виде набора координат и типа атомов и записывают эти данные на носитель информации;
в) считывают координаты атомов молекулы-мишени и молекулы-лиганда с носителя информации в память компьютера и выполняют преобразование координат атомов этих молекул таким образом, чтобы наименьшее расстояние между каждым из атомов молекулы-лиганда и заданными атомами молекулы-мишени находилось в заданном диапазоне, и записывают новые координаты атомов молекулы-мишени и молекулы-лиганда, образующих межмолекулярный комплекс мишень-лиганд, в память компьютера,
г) к множеству координат межмолекулярного комплекса мишень-лиганд добавляют параметры растворителя на основе модели явного учета растворителя и записывают координаты всех атомов межмолекулярного комплекса мишень-лиганд и растворителя в память компьютера в виде первого множества координат,
д) к множеству координат молекулы-мишени добавляют параметры растворителя на основе модели явного учета растворителя и записывают координаты всех атомов молекулы-мишени и растворителя в память компьютера в виде второго множества координат,
е) к множеству координат молекулы-лиганда добавляют параметры растворителя на основе модели явного учета растворителя и записывают координаты всех атомов молекулы-лиганда и растворителя в память компьютера в виде третьего множества координат,
ж) с помощью компьютерной программы, которая считывает из памяти компьютера первое множество координат атомов межмолекулярного комплекса и растворителя, вычисляют расстояния от атомов молекулы-лиганда до каждого атома молекулы-мишени и растворителя и проводят сортировку всех атомов первого множества таким образом, чтобы в первую группу вошли все атомы молекулы-лиганда, а также атомы молекулы-мишени и атомы растворителя, расстояния от которых до каждого из атомов молекулы-лиганда не превышают заданное значение, а во вторую группу включают все остальные атомы молекулы-мишени и растворителя,
з) проводят сортировку всех атомов второго множества таким образом, чтобы в первую группу атомов вошли те же атомы молекулы-мишени, которые входят в первую группу атомов, сформированную на этапе (ж), а во вторую группу включают все остальные атомы молекулы-мишени и все атомы растворителя, причем в первую и вторую группы атомов включают те же атомы молекул растворителя, которые входят в соответствующие группы атомов, сформированные на этапе (ж),
и) проводят сортировку всех атомов третьего множества таким образом, чтобы в первую группу атомов вошли все атомы молекулы-лиганда и те атомы молекул растворителя, которые входят в первую группу атомов, сформированную на этапе (ж), а во вторую группу включают все остальные атомы молекул растворителя,
к) формируют с использованием координат атомов первой и второй групп, сформированных на этапе (ж), входной файл для расчета межмолекулярного комплекса мишень-лиганд в растворителе с помощью соответствующей программы моделирования таким образом, что атомы упомянутой первой группы со своими ядрами и электронами моделируются методами квантовой механики, а атомы упомянутой второй группы моделируются методами классической механики,
л) формируют с использованием координат атомов первой и второй групп, сформированных на этапе (з), входной файл для расчета молекулы-мишени в растворителе с помощью соответствующей программы моделирования таким образом, что атомы упомянутой первой группы со своими ядрами и электронами моделируются методами квантовой механики, а атомы упомянутой второй группы моделируются методами классической механики,
м) формируют с использованием координат атомов первой и второй групп, сформированных на этапе (и), входной файл для расчета молекулы-лиганда в растворителе с помощью соответствующей программы моделирования таким образом, что атомы упомянутой первой группы со своими ядрами и электронами моделируются методами квантовой механики, а атомы упомянутой второй группы моделируются методами классической механики,
н) на основе физико-химических свойств соответствующих молекул определяют зарядовые состояния различных групп атомов молекулы-мишени и молекулы-лиганда в растворителе и в соответствии с этим добавляют или убирают дополнительные атомы в соответствующих местах молекулы-мишени и молекулы-лиганда,
о) определяют полный заряд молекулы-мишени, полный заряд молекулы-лиганда и полный заряд межмолекулярного комплекса мишень-лиганд,
п) модифицируют входные файлы для расчета межмолекулярного комплекса мишень-лиганд, расчета молекулы-мишени и расчета молекулы-лиганда с учетом координат соответствующих атомов, их типа, а также полных зарядов и мультиплетности этих молекул,
р) во входные файлы для расчета межмолекулярного комплекса мишень-лиганд, молекулы-мишени и молекулы-лиганда включают параметры растворителя в неявной модели, в которой с использованием координат атомов молекулы-мишени, молекулы-лиганда и молекул растворителя, координаты которых включены в соответствующие входные файлы, модифицированные на этапе (п), формируют координаты точек, находящихся на поверхности, доступной растворителю, которая охватывает молекулу-мишень, молекулу-лиганд и молекулы растворителя, или охватывает только молекулу-мишень и молекулы растворителя в случае расчета молекулы-мишени в растворителе, или охватывает только лиганд и молекулы растворителя в случае расчета молекулы-лиганда в растворителе, и с помощью этих точек формируют математическую модель неявного учета растворителя, и записывают на носитель информации эти входные файлы для расчета межмолекулярного комплекса мишень-лиганд, молекулы-мишени и молекулы-лиганда с помощью соответствующей программы моделирования,
с) вычисляют с помощью соответствующей программы моделирования полную энергию межмолекулярного комплекса мишень-лиганд и растворителя, используя соответствующий входной файл, сформированный на этапе (р), и находят минимум полной энергии межмолекулярного комплекса мишень-лиганд и растворителя при варьировании положений по меньшей мере некоторых атомов межмолекулярного комплекса и растворителя; записывают на носитель информации значение минимума полной энергии межмолекулярного комплекса мишень-лиганд и растворителя, и соответствующие координаты атомов,
т) вычисляют с помощью соответствующей программы моделирования полную энергию молекулы-мишени и растворителя, используя соответствующий входной файл, сформированный на этапе (р), и находят минимум полной энергии молекулы-мишени и растворителя при варьировании положений по меньшей мере части атомов молекулы-мишени и растворителя; записывают на носитель информации значение минимума полной энергии молекулы-мишени и растворителя, и соответствующие координаты атомов,
у) вычисляют с помощью соответствующей программы моделирования полную энергию молекулы-лиганда и растворителя, используя входной файл, сформированный на этапе (р), и находят минимум полной энергии молекулы-лиганда и растворителя при варьировании положений по меньшей мере части атомов молекулы-лиганда и растворителя; записывают на носитель информации значение минимума полной энергии молекулы-лиганда и растворителя, и соответствующие координаты атомов,
ф) используя значения минимумов полных энергий межмолекулярного комплекса мишень-лиганд, и растворителя, молекулы-мишени и растворителя, и молекулы-лиганда и растворителя, полученные на этапах (с), (т) и (у), соответственно, вычисляют энтальпию связывания молекулы-лиганда с молекулой-мишенью в растворителе, как разность между значением минимума полной энергии межмолекулярного комплекса мишень-лиганд в растворителе, вычисленным на этапе (с) с одной стороны, и суммой значений минимумов полных энергий молекулы-мишени в растворителе и молекулы-лиганда в растворителе, вычисленных соответственно на этапах (т) и (у), с другой стороны,
х) обеспечивают в процессе связывания молекулы-лиганда с молекулой-мишенью баланса молекул растворителя, когда сумма молекул растворителя, включенных в расчет молекулы-мишени, и молекул растворителя, включенных в расчет молекулы-лиганда, равна сумме молекул растворителя, включенных в расчет межмолекулярного комплекса мишень-лиганд, при этом, когда баланс молекул растворителя в процессе связывания нарушен, при расчете энтальпии связывания на этапе (ф) учитывают энергию, которую необходимо затратить, чтобы удалить из растворителя то количество молекул растворителя, которое необходимо добавить в рассматриваемую систему для соблюдения баланса по числу молекул растворителя в процессе связывания молекулы-лиганда с молекулой-мишенью.
а) получают структуру и состав молекулы-мишени в виде набора координат и типов атомов и записывают эти данные на носитель информации;
б) получают структуру и состав молекулы-лиганда в виде набора координат и типа атомов и записывают эти данные на носитель информации;
в) считывают координаты атомов молекулы-мишени и молекулы-лиганда с носителя информации в память компьютера и выполняют преобразование координат атомов этих молекул таким образом, чтобы наименьшее расстояние между каждым из атомов лиганда и заданными атомами молекулы-мишени находилось в заданном диапазоне, и записывают новые координаты атомов молекулы-мишени и молекулы-лиганда, образующих межмолекулярный комплекс мишнь-лиганд, в память компьютера,
г) к множеству координат межмолекулярного комплекса мишень-лиганд добавляют параметры растворителя на основе модели явного учета растворителя и записывают координаты всех атомов межмолекулярного комплекса мишень-лиганд и растворителя в память компьютера в виде первого множества координат,
д) к множеству координат молекулы-мишени добавляют параметры растворителя на основе модели явного учета растворителя и записывают координаты всех атомов молекулы-мишени и растворителя в память компьютера в виде второго множества координат,
е) к множеству координат молекулы-лиганда добавляют параметры растворителя на основе модели явного учета растворителя и записывают координаты всех атомов молекулы-лиганда и растворителя в память компьютера в виде третьего множества координат,
ж) используя координаты атомов межмолекулярного комплекса мишень-лиганд и растворителя, полученные на этапе (г), определяют траектории движения всех взаимодействующих друг с другом атомов молекулы-мишени и молекулы-лиганда с учетом наличия молекул растворителя путем решения уравнений Ньютона или Лагранжа при учете их теплового движения; после достижения в рассматриваемой системе атомов теплового равновесия записывают на носитель информации заданное количество раз координаты всех атомов молекулы-мишени, молекулы-лиганда и молекул растворителя через определенные промежутки времени;
з) используя координаты атомов молекулы-мишени и растворителя, полученные на этапе (д), определяют траектории движения всех взаимодействующих друг с другом атомов молекулы-мишени с учетом наличия молекул растворителя путем решения уравнений Ньютона или Лагранжа при учете их теплового движения; после достижения в рассматриваемой системе атомов теплового равновесия записывают на носитель информации заданное количество раз координаты всех атомов молекулы-мишени и молекул растворителя через определенные промежутки времени;
и) используя координаты атомов молекулы-лиганда и растворителя, полученные на этапе (е), определяют траектории движения всех взаимодействующих друг с другом атомов молекулы-лиганда с учетом наличия молекул растворителя путем решения уравнений Ньютона или Лагранжа при учете их теплового движения; после достижения в рассматриваемой системе атомов теплового равновесия записывают на носитель информации заданное количество раз координаты всех атомов молекулы-лиганда и молекул растворителя через определенные промежутки времени,
к) для каждого набора координат межмолекулярного комплекса мишень-лиганд в растворителе, записанного на этапе (ж), проводят разбиение всех атомов на группы, при этом с помощью компьютерной программы, которая считывает из памяти компьютера первое множество координат атомов межмолекулярного комплекса мишень-лиганд, включающего в себя координаты атомов молекулы-мишени, молекулы-лиганда и растворителя, вычисляют расстояния от атомов молекулы-лиганда до каждого атома молекулы-мишени и растворителя и проводят сортировку всех атомов первого множества таким образом, чтобы в первую группу вошли все атомы молекулы-лиганда, а также атомы молекулы-мишени и атомы растворителя, расстояния от которых до каждого из атомов молекулы-лиганда не превышают заданное значение, а во вторую группу включают все остальные атомы молекулы-мишени и растворителя,
л) для каждого набора координат молекулы-мишени в растворителе, записанного на этапе (з), проводят сортировку всех атомов второго множества таким образом, чтобы в первую группу атомов вошли те же атомы молекулы-мишени, которые входят в первую группу атомов, сформированную на этапе (к), а во вторую группу включают все остальные атомы молекулы-мишени и все атомы растворителя, причем в первую и вторую группы атомов включают те же атомы молекул растворителя, которые входят в соответствующие группы атомов, сформированные на этапе (к),
м) для каждого набора координат молекулы-лиганда - в растворителе, записанного на этапе (и), проводят сортировку всех атомов третьего множества таким образом, чтобы в первую группу атомов вошли все атомы молекулы-лиганда и те атомы молекул растворителя, которые входят в первую группу атомов, сформированную на этапе (к), а во вторую группу включают все остальные атомы молекул растворителя,
н) формируют с использованием наборов координат атомов первой и второй групп, сформированных на этапе (к), наборы входных файлов для расчета межмолекулярного комплекса мишень-лиганд в растворителе с помощью соответствующей программы моделирования таким образом, что атомы упомянутой первой группы со своими ядрами и электронами моделируются методами квантовой механики, а атомы упомянутой второй группы моделируются методами классической механики,
о) формируют с использованием наборов координат атомов первой и второй групп, сформированных на этапе (л), наборы входных файлов для расчета молекулы-мишени в растворителе с помощью соответствующей программы моделирования таким образом, что атомы упомянутой первой группы со своими ядрами и электронами моделируются методами квантовой механики, а атомы упомянутой второй группы моделируются методами классической механики,
п) формируют с использованием наборов координат атомов первой и второй групп, сформированных на этапе (м), наборы входных файлов для расчета молекулы-лиганда в растворителе с помощью соответствующей программы моделирования таким образом, что атомы упомянутой первой группы со своими ядрами и электронами моделируются методами квантовой механики, а атомы упомянутой второй группы моделируются методами классической механики,
р) на основе физико-химических свойств соответствующих молекул определяют зарядовые состояния различных групп атомов молекулы-мишени и молекулы-лиганда в растворителе и в соответствии с этим добавляют или убирают дополнительные атомы в соответствующих местах молекулы-мишени и молекулы-лиганда,
с) определяют полный заряд молекулы-мишени, полный заряд молекулы-лиганда и полный заряд межмолекулярного комплекса мишень-лиганд,
т) модифицируют наборы входных файлов для расчета межмолекулярного комплекса мишень-лиганд, расчета молекулы-мишени и расчета молекулы-лиганда с учетом координат соответствующих атомов, их типа, а также полных зарядов и мультиплетности этих молекул,
у) в каждый файл из соответствующего набора входных файлов мишени и молекулы-лиганда включают параметры растворителя в неявной модели, в которой с использованием координат атомов молекулы-мишени, молекулы-лиганда и молекул растворителя, координаты которых включены в соответствующие входные файлы, модифицированные на этапе (т), формируют координаты точек, находящихся на поверхности, доступной растворителю, которая охватывает молекулу-мишень, молекулу-лиганд и молекулы растворителя, или охватывает только молекулу-мишень и молекулы растворителя в случае расчета молекулы-мишени в растворителе, или охватывает только молекулу-лиганд и молекулы растворителя в случае расчета молекулы-лиганда в растворителе, и с помощью этих точек формируют математическую модель неявного учета растворителя, и записывают на носитель информации эти наборы входных файлов для расчета межмолекулярного комплекса мишень-лиганд, молекулы-мишени и молекулы-лиганда с помощью соответствующей программы моделирования,
ф) для каждого файла из набора входных файлов для расчета межмолекулярного комплекса мишень-лиганд, сформированного на этапе (у), вычисляют полную энергию межмолекулярного комплекса мишень-лиганд в растворителе с помощью соответствующей программы моделирования; вычисляют среднее значение полной энергии межмолекулярного комплекса мишень-лиганд в растворителе по результатам расчетов с помощью всех входных файлов из набора входных файлов для расчета межмолекулярного комплекса мишень-лиганд, сформированного на этапе (у),
х) для каждого файла из набора входных файлов для расчета молекулы-мишени, сформированного на этапе (у), вычисляют полную энергию молекулы-мишени в растворителе с помощью соответствующей программы моделирования; вычисляют среднее значение полной энергии молекулы-мишени в растворителе по результатам расчетов с помощью всех входных файлов из набора входных файлов для расчета молекулы-мишени, сформированного на этапе (у),
ц) для каждого файла из набора входных файлов для расчета молекулы-лиганда, сформированного на этапе (у), вычисляют полную энергию молекулы-лиганда в растворителе с помощью соответствующей программы моделирования; вычисляют среднее значение полной энергии молекулы-лиганда в растворителе по результатам расчетов с помощью всех входных файлов из набора входных файлов для расчета молекулы-лиганда, сформированного на этапе (у),
ч) используя средние значения полных энергий межмолекулярного комплекса мишень-лиганд в растворителе, молекулы-мишени в растворителе и молекулы-лиганда в растворителе, полученные на этапах (ф), (х) и (ц), соответственно, вычисляют энтальпию связывания молекулы-лиганда с молекулой-мишенью в растворителе, как разность между средним значением полной энергией межмолекулярного комплекса мишень-лиганд в растворителе, с одной стороны, и суммой средних значений полных энергий молекулы-мишени в растворителе и молекулы-лиганда в растворителе, с другой стороны.
а) получают структуру и состав молекулы-мишени;
б) получают структуру и состав молекулы-лиганда;
в) записывают данные о структуре и составе молекулы-мишени и лиганда на носитель информации в соответствующем формате;
г) выбирают параметры моделирования для использования в программе моделирования взаимодействия между молекулой-мишенью и лигандом, причем упомянутая программа моделирования осуществляет способ квантово-механического моделирования связывания молекул-лигандов с молекулами-мишенями в растворителе по п.1 или молекулярно-динамический способ квантово-механического моделирования по п.21;
д) считывают упомянутые записанные данные и осуществляют их обработку по меньшей мере одним процессором с помощью упомянутой программы моделирования взаимодействия между молекулой-мишенью и моделирования,
е) путем упомянутого квантово-механического моделирования связывания молекул-лигандов с молекулами-мишенями в растворителе получают результаты моделирования в виде числовых данных, характеризующих интенсивность связывания молекулы-лиганда с молекулой мишенью и записывают полученные числовые данные на носитель информации;
ж) осуществляют реальные химические измерения величин, характеризующих интенсивность связывания упомянутых молекул между собой;
з) сравнивают данные, полученные в измерениях на этапе (ж), с результатами моделирования, полученными на этапе (е);
и) в случае расхождения между рассчитанными и измеренными мишенью и лигандом, превышающего заданную величину, корректируют параметры моделирования, используемые программой, моделирующей взаимодействие между молекулой-мишенью и лигандом;
к) повторяют этапы (г)-(и) до тех пор, пока расхождение между рассчитанными на этапе (е) и измеренными на этапе (ж) величинами, характеризующими связывание молекул между собой, не станет меньше заданной величины;
л) повторяют этапы (а)-(к) для другой пары молекулы-мишени и лиганда;
м) повторяют этапы (а)-(л) до тех пор, пока для каждой новой пары молекул расхождение между измеренными и рассчитанными величинами, характеризующими связывание молекул между собой, не будет меньше заданной заранее величины при параметрах моделирования, полученных на этапах (а)-(л) для других пар молекул, и записывают окончательные значения параметров моделирования на носитель информации;
н) используют созданные на этапах (а)-(м) параметры моделирования связывания молекулы-лиганда с молекулой-мишенью для прогнозирования с помощью компьютерного моделирования моллекул-лигандов, которые связываются наилучшим образом с молекулой-мишенью.
| US 6230102 B1, 08.05.2001.WO 01/18627 A2, 15.03.2001.US 5495423 A, 27.02.1996.RU 2132853 C1, 10.07.1999. |
Авторы
Даты
2005-11-27—Публикация
2003-09-22—Подача