Область техники
[0001] Настоящее изобретение относится к области устройств измерения пространственного положения, в частности, к способу прецизионной калибровки систем измерения пространственного положения.
Уровень техники
[0002] Системы измерения пространственного положения имеют широкий спектр применений во многих отраслях промышленности. Системы измерения представляют собой набор устройств измерения пространственного положения объекта (т.е. угла продольного наклона, угла поперечного наклона и курсового угла). В последние годы в связи с постоянным снижением стоимости аппаратных средств различные типы систем измерения пространственного положения стали входить в повседневную жизнь огромного количества людей. Если рассматривать в качестве примера мобильные телефоны, большинство современных смартфонов содержит встроенные акселерометры, гироскопы и электронные компасы, которые представляют собой простую и недорогую систему измерения пространственного положения. Однако в настоящее время из-за ограничений по стоимости встроенные датчики большинства измерительных систем пространственного положения имеют низкую точность и стабильность, что приводит к получению неидеальных результатов измерения для всей системы измерения пространственного положения. Безусловно, калибровка датчика без изменения аппаратного обеспечения системы является очень практичным способом повышения точности измерения для всей системы. Таким образом, на практике исследование недорогого способа калибровки систем измерения пространственного положения очень полезно.
[0003] Калибровка и градуировка датчика всегда важны в области технического применения технологии датчиков. Отечественные и зарубежные ученые провели большое количество исследований, касающихся калибровки систем измерения пространственного положения. Способ многопозиционной калибровки инерциальной навигации на основе МЭМС (микроэлектромеханических систем) с использованием измерительного стенда вращения был исследован Wei Sun, Xinru Fu и др. Решение для калибровки электронного компаса, основанное на преобразовании Фурье с опорным углом, было исследовано учеными Binliang Ma и др. Ученые Wei Qin и др. исследовали способ онлайн-калибровки системы измерения пространственного положения на основе нейронной сети и UKF (сигма-точечной калмановской фильтрации).
[0004] В настоящее время исследования в основном сосредоточены на калибровке системы измерения пространственного положения с использованием калибровочных инструментов, таких как стенд вращения и т.п. Однако специализированные инструменты для калибровки дорогостоящи и многие из них сложны в эксплуатации, что обуславливает увеличение себестоимости продукции. С другой стороны, на практике характеристики датчика в системе постоянно изменяются по мере изменения окружающей среды и срока службы самого датчика. Таким образом, на практике сложно достичь высокой точности, если полагаться лишь на калибровку датчика, которая была выполнена еще на заводе. Кроме того, в некоторых текущих исследованиях калибровки без применения инструментов решения по калибровке либо слишком просты, чтобы иметь практическую значимость для повышения точности фактического измерения, либо эти решения по калибровке слишком сложны и требуют наличия у пользователя значительных технических навыков.
Раскрытие сущности изобретения
[0005] Принимая во внимание недостатки существующих на данный момент способов калибровки пространственного положения настоящее изобретение обеспечивает способ прецизионной калибровки систем измерения пространственного положения, который дает надежный результат калибровки, высокую точность и требует меньших затрат времени.
[0006] Ниже приведены технические решения, которые применены в настоящем изобретении для достижения вышеуказанной цели.
Предложен способ прецизионной калибровки систем измерения пространственного положения. Способ прецизионной калибровки системы измерения пространственного положения включает следующие этапы:
калибровка нулевого отклонения, масштабного коэффициента и неортогонального угла между осями акселерометра в системе измерения пространственного положения по модели аппроксимации эллипсоида;
компенсация исходных данных акселерометра с использованием вычисленного параметра эллипсоида;
калибровка электронного компаса по модели аппроксимации эллипсоида в соответствии со скомпенсированными данными акселерометра;
компенсация исходных данных электронного компаса с помощью вычисленного параметра эллипсоида;
вычисление пространственного положения на основании скомпенсированных данных акселерометра и скомпенсированных данных электронного компаса.
[0007] Согласно одному аспекту настоящего изобретения перед этапом калибровки нулевого отклонения, масштабного коэффициента и неортогонального угла между осями акселерометра системы измерения пространственного положения по модели аппроксимации эллипсоида выполняют следующий этап: выполнение горизонтальной калибровки на акселерометре для устранения начального нулевого отклонения акселерометра.
[0008] Согласно одному аспекту настоящего изобретения после этапа выполнения горизонтальной калибровки на акселерометре для устранения исходного нулевого отклонения акселерометра выполняют следующий этап: сбор трехосных данных акселерометра за определенный промежуток времени, причем эти трехосные данные записывают в виде 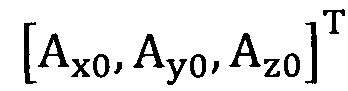 , а нулевое отклонение записывают в виде
, а нулевое отклонение записывают в виде 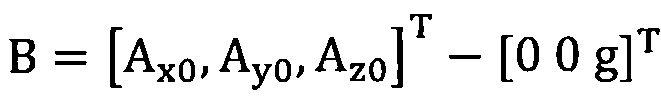 .
.
[0009] Согласно одному аспекту настоящего изобретения этап калибровки нулевого отклонения, масштабного коэффициента и неортогонального угла между осями акселерометра системы измерения пространственного положения по модели аппроксимации эллипсоида дополнительно включает следующие этапы:
подстановку вектора параметра аппроксимируемого эллипсоида, записанного как 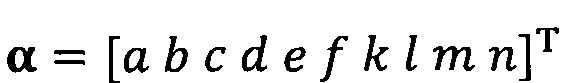 ;
;
подстановку числа n итераций калибровки, разложение первого значения 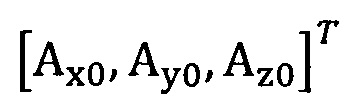 , полученного от акселерометра, в
, полученного от акселерометра, в
десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде 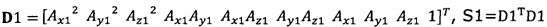 ;
;
если число раз сбора трехосных данных акселерометра не достигло значения n, обновление матрицы S с использованием вновь собранных данных акселерометра Dk, причем 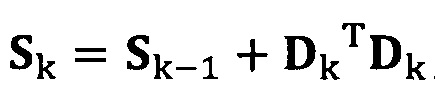 ;
;
после вычисления матрицы S, введение матрицы С ограничения эллипсоида и одновременное разложение матрицы S на блоки, причем
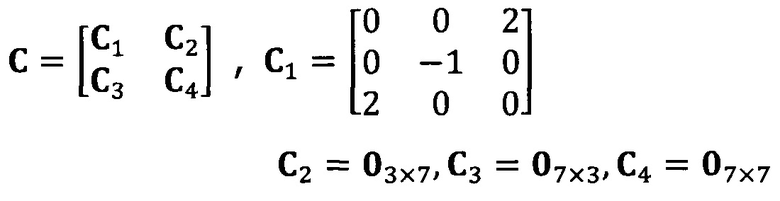
разложение матрицы S на блоки:
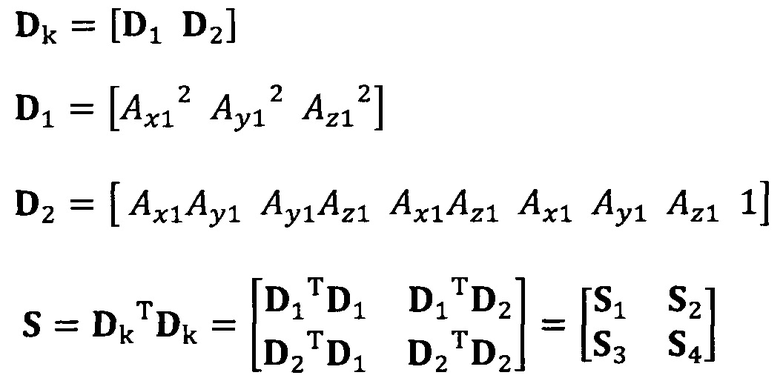
вычисление вектора аппроксимации эллипсоида с помощью следующих уравнений:
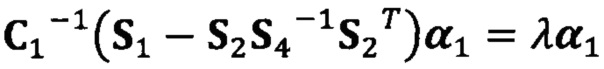
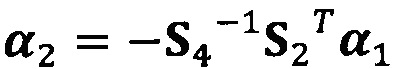 ;
;
после вычисления α1 вычисление α2 с помощью вышеприведенных уравнений для вычисления каждого параметра вектора аппроксимации эллипсоида, причем 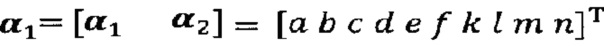 ;
;
кроме того, с учетом фактического физического соответствия трехосные масштабные коэффициенты kx, ky, kz, неортогональные углы между осями δxy, δyz, δxz и остаточные нулевые отклонения bx, by, bz могут быть вычислены с помощью следующих уравнений:
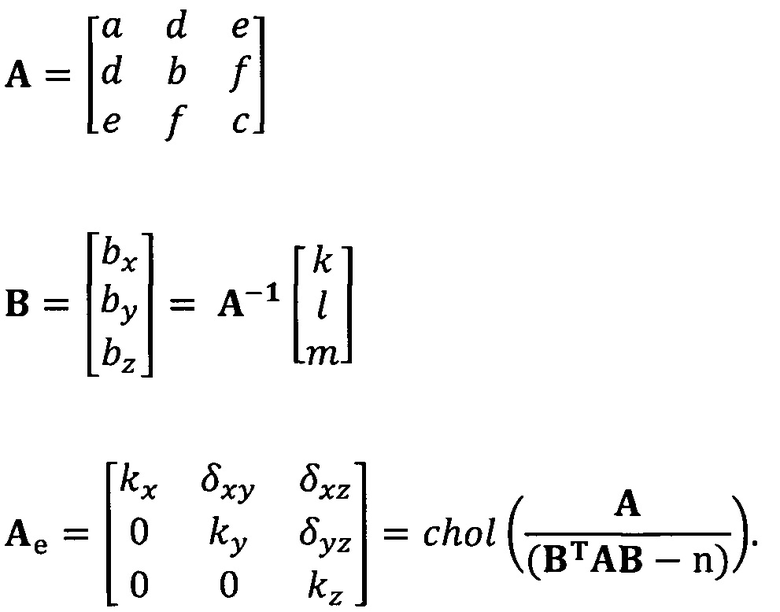
[00010] Согласно одному аспекту настоящего изобретения после выполнения этапа калибровки нулевого отклонения, масштабного коэффициента и неортогонального угла между осями акселерометра системы измерения пространственного положения по модели аппроксимации эллипсоида выполняют следующий этап: после сбора новых данных акселерометра выполняют корректирование вновь собранных данных с применением параметра эллипсоида.
[00011] Согласно одному аспекту настоящего изобретения этап калибровки электронного компаса по модели аппроксимации эллипсоида на основании скомпенсированных данных акселерометра дополнительно включает следующие этапы:
подстановку вектора параметра аппроксимируемого эллипсоида, записанного как 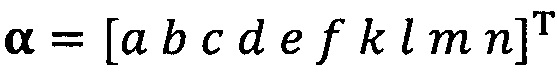 ;
;
сбор трехосных данных электронного компаса за определенный промежуток времени и проведение операции обработки собранных данных для недопущения переполнения, причем трехосные данные записывают в виде 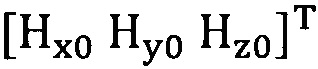 ;
;
подстановку числа n итераций калибровки, разложение первого значения 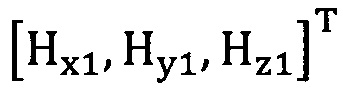 , полученного от электронного компаса, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде
, полученного от электронного компаса, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде 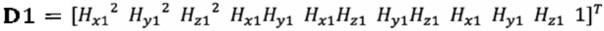 , причем
, причем 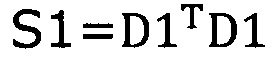 ;
;
если число раз сбора трехосных данных электронного компаса не достигло значения n, обновление матрицы S с использованием вновь собранных данных компаса Dk, причем 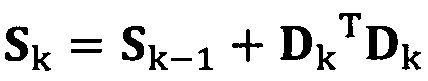 ;
;
после вычисления матрицы S введение матрицы С ограничения эллипсоида и одновременное разложение матрицы S на блоки, причем
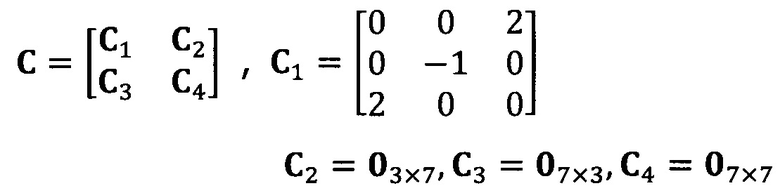
разложение матрицы S на блоки:
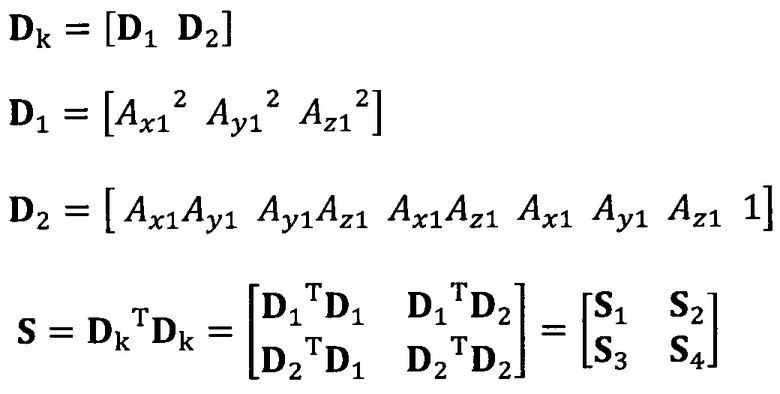
вычисление вектора аппроксимации эллипсоида с
помощью следующих уравнений:
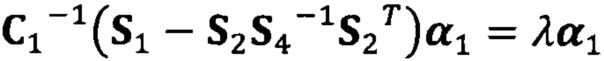
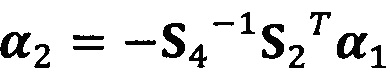 ;
;
после вычисления α1, вычисление α2 с помощью вышеприведенных уравнений для вычисления каждого параметра вектора аппроксимации эллипсоида, причем 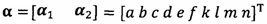 ;
;
кроме того, с учетом фактического физического соответствия трехосные масштабные коэффициенты kx, ky, kz, неортогональные углы между осями δxy, δyz, δxz и остаточные нулевые отклонения bx, by, bz могут быть вычислены с помощью следующих уравнений:
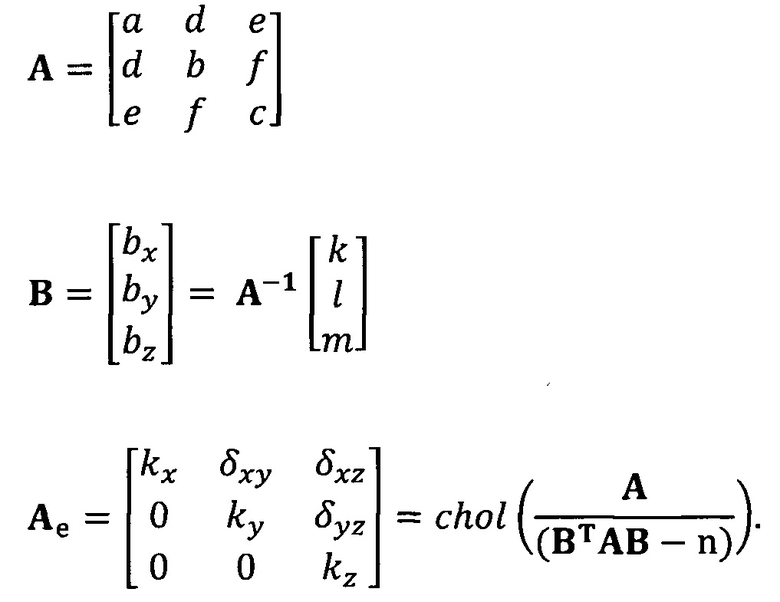
[00012] Согласно одному аспекту настоящего изобретения после выполнения этапа калибровки электронного компаса на основании скомпенсированных данных акселерометра по модели аппроксимации эллипсоида выполняют следующий этап: после сбора новых данных электронного компаса выполняют корректирование вновь собранных данных с применением параметра эллипсоида.
[00013] Согласно одному аспекту настоящего изобретения после осуществления этапа вычисления пространственного положения на основании скомпенсированных данных акселерометра и скомпенсированных данных электронного компаса выполняют следующий этап: обновление параметра эллипсоида с помощью электронного компаса с использованием данных измерений во время осуществления измерения с целью повышения точности параметра эллипсоида.
[00014] Согласно одному аспекту настоящего изобретения перед осуществлением этапа обновления параметра эллипсоида с помощью электронного компаса с использованием данных измерений во время осуществления измерения с целью повышения точности параметра эллипсоида выполняют следующий этап: удаление пропущенной расчетной точки из собранных данных электронного компаса с применением статистического правила.
[00015] Преимущества настоящего изобретения заключаются в следующем. Способ аппроксимации эллипсоида используют для калибровки электронного компаса и улучшения системы измерения пространственного положения. Таким образом, он позволяет эффективно устранять проблемы случайной выдачи датчиком неправильных данных и перескакиваний, благодаря чему фактически гарантируется надежность результата калибровки. Рекурсивную обработку выполняют в алгоритме аппроксимации эллипсоида таким образом, что устраняется необходимость хранения внутренним центральным процессором (ЦП) системы измерения пространственного положения данных всех точек, собранных ранее датчиком во время обработки данных. Необходимо сохранять лишь матрицу, полученную ранее путем рекурсии, и текущие результаты измерения. Таким образом, в той же аппаратной среде способ аппроксимации эллипсоида позволяет обрабатывать больше значений, в результате чего повышается точность аппроксимации эллипсоида. Соответственно, в случае использования обычного алгоритма аппроксимации для недопущения переполнения стека памяти в процессе эксплуатации ЦП может выполнять операцию аппроксимации лишь в нескольких точках выборки. В результате этого точность аппроксимации ограничивается. Настоящее изобретение улучшает крупномасштабное применение матрицы в алгоритме аппроксимации эллипсоида и оптимизирует процедуру вычисления, что позволяет сократить объем вычислений аппроксимации эллипсоида более чем на 90 процентов. Если в качестве примера взять программу MATLAB, основанную на традиционном алгоритме, одноразовое выполнение алгоритма аппроксимации займет 563 мс. Для сравнения, выполнение усовершенствованного алгоритма занимает всего 14 мс. Применена стратегия, в которой для калибровки используют данные измерений, благодаря чему повышается отказоустойчивость во время калибровки. Таким образом, требования, касающиеся начальной калибровки, снижаются и уменьшается сложность эксплуатации для пользователя.
Краткое описание чертежей
[00016] Чтобы понятно проиллюстрировать технические решения вариантов осуществления настоящего изобретения, кратко представим чертежи, используемые в вариантах осуществления. Безусловно, нижеописанные чертежи представляют лишь некоторые варианты осуществления настоящего изобретения. Специалистом в данной области техники без приложения творческих усилий также могут быть предложены и другие чертежи.
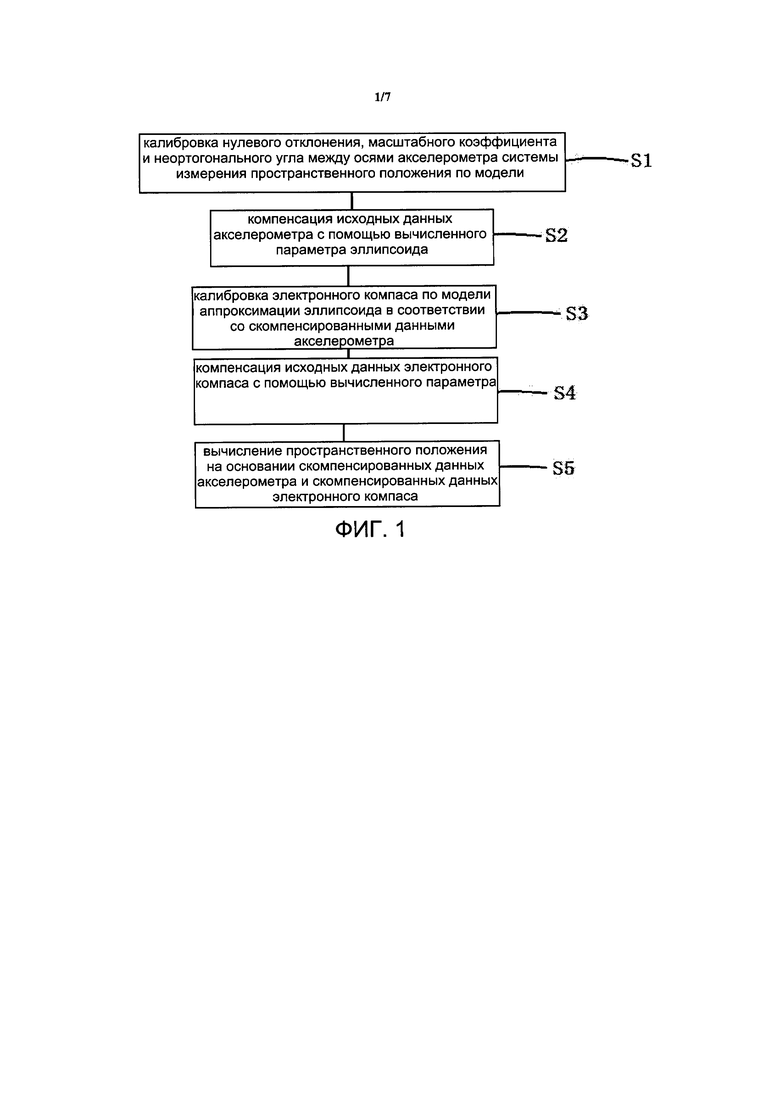
[00017] На фиг. 1 представлена блок-схема варианта осуществления 1 способа прецизионной калибровки системы измерения пространственного положения согласно настоящему изобретению;
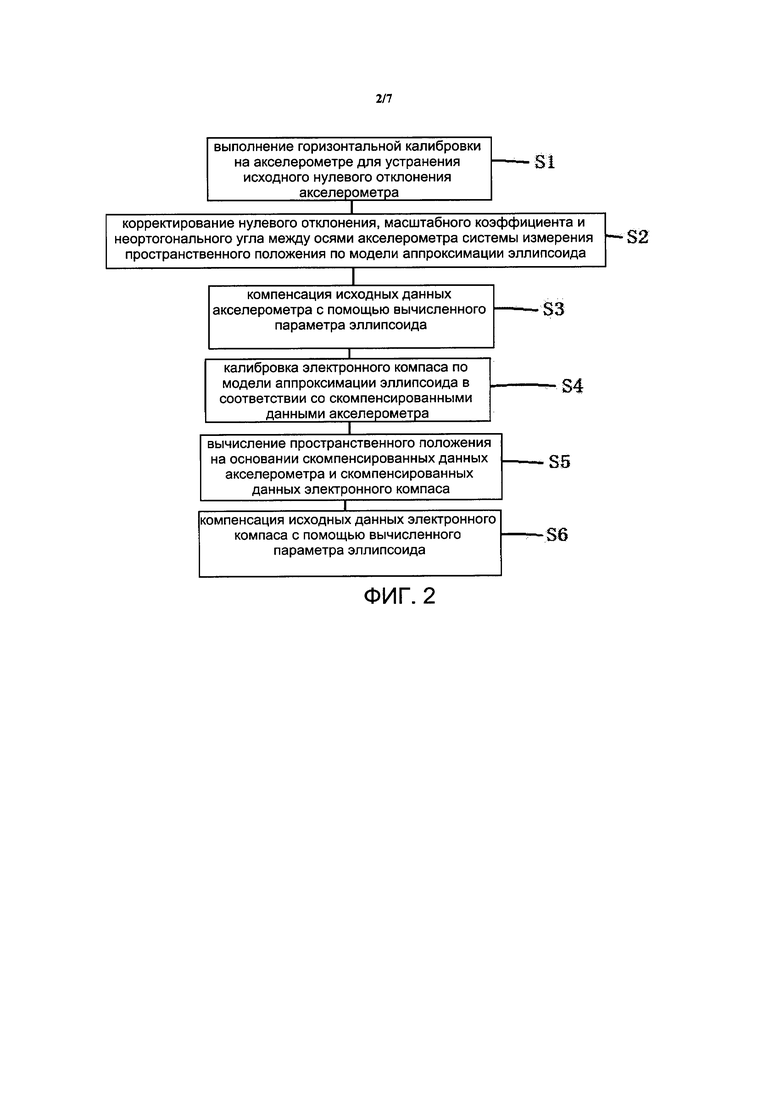
На фиг. 2 представлена блок-схема варианта осуществления 2 способа прецизионной калибровки системы измерения пространственного положения согласно настоящему изобретению;
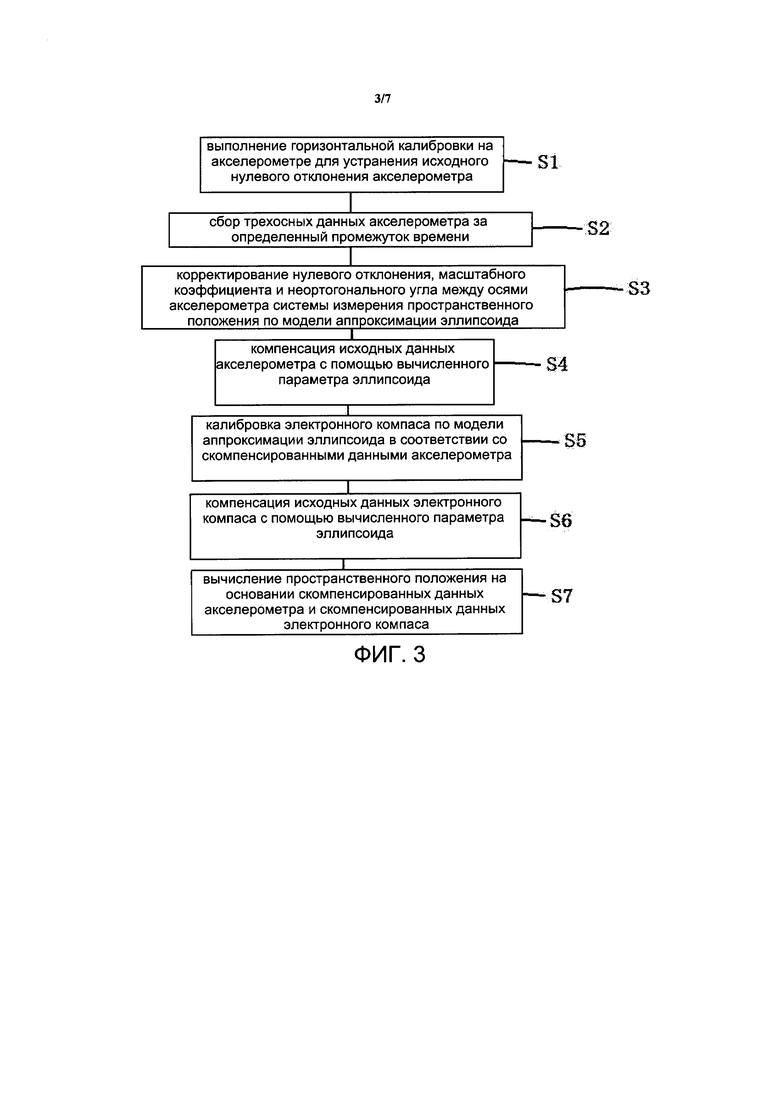
На фиг. 3 представлена блок-схема варианта осуществления 3 способа прецизионной калибровки системы измерения пространственного положения согласно настоящему изобретению;
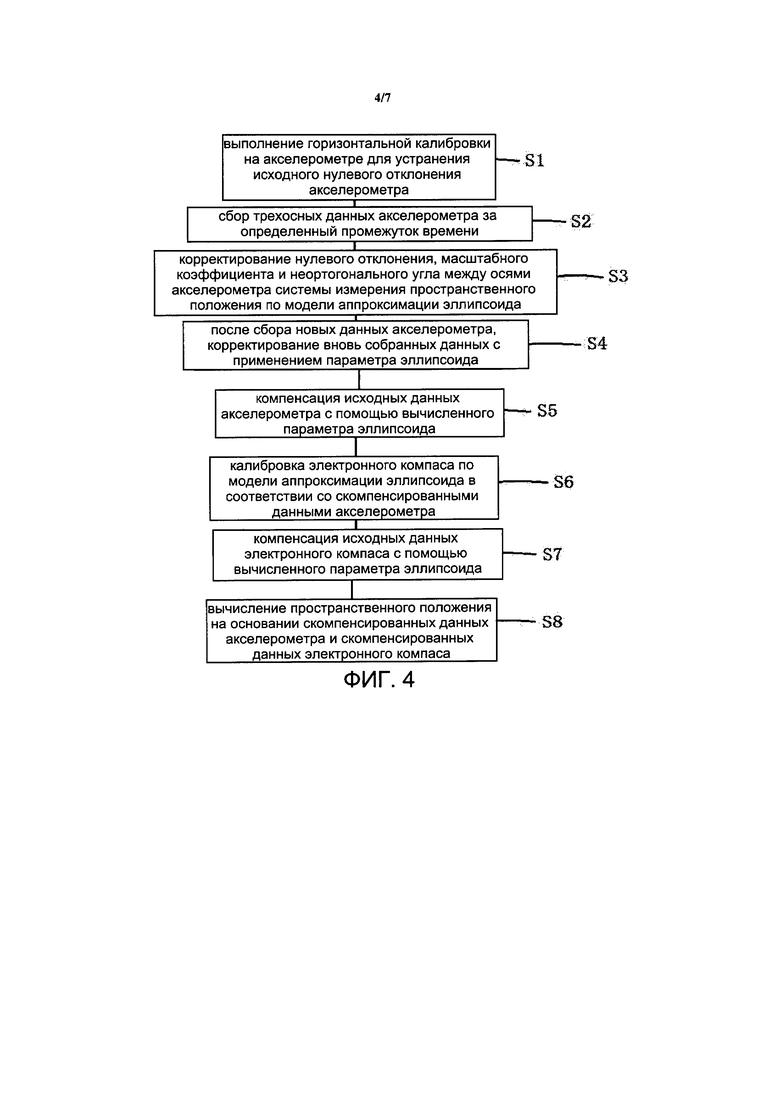
На фиг. 4 представлена блок-схема варианта осуществления 4 способа прецизионной калибровки системы измерения пространственного положения согласно настоящему изобретению;
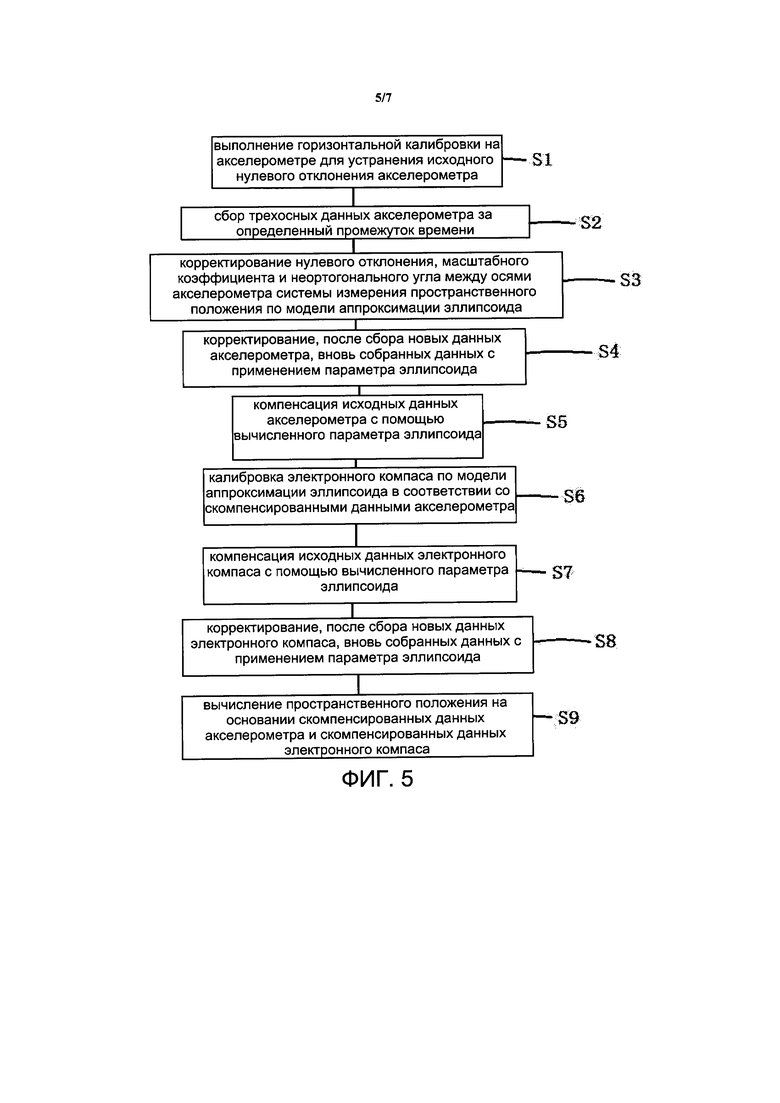
На фиг. 5 представлена блок-схема варианта осуществления 5 способа прецизионной калибровки системы измерения пространственного положения согласно настоящему изобретению;
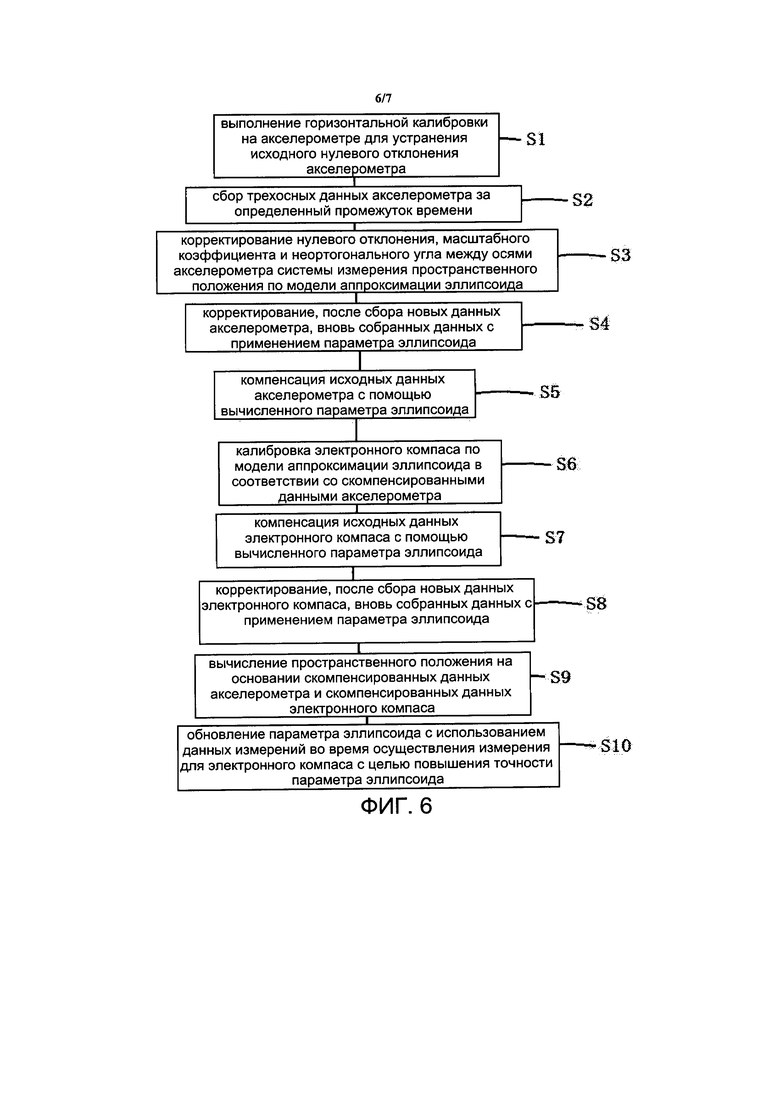
На фиг. 6 представлена блок-схема варианта осуществления 6 способа прецизионной калибровки системы измерения пространственного положения согласно настоящему изобретению;
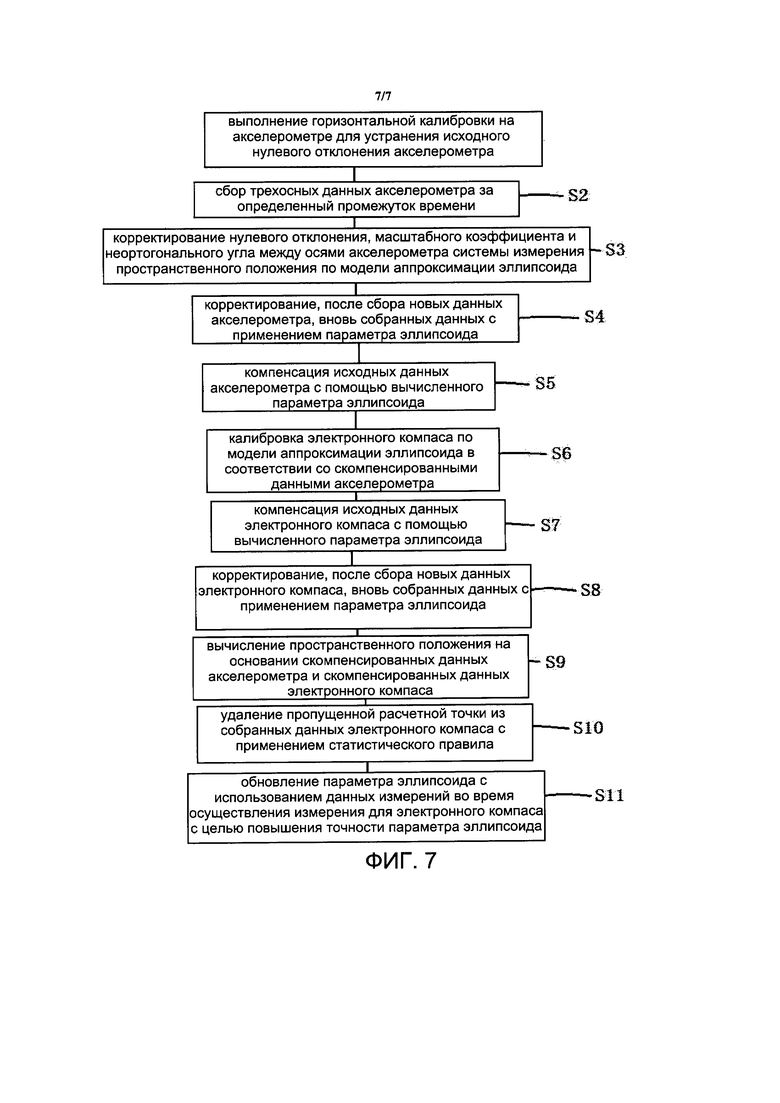
На фиг. 7 представлена блок-схема варианта осуществления 7 способа прецизионной калибровки системы измерения пространственного положения согласно настоящему изобретению.
Осуществление изобретения
[00018] В дальнейшем в этом документе технические решения вариантов осуществления настоящего изобретения явно и полностью описаны со ссылками на чертежи к вариантам осуществления настоящего изобретения. Очевидно, что описанные варианты осуществления представляют собой лишь некоторые из вариантов осуществления настоящего изобретения, а не все из них. Основанные на этих вариантах осуществления настоящего изобретения все другие варианты осуществления, предложенные специалистом в данной области техники без приложения творческих усилий, подпадают под сферу защиты настоящего изобретения.
Вариант осуществления 1
[00019] На фиг. 1 представлен способ прецизионной калибровки системы измерения пространственного положения. Способ прецизионной калибровки системы измерения пространственного положения включает следующие этапы:
Этап S1: калибровка нулевого отклонения, масштабного коэффициента и неортогонального угла между осями акселерометра системы измерения пространственного положения по модели аппроксимации эллипсоида;
На этапе S1: калибровка нулевого отклонения, масштабного коэффициента и неортогонального угла между осями акселерометра системы измерения пространственного положения по модели аппроксимации эллипсоида дополнительно включает следующие этапы:
подстановку вектора параметра аппроксимируемого эллипсоида, который можно записать как 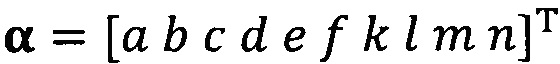 ;
;
подстановку числа т итераций калибровки, разложение первого значения 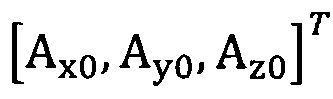 , полученного от акселерометра, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде
, полученного от акселерометра, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде 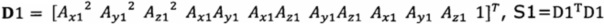 ;
;
если число раз сбора трехосных данных акселерометра не достигло значения n, обновление матрицы S с использованием вновь собранных данных акселерометра Dk, причем 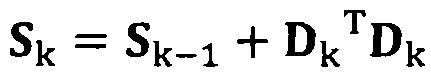 ;
;
после вычисления матрицы S, введение матрицы С ограничения эллипсоида и одновременное разложение матрицы S на блоки, причем
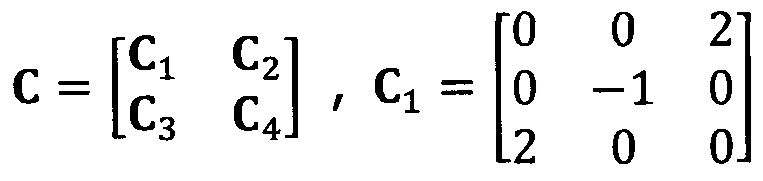
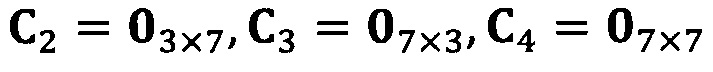
разложение матрицы S на блоки:
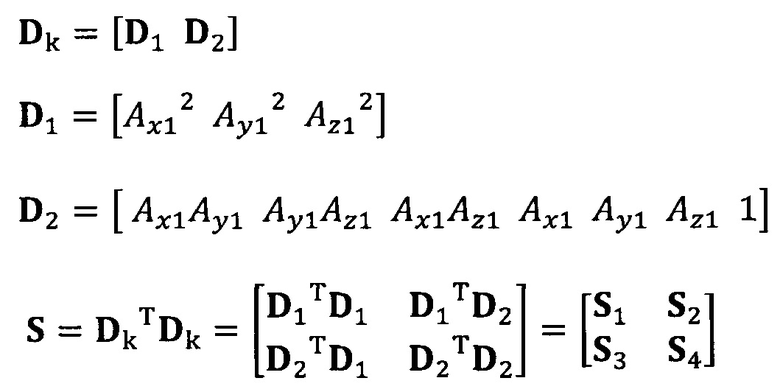
вычисление вектора аппроксимации эллипсоида с помощью следующих уравнений:
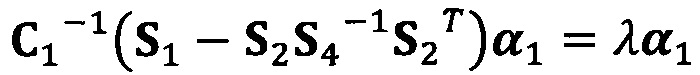
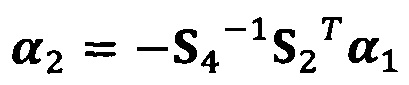 ;
;
после вычисления α1, вычисление α2 с помощью вышеприведенных уравнений для вычисления каждого параметра вектора аппроксимации эллипсоида, причем 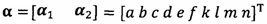 ;
;
кроме того, с учетом фактического физического соответствия трехосные масштабные коэффициенты kx, ky, kz, неортогональные углы между осями δxy, δyz, δxz и остаточные нулевые отклонения bx, by, bz могут быть вычислены с помощью следующих уравнений:
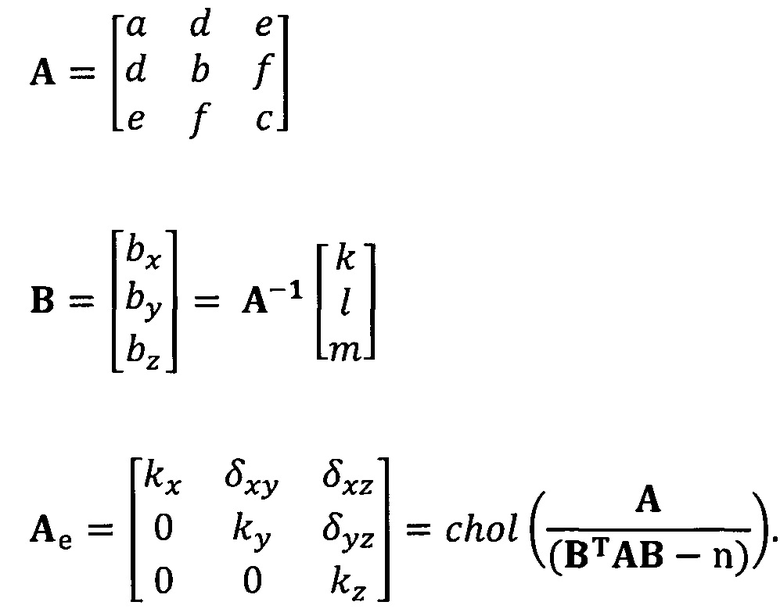
[00020] В вышеприведенных уравнениях а1 представляет собой собственный вектор, соответствующий максимальному собственному значению матрицы 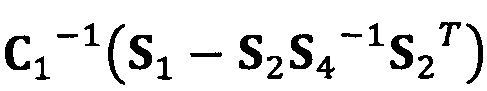 . Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
. Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
Если принять, что 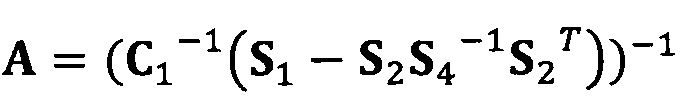 , взят вектор начальной итерации
, взят вектор начальной итерации 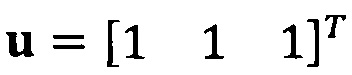 и задана точность итерации ε=1e-6;
и задана точность итерации ε=1e-6;
проводят разложение LU по А, а именно, А=LU;
решают систему линейных уравнений:
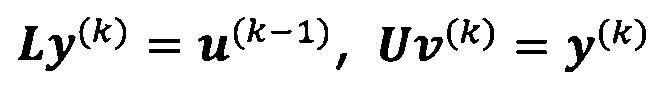
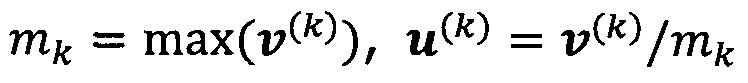
если 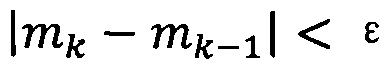 , пропускают итерацию, чтобы прекратить вычисление, причем
, пропускают итерацию, чтобы прекратить вычисление, причем 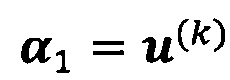 ; иначе k=k+1 и вычисление продолжают.
; иначе k=k+1 и вычисление продолжают.
[00021] Вообще говоря, если принять во внимание ε=1е-6, эта точность может быть достигнута менее, чем за 5 итераций итерационного вычисления.
[00022] Этап S2: компенсация исходных данных акселерометра с помощью вычисленного параметра эллипсоида.
[00023] Этап S3: калибровка электронного компаса по модели аппроксимации эллипсоида в соответствии со скомпенсированными данными акселерометра;
На этапе S3: калибровка электронного компаса по модели аппроксимации эллипсоида в соответствии со скомпенсированными данными акселерометра дополнительно включает следующие этапы:
подстановку вектора параметра аппроксимируемого эллипсоида, который можно записать как 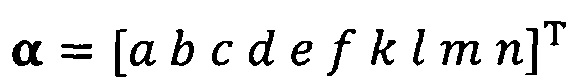 ;
;
сбор трехосных данных электронного компаса за определенный промежуток времени и проведение операции обработки собранных данных для недопущения переполнения, причем трехосные данные записывают в виде 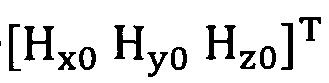 ;
;
подстановку числа n итераций калибровки, разложение первого значения 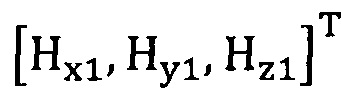 , полученного от электронного компаса, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде
, полученного от электронного компаса, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде 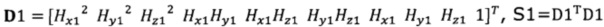 ;
;
если число раз сбора трехосных данных электронного компаса не достигло значения n, обновление матрицы S с использованием вновь собранных данных компаса Dk, причем 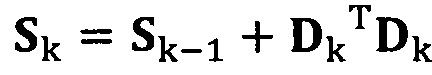 ;
;
после вычисления матрицы S введение матрицы С ограничения эллипсоида и одновременное разложение матрицы S на блоки, причем
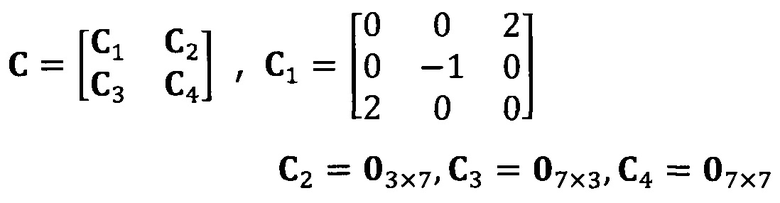
разложение матрицы S на блоки:
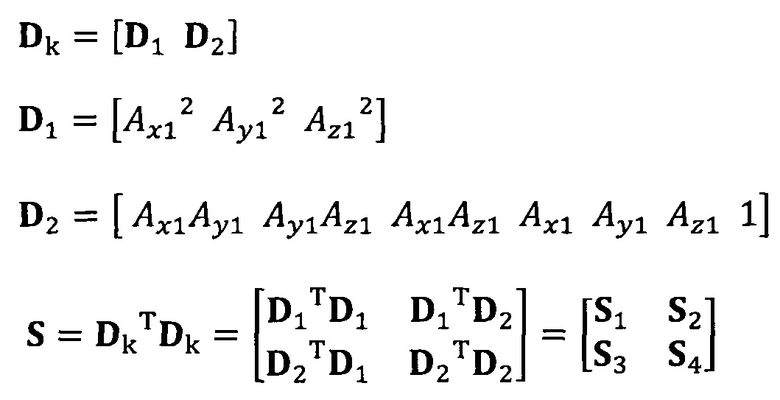
вычисление вектора аппроксимации эллипсоида с помощью следующих уравнений:
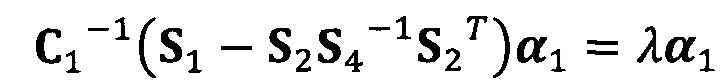
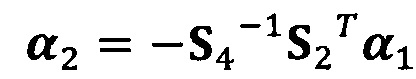 ;
;
после вычисления α1, вычисление α2 с помощью вышеприведенных уравнений для вычисления каждого параметра вектора аппроксимации эллипсоида, причем 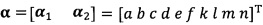 ;
;
кроме того, с учетом фактического физического соответствия трехосные масштабные коэффициенты kx, ky, kz, неортогональные углы между осями δxy, δyz, δxz и остаточные нулевые отклонения bx, by, bz могут быть вычислены с помощью следующих уравнений:
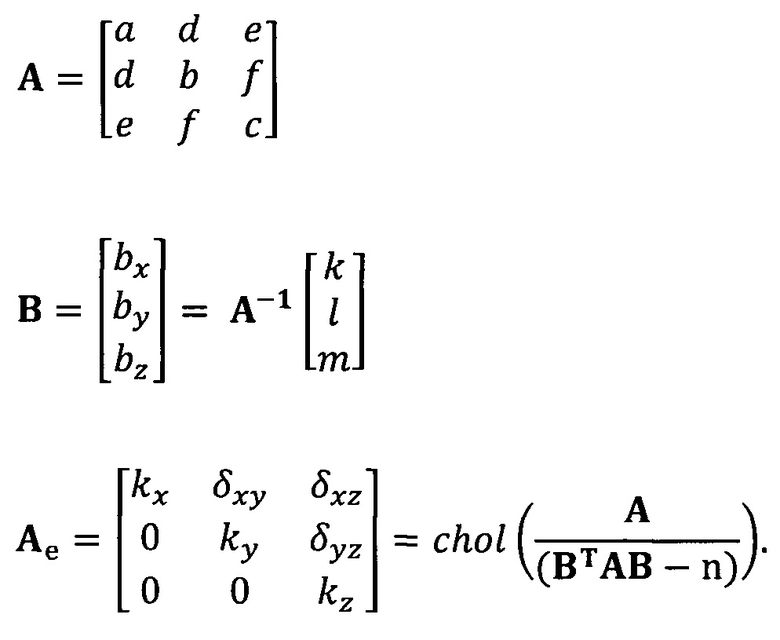
[00024] В вышеприведенных уравнениях α1 представляет собой собственный вектор, соответствующий максимальному собственному значению матрицы 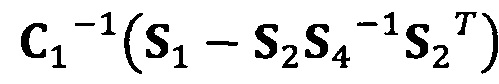 . Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
. Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
Если принять, что 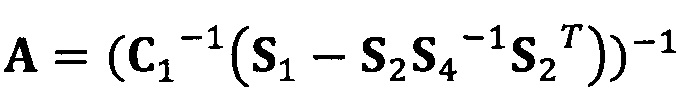 , взят вектор начальной итерации
, взят вектор начальной итерации 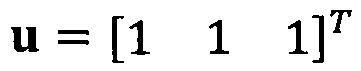 и задана точность итерации ε=1е-6;
и задана точность итерации ε=1е-6;
проводят разложение LU по А, а именно, А=LU;
решают систему линейных уравнений:
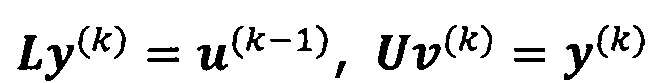
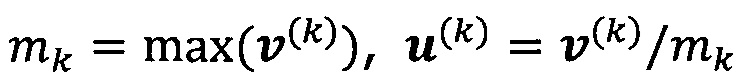
если 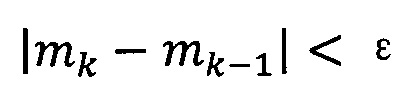 , пропускают итерацию, чтобы прекратить вычисление, причем
, пропускают итерацию, чтобы прекратить вычисление, причем 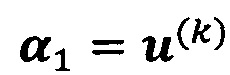 ; иначе k=k+l и вычисление продолжают.
; иначе k=k+l и вычисление продолжают.
[00025] Вообще говоря, если принять во внимание ε=1е-6, эта точность может быть достигнута менее, чем за 5 итераций итерационного вычисления.
[00026] Этап S4: компенсация исходных данных электронного компаса с помощью вычисленного параметра эллипсоида.
[00027] Этап S5: вычисление пространственного положения на основании скомпенсированных данных акселерометра и скомпенсированных данных электронного компаса.
Вариант осуществления 2
[00028] На фиг. 2 представлен способ прецизионной калибровки системы измерения пространственного положения. Способ прецизионной калибровки системы измерения пространственного положения включает следующие этапы:
Этап S1: проведение горизонтальной калибровки на акселерометре для устранения первоначального нулевого отклонения акселерометра;
установка устройства измерения пространственного положения в горизонтальное положение с помощью пузырькового уровня и выполнение горизонтальной калибровки на акселерометре для устранения нулевого отклонения акселерометра.
[00029] Этап S2: калибровка нулевого отклонения, масштабного коэффициента и неортогонального угла между осями акселерометра системы измерения пространственного положения по модели аппроксимации эллипсоида;
На этапе S2: калибровка нулевого отклонения, масштабного коэффициента и неортогонального угла между осями акселерометра системы измерения пространственного положения по модели аппроксимации эллипсоида дополнительно включает следующие этапы:
подстановку вектора параметра аппроксимируемого эллипсоида, который можно записать как 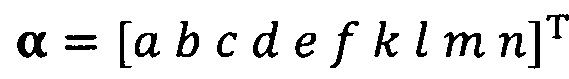 ;
;
подстановку числа n итераций калибровки, разложение первого значения 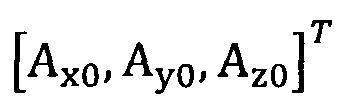 , полученного от акселерометра, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде
, полученного от акселерометра, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде 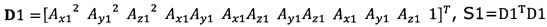 ;
;
если число раз сбора трехосных данных акселерометра еще не достигло значения n, обновление матрицы S с использованием вновь собранных данных акселерометра Dk, причем 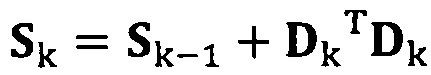 ;
;
после вычисления матрицы S, введение матрицы С ограничения эллипсоида и одновременное разложение матрицы S на блоки, причем
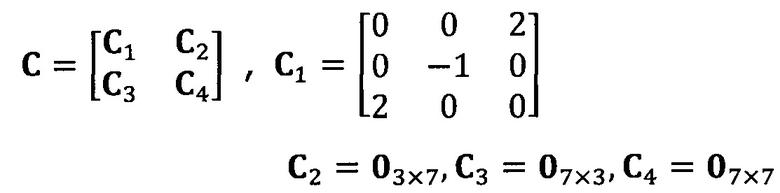
разложение матрицы S на блоки:
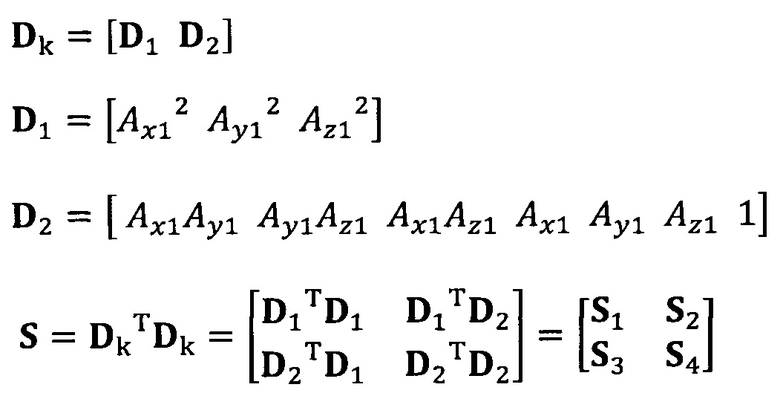
вычисление вектора аппроксимации эллипсоида с помощью следующих уравнений:
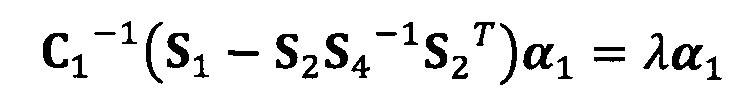
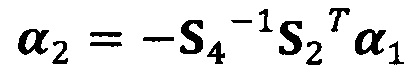 ;
;
после вычисления α1, вычисление α2 с помощью вышеприведенных уравнений для вычисления каждого параметра вектора аппроксимации эллипсоида, причем 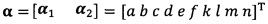 ;
;
кроме того, с учетом фактического физического соответствия трехосные масштабные коэффициенты kx, ky, kz, неортогональные углы между осями δху, δyz, δxz и остаточные нулевые отклонения bx, by, bz могут быть вычислены с помощью следующих уравнений:
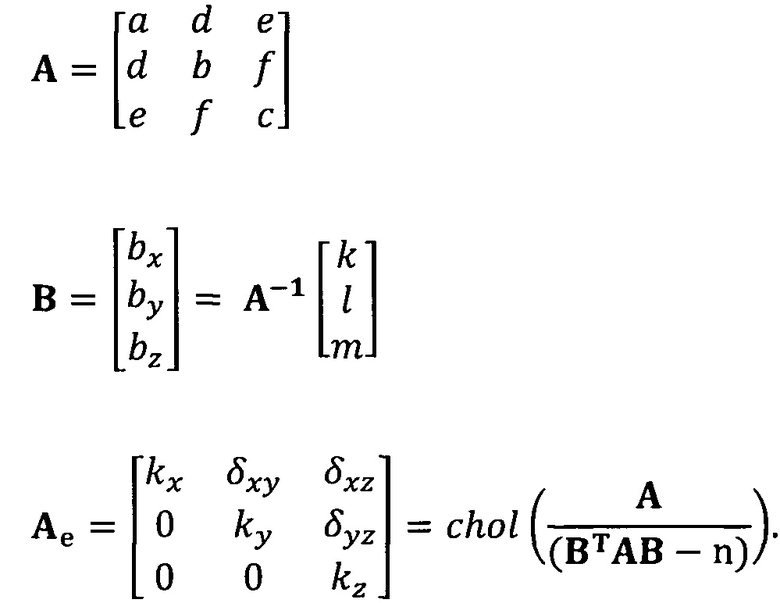
[00030] В вышеприведенных уравнениях α1 представляет собой собственный вектор, соответствующий максимальному собственному значению матрицы 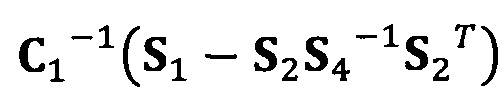 . Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
. Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
Если принять, что 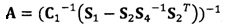 , взят вектор начальной итерации
, взят вектор начальной итерации 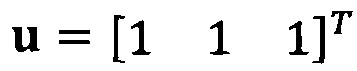 , задана точность итерации ε=1e-6;
, задана точность итерации ε=1e-6;
проводят разложение LU по А, а именно, А=LU;
решают систему линейных уравнений:
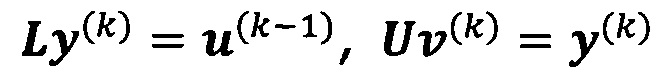
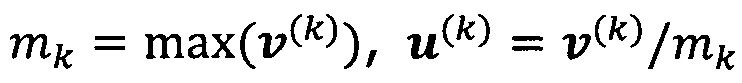
если 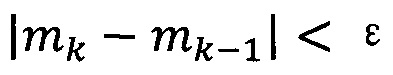 , пропускают итерацию, чтобы прекратить вычисление, причем
, пропускают итерацию, чтобы прекратить вычисление, причем 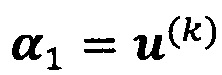 ; иначе k=k+1 и вычисление продолжают.
; иначе k=k+1 и вычисление продолжают.
[00031] Вообще говоря, если принять во внимание ε=1е-6, эта точность может быть достигнута менее, чем за 5 итераций итерационного вычисления.
[00032] Этап S3: компенсация исходных данных акселерометра с помощью вычисленного параметра эллипсоида.
[00033] Этап S4: калибровка электронного компаса по модели аппроксимации эллипсоида в соответствии со скомпенсированными данными акселерометра;
На этапе S4: калибровка электронного компаса по модели аппроксимации эллипсоида в соответствии со скомпенсированными данными акселерометра дополнительно включает следующие этапы:
подстановку вектора параметра аппроксимируемого эллипсоида, который можно записать как 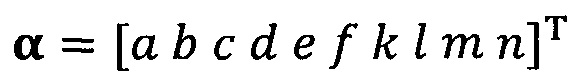 ;
;
сбор трехосных данных электронного компаса за определенный промежуток времени и проведение операции обработки собранных данных для недопущения переполнения, причем трехосные данные записывают в виде 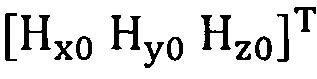 ;
;
подстановку числа n итераций калибровки, разложение первого значения 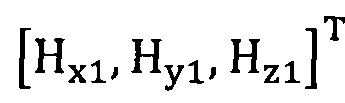 , полученного от электронного компаса, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде
, полученного от электронного компаса, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде 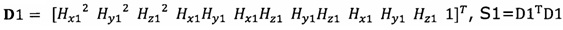 ;
;
если число раз сбора трехосных данных электронного компаса не достигло значения n, обновление матрицы S с использованием вновь собранных данных компаса Dk, причем 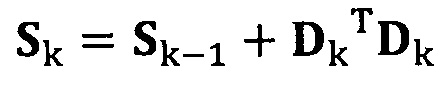 ;
;
после вычисления матрицы S введение матрицы С ограничения эллипсоида и одновременное разложение матрицы S на блоки, причем
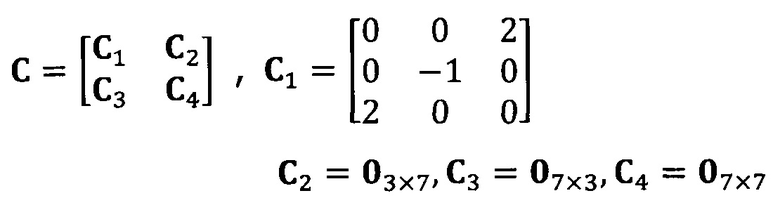
разложение матрицы S на блоки:
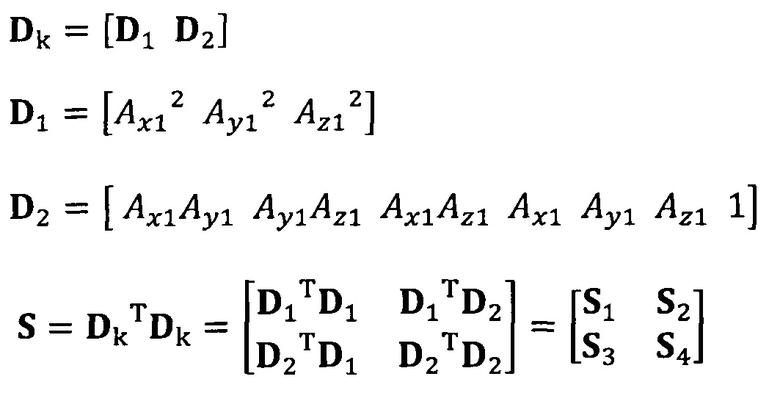
вычисление вектора аппроксимации эллипсоида с помощью следующих уравнений:
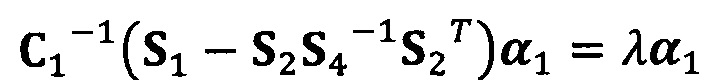
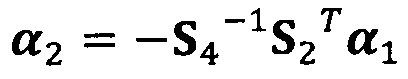 ;
;
после вычисления α1, вычисление α2 с помощью вышеприведенных уравнений для вычисления каждого параметра вектора аппроксимации эллипсоида, причем 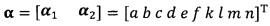 ;
;
кроме того, с учетом фактического физического соответствия трехосные масштабные коэффициенты kx, ky, kz, неортогональные углы между осями δху, δyz, δxz и остаточные нулевые отклонения bx, by, bz могут быть вычислены с помощью следующих уравнений:
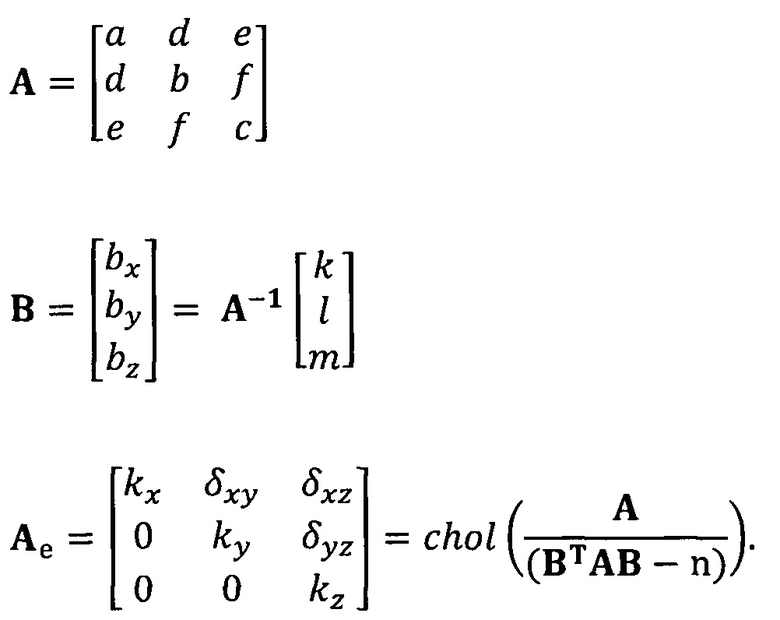
[00034] В вышеприведенных уравнениях α1 представляет собой собственный вектор, соответствующий максимальному собственному значению матрицы 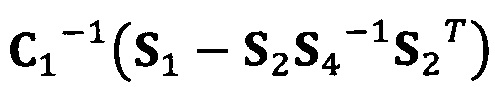 . Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
. Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
Если принять, что 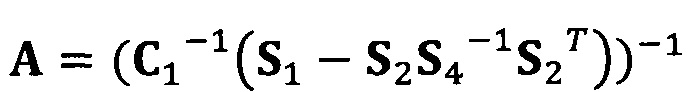 , взят вектор начальной итерации
, взят вектор начальной итерации 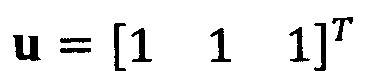 и задана точность итерации ε=1е-6;
и задана точность итерации ε=1е-6;
проводят разложение LU по А, а именно, А=LU;
решают систему линейных уравнений:
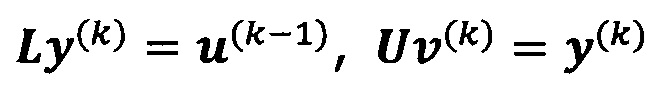
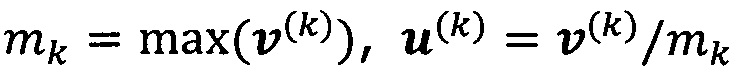
если 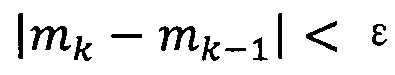 , пропускают итерацию, чтобы прекратить вычисление, причем
, пропускают итерацию, чтобы прекратить вычисление, причем 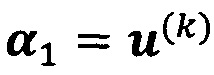 ; иначе k=k+1 и вычисление продолжают.
; иначе k=k+1 и вычисление продолжают.
[00035] Вообще говоря, если принять во внимание ε=1е-6, эта точность может быть достигнута менее, чем за 5 итераций итерационного вычисления.
[00036] Этап S5: компенсация исходных данных электронного компаса с помощью вычисленного параметра эллипсоида.
[00037] Этап S6: вычисление пространственного положения на основании скомпенсированных данных акселерометра и скомпенсированных данных электронного компаса.
Вариант осуществления 3
[00038] На фиг. 3 представлен способ прецизионной калибровки системы измерения пространственного положения. Способ прецизионной калибровки системы измерения пространственного положения включает следующие этапы:
Этап S1: проведение горизонтальной калибровки на акселерометре для устранения первоначального нулевого отклонения акселерометра;
установка устройства измерения пространственного положения в горизонтальное положение с помощью пузырькового уровня и выполнение горизонтальной калибровки на акселерометре для устранения нулевого отклонения акселерометра.
[00039] Этап S2: сбор трехосных данных акселерометра за определенный промежуток времени, причем эти трехосные данные записывают в виде 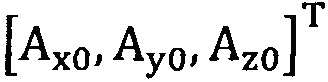 , нулевое отклонение записывают в виде
, нулевое отклонение записывают в виде 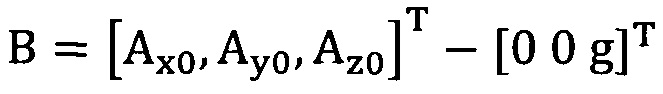 .
.
[00040] Этап S3: калибровка нулевого отклонения, масштабного коэффициента и неортогонального угла между осями акселерометра системы измерения пространственного положения по модели аппроксимации эллипсоида;
На этапе S3: калибровка нулевого отклонения, масштабного коэффициента и неортогонального угла между осями акселерометра системы измерения пространственного положения по модели аппроксимации эллипсоида дополнительно включает следующие этапы:
подстановку вектора параметра аппроксимируемого эллипсоида, который можно записать как 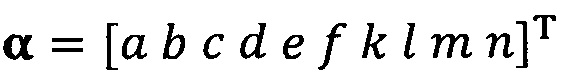 ;
;
подстановку числа n итераций калибровки, разложение первого значения 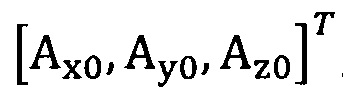 , полученного от акселерометра, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде
, полученного от акселерометра, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде 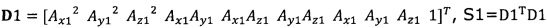 ;
;
если число раз сбора трехосных данных акселерометра не достигло значения n, обновление матрицы S с использованием вновь собранных данных акселерометра Dk, причем 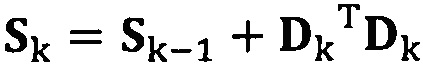 ;
;
после вычисления матрицы S, введение матрицы С ограничения эллипсоида и одновременное разложение матрицы S на блоки, причем
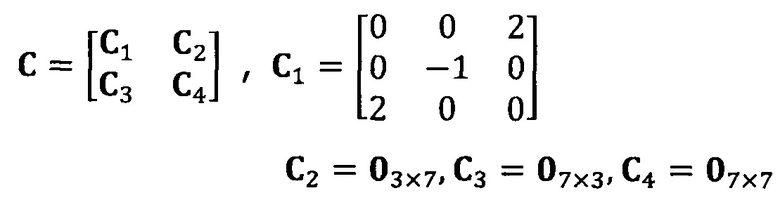
разложение матрицы S на блоки:
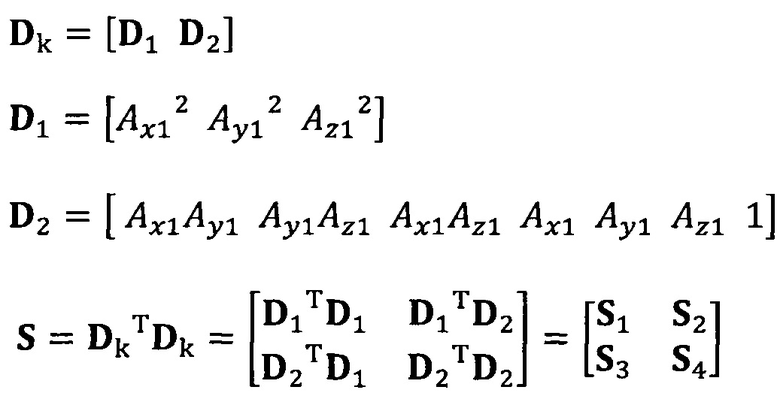
вычисление вектора аппроксимации эллипсоида с помощью следующих уравнений:
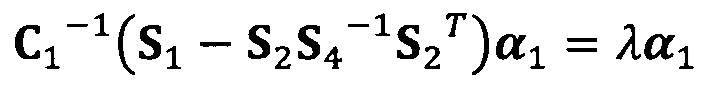
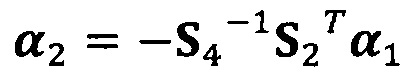 ;
;
после вычисления α1, вычисление α2 с помощью вышеприведенных уравнений для вычисления каждого параметра вектора аппроксимации эллипсоида, причем 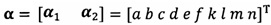 ;
;
кроме того, с учетом фактического физического соответствия трехосные масштабные коэффициенты kx, ky, kz, неортогональные углы между осями δxy, δyz, δxz и остаточные нулевые отклонения bx, by, bz могут быть вычислены с помощью следующих уравнений:
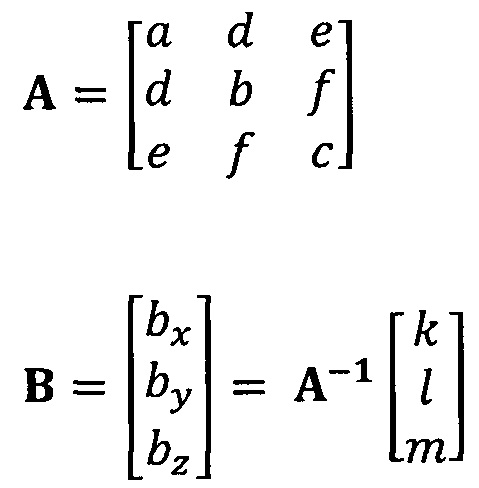
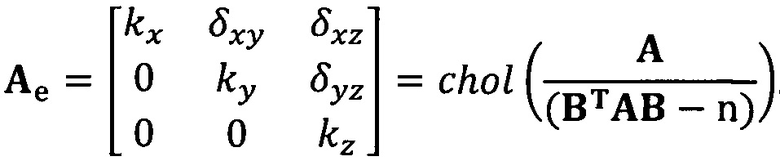
[00041] В вышеприведенных уравнениях α1 представляет собой собственный вектор, соответствующий максимальному собственному значению матрицы 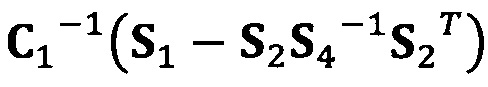 . Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
. Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
Если принять, что 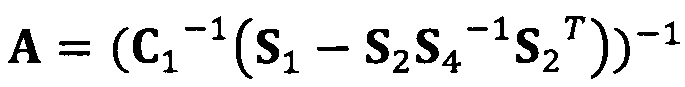 , взят вектор начальной итерации
, взят вектор начальной итерации 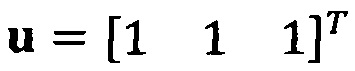 и задана точность итерации ε=1е-6;
и задана точность итерации ε=1е-6;
проводят разложение LU по А, а именно, А=LU;
решают систему линейных уравнений:
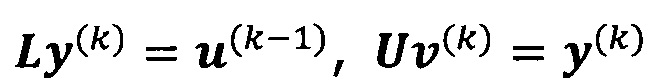
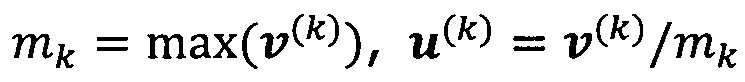
если 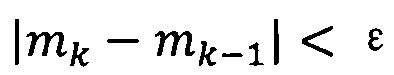 , пропускают итерацию, чтобы прекратить вычисление, причем
, пропускают итерацию, чтобы прекратить вычисление, причем 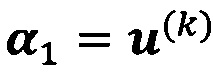 ; иначе k=k+1 и вычисление продолжают.
; иначе k=k+1 и вычисление продолжают.
[00042] Вообще говоря, если принять во внимание ε=1е-6, эта точность может быть достигнута менее, чем за 5 итераций итерационного вычисления.
[00043] Этап S4: компенсация исходных данных акселерометра с помощью вычисленного параметра эллипсоида.
[00044] Этап S5: калибровка электронного компаса по модели аппроксимации эллипсоида в соответствии со скомпенсированными данными акселерометра;
На этапе S5: калибровка электронного компаса по модели аппроксимации эллипсоида в соответствии со скомпенсированными данными акселерометра дополнительно включает следующие этапы:
подстановку вектора параметра аппроксимируемого эллипсоида, который можно записать как 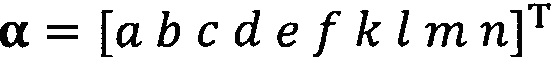 ;
;
сбор трехосных данных электронного компаса за определенный промежуток времени и проведение операции обработки собранных данных для недопущения переполнения, причем трехосные данные записывают в виде 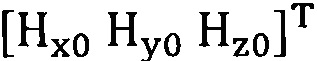 ;
;
подстановку числа n итераций калибровки, разложение первого значения 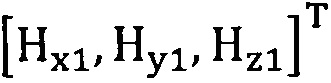 , полученного от электронного компаса, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде
, полученного от электронного компаса, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде 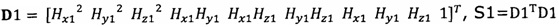 ;
;
если число раз сбора трехосных данных электронного компаса не достигло значения n, обновление матрицы S с использованием вновь собранных данных компаса Dk, причем 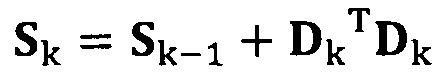 ;
;
после вычисления матрицы S введение матрицы С ограничения эллипсоида и одновременное разложение матрицы S на блоки, причем

разложение матрицы S на блоки:
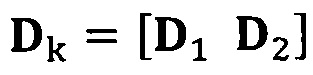
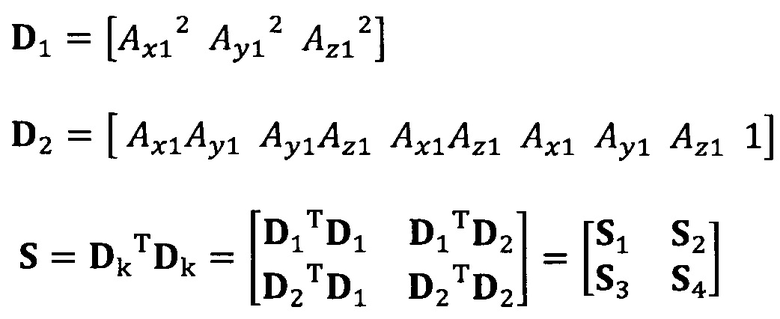
вычисление вектора аппроксимации эллипсоида с помощью следующих уравнений:
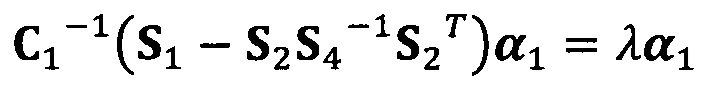
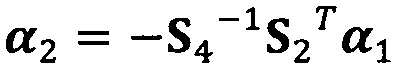 ;
;
после вычисления α1 вычисление α2 с помощью вышеприведенных уравнений для вычисления каждого параметра вектора аппроксимации эллипсоида, причем 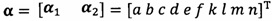 ;
;
кроме того, с учетом фактического физического соответствия трехосные масштабные коэффициенты kx, ky, kz, неортогональные углы между осями δxy, δyz, δxz и остаточные нулевые отклонения bx, by, bz могут быть вычислены с помощью следующих уравнений:
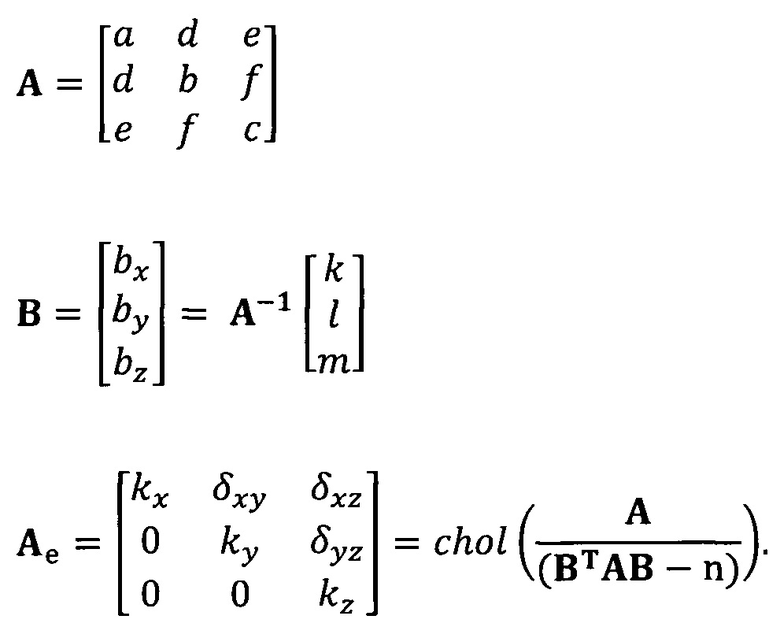
[00045] В вышеприведенных уравнениях α1 представляет собой собственный вектор, соответствующий максимальному собственному значению матрицы 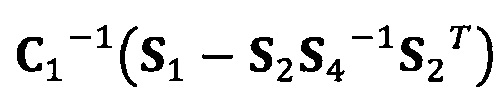 . Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
. Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
Если принять, что 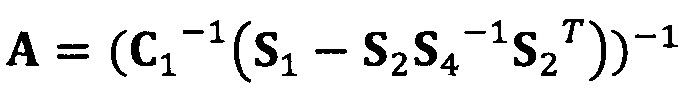 , взят вектор начальной итерации
, взят вектор начальной итерации 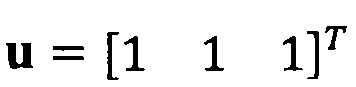 и задана точность итерации ε=1е-6;
и задана точность итерации ε=1е-6;
проводят разложение LU по А, а именно, А=LU;
решают систему линейных уравнений:
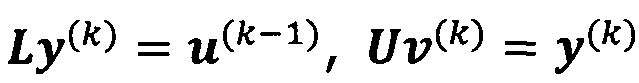
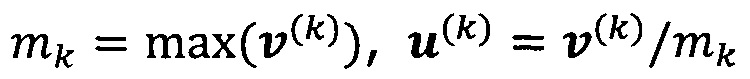
если 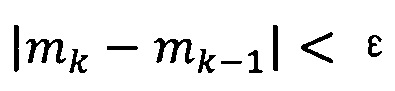 , пропускают итерацию, чтобы прекратить вычисление, причем
, пропускают итерацию, чтобы прекратить вычисление, причем 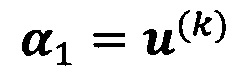 ; иначе k=k+1 и вычисление продолжают.
; иначе k=k+1 и вычисление продолжают.
[00046] Вообще говоря, если принять во внимание ε=1е-6, эта точность может быть достигнута менее, чем за 5 итераций итерационного вычисления.
[00047] Этап S6: компенсация исходных данных электронного компаса с помощью вычисленного параметра эллипсоида.
[00048] Этап S7: вычисление пространственного положения на основании скомпенсированных данных акселерометра и скомпенсированных данных электронного компаса.
Вариант осуществления 4
[00049] На фиг. 4 представлен способ прецизионной калибровки системы измерения пространственного положения. Способ прецизионной калибровки системы измерения пространственного положения включает следующие этапы:
Этап S1: проведение горизонтальной калибровки на акселерометре для устранения первоначального нулевого отклонения акселерометра;
установка устройства измерения пространственного положения в горизонтальное положение с помощью пузырькового уровня и выполнение горизонтальной калибровки на акселерометре для устранения нулевого отклонения акселерометра.
[00050] Этап S2: сбор трехосных данных акселерометра за определенный промежуток времени, причем эти трехосные данные записывают в виде 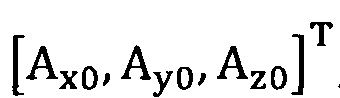 , нулевое отклонение записывают в виде
, нулевое отклонение записывают в виде 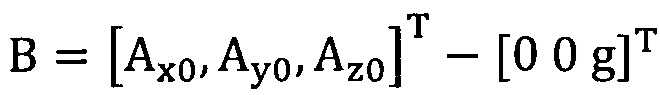 .
.
[00051] Этап S3: калибровка нулевого отклонения, масштабного коэффициента и неортогонального угла между осями акселерометра системы измерения пространственного положения по модели аппроксимации эллипсоида;
На этапе S3: калибровка нулевого отклонения, масштабного коэффициента и неортогонального угла между осями акселерометра системы измерения пространственного положения по модели аппроксимации эллипсоида дополнительно включает следующие этапы:
подстановку вектора параметра аппроксимируемого эллипсоида, который можно записать как 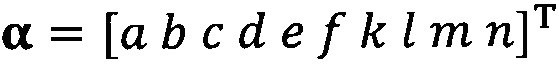 ; подстановку числа n итераций калибровки, разложение первого значения
; подстановку числа n итераций калибровки, разложение первого значения 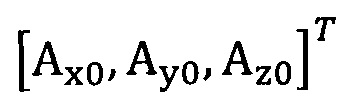 , полученного от акселерометра, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде
, полученного от акселерометра, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде 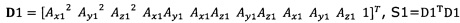 ;
;
если число раз сбора трехосных данных акселерометра не достигло значения n, обновление матрицы S с использованием вновь собранных данных акселерометра Dk, причем 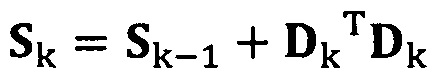 ;
;
после вычисления матрицы S, введение матрицы С ограничения эллипсоида и одновременное разложение матрицы S на блоки, причем
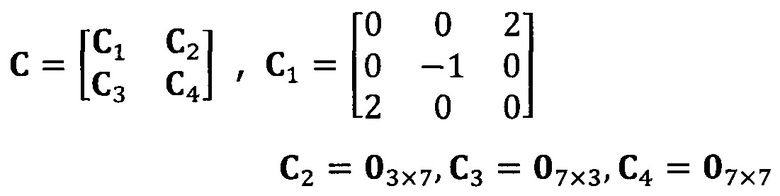
разложение матрицы S на блоки:
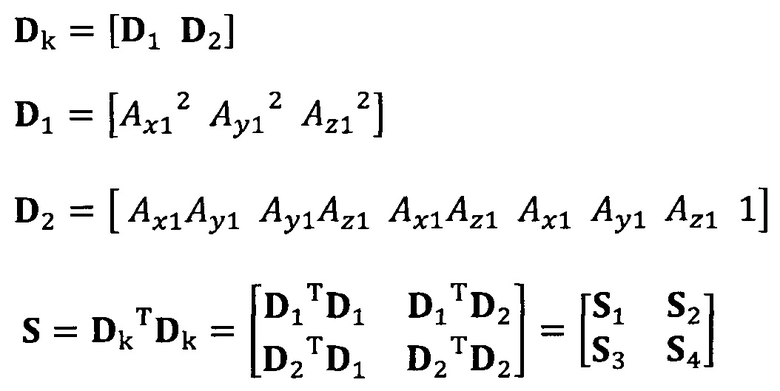
вычисление вектора аппроксимации эллипсоида с помощью следующих уравнений:
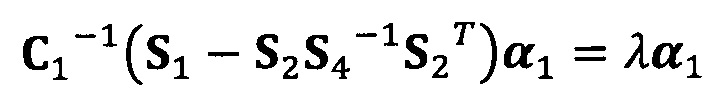
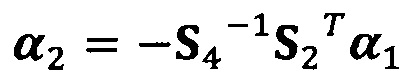 ;
;
после вычисления α1 вычисление α2 с помощью вышеприведенных уравнений для вычисления каждого параметра вектора аппроксимации эллипсоида, причем 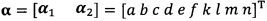 ;
;
кроме того, с учетом фактического физического соответствия трехосные масштабные коэффициенты kx, ky, kz, неортогональные углы между осями δxy, δyz, δxz и остаточные нулевые отклонения bx, by, bz могут быть вычислены с помощью следующих уравнений:
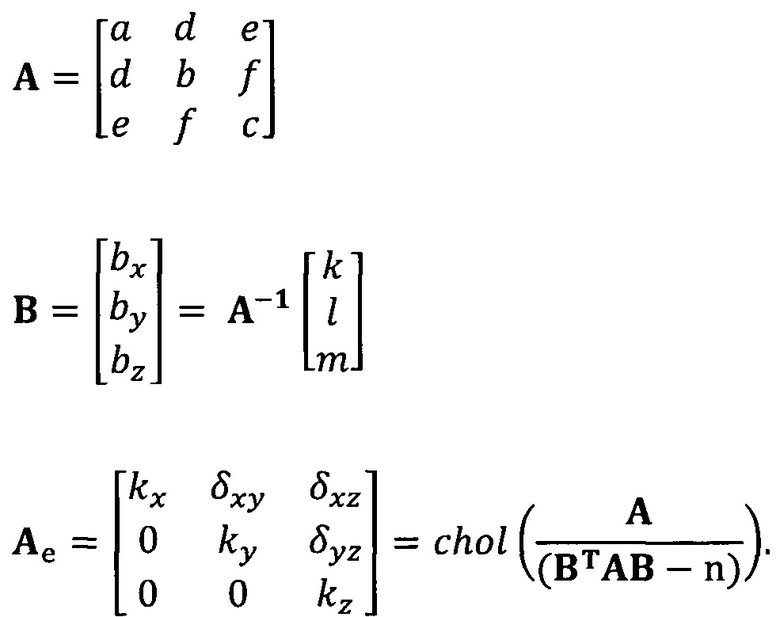
[00052] В вышеприведенных уравнениях α1 представляет собой собственный вектор, соответствующий максимальному собственному значению матрицы 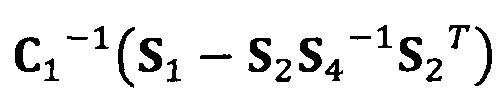 . Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
. Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
Если принять, что 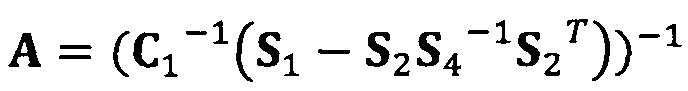 , взят вектор начальной итерации
, взят вектор начальной итерации 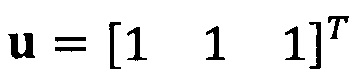 и задана точность итерации ε=1е-6;
и задана точность итерации ε=1е-6;
проводят разложение LU по А, а именно, А=LU;
решают систему линейных уравнений:
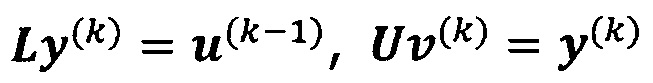
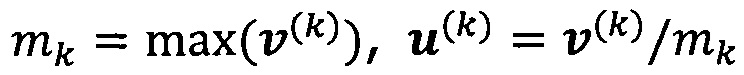
если 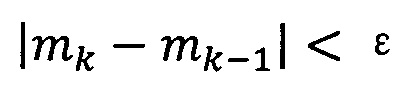 , пропускают итерацию, чтобы прекратить вычисление, причем
, пропускают итерацию, чтобы прекратить вычисление, причем 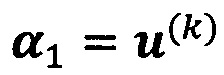 ; иначе k=k+1 и вычисление продолжают.
; иначе k=k+1 и вычисление продолжают.
[00053] Вообще говоря, если принять во внимание ε=1е-6, эта точность может быть достигнута менее, чем за 5 итераций итерационного вычисления.
[00054] Этап S4: корректирование, после сбора новых данных акселерометра, вновь собранных данных с применением параметра эллипсоида.
[00055] Этап S5: компенсация исходных данных акселерометра с помощью вычисленного параметра эллипсоида.
[00056] Этап S6: калибровка электронного компаса по модели аппроксимации эллипсоида в соответствии со скомпенсированными данными акселерометра;
На этапе S6: калибровка электронного компаса по модели аппроксимации эллипсоида в соответствии со скомпенсированными данными акселерометра дополнительно включает следующие этапы:
подстановку вектора параметра аппроксимируемого эллипсоида, который можно записать как 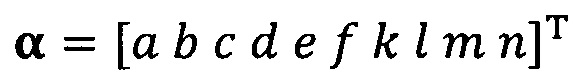 ;
;
сбор трехосных данных электронного компаса за определенный промежуток времени и проведение операции обработки собранных данных для недопущения переполнения, причем трехосные данные записывают в виде 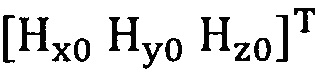 ;
;
подстановку числа n итераций калибровки, разложение первого значения 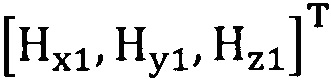 , полученного от электронного компаса, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде
, полученного от электронного компаса, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде 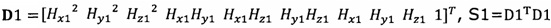 ;
;
если число раз сбора трехосных данных электронного компаса не достигло значения n, обновление матрицы S с использованием вновь собранных данных компаса Dk, причем 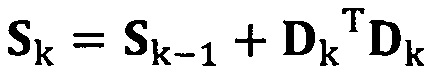 ;
;
после вычисления матрицы S введение матрицы С ограничения эллипсоида и одновременное разложение матрицы S на блоки, причем
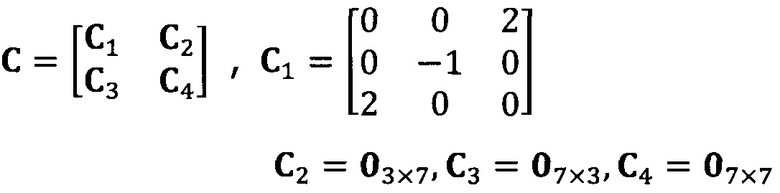
разложение матрицы S на блоки:
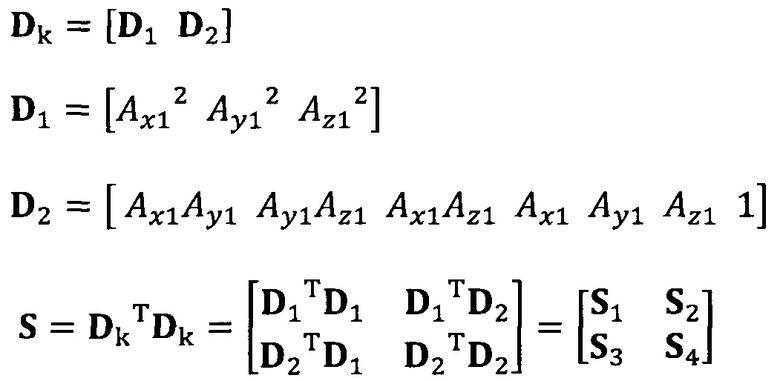
вычисление вектора аппроксимации эллипсоида с помощью следующих уравнений:
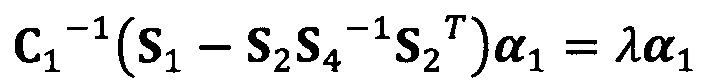
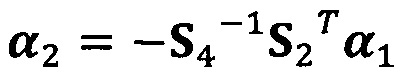 ;
;
после вычисления α1, вычисление α2 с помощью вышеприведенных уравнений для вычисления каждого параметра вектора аппроксимации эллипсоида, причем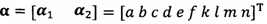 ;
;
кроме того, с учетом фактического физического соответствия трехосные масштабные коэффициенты kx, ky, kz, неортогональные углы между осями δxy, δyz, δxz и остаточные нулевые отклонения bx, by, bz могут быть вычислены с помощью следующих уравнений:
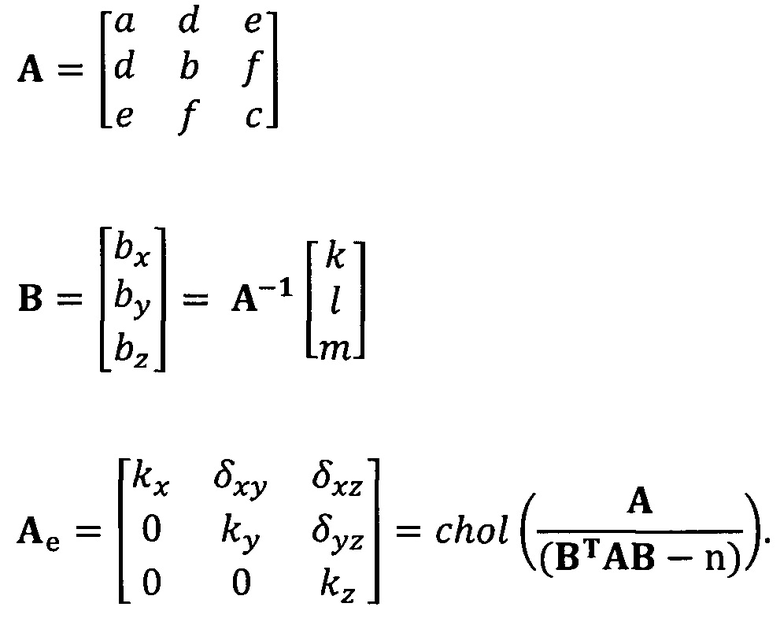
[00057] В вышеприведенных уравнениях α1 представляет собой собственный вектор, соответствующий максимальному собственному значению матрицы 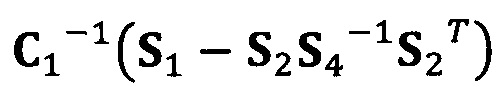 . Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
. Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
Если принять, что 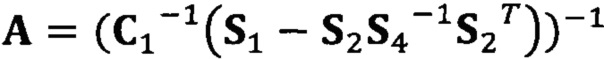 , взят вектор начальной итерации
, взят вектор начальной итерации 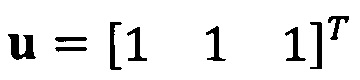 и задана точность итерации ε=1e-6;
и задана точность итерации ε=1e-6;
проводят разложение LU по А, а именно, А=LU;
решают систему линейных уравнений:
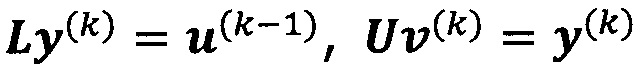
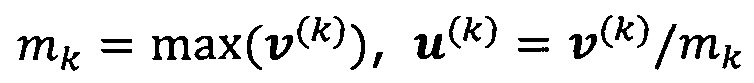
если 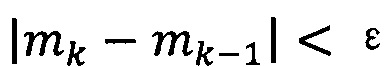 , пропускают итерацию, чтобы
, пропускают итерацию, чтобы
прекратить вычисление, причем 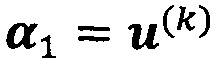 ; иначе k=k+1 и вычисление продолжают.
; иначе k=k+1 и вычисление продолжают.
[00058] Вообще говоря, если принять во внимание ε=1е-6, эта точность может быть достигнута менее, чем за 5 итераций итерационного вычисления.
[00059] Этап S7: компенсация исходных данных электронного компаса с помощью вычисленного параметра эллипсоида.
[00060] Этап S8: вычисление пространственного положения на основании скомпенсированных данных акселерометра и скомпенсированных данных электронного компаса.
Вариант осуществления 5
[00061] На фиг. 5 представлен способ прецизионной калибровки системы измерения пространственного положения. Способ прецизионной калибровки системы измерения пространственного положения включает следующие этапы:
Этап S1: проведение горизонтальной калибровки на акселерометре для устранения первоначального нулевого отклонения акселерометра;
установка устройства измерения пространственного положения в горизонтальное положение с помощью пузырькового уровня и выполнение горизонтальной калибровки на акселерометре для устранения нулевого отклонения акселерометра.
[00062] Этап S2: сбор трехосных данных акселерометра за определенный промежуток времени, причем эти трехосные данные записывают в виде 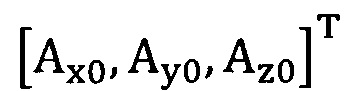 , нулевое отклонение записывают в виде
, нулевое отклонение записывают в виде 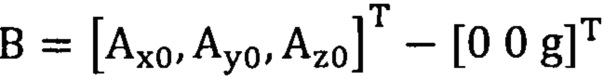
[00063] Этап S3: калибровка нулевого отклонения, масштабного коэффициента и неортогонального угла между осями акселерометра системы измерения пространственного положения по модели аппроксимации эллипсоида;
На этапе S3: калибровка нулевого отклонения, масштабного коэффициента и неортогонального угла между осями акселерометра системы измерения пространственного положения по модели аппроксимации эллипсоида дополнительно включает следующие этапы:
подстановку вектора параметра аппроксимируемого эллипсоида, который можно записать как 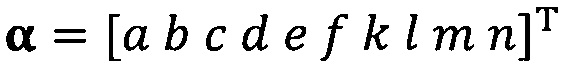 ;
;
подстановку числа n итераций калибровки, разложение первого значения 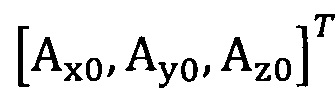 , полученного от акселерометра, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде
, полученного от акселерометра, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде 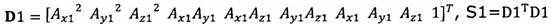 ;
;
если число раз сбора трехосных данных акселерометра не достигло значения n, обновление матрицы S с использованием вновь собранных данных акселерометра Dk, причем 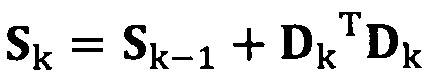 ;
;
после вычисления матрицы S, введение матрицы С ограничения эллипсоида и одновременное разложение матрицы S на блоки, причем
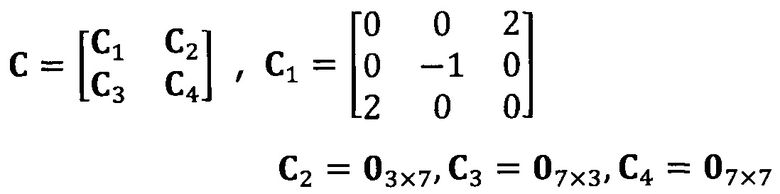
разложение матрицы S на блоки:
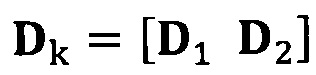
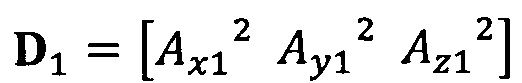
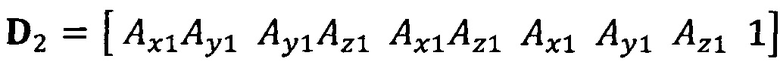
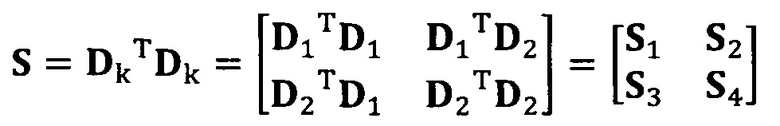
вычисление вектора аппроксимации эллипсоида с помощью следующих уравнений:
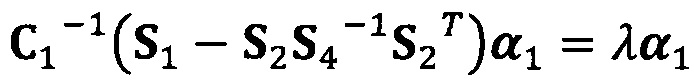
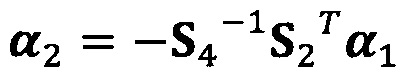 ;
;
после вычисления α1, вычисление α2 с помощью вышеприведенных уравнений для вычисления каждого параметра вектора аппроксимации эллипсоида, причем 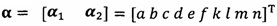 ;
;
кроме того, с учетом фактического физического соответствия трехосные масштабные коэффициенты kx, ky, kz, неортогональные углы между осями δxy, δyz, δxz и остаточные нулевые отклонения bx, by, bz могут быть вычислены с помощью следующих уравнений:
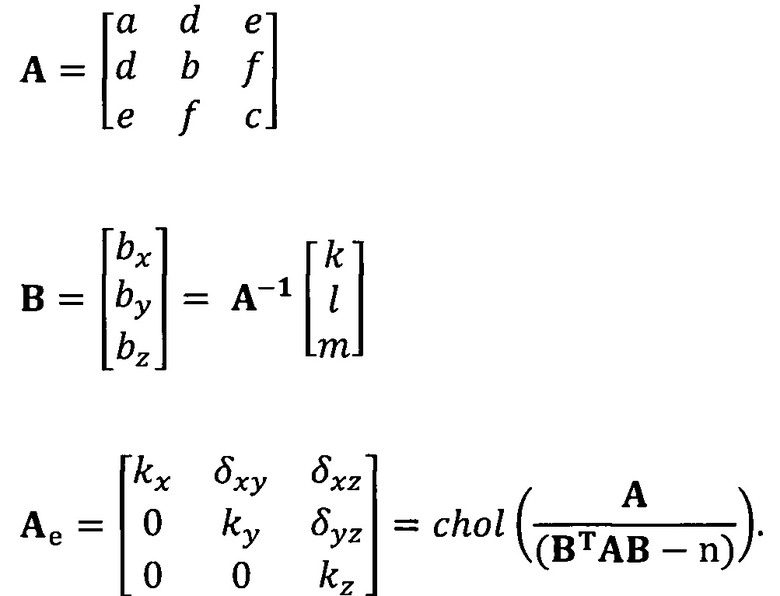
[00064] В вышеприведенных уравнениях α1 представляет собой собственный вектор, соответствующий максимальному собственному значению матрицы 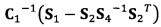 . Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
. Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
Если принять, что 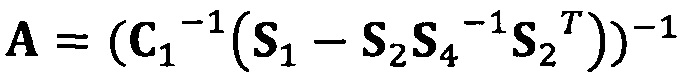 , взят вектор начальной итерации
, взят вектор начальной итерации 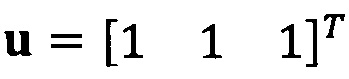 и задана точность итерации ε=1е-6;
и задана точность итерации ε=1е-6;
проводят разложение LU по А, а именно, А=LU;
решают систему линейных уравнений:
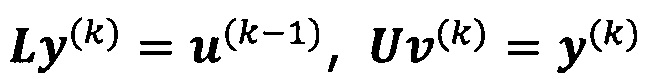
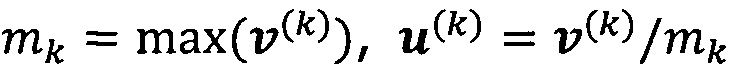
если 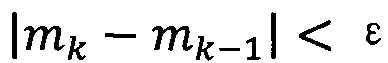 , пропускают итерацию, чтобы прекратить вычисление, причем
, пропускают итерацию, чтобы прекратить вычисление, причем 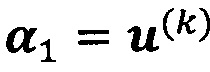 ; иначе k=k+1 и вычисление продолжают.
; иначе k=k+1 и вычисление продолжают.
[00065] Вообще говоря, если принять во внимание ε=1е-6, эта точность может быть достигнута менее, чем за 5 итераций итерационного вычисления.
[00066] Этап S4: корректирование, после сбора новых данных акселерометра, вновь собранных данных с применением параметра эллипсоида.
[00067] Этап S5: компенсация исходных данных акселерометра с помощью вычисленного параметра эллипсоида.
[00068] Этап S6: калибровка электронного компаса по модели аппроксимации эллипсоида в соответствии со скомпенсированными данными акселерометра;
На этапе S6: калибровка электронного компаса по модели аппроксимации эллипсоида в соответствии со скомпенсированными данными акселерометра дополнительно включает следующие этапы:
подстановку вектора параметра аппроксимируемого эллипсоида, который можно записать как 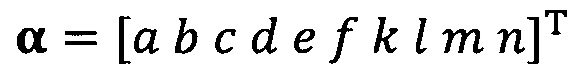 ;
;
сбор трехосных данных электронного компаса за определенный промежуток времени и проведение операции обработки собранных данных для недопущения переполнения, причем трехосные данные записывают в виде 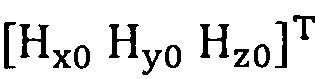 ;
;
подстановку числа n итераций калибровки, разложение первого значения 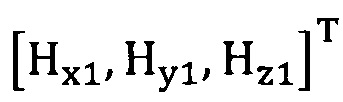 , полученного от электронного компаса, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде
, полученного от электронного компаса, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде 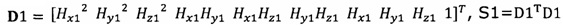 ;
;
если число раз сбора трехосных данных электронного компаса не достигло значения n, обновление матрицы S с использованием вновь собранных данных компаса Dk, причем 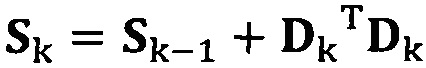 ;
;
после вычисления матрицы S введение матрицы С ограничения эллипсоида и одновременное разложение матрицы S на блоки, причем
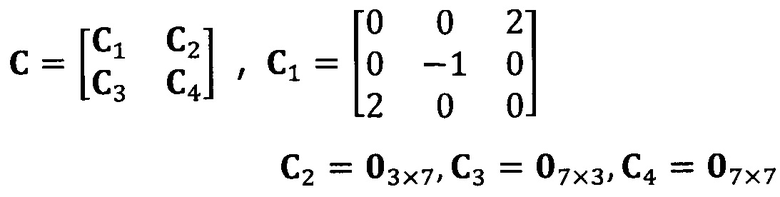
разложение матрицы S на блоки:
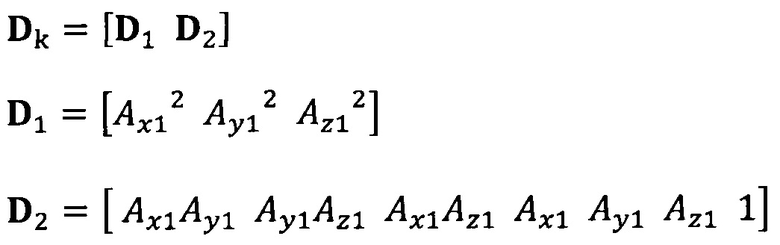
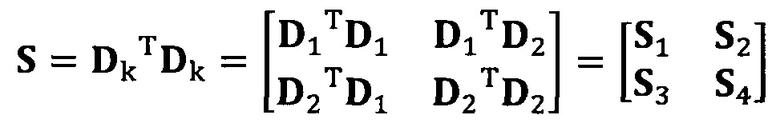
вычисление вектора аппроксимации эллипсоида с помощью следующих уравнений:
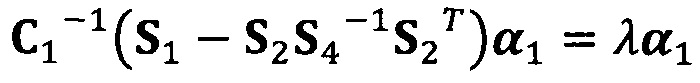
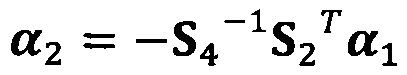 ;
;
после вычисления α1, вычисление α2 с помощью вышеприведенных уравнений для вычисления каждого параметра вектора аппроксимации эллипсоида, причем 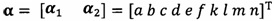 ;
;
кроме того, с учетом фактического физического соответствия трехосные масштабные коэффициенты kx, ky, kz, неортогональные углы между осями δxy, δyz, δxz и остаточные нулевые отклонения bx, by, bz могут быть вычислены с помощью следующих уравнений:

[00069] В вышеприведенных уравнениях α1 представляет собой собственный вектор, соответствующий максимальному собственному значению матрицы 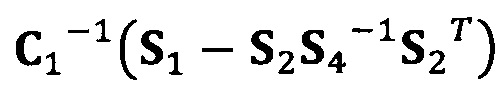 . Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
. Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
Если принять, что 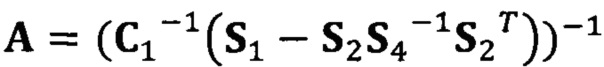 , взят вектор начальной итерации
, взят вектор начальной итерации 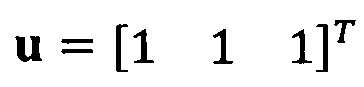 и задана точность итерации ε=1е-6;
и задана точность итерации ε=1е-6;
проводят разложение LU для А, а именно, А=LU;
решают систему линейных уравнений:
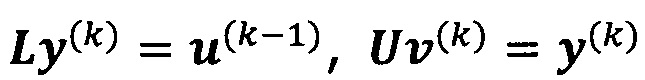
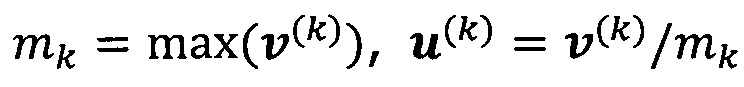
если 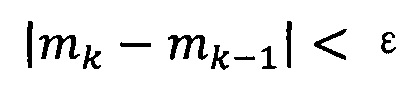 , пропускают итерацию, чтобы прекратить вычисление, причем
, пропускают итерацию, чтобы прекратить вычисление, причем 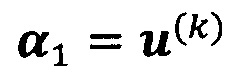 ; иначе k=k+1 и вычисление продолжают.
; иначе k=k+1 и вычисление продолжают.
[00070] Вообще говоря, если принять во внимание ε=1е-6, эта точность может быть достигнута менее, чем за 5 итераций итерационного вычисления.
[00071] Этап S7: компенсация исходных данных электронного компаса с помощью вычисленного параметра эллипсоида.
[00072] Этап S8: корректирование, после сбора новых данных электронного компаса, вновь собранных данных с применением параметра эллипсоида.
[00073] Этап S9: вычисление пространственного положения на основании скомпенсированных данных акселерометра и скомпенсированных данных электронного компаса.
Вариант осуществления 6
[00074] На фиг. 6 представлен способ прецизионной калибровки системы измерения пространственного положения. Способ прецизионной калибровки системы измерения пространственного положения включает следующие этапы:
Этап S1: проведение горизонтальной калибровки на акселерометре для устранения первоначального нулевого отклонения акселерометра;
установка устройства измерения пространственного положения в горизонтальное положение с помощью пузырькового уровня и выполнение горизонтальной калибровки на акселерометре для устранения нулевого отклонения акселерометра.
[00075] Этап S2: сбор трехосных данных акселерометра за определенный промежуток времени, причем эти трехосные данные записывают в виде 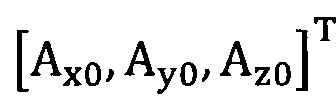 , нулевое отклонение записывают в виде
, нулевое отклонение записывают в виде 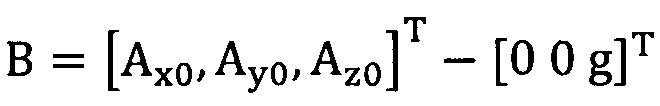 .
.
[00076] Этап S3: калибровка нулевого отклонения, масштабного коэффициента и неортогонального угла между осями акселерометра системы измерения пространственного положения по модели аппроксимации эллипсоида;
На этапе S3: калибровка нулевого отклонения, масштабного коэффициента и неортогонального угла между осями акселерометра системы измерения пространственного положения по модели аппроксимации эллипсоида дополнительно включает следующие этапы:
подстановку вектора параметра аппроксимируемого эллипсоида, который можно записать как 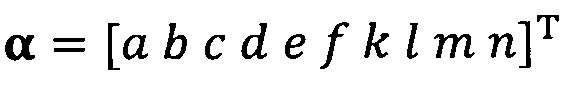 ;
;
подстановку числа n итераций калибровки, разложение первого значения 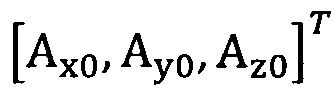 , полученного от акселерометра, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде
, полученного от акселерометра, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде 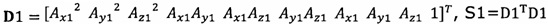 ;
;
если число раз сбора трехосных данных акселерометра не достигло значения n, обновление матрицы S с использованием вновь собранных данных акселерометра Dk, причем 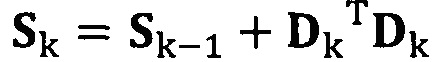 ;
;
после вычисления матрицы S, введение матрицы С ограничения эллипсоида и одновременное разложение матрицы S на блоки, причем
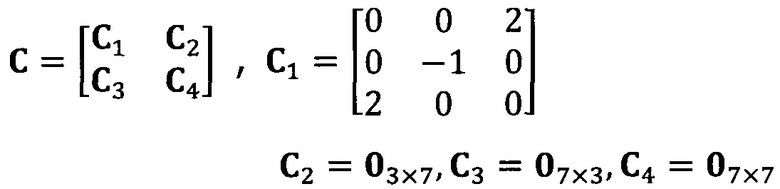
разложение матрицы S на блоки:
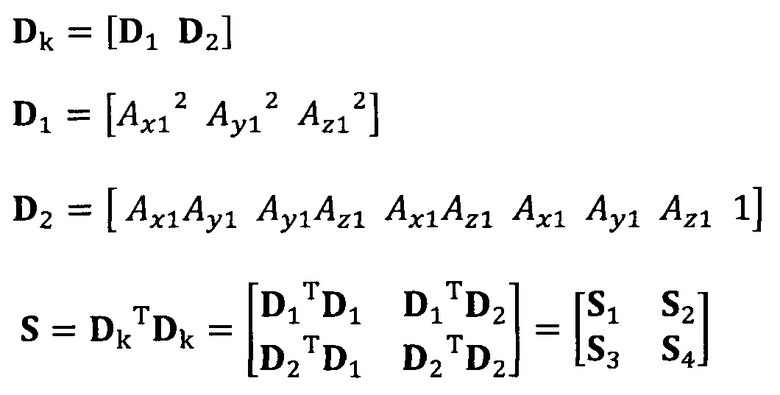
вычисление вектора аппроксимации эллипсоида с помощью следующих уравнений:
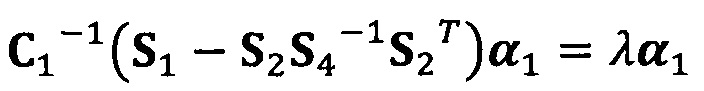
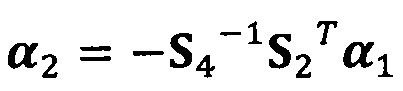 ;
;
после вычисления α1 вычисление α2 с помощью вышеприведенных уравнений для вычисления каждого параметра вектора аппроксимации эллипсоида, причем 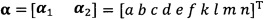 ;
;
кроме того, с учетом фактического физического соответствия трехосные масштабные коэффициенты kx, ky, kz, неортогональные углы между осями δxy, δyz, δxz и остаточные нулевые отклонения bx, by,bz могут быть вычислены с помощью следующих уравнений:

[00077] В вышеприведенных уравнениях α1 представляет собой собственный вектор, соответствующий максимальному собственному значению матрицы 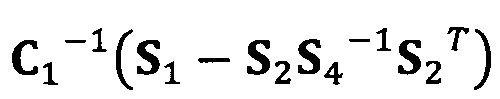 . Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
. Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
Если принять, что 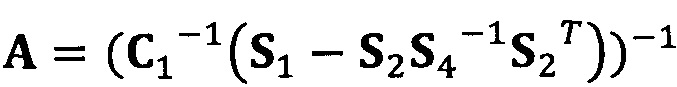 , взят вектор начальной итерации
, взят вектор начальной итерации 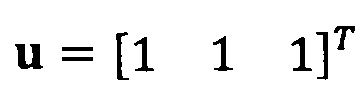 и задана точность итерации ε=1е-6;
и задана точность итерации ε=1е-6;
проводят разложение LU по А, а именно, А=LU;
решают систему линейных уравнений:
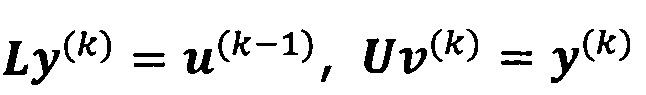
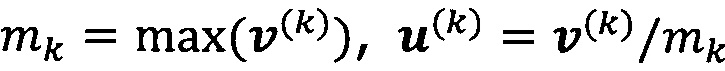
если 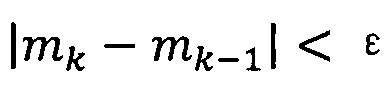 , пропускают итерацию и прекращают вычисление, причем
, пропускают итерацию и прекращают вычисление, причем 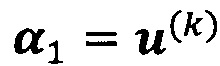 ; иначе k=k+1 и вычисление продолжают.
; иначе k=k+1 и вычисление продолжают.
[00078] Вообще говоря, если принять во внимание ε=1е-6, эта точность может быть достигнута менее, чем за 5 итераций итерационного вычисления.
[00079] Этап S4: корректирование, после сбора новых данных акселерометра, вновь собранных данных с применением параметра эллипсоида.
[00080] Этап S5: компенсация исходных данных акселерометра с помощью вычисленного параметра эллипсоида.
[00081] Этап S6: калибровка электронного компаса по модели аппроксимации эллипсоида в соответствии со скомпенсированными данными акселерометра;
На этапе S6: калибровка электронного компаса по модели аппроксимации эллипсоида в соответствии со скомпенсированными данными акселерометра дополнительно включает следующие этапы:
подстановку вектора параметра аппроксимируемого эллипсоида, который можно записать как 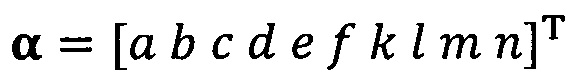 ;
;
сбор трехосных данных электронного компаса за определенный промежуток времени и проведение операции обработки собранных данных для недопущения переполнения, причем трехосные данные записывают в виде 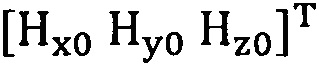 ;
;
подстановку числа n итераций калибровки, разложение первого значения 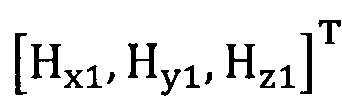 , полученного от электронного компаса, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде
, полученного от электронного компаса, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде 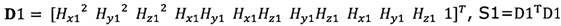 ;
;
если число раз сбора трехосных данных электронного компаса не достигло значения n, обновление матрицы S с использованием вновь собранных данных компаса Dk, причем 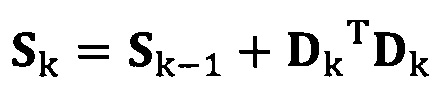 ;
;
после вычисления матрицы S введение матрицы С ограничения эллипсоида и одновременное разложение матрицы S на блоки, причем
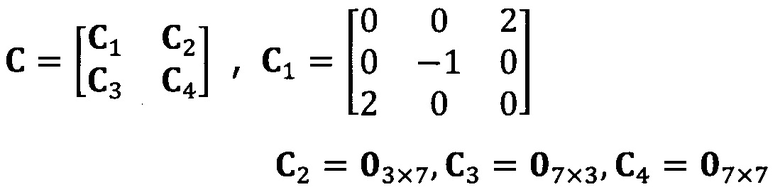
разложение матрицы S на блоки:
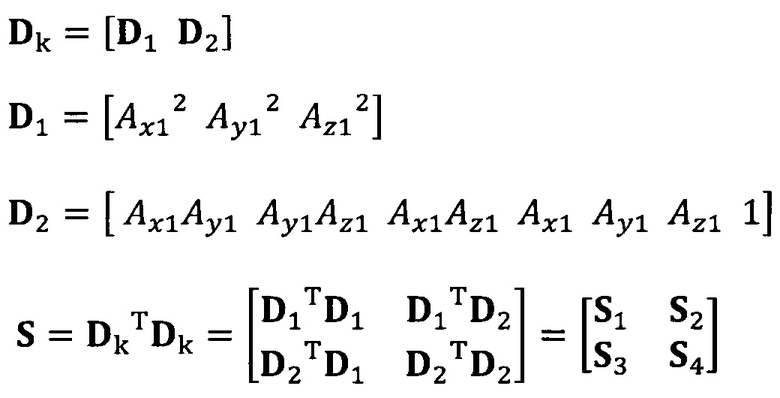
вычисление вектора аппроксимации эллипсоида с помощью следующих уравнений:
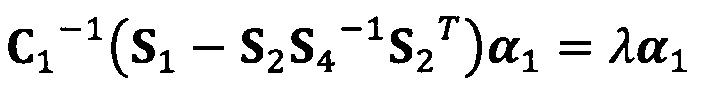
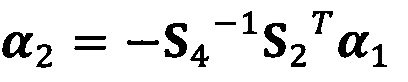 ;
;
после вычисления α1, вычисление α2 с помощью вышеприведенных уравнений для вычисления каждого параметра вектора аппроксимации эллипсоида, причем 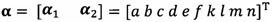 ;
;
кроме того, с учетом фактического физического соответствия трехосные масштабные коэффициенты kx, ky, kz, неортогональные углы между осями δxy, δyz, δxz и остаточные нулевые отклонения bx, by, bz могут быть вычислены с помощью следующих уравнений:
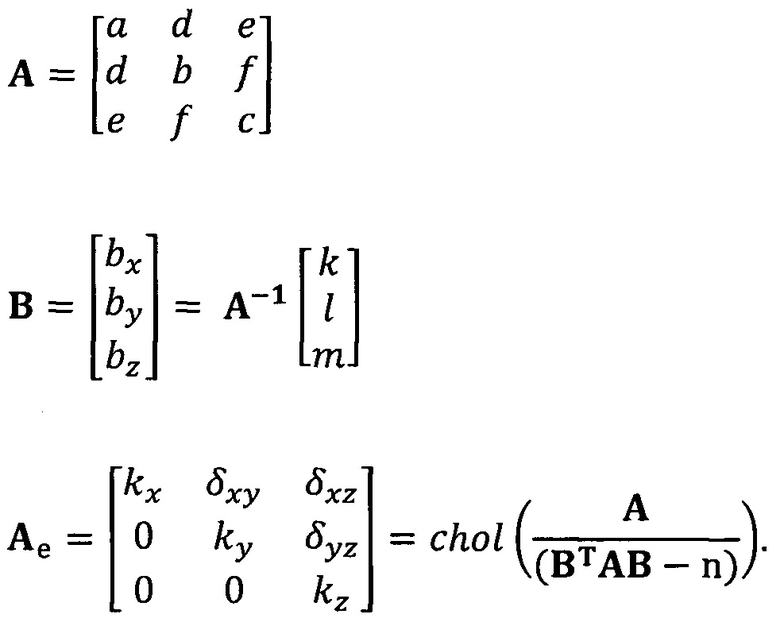
[00082] В вышеприведенных уравнениях α1 представляет собой собственный вектор, соответствующий максимальному собственному значению матрицы 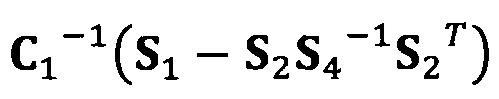 . Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
. Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
Если принять, что 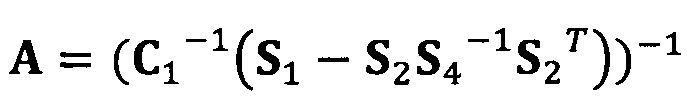 , взят вектор начальной итерации
, взят вектор начальной итерации 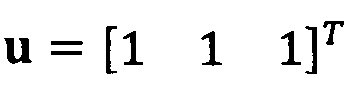 и задана точность итерации ε=1е-6;
и задана точность итерации ε=1е-6;
проводят разложение LU по А, а именно, А=LU;
решают систему линейных уравнений:
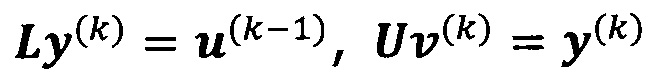
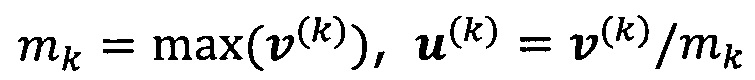
если 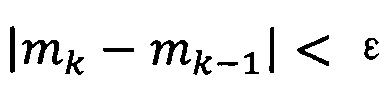 , пропускают итерацию и прекращают вычисление, причем
, пропускают итерацию и прекращают вычисление, причем 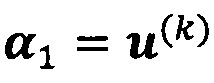 ; иначе k=k+1 и вычисление продолжают.
; иначе k=k+1 и вычисление продолжают.
[00083] Вообще говоря, если принять во внимание ε=1е-6, эта точность может быть достигнута менее, чем за 5 итераций итерационного вычисления.
[00084] Этап S7: компенсация исходных данных электронного компаса с помощью вычисленного параметра эллипсоида.
[00085] Этап S8: корректирование, после сбора новых данных электронного компаса, вновь собранных данных с применением параметра эллипсоида.
[00086] Этап S9: вычисление пространственного положения на основании скомпенсированных данных акселерометра и скомпенсированных данных электронного компаса.
[00087] Этап S10: обновление параметра эллипсоида с использованием данных измерений во время осуществления измерения для электронного компаса с целью повышения точности параметра эллипсоида.
Вариант осуществления 7
[00088] На фиг. 7 представлен способ прецизионной калибровки системы измерения пространственного положения. Способ прецизионной калибровки системы измерения пространственного положения включает следующие этапы:
Этап S1: проведение горизонтальной калибровки на акселерометре для устранения первоначального нулевого отклонения акселерометра;
установка устройства измерения пространственного положения в горизонтальное положение с помощью пузырькового уровня и выполнение горизонтальной калибровки на акселерометре для устранения нулевого отклонения акселерометра.
[00089] Этап S2: сбор трехосных данных акселерометра за определенный промежуток времени, причем эти трехосные данные записывают в виде 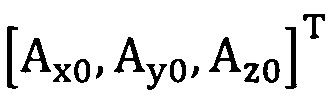 , нулевое отклонение записывают в виде
, нулевое отклонение записывают в виде 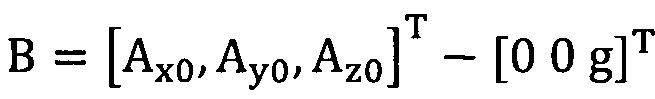 .
.
[00090] Этап S3: калибровка нулевого отклонения, масштабного коэффициента и неортогонального угла между осями акселерометра системы измерения пространственного положения по модели аппроксимации эллипсоида;
На этапе S3: калибровка нулевого отклонения, масштабного коэффициента и неортогонального угла между осями акселерометра системы измерения пространственного положения по модели аппроксимации эллипсоида дополнительно включает следующие этапы:
подстановку вектора параметра аппроксимируемого эллипсоида, который можно записать как 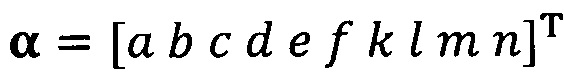 ;
;
подстановку числа n итераций калибровки, разложение первого значения 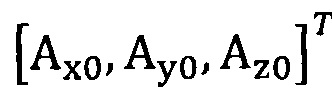 , полученного от акселерометра, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде
, полученного от акселерометра, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде 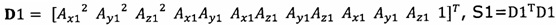 ;
;
если число раз сбора трехосных данных акселерометра не достигло значения n, обновление матрицы S с использованием вновь собранных данных акселерометра Dk, причем 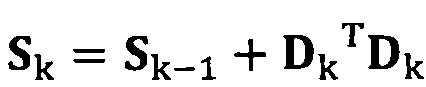 ;
;
после вычисления матрицы S, введение матрицы С ограничения эллипсоида и одновременное разложение матрицы S на блоки, причем
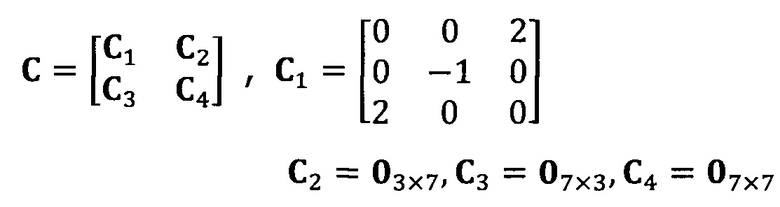
разложение матрицы S на блоки:
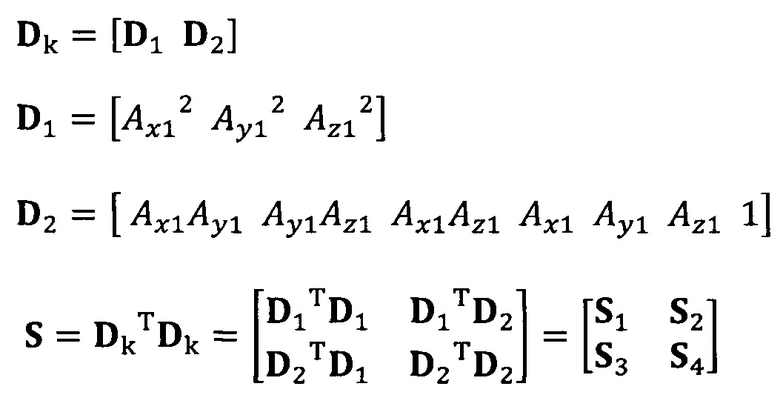
вычисление вектора аппроксимации эллипсоида с помощью следующих уравнений:
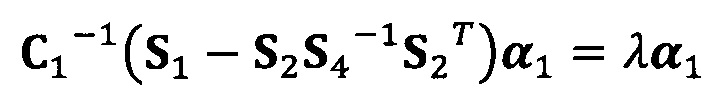
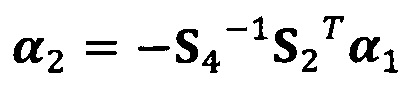 ;
;
после вычисления α1 вычисление α2 с помощью вышеприведенных уравнений для вычисления каждого параметра вектора аппроксимации эллипсоида, причем 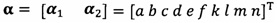 ;
;
кроме того, с учетом фактического физического соответствия трехосные масштабные коэффициенты kx, ky, kz, неортогональные углы между осями δxy, δyz, δxz и остаточные нулевые отклонения bx, by, bz могут быть вычислены с помощью следующих уравнений:
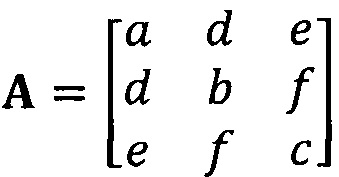
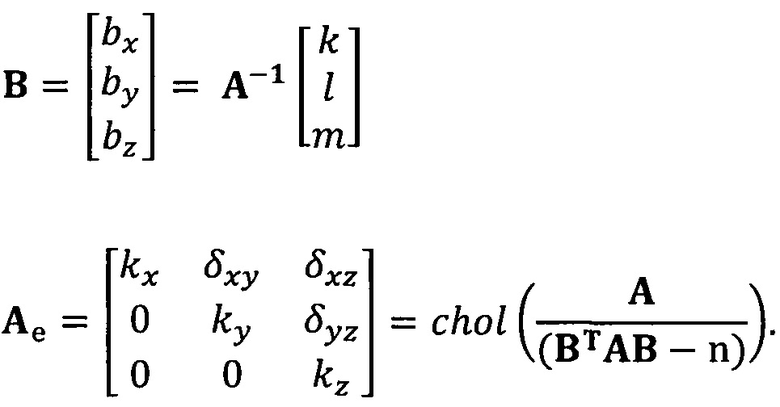
[00091] В вышеприведенных уравнениях α1 представляет собой собственный вектор, соответствующий максимальному собственному значению матрицы 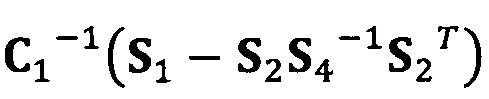 . Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
. Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
Если принять, что 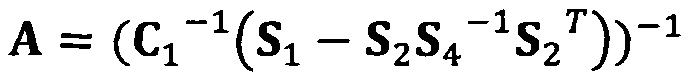 , взят вектор начальной итерации
, взят вектор начальной итерации 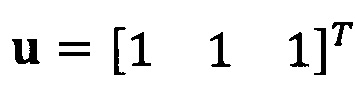 и принята точность итерации ε=1е-6;
и принята точность итерации ε=1е-6;
проводят разложение LU по А, а именно, А=LU;
решают систему линейных уравнений:
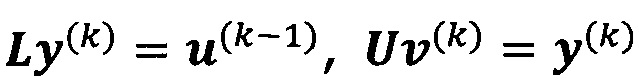
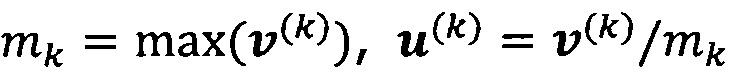
если 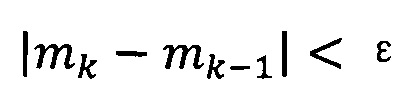 , пропускают итерацию, чтобы прекратить вычисление, причем
, пропускают итерацию, чтобы прекратить вычисление, причем 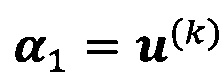 ; иначе k=k+1 и вычисление продолжают.
; иначе k=k+1 и вычисление продолжают.
[00092] Вообще говоря, если принять во внимание ε=1е-6, эта точность может быть достигнута менее, чем за 5 итераций итерационного вычисления.
[00093] Этап S4: корректирование, после сбора новых данных акселерометра, вновь собранных данных с применением параметра эллипсоида.
[00094] Этап S5: компенсация исходных данных акселерометра с помощью вычисленного параметра эллипсоида.
[00095] Этап S6: калибровка электронного компаса по модели аппроксимации эллипсоида в соответствии со скомпенсированными данными акселерометра;
На этапе S6: калибровка электронного компаса по модели аппроксимации эллипсоида в соответствии со скомпенсированными данными акселерометра дополнительно включает следующие этапы:
подстановку вектора параметра аппроксимируемого эллипсоида, который можно записать как 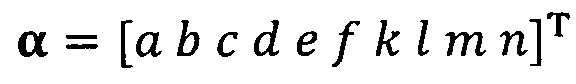 ;
;
сбор трехосных данных электронного компаса за определенный промежуток времени и проведение операции обработки собранных данных для недопущения переполнения, причем трехосные данные записывают в виде 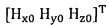 ;
;
подстановку числа n итераций калибровки, разложение первого значения 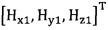 , полученного от электронного компаса, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде
, полученного от электронного компаса, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде 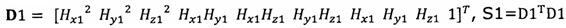 ;
;
если число раз сбора трехосных данных электронного компаса не достигло значения n, обновление матрицы S с использованием вновь собранных данных компаса Dk, причем 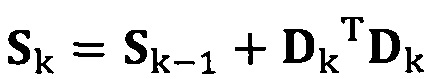 ;
;
после вычисления матрицы S введение матрицы С ограничения эллипсоида и одновременное разложение матрицы S на блоки, причем
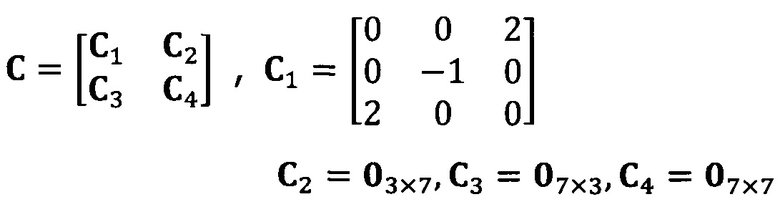
разложение матрицы S на блоки:
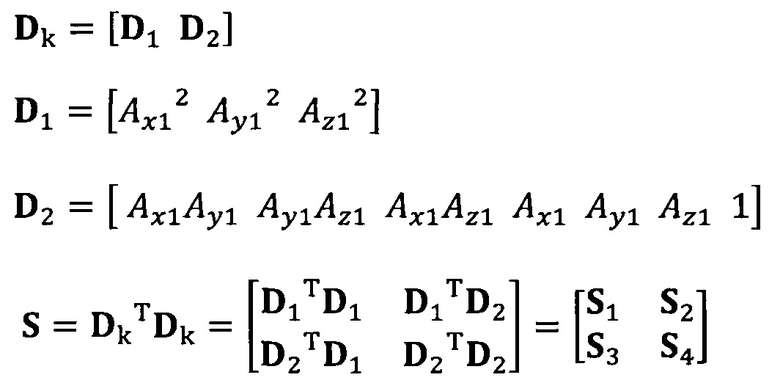
вычисление вектора аппроксимации эллипсоида с помощью следующих уравнений:
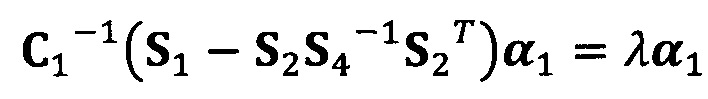
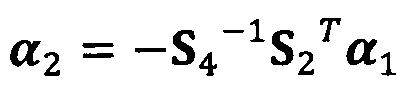 ;
;
после вычисления α1, вычисление α2 с помощью вышеприведенных уравнений для вычисления каждого параметра вектора аппроксимации эллипсоида, причем 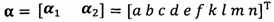 ;
;
кроме того, с учетом фактического физического соответствия трехосные масштабные коэффициенты kx, ky, kz, неортогональные углы между осями δxy, δyz, δxz и остаточные нулевые отклонения bx, by, bz могут быть вычислены с помощью следующих уравнений:

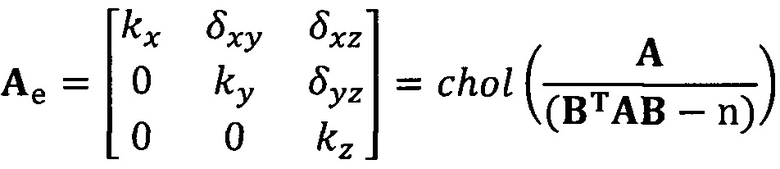
[00096] В вышеприведенных уравнениях α1 представляет собой собственный вектор, соответствующий максимальному собственному значению матрицы 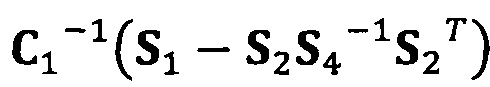 . Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
. Таким образом, при практическом вычислении не нужно вычислять все собственные значения и собственные векторы. Даже нет необходимости в вычислении собственных значений. Для вычисления максимального собственного вектора применим лишь степенной способ или обратный степенной способ. В качестве примера взят обратный степенной способ:
Если принять, что 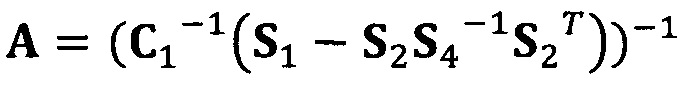 , взят вектор начальной итерации
, взят вектор начальной итерации 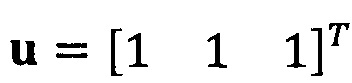 , задана точность итерации ε=1e-6;
, задана точность итерации ε=1e-6;
проводят разложение LU по А, а именно, А=LU;
решают систему линейных уравнений:
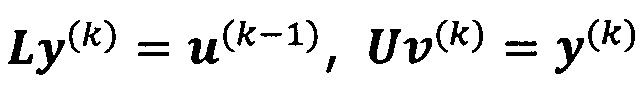
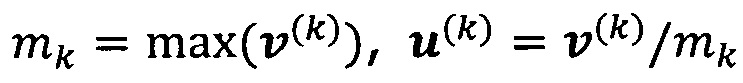
если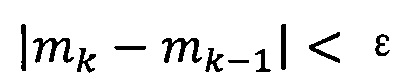 , пропускают итерацию, чтобы прекратить вычисление, причем
, пропускают итерацию, чтобы прекратить вычисление, причем 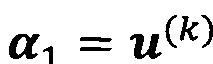 ; иначе k=k+1 и вычисление продолжают.
; иначе k=k+1 и вычисление продолжают.
[00097] Вообще говоря, если принять во внимание ε=1е-6, эта точность может быть достигнута менее, чем за 5 итераций итерационного вычисления.
[00098] Этап S7: компенсация исходных данных электронного компаса с помощью вычисленного параметра эллипсоида.
[00099] Этап S8: корректирование, после сбора новых данных электронного компаса, вновь собранных данных с применением параметра эллипсоида.
[000100] Этап S9: вычисление пространственного положения на основании скомпенсированных данных акселерометра и скомпенсированных данных электронного компаса.
[000101] Этап S10: удаление пропущенной расчетной точки в собранных данных электронного компаса с применением статистического правила.
[000102] Этап S11: обновление параметра эллипсоида с использованием данных измерений во время осуществления измерения для электронного компаса с целью повышения точности параметра эллипсоида.
[000103] Преимущества настоящего изобретения заключаются в следующем. Способ аппроксимации эллипсоида используют для калибровки электронного компаса и улучшения системы измерения пространственного положения. Таким образом, он позволяет эффективно устранять проблемы случайной выдачи датчиком неправильных данных и перескакиваний, благодаря чему фактически гарантируется надежность результата калибровки. Рекурсивную обработку выполняют в алгоритме аппроксимации эллипсоида таким образом, что устраняется необходимость хранения внутренним ЦП системы измерения пространственного положения данных всех точек, собранных ранее датчиком во время обработки данных. Необходимо сохранять лишь матрицу, полученную ранее путем рекурсии, и текущие результаты измерения. Таким образом, в той же аппаратной среде способ аппроксимации эллипсоида позволяет обрабатывать больше значений, в результате чего повышается точность аппроксимации эллипсоида. Соответственно, в случае использования обычного алгоритма аппроксимации для недопущения переполнения стека памяти в процессе эксплуатации ЦП может выполнять операцию аппроксимации лишь в нескольких точках выборки. В результате этого точность аппроксимации ограничивается. Настоящее изобретение улучшает крупномасштабное применение матрицы в алгоритме аппроксимации эллипсоида и оптимизирует процедуру вычисления, что позволяет сократить объем вычислений аппроксимации эллипсоида более чем на 90 процентов. Если в качестве примера взять программу MATLAB, основанную на традиционном алгоритме, одноразовое выполнение алгоритма аппроксимации займет 563 мс. Для сравнения, выполнение усовершенствованного алгоритма занимает всего 14 мс. Применена стратегия, в которой для калибровки используют данные измерений, благодаря чему повышается отказоустойчивость во время калибровки. Таким образом, требования, касающиеся начальной калибровки, снижаются и уменьшается сложность эксплуатации для пользователя.
[000104] Вышеупомянутое раскрытие представляет собой лишь конкретный вариант осуществления настоящего изобретения. Однако объем защиты настоящего изобретения не ограничен ним. Специалисты в данной области техники легко смогут предложить изменения или замены в пределах раскрытого объема, которые, как предполагается, входят в объем защиты настоящего изобретения. Таким образом, объем защиты настоящего изобретения входят в объем защиты прилагаемой формулы изобретения.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ повышения точности калибровки масштабных коэффициентов и углов неортогональности осей чувствительности блока датчиков ДУС | 2019 |
|
RU2718142C1 |
| Способ определения коэффициентов калибровки интегрированного блока датчиков | 2017 |
|
RU2655053C1 |
| Способ повышения точности калибровки блока микромеханических датчиков угловой скорости | 2019 |
|
RU2727344C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОШИБОК ОРИЕНТАЦИИ ИЗМЕРИТЕЛЬНЫХ ОСЕЙ ЛАЗЕРНЫХ ГИРОСКОПОВ И МАЯТНИКОВЫХ АКСЕЛЕРОМЕТРОВ В БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЕ | 2018 |
|
RU2683144C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ И КОМПЕНСАЦИИ МАГНИТНОЙ ДЕВИАЦИИ ИНКЛИНОМЕТРА | 2000 |
|
RU2186966C2 |
| СПОСОБ ЭКСПЛУАТАЦИОННОЙ КАЛИБРОВКИ ТРЕХОСЕВОГО ЭЛЕКТРОННОГО КОМПАСА С КОМПЕНСАЦИЕЙ СМЕЩЕНИЯ ОСЕЙ | 2020 |
|
RU2755400C1 |
| СПОСОБ АВТОНОМНОЙ ОРИЕНТАЦИИ ПОДВИЖНЫХ ОБЪЕКТОВ | 2017 |
|
RU2653967C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НЕОРТОГОНАЛЬНОСТИ ОСЕЙ ЧУВСТВИТЕЛЬНОСТИ ЛАЗЕРНОГО ГИРОСКОПА | 2019 |
|
RU2727318C1 |
| СПОСОБ АВТОНОМНОЙ ИНЕРЦИАЛЬНОЙ ОРИЕНТАЦИИ ПОДВИЖНЫХ ОБЪЕКТОВ | 2022 |
|
RU2800846C1 |
| СПОСОБ БЕСПЛАТФОРМЕННОЙ ОРИЕНТАЦИИ ПОДВИЖНЫХ ОБЪЕКТОВ | 2022 |
|
RU2784859C1 |
Настоящее изобретение относится к области устройств измерения пространственного положения, в частности к способу прецизионной калибровки систем измерения пространственного положения. Способ прецизионной калибровки систем измерения пространственного положения включает следующие этапы: калибровку нулевого отклонения, масштабного коэффициента и неортогонального угла между осями акселерометра в системе измерения пространственного положения по модели (S1) аппроксимации эллипсоида; компенсацию исходных данных акселерометра с использованием вычисленного параметра (S2) эллипсоида; калибровку электронного компаса по модели аппроксимации эллипсоида на основании скомпенсированных данных (S3) акселерометра; компенсацию исходных данных электронного компаса с помощью вычисленного параметра (S4) эллипсоида; вычисление пространственного положения на основании скомпенсированных данных акселерометра и скомпенсированных данных электронного компаса (S5). Технический результат заявленного изобретения – обеспечение надежного результата калибровки и высокой точности при меньших затратах времени на калибровку. 8 з.п. ф-лы, 7 ил.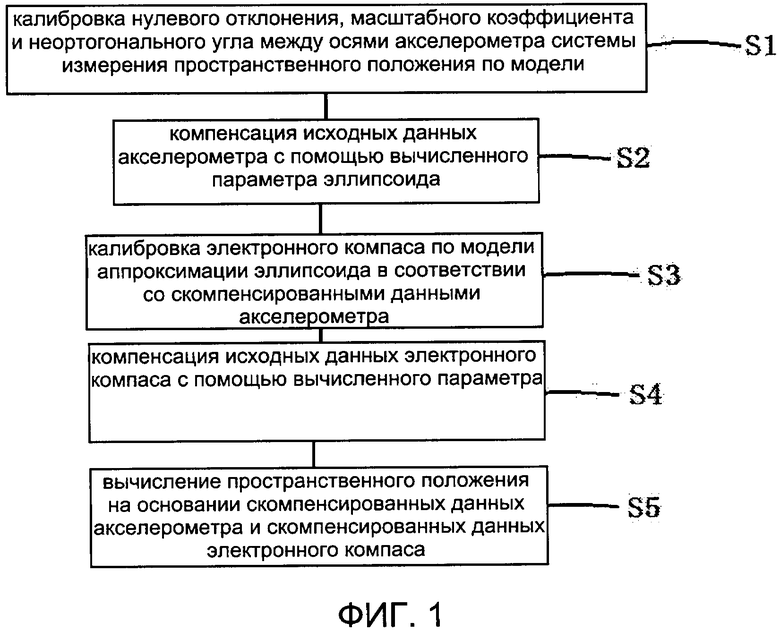
1. Способ прецизионной калибровки системы измерения пространственного положения, отличающийся тем, что он включает следующие этапы:
калибровка нулевого отклонения, масштабного коэффициента и неортогонального угла между осями акселерометра системы измерения пространственного положения по модели аппроксимации эллипсоида;
компенсация исходных данных акселерометра с использованием вычисленного параметра эллипсоида;
калибровка электронного компаса по модели аппроксимации эллипсоида в соответствии со скомпенсированными данными акселерометра;
компенсация исходных данных электронного компаса с помощью вычисленного параметра эллипсоида и
вычисление пространственного положения на основании скомпенсированных данных акселерометра и скомпенсированных данных электронного компаса.
2. Способ прецизионной калибровки системы измерения пространственного положения по п. 1, отличающийся тем, что перед этапом калибровки нулевого отклонения, масштабного коэффициента и неортогонального угла между осями акселерометра системы измерения пространственного положения по модели аппроксимации эллипсоида выполняют следующий этап:
выполнение горизонтальной калибровки на акселерометре для устранения исходного нулевого отклонения акселерометра.
3. Способ прецизионной калибровки системы измерения пространственного положения по п. 2, отличающийся тем, что после этапа выполнения горизонтальной калибровки на акселерометре для устранения исходного нулевого отклонения акселерометра выполняют следующий этап:
сбор трехосных данных акселерометра за определенный промежуток времени, причем эти трехосные данные записывают в виде 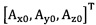 , а нулевое отклонение записывают в виде
, а нулевое отклонение записывают в виде 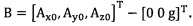
4. Способ прецизионной калибровки системы измерения пространственного положения по п. 3, отличающийся тем, что этап калибровки нулевого отклонения, масштабного коэффициента и неортогонального угла между осями акселерометра системы измерения пространственного положения по модели аппроксимации эллипсоида также включает следующие этапы:
подстановка вектора параметра аппроксимируемого эллипсоида, записанного как 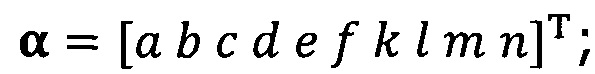
подстановка числа n итераций калибровки, разложение первого значения 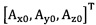 , полученного от акселерометра, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде
, полученного от акселерометра, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде 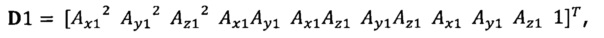 S1=D1TD1;
S1=D1TD1;
если число раз сбора трехосных данных акселерометра не достигло значения n, обновление матрицы S с использованием вновь собранных данных акселерометра Dk, причем Sk=Sk-1+DkTDk;
после вычисления матрицы S введение матрицы С ограничения эллипсоида и одновременное разложение матрицы S на блоки, причем
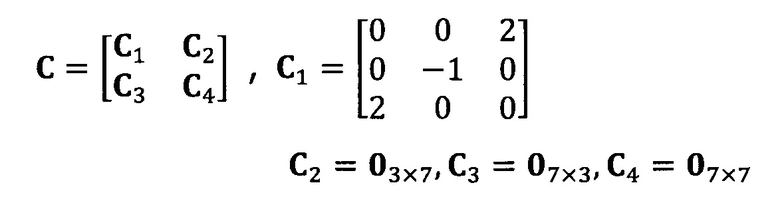
разложение матрицы S на блоки:
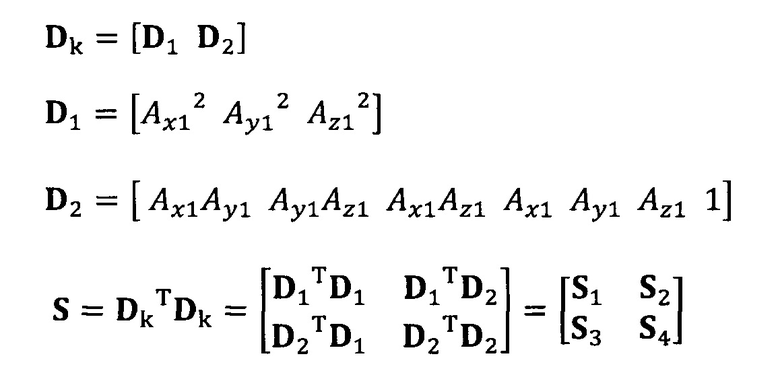
вычисление вектора аппроксимации эллипсоида с помощью следующих уравнений:
C1-1(S1-S2S4-1S2T)α1=λα1
α2=-S4-1S2Tα1;
после вычисления α1 вычисление α2 с помощью вышеприведенных уравнений для вычисления каждого параметра вектора аппроксимации эллипсоида, причем 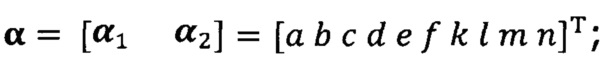
кроме того, с учетом фактического физического соответствия трехосные масштабные коэффициенты kx, ky, kz, неортогональные углы между осями δxy, δyz, δxz и остаточные нулевые отклонения bx, by, bz могут быть вычислены с помощью следующих уравнений:
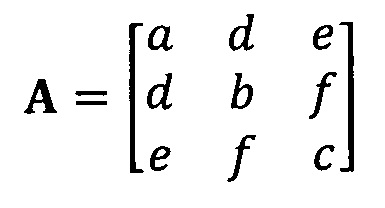
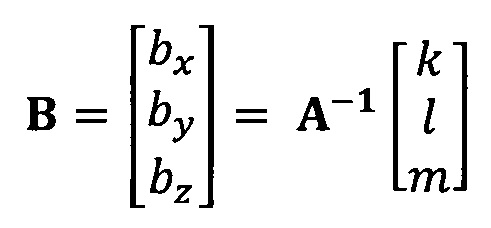
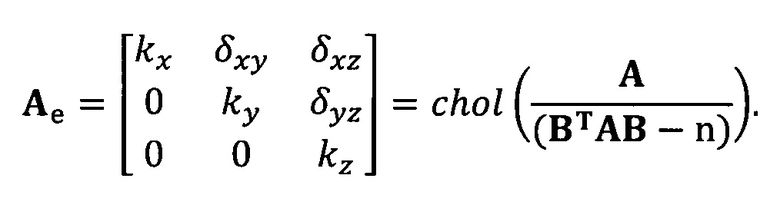
5. Способ прецизионной калибровки системы измерения пространственного положения по п. 4, отличающийся тем, что после этапа калибровки нулевого отклонения, масштабного коэффициента и неортогонального угла между осями акселерометра системы измерения пространственного положения по модели аппроксимации эллипсоида выполняют следующий этап:
после сбора новых данных акселерометра корректирование вновь собранных данных с применением параметра эллипсоида.
6. Способ прецизионной калибровки системы измерения пространственного положения по п. 5, отличающийся тем, что этап калибровки электронного компаса по модели аппроксимации эллипсоида на основании скомпенсированных данных акселерометра дополнительно включает следующие этапы:
подстановку вектора параметра аппроксимируемого эллипсоида, записанного как 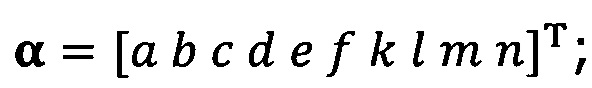
сбор трехосных данных электронного компаса за определенный промежуток времени и проведение операции обработки собранных данных для недопущения переполнения, причем трехосные данные записывают в виде 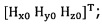
подстановку числа n итераций калибровки, разложение первого значения 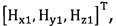 полученного от электронного компаса, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде
полученного от электронного компаса, в десятимерный вектор-столбец D1 и вычисление матрицы S1, причем D1 записывают в виде 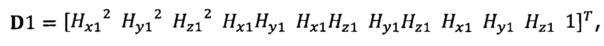 причем S1=D1TD1;
причем S1=D1TD1;
если число раз сбора трехосных данных электронного компаса не достигло значения n, обновление матрицы S с использованием вновь собранных данных электронного компаса Dk, причем Sk=Sk-1+DkTDk;
после вычисления матрицы S введение матрицы С ограничения эллипсоида и одновременное разложение матрицы S на блоки, причем
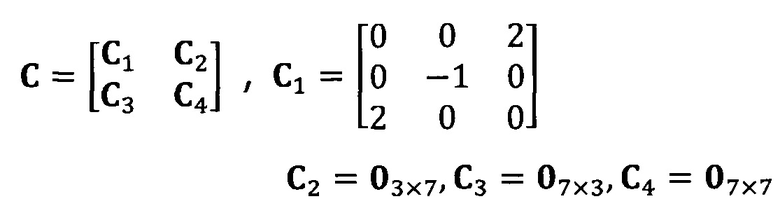
разложение матрицы S на блоки:
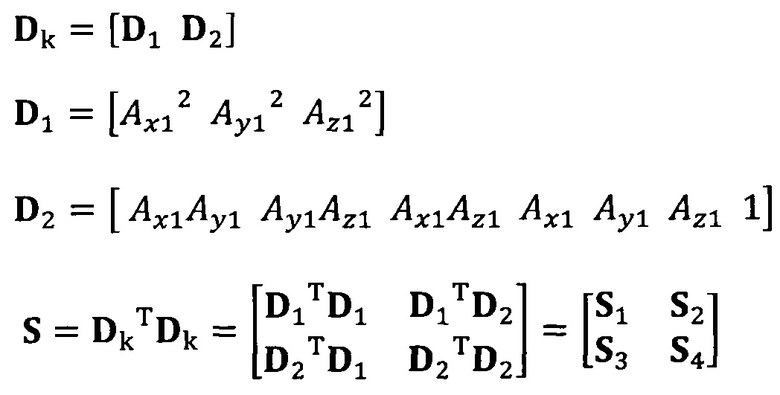
вычисление вектора аппроксимации эллипсоида с помощью следующих уравнений:
C1-1(S1-S2S4-1S2T)α1=λα1
α2=-S4-1S2Tα1;
после вычисления α1 вычисление α2 с помощью вышеприведенных уравнений для вычисления каждого параметра вектора аппроксимации эллипсоида, причем 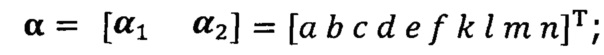
кроме того, с учетом фактического физического соответствия трехосные масштабные коэффициенты kx, ky, kz, неортогональные углы между осями δxy, δyz, δxz и остаточные нулевые отклонения bx, by, bz могут быть вычислены с помощью следующих уравнений:
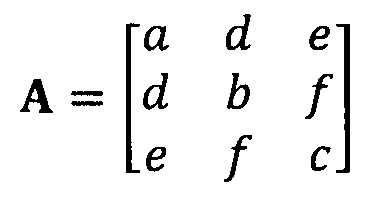
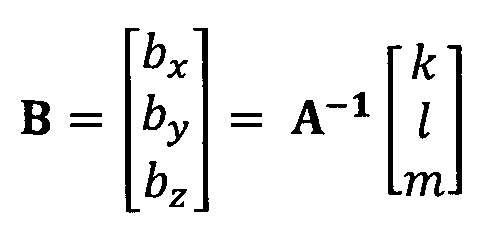
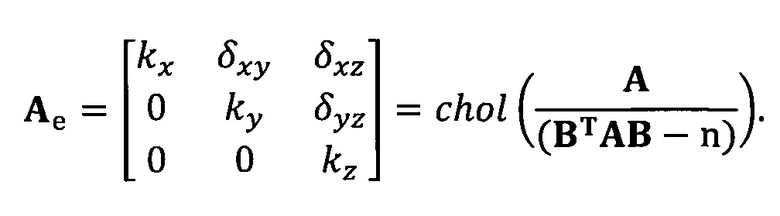
7. Способ прецизионной калибровки системы измерения пространственного положения по п. 6, отличающийся тем, что после выполнения этапа калибровки электронного компаса на основании скомпенсированных данных акселерометра по модели аппроксимации эллипсоида выполняют следующий этап:
после сбора новых данных электронного компаса выполняют корректирование вновь собранных данных с применением параметра эллипсоида.
8. Способ прецизионной калибровки системы измерения пространственного положения по п. 7, отличающийся тем, что после осуществления этапа вычисления пространственного положения на основании скомпенсированных данных акселерометра и скомпенсированных данных электронного компаса выполняют следующий этап:
обновление параметра эллипсоида с помощью электронного компаса с использованием данных измерений во время осуществления измерения с целью повышения точности параметра эллипсоида.
9. Способ прецизионной калибровки системы измерения пространственного положения по п. 8, отличающийся тем, что перед осуществлением этапа обновления параметра эллипсоида с помощью электронного компаса с использованием данных измерений во время осуществления измерения с целью повышения точности параметра эллипсоида выполняют следующий этап:
удаление пропущенной расчетной точки из собранных данных электронного компаса с применением статистического правила.
| US 7451549 B1, 18.11.2008 | |||
| WO 1998048292 A2, 29.10.1998 | |||
| WO 2013112230 A1, 01.08.2013 | |||
| US 7376507 B1, 20.05.2008 | |||
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ ПОДВИЖНЫХ ОБЪЕКТОВ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 1996 |
|
RU2098764C1 |
Авторы
Даты
2018-07-26—Публикация
2016-07-04—Подача