Изобретение относится к области бортового приборостроения и автоматики и может быть использовано для решения задач автономной ориентации при управлении наземными, плавающими, летательными, баллистическими и космическими аппаратами в околоземном пространстве.
При решении задач пространственной ориентации подвижных объектов (ПО) в околоземном пространстве предпочтение отдают способам автономной ориентации, соответствующим бесплатформенным технологиям [1, 2].
Известен геометрический способ автономной ориентации ПО в околоземном пространстве на основе использования платформенных гироскопических технологий [3, 4, 6].
В основу этого способа положены принципы физического воспроизведения (геометрическим путем) в пространстве двух или трех базовых направлений отсчета с помощью гироскопических систем ориентации (ГСО). Схемы построения ГСО могут предполагать реализацию различных вариантов схемотехнических и конструктивных решений [3,4]:
- комбинации трехстепенных (свободных и корректируемых) гироскопов в кардановых подвесах (гироскопов направления, гирокомпасов, гирорбитантов, гировертикалей, гировертикантов и пр.),
- курсовертикалей гироскопических (КВГ),
- комбинации одноосных (ОГС) и двухосных (ДГС) гиростабилизаторов,
- трехосных индикаторных, силовых и индикаторно-силовых гиростабилизаторов (ТГС) с гиростабилизированными платформами (ГСП),
- систем трех и нескольких одноосных гиростабилизаторов (ОГС),
- гироазимутгоризонтов (ГАГ) на основе использования схем ОГС, ДГС, ТГС и др.
Во всех вариантах построения ГСО используют принцип физического моделирования отсчетных базисов, воспроизводимых материально с помощью трех ортов:

где 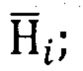 Hi - векторы кинетических моментов и их модули для i-ых гироскопов.
Hi - векторы кинетических моментов и их модули для i-ых гироскопов.
Для схем ГСО, построенных с учетом использования только двух гироскопов с кинетическими моментами 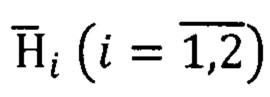 отсчетный базис
отсчетный базис 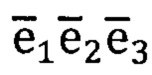 строят на основе следующих ортов:
строят на основе следующих ортов:
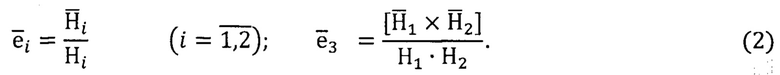
В общем случае отсчетная система координат, построенная на основе ортов 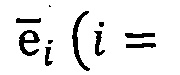
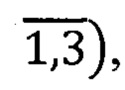 определяемых по формулам (1) или (2), для любой схемы ГСО представляет собой неортогональньш и нестационарный базис (в силу проявления геометрических свойств кардановых подвесов и свойств астатизма гироскопов).
определяемых по формулам (1) или (2), для любой схемы ГСО представляет собой неортогональньш и нестационарный базис (в силу проявления геометрических свойств кардановых подвесов и свойств астатизма гироскопов).
К недостаткам геометрического способа автономной ориентации ПО на основе использования ГСО следует отнести следующее:
- большие габариты и массы ГСО,
- необходимость проведения операций коррекций ГСО, т.к. гироскопы «уходят в пространстве» вследствие проявления их дрейфа, обусловленного свойством астатизма,
- использование ГСО на ПО накладывает некоторые ограничения на пространственные маневры объектов в силу проявления геометрических свойств выбиваемости гироскопов, обусловленных явлением «складывания рамок» кардановых подвесов.
Придание ГСО с кардановыми подвесами свойств устойчивости, невыбиваемости, пространственной всережимности и всеманевренности достигают путем усложнения схемо -технических и конструктивных решений (вводят дополнительную следящую раму, отрабатываемую в положение устойчивости гироскопа с помощью следящей системы, а также вводят коррекцию от дополнительных эталонных систем). Это усовершенствование приводит в еще большей степени к ухудшению габаритно-массовых характеристик ГСО, а также к снижению показателей технологичности, экономичности, надежности работы в эксплуатации.
Этот факт привел к тому, что в последние 20-30 лет специалисты в области управления ПО при решении задач пространственной автономной ориентации объектов предпочтение отдают бесплатформенным и бескардановым технологиям [1-6].
Известен способ автономной ориентации ПО в пространстве, основанный на формировании и обработке двухвекторной или трехвекторной информации, получаемой от пар или троек трехосных блоков гироскопов, акселерометров, магнитометров [6, 7].
В научно-технической литературе способ получил название способа аналитического горизонт-компасирования (АГК). Способ АГК реализуют в трех вариантах:
- двухвекторном АГК на основе инерциальной информации о векторах 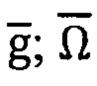 (g П - АГК),
(g П - АГК),
- двухвекторном АГК на основе магнито-интерциальной информации о векторах 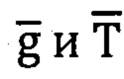 (g Т-АГК),
(g Т-АГК),
- трехвекторном комбинированном АГК на основе объединения двухвекторных способов (g Ω Т-АГК).
В вариантах способа АГК приняты обозначения векторов ГФП:
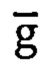 - вектора напряженности поля тяжести Земли (ПТЗ),
- вектора напряженности поля тяжести Земли (ПТЗ),
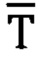 - вектора напряженности магнитного поля Земли (МПЗ),
- вектора напряженности магнитного поля Земли (МПЗ),
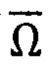 - вектора угловой скорости собственного суточного вращения Земли.
- вектора угловой скорости собственного суточного вращения Земли.
Во всех трех вариантах способа АГК информацию о векторе 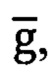 получаемую с помощью трехосных блоков акселерометров (ТБА), используют для решения задачи аналитического горизонтирования (АГ), т.е. задачи определения углов ϑ и γ отклонения ПО от плоскости горизонта аналитическим путем на основе алгоритмической обработки информации ТБА в связанном с объектом базисе m:
получаемую с помощью трехосных блоков акселерометров (ТБА), используют для решения задачи аналитического горизонтирования (АГ), т.е. задачи определения углов ϑ и γ отклонения ПО от плоскости горизонта аналитическим путем на основе алгоритмической обработки информации ТБА в связанном с объектом базисе m:

Компоненты вектора, отнесенного к осям географического базиса
q=NHE (N - направление на Север, Н - направление вертикали места,
Е - направление на Восток) вычисляют на основе использования основного уравнения гравиметрии [8]:
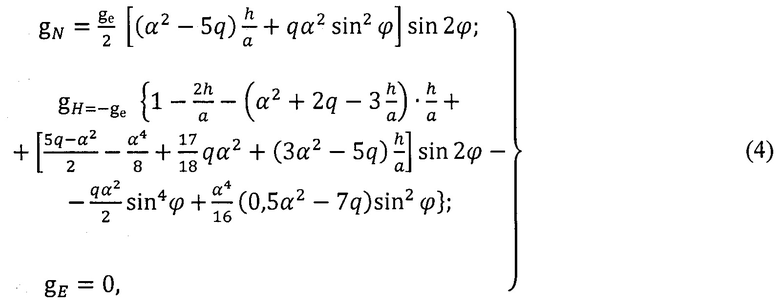
где ge - ускорение свободно падающего тела на экваторе,
ge=9,7803267715 м/с2,
а -большая полуось референц-эллипсоида фигуры Земли,
а=6378245, м,
h -географическая высота, h=r-R,
R - средний радиус Земли, R=6378211 м,
а2 - квадрат эксцентриситета сжатия Земли.

b - малая полуось фигуры Земли, b=6356863 м,
ϕ - географическая широта точки наблюдения,
q - отношение центростремительного ускорения к ускорению на экваторе:

Ω - угловая скорость вращения Земли, Ω=7,292116557⋅10-5c-1
Радиус-вектор 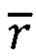 точки наблюдения с координатами ϕ, h вычисляют по формуле:
точки наблюдения с координатами ϕ, h вычисляют по формуле:
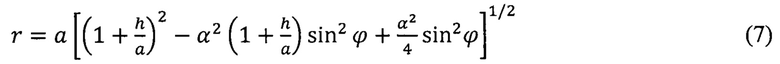
На основе компонент векторов 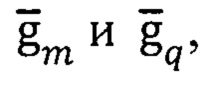 вычисленных по формулам (3), (4), формируют уравнение АГ:
вычисленных по формулам (3), (4), формируют уравнение АГ:
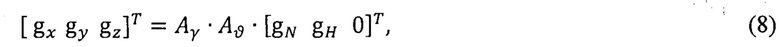
где АγАϑ - матрицы (3×3) углов крена γ и тангажа ϑ.
Путем решения скалярных уравнений, получаемых из векторно-матричного уравнения (8), формируют алгоритмы АГ:
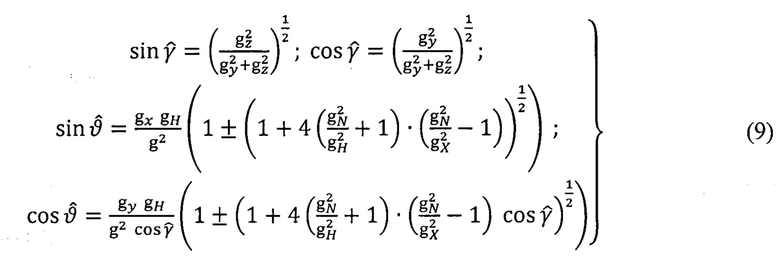
После решения задачи АГ составляют уравнения аналитического компасирования (АК) для двух вариантов:
- для аналитического компасирования инерциального (АКИ), (g Ω-АК),
- для магнитометрического аналитического компасирования (МАК), (g Т-АК).

где 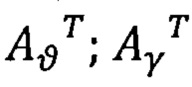 - транспонированные матрицы (3×3) углов тангажа и крена ПО,
- транспонированные матрицы (3×3) углов тангажа и крена ПО,
Тх, Ту, Tz - проекции вектора 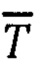 на оси связанного базиса m (определяют по показаниям трехосного блока магнитометров (ТБМ)),
на оси связанного базиса m (определяют по показаниям трехосного блока магнитометров (ТБМ)),
TN, ТH, ТE - проекции вектора 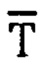 МПЗ на оси географического базиса q (вычисляют по модели нормального МПЗ [9]),
МПЗ на оси географического базиса q (вычисляют по модели нормального МПЗ [9]),
Аψ - матрица (3×3) курса ПО.
Уравнения АК (10) и (11) справедливы только в режиме неподвижности ПО (в режиме ZUPT), при котором выполняются соотношения (10) и условия для показаний ТБГ:
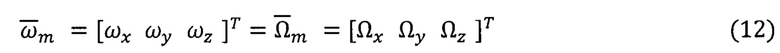
Из решений уравнений (10) и (11) получают алгоритмы АК (АКИ и МАК). Алгоритм АКИ (g Ω - вариант):
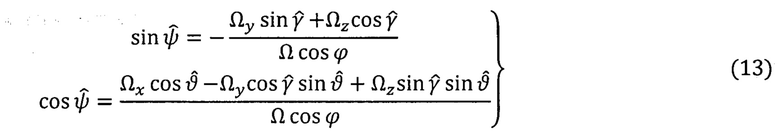
Алгоритм МАК (g Т - вариант):
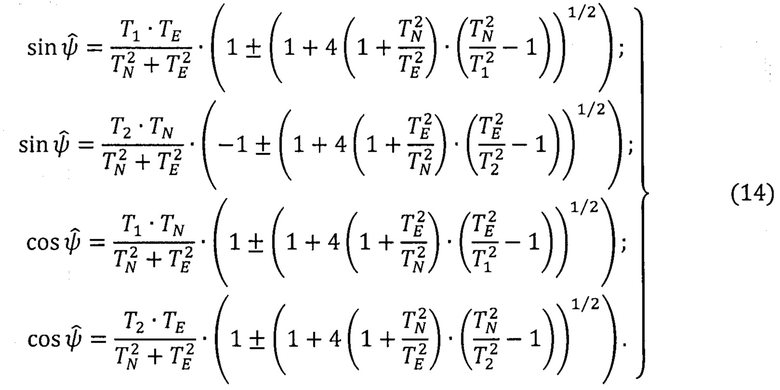
Причем
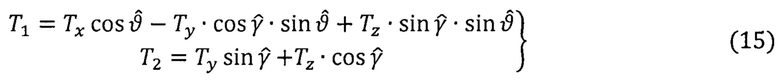
Для повышения точности решения задачи АГК, а также обеспечения условий всережимности и устойчивости алгоритмов иногда способы АКИ и МАК выполняют совместно в одном способе (комбинированный вариант АГК) с использованием расширенной магнито-инерциальной информации [9, 10, 11].
Способ ориентации инклинометра в составе подземного снаряда в скважине [11] включает измерение проекции на оси связанного базиса напряженности магнитного поля феррозондами, измерение проекции ускорения свободно падающего тела акселерометрами, измерение проекции угловой скорости вращения Земли гироскопами, преобразование первичных сигналов и определение углов пространственной ориентации объекта. При этом оценивают погрешность гироскопов с привлечением информации от спутниковой навигационной системы (СНС) и корректируют величины дрейфов гироскопов с учетом информации от феррозондов. Причем при отсутствии магнитных аномалий вычисляют углы ориентации ПО по сигналам ТБМ 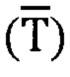 и ТБА
и ТБА 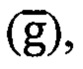 а при работе в средах с аномальными магнитными свойствами вычисляют параметры ориентации по сигналам ТБА
а при работе в средах с аномальными магнитными свойствами вычисляют параметры ориентации по сигналам ТБА 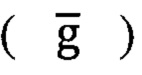 и ТБГ
и ТБГ 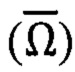 . Таким образом, обработку многомерной магнито-инерциальной информации
. Таким образом, обработку многомерной магнито-инерциальной информации 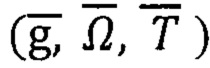 выполняют по схеме реконфигурации алгоритмов (g Ω-АГК или g Г-АГК).
выполняют по схеме реконфигурации алгоритмов (g Ω-АГК или g Г-АГК).
При отсутствии магнитных аномалий в среде реализуют схему g Т - АГК с помощью безгироскопного магнито-акселерометрического модуля (ТБМ+ТБА). При наличии же магнитных аномалий и при проявлении внешних магнитных помех реализуют автономную ориентацию по схеме gΩ-АГК с использованием только инерциальной информации (ТБА+ТБГ).
Общим недостатком способа АГК во всех вариантах (g Ω, g Т и g Ω Г) являются ограничения на условия использования измерительного модуля (ТБА, ТБМ, ТБГ) в виде требования выполнения режима остановки ПО (режима ZUPT).
Кроме того, алгоритмы АКИ (13) и МАК (14) вырождаются в районах географических (cos ϕ=0) и геомагнитных 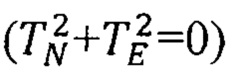 полюсов, а также не обеспечивают необходимой точности решения задачи автономной ориентации в околополярных районах (с географической широтой
полюсов, а также не обеспечивают необходимой точности решения задачи автономной ориентации в околополярных районах (с географической широтой 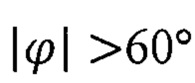 из-за близости векторов
из-за близости векторов 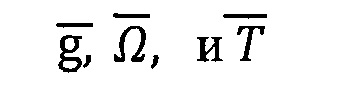 к условиям квазиколлинеарности
к условиям квазиколлинеарности 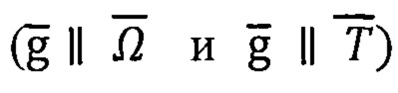 В этих же районах проявляется повышенная чувствительность алгоритмов АГК к погрешностям первичных измерений
В этих же районах проявляется повышенная чувствительность алгоритмов АГК к погрешностям первичных измерений 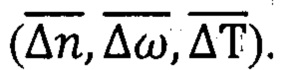
С учетом отмеченных недостатков способ АГК в основном нашел практическое применение для решения задач НАВ ПО в предстартовых условиях [12].
Однако и в этих случаях для повышения точности решения задачи автономной ориентации ПО необходимо минимизировать погрешности в магнитометрическом 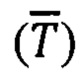 и инерциальном
и инерциальном 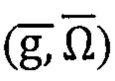 каналах измерений.
каналах измерений.
Известен способ автономной пространственной ориентации (АПО) ПО, заключающийся в составлении матричного уравнения, характеризующего преобразование векторов ГФП 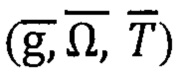 из географического базиса q=NHE в связанный с объектом базис m=XYZ, и в последующем решении этого уравнения с целью формирования алгоритмов обработки многомерной геофизической информации (ГФИ) и преобразования;ее в пилотажно-навигационную информацию (ПНИ) о параметрах ориентации объекта [13].
из географического базиса q=NHE в связанный с объектом базис m=XYZ, и в последующем решении этого уравнения с целью формирования алгоритмов обработки многомерной геофизической информации (ГФИ) и преобразования;ее в пилотажно-навигационную информацию (ПНИ) о параметрах ориентации объекта [13].
Способ оперирует с информацией о векторах ГФП 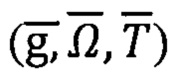 и поэтому назван способом ориентации векторным автономным (СОВА).
и поэтому назван способом ориентации векторным автономным (СОВА).
По доступной информации предварительно вычисляют векторы ПТЗ 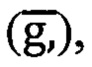 МПЗ
МПЗ 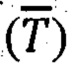 и поля вращения Земли (ПВЗ)-
и поля вращения Земли (ПВЗ)-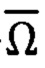 в географическом q и связанном m базисах
в географическом q и связанном m базисах
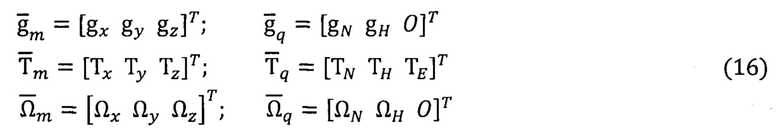
Вектор 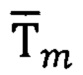 вычисляют с учетом результатов предварительно выполненных метрологических тарировок и технологических калибровок в соответствии с расширенным уравнением Пуассона [14]:
вычисляют с учетом результатов предварительно выполненных метрологических тарировок и технологических калибровок в соответствии с расширенным уравнением Пуассона [14]:
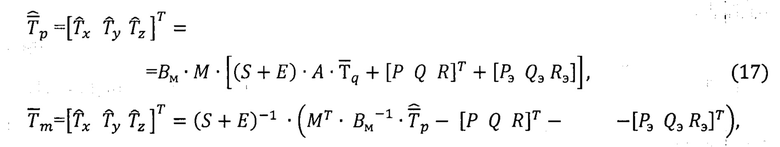
где 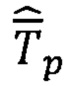 - вектор напряженности результирующего магнитного поля, сформированный по показаниям ТБМ и приведенный к осям приборного отсчетного базиса р,
- вектор напряженности результирующего магнитного поля, сформированный по показаниям ТБМ и приведенный к осям приборного отсчетного базиса р,
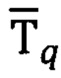 - вектор напряженности МПЗ в точке наблюдения, приведенный к географическому базису q:
- вектор напряженности МПЗ в точке наблюдения, приведенный к географическому базису q:
P,Q,R - компоненты вектора напряженности магнитного поля объекта (МПО), отнесенного к осям связанного базиса m,
Pэ,Qэ,Rэ - аналогичные компоненты вектора, обусловленного влиянием электромагнитных источников (ЭМИ) помех,
Е - единичная матрица (3×3),
S - матрица коэффициентов Пуассона (3×3),
Bм - матрица погрешностей сборки ТБМ (3×3),
М - матрица погрешностей монтажа ТБМ на объекте (3×3).
Компоненты векторов 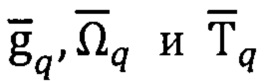 в осях географического q базиса вычисляют с учетом данных СНС (ϕ; λ; h; r) по моделям нормальных ГФП [8, 9, 14]:
в осях географического q базиса вычисляют с учетом данных СНС (ϕ; λ; h; r) по моделям нормальных ГФП [8, 9, 14]:
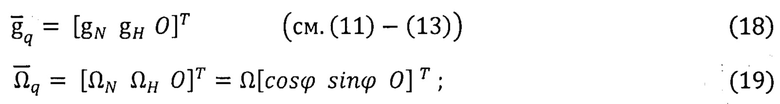
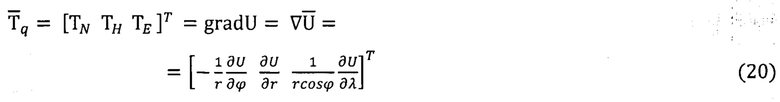
Геомагнитный потенциал представляют с помощью сферических рядов Гаусса [9]:
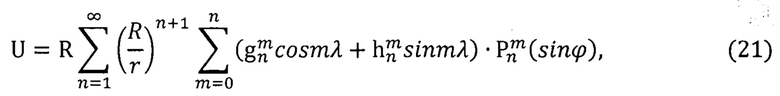
где m, n - степень и порядок членов разложения,
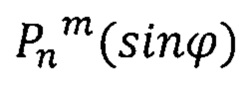 -присоединенные функции Лежандра. На основе навигационной информации (ϕ, λ, h), получаемой от СНС, вычисляют компоненты вектора кажущегося ускорения
-присоединенные функции Лежандра. На основе навигационной информации (ϕ, λ, h), получаемой от СНС, вычисляют компоненты вектора кажущегося ускорения 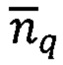 в географическом базисе [1, 2]:
в географическом базисе [1, 2]:
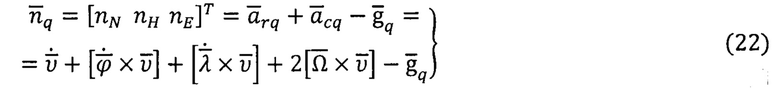
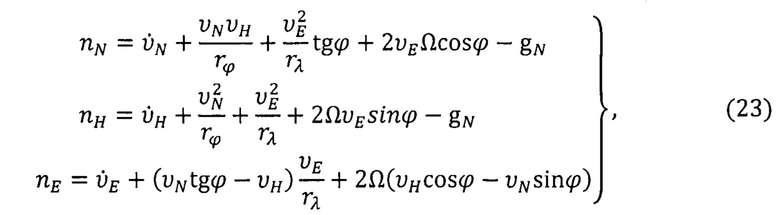
где rϕ, rλ радиусы кривизны эквидистантного референц-эллипсоида [8].
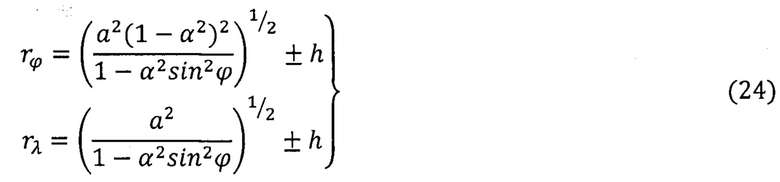
Компоненты вектора 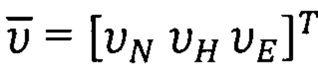 определяют на основе данных СНС [1, 2]:
определяют на основе данных СНС [1, 2]:

Вектор 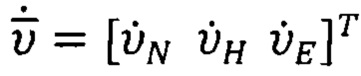 определяют путем численного дифференцирования.
определяют путем численного дифференцирования.
Расширяют ГФИ за счет вычисления на основе способа восстановления векторной информации [15] вектора 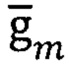 в связанном базисе, а также путем вычисления дополнительных векторов [13] в базисах m и q:
в связанном базисе, а также путем вычисления дополнительных векторов [13] в базисах m и q:

На основе вычисленных по формулам (4) - (6), (19) - (26), (16) векторов составляют матричное уравнение АПО в условиях функциональной избыточности информации:
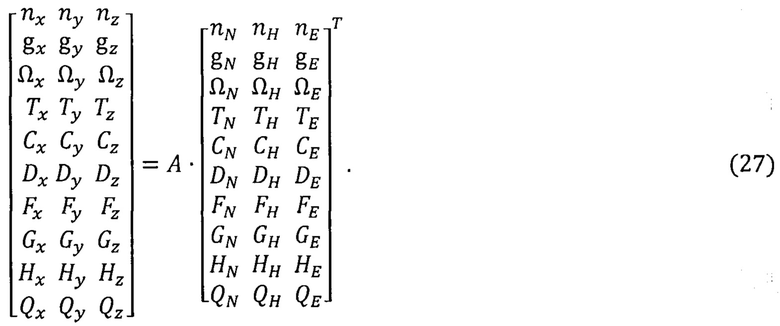
В соответствии с принципом декомпозиции разбивают матричное уравнение (27) на частные матричные уравнения идентификации с квадратными матрицами (3×3) вида:

где Рk -матрица приборной информации и ГФИ в связанном базисе m (3×3),
Nk - матрица идентификации (3×3) для k-ого варианта. Максимально возможное число вариантов построения матричных уравнений идентификации вида (28) составляет
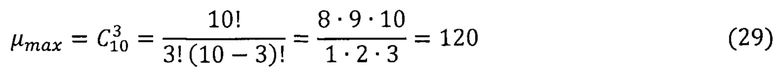
Для практических целей из соображений экономии объема оперативной памяти бортового вычислителя достаточно использовать ограниченное число вариантов (μ<μmax), например, μ≤10.
Алгоритмы АПО для способа СОВА получают путем обращения уравнений идентификации (28):
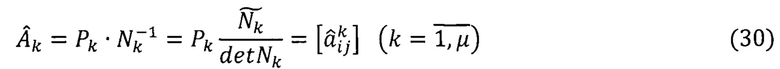
По алгоритмам АПО (30) вычисляют оценки направляющих косинусов 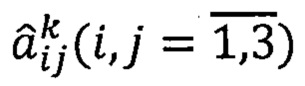 матрицы ориентации
матрицы ориентации 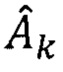 для k-ого варианта.
для k-ого варианта.
Используют операцию сравнения оценок (30) и вычисления выровненной оценки матрицы ориентации 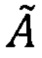 (3×3):
(3×3):
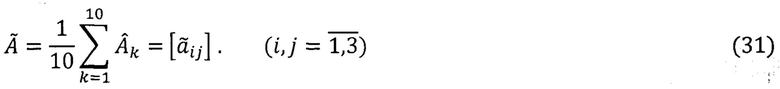
По вычисленным значениям направляющих косинусов матрицы ориентации определяют оценки эйлеровых углов по формулам [13]:

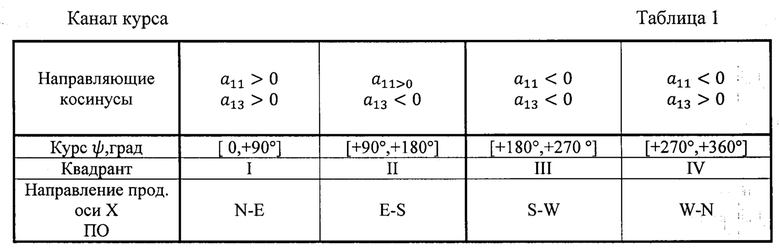
Значения, знаки оценок вычисленных эйлеровых углов 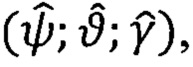 а также положение ПО относительно осей географического базиса (q=NHE) определяют с помощью табл. 1, 2, 3.
а также положение ПО относительно осей географического базиса (q=NHE) определяют с помощью табл. 1, 2, 3.
Для формирования первичной приборной информации 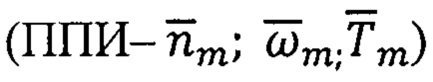 в способе СОВА используют три блока векторных ДПИ-ТБА, ТБГ, ТБМ. На основе этой ППИ могут быть реализованы трехвекторные и двухвекторные алгоритмы обработки информации (16) - (32). За счет этого реализуют условия функциональной избыточности информации, обеспечивающие свойства отказоустойчивости СОН и ее работоспособность в резервно-аварийных режимах (РАР). При этом допускается отказ любого блока или любых датчиков в пределах одного блока без потери работоспособности в РАР.
в способе СОВА используют три блока векторных ДПИ-ТБА, ТБГ, ТБМ. На основе этой ППИ могут быть реализованы трехвекторные и двухвекторные алгоритмы обработки информации (16) - (32). За счет этого реализуют условия функциональной избыточности информации, обеспечивающие свойства отказоустойчивости СОН и ее работоспособность в резервно-аварийных режимах (РАР). При этом допускается отказ любого блока или любых датчиков в пределах одного блока без потери работоспособности в РАР.
Известны способы пространственной автономной бесплатформенной ориентации ПО в околоземном пространстве, объединенных в единую группу способов трехмерной расширенной инерциальной ориентации (ТРИО) [1-6]. Варианты способов бесплатформенной автономной инерциальной ориентации ПО (способов ТРИО) отличаются друг от друга прежде всего способами описания геометрии и кинематики вращательного движения объекта [2, 3, 6].
В качестве исходной математической модели вращательного движения любого ПО в пространстве во всех способах ТРИО принимают кинематическое уравнение вращения твердого тела:

где 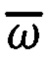 - вектор абсолютной угловой скорости вращения объекта в инерциальном пространстве, измеряемый с помощью блока гироскопов,
- вектор абсолютной угловой скорости вращения объекта в инерциальном пространстве, измеряемый с помощью блока гироскопов,
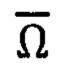 - вектор переносной угловой скорости вращения объекта вместе с вращающейся Землей в инерциальном пространстве,
- вектор переносной угловой скорости вращения объекта вместе с вращающейся Землей в инерциальном пространстве,
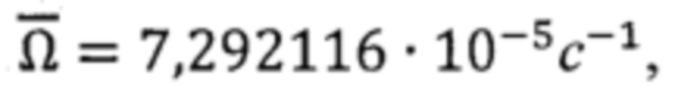
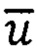 - вектор относительной угловой скорости вращения объекта относительно Земли.
- вектор относительной угловой скорости вращения объекта относительно Земли.


Достоинством способа СОВА является и то, что для его реализации не требуется выполнять операции начальной автономной выставки (НАВ) СОН.
Недостатки способа СОВА:
- применение ТБГ приводит к снижению точности решения задачи автономной ориентации из-за проявления дрейфа гироскопов,
- сложность алгоритмов обработки информации с учетом функциональной избыточности информации в способе СОВА повышает требования к вычислительным характеристикам микроконтроллера (быстродействию, длине разрядной сетки, информационной производительности).
На основе векторного уравнения (33) формируют кинематические уравнения вращательного движения ПО в околоземном пространстве в векторно-матричной и скалярной формах [6]:
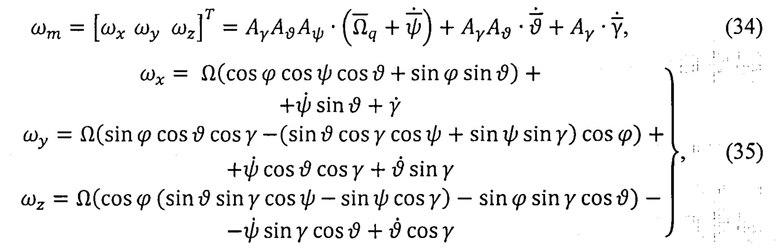
где 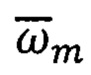 - вектор абсолютной угловой скорости вращения ПО объекта в инерциальном пространстве, заданный в связанном базисе m=XYZ,
- вектор абсолютной угловой скорости вращения ПО объекта в инерциальном пространстве, заданный в связанном базисе m=XYZ,
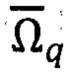 - вектор угловой скорости суточного вращения Земли в географическом базисе q=NHE,
- вектор угловой скорости суточного вращения Земли в географическом базисе q=NHE,
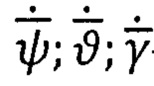 - векторы производных по времени от текущих значений углов ориентации ПО (курса - ψ, тангажа - ϑ, крена - γ),
- векторы производных по времени от текущих значений углов ориентации ПО (курса - ψ, тангажа - ϑ, крена - γ),
ϕ - географическая широта точки текущего местоположения ПО ωх; ωу; ωz - проекции вектора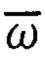 на оси связанного базиса m=XYZ. Производные по времени с учетом дискретности обработки информации вычисляют по методу численного дифференцирования:
на оси связанного базиса m=XYZ. Производные по времени с учетом дискретности обработки информации вычисляют по методу численного дифференцирования:

где Δt - интервал времени, соответствующий одному шагу вычислений, выполняемых с шаговой частотой 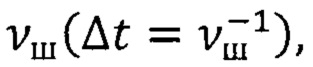
Δψ, Δϑ; Δγ - приращения (вариации) углов ориентации ПО, приходящиеся на текущий шаг вычислений.
С учетом (36) систему (35) приводят к векторно-матричному виду [1, 2, 3, 6, 16]
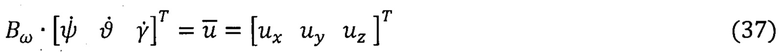
Причем
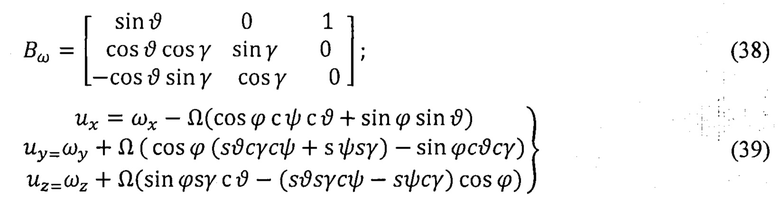
На основе векторно-матричного дифференциального уравнения (37) получают непрерывный интегральный алгоритм обработки информации в способе ТРИО-А [17]:

где 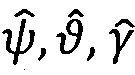 - оценки текущих значений углов ориентации ПО,
- оценки текущих значений углов ориентации ПО,
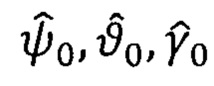 - оценки углов ориентации ПО в предстартовых условиях, определенные при начальной расширенной автономной выставке (НРАВ).
- оценки углов ориентации ПО в предстартовых условиях, определенные при начальной расширенной автономной выставке (НРАВ).
На практике обычно пренебрегают угловой скоростью вращения ПО, обусловленной вращением Земли, и принимают упрощение 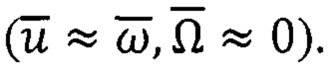
Тогда вместо выражения (40) непрерывный алгоритм ТРИО-А будет выглядеть иначе [17]:

На практике непрерывные алгоритмы (40) или (41) (алгоритмы идеальной работы системы автономной ориентации) не могут быть реализованы точно. Их воспроизводят в виде дискретных алгоритмов способов ТРИО-А [17]:
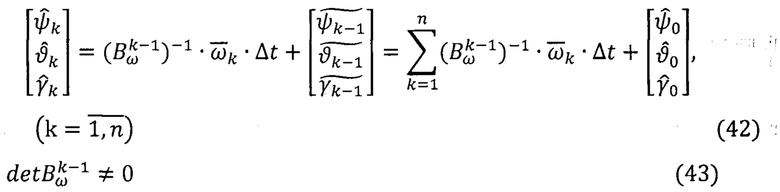
Причем матрица идентификации 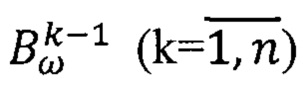 на каждом k-ом шаге вычислений
на каждом k-ом шаге вычислений
формируют на основе информации о значениях углов ориентации ПО, определенных на предыдущем (k-1)-ом, а не на текущем k-ом шаге вычислений.
В реальных условиях показания ТБГ содержат наряду с полезными сигналами 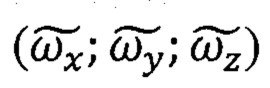 аддитивные погрешности, обусловленные дрейфом гироскопов
аддитивные погрешности, обусловленные дрейфом гироскопов 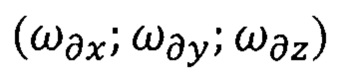
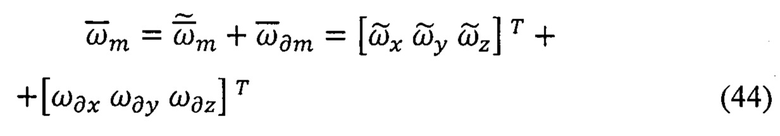
Из анализа интегральных алгоритмов ориентации ПО (40) - (43) с учетом выражений (44) для реальных измерений 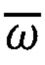 с помощью ТБГ видно, что всем вариантам способов ТРИО ПО характерен общий недостаток, заключающийся в накоплении погрешностей во времени (нерерывном и дискретном), связанном с процессом интегрирования (суммирования) как полезных сигналов
с помощью ТБГ видно, что всем вариантам способов ТРИО ПО характерен общий недостаток, заключающийся в накоплении погрешностей во времени (нерерывном и дискретном), связанном с процессом интегрирования (суммирования) как полезных сигналов 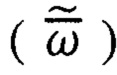 так и дрейфа гироскопов
так и дрейфа гироскопов 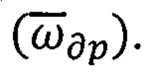
Из-за проявления этого общего недостатка все способы интегральной ориентации ПО имеют ограничения по времени работы БСО или нуждаются в использовании дополнительных приемов коррекции.
Известна группа способов инерциальной ориентации ПО, в которых для ограничения процесса непрерывного накопления погрешностей интегрирования ошибок, обусловленных дрейфом гироскопов, используют прием коррекции БСО по сигналам формирующих фильтров, наблюдающих устройств и эталонных систем ориентации [18-20].
Во всех этих вариантах способов коррекции систем инерциальной ориентации (ТРИО-К) используют принцип отрицательной обратной связи:
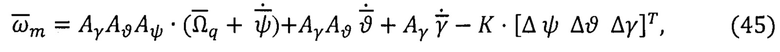
где К - матрица коррекции (3×3),
Δψ, Δϑ; Δγ - сигналы поправок.
За счет реализации способа коррекции ТРИО с помощью отрицательной обратной связи удается ограничить непрерывный рост погрешностей интегрирования (суммирования) первичных ошибок. Однако в этом случае наблюдается не неограниченный рост погрешностей, а колебательные изменения выходных погрешностей с ограничением их амплитуды роста. Свести к нулю погрешности интегрирования (суммирования) первичных ошибок в вариантах способов ТРИО-К не удается. Необходимо снижать уровень проявления первичных ошибок, в частности, снижать степень влияния первичных ошибок, обусловленных дрейфом гироскопов.
Известна группа способов двухчастотного формирования и обработки инерциальной информации при решении задачи инерциальной ориентации (способов ТРИО -Д) [21].
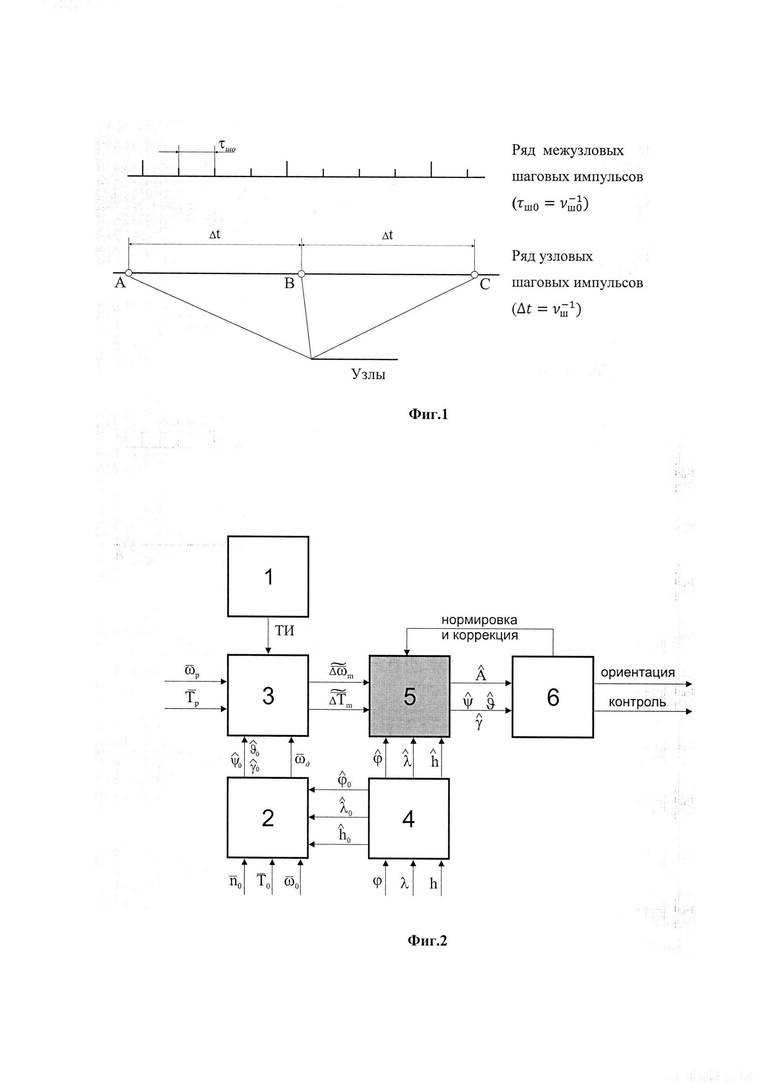
Сущность способов ТРИО -Д заключается в том, что в них реализуют двухчастотную схему получения и обработки инерциальной информации (Фиг. 1):
- получение исходной информации о векторе 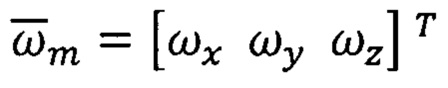 с шаговой частотой опроса датчиков (νш0) в межузловых точках,
с шаговой частотой опроса датчиков (νш0) в межузловых точках,
- обработка полученной информации 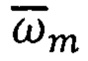 с меньшей шаговой частотой (νш) решения задачи автономной инерциальной ориентации в узловых точках.
с меньшей шаговой частотой (νш) решения задачи автономной инерциальной ориентации в узловых точках.
Процесс получения инерциальной информации является высокочастотным, а процесс обработки информации (процесс решения задачи инерциальной ориентации) -низкочастотным.
При этом выполняют условия согласования частот:

где ΔТ - максимальный интервал времени, необходимый для выполнения всех вычислительных операций в одном шаге вычислений,
νш - шаговая частота решения задачи инерциальной ориентации в узлах А, В, С, …,
νш0 - шаговая частота опроса датчиков в межузловых точках,
νп - наибольшая частота изменения помех.
Условие (46) определяет быстродействие выбранного алгоритма решения задачи ТРИО-Д. Условие (47) соответствует требованию кратности частот, характеризующему степень приближения дискретного процесса вычисления по алгоритму (42), (43) к непрерывному процессу вычислений по алгоритму (40) или (41). Условие (48) соответствует известной теореме В.А. Котельникова.
К настоящему времени разработаны различные алгоритмы двухчастотной обработки инерциальной информации для способов ТРИО-Д [20, с. 60]:
- алгоритм Миллера (1983),
- алгоритм М. Игнагни (1990),
- алгоритм П. Сэведжа (1998) и другие.
Во всех алгоритмах способов ТРИО-Д выполнение высокочастотных вычислительных операций с частотой опроса датчиков (νшо) позволяет определить производные от вектора 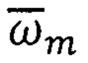 по времени в межузловых точках, что позволяет решать задачу прогнозирования в формировании приращений углов ориентации Δψ, Δϑ; Δγ в узловых точках вычислений (Фиг. 1). Таким образом, двухчастотные схемы и алгоритмы обработки инерциальной информации в задаче ТРИО-Д играют прогнозирующую и решающую роль.
по времени в межузловых точках, что позволяет решать задачу прогнозирования в формировании приращений углов ориентации Δψ, Δϑ; Δγ в узловых точках вычислений (Фиг. 1). Таким образом, двухчастотные схемы и алгоритмы обработки инерциальной информации в задаче ТРИО-Д играют прогнозирующую и решающую роль.
В двухчастотных способах ТРИО-Д используют принцип аппроксимации процессов изменения параметров ориентации и вектора угловой скорости 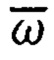 вращения ПО в межузловых интервалах времени с помощью разложения функций матриц ориентации A(t) и функций вектора
вращения ПО в межузловых интервалах времени с помощью разложения функций матриц ориентации A(t) и функций вектора 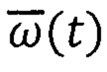 в дискретные степенные ряды [16, 20].
в дискретные степенные ряды [16, 20].
Сущность всех вариантов способов группы ТРИО-Д заключается в том, что за счет реализации двухчастотных алгоритмов обработки информации
- во-первых, обеспечивают условия для частичного разрешения противоречия несоответствия исходных значений углов ориентации ПО дискретной форме алгоритмов обработки информации,
- во-вторых, обеспечивают условия для приближения дискретного процесса вычислений параметров ориентации к непрерывному вычислительному процессу в соответствии с интегральными алгоритмами (40), (41).
К недостаткам всех способов групп ТРИО-А, К, Д следует отнести следующее:
- неустойчивость вычислительного процесса при обработке информации по интегральным алгоритмам (40), (41), при которой наблюдается рост методических погрешностей (асимптотически или колебательно), вызванных как проявлением дрейфа гироскопов 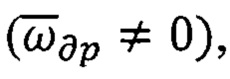 так и процессом интегрирования (суммирования) во времени погрешностей, связанных с дрейфом,
так и процессом интегрирования (суммирования) во времени погрешностей, связанных с дрейфом,
- проявление методических погрешностей в определении параметров ориентации ПО, обусловленных противоречием между исходными значениями параметров в подынтегральных выражениях (40), (41) и формой дискретных алгоритмов обработки информации (42), (43).
Причем, хотя первый недостаток (накопление погрешностей во времени), является более значимым по масштабам проявления, тем не менее, второй недостаток усугубляет степень проявления первого недостатка. Таким образом, оба недостатка способов ТРИО-А, К, Д проявляются взаимосвязано.
В задачу настоящего изобретения входит устранение недостатков, присущих способам-аналогам и способу-прототипу (ТРИО) решения задачи автономной инерциальной ориентации ПО.
В предлагаемом изобретении частично устраняют следующие погрешности:
- инструментальные погрешности, обусловленные дрейфом нулевых сигналов гироскопов,
- методические погрешности, связанные с неучетом в алгоритмах (41) обработки информации факта переносного вращения ПО вместе с вращающейся Землей 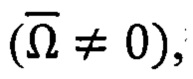
- методические погрешности, обусловленные несоответствием значений углов ориентации ПО, используемых в алгоритмах обработки информации, форме самих алгоритмов,
- исключают недостаток, связанный с усложнением алгоритмов обработки информации, вызванным необходимостью реализации двухчастотной схемы формирования и обработки ППИ.
Решение поставленной в изобретении задачи достигают путем комбинирования приемов:
- приема расширения информации, получаемой при выполнении операций НРАВ, при которой обеспечивают не только определение оценок начальных значений углов ориентации ПО 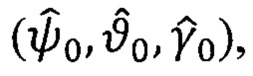 но и идентификацию аддитивных погрешностей, обусловленных дрейфом гироскопов,
но и идентификацию аддитивных погрешностей, обусловленных дрейфом гироскопов,
- приема формирования алгоритмов дискретной обработки информации, учитывающих расширенную информацию о значениях начальных углов ориентации ПО 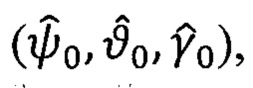 о значениях углов ориентации ПО на предыдущем (а не на текущем) шаге вычислений, о составляющих переносной угловой скорости объекта, обусловленной вращением Земли
о значениях углов ориентации ПО на предыдущем (а не на текущем) шаге вычислений, о составляющих переносной угловой скорости объекта, обусловленной вращением Земли 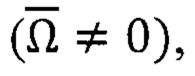 а также о составляющих аддитивных погрешностей гироскопов
а также о составляющих аддитивных погрешностей гироскопов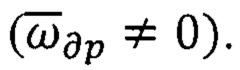
Предлагаемый способ авторы назвали способом многовариантной ориентации дифференциальной автономной (МОДА).
Предлагаемое изобретение поясняется чертежами (Фиг. 1, 2). На Фиг. 1 представлена схема формирования двух рядов импульсов в двухчастотном способе ТРИО-Д. Приняты следующие обозначения:
А, В, С… - ряд узловых импульсов с шаговой частотой νш,
Δt - длительность одного шага обработки информации 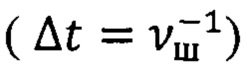
τш0; νш0 - длительность одного шага и частота опроса датчиков 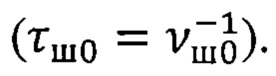
На Фиг. 2 представлена функциональная схема способа МОДА и приняты следующие обозначения,
1 - позиция, соответствующая выполнению операций метрологической тарировки, аналитической юстировки и технологической калибровки ДПИ и блоков ТБА, ТБГ, ТБМ,
2 - позиция, соответствующая выполнению операций НРАВ для определения значений углов начальной ориентации ПО в предстартовых условиях 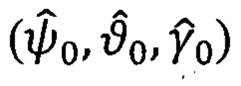 и идентификации вектора угловой скорости
и идентификации вектора угловой скорости 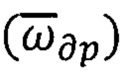 дрейфа гироскопов,
дрейфа гироскопов,
3 - позиция, соответствующая процессу измерений с помощью блоков ТБМ, ТБГ вектора напряженности результирующего магнитного поля, вектора абсолютной угловой скорости вращения ПО в инерциальном пространстве на оси приборной системы координат р=XпYпZп,
4 - позиция, соответствующая формированию навигационной информации (ϕ, λ, r, h) с помощью спутниковой навигационной системы(СНС),
5 - позиция, соответствующая процессу обработки первичной приборной информации (ППИ), технологической информации НРАВ и навигационной информации) (от СНС) по алгоритмам МОДА,
6 - позиция, соответствующая операциям автономного контроля и нормировки (АКН) по алгоритмам комбинированного автономного самотестирования, коррекции и аналитической диагностики (КАСКАД).
Способ МОДА заключается в последовательном выполнении операций технологических калибровок, НРАВ, измерений, формирования ППИ, навигационной информации и комбинированной обработки полученной многомерной многовекторной информации (ФИГ. 2):
1. Заранее (до старта ПО) выполняют операции метрологических тарировок, аналитических постировок и технологических калибровок магнитометрического и инерциальных каналов измерений (поз. 1, Фиг. 2). Технологические операции выполняют по методике, описанной в научно-технической литературе [10]. Обработку полученной информации выполняют по алгоритмам технологического обеспечения модуля (АТОМ). На выходе блока (поз. 1, Фиг. 2) формируют технологическую информацию (ТИ) об индивидуальных параметрах ДПИ, блоков и модуля.
2. Выполняют операции начальной расширенной автономной выставки (поз. 2, Фиг. 2). При этом на основе измерений с помощью блоков (ТБА, ТБГ, ТБМ) и СНС формируют начальную информацию: в связанном (m0=X0Y0Z0) и географическом (q0=N0H0E0) базисах, в предстартовых условиях в режиме остановки (ZUPT) ПО:
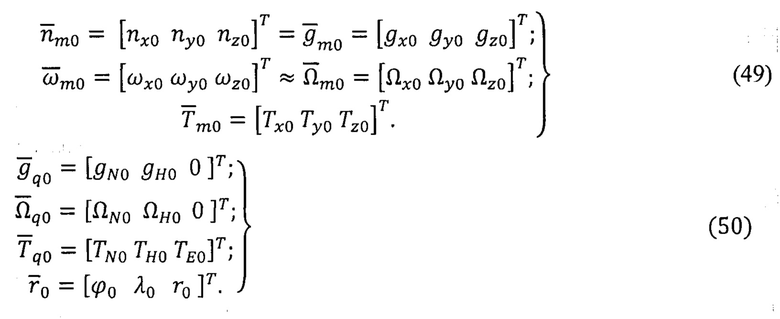
Выражения (49) реализуют на основе первичной обработки сигналов блоков (ТБА, ТБГ, ТБМ) в соответствии с формулами (3), (12) и (17).
Соотношения (50) реализуют путем организации вычислений по формулам (4) - (7), (18) - (21) компонент векторов ГФП с учетом начальной навигационной информации(ϕ0,λ0,r0) от СНС. Вычисляют компоненты производного вектора

в связанном (m0=X0Y0Z0) и географическом (q0=N0H0E0) базисах в предстартовых условиях:
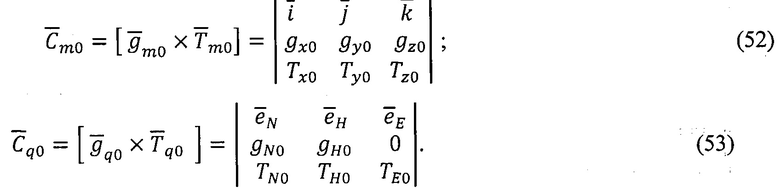
На основе информации о векторах 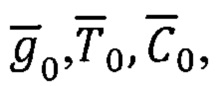 вычисленных в базисах m0 и q0, а также информации о вычисленном векторе
вычисленных в базисах m0 и q0, а также информации о вычисленном векторе 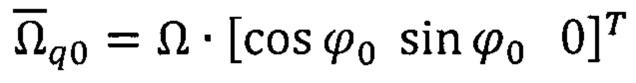 составляют систему векторно-инвариантных уравнений [15]:
составляют систему векторно-инвариантных уравнений [15]:
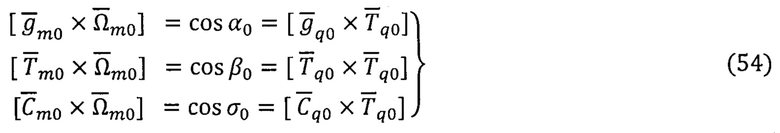
Из решения системы векторно-инвариантных уравнений (54) находят оценку вектора

а затем идентифицируют оценку вектора угловой скорости дрейфа гироскопов:
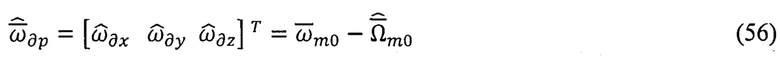
Расширяют ППИ и ГФИ путем вычисления дополнительных производных векторов виртуальных ГФП в базисах m0 и q0:

Формируют расширенное матричное уравнение начальной автономной ориентации ПО:
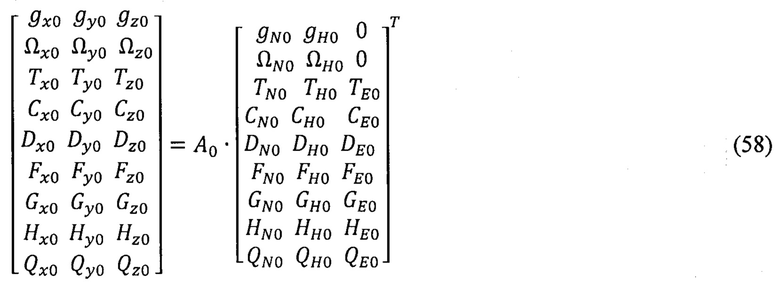
В соответствии с принципом декомпозиции разбивают матричное уравнение (58) на частные матричные уравнения идентификации с квадратными матрицами (3×3) вида:
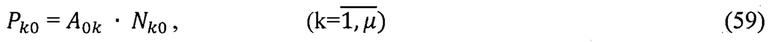
где Рk0 - матрица (3×3)приборной информации и ГФИ в связанном базисе m0=X0Y0Z0 для k-ого варианта,
Nk0 - матрица (3×3) идентификации начальных углов ориентации ПО (ψ0; ϑ0; γ0) для k-ого варианта.
Путем обращения уравнений идентификации (59) получают алгоритмы определения начальных значений углов ориентации ПО в предстартовых условиях с учетом функциональной избыточности информации 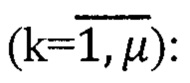
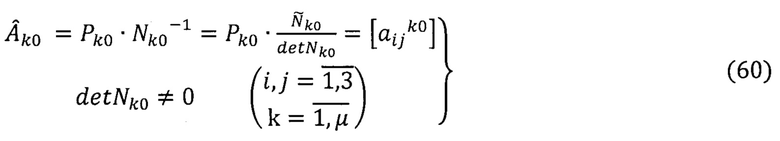
По формулам (31), (32) и табл. 1, 2, 3 вычисляют выровненную оценку матрицы 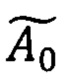 (3×3),соответствующие оценки углов ориентации
(3×3),соответствующие оценки углов ориентации 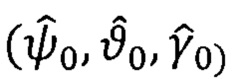 и их знаки.
и их знаки.
3. В процессе измерений вектора напряженности результирующего магнитного поля 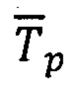 с помощью ТБМ и вектора абсолютной угловой скорости вращения ПО в инерциальном пространстве
с помощью ТБМ и вектора абсолютной угловой скорости вращения ПО в инерциальном пространстве 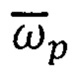 с помощью ТБГ в приборном измерительном базисе р с учетом результатов технологических калибровок (поз. 1, Фиг. 1) выполняют операции коррекции показаний блоков (ТБМ, ТБА) и приведения их к ортонормированным осям связанного базиса m=XYZ.
с помощью ТБГ в приборном измерительном базисе р с учетом результатов технологических калибровок (поз. 1, Фиг. 1) выполняют операции коррекции показаний блоков (ТБМ, ТБА) и приведения их к ортонормированным осям связанного базиса m=XYZ.
При этом используют выражения (17) для 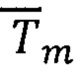 и формулы для коррекции- приведения вектора
и формулы для коррекции- приведения вектора 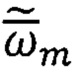 :
:
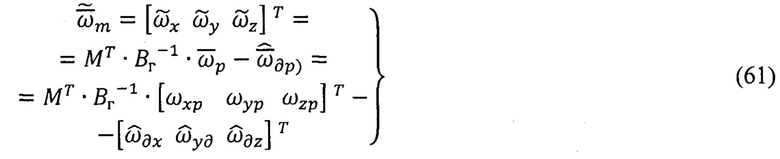
На каждом μ - шаге вычислений определяют приращения (вариации) векторов 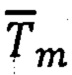 и
и 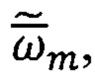 приходящиеся на интервал времени
приходящиеся на интервал времени 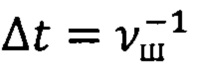 (Фиг. 1):
(Фиг. 1):
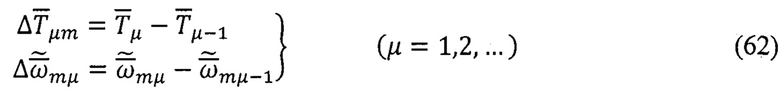
Или
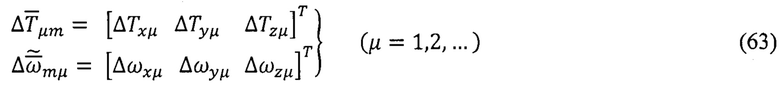
Приращения (вариации)показаний ТБМ и ТБГ вычисляют на каждом шаге вычислений по формулам:
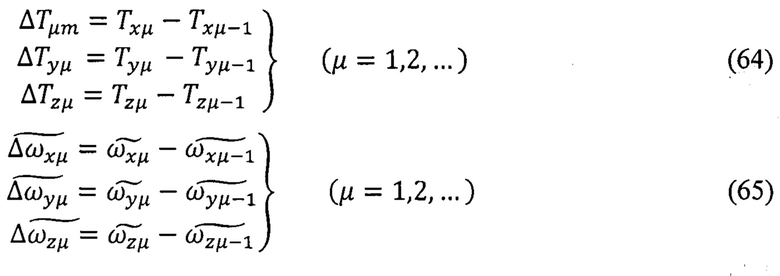
4. На каждом μ - шаге вычислений СНС измеряет текущие географические координаты точки наблюдения (ϕ, λ, h) и формирует их оценки - 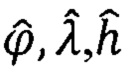 (поз. 4, Фиг. 2). При выполнении операций НРАВ с помощью СНС формируют оценки начальных значений географических координат
(поз. 4, Фиг. 2). При выполнении операций НРАВ с помощью СНС формируют оценки начальных значений географических координат 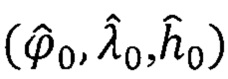 точки старта ПО (Фиг. 2).
точки старта ПО (Фиг. 2).
5. В вычислительном блоке (поз. 5, Фиг. 2) выполняют основные операции по обработке магнитно-инерциальной информации 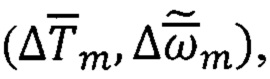 получаемой от блоков ТБМ, ТБГ.
получаемой от блоков ТБМ, ТБГ.
Для формирования дифференциальных алгоритмов по способу МОДА рассматривают кинематические уравнения вращательного движения ПО в базисах m, q для инерциального канала измерений (от ТБГ) и векторно-матричное уравнение для магнитометрического канала (от ТБМ):
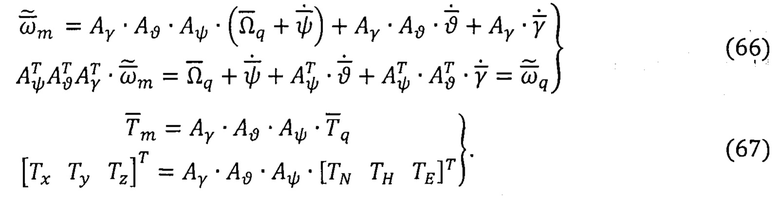
На каждом μ-ом шаге вычислений по формулам (62)-(65) определяют приращения векторов 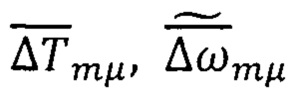 и с учетом найденных вариаций производят линеаризацию скалярных девяти уравнений, получаемых из уравнений (66), (67).
и с учетом найденных вариаций производят линеаризацию скалярных девяти уравнений, получаемых из уравнений (66), (67).
Линеаризованную систему девяти уравнений записывают в векторно-матричной форме:

где N - прямоугольная матрица (9×3) идентификации вариаций углов ориентации (Δψ, Δϑ; Δγ),
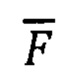 - вектор-функция (9×1) идентификации.
- вектор-функция (9×1) идентификации.
Причем

Элементы матрицы идентификации N:
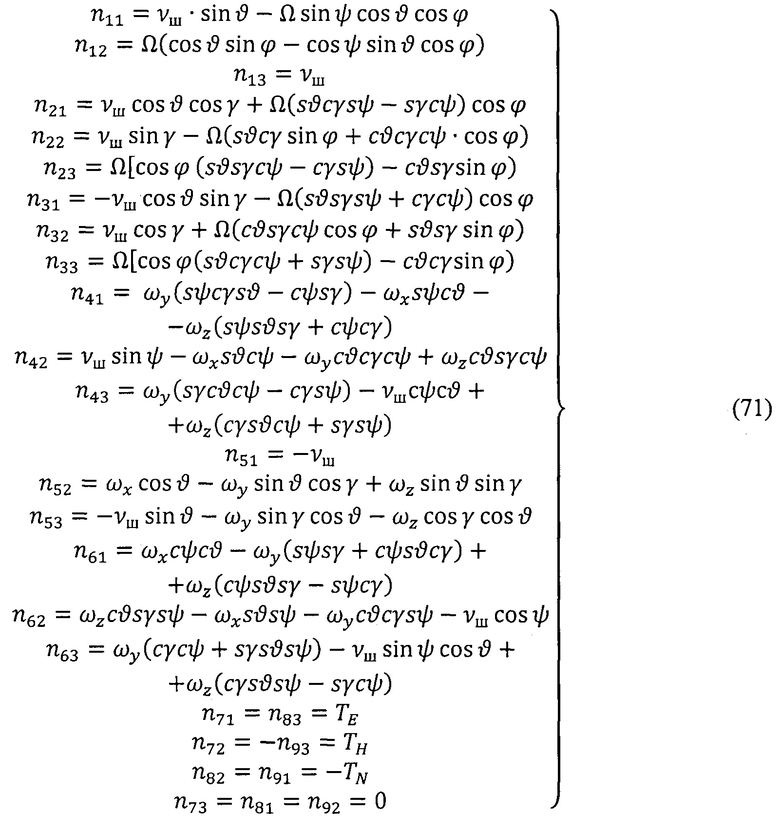
Компоненты вектор-функции 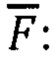
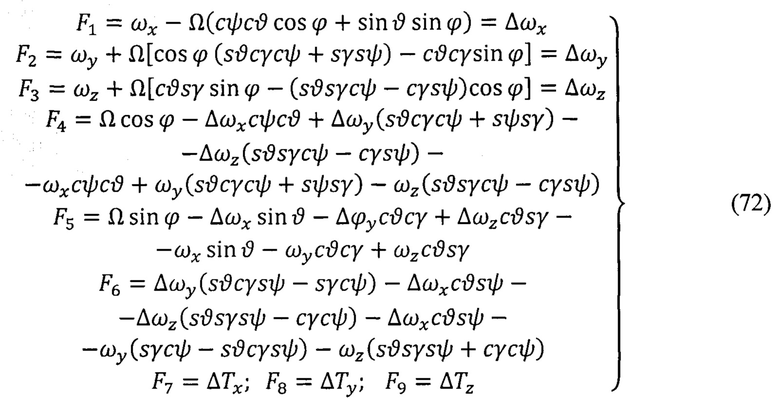
Коэффициенты 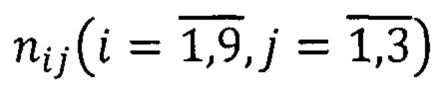 матрицы идентификации N вычисляют по формулам (71) с учетом значений параметров, зафиксированных на предыдущем (μ-1)-ом шаге вычислений. Функции идентификации
матрицы идентификации N вычисляют по формулам (71) с учетом значений параметров, зафиксированных на предыдущем (μ-1)-ом шаге вычислений. Функции идентификации 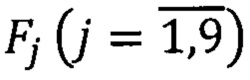 вычисляют по формулам (72) с учетом углов ориентации (ψ,ϑ,γ,ϕ) и угловых скоростей ωx,ωy,ωz, зафиксированных также в (μ-1)-ом шаге вычислений.
вычисляют по формулам (72) с учетом углов ориентации (ψ,ϑ,γ,ϕ) и угловых скоростей ωx,ωy,ωz, зафиксированных также в (μ-1)-ом шаге вычислений.
На основе декомпозиции векторно-матричного уравнения (68) формируют путем выборки тройки уравнений идентификации с квадратными матрицами:
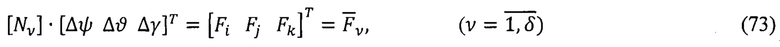
где [Nv] - квадратная матрица идентификации (3×3) для
v-ого варианта 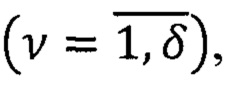
Fi;Fj;Fk - функции идентификации 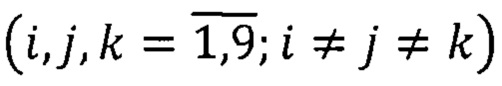 вектора
вектора 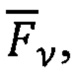 соответствующего ν-ому варианту.
соответствующего ν-ому варианту.
Причем
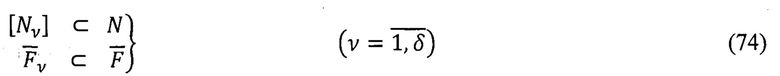
Число (δ) вариантов построения частных уравнений идентификации вида (73), (74) составляет:

Для практических целей достаточно реализовать ограниченное число каналов обработки информации (δ≤10).
Решения уравнений идентификации (73) для v-ого варианта на μ-ом шаге вычислений получают путем их обращения:
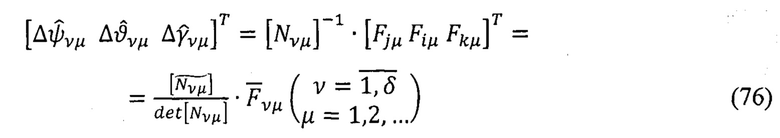
Причем
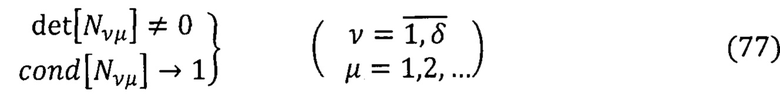
Выражения (77) соответствуют условиям невырождаемости и хорошей обусловленности решений (76).
На каждом μ-ом шаге вычислений (μ=1, 2, 3, …) с учетом наличия расширенной информации о вариациях углов ориентации 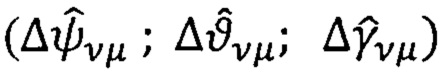 для ν вариантов каналов
для ν вариантов каналов 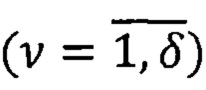 производят операции осреднения вычисленных оценок:
производят операции осреднения вычисленных оценок:
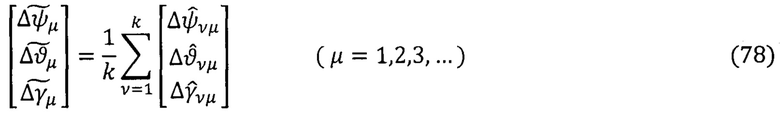
После операции осреднения вариаций углов ориентации ПО на каждом μ-ом шаге вычислений определяют оценки и знаки (табл. 1-3) конечных величин углов ориентации объекта:
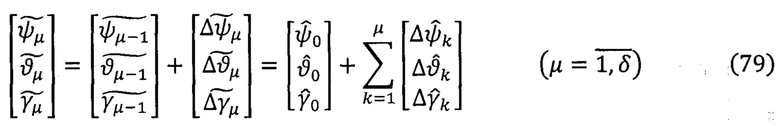
На основе вычисленных по формулам (78), (79) осредненным оценкам вычисляют направляющие косинусы 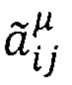 на μ-ом каждом шаге вычислений и формируют оценки матриц ориентации:
на μ-ом каждом шаге вычислений и формируют оценки матриц ориентации:
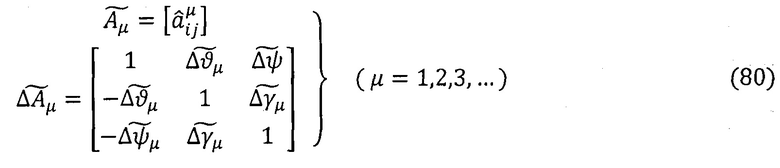
6. На каждом шаге вычислений выполняют операции автономного контроля и нормировки - АКН (поз. 6, Фиг. 2) по комбинрованным алгоритмам самотестирования, контроля и автономной диагностики (КАСКАД):

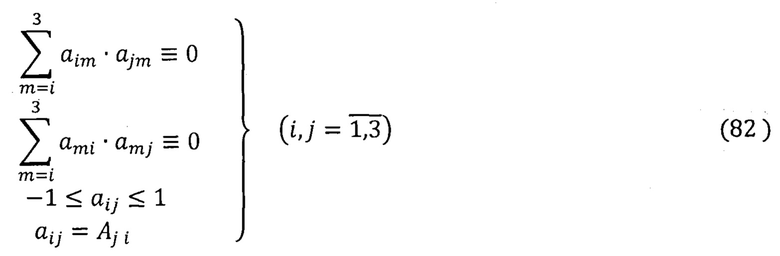
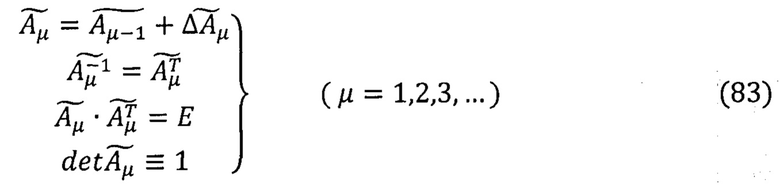
По результатам выполнения операций АКН по алгоритмам КАСКАД (81-83) в заключение производят операции коррекции и нормировки результатов вычислений (Фиг. 2).
Из анализа выражений (40) - (42) и (78), (79) видно, что способам ТРИО и МОДА характерен общий недостаток, заключающийся в явлении накопления погрешностей, обусловленном процессом суммирования показаний блоков ТБГ и ТБМ и влиянием аддитивных погрешностей гироскопов, связанных с их дрейфом. Однако это явление в способе МОДА проявляется в меньшей степени и в меньшем темпе (с меньшей скоростью), чем в способе ТРИО. Причина такого снижения степени и темпа накопления погрешностей в способе МОДА по сравнению со способом ТРИО кроется в том, что
- в способе ТРИО под знак интегралов (или сумм) попадают сами значения текущих сигналов гироскопов (ωх, ωу, ωz) вместе с величинами угловых скоростей их дрейфа 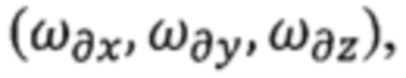 ,
,
- а в способе МОДА под знак суммы попадают не сигналы гироскопов (ωх, ωу, ωz), а функции идентификации 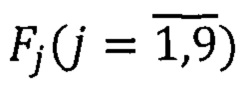 зависящие от комбинаций разноосных сигналов Δωх; Δωу; Δωz вычисляемых на основе сравнения показаний гироскопов на каждых соседних шагах вычислений.
зависящие от комбинаций разноосных сигналов Δωх; Δωу; Δωz вычисляемых на основе сравнения показаний гироскопов на каждых соседних шагах вычислений.
Кроме того сами сигналы гироскопов предварительно скорректированы 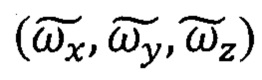 по формулам (55), (56)с учетом величин их угловых скоростей дрейфов
по формулам (55), (56)с учетом величин их угловых скоростей дрейфов 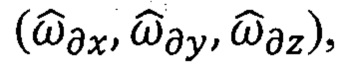 идентифицированных предварительно в предстартовых условиях по алгоритмам НРАВ.
идентифицированных предварительно в предстартовых условиях по алгоритмам НРАВ.
Точность решения задачи автономной ориентации ПО в предлагаемом способе МОДА увеличивается за счет - использования функционально избыточной информации на всех этапах (организации вычислений по ν вариантам информационных каналов на каждом μ-ом шаге вычислений),
- реализации операций осреднения оценок углов ориентации ПО на каждом μ-ом шаге вычислений,
- выполнения операций НРАВ в условиях использования расширенной магнитно-инерциальной информации 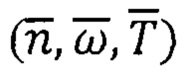 от трех блоков (ТБА, ТБГ, ТБМ).
от трех блоков (ТБА, ТБГ, ТБМ).
К числу недостатков способа МОДА следует отнести факт усложнения алгоритмов обработки расширенной многовекторной информации и увеличение требуемых показателей объема, производительности и скорости обработки информации, что в свою очередь, предъявляет повышенные требования к вычислительным характеристикам МК (табл. 1).
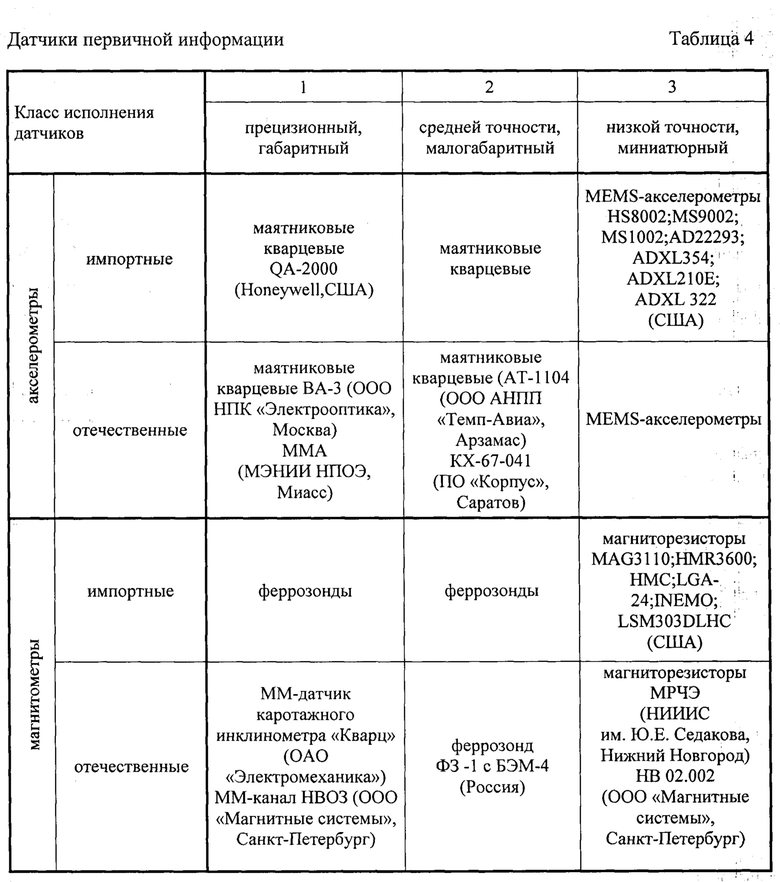
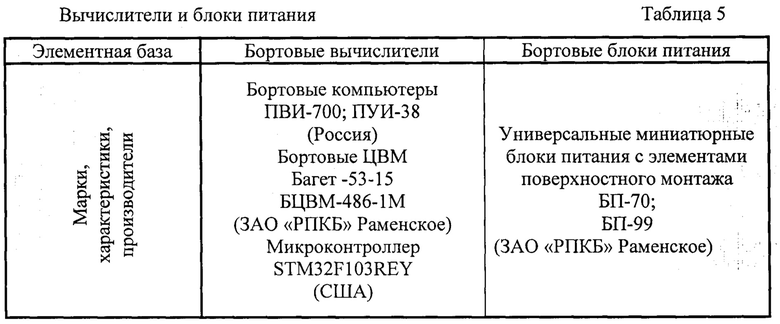
Практическая реализация предлагаемого способа МОДА может быть выполнена как на импортной, так и на отечественной элементной базе (табл. 4, 5).
Численные оценки расчетным путем показывают, что для реализации бесплатформенной системы ориентации (БСО) на основе предлагаемого способа МОДА с
допустимыми погрешностями ориентации ПО в пространстве в пределах 10'…20'
достаточно использовать в составе БСО блоки векторных датчиков, имеющих инструментальные погрешности и разрешающие способности не хуже пороговых значений:

что соответствует уровню достижимых показателей для существующих (табл. 4), а тем более для перспективных векторных датчиков.
Длина разрядной сетки МК в 24 бит, необходимая для обеспечения вычислительных операций при обработке информации с гарантированной точностью решения задачи автономной ориентации (с допустимой погрешностью и разрешающей способностью не хуже 1'') предполагает:
- измерение компонент вектора 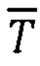 с помощью ТБМ с допустимой погрешностью ΔT≤0,3 нТл (с точностью до второго знака после запятой),
с помощью ТБМ с допустимой погрешностью ΔT≤0,3 нТл (с точностью до второго знака после запятой),
- измерение компонент вектора 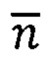 с помощью ТБА с допустимой погрешностью Δn≤5⋅10-5g(c точностью до пятого знака после запятой),
с помощью ТБА с допустимой погрешностью Δn≤5⋅10-5g(c точностью до пятого знака после запятой),
- вычисление в МК функций эйлеровых углов с допустимой погрешностью, не превышающей 0,001% (с точностью до шестого знака после запятой).
Для сравнения следует указать на то, что в современных цифровых пилотажно-навигационных комплексах обработку информации выполняют с длиной разрядной сетки в 16…32 знака.
Определение потребной частоты обновления информации связано с оценкой динамических свойств ПО, на котором предполагают реализовать БСО в соответствии с предлагаемым способом. Численный анализ показывает, что для самого динамичного канала крена (вращения) ПО частота обновления информации в БСО должна удовлетворять условию:

При допустимой погрешности δγ=1'' для высокоманевренного ПО (ωxm=360°/c=1 Гц) частота ν≈1 КГц. Для маломаневренных ПО эта частота обновления информации в БСО νш может быть снижена на 1…2 порядка. Частота обновления информации в пилотажном (БСО, νш), и навигационном (СНС, νц) должны удовлетворять условию согласования:

При частоте обновления навигационной информации νц=1…5 Гц (от СНС) условие (86) выполняется с большим запасом.
С другой стороны, шаговая частота обновления информации в БСО(νш) должна быть согласована с тактовой частотой (νТ) обработки приборной, геофизической и пилотажно-навигационной информации в МК:

При выборе современных бортовых вычислителей (табл. 4) условие (87) выполняется.
Немаловажным фактом в пользу предлагаемого способа бесплатформенной автономной ориентации ПО в пространстве является тот факт, что этот способ не накладывает никаких ограничений на выбор места установки ТБМ на объекте. В соответствии с требованиями отраслевого стандарта (ОСТ 1 00374-80 «Датчики магнитного курса. Требования к размещению на самолетах и вертолетах») в авиации существуют ограничения на выбор места установки на летательных аппаратах магнитометрических датчиков. Аналогичные ограничения существуют в морском флоте и ракетно-космической технике. Более того, для снижения уровня намагниченности плавающих аппаратов в морском флоте широко используют технологию размагничивания кораблей и подводных лодок.
В соответствии с алгоритмами обработки магнитометрической информации (17), (20), (21) в предлагаемом способе МОДА учитывают не только магнитные и электромагнитные свойства ПО, но и погрешности сборки ТБМ и ошибки его монтажа на объекте.
Кроме того, в соответствии с алгоритмами беслатформенной обработки информации (30)-(32), (табл. 1-3)
- сняты всякие ограничения на условия выполнения пространственных маневров ПО (т.е. обеспечиваются условия всеманевренности и всережимности работы БСО).
Для БСО, реализующей алгоритмы МОДА, важно выполнить три режима работы в 3 этапа:
- режим (этап) технологической подготовки,
- штатный режим (этап) работы,
- режим (этап) самотестирования и самодиагностики.
В конструктивном отношении БСО, реализующая способ МОДА, может быть построена по одному их трех вариантов:
- в виде единого моноблока (модуля),
- в виде набора отдельных блоков,
- в смешанном варианте.
Вычислитель БСО может быть реализован по схеме, встроенной в измерительный модуль конструкции или в виде отдельного вычислительного блока.
Особенность практической реализации предлагаемого изобретения заключается в том, что аппаратную часть системы выбирают исходя из конкретных требований, связанных с типом объекта, средой и условиями его применения, а достижение системой соответствующих функций обеспечивают за счет сменного универсального программно-алгоритмического обеспечения. Это означает, что предлагаемый способ может быть реализован как в существующих БСО, так и в проектируемых и перспективных разработках.
Для повышения показателей точности, надежности, самопроверяемости, отказоустойчивости и живучести БСО на аппаратном уровне блоки датчиков могут быть выполнены по схемам многоосных блоков неортогональных измерителей (гироскопов, магнитометров, ньютонометров) [6].
Анализ отечественной и зарубежной научно-технической литературы, и патентных источников за последние 30 лет показывает, что альтернативы предлагаемому изобретению в настоящее время не существует, а сам предлагаемый способ бесплатформенной автономной ориентации ПО обладает необходимыми признаками новизны, актуальности и перспективности.
Перечень литературных и патентных источников
1. Матвеев В.В., Распопов В.Я. Основы построения бесплатформенньгх инерциальных навигационных систем/Под общ. ред. д.т.н. В.Я. Распопова. - СПб.: ГНЦ РФ ОАО «Концерн «ЦНИИ «Электроприбор», 2009, -280 с.
2. Ориентация и навигация подвижных объектов. Современные информационные технологии / Под общ. ред. Б.С. Алешина, К.К. Верееменко, А.И. Черноморского.: - М.: Физматлит, 2006. -424 с.
3. Репников А.В., Сачков Г.П., Черноморский А.Н. Гироскопические системы: Учеб. пособие для авиац. вузов/Под ред. д.т.н. А.В. Репникова. - М.: Машиностроение, 1983. - 319 с.
4. Рахтеенко Е.Р.Гироскопические системы ориентации. -М.: Машиностроение, 1989.-232 с.
5. Микромеханические датчики и системы. Практические результаты и перспективы развития / XII Санкт-Петербургская международная конференция по интегрированным навигационным системам-СПб.: ГНЦ РФ ОАО «Концерн «ЦНИИ «Электроприбор», 2005, - С.262-275.
6. Проскуряков Г.М., Плотников П.К. Геометрия и кинематика пространственного состояния подвижных объектов: учебн. пособие / Сарат. техн. ун-т, Саратов, 2008. -155 с.
7. Шведов А.П. Комлексирование магнитометрических и инерциальных систем ориентации / А.П. Шведов, Ю.В. Иванов, Д.М. Малютин, Р.В. Алалуев, М.Г. Погорелов // Справочник. Инженерный журнал. Приложение №6, 2010 г. - С 15-19.
8. Руководство по Всемирной геодезической системе - 1984 (WGS-84)/-Международная организация гражданской авиации IKAO, изд.2ое, 2002, DOC 9674.
9. International Geomagnetic Reference Field IGRF WMM-20, URL: // WWW.ngdc.noaa.gov/com (дата обращения: 20.12.2021).
10. Силкин А.А. Синтез и анализ алгоритмов определения пространственной ориентации беспилотной аэродинамической платформы по измерениям магнитного поля Земли/диссерт. на соиск.уч. степени канд. техн. наук / Инст. машиноведения им.А.А. Благонравова РАН. - М., 2002.
11. Пат RU №2503 810 МПК Е21 В 47/22. Способ автономной ориентации инклинометра в скважине, опубл.10.01.2014.
12. Биндер Я.И. Падерина Т.В. Бесплатформенный инерциальный измерительный модуль: компасирование и калибровка на подвижном основании в условиях ограничения угловых перемещений / Гироскопия и навигация, №4 2003, С. 30-40.
13. Патент RU №2653967 С1 МПК G01 21/00 Способ автономной ориентации подвижных объектов / авторы: Проскуряков Г.М. и др. / Патентообладатель-ФГБОУ ВО Сарат. госуд. техн. ун-т им.Гагарина Ю.А. от 20.06.2017, опубл. 15.05.2018, Бюлл. №14.
14. Игнатьев А.А., Проскуряков Г.М. Гетеромагнитометрия: алгоритмы, методики, калибровки блоков магнитометров. Саратов: Изд-во Сарат. ун-та, 2014. - 152 с.
15. Патент RU №2757828 МПК G05D 1/00; G05В 23/00; G 06 F 11/00. Способ восстановления векторной информации в информационно-измерительных системах / авторы: Проскуряков Г.М., Голованов П.Н., Пыльский В.А. / Патентообладатель - ФГБОУ ВО Сарат.госуд. техн. ун-т им. Гагарина Ю.А. от 15.12.2020, опубл.21.10.2021, Бюлл. №30.
16. Бранец В.Н. Лекции по теории бесплатформенных инерциальных навигационных систем управления: Учеб. пособие. - М.: МФТИ,2009. - 304 с.
17. Андреев В.Д. Теория инерциальной навигации. Автономные системы. - М.: Наука, 1967. - 647 с.
18. Андреев В.Д. Теория инерциальной навигации. Корректируемые системы., - М.; Наука,1966. - 579 с.
19. Резниченко В.И., Левит Г.А.Определение скорости по сигналам спутниковых навигационных систем. - СПб.: ГНИНГИ МО РФ, 2004. - 88 с.
20. Литманович Ю.А., Марк ДЖ.Г.Прогресс в разработке алгоритмов БИНС на Западе и Востоке в материалах Санкт-Петербургских конференций: Обзор за десятилетие / Гироскопия и навигация, №3(42), 2003, С. 52-67.
21. Лесючевский В.М., Литманович Ю.А.Новые подходы в разработке дискретных алгоритмов выработки параметров поступательного движения объекта в инерциальных навигационных системах / Гироскопия и навигация, №2(5), 1994, С. 39-58.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ автономной ориентации объектов в околоземном пространстве | 2022 |
|
RU2787971C1 |
| СПОСОБ БЕСПЛАТФОРМЕННОЙ ОРИЕНТАЦИИ ПОДВИЖНЫХ ОБЪЕКТОВ | 2022 |
|
RU2784859C1 |
| АВТОНОМНЫЙ КОМПЛЕКС ДЛЯ КОРРЕКЦИИ ИНЕРЦИАЛЬНЫХ СИСТЕМ ПЛАТФОРМЕННОЙ ОРИЕНТАЦИИ И НАВИГАЦИИ ПОДВИЖНЫХ ОБЪЕКТОВ | 2022 |
|
RU2826826C2 |
| СПОСОБ БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ | 2022 |
|
RU2806707C1 |
| СПОСОБ АВТОНОМНОЙ ОРИЕНТАЦИИ ПОДВИЖНЫХ ОБЪЕКТОВ | 2017 |
|
RU2653967C1 |
| Способ восстановления векторной информации в информационно-измерительных системах | 2020 |
|
RU2757828C1 |
| СПОСОБ ПЕРСОНАЛЬНОЙ АВТОНОМНОЙ НАВИГАЦИИ | 2013 |
|
RU2523753C1 |
| Способ автономной ориентации подвижного объекта с помощью инерциального измерительного модуля | 2019 |
|
RU2738342C1 |
| ИНТЕГРИРОВАННАЯ СИСТЕМА ОРИЕНТАЦИИ И НАВИГАЦИИ ДЛЯ ОБЪЕКТОВ С БЫСТРЫМ ВРАЩЕНИЕМ ВОКРУГ ПРОДОЛЬНОЙ ОСИ | 2014 |
|
RU2561003C1 |
| Астроинерциальная навигационная система с коррекцией по гравитационному полю Земли | 2023 |
|
RU2820600C1 |
Изобретение относится к способу автономной инерциальной ориентации подвижных объектов. Для ориентации подвижных объектов измеряют вектор абсолютной угловой скорости вращения, вектор кажущегося ускорения объекта в инерциальном пространстве и вектор напряженности геомагнитного поля с помощью предварительно откалиброванных трехосных блоков гироскопов, акселерометров, магнитометров, производят обработку полученной многовекторной информации по дискретным интегральным алгоритмам определенным образом. Обеспечивается устранение инструментальных и методических погрешностей, упрощение алгоритмов обработки информации. 2 ил., 5 табл.
Способ автономной инерциальной ориентации подвижных объектов, заключающийся в измерении вектора абсолютной угловой скорости вращения, вектора кажущегося ускорения объекта в инерциальном пространстве и вектора напряженности геомагнитного поля с помощью предварительно откалиброванных трехосных блоков гироскопов, акселерометров, магнитометров и в последующей обработке полученной многовекторной информации по дискретным интегральным алгоритмам с учетом оценок начальных значений углов предстартовой ориентации объекта, определенных предварительно при начальной автономной выставке, отличающийся тем, что сначала идентифицируют оценку вектора угловой скорости собственного дрейфа гироскопов в предстартовых условиях в процессе проведения операций начальной расширенной автономной выставки, а затем учитывают оценку этого вектора вместе с технологической и предстартовой информацией, полученной при проведении операций технологических калибровок и начальной вставки, при обработке информации об изменениях сигналов гироскопов и магнитометров на каждом шаге вычислений по многовариантным дифференциальным алгоритмам автономной инерциальной ориентации объектов в условиях функциональной избыточности информации.
| СПОСОБ КОРРЕКЦИИ БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ | 2014 |
|
RU2564380C1 |
| Способ автономной ориентации объектов в околоземном пространстве | 2022 |
|
RU2787971C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ ПОДВИЖНЫХ ОБЪЕКТОВ И КОМПЛЕКСИРОВАННАЯ НАВИГАЦИОННАЯ СИСТЕМА ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2009 |
|
RU2395061C1 |
| EP 3073226 B1, 22.05.2019 | |||
| FR 2961305 B1, 22.06.2012. | |||
Авторы
Даты
2023-07-31—Публикация
2022-11-28—Подача