Общая область техники
Настоящее изобретение относится к области систем автоматизированного проектирования.
Более конкретно, оно касается способа моделирования детали, в частности, лопаточного колеса.
Уровень техники
Необходимость постоянного повышения эффективности работы оборудования, в частности, авиационного оборудования, например, роторов газотурбинных двигателей (то есть узла, образованного ступицей, на которой закреплены расположенные радиально лопатки, как показано на фиг. 1а), в настоящее время требует использования информативных инструментов моделирования.
Эти инструменты позволяют проектировать детали, автоматически оптимизируя некоторые из их характеристик. В случае лопаточного колеса (то есть узла, образованного лопатками диска газотурбинного двигателя, часть которого показана на фиг. 1b) принцип состоит в определении аэромеханического и/или акустического геометрического оптимума, закономерностей лопатки лопаточного колеса, то есть одной или нескольких кривых, описывающих значение физической величины (примеры будут представлены ниже) вдоль сечения или высоты лопатки в данной окружающей среде, посредством выполнения большого числа вычислений моделирования.
Для этого необходимо определить параметры закономерности, которую необходимо оптимизировать, то есть представить ее в виде функции N входных параметров. При этом оптимизация состоит в изменении (как правило, случайном) этих различных параметров под напряжением вплоть до определения их оптимальных значений по заранее определенному критерию. Затем на основании определенных опорных точек посредством интерполяции получают «гладкую» кривую.
Число необходимых вычислений напрямую (линейно и даже экспоненциально) связано с числом входных параметров задачи.
Существуют самые разные методы определения параметров закономерности, в частности, можно указать две большие категории:
- Дискретная модель: закономерность определяют по положению множества точек (на практике от 5 до 10 для закономерности по высоте и от 50 до 200 для сечения), поочередно перемещаемых во время оптимизации;
- Параметрическая модель: закономерность определяют через математические кривые, известные в литературе, такие как кривые Безье или кривые NURBS (неоднородные рациональные В-сплайны).
Желательно использовать большое число параметров для повышения качества закономерности (это является основополагающим фактором при проектировании лопаточных колес), однако такой подход ограничен мощностью и ресурсами современных процессоров.
Даже при использовании дорогих сверхмощных вычислительных машин время, необходимое для моделирования одной закономерности, остается достаточно большим.
Отмечается также то, что в присутствии большого числа параметров появляются проблемы: определяемые закономерности имеют слишком большое число опорных точек, которые необходимо соблюдать, и первые получаемые кривые оказываются чрезмерно «волнистыми» (что называют феноменом Рунге), что не позволяет их использовать в таком состоянии. Необходимо их трансформировать, чтобы они стали достаточно сглаженными, что приводит к увеличению времени, необходимого для получения результатов.
По всем этим причинам используют почти исключительно параметрические модели (с применением математических кривых), поскольку, как отмечается, они требуют почти в пять раз меньше параметров для модулирования закономерности равнозначного качества.
Однако отмечается, что даже при использовании параметрических моделей высокого уровня число параметров, необходимое для достаточного качества моделирования при современных стандартах, остается проблематичным (порядка десятка параметров).
Поэтому существует потребность в способе параметризации и оптимизации закономерностей лопатки (или любой другой детали), который будет более экономичным с точки зрения использования информативных ресурсов, который позволяет сохранить и даже повысить качество моделирования и одновременно ограничить риски появления «волнистых» кривых.
Раскрытие изобретения
Первый объектом изобретения является способ моделирования детали, отличающийся тем, что включает в себя осуществление следующих этапов при помощи средств обработки данных устройства:
(a) Параметризация кривой класса С1, отображающей значение характеристической физической величины указанной детали в зависимости от положения вдоль по меньшей мере части детали, при этом кривая образована:
a. Двумя крайними точками, определяющими протяженность указанной части детали;
b. По меньшей мере одной промежуточной точкой, расположенной между крайними точками;
c. По меньшей мере двумя кривыми Безье, соединенными на уровне указанной промежуточной точки;
при этом параметризацию осуществляют по одному или нескольким параметрам, определяющим указанную промежуточную точку;
(b) Определение оптимизированных значений указанных параметров указанной кривой;
(c) Воспроизведение определенных значений на интерфейсе указанного устройства.
Кривые Безье являются параметрическими полиномиальными кривыми, определяемыми как комбинации из N+1 элементарных многочленов, называемых многочленами Бернштейна: кривую Безье определяют совокупностью точек 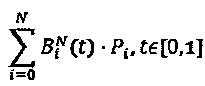 , при этом
, при этом 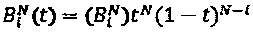 являются N+1 многочленами Бернштейна степени N.
являются N+1 многочленами Бернштейна степени N.
Точки 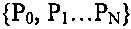 называются «имплицитными» контрольными точками кривой и представляют собой переменные, благодаря которым можно моделировать закономерность лопатки при помощи кривой Безье.
называются «имплицитными» контрольными точками кривой и представляют собой переменные, благодаря которым можно моделировать закономерность лопатки при помощи кривой Безье.
Эти точки называют «имплицитными», так как кривую Безье можно рассматривать как совокупность барицентров N+1 взвешенных контрольных точек с весовым коэффициентом, равным значению многочлена Бернштейна, соответствующего каждой контрольной точке. Иначе говоря, эти точки действуют как локальные точки, притягивающие кривую, которая при этом, как правило, через них не проходит (кроме первой и последней точек, соответствующих t=0 и t=1, и некоторых случаев совмещения точек по прямой).
Как правило, в известных методах моделирования закономерности с использованием кривой Безье крайние контрольные точки Р0 и PN используемой кривой являются фиксированными (они определяют протяженность части детали, в частности, лопатки лопаточного колеса, на которой будут производить моделирование), но другие точки 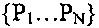 имеют подвижные координаты, образующие входные параметры для алгоритма оптимизации.
имеют подвижные координаты, образующие входные параметры для алгоритма оптимизации.
В рамках настоящего способа моделирования предложено параметрировать закономерность не через имплицитные контрольные точки сложной кривой Безье, а только через точки сопряжения (называемые «промежуточными контрольными точками пользователя (PCU)) множества элементарных кривых Безье.
Кроме того, в отличие от известных решений, в которых предлагается определять контрольные точки только по их координатам (x, y), в рамках настоящего способа предпочтительно в качестве дополнительных входных параметров предложено использовать также критерии, например, связанные с касательными.
Иначе говоря, вместо моделирования закономерности только через положения большого числа имплицитных контрольных точек используют до пяти параметров небольшого числа эксплицитных контрольных точек.
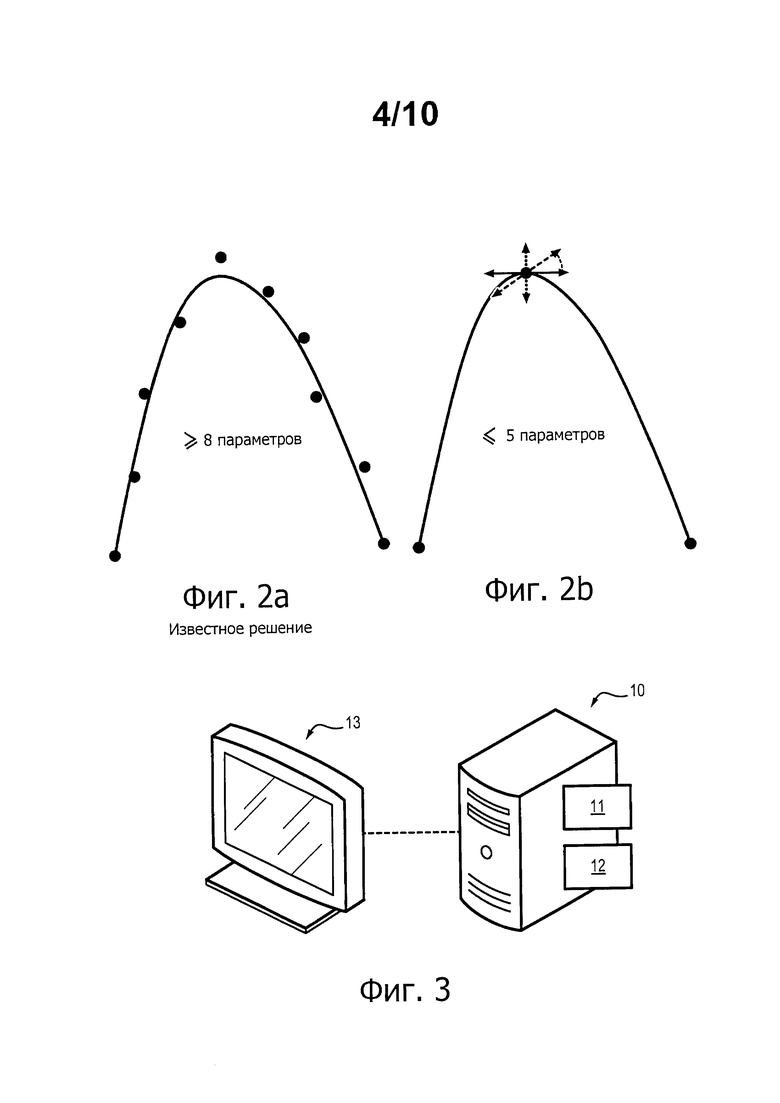
Фиг. 2а и 2b иллюстрируют этот принцип путем сравнения необходимых контрольных точек в известном способе и в заявленном способе. Заявитель установил, что этот новый метод, используя в два раза меньше параметров (и даже в некоторых случаях на 60% меньше), позволяет получить эквивалентное качество моделирования. Это позволяет существенно сократить время и/или необходимую мощность вычисления.
Кроме того, независимо от числа параметров, число контрольных точек уменьшается в три и даже в четыре раза (поскольку в промежуточных контрольных точках сконцентрировано большее число параметров). Таким образом, практически решается проблема нежелательного явления «волнистости», связанного со слишком большим числом опорных точек кривой.
Согласно другим предпочтительным и не ограничительным признакам:
- параметр или параметры, определяющие промежуточную точку, выбирают из группы, в которую входят абсцисса точки, ордината точки, ориентация касательной к кривой на уровне точки и два коэффициента натяжения, каждый из которых связан с полукасательной к кривой на уровне точки;
- параметризацию осуществляют также по одному или нескольким параметрам, определяющим по меньшей мере одну из крайних точек;
- параметр или параметры, определяющие крайнюю точку, выбирают из группы, в которую входят абсцисса точки, ордината точки, ориентация касательной к кривой на уровне точки и коэффициент натяжения, связанный с полукасательной к кривой на уровне точки;
- коэффициент натяжения, связанный с полукасательной к кривой на уровне промежуточной или крайней точки, является функцией значения производной второго порядка кривой вблизи точки;
- указанная кривая образована К-1 промежуточными точками, упорядоченными по протяженности указанной части детали, и К кривыми Безье, при К≥2;
- 1-ю кривую Безье определяют в интервале между крайней точкой, соответствующей началу указанной части детали, и 1-й промежуточной точкой, и К-ю кривую Безье определяют в интервале между К-1-ой промежуточной точкой и крайней точкой, соответствующей концу указанной части детали;
- К≥3, при этом i-ю или каждую из i-х кривых Безье определяют в интервале между i-1-ой промежуточной точкой и i-й промежуточной точкой;
- каждую кривую Безье полностью определяют по точкам, образующим ее концы;
- деталь выбирают из группы, в которую входят лопаточное колесо, площадка газотурбинного двигателя, зеркало заднего вида, элерон, крыло или несущий винт, хвостовое оперение, фюзеляж, воздушный винт, сопло, проточный тракт, обтекатель и турбины;
- деталь является лопаточным колесом, при этом часть детали является частью лопатки лопаточного колеса;
- указанная часть лопатки лопаточного колеса является частью сечения лопатки лопаточного колеса или высоты лопатки лопаточного колеса;
- указанную характеристическую физическую величину указанного лопаточного колеса выбирают из группы, в которую входят толщина лопаточного колеса, осевая линия, закономерность угла осевой линии сечения лопатки лопаточного колеса, закономерность максимальной толщины, закономерность положения максимальной толщины, угол стреловидности и двугранный угол, закономерность набора сечений, входной/выходной углы лопатки лопаточного колеса по высоте.
Вторым объектом изобретения является способ изготовления детали, содержащий следующие этапы:
- осуществляют способ, являющийся первым объектом, чтобы моделировать по меньшей мере часть детали;
- изготавливают указанную деталь в соответствии с моделью указанной по меньшей мере части детали.
Третьим объектом изобретения является устройство для моделирования детали, отличающееся тем, что содержит средства обработки данных, выполненные с возможностью применять:
- Модуль параметризации кривой класса С1, отображающей значение характеристической физической величины указанной детали в зависимости от положения вдоль по меньшей мере части детали, при этом модуль определяет кривую:
a. по двум крайним точкам, определяющим протяженность указанной части детали;
b. по меньшей мере по одной промежуточной точке, расположенной между крайними точками;
c. по меньшей мере по двум кривым Безье, соединенным на уровне указанной промежуточной точки;
при этом параметризацию осуществляют по одному или нескольким параметрам, определяющим указанную промежуточную точку;
- Модуль определения оптимизированных значений указанных параметров указанной кривой;
- Модуль воспроизведения определенных значений на интерфейсе указанного оборудования.
Четвертым и пятым объектами изобретения являются соответственно компьютерный программный продукт, содержащий командные коды для осуществления способа моделирования детали, являющегося первым объектом изобретения; и средство хранения информации, которое выполнено с возможностью считывания информативным устройством и на котором компьютерный программный продукт содержит командные коды для осуществления способа моделирования детали, являющегося первым объектом изобретения.
Описание чертежей
Другие отличительные признаки и преимущества настоящего изобретения будут более очевидны из нижеследующего описания предпочтительного варианта выполнения со ссылками на прилагаемые чертежи, на которых:
Фиг. 1а (уже описана) - пример газотурбинного двигателя.
Фиг. 1b (уже описана) - пример лопаточного колеса, для которого применяют заявленный способ.
Фиг. 1c-1d - сечение лопатки лопаточного колеса.
Фиг. 2а-2b (уже описаны) - сравнение параметризации кривой при помощи известного способа и при помощи заявленного способа.
Фиг. 3 - система для осуществления заявленного способа.
Фиг. 4 - кривая, используемая в рамках заявленного способа.
Фиг. 5а-5е - примеры, иллюстрирующие применение изобретения для закономерности толщины на лопатке лопаточного колеса.
Фиг. 6а-6е - примеры, иллюстрирующие применение изобретения для закономерности угла осевой линии на лопатке лопаточного колеса.
Осуществление изобретения
Настоящий способ предпочтительно предназначен для моделирования детали газотурбинного двигателя, в частности, лопаточного колеса (любого лопаточного колеса), однако он не ограничивается этой деталью и даже областью авиации. При помощи этого способа можно моделировать и оптимизировать любую «деталь», то есть любой промышленно изготавливаемый элемент, дизайн которого соответствует внешним физическим условиям (в частности, аэромеханического и/или акустического, а также гидродинамического типа).
В дальнейшем тексте описания в качестве примера будет рассмотрена лопатка лопаточного колеса, но специалист может транспонировать способ, например, чтобы моделировать:
- в области турбореактивных двигателей: проточные тракты (внутреннюю и наружную стенки каждого из потоков), 3D-площадки (не осесимметричный дизайн площадки моноблочного лопаточного диска или обечайки спрямляющего аппарата). На фигуре 1а от входа к выходу газотурбинного двигателя последовательно представлены примеры зон газотурбинного двигателя, для которых моделирование при помощи настоящего способа представляет особый интерес: так называемая «С-образная» часть проточного тракта (то есть участок проточного тракта, расположенный между выходом компрессора низкого давления и входом компрессора высокого давления, турбина (на выходе камеры сгорания) и сопло (на выходе турбины);
- в автомобильной области (в частности, для «Формулы 1»): зеркала заднего вида, элероны;
- в области авиации: крыло самолета, хвостовые оперения, фюзеляж, лопасти винта вертолета, хвостовое оперение вертолета, воздушные винты самолета;
- в космической области: реактивное сопло ракетного двигателя (и в целом дизайн любого типа сопла);
- в железнодорожной области: передние и задние обводы поезда;
- в области гидродинамики: лопасти, используемые в чанах обработки воды, лопасти вентилятора, винты судна, лопатки турбины гидростанции;
- и многие другие детали в различных областях, например, форма руля велосипеда или мотоцикла.
Понятно, что настоящий способ представляет интерес для моделирования любой детали, которая должна быть подвижной относительно входящей с ней в контакт текучей среды и форма которой влияет на характеристики, в частности, деталей транспортного средства (в самом широком смысле: наземного, морского, воздушного, космического и т.д.) и промышленных вращающихся деталей (лопасти, турбины и т.д.). В области газотурбинных двигателей деталь 1 предпочтительно выбирают из группы, в которую входят лопаточное колесо, площадка, проточный тракт и сопло (газотурбинного двигателя).
Показанное на фиг. 1b лопаточное колесо содержит множество лопаток 2 (на фигуре показано основание одной лопатки), расположенных радиально от центральной части диска. На фиг. 1с представлен вид части лопатки 2, на которой идентифицировано «сечение» лопатки 2, проходящее от передней кромки ВА к задней кромке BF. Под сечением следует понимать поперечное сечение лопатки 2.
На фиг. 1d более детально показано это сечение BA-BF (можно заметить вогнуто-выпуклый профиль). Следует отметить «хорду», то есть прямую линию, которая соединяет крайние точки сечения. Как будет показано ниже, эта хорда служит ориентиром для определения расположения точек вдоль сечения. На этой фиг. 1d показана также центральная линия или «осевая линия» лопатки 2. Ортогонально к сечению находится «высота» лопатки 2. На фигуре показаны и будут описаны ниже различные физические величины лопатки. Как было указано выше, эти величины можно моделировать вдоль сечения или высоты лопатки 2.
Такое лопаточное колесо моделируют в ходе его проектирования при помощи информативного устройства 10, показанного на фиг. 3. Оно содержит средства 11 обработки данных (один или несколько процессоров), средства 11 хранения данных (например, один или несколько жестких дисков), интерфейсные средства 13 (включающие в себя средства ввода, такие как клавиатура и мышь или сенсорный интерфейс, и средства воспроизведения, такие как экран для отображения результатов). Предпочтительно устройством 10 является сверхмощная вычислительная машина, но, понятно, что можно способ можно осуществлять на самых разных платформах.
Можно выбирать самые разные критерии, оптимизируемые во время моделирования лопатки или другой детали. Например, в случае лопатки можно попытаться максимизировать ее механические свойства, такие как стойкость к механическим напряжениям, частотные реакции лопатки, перемещения лопатки, аэродинамические свойства, такие как КПД, повышение давления, пропускная способность или граница помпажа и т.д.
Параметризация
Этап (а), осуществляемый при помощи средств 11 обработки данных под контролем оператора, является первым этапом параметризации кривой, отображающей значение характеристической физической величины указанного лопаточного колеса 1 (или любой другой детали) в зависимости от положения вдоль по меньшей мере части лопатки 2 лопаточного колеса 1 (или, в целом, части детали), в частности, части сечения или высоты лопатки 2. Под «частью сечения» следует понимать все или часть пространства, расположенного от передней кромки ВА до задней кромки BF. Под «частью высоты» следует понимать все или часть пространства, расположенного от проксимального конца к дистальному концу лопатки 2.
В дальнейшем тексте настоящего описания будет рассмотрен пример сечения лопатки 2, однако понятно, что способ можно транспонировать на любую определенную часть пространства детали.
Как было указано выше, положение вдоль кривой выражают в зависимости от длины кривой (по оси абсцисс) и, в частности, «нормализованной» длины хорды, то есть выраженной от 0 до 1, если пресекать лопатку 2, чтобы достичь проекции (ортогональной) этой точки на хорде. Иначе говоря, это соответствует координате х, которую точка сечения имела бы в ортонормированной системе координат, в которой точка ВА в качестве координат имела бы (0,0), а точка BF - (0,1). Например, точка сечения, соответствующая «нормализованной» длине сечения «0,5», находится на медиатрисе хорды. Следует отметить, что, поскольку кривая может располагаться только на части (сплошной) сечения лопатки, соответствующую функцию определяют в подинтервале [0,1].
Однако понятно, что изобретение ни в коем случае не ограничивается выражением кривой, отображающей значение величины в зависимости от длины хорды, и можно использовать другие точки отсчета.
Эту кривую, отображающую значение физической величины, следует рассматривать как моделирование закономерности этой физической величины (в связи с этим ее называют «кривой моделирования», чтобы отличать ее от кривых Безье с точки зрения терминологии). Указанная физическая величина может быть любой величиной, имеющей аэромеханическое и/или акустическое значение при проектировании деталей, и в случае лопаточного колеса в качестве не ограничительных примеров можно указать:
- Функция хорды (видение в сечении)
° Закономерность толщины
° Закономерность угла осевой линии
- Функция высоты лопатки (объемное видение)
° Максимальная толщина, положение максимальной толщины
° Закономерности стреловидности и двугранного угла (BA, BF, …)
° Закономерность набора сечений
° Закономерности входных/выходных углов (β1, β2).
Соответствующие примеры будут представлены ниже.
В случае, когда деталь 1 является соплом, физической величиной может быть сечение сопла, что позволяет определять минимальное сечение сопла, контролировать изменение эффективного числа Маха в сопле и т.д. В случае проточного тракта, физической величиной может быть сечение проточного тракта, соотношение сечения (входное сечение/выходное сечение), замедление (которое является соотношением между выходной скоростью и входной скоростью. Кроме всего прочего, этот параметр позволяет судить о способности текучей среды следовать необходимым изменениям угла).
Кривая моделирования имеет класс равномерности не менее С1, то есть она соответствует непрерывной функции, и имеет по меньшей мере 1-ю непрерывную производную на своем пространстве образования (части детали). Далее будет показано значение этого условия. На практике, полученная кривая является С∞ по кускам (бесконечно дифференцируемые функции на каждом интервале) с непрерывностью кривой и производной на уровне сопряжений (промежуточные контрольные точки). Понятно, что речь идет о минимальных условиях и что кривая вполне может быть С∞ на всем пространстве образования.
Кривую определяют при помощи ее контрольных точек. Как в известных решениях, устанавливают две крайние контрольные точки пользователя PCU0 и PCUK, которые определяют протяженность части детали (то есть область образования кривой). Кроме того, кривая моделирования содержит по меньшей мере одну промежуточную контрольную точку пользователя PCUi, i∈[1,K-1], расположенную между этими двумя крайними точками PCU0 и PCUK.
Промежуточная точка или промежуточные точки являются «эксплицитными» контрольными точками, так как через них проходит кривая. Действительно, эта кривая содержит по меньшей мере две кривых Безье, соединенных на уровне указанной промежуточной точки.
Как видно, например, из фиг. 4, кривая моделирования может состоять только из последовательности кривых Безье, каждая из которых проходит между одной из крайних точек PCU0, PCUK и промежуточной точкой PCUi или между двумя промежуточными т очками PCUi и PCUi+1.
Иначе говоря, все контрольные точки пользователя PCU0, PCU1 … PCUK-1, PCUK (крайние или промежуточные) кривой являются крайними точками Р0, PN кривой Безье.
Поскольку кривая является кривой класса С1, это предполагает, что каждая промежуточная точка PCUi обеспечивает непрерывность, в том числе на производной (даже касательной).
Как будет видно из примеров, использования только одной промежуточной точки PCU1 (то есть двух кривых Безье) достаточно для очень удовлетворительного построения кривой, отображающей закономерность. Вместе с тем, понятно, что способ можно обобщить до использования К-1 (при К≥2) промежуточных точек PCUi, i∈[1,K-1], упорядоченных по протяженности указанной части 1 детали (лопатки 2 в случае лопаточного колеса), то есть К кривых Безье (по одной между каждой парой контрольных точек 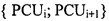 ).
).
Во всех случаях кривая моделирования содержит по меньшей мере две «крайних» кривых Безье, то есть кривые, концом которых является одна из двух крайних контрольных точек пользователя PCU0 и PCUK: первая кривая Безье образована в интервале между крайней точкой PCU0, соответствующей началу указанной части детали 1, и 1-й промежуточной точкой PCU1, и К-я кривая Безье (другая крайняя кривая) образована в интервале между К-1-ой промежуточной точкой PCUК-1 и крайней точкой PCUК, соответствующей концу указанной части детали 1.
Иначе говоря, в случае по меньшей мере двух промежуточных точек PCUi, если К≥3, кривая моделирования содержит «промежуточные» кривые Безье: каждая из i-ых (∀i i∈[1,K-1] кривых Безье образована в интервале между i-1-й промежуточной точкой PCUi-1 и i-й промежуточной точкой PCUi.
Параметры контрольной точки пользователя
Обработка служит для параметризации кривой моделирования не в зависимости от параметров имплицитных контрольных точек кривой Безье, а в зависимости от параметров промежуточных (и, возможно, крайних) контрольных точек, образующих концы кривых Безье, составляющих кривую моделирования.
В частности, каждая кривая Безье может быть полностью определена точками PCU, образующими ее концы. Иначе говоря, параметры точек PCU (с точки зрения координат и производных) служат условиями пределов при вычислении при помощи средств 11 обработки данных координат имплицитных контрольных точек различных кривых Безье, которые выбирают с достаточной минимальной степенью, чтобы удовлетворять этим предельным условиям. При этом этап (а) включает в себя определение имплицитных точек кривых Безье в зависимости от параметров точек PCU, образующих их концы.
Параметр или параметры, определяющие промежуточную точку PCUi, выбирают из группы, в которую входят абсцисса точки, ордината точки, ориентация касательной к кривой на уровне точки и два коэффициента натяжения, каждый из которых связан с полукасательной к кривой на уровне точки.
Учитывая, что кривая является кривой класса С1 (непрерывная производная), ориентация касательной должна быть одинаковой по обе стороны от промежуточной точки PCUi. С другой стороны, «длина» двух полукасательных может быть разной по обе стороны от точки и выражает стремление каждой кривой Безье «примыкать» к касательной с двух сторон от точки. Именно это и моделируют вышеупомянутые «коэффициенты натяжения».
В частности, каждый коэффициент натяжения, связанный с полукасательной к кривой на уровне промежуточной точки, является функцией значения производной второго порядка кривой вблизи точки. Действительно, значение производной второго порядка вблизи контрольной точки выражает «скорость», с которой кривая отходит от касательной.
Тот факт, что кривая моделирования не обязательно является кривой класса С2, допускает прерывистость производной второго порядка на уровне промежуточных точек.
В случае параметризации крайней точки PCU0 и PCUK параметр или параметры, определяющие эту крайнюю точку, выбирают из группы, в которую входят абсцисса точки, ордината точки, ориентация касательной к кривой на уровне точки, и коэффициент натяжения, связанный с полукасательной к кривой на уровне точки.
Иначе говоря, можно учитывать только полукасательную в области образования кривой (то есть полукасательную справа для PCU0 и слева для PCUK).
Необходимо отметить, что не обязательно реально использовать вышеупомянутые параметры (в частности, для крайних точек). Действительно, в большинстве случаев один или несколько из этих параметров (абсцисса точки, ордината точки, ориентация касательной к кривой на уровне точки, и два коэффициента натяжения, связанные, каждый, с полукасательной к кривой на уровне точки) имеют заранее определенное значение, зафиксированное пользователем, и, следовательно, их не используют в качестве «переменных» в ходе способа.
Примеры
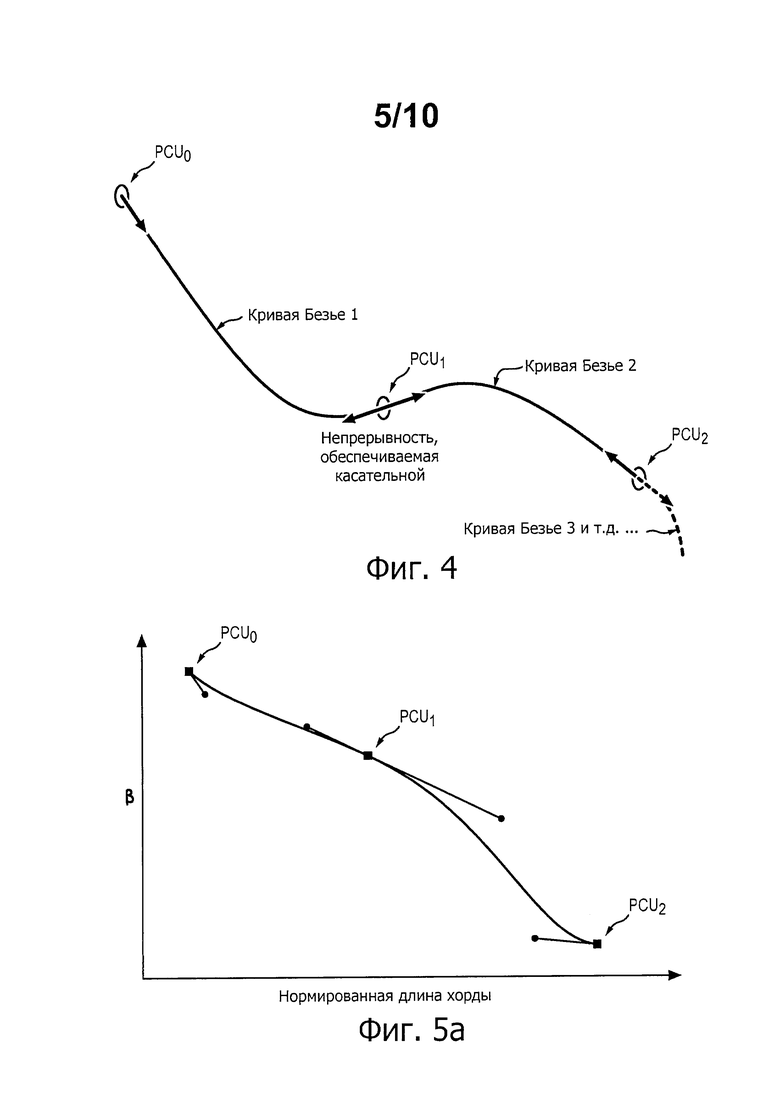
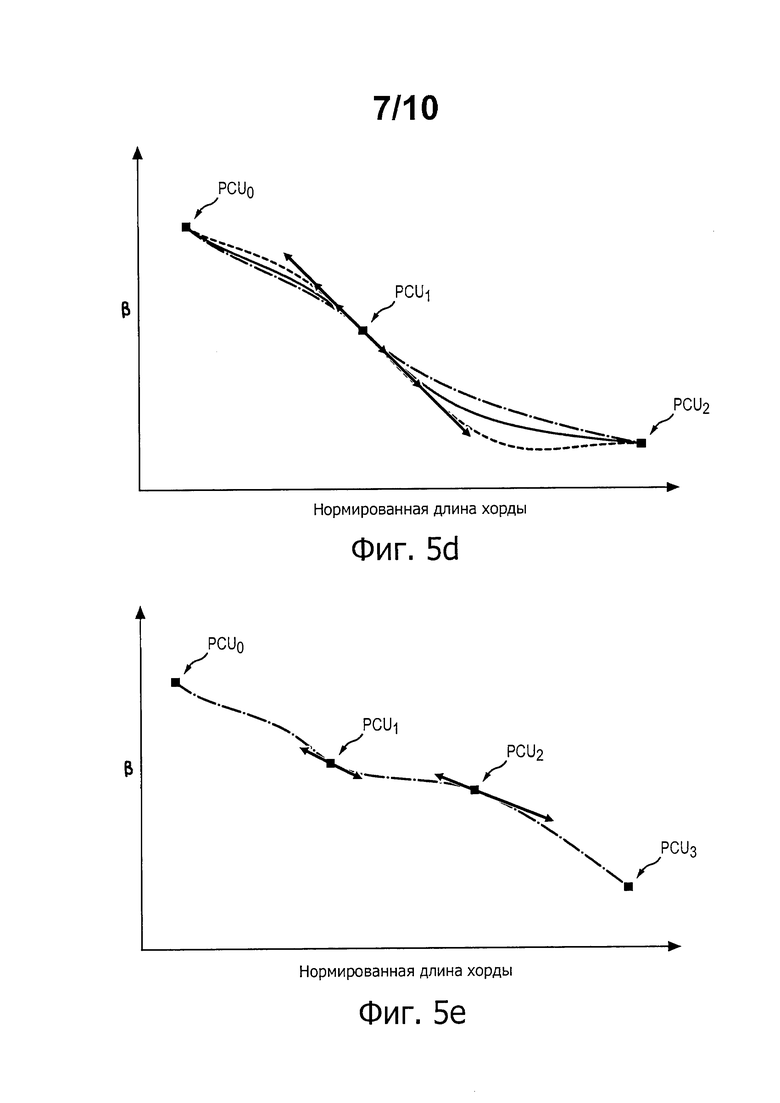
На фиг. 5а-5е представлены различные кривые, которые можно использовать при моделировании величины, называемой «закономерностью угла осевой линии (β)», которая соответствует производной осевой линии сечения лопатки 2 (см. фиг. 1d).
На фиг. 5а закономерность моделируют, используя только одну промежуточную точку PCU1 с более значительным натяжением справа, чем слева.
На фиг. 5b учитываемым параметром является координата у промежуточной точки PCU1. Здесь показаны 3 варианта кривой, соответствующие трем разным значениям этого параметра.
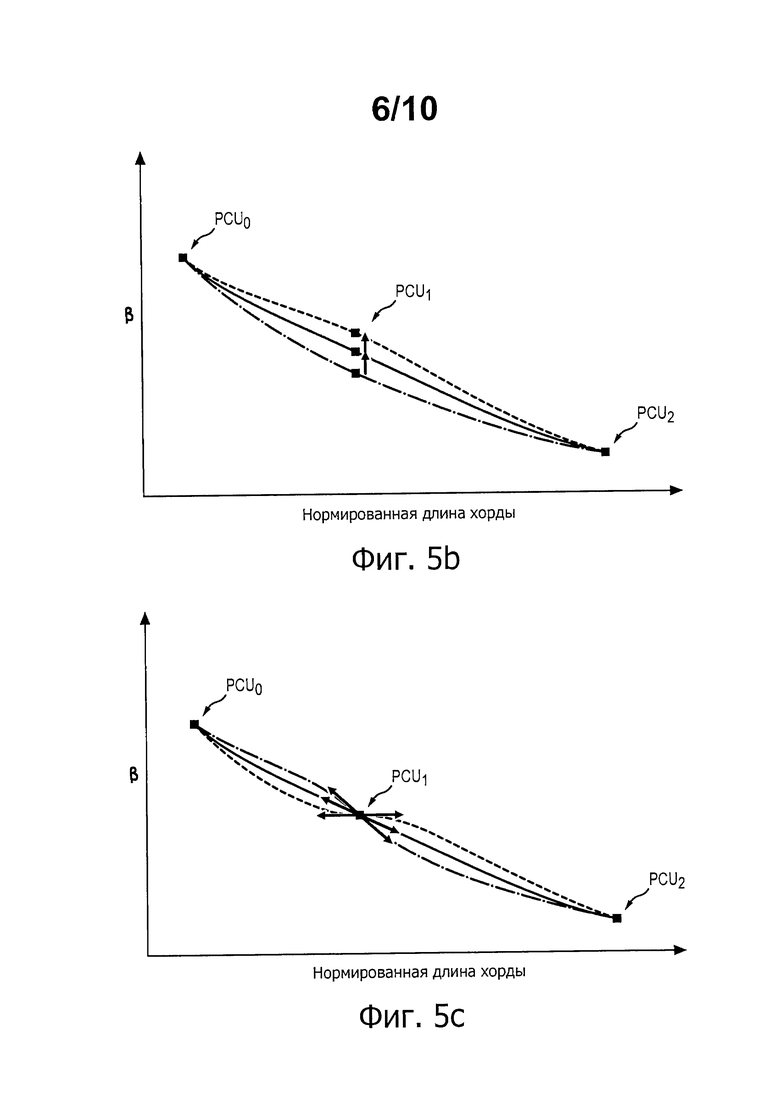
На фиг. 5с учитываемым параметром является ориентация касательной к кривой на уровне промежуточной точки PCU1 (иначе говоря, значение производной в этой точке). Здесь показаны 3 варианта кривой, соответствующие трем разным значениям этого параметра.
В примере на фиг. 5d учитывают два параметра, а именно коэффициенты натяжения, каждый из которых связан с полукасательной к кривой на уровне промежуточной точки PCU1. Здесь показаны 3 варианта кривой, соответствующие трем парам значений для этих параметров.
На фиг. 5е показан альтернативный пример, в котором используют две промежуточные точки PCU1 и PCU2.
На фиг. 6а-6е представлены различные кривые, которые можно использовать при моделировании величины, называемой «закономерностью толщины», которая соответствует просто толщине лопатки 2 вдоль сечения.
На фиг. 6а закономерность моделируют, используя только одну промежуточную точку PCU1 с горизонтальной касательной (локальный максимум).
На фиг. 6b учитываемым параметром является координата y промежуточной точки PCU1. Здесь показаны 3 варианта кривой, соответствующие трем разным значениям этого параметра.
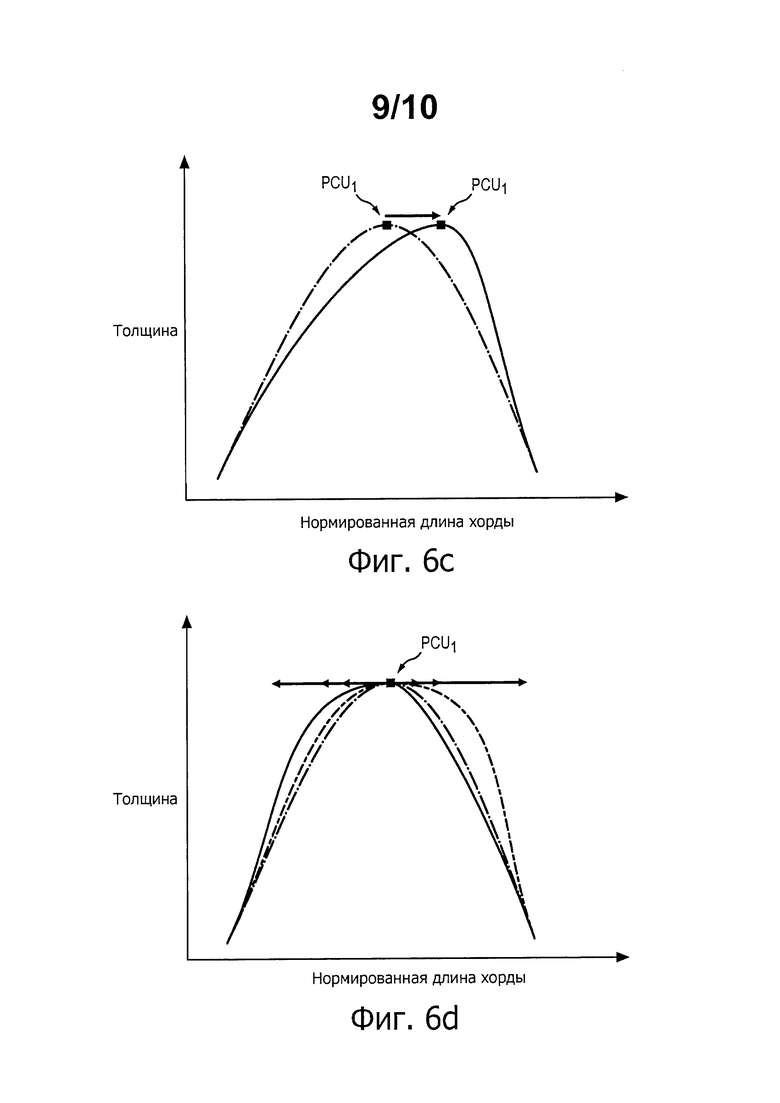
На фиг. 6с учитываемым параметром является координата x промежуточной точки PCU1. Здесь показаны 3 варианта кривой, соответствующие трем разным значениям этого параметра. Отмечается адаптация двух кривых Безье по обе стороны от промежуточной точки PCU1, чтобы соблюдать условия, задаваемые параметром этой точки.
В примере на фиг. 6d опять учитывают два коэффициента натяжения, каждый из которых связан с полукасательной к кривой на уровне промежуточной точки PCU1. Здесь показаны 3 варианта кривой, соответствующие трем парам значений для этого параметра. В частности, показана кривая, для которой коэффициенты являются разбалансированными, что обуславливает наблюдаемую асимметрию.
На фиг. 6е показан более сложный альтернативный вариант, в котором используют три промежуточные точки PCU1, PCU2 и PCU3.
Оптимизация и воспроизведение
Второй этап (b) способа представляет собой этап определения оптимизированных (и по возможности оптимальных) значений указанных параметров указанной кривой при помощи средств 11 обработки данных. Речь идет об этапе оптимизации.
Специалисту известны различные методы для осуществления этого этапа, и, например, можно просто псевдослучайно менять выбранные переменные параметры, одновременно осуществляя моделирования для определения этих оптимизированных значений (то есть значений, для которых выбранный критерий максимизирован) параметров контрольных точек PCUi. Однако изобретение не ограничивается этой возможностью.
На последнем этапе (с) интерфейсные средства 13 устройства 10 воспроизводят определенные значения параметров для использования, например, путем отображения кривой моделирования, в которой параметры установлены по этим оптимизированным значениям.
В альтернативном варианте интерфейсные средства 13 могут просто отображать этих цифровые значения.
Способ изготовления детали
После моделирования деталь 1 можно изготовить. Изобретением предложен способ изготовления детали 1 (в частности, лопаточного колеса), содержащий следующие этапы:
- осуществляют способ, являющийся первым объектом изобретения, чтобы моделировать по меньшей мере часть детали 1 (часть лопатки 2 лопаточного колеса);
- изготавливают указанную деталь 1 в соответствии с полученной моделью указанной по меньшей мере части детали 1.
В результате можно получить лопаточное колесо 1, содержащее множество выполненных таким образом лопаток 2. Устройство
Устройство 10 (показано на фиг. 4) для моделирования детали 1 содержит средства 11 обработки данных, выполненные с возможностью применять:
- Модуль параметризации кривой класса С1, отображающей значение характеристической физической величины указанной детали 1 в зависимости от положения вдоль по меньшей мере части детали 1, при этом модуль определяет кривую:.
° по двум крайним точкам PCU0, PCUK, определяющим протяженность указанной части детали;
° по меньшей мере по одной промежуточной точке PCUi, i∈[1,K-1], расположенной между крайними точками PCU0, PCUK;
° по меньшей мере по двум кривым Безье, соединенным на уровне указанной промежуточной точки;
при этом параметризацию осуществляют по одному или нескольким параметрам, определяющим указанную промежуточную точку;
- Модуль определения оптимизированных значений указанных параметров указанной кривой;
- Модуль воспроизведения определенных значений на интерфейсе указанного устройства.
Компьютерный программный продукт
Четвертым и пятым объектами изобретения являются соответственно компьютерный программный продукт, содержащий командные коды для осуществления (при помощи средств 11 обработки данных, в частности, входящих в состав устройства 10) заявленного способа моделирования детали 1, а также средства хранения информации, которые выполнены с возможностью считывания информативным устройством (например, память 12 этого устройства 10) и на которых записан этот компьютерный программный продукт.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ МОДЕЛИРОВАНИЯ НЕОСЕСИММЕТРИЧНОЙ ПОВЕРХНОСТИ | 2014 |
|
RU2670380C2 |
| ДЕТАЛЬ ГАЗОТУРБИННОГО ДВИГАТЕЛЯ С НЕОСЕСИММЕТРИЧНОЙ ПОВЕРХНОСТЬЮ | 2014 |
|
RU2672990C1 |
| СПОСОБ МОДЕЛИРОВАНИЯ ЛОПАСТИ НЕКАПОТИРОВАННОГО ВИНТА | 2014 |
|
RU2670330C2 |
| ДЕТАЛЬ ИЛИ УЗЕЛ ГАЗОТУРБИННОГО ДВИГАТЕЛЯ И СООТВЕТСТВУЮЩИЙ ГАЗОТУРБИННЫЙ ДВИГАТЕЛЬ | 2014 |
|
RU2666933C1 |
| ДЕТАЛЬ ГАЗОТУРБИННОГО ДВИГАТЕЛЯ С НЕОСЕСИММЕТРИЧНОЙ ПОВЕРХНОСТЬЮ | 2014 |
|
RU2675980C2 |
| РАДИАЛЬНАЯ ДИФФУЗОРНАЯ ЛОПАТКА ДЛЯ ЦЕНТРОБЕЖНЫХ КОМПРЕССОРОВ | 2010 |
|
RU2581686C2 |
| СПОСОБ РЕМОНТА МЕХАНИЧЕСКИ ОБРАБАТЫВАЕМЫХ ДЕТАЛЕЙ, ТАКИХ КАК ЛОПАТКИ ТУРБОМАШИН ИЛИ ЛОПАТКИ МОНОБЛОЧНОГО ЛОПАТОЧНОГО ДИСКА | 2008 |
|
RU2476301C2 |
| СПОСОБ МОДЕЛИРОВАНИЯ ВАННЫ ЛОПАТКИ | 2015 |
|
RU2695502C2 |
| СПОСОБ ПРОЕКТИРОВАНИЯ ЦЕНТРОБЕЖНЫХ НАСОСОВ | 2013 |
|
RU2542160C1 |
| Радиально-осевая гидротурбина и способ её изготовления | 2020 |
|
RU2757242C1 |





Изобретение относится к автоматизированному проектированию. Техническим результатом является сокращение времени при проектировании детали. Способ содержит следующие этапы, осуществляемые при помощи средств обработки данных устройства: (а) осуществляют параметризацию кривой класса С1, представляющей значение характеристической физической величины указанной детали в зависимости от положения по меньшей мере вдоль части детали, при этом кривая определяется: а) двумя крайними точками (PCU0, PCUK), определяющими протяженность указанной части детали; b) по меньшей мере одной промежуточной точкой (PCUi, i∈[1,K-1]), расположенной между крайними точками (PCU0, PCUK); с) по меньшей мере двумя кривыми Безье, соединенными на уровне указанной промежуточной точки; при этом параметризацию осуществляют по одному или множеству параметров, определяющих указанную промежуточную точку; (b) определяют оптимизированные значения указанных параметров указанной кривой; (с) воспроизводят определенные значения на интерфейсе указанного устройства. 4 н. и 12 з.п. ф-лы, 18 ил.
1. Способ моделирования детали (1), содержащий этапы, осуществляемые при помощи средств (11) обработки данных устройства (10):
осуществляют параметризацию кривой класса С1, представляющую значение характеристической физической величины указанной детали (1) в зависимости от положения по меньшей мере вдоль части детали (1), при этом кривая определяется:
двумя крайними точками (PCU0, PCUK), определяющими протяженность указанной части детали (1);
по меньшей мере одной промежуточной точкой (PCUi, i∈[1, K-1]), расположенной между крайними точками (PCU0, PCUK);
по меньшей мере двумя кривыми Безье, соединенными в указанной промежуточной точке;
при этом параметризацию осуществляют по одному или множеству параметров, определяющих указанную промежуточную точку;
определяют оптимизированные значения указанных параметров указанной кривой;
воспроизводят определенные значения на интерфейсе (13) указанного устройства (10).
2. Способ по п. 1, в котором параметры, определяющие промежуточную точку (PCUi), выбирают из группы, в которую входят абсцисса точки, ордината точки, ориентация касательной к кривой на уровне точки и два коэффициента натяжения, каждый из которых связан с полукасательной к кривой на уровне точки.
3. Способ по п. 1 или 2, в котором параметризацию осуществляют также по одному или множеству параметров, определяющих по меньшей мере одну из крайних точек (PCU0, PCUK).
4. Способ по п. 3, в котором параметры, определяющие крайнюю точку (PCU0, PCUK), выбирают из группы, в которую входят абсцисса точки, ордината точки, ориентация касательной к кривой на уровне точки и коэффициент натяжения, связанный с полукасательной к кривой на уровне точки.
5. Способ по п. 2 или 4, в котором коэффициент натяжения, связанный с полукасательной к кривой на уровне промежуточной или крайней точки, является функцией значения второй производной кривой вблизи точки.
6. Способ по п. 1, в котором указанная кривая определяется К-1 промежуточными точками (PCUi, i∈[1, K-1]), упорядоченными по протяженности указанной части детали (1), и К кривыми Безье, где К≥2.
7. Способ по п. 6, в котором первую кривую Безье определяют в интервале между крайней точкой (PCU0), соответствующей началу указанной части детали (1), и первый промежуточной точкой (PCU1), а К-ю кривую Безье определяют в интервале между К-1-й промежуточной точкой (PCUК-1) и крайней точкой (PCUК), соответствующей концу указанной части детали (1).
8. Способ по п. 7, в котором К≥3, при этом i-ю или каждую из i-х (i∈[2, K-1]) кривых Безье определяют в интервале между i-1-й промежуточной точкой (PCUi-1) и i-й промежуточной точкой (PCUi).
9. Способ по п. 1, в котором каждую кривую Безье полностью определяют по точкам (PCU), определяющим ее концы.
10. Способ по п. 1, в котором деталь выбирают из группы, в которую входят лопаточное колесо, площадка газотурбинного двигателя, зеркало заднего вида, элерон, крыло или несущий винт, хвостовое оперение, фюзеляж, воздушный винт, сопло, проточный тракт, обтекатель и турбина.
11. Способ по п. 10, в котором деталь (1) является лопаточным колесом, при этом часть детали (1) является частью лопатки (2) лопаточного колеса;
12. Способ по п. 11, в котором указанная часть лопатки (2) лопаточного колеса (1) является частью сечения лопатки (2) лопаточного колеса (1) или высоты лопатки (2) лопаточного колеса (1).
13. Способ по п. 12, в котором указанную характеристическую физическую величину указанного лопаточного колеса (1) выбирают из группы, в которую входят толщина лопаточного колеса (1), осевая линия, закономерность угла осевой линии сечения лопатки (2) лопаточного колеса (1), закономерность максимальной толщины, закономерность положения максимальной толщины, угол стреловидности и двугранный угол, закономерность набора сечений, входной/выходной углы лопатки (2) лопаточного колеса (1) по высоте.
14. Способ изготовления детали, содержащий этапы, на которых:
осуществляют способ по любому из пп. 1-13 для моделирования по меньшей мере части детали (1);
изготавливают указанную деталь (1) в соответствии с полученной моделью указанной по меньшей мере части детали (1).
15. Устройство (10) для моделирования детали (1), содержащее средства (11) обработки данных, выполненные с возможностью использовать:
модуль параметризации кривой класса С1, представляющей значение характеристической физической величины указанной детали (1) в зависимости от положения по меньшей мере вдоль части детали (1), при этом модуль определяет кривую:
по двум крайним точкам (PCU0, PCUK), определяющим протяженность указанной части детали (1);
по меньшей мере по одной промежуточной точке (PCUi, i∈[1, K-1]), расположенной между крайними точками (PCU0, PCUK);
по меньшей мере по двум кривым Безье, соединенным в указанной промежуточной точке;
при этом параметризация осуществляется по одному или множеству параметров, определяющих указанную промежуточную точку;
модуль определения оптимизированных значений указанных параметров указанной кривой;
модуль воспроизведения определенных значений на интерфейсе (13) указанного устройства (10).
16. Средство хранения информации, выполненное с возможностью его считывания вычислительным устройством, на котором записан компьютерный программный продукт, содержащий командные коды для осуществления способа по любому из пп. 1-13 моделирования детали (1).
| Giannakoglou K | |||
| C., "A Design Method For Turbine Blades Using Genetic Algorithms On Parallel Computers", Computational Fluid Dynamics, 01.01.1998 | |||
| US20090319224 A1, 24.12.2009 | |||
| US20090104023 A1, 23.04.2009 | |||
| СПОСОБ АВТОМАТИЧЕСКОГО ПОСТРОЕНИЯ ТРЕХМЕРНОЙ ГЕОМЕТРИЧЕСКОЙ МОДЕЛИ ИЗДЕЛИЯ В СИСТЕМЕ ГЕОМЕТРИЧЕСКОГО МОДЕЛИРОВАНИЯ | 2006 |
|
RU2325691C1 |
Авторы
Даты
2018-08-28—Публикация
2014-04-16—Подача