Изобретение относится к измерительной технике, в частности к измерению диэлектрической проницаемости материала в свободном пространстве.
Известны способы измерения диэлектрической и магнитной проницаемостей материалов в объемном резонаторе на фиксированной частоте, когда образец измеряется в двух положениях: на поршне и на подставке [Е.Б. Зальцман. Измерение параметров магнитодиэлектриков и не намагниченных ферритов при помощи прямоугольного резонатора на волну Н10. // Радиотехника. - 1958. - Т.13. - №10. - С. 76-80.].
Недостатком способов является узкополосность проводимых измерений. При измерении парамагнитных и ферромагнитных материалов точность измерения снижается, так как из-за вносимых материалами искажения поля резонатора, метод малых возмущений, используемый в резонансном методе измерений, не выполняется.
Волноводные и резонаторные методы измерения диэлектрической и магнитной проницаемостей материалов имеют высокую точность и чувствительность измерения сверхвысокочастотных параметров, но обладают существенным недостатком узкополосностью проводимых измерений [В.Н. Егоров. Резонансные методы исследования диэлектриков на С.В.Ч.// Приборы и техника эксперимента. 2007. - №2. - С.5-38.].
Описаны способы определения диэлектрической проницаемости материала по мощности и фазе прошедшей и отраженной волны, а также применение СВЧ-измерителя в качестве приемной аппаратуры [Е.А. Воробьев. Радиоволновой контроль судовых радиотехнических конструкций и материалов. - Л.: Судостроение, 1986. - 81 с. (22 стр.).].
Известны амплитудно-фазовые приборы, работающие на «прохождение» и «отражение» электромагнитной волны в свободном пространстве, используемые для измерения диэлектрической и магнитной проницаемости материалов [Приборы для неразрушающего контроля материалов и изделий. Справочник. В 2-х книгах. Кн.1 /Под ред. В.В. Клюева. - 2-е изд., перераб. и доп. - М: Машиностроение. 1986.- 488 с. (стр. 220-224, 233-234; рис. 17 стр. 217-219).].
Известны способы определения диэлектрической проницаемости материалов основанные на анализе прошедших и отраженных от пластины диэлектрика электромагнитных волн в свободном пространстве с использованием векторных анализаторов цепей [Семененко В.Н., Чистяев В.А. Методики измерения диэлектрической проницаемости листовых образцов материалов в СВЧ диапазоне частот в свободном пространстве Материалы 20-й Международной Крымской конференции «СВЧ-техника и телекоммуникационные технологии», 13-17 сентября, Севастополь, Крым, 2010 г., с. 1091-1092.].
Диэлектрические свойства материала в свободном пространстве определяют сравнительными измерениями мощности и фазы волны, распространяющейся между передающей и приемной антеннами без образца материала, и проходящей через образец материала или отражающейся от него [А.А. Брандт. Исследование диэлектриков на сверхвысоких частотах М.: Физматгиз, 1963. - 404 с.; D. K. Ghodgaonkar, V. V. Varadan and V. K. Varadan. Free-Space Measurement of Complex Permittivity and Complex Permeability of Magnetic Materials at Microwave Frequencies. IEEE Transactions on Instrumentation and Measurement. Vol. 39 № 2, April, 1990; В.И. Сусляев, В.А. Журавлев, Е.Ю. Коровин, Ю.П. Землянухин. Рупорный метод измерения электромагнитного отклика от плоских образцов в диапазоне частот 26-37,5 ГГц с улучшенными метрологическими характеристиками. Радиотехника. Телекоммуникация. Антенны. Микроволновые устройства. Доклады ТУСУРа, №2 (24) часть 1, декабрь 2011. с. 227-231.].
Известен способ определения диэлектрического коэффициента и проводимости материалов на сверхвысоких частотах [А.с. № 62894, опубл. 30.06.1943], в котором на лист исследуемого материала под прямым углом излучают плоскую поляризованную электромагнитную волну и определяют коэффициент бегущей волны и положения пучностей и узлов возникающих стоячих волн, по которым определяют коэффициент Френеля.
Известен способ измерения диэлектрической и магнитной проницаемостей материала в свободном пространстве и устройство для его реализации, включающий измерение мощности и фазы прошедшей волны через образец материала, измерение мощности и фазы отраженной волны от образца материала, вычисление изменения мощности и фазы с образцом материала и без него, определение по изменениям величин мощностей и фаз комплексных S-параметров матрицы рассеяния диэлектрической и магнитной проницаемостей образца материала при неизменном взаимном положении приемной и передающей антенн [Nicolson, A.M. and G.F. Ross, “Measurement of the intrinsic properties of materials by time-domain techniques,”IEEE Trans. Instrum. Meas., Vol. 19, No. 4, 377-382, 1970.; А.А. Беляев, А.М. Романов, В.В. Широков, Е.М. Шульдешов. Измерение диэлектрической проницаемости стеклосотопласта в свободном пространстве. Электронный научный журнал «ТРУДЫ ВИАМ» - 2014. - №5. - С1-8.]
Условия проведения измерений в способе являются статическими для одного, неизменяемого взаимного положения антенн по анализу результатов измерения и для одной, неизменяемой поляризации падающей волны. Все эти условия проведения экспериментальных измерений не являются оптимальными для определения сверхвысокочастотных параметров, так как в известных способах недостаточно экспериментальных данных для реализации высокой точности измерения и получения однозначных значений комплексных диэлектрической и магнитной проницаемостей. Кроме того, накладываются ограничения на толщину образца и диапазон изменения определяемых сверхвысокочастотных параметров.
Наиболее близким к заявляемому изобретению является способ измерения относительной диэлектрической проницаемости диэлектрика [А.с. № 317995, МПК G 01r 31/00, опубл. 19.10.1971 бюл. №31], основанный на явлении отражения электромагнитной энергии от диэлектрика, в котором, с целью повышения точности и упрощения процесса измерения, измеряют отношение уровня сигнала, отраженного от диэлектрика, к уровню сигнала, падающего на диэлектрик, измеренных в одном канале.
Недостатком этого способа является неоднозначность определения диэлектрической проницаемости материала и необходимость использования дополнительных образцов материала различной толщины для её разрешения.
Недостатком всех представленных способов является низкая точность измерения диэлектрической проницаемости материала из-за неоднозначности получаемых измерений.
Задачей настоящего изобретения является повышение точности измерения диэлектрической проницаемости образца материала в свободном пространстве.
Способ определения диэлектрической проницаемости материала, основанный на явлении отражения электромагнитной энергии от пластины из диэлектрического материала, отличающийся тем, что измеряют толщину пластины из диэлектрического материала и зависимость сдвига фазы отраженной волны относительно падающей и прошедшей волн в диапазоне частот, по которой определяют частоту, соответствующую полуволновой толщине пластины из диэлектрического материала, а диэлектрическую проницаемость материала рассчитывают по формуле:
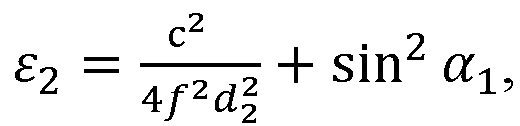
где с - скорость света;
f - частота измерения, соответствующая полуволновой толщине пластины из диэлектрического материала;
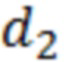 - геометрическая толщина пластины из диэлектрического материала;
- геометрическая толщина пластины из диэлектрического материала;
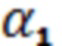 - угол падения волны на пластину из диэлектрического материала;
- угол падения волны на пластину из диэлектрического материала;
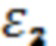 - диэлектрическая проницаемость пластины из диэлектрического материала.
- диэлектрическая проницаемость пластины из диэлектрического материала.
В предлагаемом техническом решении проводится предварительное измерение геометрической толщины пластины из диэлектрического материала, измерение зависимости сдвига фазы отраженной волны относительно падающей и прошедшей волн по экспериментально измеренной частотной зависимости сдвига фазы и определение частоты, соответствующей половине длины волны для толщины пластины из диэлектрического материала, с использованием которой рассчитывают диэлектрическую проницаемость пластины из диэлектрического материала.
Предложенный способ позволяет устранить неоднозначность полученных измерений, которая возникает из-за гармонического характера решений алгоритмов при определении диэлектрической проницаемости материала.
В предлагаемом техническом решении повышение точности определения диэлектрической проницаемости материала происходит с использованием измерений сдвига фаз отраженной относительно проходящей волны для реперных точек на частотной оси, соответствующих электрическим толщинам образца материала кратным половине длины волны в материале для которых точность измерений наиболее высокая.
Авторами установлено, что изменение фазы прошедшей и отраженной волн для любой частоты и при обеих поляризациях, любых углов падения волны на плоскую пластину из диэлектрического материала, при взаимодействии падающей и отраженной волн, в зависимости от электрической толщины пластины имеют гармонический вид, кроме случая при падении плоской волны с параллельной поляризацией под углом Брюстера для которой зависимость изменения фазы от толщины пластины из диэлектрического материала линейна из-за отсутствия отраженной волны. Минимальные искажения возникают также в точках соответствующих электрической толщине пластины из диэлектрического материала равной половине длины волны, соответствующие предлагаемому техническому решению.
Это приводит к тому, что методы определения, например, диэлектрической проницаемости материала в свободном пространстве, основанные на измерениях фазы прошедшей и отраженной волн, для несогласованной по электрической толщине стенки пластины из диэлектрического материала имеют значительную погрешность.
Для определения величины погрешности диэлектрической проницаемости материала методом свободного пространства при нулевом угле падения волны на плоскую пластину из диэлектрического материала промоделируем условия эксперимента, определив зависимость диэлектрической проницаемости материала от частоты в полосе частот от 1 до 20 ГГц, считая пластину однородной и изготовленной из однородного материала толщиной d = 9 мм, например, из диоксида кремния (кварцевого стекла) с диэлектрической проницаемостью ε = 3,81 и тангенсом угла диэлектрических потерь tgδ = 0,0001, которые измерены на частоте 10 ГГц по ГОСТ Р 8.623-2015 резонаторным методом.
На первом этапе рассчитываем мощность и фазу прошедшей волны (Δϕ(f)) для параллельной поляризации падающей волны в диапазоне частот от 1 до 20 ГГц, затем из этих расчетных данных определяем величину диэлектрической проницаемости материала по формуле:
 , (1)
, (1)
где с - скорость света;
 - фаза прошедшей волны;
- фаза прошедшей волны;
 толщина пластины из диэлектрического материала;
толщина пластины из диэлектрического материала;
 частота;
частота;
 - угол падения волны на пластину из диэлектрического материала.
- угол падения волны на пластину из диэлектрического материала.
Авторами установлено, что при наклонном падении плоской электромагнитной волны с вектором электрического поля произвольной поляризации на пластину из диэлектрического материала угловая зависимость сдвига фазы между падающей и отраженной волнами на частоте, соответствующей половине длины волны для диэлектрической проницаемости пластины составляет 180 градусов (±90 градусов), а угловое положение точки «нулевого» сдвига фазы соответствует углу падения падающей волны на пластину из диэлектрического материала.
На фиг.1 представлено расположение пластины из диэлектрического материала с диэлектрической 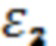 и магнитной
и магнитной 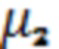 проницаемостями в свободном пространстве с диэлектрической
проницаемостями в свободном пространстве с диэлектрической  и магнитной
и магнитной 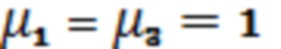 проницаемостями, относительно падающей плоской волны, с электрическим вектором
проницаемостями, относительно падающей плоской волны, с электрическим вектором  под углом
под углом 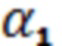 относительно нормали к поверхности
относительно нормали к поверхности  . В рамках геометрической оптики условно изображено положение отраженного луча под углом
. В рамках геометрической оптики условно изображено положение отраженного луча под углом 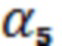 и преломленного луча под углом
и преломленного луча под углом 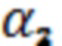 . Угол падения волны из среды диэлектрической пластины на границу диэлектрического материала (
. Угол падения волны из среды диэлектрической пластины на границу диэлектрического материала ( ) - свободное пространство (
) - свободное пространство (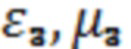 ) на фиг.1 обозначен
) на фиг.1 обозначен 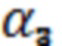 . Угол
. Угол 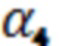 образован лучом прошедшей через пластину волны и нормалью к поверхности диэлектрической пластины в точке выхода волны.
образован лучом прошедшей через пластину волны и нормалью к поверхности диэлектрической пластины в точке выхода волны.
Для пластины из диэлектрического материала проведено расчетное моделирование сдвига фазы отраженной ТМ волны в соответствии с матричным методом [Борн М., Вольф Э. Основы оптики. - М.: Наука, 1973. - 720 с.]:
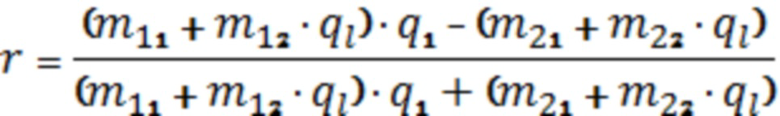 , (1)
, (1)
где r - коэффициент отражения;
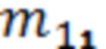 - элементы характеристической матрицы среды распространения электромагнитной волны, определяемые как:
- элементы характеристической матрицы среды распространения электромагнитной волны, определяемые как:
 ;
;  ;
; 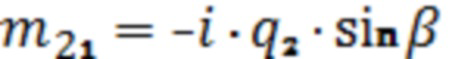 ;
;
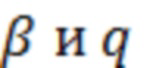 - коэффициенты, введённые для упрощения записи уравнения (1):
- коэффициенты, введённые для упрощения записи уравнения (1):
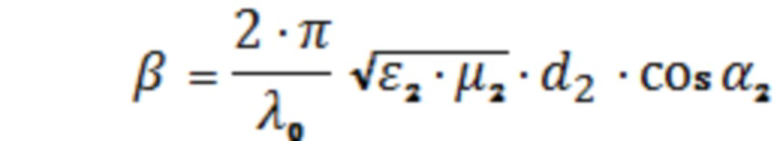 ;
;
 - длина волны;
- длина волны;
с - скорость света;
f - частота измерения;
 - угол преломления;
- угол преломления;
 - толщина пластины из диэлектрического материала;
- толщина пластины из диэлектрического материала;
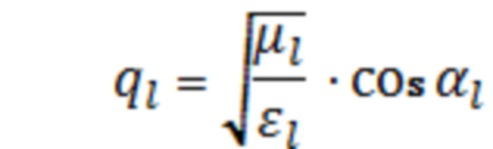 - для угла падения между слоями;
- для угла падения между слоями;
 - количество слоёв рассматриваемой диэлектрической пластины.
- количество слоёв рассматриваемой диэлектрической пластины.
Для однослойной пластины (при 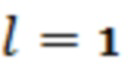 ) сдвиг фазы отраженной ТМ волны равен:
) сдвиг фазы отраженной ТМ волны равен:
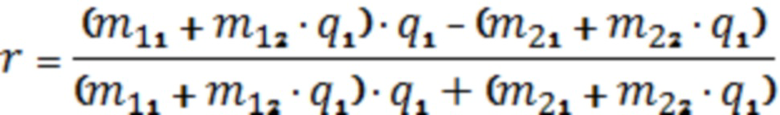 , (2)
, (2)
Для параллельной поляризации сдвиг фазы отраженной ТМ волны, когда вектор электрического поля лежит в плоскости падения, равен:
 , (3)
, (3)
где 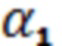 - угол падения волны на пластину из диэлектрического материала.
- угол падения волны на пластину из диэлектрического материала.
Используя закон Снеллиуса и условия, следующие из фиг.1, предполагая, что материал пластины имеет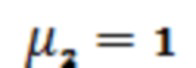 , запишем для продольной поляризации ТМ волны:
, запишем для продольной поляризации ТМ волны:
 ,
,  ,
, 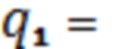

Сдвиг фазы отраженной ТМ волны равен:
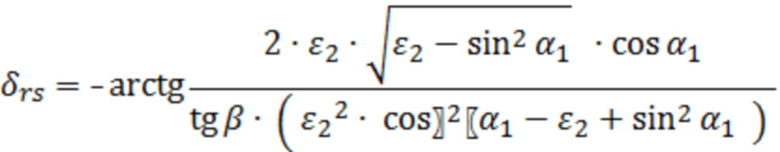 (4)
(4)
Для перпендикулярной поляризации ТЕ волны, когда вектор электрического поля перпендикулярен плоскости падения, сдвиг фазы отраженной ТЕ волны равен:
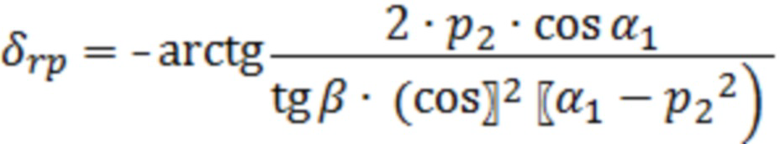 , (5)
, (5)
 ,
,  ,
, 
 .
.
Сдвиг фазы отраженной TE волны равен:
 . (6)
. (6)
где 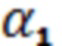 - угол падения волны на пластину из диэлектрического материала;
- угол падения волны на пластину из диэлектрического материала;
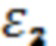 - диэлектрическая проницаемость пластины из диэлектрического материала.
- диэлектрическая проницаемость пластины из диэлектрического материала.
Как следует из анализа формулы (6), во всем диапазоне изменений угла падения отраженной ТЕ волны скачкообразного изменения сдвига фазы не наблюдается, как видно из выражения (4), сдвиг фазы отраженной ТМ волны имеет скачок, возникающий в точке неопределенности функции  при условии, когда:
при условии, когда:
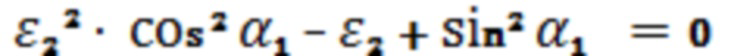 , (7)
, (7)
которое выполняется для  при
при 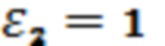 и соответствует углу Брюстера при отражении ТМ волны от пластины из диэлектрического материала, что соответствует условию пеленгации по прототипу [Калитиевский Н.И. Волновая оптика. Учеб. Пособие для ун-тов. Изд. 2-е, испр. И доп. М., «Высшая школа». 1978 г. 383 с.].
и соответствует углу Брюстера при отражении ТМ волны от пластины из диэлектрического материала, что соответствует условию пеленгации по прототипу [Калитиевский Н.И. Волновая оптика. Учеб. Пособие для ун-тов. Изд. 2-е, испр. И доп. М., «Высшая школа». 1978 г. 383 с.].
Второй скачок сдвига фазы, соответствующий условию
 , (8)
, (8)
выполняется для сдвига фазы отраженной, как ТМ, так и ТЕ волны, в точках разрыва функции , когда аргумент равен 
 или
или 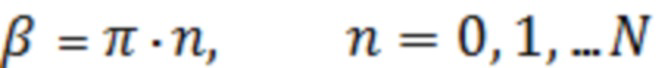
 ,
,
и выполняется для толщины пластины из диэлектрического материала кратной половине длины волны в материале при угле падения волны 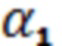 для обеих поляризаций отраженных ТЕ и ТМ волн:
для обеих поляризаций отраженных ТЕ и ТМ волн:
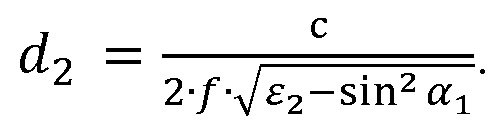 (9)
(9)
Условие (9) используется в предполагаемом изобретении для расчета диэлектрической проницаемости пластины при которой выполняется условие скачка сдвига фазы между падающей и отраженной волнами:
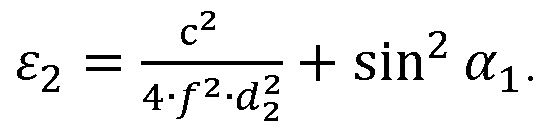 (10)
(10)
На фиг. 2 и 3 представлены расчетные зависимости сдвига фазы отраженной волны при нормальном падении волны на пластину из кварцевого стекла с диэлектрической проницаемостью  .
.
Из зависимости сдвига фазы отраженной волны от электрической толщины пластины в долях длины волны на фиг. 2 видно, что вид кривой соответствует функции арктангенса, а в области толщины кратной половины длины волны, где арктангенс терпит разрыв, наблюдается скачкообразное изменение сдвига фазы на π.
Из зависимости сдвига фазы отраженной волны от частоты падающей волны на фиг. 3 также видно, что вид кривой соответствует функции арктангенса, а в области частоты для которой электрическая длина волны соответствует кратной половине длины волны наблюдается скачкообразное изменение сдвига фазы на π.
На фиг. 4 представлен снимок с экрана векторного анализатора цепей с изображением зависимостей фазы и амплитуды от частоты для отраженной волны от диэлектрической пластины волны при нормальном угле падения на пластину. Как видно на частоте, соответствующей полуволновой электрической толщине пластины наблюдается минимальная амплитуда отраженной волны и скачкообразное изменение сдвига фазы между падающей и отраженной волнами на величину порядка 180°. Рассчитанное значение диэлектрической проницаемости пластины 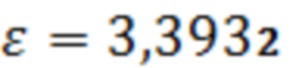 из экспериментальных данных по формуле (10) соответствует измеренной для этой пластины другими методами. Сдвиг фазы изображен так, как он наблюдался на экране анализатора цепей с падением по частоте.
из экспериментальных данных по формуле (10) соответствует измеренной для этой пластины другими методами. Сдвиг фазы изображен так, как он наблюдался на экране анализатора цепей с падением по частоте.
Как видно на фиг.4 эксперимент проведён для пластины из диэлектрического материала с потерями, поэтому на частотной зависимости изменения сдвига фазы наблюдается наклон в области центральной частоты и более ярко выраженный минимум амплитуды отраженного сигнала, в отличие от теоретически рассчитанных частотных зависимостей амплитуды и фазы для различных материалов, представленных на фиг. 5, 6.
Таким образом, использование в способе измерения диэлектрической проницаемости материала по анализу фазы отраженной волны в полосе частот для определения частоты, соответствующей электрической толщине пластины равной половине длины волны, и определение по величине этой частоты диэлектрической проницаемости пластины по процедуре, изложенной в предлагаемом техническом решении, позволяет определить диэлектрическую проницаемость материала с более высокой точностью, чем при использовании известных способов определения диэлектрической проницаемости материала по отраженной волне.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения сверхвысокочастотных параметров материала в полосе частот и устройство для его осуществления | 2018 |
|
RU2688588C1 |
| Способ пеленгации и устройство для его осуществления | 2019 |
|
RU2716273C1 |
| Способ измерения диэлектрических свойств материала и устройство для его осуществления | 2017 |
|
RU2665593C1 |
| СПОСОБ ДИСТАНЦИОННОГО ИЗМЕРЕНИЯ КОМПЛЕКСНОЙ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ ПЛОСКОСЛОИСТЫХ ДИЭЛЕКТРИКОВ ЕСТЕСТВЕННОГО ПРОИСХОЖДЕНИЯ | 2022 |
|
RU2790085C1 |
| Способ измерения относительной комплексной диэлектрической проницаемости материала с потерями | 2022 |
|
RU2789626C1 |
| Способ определения тангенса угла диэлектрических потерь материала | 2022 |
|
RU2787642C1 |
| Способ оптимизации радиотехнических характеристик антенного обтекателя со стенкой из многокомпонентного материала | 2017 |
|
RU2653185C1 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ ОБРАЗЦА МАТЕРИАЛА ПРИ ВОЗДЕЙСТВИИ ВНЕШНИХ ФАКТОРОВ | 2011 |
|
RU2453856C1 |
| ШИРОКОПОЛОСНАЯ СИСТЕМА "АНТЕННА-ОБТЕКАТЕЛЬ" | 2011 |
|
RU2446520C1 |
| Широкополосный пеленгатор | 2023 |
|
RU2811893C1 |



Изобретение относится к измерительной технике, в частности к измерению диэлектрической проницаемости материала в свободном пространстве. Предложен способ определения диэлектрической проницаемости материала, основанный на явлении отражения электромагнитной энергии от пластины из диэлектрического материала, согласно изобретению измеряют толщину пластины из диэлектрического материала и зависимость сдвига фазы отраженной волны относительно падающей и прошедшей волн в диапазоне частот, по которой определяют частоту, соответствующую полуволновой толщине пластины из диэлектрического материала, а диэлектрическую проницаемость материала рассчитывают по формуле:
 ,
,
где с - скорость света; f - частота измерения, соответствующая полуволновой толщине пластины из диэлектрического материала;  - геометрическая толщина пластины из диэлектрического материала;
- геометрическая толщина пластины из диэлектрического материала;  - угол падения волны на пластину из диэлектрического материала;
- угол падения волны на пластину из диэлектрического материала;  - диэлектрическая проницаемость пластины из диэлектрического материала. Задачей настоящего изобретения является повышение точности измерения диэлектрической проницаемости образца материала в свободном пространстве. 6 ил.
- диэлектрическая проницаемость пластины из диэлектрического материала. Задачей настоящего изобретения является повышение точности измерения диэлектрической проницаемости образца материала в свободном пространстве. 6 ил.
Способ определения диэлектрической проницаемости материала, основанный на явлении отражения электромагнитной энергии от пластины из диэлектрического материала, отличающийся тем, что измеряют толщину пластины из диэлектрического материала и зависимость сдвига фазы отраженной волны относительно падающей и прошедшей волн в диапазоне частот, по которой определяют частоту, соответствующую полуволновой толщине пластины из диэлектрического материала, а диэлектрическую проницаемость материала рассчитывают по формуле:
 ,
,
где с – скорость света;
f – частота измерения, соответствующая полуволновой толщине пластины из диэлектрического материала;
d2 – геометрическая толщина пластины из диэлектрического материала;
α1 – угол падения волны на пластину из диэлектрического материала;
 – диэлектрическая проницаемость пластины из диэлектрического материала.
– диэлектрическая проницаемость пластины из диэлектрического материала.
| СПОСОБ ИЗМЕРЕНИЯ ОТНОСИТЕЛЬНОЙ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ ДИЭЛЕКТРИКА | 0 |
|
SU317995A1 |
| US 9151793 B1, 06.10.2015 | |||
| US 2017336452 A1, 23.11.2017 | |||
| Способ измерения диэлектрических свойств материала и устройство для его осуществления | 2017 |
|
RU2665593C1 |
Авторы
Даты
2020-02-04—Публикация
2019-07-29—Подача